On the geometry of a class of conformal harmonic maps of surfaces into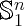

Eduardo Hulett

Abstract: This paper deals with certain advances in the understanding of the geometry of superconformal harmonic maps of Riemann surfaces into De Sitter space . The character of these notes is mainly expository and we made no attempt to provide complete proofs of the main results, which can be found in reference [12]. Our main analytic tool to study superconformal harmonic maps is a Gram-Schmidt algorithm to produce adapted frames for such maps. This allows us to compute the normal curvatures and obtain identities which are used to study their geometry. Some global properties such as fullness and rigidity are considered and a highest order Gauss transform or polar map is constructed and its main properties are discussed.

2000 Mathematics Subject Classification. 53C42, 53C50

Key words and phrases. De Sitter space-time, superconformal harmonic maps, harmonic sequences.

Partially supported by Fundación Antorchas, CONICET, FONCYT and SECYT-UNCba

1. Introduction

The purpose of these notes is to present some recent advances on the geometry of a class of harmonic maps of surfaces into De Sitter space . As we shall see these maps have many properties in common with their natural relatives: the so-called superconformal harmonic maps of surfaces into Euclidean (round) spheres , introduced and studied by Bolton, Pedit and Woodward in [2] and also by Miyaoka in [14].

The style of the paper is expository so that we have omitted the proofs of the main results. The interested reader can consult reference [12] for details.

Let denote the flat Lorentz -space i.e. equipped with the Lorentz inner product

(1)

The -dimensional De Sitter space-time of radius is by definition the pseudosphere

on which the ambient metric induces a metric also denoted by of signature , hence is a Lorentz manifold of constant sectional curvature . A smooth map from a Riemann surface is harmonic if its tension field vanishes on :  [7]. It is easily seen that is harmonic if and only if on any local complex coordinate in the following PDE is satisfied by :

(2)

where denotes the complex bilinear extension of to and

Note that equation (2) does not depend on a particular metric on but only on the conformal structure of . This is characteristic of harmonic maps of Riemann surfaces.

Let and or and a smooth map from a connected Riemann surface and assume that there is an integer such that

where . It is not difficult to show that such integer is independent of complex coordinates on , so that it depends only on the map itself. It is called the isotropy dimension of and is denoted by . A smooth map is called superconformal if , where . Here we adapted the notion of isotropy dimension which F. Burstall introduced in [5] to study harmonic maps of surfaces into and .

Let be a harmonic map with isotropy dimension . Then equation (2) implies that the locally defined non-vanishing complex function is holomorphic, hence its zeros are isolated. Moreover the formal expression

is globally defined on . It is called the -th complex Hopf differential of . We notice here that the topology of the Riemann surface plays a role. In fact, applying the Riemann-Roch Theorem [13], Ejiri in [8] shows that every space-like harmonic map is isotropic:

for every pair of integers such that . This says that the isotropy dimension of is infinite. Then if is harmonic with finite isotropy dimension and is compact, then genus. Harmonic maps of infinite isotropy dimension in have been considered by Ejiri [8] and also by Erdem [9].

It is well known that harmonic maps of surfaces into are related to Willmore surfaces in and . In fact harmonic maps (superconformal or not) of surfaces in arise as images of the conformal Gauss map of immersed Willmore surfaces in and in (see [1, 15]).

Also in [1] Alías and Palmer considered space-like superconformal minimal surfaces into four dimensional Lorentz spaceforms and studied the behaviour of their normal and Gaussian curvatures obtaining interesting results.

On the other hand Sakaki in [16] studied superconformal minimal space-like surfaces in four dimensional Lorentz spaceform satisfying a generalized Ricci-condition. Harmonic maps of surfaces with infinite isotropy dimension (also called isotropic) into were considered by Ejiri [8]. Erdem in [9] obtained a classification of harmonic isotropic maps of Riemann surfaces into with non-degenerate osculating bundle.

The layout of the paper is as follows. Section 1 introduces the Gram-Schmidt algorithm for the construction of harmonic sequences which give rise to the complex line sub bundles . In Section 2 we compute the normal curvatures of a superconformal harmonic map and derive the structural equations. Section 3 deals with global rigidity and Section 4 is devoted to the construction and main properties of the highest order Gauss transform or polar map.

2. Harmonic sequences

In what follows we shall consider only the class of superconformal harmonic maps with or (), i.e. those with maximal finite isotropy dimension: . Hence in particular is a (weakly) conformal map

(3)

At any point condition (3) above is equivalent to

Now since the ambient metric has signature , for any such that is non-singular we have , so that is a space-like map i.e. the pull-back metric is Riemannian at those points for which is non-singular.

Conversely, if is an orientable surface and is a space-like immersion, then the pullback is a Riemannian metric on which determines a conformal or Riemann surface structure on such that is a conformal immersion [13]. Hence if one considers on the induced metric , then is an isometric space-like immersion.

Let us denote by simplicity. Now fix a local chart and set

(4)

Note that is just the component of orthogonal to . Moreover is defined away from the zeros of which are called the higher order singularities of .

The following is our main technical result. It establishes the consistency of the Gram-Schmidt process (4) and assures that the vectors have positive square norms open densely in . Its proof relies on the fact that harmonic maps of Riemann surfaces into pseudospheres are real analytic maps, an essential observation due to Ejiri [8]. For details, see [12], Section 3.

Lemma 1.  [12] Let be a connected Riemann surface and a superconformal harmonic map, where or , (). On any fixed complex chart of , formula (4) generates -valued maps , defined on an open and dense subset of satisfying the following properties: i) For each the zeros of are isolated in and on an open and dense subset of . ii) for . iii) for .

By the above Lemma every superconformal harmonic map has isolated higher-order singularities. Moreover it is space-like and is non-singular on an open and dense subset of . In particular the induced metric is a Riemannian metric on with isolated singularities. Considering with the induced metric then is a branched isometric minimal space-like immersion. The globally defined complex differential , where , measures the failure of and to be orthogonal. It is called the Hopf differential of and is an important invariant of . If the map is called isotropic.
Let be the finite sequence generated by (4) on . Defining

(5)

then a straightforward computation shows that the augmented sequence satisfies the following formulae

(6)

Also from (5) it follows that , hence the extremes are orthogonal only at the zeros of the -th Hopf differential.

Harmonic sequences were thoroughly studied by Bolton and Woodward in [4], who considered harmonic maps of surfaces into complex projective spaces and spheres.

2.1. The line bundles . The (pseudo) hermitian inner product on is defined by

(7)

We denote by the complex vector space equipped with the (pseudo-hermitian) inner product (7). Let be the trivial bundle equipped with the canonical connection where is any smooth local section of and . The map determines a complex line subbundle

equipped with the metric-compatible connection , where the projection along is well defined since . By the well known Theorem of Koszul-Malgrange [7], determines a unique compatible holomorphic structure on such that a local smooth section of is holomorphic if and only if , where . Hence is holomorphic if and only if . In particular by the harmonic map equation (2) is a global holomorphic section of . On the other hand the fibers of determine a map by . Since is the composition of followed by the totally geodesic imbedding , it results also harmonic.

In general a complex vector subbundle can be equipped with the Koszul-Malgrange holomorphic structure provided it is non-degenerate respect to the ambient hermitian indefinite inner product . That is, fiberwise, where denotes -orthogonal complement.

The bundle operator given by splits up into its and parts and , according to . It is shown in [11] that both operators are related by the identity

(8)

Now since is a harmonic map, takes holomorphic sections of to holomorphic sections of . This is equivalent to

which also says that is a holomorphic section of and by (8) is antiholomorphic. Let be the unique complex line sub bundle of containing the image of . Define by continuity across the isolated zeros of , hence is a well defined non-degenerate complex line subbundle of on which the ambient metric is positive definite by Lemma 1, i.e. is a space-like subbundle of . In particular it has a well defined metric connection and hence a unique compatible holomorphic structure. From (4) it follows that sends holomorphic sections of to holomorphic sections of , in particular is a local holomorphic section of . In the same way the image of the operator determines a unique space-like (hence non-degenerate) complex line subbundle . Thus it has also a well-defined metric connection and hence a unique compatible holomorphic structure. Also from (4) is a local holomorphic section of . The process continues producing a sequence of mutually orthogonal space-like holomorphic complex line subbundles where each has a well-defined metric connection and a compatible holomorphic structure via the Koszul-Malgrange Theorem. However the last complex subbundle containing the image of may degenerate at some points and its signature may change.

The conjugate bundles are also space-like. Including the possibly degenerate subbundles , then Lemma 1 and formulae (6) imply that the whole sequence satisfies orthogonality relations

(9)

Also from (6) we conclude that defined by

satisfy . Hence for the bundle operators are holomorphic, i.e. they send holomorphic sections to holomorphic sections. This fact is expressed in an equivalently way by equation

which follows from (4) and the definition of and . Also for the operators are anti-holomorphic bundle operators as a consequence of the identity (see [12], page 190, for details). It is not difficult to show that the maps defined by are harmonic for . The finite sequence of harmonic maps is called the harmonic sequence of the initial superconformal harmonic map .

The curvature of . The intrinsic curvatures of the complex line bundles are obtained using the Koszul-Malgrange holomorphic structure. In fact, we have

In the next section we shall see that the quantity is just a multiple of the -th normal curvature by a factor depending on the induced metric on .

3. Normal curvatures and Structure equations

We fix the induced metric on , hence the computations that follow hold away from the isolated singularities . Let be the pseudo-Riemannian Levi-Civita connection of determined by the Lorentz metric and consider the pull-back bundle

with the pull-back connection denoted also by , and the pull-back Lorentz metric . The subspace of generated by the -derivatives of up to order at is called the -th osculating space at and is denoted by . Then and is a subspace of . The orthogonal complement of in , denoted by , is called the -normal space at . Thus

(10)

At generic points one can consider the -th osculating bundle with -dimensional fibers , and also the -th normal bundle with -dimensional fibers . A point is said to be generic if the fiber of over coincides with the -th osculating space at . It is known that the set of generic points is open and dense in (see [17]). The set of non-generic points, are nothing but the higher-order singularities of and consists of isolated points (cf. [6, 17]).

For the fibres of each complex line bundle determined by are isotropic space-like complex lines in . Hence each , may be identified with an oriented real space-like 2-plane subbundle of in the following way: on a complex chart is a local holomorphic section of generated by (4). We define real vector fields on by setting

(11)

Then since , the fields are orthogonal and of unit norm . Thus, for , are local generating sections of the first osculating bundle (or tangent bundle) of , and for are local generating sections of the -th normal bundle of . This exhibits the identification of and of for . Consequently the (complex) maximal isotropic space-like subbundle

identifies with the -th osculating bundle of . Also from (11) we have

It follows from Lemma 1 and our discussion above that is a real space-like -dimensional vector subbundle of . Now if is linearly full, we have and by (10) the last normal bundle of is a real non-degenerate oriented Lorentz 2-plane subbundle of : i.e. the restriction of the Lorentz metric to the fibers of has signature . Then it is easily seen that there are local generating sections of satisfying

(12)

In particular and hence there are (local) complex functions such that

(13)

so that identifies with . Note that the direct sum subbundle identifies with the normal bundle of

and restricted to coincides with the normal connection on . Also restricted to coincides with the Levi-Civita Riemannian connection on determined by the induced metric . The projection of onto each normal 2-plane subbundle defines a metric-compatible connection which is Riemannian for , whereas is pseudo-Riemannian.

Let be the connection forms of , . Then the equation defines the curvature function , where

is the area element of the induced metric respect to a local complex coordinate (cf. [17]). It is shown in [12] that

(14)

where

(15)

is the Laplacian operator of the induced metric on . Note that is just the Gauss curvature of the induced metric . The expression of the last normal curvature looks a little bit different

(16)

where are given by (13). See [12], page 194 for details.

3.1. Curvature identities and consequences. The compatibility or integrability equations satisfied by the harmonic sequence of a superconformal harmonic map are , which as consequence of (4) and (6) are given by

In terms of the functions , , and , such that , the compatibility equations above are expressed by the following system of partial differential equations

(17)

Using the expressions for obtained before, and (15), we obtain the normal curvatures in terms of and :

(18)

Hence the sum of the first curvatures gives

(19)

Note that from (19) the sign of depends on the sign of .

On the other hand squaring (16) and adding (19) we obtain

(20)

Away from the zeros of the -th Hopf differential we can take at both sides of (20) and since is a local harmonic function, we obtain the following identity

(21)

This identity generalizes a formula obtained by Alías and Palmer in [1] and is the key point to prove the following characterization of superconformal harmonic maps of tori given in [12], which is a generalization of a Theorem by Sakaki in [16]

Theorem 1. ([12], Theorem 8.1) Let be a compact connected Riemann surface and a linearly full superconformal harmonic map having no higher-order singularities. If the Gaussian and normal curvatures of satisfy on , then is topologically a -torus.

Conversely, if is a 2-torus then passing to the universal covering space of it is possible to normalize globally on . Hence if the full superconformal harmonic map has no higher-order singularities, the inequality holds on as a consequence of (20).

Also as an application of identities (19) and (20) we obtain the following result which gives information on the global behaviour of a non-full superconformal harmonic map in terms of the normal curvatures

Theorem 2. ([12], Theorem 5.4) Let be a superconformal harmonic map of a Riemann surface. Then if and only if lies fully in a unique non-degenerate hyperplane . In this case
a) if and only if the induced metric on has signature and is superconformal harmonic full into .
b) if and only if is space-like and is a superconformal harmonic full into the Euclidean unit sphere .
In both cases identity (20) implies that can occur only at the zeros of which are isolated.

3.2. Toda affine equations and Toda frames.. Away from the isolated zeros of the -th Hopf differential of it is possible to find a local complex coordinate which normalizes , i.e. on (a proof of this fact is given in [2]). In terms of and condition, is just on , so let be a complex function defined on such that and . Introduce new local sections of by

(22)

where . It is easily seen that and . In this new frame we have

so that , where . It follows that . The fourth and fifth compatibility equations in (17) yield and hence . Also from the third equation of (17) we get , from which satisfies

(23)

We have shown that in a local coordinate chart where it is possible to find a local frame

such that its compatibility equations become the following system of elliptic non-linear partial differential called Toda affine equations associated to the pair

(24)

Thus locally and away from the zeros of the -th Hopf differential the geometry of a superconformal harmonic map is completely determined from a solution of the above system. The frame considered above is called a Toda frame by Bolton Pedit and Woodward (cf. [2]). Toda equations are well known examples of completely integrable systems. For a survey on Toda equations and other soliton equations arising in geometry, see [10] and the bibliography cited there.

In terms of the last normal curvature is given by

(25)

Also from (19) we see that

(26)

Thus at points where (hence on an open and dense subset) we have

(27)

Applying to both sides of (27) we get the following identity which generalizes formula (3.1) of Alías and Palmer in [1]

(28)

Integrating this identity respect to and using the Divergence Theorem we obtain the following result

Theorem 3. ([12], Lemma 5.5) Let be a compact connected Riemann surface and a full superconformal harmonic immersion for which at each point of . Then

Note that under the hypothesis of Theorem 3, so that must be a signed function on .

4. Rigidity

Here we consider the problem of determining invariants which determine a superconformal harmonic map up to ambient isometries. We obtained the following result which is analogous to that obtained in [4, 11] when the target is and respectively

Theorem 4. ([12], Theorem 6.1) Let be superconformal harmonic maps from a connected Riemann surface. If they induce the same metric on and have the same -th Hopf differentials, then there is an isometry of such that .

The construction of the isometry uses the harmonic sequence of which by hypothesis coincides with that of , and the Toda equations (24).

A manifestation of the complete integrability of the Toda system (24) describing the geometry of a superconformal harmonic map is the fact that for a simply connected there is an associated -family of isometric deformations of the given . The proof of the following Theorem is consequence of a result by Bolton and Woodward in [4] when the target is the Euclidean sphere . For superconformal harmonic maps into , the proof is analogous and uses the machinery of harmonic sequences which we developed before.

Theorem 5. Let be a simply connected Riemann surface and let be full superconformal harmonic maps inducing the same metric on . If for some function , then is constant and is congruent with some of the family.

5. A higher order Gauss transform

According to Theorem 2 the image of a non-linearly full superconformal harmonic map lies fully in a non-degenerate hyperplane which may be either space-like or have signature . In this case the sequence generated by is periodic:

(29)

and the last line bundle of is non-degenerate and satisfies . Our discussion below needs the following result which also has an independent interest

Proposition 1. ( [12], Proposition 4.2) Let be a superconformal harmonic map. Then for every local complex chart on the following inequality holds

(30)

If is not full then its image lies fully in a non-degenerate hyperplane and equality holds in (30).

We are ready now to define the higher order Gauss transform or polar map of as follows. If the equality holds in (30) we have . Then according to the signature of the metric induced on we have:

(i) The hyperplane is space-like and consequently . In particular and have the same order zeros so that one can extend the vector across its singularities by continuity (cf. [14]). It can be easily checked that it is a real vector and has square norm one. Moreover is independent of coordinates of . The Gauss transform of is well defined by

(31)

where is the unit sphere of .

(ii) The induced metric on the hyperplane has signature and so it is isometric to . Here note that the square norm of is non-positive since . Like in the previous case the vector can be extended by continuity across its singularities and does not depend on local coordinates in . However it is not a real vector since as consequence of we have,

In this case defining (), it follows that is a real vector with square norm lying in which is independent of local coordinates of . We define the Gauss map of in this case by

(32)

where the sign in (32) depends on a choice of the sheets of the hyperboloid defining the hyperbolic space .

The main result of this section is the following

Theorem 6. ([12], Theorem 7.1) Let be a non-full superconformal harmonic map. If the image lies in a space-like hyperplane then the Gauss transform is a full superconformal harmonic map into the Euclidean unit sphere of which has the same -th Hopf differential as .

If lies in a -hyperplane then the Gauss transform is a full superconformal harmonic map in the sense of [11]. In this case the -th Hopf differentials of and have opposite signs.

Since there are no non-constant harmonic maps of compact surfaces into we obtain

Corollary 1. There exist no non-constant superconformal harmonic map of a compact surface into odd-dimensional De Sitter space ().

Note that the simplest case in the above Corollary is interesting since a conformal minimal immersion is superconformal if and only if its umbilic points are isolated.

Corollary 2. There is no non-constant conformal minimal immersion of a compact surface into with isolated umbilic points.

Other applications of higher order Gauss transforms of maps into will be discussed elsewhere.

References

[1]    L.J. Alías, B. Palmer, Curvature properties of zero mean curvature surfaces in four-dimensional Lorentzian space-forms, Math. Proc. Camb. Phil. Soc. (1998).        [ Links ]

[2]    J. Bolton, F. Pedit and L. Woodward, Minimal surfaces and the affine Toda field model J. Reine u. Angew. Math. 459 (1995), 119-150.        [ Links ]

[3]    J. Bolton, L. Woodward, On immersions of surfaces into Space forms, Soochow Journal of Math. Vol. 14, No. I (1988), 11-31.        [ Links ]

[4]    J. Bolton, L. Woodward, Congruence Theorems for harmonic maps from a Riemann surface into and , J. London Math. Soc. (2) 45 (1992), 363-376.        [ Links ]

[5]    F.E. Burstall, Harmonic tori in spheres and complex projective spaces, J. Reine u. Angew. Math. 469 (1995), 149-177.        [ Links ]

[6]    S.S. Chern, On minimal immersions of the two sphere in a space of constant curvature, Problems in Analysis, Princeton University Press (1970), 27-40.        [ Links ]

[7]    J. Eells and L. Lemaire, Selected topics on Harmonic maps, C.B.M.S. Regional Conference Series 50, Am. Math. Soc. 1983.        [ Links ]

[8]    N. Ejiri, Isotropic Harmonic maps of Riemann surfaces into the De Sitter space-time, Quart. J. Math. Oxford (2), 39 (1988), 291-306.        [ Links ]

[9]    S. Erdem, Harmonic maps from surfaces into pseudo-Riemannian spheres and hyperbolic spaces, Math. Proc. Camb. Phil. Soc. (1983), 483-494.        [ Links ]

[10]    A.P. Fordy and J.C. Wood, eds., Harmonic maps and integrable systems, Aspects of Mathematics, Vieweg 1994.        [ Links ]

[11]    E. Hulett, Harmonic superconformal maps of surfaces into , Journal of Geometry and Physics 42 (2002), 139-165.        [ Links ]

[12]    E. Hulett, Superconformal harmonic surfaces in De Sitter space-times, Journal of Geometry and Physics 55 (2005), 179-206.        [ Links ]

[13]    J. Jost, Compact Riemann Surfaces, Universitext, Springer Verlag, Berlin Heidelberg 1997.        [ Links ]

[14]    R. Miyaoka, The family of isometric superconformal harmonic maps and the affine Toda equations, J. Reine angew. Math 481 (1996), 1-25.        [ Links ]

[15]    B. Palmer, The conformal Gauss Map and the Stability of Willmore Surfaces, Ann. Global Anal. Geom. Vol 9, No.3 (1991), 305-317.        [ Links ]

[16]    M. Sakaki, Spacelike Minimal surfaces in 4-dimensional Lorenzian Space Forms, Tsukuba J. Math. Vol. 25 No. 2 (2001), 239-246.        [ Links ]

[17]    M. Spivak, A comprehensive introduction to Differential Geometry Vol.IV, Berkeley: Publish or Perish, 1979.        [ Links ]

 Eduardo Hulett
FaMAF-CIEM, Universidad Nacional de Córdoba,
Córdoba 5000, Argentina
hulett@famaf.unc.edu.ar

Recibido: 16 de noviembre de 2005
Aceptado: 18 de septiembre de 2006