Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.36 n.1 Bahía Blanca ene./mar. 2006
Rotor support stiffness estimation by sensitivity analysis
L. P. Nascimento1 and L. Caldiron2
Department of Mechanical Engineering, São Paulo State University,
15385-000 – Ilha Solteira – SP - Brazil
1 depaula@dem.feis.unesp.br
2 leonardo@dem.feis.unesp.br
Abstract — In the present work, a method for rotor support stiffness estimation via a model updating process using the sensitivity analysis is presented. This method consists in using the eigenvalues sensitivity analysis, relating to the rotor support stiffnesses variation to perform the adjustment of the model based on the minimization of the difference between eigenvalues of reference and eigenvalues obtained via mathematical model from previously adopted support bearing stiffness values. The mathematical model is developed by the finite element method and the method of adjustment should converge employing an iterative process. The performance and robustness of the method have been analyzed through a numerical example.
Keywords — Parameter Estimation. Rotor Support. Sensitivity Analysis.
I. INTRODUCTION
Mathematical models have been used to simulate and to accomplish predictions of the vibratory behavior of the dynamic systems. In fault detection and model updating there is a particular interest in obtaining relationships between the parameter variations of the system and its modal behavior or its response due to different excitation forces. In this case, the sensitivity analysis has been successfully used (Zimock, 1987).
In general, the model adjustment is carried out in terms of the mass and stiffness parameters of the system. In the publication of Zhang et al. (2000), a successfully model updating method to reduce the difference between the measured and calculated natural frequencies was presented. Sun et al. (2000) also present a sensitivity-based model updating method to automatically minimize the difference between the analytical and experimental model by using the least square algorithm. Several works (Sheinman, 1996; Kosmatka and Ricles, 1999; Dems and Mróz, 2001) have been devoted to model updating in the process of fault detection employing modal parameter sensibility.
An application that has demanded a lot of interest in the model adjustment is the identification of stiffness of supports of rotating systems (Su and Huang, 1997; Rajan et al., 1986). In the rotating machines, the support stiffness values normally are very difficult to be determined and they are not directly found in the literature. They are function of the bearing type, rotating speed of the machine, characteristics of the oil lubricant or rolling bearing employed, pedestal and foundation. However, the other dynamic parameters of the machine can be calculated with satisfactory accuracy from its design and from user or manufacturer information. The support stiffness identification is very important in the development of mathematical models with guaranteed accuracy in representing the dynamic of the system, and it is known that it is only possible when the parameter uncertainties are significantly reduced (Smart et al., 2000; Sinha et al., 2002).
Although numerous papers on support stiffness identification have been published, most of them just work with flexible supports. However it is known when the supports have high stiffness, their sensibility with respect to the modal response becomes very small, and it can induce instability in the algorithm, hindering the convergence, so a robust algorithm is necessary.
II. SENSITIVITY ANALYSIS
Consider a multi-degree-of-freedom undamped mechanical system described by equation,
[M]{ÿ} + [K]{y}, (1)
where [M] and [K ] are matrices of mass and stiffness respectively, and {y} is the displacement response vector. Now, it is admitted that in the eigenproblem solution the vibration modes are conveniently normalized to produce,
[Φ]T[M][Φ] = [I], (2a)
[Φ]T[K][Φ] = [Λ], (2b)
where [Φ] and [Λ] are the eigenvector and eigenvalue matrices respectively, and [I] is the identity matrix. Mathematical sensitivity analysis relations are now sought that show how the matrices [Λ] and [Φ] change when the matrices [M] and [K] change. For this purpose the matrix Taylor expansion can be used. For sufficiently small changes in the parameters of the system (1), only the first term in the expansions need to be retained, i.e.,
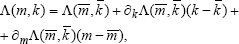 | (3a) |
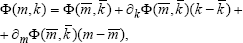 | (3b) |
where the partial derivative of the modal characteristics matrices are called the sensitivity matrices of the mechanical system (1) and the over-marks indicate the initial values of the parameters. The sensitivity of the modal parameters with respect to the stiffness matrix change can be obtained by derivative expressions,
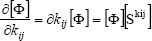 | , (4) |
 | . (5) |
Differentiating Eq. (2a) with respect to an arbitrary element of the stiffness matrix gives the relationship,
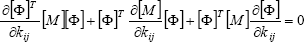 | . (6) |
Since the partial derivative of the mass matrix [M] with respect to stiffness is null and introducing Eq. (4) into Eq. (6), it results,
[Skij]T[Φ]T[M][Φ] + [Φ]T[M][Φ][Skij] = 0. (7)
The Eq. (7) can be simplified by using Eq. (2a) to give,
[Skij]T + [Skij] = 0. (8)
In the same way, differentiating Eq. (2b) with respect to the stiffness, it results,
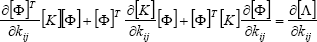 | , (9) |
and introducing Eq. (4), we have,
[Skij]T[Φ]T[K][Φ] + [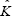 kij] + [Φ]T[K][Φ][Skij] = ∂kijΛ, (10)
kij] + [Φ]T[K][Φ][Skij] = ∂kijΛ, (10)
and finally, by using Eq. (2b) the Eq. (10) can be simplified to give:
[Skij]T[Λ] + [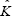 kij] + [Λ][Skij] = ∂kijΛ, (11)
kij] + [Λ][Skij] = ∂kijΛ, (11)
-[Skij][Λ] + [Λ][Skij] + [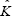 kij] = ∂kijΛ, (12)
kij] = ∂kijΛ, (12)
where,
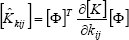 | , (13) |
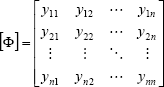 | . (14) |
The eigenvalue and eigenvector sensitivities due to small changes in a particular element of the stiffness matrix with indexes i = 1 and j = 2 can be determined by using the Eq. (12), in which the matrices will be developed in the form,
 | , (15) |
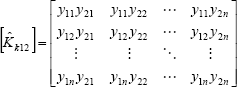 | , (16) |
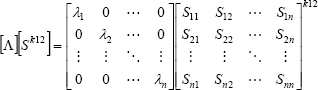 | , (17) |
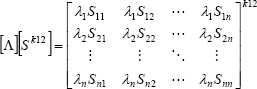 | . (18) |
Proceeding analogously one obtains,
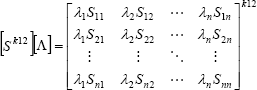 | , (19) |
and finally,
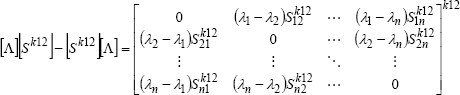 | . (20) |
In the Eq. (12), by considering the elements of the main diagonal of the matrices, the following expressions can be described,
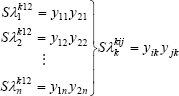 | , (21) |
and, by taking the elements out of the main diagonal of the matrices, one can then determine the expressions,
 | (22) |
The elements of the sensitivity matrix of the eigenvalues with respect to the stiffness changes are determined by Eq. (21). On the other hand, the elements of the sensitivity matrix of the eigenvectors are obtained by Eqs. (4) and (22).
III. ESTIMATION METHOD
Consider that one wants to estimate the stiffness values of the support of a real rotating system. A mathematical model for that system is developed, in which the initial support stiffness values are arbitrarily adopted. Thus, the theoretical eigenvalues, λ k (k = 1, 2, ..., N), can be can be determined, where N is the number of bearings of the system. The sensitivity of these eigenvalues with respect to changes in the stiffness value of each support, 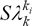 , also can be given from modeling by using the Eq. (21). Also consider that a modal analysis was accomplished and the first experimental natural frequencies of the system, ωek, were determined. The experimental eigenvalues can be given by,
, also can be given from modeling by using the Eq. (21). Also consider that a modal analysis was accomplished and the first experimental natural frequencies of the system, ωek, were determined. The experimental eigenvalues can be given by,
λek = (2πωek)2 ; (k = 1, 2, ..., N). (23)
In this system if one considers that the support stiffnesses are the only parameters that will vary, then the Eq. (3a) regarding the first term in the Taylor expansions can be simplified as,
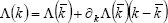 . (24)
. (24)
Admitting small changes in the elements of the stiffness matrix of the system, then the Eq. (24), when described to a particular eigenvalue, can be expressed as,
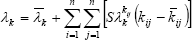 | . (25) |
The aim of the proposed method is having an adjustment of the support bearing stiffnesses. In modeling terms the support stiffnesses are finite elements just connected to one nodal point, so each stiffness value will be allocated in an element of the main diagonal of the stiffness matrix, simplifying the use of the Eq. (25). In that equation, in taking λk as experimental eigenvalues and  as theoretical eigenvalues obtained by using the initial values of the support stiffnesses, then it can be established a linear system of equations given by,
as theoretical eigenvalues obtained by using the initial values of the support stiffnesses, then it can be established a linear system of equations given by,
 | (26) |
and in the matrix form, the equation system (26) become,
 | , (27) |
or
[Sλk]{Δk} = {Δλ}. (28)
The solution of the Eq. (28) will determine the Δk values to adjust the stiffnesses of the supports, in such manner that the theoretical eigenvalues of the machine given by using de mathematical model become very close to the experimental eigenvalues. From equation system (27), it can be seen that the number of equation is equal to the number of bearings of the machine.
It is known that the sensitivity matrix in Eq. (28) has guaranteed accuracy only for small stiffness changes since that equation has been deduced just regarding the first term in the Taylor expansions. Therefore, its solution is conveniently obtained by using iterative procedure, and the convergence occurs minimizing the differences between the theoretical and experimental eigenvalues. The convergence process finishes when these differences are smaller than a previous established tolerance. Figure 1 shows the block diagram of the computational program implemented for adjustment of the support bearing stiffnesses. It can be observed that in each iteration the Δki values are algebraically added to their respective ki and the elements of the {Δλ} vector tend to zero.
As the method uses only the first term in the Taylor expansions, when the differences between the theoretical and experimental eigenvalues are significantly high, it can occur numerical problems for convergence during the first iterations, since the solution of the equation system (28) can result in very high values of Δ k (unreal). To deal with this problem, when the differences are higher than a previous established tolerance (tol2), they are automatically divided in p parts so that the algorithm convergence will happen in p steps. Therefore, a loop process occurs in each step until the current differences become lower than a certain tolerance (tol1), and thus the process goes to the following step, successively, as it is shown in Fig. 1. That resource improves the robustness of the method to estimate very rigid supports, which provide very small eigenvalue sensibilities making more difficult the convergence of the system of Eq. (28).
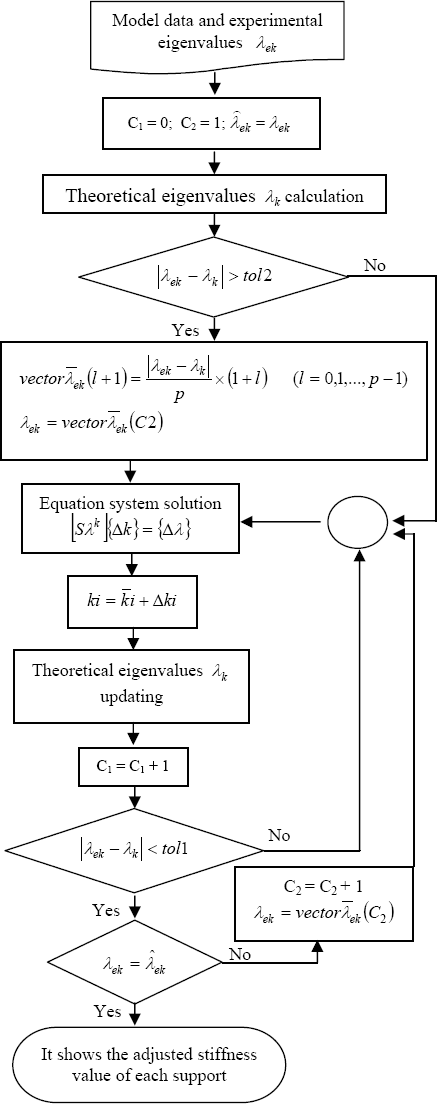
Figure 1. Block diagram of the estimation algorithm
IV. ROTOR MODELLING FOR SUPPORT STIFFNESS ESTIMATION
In this section a simplified model of rotor vibration in the vertical direction will be described. Figure 2 shows the schematic of the rotor-bearing system, which was modeled by using the finite elements method. The rotor consists of a 500 mm long shaft that is 14 mm in diameter and was considered to be a flexible beam divided into elements having distributed mass and elasticity. The two disks were modeled as lumped masses of 0.4 and 1.35 kg attached to the shaft, which is supported by bearings modeled as springs with stiffnesses K1 and K2 as shown in Fig. 2.
The rotor has been modeled into 14 finite elements and 11 nodal points with two degrees of freedom each, displacement in vertical axis and rotation around the perpendicular axis. The model does not include the gyroscopic effects.

Figure 2. Model of rotor for support stiffnesses estimation
V. NATURAL FREQUENCIES OF REFERENCE
To accomplish the simulations, at the beginning it was determined the first two natural frequencies of the rotor regarding different sets of support stiffnesses. Table 1 shows these natural frequencies, which will be used as references in analyzing the method and its robustness. The analysis is carried out by taking arbitrary stiffness values for the rotor supports so that the method processes the adjustment based on these reference frequencies.
In general the support stiffness is the most influential factor in determining critical speeds of the rotors. At low support stiffnesses relative to shaft stiffness the natural frequencies of the rotor are almost entirely dependent upon the stiffness of the bearings. When the supports become very stiff, the rotor is said to be shaft dependent because bearing stiffness changes cannot raise natural frequencies significantly. In this case only changes on the shaft geometry have important influence on the natural frequencies. The intermediate condition is when the supports and shaft stiffnesses contribute to natural frequencies determination.
It can be observed in Table 1 that practically there are no changes in natural frequencies when the stiffnesses are higher than 1.0x108 N/m, where the system has reached the zone of shaft dependent. Therefore, the robustness of the method has been tested for this condition, as well as for very flexible rotor support within of the zone of bearings dependent (1.0x102 N/m) and for an intermediate condition (1.0x105 N/m).
VI. NUMERICAL RESULTS
Table 2 shows the results of the supports stiffness estimation by taking different initial stiffnesses and using the natural reference frequencies (1.408 Hz and 2.827 Hz) related to the rotor with supports of 1.0x102 N/m (see Table 1). These results indicate that the method is quite effective to estimate the stiffness of the rotor supports when they are very flexible, in the zone where the variation of the critical frequencies is completely dependent of the characteristics of the support stiffness. It can be observed that the adjustment does happen even when it is taken quite high initial stiffnesses (higher than 105 N/m) as data for the adjustment process, however there is an increase in the number of iterations to converge to the solution.
Table 1. Stiffnesses x rotor natural frequencies
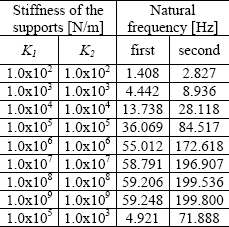
Table 3 demonstrates that when the rotor possesses supports with stiffness around the transition zone between bearing dependent and shaft dependent (represented here by 1.0x105 N/m), the method is still quite robust to converge for the solution. This result also shows that the convergence will certainly occur if lower initial stiffness values are taken and that the solution is not gotten for initial stiffness values above 5.0x106 N/m.
The estimation results for very rigid supports are presented in Table 4, where it can be verified that the method can still reach the convergence even when the rotor has very rigid supports, already in the zone of rotor shaft dependent. However, in this case it is recommended taking initial stiffness values as close as possible to the values to be estimated, so that the convergence can surely happen. Table 4 shows that the convergence only occurs for initial values higher than 1.0x105 N/m, approximately.
Table 2. Estimation of flexible supports (1.0x102 N/m)

Table 3. Estimation of supports with stiffness of 1.0x105 N/m

Table 4. Estimation of rigid supports (1.0x108 N/m)

Table 5 presents the results of the convergence analysis when the rotor possesses supports with very different stiffness (one is a hundred higher than the other). Even with that high stiffness difference the method converges normally. Also, in this case it is recommended to take low initial support stiffnesses to assure the convergence.
Table 5. Estimation of supports with different stiffnesses (1.0x105 N/m and 1.0x103 N/m)
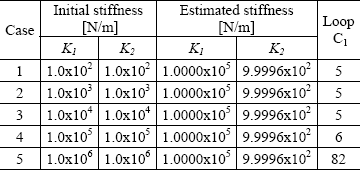
In general, the convergence for the solution occurs with a reduced number of iterations and the relative errors in estimating the stiffness are very small, being lower than 3% in the case of rotor with high support stiffnesses (see estimated stiffnesses in Tab. 4). In the other cases the relative errors were null practically. It is important to highlight that those results with small relative errors have been obtained with a tolerance (maximum difference) of 0.01 Hz between the adjusted natural frequencies and the natural frequencies of reference.
VII. CONCLUSIONS
In this work a method for estimation of rotor support stiffnesses using the sensitivity analysis is presented. A theoretical rotor modeled through a finite elements code was used to analyze the performance of the method and interesting results were obtained. It is important having an accurate model to represent the dynamics of the rotor to assure a reliable process for model updating. In general the implemented method has demonstrated to be efficient and robust to estimate the stiffnesses of rotor supports. When the method is applied to estimate flexible supports, in the zone of bearing dependent rotor, the probability of occurring problems of convergence is very small, even when the convergence process begins with initial stiffness values very different from the values that will be estimated. When the rotor is in the zone of shaft dependence, with very stiff supports, the convergence can be more difficult; therefore, it is interesting to take initial stiffness values as close as possible of the values that will be estimated. In this case the user's experience in dynamics of systems can help considerably.
Another interesting fact is that the probability of occurring convergence problems is quite reduced when it is taken smaller initial stiffness values than the values that will be estimated. This happens because the convergence process begins in such condition where the eigenvalue sensitivities respect to the support stiffness are considerably high, and for consequence, the stability of the method become higher.
An interesting characteristic of the method is the high speed of the model adjustment shown by the low number of iterations to obtain the solution. Another important characteristic of the method is its accuracy, once the convergence process can precisely reaches the natural frequencies of reference and, consequently, the estimated stiffnesses.
ACKNOWLEDGMENTS
The authors would like to acknowledge de "FAPESP – Fundação de Amparo à Pesquisa do Estado de São Paulo", the Brazilian research funding agency for financial support of this work.
REFERENCES
1. Dems, K. and Z. Mróz, "Identification of damage in beam and plate structures using parameter-dependent frequency changes", Journal of Engineering and Computations, 18, 96-120 (2001). [ Links ]
2. Kosmatka, J.B. and J.M. Ricles, "Damage detection in structures by modal vibration characterization", Journal of Structural Engineering, DEC/99, 1384-1392 (1999). [ Links ]
3. Rajan, M., H.D. Nelson and W.J. Chen, "Parameter sensitivity in the dynamic of rotor-bearing systems", Journal of vibration, Acoustics, Strees and Reliability in Design, 108, 197-206 (1986). [ Links ]
4. Sheinman, I., "Damage detection and updating of stiffness and mass matrices using model data", Journal of Computers and Structures, 59, 149-156 (1996). [ Links ]
5. Sinha, J.K., M.I. Friswell and A.W. Less, "The identification of the unbalance and the foundation model of a flexible rotating machine from a single run-down", Journal of Mechanical Systems and Signal Processing, 12, 255-271 (2002). [ Links ]
6. Smart, M.G., M.I. Friswell and A.W. Less, "Estimating turbo generator foundation parameters: model selection and regularization", Proc. of The Royal Society London, 456, 1583-1607 (2000). [ Links ]
7. Su, C. and S. Huang, "Receptance for the sensitivity analysis of critical speed to rotor support stiffness", Journal of Engineering for Gas Turbines and Power, 119, 736-739 (1997). [ Links ]
8. Sun, L.Y., C.S. Yu, B.J. Zhang, N. Chen and Q.H. Sun, "Finite element model updating via automatic optimization of physical parameters", Proc. OFIMAC, 2, 1544-1549 (2000). [ Links ]
9. Zhang, Q.H., C.C. Chang and T.Y.P. Chang, "Finite element model updating for structures with parametric constraints", Earthquake Engineering and Structural Dynamics, 29, 927-944 (2000). [ Links ]
10. Zimock, Z., "Sensitivity analysis of vibrating systems", Journal of Sound and Vibration, 115, 447-458 (1987). [ Links ]














