Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista electrónica de investigación en educación en ciencias
versión On-line ISSN 1850-6666
Rev. electrón. investig. educ. cienc. vol.2 no.1 Tandil ene./jul. 2007
ARTÍCULOS ORIGINALES
Las ideas de algunos estudiantes acerca de la enseñanza - aprendizaje de la Matemática en el Nivel Medio
Corica, Ana Rosa1;2
acorica@exa.unicen.edu.ar
Otero Maria Rita1;2
rotero@exa.unicen.edu.ar
1NIECYT-UNCPBA; Tandil- Buenos Aires, Argentina;
2 CONICET-Argentina
Resumen
Este trabajo forma parte de un proyecto más amplio en el que se estudia las ideas de alumnos y profesores -de nivel medio y universitario- acerca del saber matemático, su enseñanza y aprendizaje y se exploran posibles factores que intervienen en el fracaso en Matemática de los estudiantes. Se discuten aquí resultados parciales obtenidos con estudiantes de Nivel Medio. Se realizaron dos estudios: uno cualitativo y otro cuantitativo. Ambos estudios indican que los estudiantes atribuyen como tarea del profesor la de "explicar" los conocimientos en forma exhaustiva y detallada, y de esto hacen depender que ellos "entiendan" y "aprendan".
Palabras claves: Estudiantes; Matemática; Nivel medio; Teoría Antropológica de lo Didáctico; Teoría del Aprendizaje Significativo.
Abstract
This work comprises of a ampler project in the than he study the ideas of students and professors - of mean level and university- about the mathematical knowledge, their teaching and learning and explore possible factors that take part in the failure in Mathematical of the student's. Obtained partial results with students of Mean Level are discussed here. In order to carry out our investigation two studies were made: one qualitative and another quantitative. Both studies indicate that the students attribute as task of the professor the one "of explaining" the knowledge in exhaustive and detailed form, and of this they make depend that they "understands" and they "learns".
1. Introducción
Es ampliamente conocido que los aprendizajes escolares en el área de Matemática son insuficientes y que los estudiantes en general y los de la educación media en particular, no consiguen construir conceptos matemáticos complejos ni utilizarlos en situaciones nuevas. Numerosas investigaciones confirman el elevado índice de estudiantes que fracasan en Matemática (Badano, Dodera, 1999; Bolea, Bosch, Gascón, 2001; Corica, 2007; Gascón, Bosch, Bolea, 2001; Miguez Escorcia, 2003; Otero, Fanaro, Elichiribehety, 2001), expresado tanto en el conocimiento, las competencias y habilidades que efectivamente adquieren los alumnos, como en su valoración acerca de esta ciencia.
Ante esta situación nos cuestionamos ¿porqué se produce el mencionado "fracaso"1? Iniciamos un proyecto de investigación con estudiantes y profesores de Nivel Medio y Universitario (Corica, 2007) para tratar de explorar este "fracaso", intervenir y sugerir algunas líneas de acción. En otros trabajos (Corica, Otero, 2005a, 2005b) destacamos que los estudiantes sostienen y demandan que la principal tarea del profesor es la de explicar los contenidos de la forma más exhaustiva y detallada posible, para que ellos puedan "entender" y "aprender. El profesor tendría el papel protagónico en el proceso de enseñanza - aprendizaje de la Matemática, y sobre sus espaldas recaería la responsabilidad de que los estudiantes aprendan o no. Esta idea se corresponde con lo que se considera en la cultura corriente, y en lo que sostienen algunos documentos curriculares:
"Motivar a los alumnos y conseguir que mejoren su actitud respecto a lasmatemáticas y su aprendizaje es una de las responsabilidades principales del profesor de matemáticas y constituye uno de los factores que determinan el éxito o el fracaso de la enseñanza de las matemáticas" (Bolea, Bosch, Gascón, 2001: 247 - 304).
Además de los estudiantes, los profesores de la escuela Media también adhieren al supuesto de que el profesor debe "explicar" los conocimientos, de la forma más exhaustiva y detallada posible, de lo cual a su vez depende que el alumno "entienda" y "aprenda" (Corica, Otero, Sureda; 2005).
En este trabajo se presentan resultados parciales de dos estudios realizados con estudiantes, cuyo objetivo fue conocer y comprender las experiencias vividas por los estudiantes de la Escuela Media en las clases de Matemática. En particular, nos interesa buscar respuestas a las siguientes cuestiones: ¿cuáles son las ideas de los estudiantes acerca de la enseñanza - aprendizaje de la Matemática en el Nivel Medio? ¿Cómo se relacionan estas ideas con el fracaso de los estudiantes?
Para abordar aspectos didácticos de nuestra investigación, se adoptó como referencial teórico a la Teoría Antropológica de lo Didáctico (Chevallard 1999; 2000; 2002a; 2002b). En esta teoría se ve al profesor en el aula como el director de una comunidad de estudio, que integra junto con sus alumnos. Este punto de vista permite, entre otras cosas, considerar al profesor como una más de las figuras integrantes de la comunidad de estudio y, en particular, atenuar el protagonismo que la cultura pedagógica tradicional suele adjudicarle. (Bosch, Espinoza, Gascón, 2003). Por otro lado, para abordar aspectos cognitivos nuestro referencial teórico es la Teoría del Aprendizaje Significativo (TAS) (Ausubel; 1963; 1968; 1976; Moreira, 2000). Un punto central de la TAS es que el alumno es responsable de su propio aprendizaje, a tal punto que puede decidir no aprender, condición que está alineada con la idea de acotar la asignación de responsabilidades únicamente al profesor.
2. Metodología
Si bien situamos la naturaleza de nuestro trabajo en el ámbito de la investigación básica en educación matemática y lo hacemos dentro de un paradigma cualitativo, no podemos dejar de reconocer que a raíz de los referenciales que se utilizan y de los problemas que se abordan en este campo, es recomendable la integración de técnicas metodológicas provenientes tanto de abordajes cualitativos como cuantitativos (Greca, 2002).
Nuestra investigación es de carácter exploratorio, pues nuestro objetivo fue identificar tendencias en el grupo de estudiantes En una primera instancia, se recolectó información de las vivencias de los estudiantes de Nivel Medio en las clases de Matemática a través de un Diario de clase2 (Estudio I). Dicho estudio se realizó con alumnos de 9º EGB, 1º, 2º y 3º año de Polimodal. La elección de estos años escolares tuvo como objetivo establecer si existían cambios significativos entre los estudiantes de un año escolar a otro, o de un nivel escolar a otro. Se invitaron a participar voluntariamente estudiantes de distintas 6 escuelas públicas de una ciudad del centro de la provincia de Buenos Aires. Se trabajo con un grupo compuesto por N = 24 estudiantes.
Los Diarios de Clase que fueron entregados a los alumnos, comenzaban con la siguiente leyenda:
"En este cuaderno se encuentran representadas mis vivencias personales acerca de lo que ocurre durante las horas de Matemática, y se va construyendo con relatos sinceros que escribo después de cada clase. Esto no implica de ninguna manera que critique a mis compañeros, ni al profesor ni a la escuela, solo intento transmitir mis vivencias respecto a esta materia".
Los Diarios pretendían que los estudiantes registren sus vivencias en las clases de Matemática. Al entregarles los cuadernos, se indicó que no se admitirían comentarios descalificantes hacia el profesor, la institución, o del grupo de compañeros, lo que se buscaba comprender eran sus vivencias en las clases de Matemática. A partir del estudio de los Diarios se generaron categorías3, y luego se describe a estos Diarios a partir de las categorías de análisis que se encuentran presentes en la mayor parte de las manifestaciones de los estudiantes. La formulación de categorías se realizó mediante inducción analítica puesto que no se está interesado en la incidencia o frecuencia de ciertas cualidades, sino en la generación de conceptos y categorías teóricas que se ajusten a la realidad. Se pretende generalizar a partir de la abstracción efectuada en el estudio de unos pocos casos (Branen, 1992).
En una segunda instancia, atendiendo a los resultados obtenidos en el primer estudio, se diseñó y puso a prueba una encuesta de respuesta cerrada (Estudio II). En vistas de elaborar un instrumento que facilite la indagación, con profundidad, sobre las concepciones de lo sujetos acerca del saber matemático, su enseñanza y aprendizaje se realizaron una serie de preguntas focalizadas, cuidadosamente diseñadas, para ser contestadas en forma individual y por escrito. Optándose por la modalidad escrita porque consideramos que permite encuestar a un importante número de sujetos, lo que a su vez nos permite aplicar procedimientos del análisis multivariado.
Para la elaboración del cuestionario se diseñó, en primera instancia, un listado de preguntas que, a nuestro criterio, nos darían indicadores sobre las concepciones de lo sujetos acerca del saber matemático, su enseñanza y aprendizaje. Estas preguntas se ensayaron con diversos colaboradores, se corrigieron en aspectos de forma y contenido para luego ser aplicadas en una prueba piloto a estudiantes de los niveles propuestos para este estudio.
En forma definitiva, el cuestionario (Anexo I) mantuvo la modalidad de individual y escrito. Se optó por preguntas cerradas con opciones de respuesta, considerando que esto ayudaría a centrar la atención de los sujetos en el tema que nos interesa y nos permitiría una más rápida y clara tabulación. Las preguntas fueron pensadas de manera que cada una poseyera una y sólo una opción de respuesta y que la elección de la respuesta a modo cerrado fuera suficientemente informativa.
El cuestionario se administró en forma personal a N = 857 estudiantes pertenecientes 9º año de EGB, 1º, 2º y 3º año de Polimodal de las mismas instituciones que participaron en el estudio I. El cuestionario fue aplicado a los estudiantes de los mismos cursos a los que pertenecían los estudiantes que realizaron los diarios de clase.
El segundo estudio es cuantitativo y para el análisis de datos se emplearon técnicas provenientes del Análisis Multivariado de Datos (Lebart & Morineau, 1994; Lebart Morineau y Fenelón, 1985) que permite clasificar la población de estudiantes considerando un conjunto importante de variables. Se utilizó el paquete SPAD 3.5. Las técnicas de reducción factorial proporcionan una simplificación y síntesis de la información que permite analizar las principales conjunciones-oposiciones entre las variables y la representación gráfica de las diferentes modalidades de las variables en planos factoriales, y proporciona una visión directa y global de los principales aspectos de la información a tener en cuenta (Crivisqui E. & Villamonte G., 1997; Benzécri, 1980). El análisis factorial es un requisito previo para el análisis de clúster que permite encontrar tipologías y detectar asociaciones de variables, o características relacionadas con los grupos de estudiantes.
3. Resultados y análisis
3.1 Estudio I: Los Diarios de clase
En la Tabla I del Anexo II se indica, para cada uno de los Diarios de Clase: el año escolar del estudiante que redactó el Diario (Año), el número de clases en los que se han realizado registros (Clases), el número de inasistencias del estudiante (Inasistencia del alumno), el número de días sin clases de Matemática durante el período que se redactó el Diario, por ausencia del profesor o algún evento institucional (Días sin clase de Matemática) y el período en el que los estudiantes indican haber realizado registros (Fechas).
3.1.1 Análisis de los Diarios
A continuación se transcriben y describen algunos rasgos sobresalientes de los Diarios, de algunos de los estudiantes, que intervinieron en el estudio. En esta instancia, sólo presentamos fragmentos que hacen referencia a manifestaciones relacionadas con la dependencia de los estudiantes hacia el profesor. Resaltamos este aspecto porque todos los estudiantes que participaron en el Estudio I hicieron algún comentario acerca del mismo.
Los fragmentos que se presentan a continuación permiten entender de qué manera los estudiantes le asignan al profesor el papel principal en las clases de Matemática. Se destaca la necesidad de los estudiantes porque el profesor les explique todo lo que deben hacer: el profesor ocupa el centro del proceso de enseñanza - aprendizaje, todo gira alrededor de él y fundamentalmente entorno a sus explicaciones.
A cada estudiante se lo identifica por su año escolar y el número de intervenciones que se registran en los Diarios ((año escolar; número de intervenciones realizadas)).
El alumno A2 (9; 43)
Empezamos un cuadernillo nuevo, de expresiones algebraicas, no nos explica ya que hay explicaciones en el cuadernillo. Por ahora voy entendiendo, pero necesito mucho de la profesora y no estoy segura de poder hacerlo sola. En estas expresiones advertimos que el estudiante destaca que el profesor "no explica" pero que necesitaría que lo hiciera. Su necesidad de explicación también se reafirma cuando indica: "Tema: Racionalización de números irracionales. Lo entiendo bien, el problema es que nos queda sólo el Jueves para terminar de dar la explicación y practicar y el Viernes tenemos la prueba".
Como el estudiante no esta seguro de poder realizar la tarea sólo, le interesa que se corrija en el pizarrón. También, reconocemos la preocupación de A2 (9, 43) debido a la proximidad de la evaluación y a la ausencia de tiempo para ejercitar en presencia del profesor. Esto muestra la baja autonomía del alumno y su dependencia con el profesor.
El alumno A5 (9; 9)
Tema nuevo, Teorema de Pitágoras, aunque no le presté bastante atención, la explicación no fue bastante clara, ya que por un lado, tiene voz clara pero por el otro, no se sabe explicar bien en éste tema, igualmente cuesta mucho cazar la idea desde el principio. Nos dio ejercicios que hice mal, y nos dijo que íbamos a estar con esto hasta fin de año. El alumno reconoce no prestar atención en clase pero de todas formas, atribuye al profesor la responsabilidad de que no entiende. Inferimos que A5 (9; 9) transfiere su compromiso de aprendizaje al profesor. Este estudiante se encuentra poco preparado para realizar un aprendizaje autónomo.
El alumno A10 (1; 55)
"Operaciones combinadas" (repaso del año pasado). Entiendo el tema porque hace dos años que lo vengo repasando. Me parece que es un tema fácil, pero siempre me pasa lo mismo, que en las pruebas aparece algo que me despista. A10(1;55) se encuentra escasamente preparado, es decir, inferimos que el estudiante, no estaría capacitado para utilizar sus conocimientos en situaciones distintas a las que dieron origen al estudio (en el aula) del saber en cuestión, pues considera que las tareas propuestas para ser evaluado son distintas a las trabajadas en clase.
Clase nº 22. 30/4/03. 1 hora."Corrección de los ejercicios y vuelta a hacerlos en el frente". Bueno esta clase me sirvió para darme cuenta de un error muy tonto que tenía y que hacia que me de otro resultado. En las expresiones de A10 (1; 55) se destaca el interés por la corrección de las tareas en clase. Interpretamos que se trata de un estudiante que no posee medios para controlar sus propias producciones y con poca autonomía para el estudio de la Matemática.
El alumno A19 (3; 7)
... estuvimos realizando algunos ejercicios de una guía que se nos dio, que contenía distintos temas. La forma en la que trabajamos fue en grupo y me pareció muy bien, ya que de esta forma nos vamos ayudando entre nosotros, lo que si creo que faltó, fue una breve explicación por parte de la profesora, para refrescar un poco la memoria antes de comenzar a resolver los ejercicios. De las manifestaciones de A19 (3; 7) inferimos que comprende Matemática compartiendo significados con sus compañeros pero necesita también que el docente le explique los conceptos.
El alumno A21 (3, no se registra)
Después vimos cambio de base de los logaritmos, otra vez tuve unos inconvenientes pero los solucioné rápido, nos dieron una parva de ejercicios, yo pensaba que a esto lo sabia de memoria, pero cuando llegó el día de la prueba me fue re mal me saqué un 4, no entendía como, si lo sabía de memoria, yo no soy de esos que le echan la culpa al profesor porque este explica re bien, además si no lo entendés te lo vuelve a explicar, en eso es muy bueno. Inferimos que A21(3, no se registra) desconoce las limitaciones de su aprendizaje. Como no obtiene los resultados esperados en las evaluaciones, no se explica cómo desaprueba si el profesor "explica bien" y el creía saber. Esto da sustento empírico al hecho de que, aunque un sujeto reciba explicaciones correctas y claras, no es suficiente para que pueda realizar un aprendizaje significativo.
El alumno A22 (3, 13)
Hoy repasamos el tema, pasamos al pizarrón a realizar aquellos ejercicios con los que teníamos dudas. La clase me pareció aburrida porque no podíamos avanzar nada. Aún así pude comprobar que mis compañeros les cuesta entender bien el tema. Gran parte de la hora estuve trabajando en otra materia. De estas manifestaciones inferimos que a A22 (3; 13) le agradan las clases de Matemática cuando tiene algo que hacer o siente alguna dificultad para resolver. Estamos ante el caso de un estudiante que no evidenciaría una fuerte dependencia hacia las explicaciones de su profesor, como ocurre con los casos que se presentaron anteriormente.
El análisis completo de los Diarios permitió realizar las siguientes generalizaciones y que han conducido a la formulación de las categorías descriptas en el Anexo III:
- Las manifestaciones de los estudiantes no son propias de ningúnaño escolar. En general, los comentarios que se recogen de los Diarios se refieren a críticas sobre las prácticas llevadas a cabo por el profesor. Así, para los estudiantes del Nivel Medio, las acciones de sus profesores son las que determinan si aprenden o no Matemática.
- Los estudiantes no tienen autonomía para aprender Matemática. Ninguno de los 24 casos de estudiantes considerados parece asumir su responsabilidad en su aprendizaje. Por lo tanto, no reúnen los requisitos para aprender significativamente este campo de conocimiento Parece difícil frente a esta actitud, no dirigir la mirada y las correspondientes responsabilidades, al sistema escolar y a la formas de gestión didáctica de los profesores de matemática.
- Los estudiantes tienen baja resistencia a la frustración. Es decir, los estudiantes no son colocados en situaciones cuya solución es laboriosa, no inmediata, no trivial. Les agrada Matemática siempre y cuando no existan obstáculos, así, frente a la primera dificultad se sienten frustrados y abandonan su intento o acuden al profesor, quien "salva" la situación entregando la respuesta en lugar de reorientar las preguntas. De esta manera, la escuela ofrece una visión muy empobrecida de la actividad Matemática en particular y de la ciencia en general. Como resultado, los estudiantes consideran ingenuamente que se aprende por desvelamiento como si el conocimiento fuera producto de la visión de un objeto externo, más que de una acción constitutiva del mismo.
- El profesor debe explicar los conceptos. Para los estudiantes el profesor es el protagonista de la clase y su rol es el de "explicar los conceptos" y no el de "conversar"4 con los estudiantes para compartir un lenguaje y elementos de una cultura en común. Se lo percibe como a un "iluminador" de los objetos matemáticos, sólo el conocería la verdad de los mismos.
- Los estudiantes muestran desinterés por aprender Matemática. El interés de los estudiantes por aprender Matemática, se encuentra vinculado con la aprobación de la materia y no con el aprendizaje de este campo de conocimiento. La expectativa de los estudiantes es aprender de una sola vez y ante una primera explicación, al no conseguirlo, lo único que les interesa es aprobar.
- Los estudiantes no se sienten responsables de su fracaso. Los estudiantes miden su fracaso por la aprobación/desaprobación de los exámenes y no se sienten responsables de su propio fracaso, lo atribuyen a las prácticas desarrolladas por el profesor. Sin embargo, los estudiantes se perciben capaces de aprender Matemática, si les explican "bien" entienden.
A modo de síntesis, se presenta el Gráfico I que permite visualizar la frecuencia de cada subcategoría formulada.

Grafico 1 - Frecuencia de cada subcategoría formulada para el análisis de los Diarios
Los Diarios de clase permitieron generalizar tres grandes grupos de metacategorías5: Referencias al profesor, La clase de Matemática y la Evaluación. Con relación a la primera de ellas, en el Gráfico 1, se destaca el número de estudiantes que identificamos con la subcategoría Agrado (correspondiente a la categoría Explicación). A estos estudiantes les agradan las explicaciones del profesor porque este explica bien. Los alumnos coinciden en que si se les explica "bien" entienden.
Con respecto al aprendizaje de la Matemática, la mitad de los estudiantes que participaron en este estudio, sostienen su necesidad de que el profesor les explique lo que deben hacer (subcategoría: necesidad del profesor). Este punto se corresponde con lo mencionado en el párrafo anterior: es notable la dependencia que existe entre los estudiantes y las explicaciones del profesor. Aparentemente, estamos en presencia de estudiantes con poca o ninguna autonomía para el estudio de la Matemática.
Términos
Del Gráfico I también se destaca que un importante número de estudiantes coinciden en que no pueden realizar "solos" las tareas propuestas (subcategoría: Dudas en algunas tareas). También se destacan aquellos que consideran importante la corrección de tareas en clase (subcategoría: corrección de errores). Estos estudiantes parecerían no conocer medios para validar sus realizaciones y nuevamente necesitan que el profesor les explique qué deben hacer. De este modo, el topos del alumno es ocupado por el profesor.
Con respecto a la metacategoría La evaluación, destacamos el número de estudiantes que representa a la subcategoría Aprobación. Estos estudiantes tratan de hacer especulaciones acerca de la aprobación/desaprobación de las evaluaciones realizadas y como anticipáramos en párrafos anteriores, su interés por aprender Matemática es aprobar la materia más que adquirir conocimientos Matemáticos.
3.2 Estudio II: La Encuesta
La totalidad de los Diarios analizados indican, cualitativamente, la relevancia que tiene la actividad del profesor en la clase de Matemática. Para profundizar estos resultados, y con el objeto de ampliar y precisar la respuesta a las preguntas de investigación que nos formulamos, se diseño e implementó una encuesta de respuesta cerrada, a estudiantes de los mismos niveles que participaron en el estudio anterior. Para el diseño de la encuesta, se tuvieron en cuenta las categorías construidas en el Estudio I. Así, indagamos a los estudiantes acerca de: la concepción sobre la dificultad para el aprendizaje de la Matemática; la importancia otorgada a dicho aprendizaje, el interés por el aprendizaje de la Matemática, el tiempo de dedicación al estudio de la Matemática; la relación que establecen con su profesor (dependencia o independencia); sus actitudes frente a los errores cometidos; la elección de carreras vinculadas con la Matemática y la adhesión a ciertos mitos de la cultura popular sobre el saber matemático, su enseñanza y aprendizaje.
Para el análisis de datos, en este caso, se emplearon técnicas cuantitativas. En la tabla del anexo IV se presentan las variables, y sus correspondientes modalidades, formuladas para este estudio.
3.2.1 Presentación y discusión de resultados
La confiabilidad de los registros se cuantificó por el cálculo del coeficiente alfa (α) de Cronbach (Cronbach, 1996; Silveira, 1993, 1996, 1997).El paquete SSPS 11.5 permite calcular un coeficiente alfa corregido, que es el coeficiente de correlación entre el puntaje en cada ítem con el con el que se obtendría si ese ítem fuese eliminado. Este coeficiente es más aconsejable que el que se calcula sin excluir el ítem, porque el puntaje total ya lo incluye.
Para nuestro estudio, las variables que permiten obtener un α ≈ 0,7 son: CONCEPCIÓN DE DIFICULTAD PARA EL APRENDIZAJE DE LA MATEMÁTICA; EXPLICACIÓN DEL PROFESOR; ACTITUD FRENTE A LOS ERRORES; ELECCIÓN DE CARRERAS UNIVERSITARIAS VINCULADAS CON LA MATEMÁTICA; CONCEPCIÓN DE LA IMPORTANCIA DE APRENDIZAJE DE LA MATEMÁTICA; INTERÉS POR EL APRENDIZAJE DE LA MATEMÁTICA; RELACIÓN CON EL PROFESOR; APRENDER MATEMÁTICA ES APRENDER UN CONJUNTO DE FORMULAS, REGLAS Y PROCEDIMIENTOS DE CALCULO; LA MATEMÁTICA ES UNA DISCIPLINA FRÍA, POCO CREATIVA Y CERRADA; PARA LA MATEMÁTICA SE NACE; PERFIL DEL ALUMNO COMO ESTUDIANTE.
El análisis factorial se realizó con el paquete estadístico SPAD 3.5. (Cisia- Ceresta, 1998) La técnica de reducción factorial es una herramienta de estadística descriptiva que proporciona una simplificación y síntesis de la información y permite analizar las principales conjunciones-oposiciones entre las variables y los individuos mediante procesos de clasificación. En primer lugar aplicamos un Análisis de Correspondencias Múltiples, y luego una Clasificación sobre coordenadas factoriales.
Para el análisis factorial se tomaron como activas las variables: CONCEPCIÓN DE LA DIFICULTAD DEL APRENDIZAJE DE LA MATEMÁTICA, EXPLICACIÓN DEL PROFESOR, CONCEPCIÓN DE LA IMPORTANCIA DEL APRENDIZAJE DE LA MATEMÁTICA, INTERÉS POR EL APRENDIZAJE DE LA MATEMÁTICA, APRENDER UN CONJUNTO DE FÓRMULAS, PERFIL DEL ALUMNO. Con las variables mencionadas se acumula en los tres primeros factores el 62% de la varianza explicada. Las demás variables se tomaron como ilustrativas. Debemos señalar que la determinación de los elementos activos es una elección importante que debe realizar el investigador, y esta elección obedece a condiciones de homogeneidad y exhaustividad de las variables (deben pertenecer a un mismo tema o punto de vista, y describir completamente el tema).
Luego del análisis factorial, se realizó una clasificación para encontrar una posible tipología de los sujetos encuestados. La clasificación es inductiva y se basa en la búsqueda de semejanzas. Se parte de los individuos (en nuestro caso de estudiantes) y se procede por agrupamientos sucesivos, tratando de descubrir tras los detalles, las grandes líneas que describen al conjunto. Este método de clasificación ascendente origina clases politéticas (Benzécri, 1980). Es decir, las clases no se forman por la estricta conjunción lógica de propiedades correspondientes a todos los sujetos que las componen (clase monotética), sino por aquellos con un alto grado de semejanza (clase politética). Se busca una partición del conjunto de estudiantes en partes bien separadas y que a su vez reúna a los más próximos entre sí, a partir de sus distancias en una representación espacial.
La metodología para construir una tipología no consiste en la mera aplicación mecánica de los procedimientos apropiados, es un trabajo recursivo, que requiere de la consideración de varias alternativas hasta lograr una, que resulte satisfactoria por su coherencia lógica. En este caso se seleccionó una partición en tres clases y nuestro análisis fue realizado con relación a esta partición óptima. Las clases tienen asociadas ciertas características que se detallan a continuación.
La clase 1 reúne al 27% de los individuos, a ella pertenecen los sujetos que denominamos "Independientes del profesor". Todos los individuos de esta clase se caracterizan por reconocerse curiosos con relación al aprendizaje de la Matemática e independientes del profesor, es decir les gusta aprender cosas nuevas y realizar preguntas sobre temas que van mas allá de los tratados en clase, buscando resolver ellos mismos los problemas propuestos sin depender del docente. Posiblemente como se trata de estudiantes comprometidos con su aprendizaje no se ciñen únicamente a las explicaciones del profesor aunque aproximadamente el 80% de esta clase casi siempre entiende las explicaciones recibidas y no tiene dificultades en Matemática. Este tipo de estudiante considera importante aprender Matemática (90%), esta buena predisposición parecería estar vinculada con la elección de carreras universitarias relacionadas con la Matemática (60%). Por otro lado quienes componen la clase consideran que la Matemática no es una disciplina, fría, cerrada y poco creativa (80%).
La clase 2 reúne al 56% de los sujetos encuestados y la hemos denominado "Dependientes del profesor". Todos los individuos que conforman esta clase se identifican con la modalidad que expresa la dependencia del profesor. Es decir, necesitan que el profesor les explique y les diga qué tienen que hacer y cómo tienen que hacerlo, y tratan de seguir los procedimientos realizados por el docente, ellos manifiestan que cuando resuelven y corrigen las tareas con el profesor se sienten seguros. Podría decirse que como es frecuente observar en el ámbito escolar, estos sujetos tratan de "responder" a las demandas del profesor. Reconocemos en este grupo a un tipo de estudiante que coloca fuera de él la responsabilidad del aprendizaje, transfiriendo esta responsabilidad al docente. Alrededor del 70% de los sujetos de la clase manifiestan que no elegirían una carrera vinculada con la Matemática. En este grupo la motivación estaría casi exclusivamente vinculada con aprobar la asignatura.
La clase 3 reúne al 17% de los individuos y la denominamos "Despreocupados por aprender Matemática". Todos los individuos de esta clase se caracterizan por declarar su despreocupación por aprender Matemática. El 90% manifiesta no estar interesado en aprender Matemática. El 75% casi nunca entiende las explicaciones del profesor y además el 82% casi nunca pide explicación al profesor sobre los errores que comente, lo cual es otro indicador de despreocupación. Estos resultados son compatibles con la decisión de no elegir carreras vinculadas con la Matemática que el 80% de los individuos de esta clase manifiesta. El 60% considera que la Matemática es una disciplina fría, cerrada y poco creativa.
Las modalidades de la variable AÑO ESCOLAR no caracterizan a ninguna de las clases anteriores, lo cual permite inferir que la tipología es independientemente de la evolución escolar de los sujetos. Esto estaría indicando un fenómeno propio de la institución alumno y de la institución profesor: la dependencia del alumno de las explicaciones del profesor.
Con el objetivo de visualizar algunas de las relaciones existentes entre las variables se presentan gráficos obtenidos a partir de la tabla de contingencias de Burt, que permite analizar como se construyen las modalidades de una variable en términos de las modalidades de cada una las variables restantes.
El alumno y sus ideas sobre el aprendizaje de la Matemática
Los gráficos que se presentan a continuación describen la relación entre el perfil de alumno (Independiente, Dependiente, Despreocupado) y las variables que describen su concepción acerca del aprendizaje de la Matemática.
El Gráfico 2 muestra cómo se desagregan las modalidades de la variable PERFIL DE ALUMNO con respecto a las modalidades de la variable AÑO ESCOLAR. Se puede advertir que las 3 modalidades de la variable PERFIL DE ALUMNO se hallan presentes en los 4 años escolares en aproximadamente la misma proporción. Por ejemplo, los estudiantes identificados como dependientes del profesor constituyen entre el 51% y 61% de los sujetos de cada año escolar. Estos resultados se corresponden con lo expuesto en párrafos anteriores: el año escolar no caracteriza a ninguna de las clases en la clasificación que se presentó anteriormente. Entonces, a lo largo del tránsito por la educación media, la enseñanza de la Matemática no produciría modificaciones en el perfil del alumno que se traduzcan en el desarrollo de una mayor autonomía para estudiar Matemática, esto no puede ser analizado con independencia de las restricciones institucionales en juego que determinan la praxeología del profesor y el papel del alumno.

Gráfico 2 - Perfil de los alumnos y Año escolar
Aparentemente, la concepción de dificultad en el aprendizaje de la Matemática varía según se trate de un estudiante autónomo para el estudio o no. En el Gráfico 3 se muestra que el 88% de los estudiantes Independiente no tendrían dificultad en Matemática, mientras que para los Dependientes y Despreocupados más de la mitad tiene dificultad.

Gráfico 3 - Perfil de los alumnos y concepción de dificultad
En el Gráfico 4 podemos observar que el 90% de los estudiantes que se identifican con el perfil de alumno Despreocupado no tiene interés por aprender Matemática. Entre los estudiantes que se perciben como Dependientes del profesor, también el interés por aprender Matemática es bajo, siendo los Independientes quienes tendrían mayor interés por aprender este campo de conocimiento.
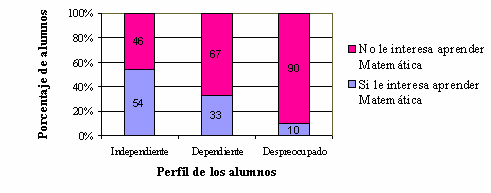
Gráfico 4 - Perfil de los alumnos e interés por el aprendizaje de la Matemática
El Gráfico 5 muestra que aunque el interés sea escaso, un muy elevado porcentaje -más del 82 % de los estudiantes que se identifican con los perfiles Independiente y Dependiente del profesor consideran que es importante aprender Matemática. Coincidentemente, el 79% del total de sujetos encuestados considera importante aprender Matemática, lo cual indicaría que en la educación media, el saber matemático se encuentra valorizado aunque no resulte interesante.

Gráfico 5 - Perfil de los alumnos y concepción de la importancia del aprendizaje de la Matemática
Alumnos y algunos mitos sobre el saber matemático
Los gráficos que se presentan a continuación muestran la relación entre la tipología y la concepción que tienen los estudiantes acerca del saber matemático.
En el Gráfico 6 podemos observar que independientemente del perfil de los estudiantes, más del 65% coincide en indicar que aprender Matemática es aprender un conjunto de fórmulas, reglas y procedimientos de cálculo. Estos resultados sugieren considerar que la concepción de los profesores sobre el saber Matemático, que subyace a las praxeologías que implementan, explicaría las ideas de los alumnos.

Gráfico 6 - Perfil de los alumnos y concepción de que aprender Matemática es aprender un conjunto de fórmulas
En el Gráfico 7 observamos que los alumnos que se identifican con los perfiles Independientes y Dependientes del profesor, no consideran a la Matemática como una disciplina fría, cerrada y poco creativa. Por el contrario, los Despreocupados si la consideran fría y poco creativa, lo cual se corresponde con las características de este perfil de alumno.

Gráfico 7 - Perfil de los alumnos e idea de que la Matemática es una disciplina fría
Alumnos y algunos mitos sobre la enseñanza de la Matemática
Los gráficos que se presentan a continuación muestran la relación entre la tipología y la concepción que tienen los estudiantes acerca de la utilización de algunos recursos para la enseñanza de la Matemática.
En el Gráfico 8 se puede observar que independientemente, de la tipología considerada, aproximadamente el mismo porcentaje de estudiantes coincide en que resultaría más beneficioso el aprendizaje de la Matemática mediante situaciones de la vida cotidiana. Esto reafirma en el espacio del alumno, lo señalado por Chevallard (1999) acerca de los mitos pedagógicos asumidos por los profesores. Nos preguntamos entonces ¿cuál es el origen de esta mitología que también estaría presente en los alumnos? Sobre todo, porque el trabajo con las llamadas situaciones de la vida cotidiana remitiría a una idea de sentido común que vincula linealmente al conocimiento escolar con su utilidad para "la vida". Esta mitología parece nacer desde lugares muy alejados del sistema de enseñanza, desde donde se piensa su funcionamiento, pero aunque los profesores la sientan como una demanda que se agrega a sus obligaciones, su realización parece de difícil concreción. ¿Qué se entiende por situaciones de la vida cotidiana? ¿Se reconoce que buena parte de los problemas así llamados son imposibles de abordar en un contexto escolar? ¿Se entiende que ninguna ciencia estudia directamente la realidad sino que modela y recorta los problemas para convertirlos en fenómenos que puedan estudiarse? Por ejemplo, para calcular la velocidad con que llega al piso una hoja que cae de un árbol se precisan tener en cuenta numerosos factores, que escapan al simple cálculo. Destacamos que los profesores de la escuela media también coinciden en que la enseñanza de la Matemática deben utilizarse situaciones de la vida cotidiana, aunque si analizamos las organizaciones didácticas de los profesores advertimos que esto no se pone en práctica. (Corica, 2007). Sería relevante considerar las concepciones de los estudiantes y profesores sobre las llamadas situaciones de la vida cotidiana, y problematizar cuáles admitirían un tratamiento didáctico adecuado.

Gráfico 8 - Perfil de los alumnos y enseñanza de la Matemática a partir de situaciones de la vida cotidiana
El Gráfico 9 muestra que alrededor del 60% de los estudiantes de las tres tipologías coinciden en que el uso de herramientas informáticas sería más beneficioso para aprender Matemática. Analizamos la adhesión de los estudiantes a este mito que se atribuye a los profesores, en los mismos términos mencionados antes sobre la utilidad del conocimiento escolar y sobre las restricciones que provienen de demandas sociales dirigidas a la institución escolar y que están muy alejadas de las posibilidades concretas del profesor de Matemática en su clase. Por otro lado, en un trabajo sobre las ideas de los profesores de Matemática y su práctica didáctica encontramos que aunque adhieren al mito, no usan herramientas informáticas (Corica, 2007), lo cual indicaría que la coincidencia entre profesores y estudiantes esta enraizada en una demanda social que se agrega a las restricciones ya existentes.

Gráfico 9 - Perfil de los alumnos y enseñanza de la Matemática a partir de herramientas informáticas
En síntesis
- El Estudio I puso de manifiesto la dependencia que existiría entre los estudiantes y las explicaciones del profesor, resultado que se confirma en el Estudio II. En cuanto a la enseñanza - aprendizaje de la Matemática sólo una minoría de alumnos se sentiría autónomo para aprender esta disciplina. Así, en todo en nivel medio encontramos un alto porcentaje de sujetos que sólo tratan de responder a las demandas del profesor y colocan fuera de ellos la responsabilidad de aprender, trasfiriéndosela al docente. Esto último también podría indicar que los estudiantes también subestiman sus propias capacidades y consideran que el docente es una fuente cierta de conocimiento. Estos resultados dan sustento al hecho de que los alumnos, atribuyen como principal tarea del profesor la de "explicar" los conocimientos en la forma más exhaustiva y detallada posible, de lo cual a su vez, hacen depender que el estudiante "entienda" y "aprenda".
- Los estudiantes de Nivel Medio consideran, sostienen y demandan al profesor su papel de "explicador" quien debe centrar la mayor parte de su actividad en explicarles. La tarea del profesor es "iluminar" los conceptos, como si los objetos matemáticos estuviesen en un lugar oscuro y fuese necesario echar luz sobre ellos para "verlos". De esta forma, el topos del alumno en el proceso de estudio acaba siendo reducido, por los mismos alumnos.
- Un elevado porcentaje de alumnos encuestados considera que estudiar Matemática consiste en aprender un conjunto de reglas, fórmulas y procedimientos de cálculo. Tales reglas no se derivan de la construcción y desarrollo de técnicas sustentadas en un logos tecnológico - teórico. Los estudiantes se perciben sólo como usuarios de fórmulas previamente elaboradas y auto evidentes, y no como desarrolladores de técnicas. En la escuela las fórmulas se memorizan, se aplican, pero difícilmente se ofrece la oportunidad de construirlas. Así se genera una fuerte dependencia de las fórmulas, que inhibe la búsqueda de procedimientos alternativos, personales, "informales" y que anula el cuestionamiento de las técnicas como cimiento para el desarrollo de otras y como instrumento para su validación a partir del bloque teórico. Este hecho ha sido bien establecido en la Teoría Antropológica de lo Didáctico (Chevallard, 1999): el bloque técnico, como por ejemplo la aplicación de fórmulas y reglas, y la realización de cálculos, suelen prevalecer en las organizaciones didácticas escolares.
- El estudio II pone en evidencia que los estudiantes de la Escuela Media valorizan el saber Matemático, posiblemente, debido a que existe un reconocimiento social hacia dicho saber. Sin embargo, muy pocos manifiestan interés en aprender Matemática. Este resultado coincide con lo anticipado en el Estudio I: el interés de los estudiantes por aprender Matemática, se centra en aprobar la materia.
4. Conclusiones Finales
- Los estudios realizados permiten afirmar que, según los estudiantes de escuela media, la actividad principal del profesor se encuadra en lo que denominamos la Metáfora del Profesor Explicador: un profesor cuyo rol sería el de "iluminar" los conceptos para que los estudiantes puedan "verlos". Mientras que la actividad del alumno se resume en la Metáfora del Estudiante dependiente del Profesor. Una característica esencial de este estudiante es su necesidad de que el profesor le diga todo lo que debe hacer.
- La metáfora del profesor explicador y del estudiante dependiente del profesor parecen alimentarse mutuamente. Sin embargo, la función del profesor tal como es vista por los alumnos obedece a que ellos han sido expuestos a este modelo que genera su dependencia por un tiempo muy prolongado. En este sentido, nuestros resultados son compatibles con investigaciones que señalan que el perfil cognitivo de los estudiantes de secundaria es mayoritariamente reflexivo y teórico, poco creativo y poco activo, siendo esto una consecuencia de la forma de enseñanza predominante en la escuela (Alonso, Gallego, Honey ,1995).
- Los resultados de los estudios I y II conducen directamente al análisis de la actividad del profesor. El fracaso escolar en Matemática -detectado en toda la escolaridad media por diversas investigaciones y reconocido por docentes, de los estudiantes que intervinieron en nuestro proyecto de investigación (Corica, 2007)- no consiste en que los alumnos desaprueben los exámenes, sino en la resignación y desvalorización de los profesores acerca del saber: los estudiantes aprueban contenidos que tienen poca relevancia. Esto confirma la validez de que la conciencia didáctica de los profesores esta cerrada (Bosch et. al., 2003) y que por lo tanto, ellos no consiguen ver que el fracaso de los estudiantes está relacionado con la forma en que se enseña, sino que lo atribuyen a factores exógenos.
- Es evidente entonces, que el fracaso de los estudiantes se encuentra vinculado con las praxeologías didácticas que viven en la institución escuela. Esta situación nos conduce al problema del cambio, urgente y necesario, de dichas praxeologías. Los involucrados directamente en este cambio serían los profesores, quienes deberían modificar su perfil de profesor, identificado con la Metáfora del Profesor Explicador, por la Metáfora del Profesor Cuestionador: un profesor predispuesto a cuestionar a los estudiantes, creando en el aula un ámbito donde el profesor plantee preguntas interesantes y no se limite sólo a explicar conceptos; las cuestiones son y deben ser las que despierten el interés por conocer. Pero esto también nos enfrenta a cuestiones como ¿qué posibilidades de sobrevivir en una institución escolar tiene un profesor, que se identifique con la Metáfora del Profesor Cuestionador? Seguramente este profesor se encuentre implicado en un gran esfuerzo, tratando de lidiar con la oposición de sus estudiantes a la innovación, quienes también se ven afectados directamente, inmersos en un gran esfuerzo, tratando de adoptar un nuevo perfil de estudiante: independiente del profesor.
- Si bien es cierto que el sistema impone restricciones muy fuertes al oficio del profesor, no es menos cierto que ningún cambio profundo puede hacerse sin ellos. Los alumnos también se encuentran implicados, pero en un cambio de las praxeologías discentes. Nuestra línea de investigación se orienta a tratar estas cuestiones en el Nivel Medio y los primeros dos años de la Universidad: la inserción de un nuevo modelo didáctico que implica un "nuevo" profesor y alumno.
1 El fracaso de los estudiantes puede mirarse desde diversas perspectivas (Cabrera, et. al, 2006). En nuestro caso es interpretado en un sentido amplio, en términos del saber matemático, las competencias y habilidades que efectivamente deben adquirir los alumnos para lograr una formación de calidad.
2 Transcripciones personales de los estudiantes sobre sus vivencias en las clases de Matemática.
3 Término que agrupa a una clase de manifestaciones según una regla de correspondencia unívoca.
4 Conversar viene del latín conversare y significa dar vueltas junto con otros.
5 Metacategoría: término general que engloba a otros (categorías) y que hacen referencia, de forma más específica, al mismo. Del mismo modo son interpretadas las categorías respecto de las subcategorías.
La encuesta
Edad................. Facultad: .................
Elegí solo una opción, marcando con un óvalo la respuesta.
1. ¿Te parece difícil la Matemática? Si No
2. ¿Cuánto tiempo por día dedicás al estudio de la Matemática, comparado con otras materias?
Igual que a todas Más Menos
3. Cuando tu actual profesor de Matemática explica un tema ¿Le entendés? Casisiempre Casi nunca
4. Cuando te equivocás en Matemática, ¿Le pedís al profesor que te explique las causas del error?
Casi siempre Casi nunca
5. ¿Elegirías una carrera universitaria vinculada a Matemática? SiNo
6. ¿Crees que es importante aprender Matemática? Si No
7. ¿Te sentís interesado por aprender Matemática? Si No
8. ¿Cómo ves tu relación con el profesor de Matemática?
a) Siento que tengo el compromiso de entender y hacer las cosas que pide, porque el profesor es muy simpático y bueno con nosotros.
b) Siento que debo prestar atención y hacer las cosas, porque el profesor es quien manda, y hay que obedecer.
c) Siento que todos le debemos prestar atención y hacer las cosas porque nuestro mayor interés es construir conocimiento matemático.
9. ¿Estás de acuerdo o en desacuerdo con cada una de las siguientes frases?

10. Identifica con una cruz con cuál de los siguientes chicos te identificas más: A, B, C.
A) Soy muy curioso/a y me encanta aprender cosas nuevas. Me agradan mucho las clases de Matemática y siempre pregunto cosas que no se dan en clase. Cuando me dan ejercicios disfruto si puedo resolverlos de un modo creativo. Generalmente me va bien en las pruebas.
B) Me cuesta mucho aprender Matemática pero me preocupo y presto atención en clase. Me gusta que el profesor me explique claramente todo y que me diga lo que tengo que hacer y cómo hacerlo, trato de seguir los procedimientos que realiza para resolver los ejercicios. Al resolver y corregir esos ejercicios con el profesor, me siento seguro de mí mismo. A veces apruebo los exámenes.
C) No me agradan las clases de Matemática, no me parecen interesantes, por lo que en general no presto atención. Soy muy distraído, estudio muy poco y suelo faltar bastante, por lo que casi siempre me va mal en las evaluaciones.

Las categorías
A continuación se describen las categorías que se originaron a partir del estudio de los Diarios
1. Referencias al Profesor
Se refiere a las opiniones de los estudiantes acerca del profesor de Matemática.
1.1. Explicación. Actitudes frente a las explicaciones realizadas, por el profesor, de los contenidos.
1.1.1- Desagrado. Razones por las que los estudiantes sienten desagrado a las explicaciones recibidas.
1.1.1.1- Incomprensión. A estos estudiantes les desagradan las explicaciones dadas por sus profesores. Consideran que no entienden el vocabulario que emplea y no comprenden los procedimientos que lleva a cabo cuando resuelve tareas en el pizarrón.
1.1.1.2- Desgano. Estos estudiantes indican que al solicitarle al profesor reiteradas explicaciones de conceptos ya estudiados, éste lo hace con desgano y eso los desanima.
1.1.2- Agrado. Los alumnos manifiestan que les agradan las explicaciones del profesor cuando explica bien. Consideran que si a ellos se les explica bien, entienden.
1.2- Críticas a las calificaciones. Todas las manifestaciones de los estudiantes sobre las calificaciones se refieren a desacuerdos con la calificación asignada. Los estudiantes señalan que se aprueba a aquellos alumnos que no trabajan en el aula. También, indican su disconformidad con respecto a la anulación de las calificaciones, cuando hay demasiadas evaluaciones desaprobadas, siendo que ellos aprobaron.
1.3. Propuestas de clase. Las clases de Matemática son más organizadas cuando el profesor propone trabajar con fotocopias.
1.4. Incumplimiento, del profesor, en sus tareas. Recoge las manifestaciones, de los estudiantes, acerca del incumplimiento, por parte del profesor, en sus tareas.
1.4.1. Inasistencia del profesor. Los estudiantes manifiestan disconformidad con los profesores que no cumplen los horarios porque a raíz de esto "no se hace nada en la clase". También, a los estudiantes les desagrada el cambio de un profesor por otro, dicen que deben adaptar a otra persona, con otras formas de trabajar.
1.4.2. Entrega de evaluaciones. Estos estudiantes se sienten molestos cuando se demora en la entrega de las evaluaciones corregidas.
2. La clase de Matemática
Se refiere a las experiencias de los estudiantes en las clases de Matemática.
2.1 Cómo se aprende en Matemática. Recoge las manifestaciones, de los estudiantes, con respecto al primer encuentro con el saber matemático.
2.1.1. Ayuda de compañeros. Entienden Matemática cuando les explican sus compañeros.
2.1.2. Necesidad del profesor. Necesitan que el profesor les explique los conceptos, todas las veces que sea necesario y en lo posible, empleando ejemplos.
2.2- Tareas propuestas por el profesor. Indica las experiencias de los estudiantes acerca de las tareas propuestas por el profesor.
2.2.1- Puede realizar las tareas. Estos estudiantes pueden realizar las tareas sin dificultad porque consideran que comprenden.
2.2.2- Dudas en algunas tareas. Estos estudiantes tienen dudas para poder realizar las tareas y por esta razón no pueden culminarlas solos.
2.2.3- No puede realiza la tarea. Estos estudiantes manifiestan no poder realizar las tareas porque no entienden la consigna y optan por recurrir al docente.
2.2.4- Falta de tiempo. Los estudiantes se sienten preocupados por el poco tiempo que queda para ejercitar -en clase- antes de la evaluación programada.
2.3 Corrección de errores. A estos estudiantes les interesa que se corrijan las tareas en el pizarrón porque consideran que los ayuda a comprender y a tener todas las tareas resueltas.
2.4. Actitudes en las clases de Matemática. Hace referencia a las actitudes de los estudiantes en la clase de Matemática.
2.4.1 Aburrimiento. Razones por las cuales los estudiantes se sienten aburridos en la clase de Matemática.
2.4.1.1 Cuando entienden. Se aburren cuando el profesor no propone tareas para realizar.
2.4.1.2 Cuando no entienden. Se aburren cuando no entienden los conceptos.
2.4.1.3 Cuando el profesor no indica ninguna tarea. Se aburren cuando no tienen tareas para realizar.
2.4.2- Agrado por la Matemática. Razones por las que, a los estudiantes, les gustan las clases de Matemática.
2.4.2.1- Trabajo en grupo. Les gusta Matemática cuando trabajan en grupo porque pueden ayudarse entre ellos.
2.4.2.2- Comprensión ante una primera explicación. Les gusta Matemática cuando comprenden a partir de la primera explicación dada por el profesor.
2.4.2.3- Tarea. Les gusta las clases de Matemática cuando tienen tareas para realizar.
1. La Evaluación
Se refiere a las manifestaciones de los estudiantes, acerca de las evaluaciones propuestas por el profesor.
3.1- Actitud frente a la evaluación realizada. Hace referencia a las especulaciones que realizan los estudiantes, acerca de las evaluaciones escritas realizadas.
3.1.1- Desaprobación. Estos estudiantes saben cuando desaprueban.
3.1.2. Aprobación. Estos estudiantes saben cuando aprueban.
3.1.3 Concepción incorrecta de resultados. Estos estudiantes, al finalizar la evaluación, aseguran que aprueban pero ocurre lo contrario.
3.2. Evaluación propuesta. Registra las manifestaciones de los estudiantes acerca de las tareas propuestas para ser evaluados.
3.2.1 Tareas distintas a las propuestas en clase. Estos estudiantes indican que en la evaluación, se proponen tareas distintas a las trabajadas en clase.
3.2.2 Dudas al realizar algunas tareas de la evaluación. Estos estudiantes llegan con dudas, a las instancias de evaluación.
3.2.3 Evaluación de prácticos. Estos estudiantes consideran útil calificar los trabajos prácticos porque les es útil para su control y para tener una nota más.

Bibliografía
1. ALONSO, C., GALLEGO, D. y HONEY, P. (1999). Los estilos de aprendizaje: procedimientos de diagnósticos y mejora. Universidad de Deusto. Madrid: Ed. Mensajero. [ Links ]
2. AUSUBEL, D. (1963). The psychology of meaningful verbal learning. New York: Grune and Stratton. [ Links ]
3. AUSUBEL, D. (1968). Educational psychology: a cognitive view. New York: Holt, Rinehart and Winston. [ Links ]
4. AUSUBEL, D.(1976). Psicología educativa: un punto de vista cognoscitivo. México: Editorial Trillas. Traducción al español de Roberto Helier D., de la primera edición de Educational psychology: a cognitive view. [ Links ]
5. BADANO, C. y DODERA, M. (1999). Un estudio de la influencia de la representación de la matemática en el rendimiento académico del alumno de primer año de la universidad. Educación Matemática, 11(3), 79-88. [ Links ]
6. BENZÉCRI, J. (1980) Practique de l'Anályse des Donneés T 1 y 2. Paris: Dunod. [ Links ]
7. BOLEA P., BOSCH M., Y GASCÓN J. (2001). La transposición didáctica de organizaciones matemáticas en proceso de algebrización: el caso de la proporcionalidad. Recherches en Didactique des Mathématiques, 21 (3),.247-304. [ Links ]
8. BOSCH, M. ESPINOZA, L. y GASCÓN, J. (2003). El profesor como director de procesos de estudios. Análisis de organizaciones didácticas espontáneas. Recherches en Didactique des Mathématiques, 23(1), 79 - 136. [ Links ]
9. BRANEN (1992); Combining Qualitative and Quantitative approaches: an overview en J. Brannen (ed.) Mixing Methods: Qualitative and Quantitative Research, Aldershot, Avenbury. [ Links ]
10. CABRERA, L. ; BETHENCOURT, J. M.; PÉREZ, P. A. ; GONZÁLEZ AFONSO M. (2006); El problema del abandono de los estudiantes universitarios; RELIEVE.12(2). España. [ Links ]
11. CHEVALLARD, Y (2002a); Organiser l' étude 1. Structures et fonctions. In Dorier J. - L. et al. (eds) Actes de la 11 École d'Été de didactique des mathématiques - Corps - 21 - 30 Aoüt 2001 (pp. 3 - 22) Grenoble : La Penseé Sauvage. [ Links ]
12. CHEVALLARD (2002b); Organiser l' étude 3. Écologie & régulation. In Dorier J. - L. et al. (eds) Actes de la 11 École d'Été de didactique des mathématiques - Corps - 21 - 30 Aoüt 2001 (pp. 41 - 56) Grenoble: La Penseé Sauvage. [ Links ]
13. CHEVALLARD (2000); La recherche en didactique et la formation desprofesseurs: problématiques, concepts, probléms. In Bailleul M. (ed) Actes de la X° École d'été de didactique des mathématiques (Houlgate, 18 - 25 aoüt 1999) (pp. 98 - 112). Caen: ARDM et IUFM de Caen. [ Links ]
14. CHEVALLARD, Y; (1999) El análisis de las prácticas docentes en la teoría antropológica de lo didáctico. Recherches en Didactique des Mathématiques; 19(2), pp 221 - 266. [ Links ]
15. CISIA-CERESTA. SPAD. 3.5 (1998) integrado versión PC, Centre International de Statistique et d´Informatique Appliquées, Francia. [ Links ]
16. CORICA, A. (2007). El saber matemático, su enseñanza y su aprendizaje: la mirada de alumnos y profesores. Tesis de Licenciatura. Director: Otero, M R., Argentina: Editado por el Departamento de Formación Docente y NIECYT - Facultad de Ciencias Exactas - UNICEN. [ Links ]
17. CORICA, A. y OTERO, M. R (2005a). El desempeño escolar en Matemática y las representaciones de los alumnos. En Sagula y otros (Ed), Actas del VII SEM, Argentina. [ Links ]
18. CORICA, A.; OTERO, M. R. (2005b) Ideas de los profesores acerca de la Enseñanza Aprendizaje de la Matemática y Aprendizaje Significativo. En M. Moreira (Ed), Actas del I Encontro Nacional de Aprendizagem Significativo, Brasil. [ Links ]
19. CORICA, A., OTERO, M. y SUREDA, P. (2006). El saber matemático, su enseñanza y su aprendizaje: la mirada de alumnos y profesores. Acta Latinoamericana de Matemática Educativa. 19, México: Comité Latinoamericano de Matemática Educativa. [ Links ]
20. CRIVISQUI E. & VILLAMONTE G. (1997) Presentación de los métodos de análisis factorial de correspondencias múltiples. PRESTA Programme de recherche et d' enseignement en statistique apliqueé, Bruxelles, Belgique. [ Links ]
21. CRONBACH, L.J. (1996) Coefficient alpha and the internal structure of tests. In: MEHRENS, W. A. e EBEL, R. L. (org.) Principles of educational and psychological measurement. Chicago: Rand McNally, 1967. Fundamentos da testagem psicológica. Porto Alegre: Artes Médicas. [ Links ]
22. GASCÓN, J. BOSCH, M. y BOLEA, P. (2001). ¿Cómo se construyen los problemas en didáctica de las matemáticas?. Educación Matemática, 13 (3), 22 -63. [ Links ]
23. GRECA, I. (2002). Avaliando A Qualidade Da Pesquisa Na Área Em Ensino De Ciências: Algumas Questões Metodológicas Para Refletir. Revista Brasileira de Pesquisa em Educação em Ciências, 2(1) 73-82. [ Links ]
24. LEBART, L.y MORINEAU A. SPAD (1994). Systéme portable d'Anályse des Données Numeriques, CISIA, Saint Mandé [ Links ].
25. LEBART, L. MORINEAU, A. y FENELON J.P. (1985). Tratamiento estadístico de datos. Barcelona: Editorial Marcombo. [ Links ].
26. MIGUEZ ESCORCIA, M. (2003). El rechazo hacia las Matemáticas, una primera aproximación. Acta Latinoamericana de Matemática Educativa, 17, 292 - 298. [ Links ]
27. MOREIRA M. A. (2000) Subversive meaningful learning. Actas del III Encuentro Internacional sobre Aprendizaje Significativo, 33-45, Lisboa. [ Links ]
28. OTERO, M. FANARO, M. y ELICHIRIBEHETY, I. (2001). El conocimiento Matemático de los Estudiantes que ingresan a la Universidad; Revista Latinoamericana de Investigación en Matemática, 4(3), 267 - 287. [ Links ]
29. SILVEIRA, F. L. (1993) Validação de testes de papel e lápis. In: MOREIRA, M. A. e SILVEIRA, F.L. Instrumentos de pesquisa em ensino e aprendizagem. Porto Alegre: EDIPUCRS. [ Links ]
30. SILVEIRA, F. L. (1996) Relação do desempenho no concurso vestibular da Universidade Federal do Rio Grande do Sul com diversas variáveis. Estudos em Avaliação Educacional, 14, 83-103. [ Links ] Las ideas de algunos estudiantes acerca de la enseñanza - aprendizaje de la Matemática en el Nivel Medio Ana Rosa Corica, María Rita Otero REIEC Revista Electrónica de Investigación en Educación en Ciencias Año 2 - Número 1 -julio de 2007-Página 61
31. SILVEIRA, F. L. (1997) Comparação entre três argumentos de concorrência para o concurso vestibular da Universidade Federal do Rio Grande do Sul. Estudos em Avaliação Educacional, 16, 43-57. [ Links ]














