Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Geoacta
versión On-line ISSN 1852-7744
Geoacta vol.38 no.2 Ciudad Autónoma de Buenos Aires dic. 2013
TRABAJOS DE INVESTIGACIÓN
La elección de días geomagnéticamente tranquilos
The choice of the geomagnetically quiet days
María Andrea Van Zele
IGeBA de CONICET en Facultad de Ciencias Exactas y Naturales (UBA) Facultad de Ciencias Exactas y Naturales - Departamento de Ciencias Geológicas Ciudad Universitaria - 1428 Buenos Aires - Argentina avanzele@gl.fcen.uba.ar
RESUMEN
Las variaciones geomagnéticamente tranquilas en latitudes bajas y medias son aquellas debidas al movimiento de iones y electrones en la región E ionosférica. Para el estudio de estas variaciones (Sq), de perturbaciones y de tormentas, es necesario identificar cuáles días pueden considerarse tranquilos. El objetivo del trabajo es poner en evidencia la presencia de variaciones debidas a diferentes causas en algunos de los 5 días más tranquilos de un mes (aún con el mismo nivel de perturbación geomagnética) y mostrar que la identificación de esos días (Q) es conveniente hacerla para cada caso en particular.
Palabras claves: Variaciones geomagnéticas tranquilas; Sq; Criterios de selección.
ABSTRACT
Quiet geomagnetic variations in low and middle latitudes are those due to the movement of ions and electrons in the ionospheric E region. To study these variations (Sq), disturbances and storms, it is necessary to identify which days may be considered as quiet. The aim of this work is to demonstrate the presence of variations due to different causes in some of the 5 quietest days a month (even with the same level of geomagnetic disturbance) and show that the identification of those days (Q) should be made for each particular case.
Key words: Quiet geomagnetic variations; Sq; Selection criteria.
INTRODUCCIÓN
Las variaciones geomagnéticamente tranquilas en latitudes bajas y medias son aquellas debidas al movimiento de iones y electrones en la región E ionosférica. Para el estudio de estas variaciones (Sq), de perturbaciones y de tormentas, es necesario identificar cuáles días pueden considerarse tranquilos. Los centros mundiales de datos estipulan cuales son los 5 días más tranquilos de cada mes en orden decreciente de tranquilidad; en ellos i) las variaciones son lentas, recurrentes y regulares, fácilmente reconocibles a partir de magnetogramas; ii) se observa una clara ausencia de variaciones de alta frecuencia lejos de la región auroral (Campbell, 1989).Sin embargo esto no sobreentiende que ellos sean igualmente tranquilos. El objetivo del trabajo es poner en evidencia la presencia de variaciones debidas a diferentes causas en algunos de los 5 días más tranquilos de un mes (aún con el mismo nivel de perturbación geomagnética) y mostrar que la identificación de esos días (Q) es conveniente hacerla para cada trabajo en particular.
En períodos de baja actividad solar la radiación incidente es más estable (medida por ejemplo con el índice F10.7 o sus derivados) (Yamazaki et al., 2011; Van Zele, 2013), las fulguraciones solares son menos numerosas (Van Zele and Meza, 2011) y el número de manchas solares (indicador de la eyección de partículas solares que alcanzarían a la magnetosfera, ingresarían en ella y la perturbarían) es menor; lo contrario sucede en intervalos de alta actividad solar. Por ello, si se buscan días de actividad geomagnética similar, los hay en mayor cantidad en años de baja actividad solar, y viceversa (Van Zele, 2013). Estudiando la amplitud de la componente Y entre las 6 y las 18 TU en días en que los Kp = 3+ en ese intervalo (considerada como Sq), a lo largo de 21 años, Takeda (2002) concluye que en cada mes, la dependencia de Sq a la actividad solar es causada por la conductividad local.
Es habitual utilizar índices de actividad geomagnética para identificar días Q; uno adecuado para observatorios en latitudes bajas y medias es el trihorario Km (Menvielle and Berthelier, 1991). El orden de los 5 días más tranquilos no necesariamente coincide con el orden creciente de ? Km, resultante de la suma de los 8 Km de ese día. También puede utilizarse el más antiguo Kp (Mayaud, 1980). Algunos autores eligen como Q los 5 días más tranquilos de cada mes y usan el promedio como representación correspondiente a ese mes, suponiendo que las pequeñas irregularidades que pueden ocurrir en días individuales están suavizadas en el promedio; otros usan los días en que la suma de los 8 Kp o de los 8 Km están por debajo de un nivel elegido; otros agregan además cotas para cada Kp o Km de ese día.
Para este trabajo se estudian las variaciones geomagnéticas de la componente norte X(t), este Y(t) y vertical hacia el centro de la tierra Z(t), de 5 observatorios de baja latitud. En cada día universal, son registrados 1440 valores (cada minuto del día universal: t ? [0, 1439]). A fin de eliminar la influencia de la corriente anillo simétrica y las corrientes de Chapman-Ferraro (Parks, 1991) se calculan sym X(t) y sym Y(t) a partir de los índices sym H(t) y sym D(t) (Iyemori et al., 2010):
Sym X(t) = symH(t).cos ?.sen (sym D(t)); sym Y(t) = sym H(t).cos ?.cos (sym D(t));
el factor cos ? considera la influencia de la corriente anillo (supuesta en el ecuador geomagnético) en la latitud del observatorio. Los valores de la medianoche local (Xo, Yo, Zo), se calculan como Xo = X(0) - sym X(0), Yo = Y(0) - sym Y(0), Zo = Z(0). Las variaciones diarias sin la contribución de las variaciones de la corriente anillo simétrica o de la magnetopausa, y medidas a partir del valor de la medianoche local resultan:
dX(t) = X(t) - sym X(t) - Xo; dY(t) = Y(t) - sym Y(t) - Yo; dZ(t) = Z(t) - Zo, (1).
En todos los casos el error considerado en los datos es de 1 nT. De ello resulta que las variaciones geomagnéticas de origen externo dX, dY, dZ, si correspondieran a un día Q, resultarían de los movimientos de las partículas cargadas en la región E ionosférica y las que ellas inducen en la corteza terrestre, si se hace caso omiso de las corrientes de las mareas lunisolares (de baja amplitud). En una localidad particular los días Q deben ser de apariencia similar, con pequeños cambios de forma a través de las estaciones del año (Campbell, 1989). Con el cambio de latitud la variación es evidente: dX es aproximadamente igual en ambos hemisferios mientras que dY y dZ son opuestos.
Una adecuada representación de Sq en baja actividad solar puede obtenerse con sólo 4 armónicos (Campbell, 1989): las componentes espectrales (n = 1, 2, 3, 4) correspondientes a períodos de 24, 12, 8 y 6 horas. Por ello sería adecuado representar a dX, dY y dZ (representadas por v en lasec. 2, 3 y 6) como (Chapman and Bartels, 1940) la síntesis v(t) de los coeficientes:

LOS DATOS
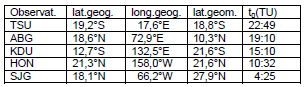
Los observatorios de baja latitud estudiados figuran en la Tabla 1, donde se indican las coordenadas y la hora (TU) de la medianoche.
Tabla 1: siglas IAGA de los observatorios, coordenadas y hora TU a la medianoche
Table 1: IAGA code for the observatories, coordinates and UT at midnight.
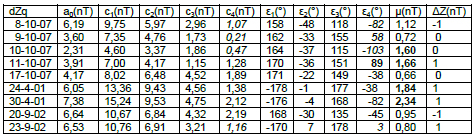
A modo de ejemplo se estudian los 5 días Q de octubre de 2007 (baja actividad solar), y días Q con valores de ? Km extremos en 2 meses de alta actividad solar (http://wdc.kugi.kyoto-u.ac.jp/); los valores de Km se reproducen en la Tabla 2 (http://isgi.cetp.ipsf.fr/). En todos los casos ninguno de los 8 Km de un día supera el valor 1-, que es el tercer valor más bajo de los 28 posibles.
Tabla 2: las columnas indican los días Q de octubre de 2007 y aquellos con valores de ?Km extremos para abril 2001 y setiembre 2002, los valores de los 8 Km en cada intervalo y la suma de ellos.
Table 2: the columns indicate the Q days for October 2007 and those ones corresponding to extreme values of ?Km for April 2001 and September 2002, the 8 Km corresponding and its sum.

METODOLOGÍA
Las figuras a continuación representan las variaciones diarias dXq, dYq o dZq (ec.1) en TU de los días elegidos como tranquilos en baja y alta actividad solar, calculadas para los observatorios de la Tabla 1; en cada par de figuras la ordenada tiene la misma escala a fin de evidenciar la variación de amplitud con el cambio de actividad. Las líneas verticales negras punteadas representan t=00:00 TL (medianoche); se han graficado con trazo grueso aquellos días que muestran variaciones no regulares o ?X, ?Y o ?Z (ec.7) que superen los 10 nT.
Las Tablas presentan los 5 primeros coeficientes de Fourier correspondientes a los desarrollos (ec.3 y 4) de las variaciones mostradas en las Figuras inmediatamente anteriores; en cursiva se han mostrados aquellos armónicos que no son importantes por ser las amplitudes menores que 1 nT (error considerado en los datos). En negrita se realzan aquellas variaciones que no pueden considerarse tranquilas: i) varianzas que evidencian la necesidad de considerar armónicos de mayor grado para una adecuada representación de la variación: en este trabajo se establece como cota para definir matemáticamente un criterio de tranquilidad que 2µ (ec.6) debe ser menor que cualquier coeficiente ci; ii) las amplitudes y fases deben mostrar una variación que responda a una corriente esperada para una capa a Chapman (Heargraves, 1992); iii) las fases deben ser similares; iv) ?X, ?Y o ?Z (ec.7) no deben superar los 10 nT.
Los parámetros del viento solar que pueden estar afectando a las variaciones geomagnéticas son Bz(IMF) y la presión del flujo, pues ellos condicionan el estado de la magnetosfera (Parks, 1991), el primero abriéndola, el segundo indicando la cantidad de partículas que pueden ingresar. En los días elegidos se observa que i) el 10-10-2001 en [2, 8] TU y [10, 19] TU Bz(IMF) < 0; ii) el 11-10-2007 en [19:30; 22] TU Bz(IMF) < 0; iii) el 17-10-2001 en [0, 1] Bz< 0; iv) el 24 -4-01 en [3, 9] TU Bz(IMF) < 0; v) del 30-4-2001 faltan datos y por lo tanto las variaciones irregulares no podrán asignarse a inestabilidades del viento solar; el 23-9-2002 en [2, 3] TU y [17, 19] TU Bz(IMF) < 0;en todos los casos la apertura es mínima y las variaciones de la presión también (http://cdaweb.gsfc.nasa.gov/cgi-bin/eval2.cgi).
Los efectos de las fulguraciones solares de intensidad media clasificadas como M pueden observarse (según la hora en que se producen) superpuestas a las Sq: i) los satélites GOES no las han registrado los días elegidos en baja actividad solar; en alta actividad i) en TSU: la del 24-04-2001 a las 12:38 TU (M16) en dXq y dYq; las del 20-9-2002 a las 05:08 TU (M15) y a las 09:21 TU (M18) en dY; ii) en ABG: la del 20-9-2002 a las 9:21 TU (M18) en dY; iii) en KDU: la del 24-4-2001 a las 22:14 TU (M18) en dY; iv) en SJG: la del 24-2-2001 a las 18:04 (M23) en dY; aunque pequeñas, contribuyen a la dispersión. El día 24-4-2001 se producen otras 2: a las 05:33 TU (M21) y a las 06: 53 TU (M31) que no pueden distinguirse dado que suceden en un intervalo perturbado (http://satdat.ngdc.noaa.gov/sem/goes/data).
En las Figuras 1 se han representado dXq (TSU) para los 5 días Q elegidos para baja actividad solar (a), y los 4 para alta (b). A lo largo del día local, regularmente, muestra un máximo previo al mediodía. Las variaciones no regulares de los días 10-10-2007 y 24-4-2001 podrían corresponderse al ingreso de partículas del viento solar. Las variaciones irregulares de dXq los días 11 y 17-10-2007, 30-4-2001 y 20-9-2002 no se relacionarían con Bz (IMF). La Tabla 3 indicaría que según dXq (TSU) el 9-10-07, 10-10-07, 17-10-07 y 23-9-02 son días Q.

Fig. 1: variaciones dXq en TSU: a) en baja actividad solar; b) en alta
Fig. 1: dXq variations at TSU: a) for low solar activity; b) for high solar activity
Tabla 3: coeficientes armónicos de dXq(TSU) para los 9 días Q elegidos
Table 3: harmonic coefficients ofdXq(TSU) for the 9 Q days.

En las Figuras 2 se han graficado las variaciones (ec.1) dYq (TSU) para a) baja y b) alta actividad solar; las variaciones no regulares de los días 10-10-2007 y 24-4-2001 podrían corresponderse al ingreso de partículas del viento solar. La Tabla 4 mostraría según dXq (TSU) el 8-10-07, 10-10-07, 17-10-07, 30-4-2001 y 20y23-9-02 son días Q.

Fig. 2: variaciones dYq en TSU: a) en baja actividad solar; b) en alta
Fig. 2: dYq variations at TSU: a) for low solar activity; b) for high solar activity
Tabla 4: coeficientes armónicos de dYq(TSU) para los 9 días Q elegidos
Table 4: harmonic coefficients ofdYq(TSU) for the 9 Q days.

En las Figuras 3 se han graficado las variaciones (ec.1) dZq (TSU) para a) baja y b) alta actividad solar; las variaciones no regulares de los días 10-10-2007 y 24-4-2001 podrían corresponderse al ingreso de partículas del viento solar. La Tabla 5 mostraría según dXq (TSU) que el 8-10-07, 9-10-07, 17-10-07 y 20-9-02 y 23-9-02 son días Q.

Fig. 3: variaciones dZq en TSU: a) en baja actividad solar; b) en alta
Fig. 3: dZq variations at TSU: a) for low solar activity; b) for high solar activity
Tabla 5: coeficientes armónicos de dYq(TSU) para los 9 días Q elegidos
Table 5: harmonic coefficients ofdYq(TSU) for the 9 Q days.
En las figuras 4, 5 y 6 se han representado respectivamente dXq (ABG), dYq (ABG) y dZq (ABG) para los 5 días Q elegidos para baja actividad solar (a) y los 4 para alta. Las Tablas 6, 7 y 8 indican los días Q según los criterios establecidos para los coeficientes de Fourier.

Fig. 4: variaciones dXq en ABG: a) en baja actividad solar; b) en alta
Fig. 4: dXq variations at ABG: a) for low solar activity; b) for high solar activity

Fig. 5: variaciones dYq en ABG: a) en baja actividad solar; b) en alta
Fig. 5: dYq variations at ABG: a) for low solar activity; b) for high solar activity

Fig. 6: variaciones dZq en ABG: a) en baja actividad solar; b) en alta
Fig. 6: dZq variations at ABG: a) for low solar activity; b) for high solar activity
Tabla 6: coeficientes armónicos de dXq(ABG) para los 9 días Q elegidos
Table 6: harmonic coefficients ofdXq(ABG) for the 9 Q days.

Tabla 7: coeficientes armónicos de dYq(ABG) para los 9 días Q elegidos
Table 7: harmonic coefficients ofdYq(ABG) for the 9 Q days.

Tabla 8: coeficientes armónicos de dZq(ABG) para los 9 días Q elegidos
Table 8: harmonic coefficients ofdZq(ABG) for the 9 Q days.

Análogamente las Figuras 7, 8 y 9, y las Tablas 9, 10 y 11 corresponden a KDU; las Figuras 10, 11 y 12, y las Tablas 12, 13 y 14 corresponden a HON; y las Figuras 13, 14 y 15 y las Tablas 15, 16 y 17 corresponden a SJG.
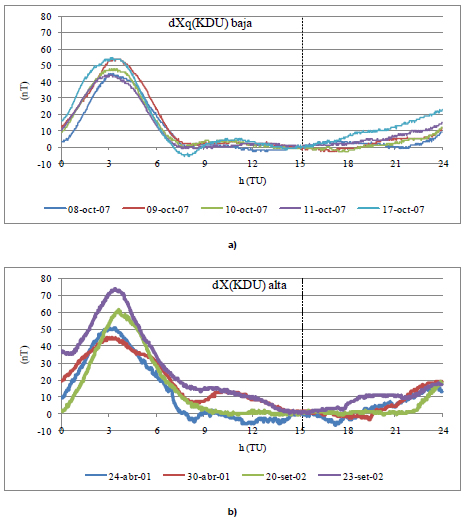
Fig. 7: variaciones dXq en KDU: a) en baja actividad solar; b) en alta
Fig. 7: dXq variations at KDU: a) for low solar activity; b) for high solar activity
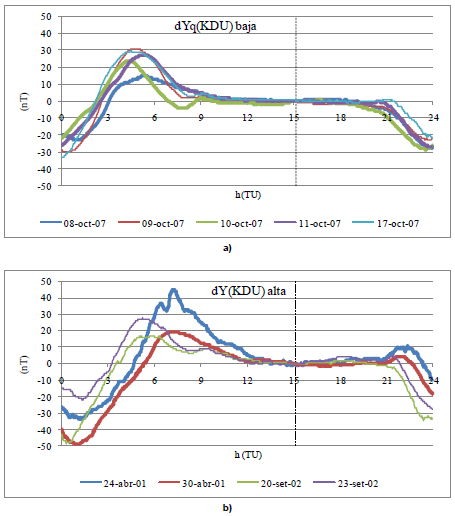
Fig. 8: variaciones dYq en KDU: a) en baja actividad solar; b) en alta
Fig. 8: dYq variations at KDU: a) for low solar activity; b) for high solar activity
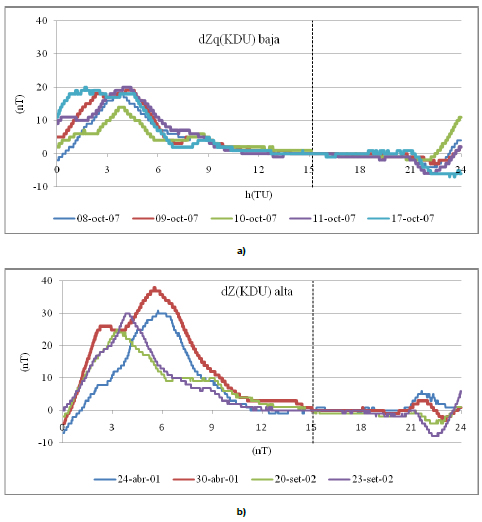
Fig. 9: variaciones dZq en KDU: a) en baja actividad solar; b) en alta
Fig. 9: dZq variations at KDU: a) for low solar activity; b) for high solar activity
Tabla 9: coeficientes armónicos de dXq(KDU) para los 9 días Q elegidos
Table 9: harmonic coefficients ofdXq(KDU) for the 9 Q days.
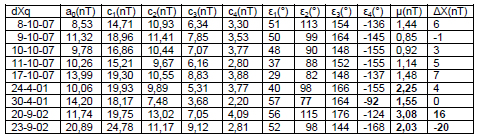
Tabla 10: coeficientes armónicos de dYq(KDU) para los 9 días Q elegidos
Table 10: harmonic coefficients of dYq(KDU) for the 9 Q days.

Tabla 11: coeficientes armónicos de dZq(KDU) para los 9 días Q elegidos
Table 11: harmonic coefficients ofdZq(KDU) for the 9 Q days.

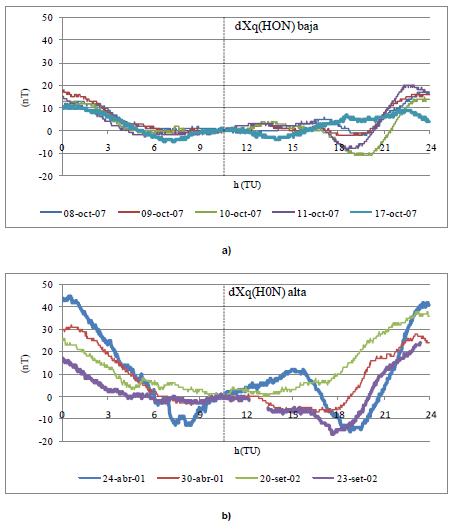
Fig. 10: variaciones dXq en HON: a) en baja actividad solar; b) en alta
Fig. 10: dXq variations at HON: a) for low solar activity; b) for high solar activity
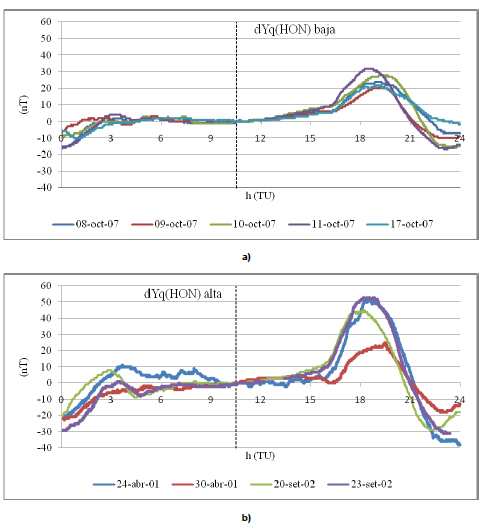
Fig. 11: variaciones dYq en HON: a) en baja actividad solar; b) en alta
Fig. 11: dYq variations at HON: a) for low solar activity; b) for high solar activity
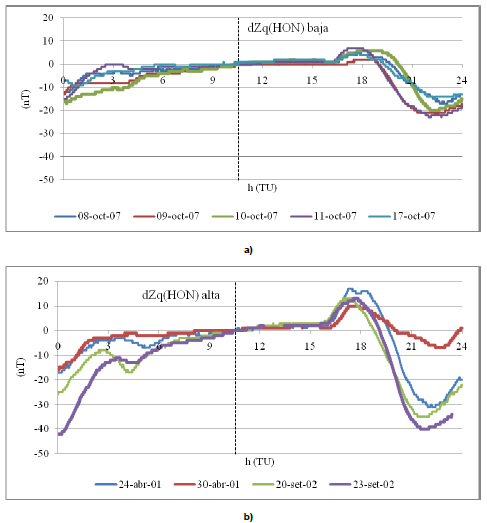
Fig. 12: variaciones dZq en HON: a) en baja actividad solar; b) en alta
Fig. 12: dZq variations at HON: a) for low solar activity; b) for high solar activity
Tabla 12: coeficientes armónicos de dXq(HON) para los 9 días Q elegidos
Table 12: harmonic coefficients ofdXq(HON) for the 9 Q days.
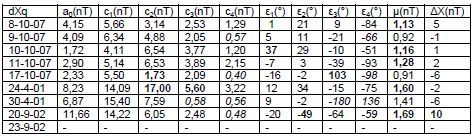
Tabla 13: coeficientes armónicos de dYq(HON) para los 9 días Q elegidos
Table 13: harmonic coefficients ofdYq(HON) for the 9 Q days.
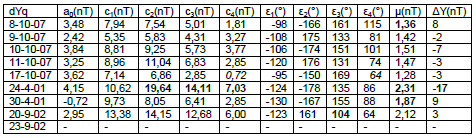
Tabla 14: coeficientes armónicos de dZq(HON) para los 9 días Q elegidos
Table 14: harmonic coefficients ofdZq(HON) for the 9 Q days.
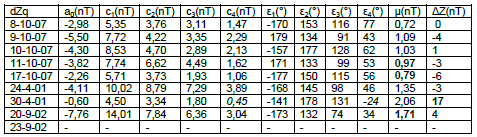

Fig. 13: variaciones dXq en SJG: a) en baja actividad solar; b) en alta
Fig. 13: dXq variations at SJG: a) for low solar activity; b) for high solar activity

Fig. 14: variaciones dYq en SJG: a) en baja actividad solar; b) en alta
Fig. 14: dYq variations at SJG: a) for low solar activity; b) for high solar activity
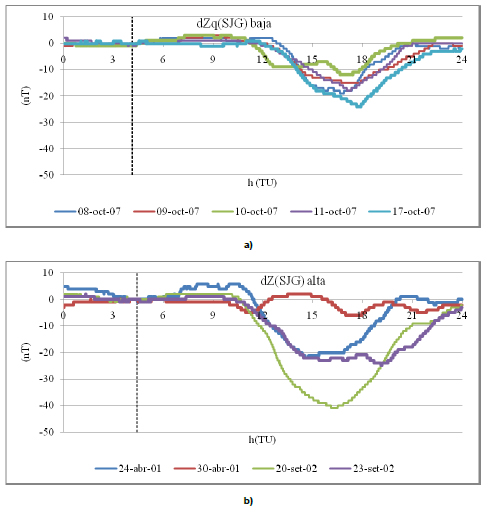
Fig. 15: variaciones dZq en SJG: a) en baja actividad solar; b) en alta
Fig. 15: dZq variations at SJG: a) for low solar activity; b) for high solar activity
Tabla 15: coeficientes armónicos de dXq (SJG) para los 9 días Q elegidos
Table 15: harmonic coefficients of dXq (SJG) for the 9 Q days.
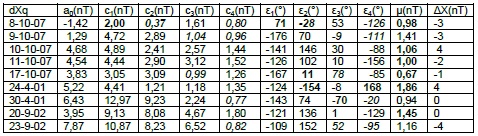
Tabla 16: coeficientes armónicos de dYq(SJG) para los 9 días Q elegidos
Table 16: harmonic coefficients ofdYq(SJG) for the 9 Q days.

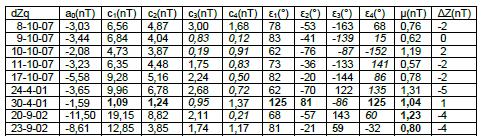
Tabla 17: coeficientes armónicos de dZq(SJG) para los 9 días Q elegidos
Table 17: harmonic coefficients ofdZq(SJG) for the 9 Q days.
DISCUSIÓN
Según los índices Km, en alta actividad solar, los días menos tranquilos de los elegidos próximos a los equinoccios corresponderían a alta actividad solar: el 24-4-2001 y el 20-9-2002. En todos los casos, como ya está establecido, las amplitudes de las variaciones en alta actividad solar son mayores que en baja.
Si bien los gráficos de dXq, dYq y dZq son una valoración subjetiva para establecer que un día es tranquilo, son a menudo usados; los días Q según los gráficos aquí presentados resultan:
De la Tabla 18 se infiere que los observatorios o sus componentes no indican la tranquilidad de igual manera; es de notar, sin embargo que el 24-4-01 se manifiesta como el menos tranquilo, acordando con los índices Km. Por otra parte, ABG (el de menor latitud geomagnética) parece ser el observatorio menos perjudicado por las perturbaciones, mientras que TSU y KDU (en el hemisferio sur) parecen ser los más afectados por ellas.
Tabla 18: síntesis de los 9 días subjetivamente elegidos como Q según los gráficos de dXq, dYq y dZq para los 5 observatorios.
Table 18: Synthesis of the 9 days subjectively chosen as Q after the dXq, dYq and dZq graphs for the 5 observatories

De acuerdo con las cotas establecidas para los coeficientes de Fourier se han definidos los días Q como se indican en la Tabla 19
Tabla 19: síntesis de los 9 días elegidos como Q según las cotas establecidas para los coeficientes de Fourier de dXq, dYq y dZq para los 5 observatorios.
Table 19: synthesis of the 9 days subjectively chosen as Q after the dimensions give to the Fourier coefficients for dXq, dYq and dZq for the 5 observatories

De la Tabla 19 se infiere que los observatorios o sus componentes no indican la tranquilidad de igual manera; es de notar, sin embargo que el 24-4-01 se manifiestan como el menos tranquilo, acordando con los índices Km, y el día 9 el más tranquilo. El número de días seleccionables en cada componente no permite establecer una estadística acerca de si existe o no variación de la fase con el cambio de la actividad solar.
CONCLUSIONES
En las tablas presentadas en la Discusión puede verse que de los gráficos y el análisis armónico no se extraen las mismas conclusiones respecto de cuales considerar días Q; si bien las características resaltadas para definir la no tranquilidad de una variación diaria en un gráfico son subjetivas, también lo son las cotas impuestas a los parámetros de un análisis armónico.
Se observa también que la condición de tranquilidad depende de la componente observada, del observatorio y de la actividad solar, por lo que definir como tranquilo un día para varios observatorios es, al menos, arriesgado.
De ello se concluye que, es admisible en baja actividad solar, elegir los 5 días Q definidos por algún índice de actividad geomagnética dada la baja amplitud de las variaciones y perturbaciones, aunque; el 11-10-07 en TSU y el 8, 10 y 17-10-07 en SJG distorsionarían el promedio. En alta actividad solar elegir el promedio puede ser altamente inadecuado. Para cada día universal, para cada componente, las variaciones geomagnéticas están modeladas por la radiación solar que afecta el nivel de concentración de iones y el movimiento térmico de la alta atmósfera, el viento solar, y la posición geográfica del observatorio que la registra; de allí que sea conveniente estudiar, según la necesidad, en cada caso, cada día tranquilo elegido.
Agradecimientos
La autora agradece al IGeBA-CONICET y a la Facultad de Ciencias Exactas y Naturales (UBA) por las facilidades otorgadas para el desarrollo de este trabajo; y al World Data Center for Geomagnetism de Kyoto (Japón), al Service International des Indices Geomagnetiques (Francia) y a la NASA (EEUU) por la facilidad de disponibilidad de los datos utilizados, y a los árbitros que contribuyeron a una mejor presentación del trabajo.
REFERENCIAS
1. Campbell, W.H., 1989. The regular geomagnetic field variations during quiet solar conditions; en Geomagnetism, vol.3; 385-460. Academic Press Limited. [ Links ]
2. Chapman, S. and J. Bartels; 1940. Geomagnetism, Oxford at the Clarendon press, vol. I, pp 542. [ Links ]
3. Hargreaves, J.K., 1992; The solar-terrestrial environmental. Cambridge atmospheric and space science series 5, pp 420 [ Links ]
4. Iyemori T., M. Takeda, M. Nose, Y. Odagi and H. Toh, 2010. Mid-latitude Geomagnetic Indices "ASY" and "SYM" for 2009 (Provisional).Data Analysis Center for Geomagnetism and Space Magnetism, Graduate School of Science, Kyoto University, Japan. [ Links ]
5. Mayaud P.N., 1980. Deviation, meaning and use of Geomagnetic Indices. AGUGeophysical. Monograph 22, pp154. [ Links ]
6. Menvielle M. and A.Berthelier, 1991. The K derived planetary indices. Description and availability. Reviews of Geophysics 30. [ Links ]
7. Parks, G.K., 1991. Physics of space plasma, an introduction. Addison-Wesley publishing Company,pp 538. [ Links ]
8. Takeda, M. ,2002. The correlation between the variation in ionosphericconductivity and that of the geomagnetic Sq field. Journal of Atmospheric and Solar-Terrestrial Physics 64 (2002) 1617- 1621. [ Links ]
9. Van Zele, M.A.and A. Meza 2011. The geomagnetic solar flare effect identify by SIIG as an indicatorof solar flare observed by GOES satellite. Advances in Space Research 48, 826-836. [ Links ]
10. Van Zele, M.A., 2013. Las variaciones geomagnéticas tranquilas Sq y su relación con parámetrossolares. GEOACTA 38(1): 30-47 (2013). [ Links ]
11. Yamazaki,Y., K. Yumoto, M. G. Cardinal, B. J. Fraser, P. Hattori, Y. Kakinami, J. Y. Liu, K. J. W. Lynn, R. Marshall, D. McNamara, T. Nagatsuma, V. M. Nikiforov, R. E. Otadoy, M. Ruhimat, B. M. Shevtsov, K. Shiokawa, S. Abe, T. Uozumi and A. Yoshikawa; 2011. An empirical model of the quiet daily geomagnetic field variation, Journal of Geophysical Research, 116, A10312, doi:10.1029/2011JA016487. [ Links ]
Recibido: 06-09-2013
Aceptado: 16-10-2013














