Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Geoacta
versión On-line ISSN 1852-7744
Geoacta vol.39 no.2 Ciudad Autónoma de Buenos Aires dic. 2014
TRABAJOS DE INVESTIGACIÓN
Estadística de manchas solares y terremotos en Chile
Statistics of sunspots and earthquakes in Chile
Virginia Mabel Silbergleit 1,2 y Patricia Alejandra Larocca3
1Instituto de Gas y Petróleo, Facultad de Ingeniería, UBA
2Consejo Nacional de Investigaciones Científicas y Técnicas
3Instituto de Geodesia y Geofísica Aplicadas, Facultad de Ingeniería, UBA
RESUMEN
La actividad solar influye sobre el geosistema y una manifestación de esta actividad son las manchas solares. En el presente trabajo se realiza un estudio estadístico del número de manchas solares y del momento sísmico para terremotos con epicentros en Chile, durante los años 1906 al 2011. Se estudian periodogramas donde se verifican periodicidades de aproximadamente 11 y 22 años para el Sol y entre 2.4 y 8.5 años; 11-14 y 26.2 años para la magnitud sísmica. El coeficiente de correlación hallado para las series mencionadas fue de C = 0.6. Se obtuvieron buenos ajustes utilizando la función de Weibull para ambas series.
Palabras claves: Manchas solares; Periodicidades; Sismos; Estadísticas.
ABSTRACT
Solar activity influences the geosystem and this activity could be studied by sunspots. In this paper a statistical study of sunspots and the seismic moment of earthquakes with epicenters in Chile during the years 1906 to 2011 is done. We study periodograms in which periodicities of about 11 and 22 years for the Sun and between 2.4 and 8.5 years; 11-14 and 26.2 years for the earthquake magnitude are observed. The correlation coefficient between the above mentioned data was C = 0.6. For both data series the Weibull function showed good fits.
Keywords: Sunspots; Periodicities; Earthquakes; Statistics.
INTRODUCCIÓN
El objetivo del estudio es observar las semejanzas y diferencias estadísticas entre el número de manchas solares y los terremotos en Chile. La ocurrencia de los terremotos tiene una distribución no homogénea sobre la superficie terrestre, en general, se producen en áreas donde se dan límites tectónicos diferentes. En el caso de Chile, el gran terremoto de magnitud sísmica 9.5 ocurrido en Valdivia, el 22 de mayo de 1960, (el mayor de la historia de la humanidad) se originó debido al desplazamiento súbito de la placa de Nazca bajo la placa Sudamericana.
Chile se encuentra dentro del cinturón de fuego del Pacífico (larga cadena de volcanes y estructuras tectónicas activas que rodea el Océano Pacífico). Este es uno de los países con mayor sismicidad en el mundo. Durante el último siglo se observó un promedio de ocurrencia de terremotos destructores cada 10 años liberándose un alto porcentaje de la energía sísmica, debido principalmente a la interacción entre las placas de Nazca y Sudamérica. Estas placas convergen con una velocidad relativa del orden de 8 cm/a en la dirección N78°E, (Compte y Pardo, 1991). Esta tectónica provoca la subducción de la placa oceánica (Placa de Nazca) bajo el continente (Placa Sudamericana), proceso que genera esfuerzos suficientes para dar origen a sismos.
En la zona central de Chile, el rasgo batimétrico más destacado de la placa oceánica de Nazca es la dorsal de Juan Fernández, cadena de volcanes extintos, que es subductada alrededor de los 33°S.
Algunos de los montes submarinos más importantes de esta cadena son las islas de Juan Fernández que emergen sobre el nivel del mar y bajo el mar el monte O'Higgins pronto a subductar, cercano a la fosa oceánica, (Pardo, 2001).
Del estudio de la ocurrencia de sismos en sus países, diversas autores publicaron los siguientes resultados: a) Du Xinxing, S. (1997) frecuencias de 7; 14; 22 y 42 años, b) Liritzis y Tsapanos( 1992) frecuencias de 3; 4.5; 6.5: 8: 9, 14-20 y 31-34 años y c) Madhava Rao and Kaila (1986) valores entre 3 y 12 años.
De acuerdo a las observaciones mostradas en USGS (http://pubs.usgs.gov/ gip/earthq1/measure.html), la cantidad de sismos débiles es mayor que la correspondiente a sismos destructivos, a sismos mayores y a grandes sismos.
Ritz (1984) y Serrano y col, (2003) han investigado la relación entre las actividades solar y sísmica. Mazzarella y Palumbo (1988) a partir de estudios de terremotos en Italia indicaron que la actividad solar y las anomalías magnéticas son propensas a desencadenar terremotos.
Han y col. (2004) estudiaron la relación entre la actividad solar y los grandes terremotos (Mw ≥ 8) en China. Ellos observaron un aumento en la cantidad de sismos en los años de máxima actividad solar. Sobolev y col. (1998) y Zolotov y col. (2010) proponen la existencia de una interacción entre el viento solar, la radiación de partículas y los terremotos.
Tavares y Acevedo (2011) encontraron relaciones entre el incremento de eventos solares durante la última mitad del siglo XX y la intensificación de la ocurrencia de terremotos.
Simpson (1967) vinculó la máxima frecuencia en la aparición de terremotos con la moderada y alta actividad solar.
Las manchas solares son áreas oscuras sobre la superficie del mismo que contienen fuertes campos magnéticos. El tamaño de una mancha solar moderada es muchas veces mayor que el de la Tierra, las mismas pueden permanecer por semanas o meses antes de desaparecer. Debido a la rotación solar, las manchas muestran movimientos de izquierda a derecha.
La periodicidad media de 11 años fue observada por primera vez por Heinrich Schwave (1789-1875) y la de 22 años lleva el nombre de George Ellery Hale (1868-1938) quién descubrió que las manchas solares se deben a la acción del campo magnético solar que limita la emisión de radiación del Sol. El número de manchas solares (Rz) es un observable vinculado con la intensidad de la componente toroidal del campo solar global.
Duhau y Martinez (2012) estudiaron las transiciones de la dínamo solar y su vinculación con los rápidos cambios climáticos. Presentaron variables solar-terrestres asociadas a fenómenos solares algunas de ellas aptas para producir actividad sísmica.
En el presente trabajo se estudiaron los valores de la magnitud sísmica superficial (Ms) y del número de manchas solares (Rz) utilizando:
a) Periodogramas de Rz y Ms obtenidos mediante la transformada rápida de Fourier.
b) Regresión lineal entre Rz y Ms considerando los valores máximos anuales.
c) Distribuciones estadísticas aplicadas a los máximos del momento símico, Ms y de las manchas solares Rz.
DATOS Y METODOLOGÍA
Una magnitud sísmica es una medida relacionada con la cantidad de energía liberada en forma de ondas. Se puede considerar como el tamaño relativo de un temblor y se determina tomando el logaritmo (base 10) de la amplitud máxima de movimiento de alguna onda superficial a la que se le aplica una corrección por distancia al epicentro y profundidad local. Se define Ms a la magnitud adimensional de ondas superficiales por:
Ms= log(A/T)+1,66 log(D) + 3,3
Donde:
D= distancia foco-estación
A= amplitud de movimiento de suelo
T=período de la onda lineal
Los datos sísmicos se obtuvieron a través del Servicio Sismológico de la Universidad de Chile (http://ssn.dgf.unchile.cl). Se consideraron los sismos con Ms≥7 para el período 1906-2011 (La Figura 1 muestra el gráfico de los datos correspondientes).
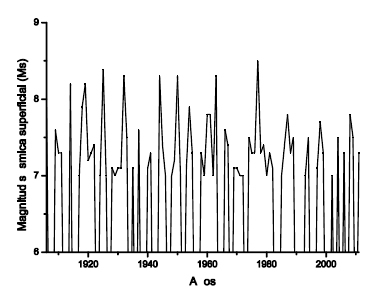
Figura 1. Ms para terremotos de Chile (valor medio anual) desde 1906 a 2011.
Figure 1. Ms for Chilean earthquakes (annual average) since 1906 to 2011.
Terremotos observados en Chile han sido estudiados previamente por Silbergleit y Prezzi (2012) quienes estimaron los valores máximos esperables para la próxima década.
El número de manchas solares Rz es la magnitud que mide el número y tamaño de las manchas solares. Los valores promedios anuales de Rz se obtuvieron a través de Nacional Geophysical Data Center (http://www.ngdc.noaa.gov/), la Figura 2 muestra el gráfico de los datos correspondientes.

Figura 2. Número de manchas solares (promedio anual) desde 1906 a 2011.
Figure 2. Number of sunspots (annual average) since 1906 to 2011.
Trabajos vinculados a la actividad solar fueron previamente publicados por Silbergleit y Larocca, (2001, 2005).
RESULTADOS DEL ANALISIS DE LAS SERIES
a) Estudio de periodogramas
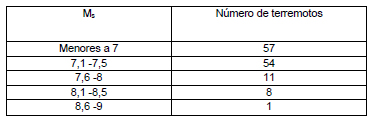
Tabla 1. Número de terremotos observados en Chile entre 1906 y 2011 según su magnitud sísmica superficial.
Table 1. Number of earthquakes observed in Chile between 1906 and 2011 according to their surface seismic magnitude.
Los picos de 11 y 26,2 años podrían asociarse con los que aparecen en la Figura 4 para Rz.
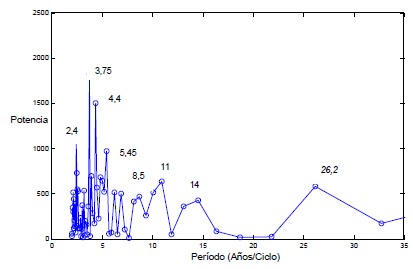
Figura 3. Periodograma correspondiente al Ms para el período 1906-2011 (el máximo corresponde a 3,75 años y luego pueden notarse picos de 4,4; 5,45; 8,5; 11; 14 y 26,2 años).
Figure 3. Ms periodogram for the period 1906-2011 (the maximum corresponds to 3.75 years and spikes of 4.4; 5.45; 8.5; 11; 14 and 26.2 years can be identified)

Figura 4. Periodograma correspondiente a Rz para el intervalo 1906-2011 (el máximo corresponde a 10,5 años).
Figure 4. Rz periodogram for the period 1906-2011 (the maximum corresponds to 10.5 years)
En la Figura 4 se muestra el espectro de potencia de las serie Rz en función del tiempo. Se observan dos picos de 10.5 años y de 22 años, que se corresponden con el ciclo de Schwabe y el de Hale respectivamente.
b) Regresión lineal entre Ms y Rz
Se analizó la correlación temporal entre los promedios anuales de Ms y Rz . El coeficiente de correlación entre ambas series temporales fue de C= 0.6. La Figura 5 muestra el ajuste y la ecuación de la recta de regresión.

Figura 5. Rz vs Ms para el período 1906-2011.
Figure 5. Rz vs. Ms for the period 1906-2011.
c) Análisis de funciones de distribución
Cada fenómeno aleatorio genera su propia variable aleatoria que se distingue además por su naturaleza física, por la probabilidad asociada a cada valor posible caracterizada por su función de distribución o probabilidad acumulada. Muchas veces es conveniente calcular la derivada de la función de distribución llamada densidad de probabilidad pues ésta mide la forma en que se agrupan las observaciones de una eventual muestra para distintos valores de la variable.
Se analizaron distintas funciones de densidad de probabilidad para los valores máximos de Rz por ciclo solar y Ms.
La determinación, el análisis y la validación a partir de la prueba de Kolmogorov-Smirnov permite obtener una estimación de la curva representativa a partir de los resultados muestrales. En las Tablas 2 y 3 se muestran los ajustes de dichas funciones para RzMax y su ordenamiento por el criterio de máxima verosimilitud y calidad de ajuste ( Mermoz y García, 2006).
Tabla 2 Modelos de distribuciones propuestos para RzMax. (L es el logaritmo de la máxima verosimilitud y P es el parámetro de ajuste lineal).
Table 2. Distribution models proposed for RzMax. (L is the logarithm of the maximum verisimilitude and P is the linear adjustment parameter).

Tabla 3. Coeficientes de la distribución de Weibull, obtenidos a partir de los distintos ajustes.
Table 3. Coefficients of the Weibull distribution, calculated for the different adjustments.
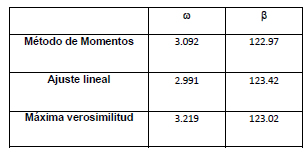
En la Tabla 2 se observa que las distribuciones que mejor ajustan RzMax son las de Weibull y la Normal (con P = 0.99). En la Tabla 4 se muestra que las mismas funciones de distribución son las que también mejor ajustan MsMax (con P=0.96). Se consideraron los valores de los parámetros obtenidos por el método de ajuste lineal que son mostrados en las Tablas 3 y 5, respectivamente.
Tabla 4 Modelos de distribuciones propuestos para MsMax L es el logaritmo de la máxima verosimilitud y P es el parámetro de ajuste lineal.
Table 4. Distribution models proposed for MsMax. L is the logarithm of the maximum verisimilitude and P is the linear adjustment parameter.

Tabla 5. Coeficientes de la distribución de Weibull, para MsMax por los métodos especificados.
Table 5. Coefficients of the Weibull distribution, calculated for MsMax using the specified methods.

Los datos fueron procesados con el programa MOVAC (Mermoz y García, 2006). Los resultados se muestran en las Figuras 6 y 7.
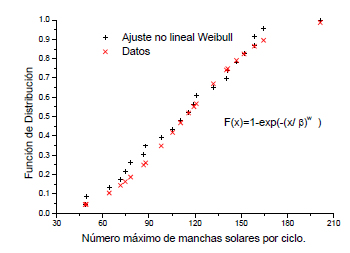
Figura 6. Función de distribución para el número máximo de RzMax desde el ciclo solar 1 al 23.
Figure 6. Distribution fuction for the maximum number of RzMax since solar cycle 1 to 23.
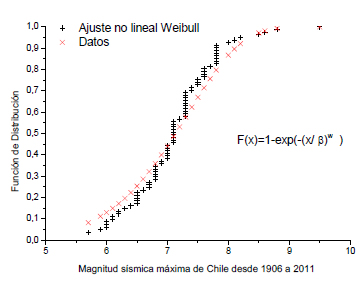
Figura 7. Función de distribución para MsMax.
Figure 7. Distribution function for MsMax.
En las Figuras 8 y 9 se muestran los histogramas para el número RzMax y MsMax Se representaron las funciones de densidad de probabilidad obteniéndose que el 66% de los RzMax y el el 72% de los MsMax se encuentran en los intervalos 70 ≤ RzMax ≤ 150 manchas y 7.5 ≤ MsMax ≤ 8.5 respectivamente.

Figura 8. Histograma correspondiente a RzMax y la función de densidad de Weibull.
Figure 8. Histogram corresponding to RzMax and Weibull density fuction.
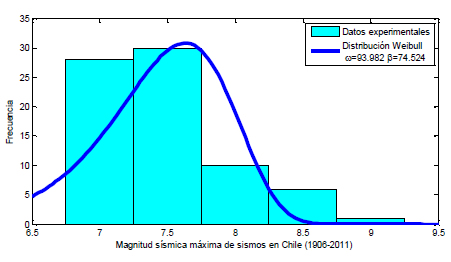
Figura 9. Histograma correspondiente a MsMax y la función de densidad de Weibull.
Figure 9. Histogram corresponding to a MsMax and Weibull density function.
CONCLUSIONES
A partir del presente estudio se concluye que:
1- utilizando el método de Transformada Rápida de Fourier para el análisis de las periodicidades en Ms y Rz durante los últimos cien años se encontraron periodicidades similares a las obtenidas en trabajos previos. Estos corresponden a distintos países, sin embargo loe resultados son consistentes, y podrían explicarse considerando que el número de sismos débiles es mayor que el correspondiente a sismos destructivos, sismos mayores y grandes sismos, en consecuencia las frecuencias que aparecen en la Figura 3 estarían vinculadas a los diferentes períodos de ocurrencia sísmica. Para el caso de Rz aparece claramente el período conocido como ciclo de Schwave (en 10.5 años ver Figura 4) y el de Hale. Periodicidades similares se observaron en Ms (con valores de 11 y 26.4 años, (ver Figura 3).
2- el coeficiente de correlación entre el Rz y Ms (C=0.6) ) muestra una intensi-dad de la relación lineal entre ellos que podría ser denominada "moderada" ya que es un 40% menor que una correlación fuerte y un 60% mayor que una débil. Este resultado podría deberse al azar por lo cual no significa que obligadamente exista una relación lineal causa-efecto entre la dos variables.
3- a partir del análisis de funciones de probabilidad para RzMax y MsMax, y utilizando para ambas series la distribución de Weibull se obtuvieron buenos ajustes en los dos casos, por lo tanto podemos asegurar que esta distribución es apropiada para utilizarse con los datos estudiados. Este hecho también se manifiesta en las funciones de densidad de probabilidad graficadas sobre los histogramas para RzMax y MsMax.
Los resultados antes mencionados muestran las semejanzas y diferencias obtenidas para las series estudiadas. Futuros estudios de modelado físico y estadístico contribuirán a completar el análisis aquí presentado.
Agradecimientos. Este trabajo se ha realizado con recursos económicos correspondientes a los proyectos: PIP N° 11420090100258 (CONICET) y PIP N° 20020090100131 (UBACYT), Argentina. Las autoras agradecen las importantes correcciones y sugerencias realizadas por los revisores.
REFERENCIAS
1. Comte, D., y M. Pardo, 1991.Readpraisal of great historical earthquakes in the northen Chile y Southerm Peru seismic gap: Natural Hazards 4: 23-44. [ Links ]
2. Duhau, S. y E. A. Martinez, 2012.Solar dynamo transitions as driver of sudden climate changes.In Global Warming-Impacts y Future Perspective. Ed. Bharat Raj Singh, ISBN 978-953-51-0755-2, In Tech. doi: 105772/51814. [ Links ]
3. Du Xinxing, S., 1997. Wavelets data based analysis of dynamic seismicity period: Earthquake, 17,3: 259-264. [ Links ]
4. Han, Y.B., Guo, Z.J., Wu, J. y L.H. Ma , 2004. Possible triggering of solar activity to big earthquakes (Ms ≥ 8) in faults with near west-east strike in China: Science in China Series GPhysics, Mechanics y Astronomy, 47: 173-181.
5. Liritzis I. y T. M. Tsapanos , 1992. Probable evidence for periodicities in global seismic energy release: Earth, Moon y Planets, 60 (2): 93-108. [ Links ]
6. Madhava Rao, N. y K. L. Kaila , 1986. Model of earthquake energy periodicity in the Alpide-Himalayan seismotectonic belt: Tectonophysics, 124 (3-4): 261-270. [ Links ]
7. Mazzarella, A. y A. Palumbo , 1988. Solar geomagnetic and seismica ctivity: Nuovo Cimento C, Serie 1: 353-364. [ Links ]
8. Mermoz O. y R. García, 2006. Distribuciones univariantes de probabilidad: modelos y su identificación. Edit. Nueva Librería. Buenos Aires, Argentina. 1ra. Ed. 218p. [ Links ]
9. Pardo M., Informe de la Actividad Sísmica del 09 de Abril de 2001. Servicio Sismológico. Departamento de Geofísica. Facultad de Ciencias Físicas y Matemáticas. Universidad de Chile.(http://ssn.dgf.unchile.cl). [ Links ]
10. Ritz, M. 1984. Short communication: A high conductivity anomaly on the West African craton (MALI). Journal of Geophysics, 55: 182-184. [ Links ]
11. Serrano I., Zhao, D., Morales, J. y F. Torcal , 2003. Seismic tomography from local crustal earthquakes beneath eastern Rif Mountains of Morocco: Tectonic Physics, 367: 187-201. [ Links ]
12. Silbergleit V. y P. Larocca, 2001. Estimate of the upper limit of amplitude of solar cycle no.23, Atmósfera. 3. [ Links ]
13. Silbergleit, V.M. y P. A. Larocca, 2005. Geomagnetic activity y solar cycles. Advances in Space Research vol. 36 issue 12 2005. 2384-2387. [ Links ]
14. Silbergleit V. M. y C. Prezzi., 2012.Statistics of major Chilean earthquakes recurrente. Natural Hazards, 62, 2 , 445-458. DOI: 10.1007/s11069-012-0086-8. [ Links ]
15. Simpson J. F.,1967. Solar Activity as a triggering mechanism for earthquakes.Earth y Planetary Science Letters, 3.417-425. [ Links ]
16. Sobolev, G.A., Shestopalov, I. P. y E.P Kharin, 1998. Geoeffective solar flashes and seismica activity of the Earth: Fizika Zemli (in Russian), 7: 85-90. [ Links ]
17. Tavares, M. y A. Azevedo , 2011. Influences of Solar Cycles on earthquakes: Natural Science,3 6: 436-443. [ Links ]
18. Zolotov O.V., Namgaladze, A. A., Zkharenkova, I. E., Shagimuratov, I. I. y O.V. Martynenko, 2010. Modeling of ionospheric earthquake precursors generated by various electric field sources: Natural Hazards Earth System Sciences, 10: 7-18. obtained from different Ms settings. [ Links ]
Recibido: 15-10-2013
Aceptado: 06-08-2014














