Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ameghiniana
versión On-line ISSN 1851-8044
Ameghiniana v.42 n.4 Buenos Aires sept./dic. 2005
Swerving as the escape strategy of Macrauchenia patachonica Owen (Mammalia; Litopterna)
Richard A. Fariña 1 , R. Ernesto Blanco 2 and Per Christiansen 3
1Departamento de Paleontología, Facultad de Ciencias, Universidad de la República, Iguá 4225, 11400 Montevideo, Uruguay. fari~a@fcien.edu.uy
2Instituto de Física, Facultad de Ingeniería, Universidad de la República, Julio Herrera y Reissig 565, 11300 Montevideo, Uruguay. blanco@fing.edu.uy
3Department of Vertebrates, Zoological Museum, Universitetsparken 15, DK, 2100 Copenhagen O, Denmark. p2christiansen@zmuc.ku.dk
Abstract. The Lujanian megamammals (late Pleistocene of South America) show many palaeoautecological peculiarities. The present paper studies one of them, the locomotor habits of Macrauchenia patachonica Owen, through those morphological features related with its possible antipredation strategy. To avoid predation (especially by the sabre-tooth Smilodon Lund), this large litoptern seems to have been particularly adapted to swerving behaviour. This is suggested by the fact that its limb bones have indicators of higher transverse than anteroposterior strength (significantly so in the case of the femur), a feature which is also observed in modern swervers, and not so clearly in other fast running herbivores that do not use swerving so much.
Resumen. El esquive como la estrategia de escape de Macrauchenia patachonica Owen (Mammalia; Litopterna) . La megafauna lujanense (Pleistoceno tardío de Sudamérica) muestra muchas peculiaridades paleoautecológicas. El presente trabajo estudia una de ellas, los hábitos locomotores de Macrauchenia patachonica , a través de aquellas características morfológicas relacionadas con su posible estrategia contra los depredadores. Para evitar la depredación (especialmente por el félido de dientes de sable Smilodon Lund), este gran litopterno parece haber estado particularmente adaptado para el comportamiento de esquive, como lo sugiere el hecho de que sus huesos largos de las extremidades son más fuertes en el sentido transverso que en el anteroposterior (y muy significativamente en el caso del fémur). Este carácter se observa también en animales modernos que esquivan y no tan claramente en otros herbívoros que corren rápido pero no usan tanto el esquive.
Key words. Palaeoecology; Megafauna; Pleistocene; South America; Biomechanics; Locomotion.
Palabras clave. Paleoecología; Megafauna; Pleistoceno; Sudamérica; Biomecánica; Locomoción.
Introduction
Previous palaeobiological studies (Fariña and Vizcaíno, 1999, and references therein) have shown that the Lujanian megafauna (late Pleistocene-early Holocene of South America) had very peculiar ecological features, including numerous species whose adult body mass exceeded a metric tonne (Fariña et al ., 1998; Bargo et al ., 2000; Christiansen and Fariña, 2003). These include proboscideans, extinct ungulates (Litopterna and Notoungulata) and xenarthrans (glyptodonts and giant ground sloths). Although some taxonomic revision may be needed, as many as 19 species of megamammals have been cited for some localities (Fariña, 1996), an abundance of megamammals that must have placed a severe stress on the habitat.
Autecological characteristics of some of the Lujanian species have been previously studied. In this paper we intend to establish the behaviour of one of the megaherbivores found in this palaeofauna, the last litoptern Macrauchenia patachonica Owen, by evaluating its locomotor adaptations and potential escape strategies, possibly from such predators as the sabre-tooth felid Smilodon bonaerensis (Muñiz) (figure 1), some of whose morphological locomotory characteristics are also assessed. These studies are based on our assumptions that these strategies are relevant in terms of the selective pressure acting upon the herbivores and that the locomotor behaviour of those herbivores are reflected in their limb bone dimensions, following an approach used in works by Alexander (1985), Gatesy (1991) and Carrano (1998), among others. A similar approach can be applied to the predator.

Figure 1. Reconstructions of Smilodon (A), Macrauchenia (B) and Hippidion (C) (modified from Fariña and Vizcaíno, 1995) / Reconstrucciones de Smilodon (A), Macrauchenia (B) e Hippidion (C) (modificados de Fariña y Vizcaíno, 1995).
The litoptern Macrauchenia patachonica (whose palaeobiology was studied as long as 80 years ago in the work by Sefve, 1924) was chosen for this study because it represents a peculiar adaptive type, with a distinctive South American phylogenetical and biogeographical histories. Indeed, the extinct order Litopterna was among the ancient inhabitants of South America, which were present in this continent at least from the early Tertiary (Pascual et al ., 1965).
For comparative purposes, some modern large felids were considered, as well as some Lujanian and modern mammalian herbivores, including living and extinct equids, living artiodactyls and ratites.
Material and methods
The bone dimensions referred to below were taken from the following specimens: Smilodon bonaerensis [holotype, Museo Argentino de Ciencias Naturales [hereafter MACN]- 46], Macrauchenia patachonica [Museo de La Plata [hereafter MLP] - DP 12-1424], Hippidion principale (Lund) [MLP - 6-64, exhibited in Sala VIII of the MLP, a cast of the holotype of H . bonaerense Owen, considered a junior synonym of H . principale by Alberdi and Prado [1993]], Equus zebra Linnaeus [a juvenile specimen, MLP-DZV 948], Equus burchelli Gray [CN 3421], Struthio camelus Linnaeus [MLP-DZV 660 and CN 70], Rhea americana (Linnaeus) [Facultad de Ciencias, Montevideo, unnumbered], Pterocnemia pennata (d'Orbigny) [MLPDZV 662], Connochaetes gnou (Zimmermann) [MLPDZV 956, British Museum Natural History [hereafter BMNH] 1850.11.22.70, BMNH 1981.800], Connochaetes taurinus (Burchell) [MLP-DZV 1529], Gazella thomsoni (Gunther). BMNH [1936.9.5.4, BMNH 1936.9.5.4], Felis concolor Linnaeus [Zoological Museum, University of Copenhagen [hereafter CN] 5663], Panthera leo (Linnaeus) [CN 6043], Panthera onca (Linnaeus) [CN 5660], Panthera pardus (Linnaeus) [CN 5661], Panthera tigris tigris (Linnaeus) [CN 5667], Panthera tigris altaica (Temminck)[CN 5698] and Panthera uncia (Schreber) [CN 5216].
Estimation and distribution of body mass
Several methods were used to estimate body masses of the fossil species considered. Alexander's (1985, 1989) procedure of calculating volumes of scale models by submerging them in water and weighing the displaced liquid was performed in the cases of Macrauchenia and Smilodon . These models were made of a synthetic modelling clay specifically for the purposes of this paper. After that, volume estimates for these animals were obtained by multiplying the volumes of the models by the cubes of their respective scales. A precision balance was used, the error in taking the model mass being less than 0.5 gram, or about 3%. Therefore, the final error introduced by multiplying by the scale is negligible. A density of 1,000 kg m-3 was assumed for the animal when alive, as is usual when studying fossil mammals (Alexander, 1985, 1989; Fariña, 1995).
Some alternative methods of estimating mass, based on allometric relationships (Alberdi et al ., 1995, Fariña et al ., 1998), were compared to our results and yielded very similar values to those used here. Furthermore, the procedure described above has been preferred for the purposes of this paper because it is less dependent of the dimensions of the bones whose strength is under analysis.
The models were suspended to determine the centre of mass, as described by Alexander (1985:3); i.e ., hanging them from two points in the sagittal plane (for instance, the head and the tail) and extending the lines of the thread until they crossed each other. The position of the centre of mass was used to determine the proportion ( a , see below) of the weight supported by each pair of limbs (see below), as explained in Alexander (1985), Fariña (1995) and Christiansen (1997). In the case of the equids, the value given in the literature for this proportion in the domestic horse was taken (Björck, 1958). The masses of some of the African mammals were taken from Nowak (1991), except for extant felids (which had been weighed prior to death) and the large subadult specimen of Equus burchelli , for which the actual body mass of the skeletal specimen used for analysis had been recorded (see below). In the case of Equus zebra , the mass value obtained from the literature was corrected assuming geometric similarity, as our specimen was a juvenile. It should be mentioned that juveniles and subadult have relatively stronger limbs than those of full grown adults (Christiansen, 2000, and unpublished observations), but this cannot be assumed to have affected the ratios IACt / IACap. In the case of the ostrich, the mass was estimated after the data in Alexander (1983b), again assuming geometric similarity between his specimen and ours. Another specimen (see below) was weighed prior to death (Christiansen, 2000). In the case of the greater rhea, an unpublished estimation kindly supplied by Ms Olivia Lluch was used. No mass estimation was available for the lesser rhea. The percentage of mass supported by the hind limbs in the big cats was set at 45%, following Rollinson and Martin (1981) who gave a value of 48% for ahind in Acinonyx , which is somewhat lighter in the forequarters than the others.
Limb bone strength
Limb long bones are vulnerable to forces that impose bending moments on them (Rubin and Lanyon, 1982; Carrano, 1998). During locomotion the forces acting on the bones will vary during the stride in a very complex pattern (Alexander, 1989) but it is convenient to divide these forces into two main components (Alexander, 1985, 1989): a) an axial component, acting along the long axis of the bone and setting up a compressive stress which is proportional to bone cross sectional area, and b) a bending component, acting at right angles to the long axis of the bone, and distorting it about its long axis. The latter component is the most important in most cases during locomotion (Alexander, 1989).
All stresses (and even bending components) are particularly important in large animals, as great mass exerts large moments on the bones due to inertia alone. Consequently, large animals also use postural changes to aid in supporting their body weight (Biewener, 1983, 1989a, 1989b, 1990; Carrano, 1998), progressively aligning their long bones closer to vertical with increasing size, in order to reduce the bending induced moments. This is brought about, as the postural change increases the effective mechanical advantage of the muscles (for definitions see Biewener, 1989b).
When a bone has to withstand a force exerted at its distal end at right angles to its long axis, its strength is directly related to its section modulus for bending in a parasagittal plane ( Z ), obtained from its cross section (Alexander, 1983a: 129), and inversely related to the bone length and to the force exerted. This force is proportional to the fraction ( a ) of the animal's weight ( mg ) supported by the corresponding pair of limbs. Thus, a strength indicator (or indicator of athletic capability in a parasagittal plane, hereafter referred to as IACap) is derived, expressed as Z/amgx , where x is the distance from the distal end at which the section is taken, usually half way along the bone, or near it, if a large process for muscle attachment was present in this precise place (see Alexander, 1985, for further explanations). Units are the inverse of those of pressure (Pa-1). Notice that this approach allows a comparison between a biped and a quadruped, as, in the latter case, only the fraction of the body weight withstood by the appropriate pair of limbs ( a ) is taken into account for the calculation of its strength indicators.
In contrast to previous studies, we also computed a transverse strength indicator (IACt). In doing so, the section modulus for bending in a transverse plane was obtained from the appropriate bone cross section. The rest of the procedure was the same used for calculating IACap. A ratio between IACt and IACap was calculated to assess the differential anteroposterior and transverse strengths. Also the ratio of the diameters would yield the same information in part; i.e ., the relative strength to resist anteroposterior or transverse forces, but not on the absolute strength for each direction of bending. A potentially important issue is whether there are significant errors in between-taxon comparisons due to phylogenetic variations in medullary cavity size, which cannot be corrected for at this time.
Bone strengths of the extinct animals were computed by using external bone dimensions, as is customary in such analyses ( e.g . Alexander, 1985, 1989; Fariña, 1995; Christiansen, 1997, 1998; Christiansen and Paul, 2001). In animals with hollow long bones the section modulus for the medullary cavity must be subtracted from the section modulus based on external dimensions, thus lowering the strength indicator value. However, even among large theropod dinosaurs with rather large femoral medullary cavities the values computed from external bone dimensions are only slightly inflated, indicating that the usage of external bone dimensions in extinct animals should lead to relatively little error. The exception to this condition would be the presence of an extremely large marrow cavity, which appears never to be the case among large animals (see Christiansen, 2000). In this particular case, we compared the results obtained using both external dimensions ( i.e ., computing the section moduli assuming solid cross sections and using this as the independent variable) and Xray ( i.e ., computing the section modulus for the bone after having subtracted the section modulus for the marrow cavity and using it as the dependent variable) in the following specimens: Ursus maritimus Phipps [CN 1965], Paradoxurus hermaphroditus (Pallas) [CN 1587], Ailurus fulgens Cuvier [CN 4451], Hyaena hyaena (Linnaeus) [CN 1597], Felis concolor [CN 5663], Felis lynx Linnaeus [CN 120], Panthera leo [CN 6043], Panthera tigris (Linnaeus) [CN 5667], Canis lupus Linnaeus [CN 713], Vulpes vulpes Linnaeus [CN 302], Elephas maximus (Linnaeus) [CN 1399], Equus burchelli [CN 3421], Diceros bicornis (Linnaeus) [CN 3729], Tapirus terrestris (Linnaeus) [CN 2866], Hemitragus jemlahicus Smith [CN 4104], Okapia johnstoni Sclater [CN 3566], Tragulus javanicus Osbeck [CN 339], Hippopotamus amphibius Linnaeus [CN 4115], Potamochoerus porcus (Linnaeus) [CN 3450], Syncerus caffer (Sparrman)[CN 3050], Tragelaphus strepsiceros (Pallas)[CN 3793], Gazella dorcas (Linnaeus) [CN 1515], Antidorcas marsupialis (Zimmermann)[ CN 3134], Alces alces (Linnaeus)[CN 3522], Cervus timorensis Blainville [CN 699] and Dama dama (Linnaeus) [CN 1495].
Cross-sections of femora and humeri were measured directly with the aid of a profile gauge at distances x from the distal end or by approximation to an ellipse. To assess bone strength and other cursorial features of Macrauchenia patachonica , limb bone dimensions and distance from right acetabulum to left acetabulum were taken from the same specimen as above, i.e ., MLP-DP 12-1424.
Statistical analyses
The departure of the IACt / IACap ratio from one (see table 1), i.e ., from the circular cross section, was assessed by subtracting the appropriate value for each bone of each species from one and dividing the result so obtained by the standard deviation of this sample. This figure was compared with the values given in a t table.

Table 1. Masses, their distribution (ahind is the proportion of the body weight supported by the hind limbs) and anteroposterior (IACap) and transverse (IACt) strength indicators in several extinct and modern mammals and birds. The values of the ratios of the transverse and anteroposterior strength indicators that are significantly different from one are shown in bold characters. Modern animals that are observed to swerve are marked with an asterisk (*) / Masas, su distribución (ahind es la proporción del peso corporal que soportan las extremidades posteriores) y los indicadores de resistencia anteroposterior (IACap) y transverso (IACt) en varios mamíferos y aves extinguidas y actuales. Los valores de los cocientes de los indicadores de resistencia anteroposterior y transverso que son significativamente diferentes de uno se muestran en negrita. Los animales modernos en los que se observa esquive se marcan con un asterisco (*).
Results
Body mass
The mass of Smilodon was estimated using scale models as 400 kg (table 1). Thus, this animal was larger than the any modern felid (for instance, the mass of our specimen of Panthera tigris altaica was 230 kg), which corroborates the results obtained by averaging allometric equations (Fariña et al ., 1998). Macrauchenia exceeded the metric tonne of body mass, thus qualifying as a megaherbivore, but likely in the range of Smilodon's prey size (see Anyonge, 1993, for further discussion). The mass of Hippidion was 400 kg, slightly larger than those of modern wild equids.
Limb bone strength
Calculations of section moduli using external dimensions ( i.e ., assuming a solid cross section) are very highly correlated with those using X-ray pictures, which account for the marrow cavity, both for the humeri ( a = 1.023; b = 0.072; r2 = 0.9993) and for the femora ( a = 0.127; b = 1.031; r2 = 0.9992). Therefore, we assumed that both sources can be safely used for our study, particularly because some of our most important conclusions are based on ratios between those indicators.
The segment lengths of the hindlimb of Macrauchenia have the following values: femoral length is 59 cm (47.2% of the total limb length, less than one standard deviation longer than the mammalian average given by Carrano, 1998); tibial length is 42 cm (33.6%, about one standard deviation shorter than the average in Carrano, 1998); metatarsal length is 24 cm (19.2%, about the average in Carrano, 1998). Macrauchenia shows a value of IACap for the femur about 50% higher than expected for a 1100-kg mammal, according to the allometric equations in Fariña et al . (1997). However, the value of the IACt for that bone is significantly higher (ratio = 1.45, p < 0.05), although not so in the humerus (ratio = 1.16, p > 0.4, not significant).
The results are also shown in table 1. All the IACap values of the indicator of athletic capability obtained for the fossil mammals lie above 20 GPa-1. When other mass estimates, based on allometric equations, were used these results did not change very much. These figures indicate that the long bone strength must have allowed them to perform strenuous locomotor activities, such as fast running. For instance, the African buffalo Syncerus caffer is capable of galloping and has IACap values of 21 and 22 GPa-1 for humerus and femur, respectively; non-galloping elephants have much lower values, 11 and 7 GPa-1 for humerus and femur, respectively (Alexander, 1985; see also Fariña et al ., 1997; Christiansen, 2000).
In the case of Smilodon, IACt of the humerus is much lower than the IACap. The ratio between those values is 0.65, which is marginally significant ( p < 0.05). The opposite condition occurs in the case of the femur, but the differences between the two values are much smaller (ratio = 1.17, p > 0.4, not significant). A similar pattern is observed in the tiger and the other extant large felids (table 1); the jaguar and the puma show similar figures for the humeri, but have lower ratios for the femora (for both species, ratio = 0.9, not significant).
Among the other herbivores, the equids (the fossil Hippidion , and the two living zebra Equus zebra and E. burchelli ) show high values of the IACap, which is consistent with their observed or inferred fast galloping gait (although it should be taken into account that E . burchelli is a large subadult, and so may have relatively stronger bones than full grown adults), as well as with the fact that they are of large body size and have sharply inclined humeri. In other words, humeri appear stronger than femora in the same animal in all mammals so far studied (see Christiansen, 2000) because humeri are held more inclined than are femora, and thus subjected to greater amounts of bending and torsional stresses. Furthermore, the IACap of the humeri in two species are substantially greater than the IACt. The IACt / IACap ratio was statistically different from one in Hippidion (0.60, p < 0.05), although not so in E. zebra (0.69, p > 0.1, not significant), and it was very close to 1 in E. burchelli . The femoral sections of the three species are fairly circular (ratio around 1).
Thomson's gazelles and both wildebeests yielded high values for both IACs. Their ratios IACt / IACap do not differ significantly from one, although the femora of the gazelle tend to have a larger ratio (ratio = 1.13, p > 0.3, not significant).
The femora of ratites have unusually high absolute values for both IACap and IACt, which is a reflection of their capability to run fast (Alexander et al ., 1979) with femora that are held nearly horizontally, and thus subjected to large amounts of torsional stress (Christiansen, 2000; Carrano, 1998). The angle to vertical of the tibiae of ratites is more comparable to the angles at which mammalian long bones are held, and, conversely, the tibia of the ostrich has a strength indicator value rather similar to the femora and tibiae of fast-moving mammals (Christiansen, 2000). The ratio in the greater rhea was highly significant (ratio = 1.65, p < 0.01).
Discussion
Seizing large prey
The humeri in Smilodon are stronger than the femora, which can be related to the functions of seizing and killing the prey with the fore limbs (Akersten, 1985; Anyonge, 1996). In felines, canines and incisors are normally used in killing, and have circular sections to withstand unpredictably directed bending stresses due to the twisting and struggling of the prey (see also Farlow et al ., 1991); but sabretooths are prevented from that style of dispatching prey by their long, highly specialised canines (Biknevicius and Van Valkenburgh, 1996) that had to penetrate tissues without the prey moving in such a way that could break them. Consequently, those inferred habits would require extremely strong humeri to properly seize and immobilise prey.
Very large herbivores escape predation by virtue of their size, at least as adults (Owen-Smith, 1988). In Africa and Asia today, the adult body mass of 1,000 kg seems to be the boundary between those mammals that are susceptible to predation and those that are not. Particularly interesting is the case of the giraffe ( Giraffa camelopardalis [Linnaeus]). Male giraffes have an adult body mass larger than one tonne and are not do not usually fall victim to predation, while females seldom reach one tonne and are sometimes successfully attacked by lions (Owen-Smith, 1988). A similar phenomenon, i.e. that a size threshold existed for escaping predation by size alone, might have been present in the Lujanian, especially with regard to juveniles, although perhaps that threshold could have been somewhat higher. Indeed, Smilodon may have been capable of bringing down larger prey than could a conical-toothed feline (Akersten, 1985). Even the short-faced bear Arctodus may have been able to hunt large prey, although the South American species was not as large as its North American relative, A . simus (Cope), whose colossal mass, skull morphology, teeth and limbs would certainly indicate that hunted large prey, perhaps even subadult proboscideans (Christiansen, 1999). Therefore, it seems very likely that Macrauchenia must have needed locomotory adaptations to escape predation from these very large carnivores.
Dodging and swerving
As shown by Howland (1974), terrestrial prey can successfully escape from a faster predator if it can swerve on an arc of a circle of lower radius. Another condition to be satisfied is that the prey must not dodge too soon, as in this case the predator can dodge too and catch it. Thus, for optimum efficiency dodging and swerving should be performed with the predator close by. Extant predators, such as the big cats, simply chase after the prey at the initial phases of the hunt, but as they get closer to the prey they synchronise their stride frequency to match that of the prey (Thomas, 1996). A change of direction at close distance can help in breaking this synchrony of strides and enhance escape chances.
An animal running with a speed v along a circular arc of radius r has acceleration towards the centre of the circle. Let v2/r be the acceleration of the prey and V2/R that of the predator (figure. 2). The inequality v2/r > V2/R should hold for prey to escape. If both terms are divided by g (the acceleration of free fall), the inequality remains unchanged, and an analogue of the Froude number (a dimensionless speed, Alexander, 1982) is obtained for circular motion. McMahon and Bonner (1983) studied this movement for a turning bicycle, and found that the angle of inclination áis a function of that dimensionless quantity. In their illustration, v2/gr =1 when the angle α=45º. The curve relating both variables can be regarded as linear within the interval between α=10º and α=45º. Additionally, the swerving capability of running animals may be limited by the coefficient of friction µm between the feet and the ground (figure 3). The mean vertical component of the force on the feet equals the weight of the animal so the mean frictional force cannot exceed µmg and the greatest possible sideways acceleration is µg . Since tan α is ?mg/mg, it can be stated that tan α max = µ and hence α max = Arctan µ . A swerving animal must lean over as shown in figure 3; but in a steady circular motion the ground reaction force (including the friction force) will lie approximately (although not necessarily exactly) in the sagittal plane of the leg. In that case, transverse bending moments on leg bones would not be significantly larger than when running straight. Unfortunately, we are not aware of any experimental evidence either from force plate measurements or from implanted strain gauges that show that large transverse moments act on bones in swerving. However, it is theoretically expected that during the change of the motion from a straight line to a circular one, an acceleration appears that is related with the rotation to the body in a sagittal plane, and the ground reaction force would produce important transversal bending in the limb long bones.
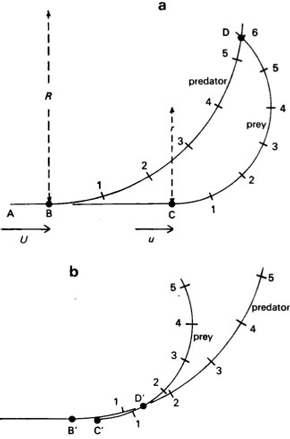
Figure 2. a, Diagram of a predator chasing a slower prey along the line ABC. At C, the prey swerves to the left, and continues at speed u along a circular arc of radius r. At B, the predator starts swerving at speed U along an arc of radius R , and intersects the prey path at D. A. A chase with u =0.75 U , r =0.5 R : the prey arrives at D after 6 units of time and the predator after only 5.4. Therefore, it can intercept and capture the prey at D. b, another chase in which the prey delays its swerve until the predator is much closer. The arcs intersect at D', and the prey escapes because it arrives there after 1.3 time units and the predator after 1.4 units (modified from Alexander, 1982) / Diagrama de un depredador persiguiendo una presa más lenta a lo largo de la línea ABC. En C, la presa dobla hacia la izquierda y continúa a velocidad u a lo largo de un arco de círculo de radio r . En B, el depredador empieza a doblar a velocidad U a lo largo de una arco de radio R , e intersecta el camino de la presa en D.A. Un persecución con u =0,75 U , r =0,5 R : la presa llega a D después de seis unidades de tiempo y el depredador después de solamente 5,4. Por lo tanto, puede interceptar y capturar la presa en D.B. Otra persecución en la cual la presa demora su giro hasta el depredador está mucho más cerca. Los arcos se intersectan en D' y la presa escapa porque llega a ese punto después de 1,3 unidades de tiempo y el depredador después de 1,4 unidades (tomado de Alexander, 1982).

Figure 3. Diagram showing external forces acting on a mammal running on a curve and the inclination angle α (modified from Alexander, 1982) / Diagrama mostrando las fuerzas externas que actúan en un mamífero corriendo en una curva y el ángulo de inclinación α (tomado de Alexander, 1982).
The parasagitally inclined humeri of larger mammals should be expected to have higher strength indicator values in the anteroposterior than in the mediolateral planes, and to be stronger than the femora, which are held substantially more vertically. As is evident from table 1, this is exactly the observed pattern, although this primarily relates to how the bones are held (their angle to vertical) - i.e ., bending moments.
The humerus of Macrauchenia is, however, markedly stronger in the mediolateral than anteroposterior plane, a very unusual condition in an animal with elbow flexure and parasagittal limbs. With such a limb posture, bending moments are expected to be stronger in the anteroposterior direction. However, this condition is not reflected in the morphology of the proximal element of the forelimb, although the radius shows an unusual medial flange.
Limb postures in large animals are more upright than in small forms, as a means of preserving resistance to bending moments at a large body size (Biewener, 1989a, 1989b, 1990). In animals with near columnar limbs, such as elephants or sauropod dinosaurs, this vertical limb pattern reaches its extreme. The significance of mediolateral as opposed to anteroposterior loading of elephant limbs is easily observed in the great mediolateral bone diameter of the femur compared to its anteroposterior diameter (Carrano, 1998).
However, not even elephants or rhinos have such a large t/ap strength indicator value ratios in the humerus as Macrauchenia (0.9 Loxodonta - 1.10 in Ceratotherium simum (Burchell), with Diceros , Tapirus and Elephas falling in between [Christiansen, 1997, 1998; Christiansen and Paul, 2001]). The femur of elephants is much stronger mediolaterally than anteroposteriorly ( t/ap ratios of 1.33-1.42 in Elephas and Loxodonta ), but in the smaller Macrauchenia the value is even higher (1.45, table 1). As Macrauchenia was a flexed-limbed animal evidently capable of true running with a suspended phase, a change in limb postures associated with its rather large size (1,100 kg) is not able to explain the unusual limb bone cross section. In fact, the contrary situation should be expected, as noted above; i.e ., that the bones would be stronger in the anteroposterior plane.
Although caution is always urged when dealing with fossil species with no living relatives or modern analogues, we propose here that swerving and dodging rather than higher speed might have been the strategy that Macrauchenia used to flee from the attack of Smilodon , given that this felid was proposed to have been an ambushing predator (see below) whose attack could only have been avoided by a sudden acceleration, either forward or lateral.
This possibility, i.e. that of a lateral acceleration due to swerving, might produce a loading pattern that could explain the unusual bone proportions. This proposal would be weaker if this condition was a phylogenetic landmark of the whole group, although in that case the fact that the whole clade might have had the same behaviour could not be ruled out. In any case, the personal observations of one of us (RAF) on the admittedly much smaller (and hence potentially allometrically different) Tertiary litopterns do not support this possibility.
The transverse bending moment due to the lateral displacement of centre of mass with respect to the limb axis increases as the animal starts to swerve. The transverse bending moment in static position depends mainly on the distance between the centre of mass and the shoulder or the hip joint, as well as the orientation of the limb bone to vertical, as torsional moments about the diaphyses are included in the bending component.
Interestingly, Howland's (1974) model predicts that pack hunters have more chances to succeed than lone hunters. As noted above, the prey may evade the leading predator by swerving when this predator is close behind, but other predators further back in the pack may be well placed to catch it as it swerves. Moreover, swerving seems to be a better strategy to escape from ambushers or short-distance chasers than from long distance chasers, which may be able to catch up a number of times when avoided.
Anyonge (1996) related limb bone dimensions and habits in several carnivores, and obtained results for the North American species Smilodon fatalis that placed it as an ambusher, with ambulator being the second best interpretation. In most studies of the North American species (see Palmqvist and Arribas, 2001, for review), there is a wide consensus that Smilodon was an ambush predator like all modern felids (with the exception of the cheetah), although with some differences, such as its plantigrade hindlimb. Further, Akersten (1985) suggested that S . fatalis might have been a social hunter, by counting the entrapped mammals in the tar pits of Rancho La Brea. Although this kind of evidence is not available for the South American species, its proposed presence in a closely related species is suggestive.
Macrauchenia is placed in the mediportal group in plots of mammalian limb bone relative dimensions by Carrano (1998), Christiansen (1998) and Christiansen and Paul (2001). It has a metatarsus length/femur length ratio (0.407), which is similar to a smaller ceratomorph such as a tapir (0.37); lower than those of large bovids and equids ( e.g . Syncerus 0.55, Bison bison 0.56, eland antelopes 0.75-0.85, equids 0.63-0.71); somewhat higher than in rhinos (which can gallop; white rhino 0.34, black rhino 0.33); and much higher than in elephants (0.20-0.25). It should be noted that there is a correlation between speed and MT/F ratio, at least when cursorial and non-cursorial forms are compared (Garland and Janis, 1993), and also that this ratio decreases with body mass (Janis and Wilhelm, 1993). Furthermore, Christiansen (2002) found significant relationship between MT/F ratio and speed, but radius/humerus was equally good. Bone ratios overall (including MT/F) do not correlate well at all with speed, probably because energetical locomotion is more important than just running fast.
Therefore, Macrauchenia could have been a rather fast runner, perhaps as fast as or even faster than a rhinoceros, which is also suggested by the value of the IACap for the femur, which is 50% higher than expected for a mammal of its size. Although they do not run over long distances, black rhinos are rather fast gallopers (Paul, 1988; see also Garland and Janis, 1993, who cite a speed of 45 km h-1, and Nowak, 1991, who cites 50 km h-1 in black rhinos and 40 km h-1 in white rhinos). As Owen-Smith (1988) notes, no present megaherbivore mammal has a special response to predators, because they have no natural enemies as adults. However, the Pleistocene large mammals may well have had predators, as sabretooths and short-faced bears, and perhaps even others like the giant sloth Megatherium (Fariña and Blanco, 1996).
However, speed might have not been enough for Macrauchenia to avoid predation, as sabre-tooths might have ambushed and chased it from a very short distance. Also, and in contrast with the smaller equid Hippidion (as inferred from its strength indicators values and by analogy with modern equids such as those studied here), it could not have had a particularly high forward acceleration given its larger size. Therefore, we propose here that Macrauchenia might have relied mainly on sudden dodging. Indeed, its antero-posterior bone strength was not as high as those observed in the fast runners studied here, and therefore it can be assumed that this species was not designed to optimise speed in one direction. Moreover, the proposed behaviour would explain the observed higher transverse strength, as swerving might have been an activity that imposed severe transverse bending stress to the limb bones. The same pattern is found in the ratites, which swerve when attacked by a faster predator (Rodríguez de la Fuente, 1979; Lluch and Fariña unpublished). The fact that bipedal running birds are used as a modern analogue of a quadrupedal mammal does not introduce any error in our analysis, as it can be safely assumed that the reactions of their long bones to the imposed maximum stresses are not different, although there might possibly be some differences in manoeuvrability. Furthermore, the retention of three digits in both pairs of limbs in Macrauchenia can be regarded as another feature presumably favourable to dodging, as it may increase manoeuvrability. The mammalian swervers considered here had ratios that were not significantly different from one, although the femora of the gazelle tend to be stronger transversely than anteroposteriorly.
A word must be said about the biological meaning of the ratio IACt / IACap and its statistical significance. It is unlikely that this ratio would turn out to be different from one at a statistically significant level in all swervers. That would imply that swerving is not only frequent, but significantly preferred. In other words, our applying this simple statistic should be regarded as conservative. The modern mammalian swervers studied here tend to escape by running fast, and often swerve as well. Therefore, even ratios that are below statistical significance, but still high, might be interpreted as indicating swerving abilities.
A simple bipedal posture, as in the two-legged high browsing by Waller's gazelle Lithocranius walleri , does not apply bending stresses on the long bones great enough to risk failure. Instead, peak velocity and jumping place the greatest amount of stress on the long bones (although in the horse metacarpus it is during cantering). It should therefore be expected that the appendicular anatomy be primarily adapted to cope with stresses imposed on it by these activities.
The disparity in the strength indicators between the humeri and the femora in Macrauchenia remains unexplained. Perhaps it was related to a strenuous fighting activity, although horses fight with their hind limbs some times and do not show this morphology, or to a differential demand imposed by details in the way of swerving upon one and other pair of limbs. Although large mammals nearly always have considerably stronger humeri than femora (since the strength indicator does not take bone angle into account), the difference in Macrauchenia is rather large and seems difficult to explain it only by this factor.
Fast running
As for a different strategy, Hippidion seems likely to have relied primarily upon fast running without swerving, as its humerus dimensions are much stronger anteroposteriorly than transversely. Zebras also run fast to escape predators (Nowak, 1991). The pattern of bone strength shown by one of the zebras is almost exactly the same observed in the Lujanian equid species. Also, and although horses do swerve well, the single hoof is an appropriate adaptation for high ground reaction forces, but not for higher manoeuvrability (see Hildebrand et al ., 1985). The femora of zebra and Hippidion (and a similar pattern is observed in the tiger) are very similar too, as they have circular sections. This might mean that the stresses imposed on the femora are less predictable than those imposed on the humeri. Indeed, when stresses are more predictable, the shape of the structure tends to optimise its design to withstand those particular stresses. A circular cross-section would be optimal to withstand stresses that may be exerted in any directions (see Biknevicius and Van Valkenburgh [1996] for discussion of cross-section shapes in differentially strong canine in felids and canids).
Conclusions
Although the Lujanian fauna is different from other mammalian faunas in several respects (Fariña, 1996; Fariña and Vizcaíno, 1999), the antipredator strategy of one of its members, Macrauchenia , can be interpreted in terms of modern mammals. Our current understanding of terrestrial locomotor biomechanics adequately explains its features as related to the ability to swerve and dodge. Modern ostriches behave in the way we propose for this Lujanian species, and they have comparable leg bone dimensions. Another member of this fauna used for comparison, the fossil horse Hippidion , may have relied primarily on fast running, as modern related species and as suggested also by its appendicular morphology, to escape predation.
Acknowledgements
We are most grateful to the following people for critical reading of earlier versions of this paper: Robert McNeill Alexander, Christine Janis, Leo Joseph, Bruce Shockey, Sergio F. Vizcaíno and Blaire Van Valkenburgh. Susana Bargo and Sergio F. Vizcaíno helped with many of the measurements. Olivia Lluch allowed us to use her data on rheas. This paper is a contribution to the projects Fondo Clemente Estable 6057, CONICYT, Uruguay, IGCP 449, N336, Universidad Nacional de La Plata, and PICT 7-6348.
References
Alberdi, M.T. and Prado, J.L. 1993. Review of the genus Hippidion Owen, 1869 (Mammalia: Perissodactyla) from the Pleistocene of South America. Zoological Journal of the Linnean Society 108: 1-22. [ Links ]
Alberdi, M.T., Prado, J.L. and Ortiz-Jaureguízar, E. 1995. Patterns of body size changes in fossil and living Equini (Perissodactyla). Biological Journal of the Linnean Society 54: 349-370. [ Links ]
Alexander, R.McN. 1982. Locomotion of Animals . Blackie, Glasgow, 163 pp. [ Links ]
Alexander, R.McN. 1983a. Animal Mechanics , 2nd edn. Blackwell Scientific, London, 301 pp. [ Links ]
Alexander, R.McN. 1983b. Allometry of the leg bones of moas (Dinornithes) and other birds. Journal of Zoology 200: 215-231. [ Links ]
Alexander, R.McN. 1985. Mechanics of posture and gait of some large dinosaurs. Zoological Journal of the Linnean Society 83: 1-25. [ Links ]
Alexander, R.McN. 1989. Dynamics of Dinosaurs and other extinct giants . Columbia University Press, New York, 167 pp. [ Links ]
Alexander, R.McN., Jayes, A.S., Maloiy, G.M.O. and Wathuta, E.M. 1979. Allometry of the limb bones of mammals from shrews (Sorex) to elephant (Loxodonta). Journal of Zoology 189: 305-314. [ Links ]
Akersten, W.A. 1985. Canine function in Smilodon (Mammalia; Felidae; Machairodontidae). Contributions in Science 365: 1-22. Natural History Museum of Los Angeles County . [ Links ]
Anyonge, W. 1993. Body mass in large extant and extinct carnivores. Journal of Zoology 231: 339-350. [ Links ]
Anyonge, W. 1996. Locomotor behaviour in Plio-Pleistocene sabre-tooth cats: a biomechanical analysis. Journal of Zoology 238: 395-413. [ Links ]
Bargo, M.S., Vizcaíno, S.F., Archuby, F. and Blanco, R.E. 2000. Limb bone proportions, strength and digging in some Lujanian (Late Pleistocene-Early Holocene) mylodontid ground sloths (Mammalia, Xenarthra). Journal of Vertebrate Paleontology 20: 601-610. [ Links ]
Biewener, A.A. 1983. Allometry of quadrupedal locomotion: The scaling of duty factor, bone curvature and limb orientation to body size. Journal of Experimental Biology 105: 147-171. [ Links ]
Biewener, A.A. 1989a. Scaling body support in mammals: Limb posture and muscle mechanics. Science 245: 45-48. [ Links ]
Biewener, A.A. 1989b. Mammalian terrestrial locomotion and size. Mechanical design principles define limits. Bioscience 39: 776-783. [ Links ]
Biewener, A.A. 1990. Biomechanics of mammalian terrestrial locomotion. Science 250: 1097-1103. [ Links ]
Biknevicius, A.R. and Van Valkenburgh, B. 1996. Design for killing: craniodental adaptations of predators. In: J.L. Gittleman (ed.), Carnivore Behavior, Ecology, and Evolution 2: 393-428. Cornell University, Ithaca, New York. [ Links ]
Björck, G. 1958. Studies on the drag force of horses. Acta Agrícola Scandinavia ( Supplement ) 4: 1-109. [ Links ]
Carrano, M. 1998. Locomotion in non-avian dinosaurs: integrating data from hindlimb kinematics, in vivo strains, and bone morphology. Paleobiology 24: 450-469. [ Links ]
Christiansen, P. 1997. Locomotion in sauropod dinosaurs. Gaia 14: 45-75. [ Links ]
Christiansen, P. 2000. Strength indicator values of theropod long bones, with comments on limb proportions and cursorial potential. In: B. Pérez-Moreno, T.R. Jr., Holtz, J.L. Sanz and J.J. Moratalla (eds.), Theropod Paleobiology Special Volume. Gaia 15: 241-255. [ Links ]
Christiansen, P. 1999. What size were Arctodus simus and Ursus spelaeus (Carnivora: Ursidae)? Annales Zoologica Fennici 36: 93-102. [ Links ]
Christiansen, P. 2002. Locomotion in terrestrial mammals: the influence of body mass, limb length and bone proportions on speed. Zoological Journal of the Linnean Society 136: 685-714 [ Links ]
Christiansen, P. and Fariña, R.A. 2003. Mass estimation of two fossil ground sloths (Xenarthra; Mylodontidae). Senckerbergiana Biologica 83: 95-101. [ Links ]
Christiansen, P. and Paul, G.S. 2001. Limb bone scaling, limb proportions and bone strength in neoceratopsian dinosaurs. Gaia 16: 13-29. [ Links ]
Fariña, R.A. 1995. Bone strength and habits in large glyptodonts. Lethaia 28: 189-196. [ Links ]
Fariña, R.A. 1996. Trophic relationships among Lujanian mammals. Evolutionary Theory 11: 125-134. [ Links ]
Fariña, R.A. and Blanco, R.E. 1996. Megatherium, the stabber. Proceedings of the Royal Society B 263: 1725-1729. [ Links ]
Fariña, R.A. and Vizcaíno, S.F. 1995. Hace Sólo Diez Mil Años. Fin de Siglo , Montevideo, 125 pp. [ Links ]
Fariña, R.A. and Vizcaíno, S.F. 1999. A century after Ameghino: the palaeobiology of the large Quaternary mammals of South America revisited. Quaternary of South America and the Antarctic Peninsula 12: 255-277. [ Links ]
Fariña R.A., Vizcaíno, S.F. and Bargo, M.S. 1998. Body mass estimations in Lujanian (Late Pleistocene-Early Holocene of South America) mammal megafauna. Mastozoología Neotropical 5: 87-108. [ Links ]
Fariña, R.A., Vizcaíno, S.F. and Blanco, R.E. 1997. Scaling of the indicator of athletic capability in fossil and extant land tetrapods. Journal of theoretical Biology 185: 441-446. [ Links ]
Farlow, J.O., Brinkman, D.L., Abler, W.L. and Currie, P.J. 1991. Size, shape, and serration density of theropod dinosaur lateral teeth. Modern Geology 16: 161-198. [ Links ]
Garland Jr., T. and Janis, C.M. 1993. Does metatarsal/tarsal ratio predict maximal running speed in cursorial mammals? J ournal of Zoology 229: 133-151. [ Links ]
Gatesy, S.M. 1991. Hindlimb scaling in birds and other theropods: Implications for terrestrial locomotion. Journal of Morphology 209: 83-96. [ Links ]
Hildebrand, M., Bramble, D.M., Liem, K.F. and Wake, D.B. (eds.). 1985. Functional vertebrate morphology . Harvard University, Cambridge, Mass., 430 pp. [ Links ]
Howland, H.C. 1974. Optimal strategies for predator avoidance: the relative importance of speed and manoeuvrability. Journal of theoretical Biology 47: 333-350. [ Links ]
Janis, C. and Wilhelm, P.B. 1993. Were there mammalian pursuit predators in the Tertiary? Dancing with wolf avatars. Journal of Mammalian Evolution 1: 103-125. [ Links ]
McMahon, T.A. and Bonner, J.T. 1983. On Size and Life. Scientific American Library, New York, 255 pp. [ Links ]
Nowak, R.M. 1991. Walker's Mammals of the World . Johns Hopkins University, Baltimore, 1629 pp. [ Links ]
Owen-Smith, R.N. 1988. Megaherbivores: The influence of very large body size on Ecology . Cambridge University, Cambridge, 369 pp. [ Links ]
Palmqvist, P. and Arribas, A. 2001. Taphonomic decoding of the paleobiological information locked in a lower Pleistocene assemblage of large mammals. Paleobiology 27: 512-530. [ Links ]
Pascual, R., Hinojosa, E., Gondar, D. and Tonni, E. 1965. Las Edades del Cenozoico mamalífero de la Argentina, con especial atención a aquéllas del territorio bonaerense. Anales de la Comisión de Investigación Científica de Buenos Aires 6: 165-193. [ Links ]
Paul, G.S. 1988. Predatory Dinosaurs of the World . A Complete Illustrated Guide. Simon and Shuster, New York, 464 pp. [ Links ]
Rodríguez de la Fuente, F. 1979. Enciclopedia Salvat de la fauna . I. África (Región Etiópica). Salvat, Pamplona, 247 pp. [ Links ]
Rollinson, J. and Martin, R.D. 1981. Comparative aspects of primate locomotion, with special reference to arboreal cercopithecines. Symposium of the Zoological Society of London 48: 377-427. [ Links ]
Rubin, C.T. and Lanyon, L.E. 1982. Limb mechanics as a function of speed and gait: a study of functional strains in the radius and tibia of horse and dog. Journal of Experimental Biology 101: 187-211. [ Links ]
Sefve, I. 1924. Macrauchenia patachonica . Bulletin of the Geological Institute of the University of Upsala 19: 1-21. [ Links ]
Thomas, D.A. 1996. Dancing predators: Modern predators pick up prey's rhythm to facilitate attacks. Journal of Vertebrate Paleontology ( supplement ) 16: 68A-69A. [ Links ]
Recibido: 6 de junio de 2003.
Aceptado: 1 de enero de 2005.














