Aproximaciones para el cálculo del geoide isostático

Crovetto, C.¹, Molinari, R.², Introcaso, A.³

Grupo de Geofísica - Instituto de Física Rosario (CONICET - UNR) - Facultad de Ciencias Exactas, Ingeniería y Agrimensura - Universidad Nacional de Rosario, Av. Pellegrini 250 - (2000) Rosario - Santa Fe
Emails: ¹crovetto@fceia.unr.edu.ar;
² molinari@fceia.unr.edu.ar;
³ geofisic@fceia.unr.edu.ar

RESUMEN
El objetivo de este trabajo es evaluar las fórmulas aproximadas en una y dos dimensiones para calcular las ondulaciones del geoide de una estructura compensada, con el fin de realizar rápidos estudios isostáticos. Se analizan casos de estructuras topográficas elevadas y de cuencas sedimentarias considerando la hipótesis de Airy y la hipótesis de Pratt, para determinar la confiabilidad de estas aproximaciones en cada caso. Se presentan dos ejemplos reales que coinciden con las tendencias encontradas.
Palabras claves: Geoide; Isostasia.

ABSTRACT
Approximations to evaluate the isostatic geoid. The aim of this work is to evaluate the approximate expressions in one and two dimensions to obtain geoid undulations of balanced structures, with the purpose of performing rapid isostatic analysis. We analyse topographic elevations and sedimentary basins, considering Airy's and Pratt's hypothesis. We present two real examples that support our results.
Keywords: Geoid; Isostasy.

Introducción

Los análisis isostáticos de las estructuras geológicas se realizan usualmente a través de las anomalías isostáticas. Dichas anomalías se calculan a partir de las anomalías de aire libre, aplicando dos correcciones: una por el efecto de la masa topográfica, y otra por el efecto de la masa compensadora teórica que requiere dicha estructura para estar en equilibrio (Heiskanen y Moritz 1967).

Para estimar el efecto de la masa topográfica generalmente se la divide en cuerpos elementales (como paralelepípedos o poliedros), y se calcula la atracción total como suma de las atracciones individuales de dichos cuerpos. Este proceso consume un tiempo de cálculo relativamente importante, sobre todo cuando la descripción de la masa es muy detallada. En el siglo XVIII, Pierre Bouguer propuso una relación sumamente sencilla para encontrar el efecto gravitatorio producido por la masa topográfica sobre una estación, en la cual dicha masa se reemplaza por una losa plana indefinida cuyo espesor coincide con la altura de la estación (Heiskanen y Moritz, 1967). Esta aproximación, que en principio parece descabellada, resulta ampliamente satisfactoria debido a que si bien considera una masa más extensa que la realmente existente, la influencia de las masas más lejanas sobre una estación es muy poco significativa. La diferencia entre la atracción generada por la masa real finita y la generada por esta losa plana indefinida resulta muy pequeña, y en general puede despreciarse. Para tener una idea concreta del error que se comete al considerar la gravedad producida por esta losa plana equivalente, podemos observar la figura 1. Allí se muestran la atracción que genera un paralelepípedo de base cuadrada de 2 km de altura y densidad igual a r = 2,67 g/cm³ y la atracción de una losa plana indefinida de igual altura y densidad, en función del ancho del paralelepípedo (arista de la base). Como se observa, las diferencias son apreciables sólo para estructuras muy angostas, siendo menores al 10% (20 mGal) para cuerpos de más de 50 km de ancho. Esto nos permite ver que esta aproximación, que parecía sumamente grosera, proporciona muy buenos resultados en forma sencilla. Debido a esta practicidad, Bouguer propuso esta forma de cálculo para eliminar el efecto topográfico de las anomalías de aire libre, y obtener las denominadas anomalías simples de Bouguer, que reflejan solamente el efecto de las masas compensadoras ocultas.

Figura 1: Comparación de la gravedad producida por un paralelepípedo de sección cuadrada, densidad igual a r = 2,67 g/cm³ , 2 km de altura y ancho variable (en línea sólida), con la gravedad producida por una losa plana indefinida de igual altura y densidad (en línea a trazos y puntos).

Siguiendo la misma idea de Bouguer, Haxby y Turcotte (1978) propusieron expresiones aproximadas para el cálculo de las ondulaciones del geoide generadas por estructuras isostáticamente compensadas. Estas aproximaciones reemplazan la estructura y su masa compensadora por losas planas indefinidas, para las cuales se calculan los potenciales gravitatorios, y finalmente las ondulaciones del geoide a través de la conocida fórmula de Bruns (Heiskanen y Moritz 1967):

          (1)

en donde N(x, y) representa la ondulación del geoide en un punto de coordenadas (x, y), V(x, y, 0) es el potencial perturbador total sobre el geoide generado por ambas losas y g = 980 Gal es la gravedad general adoptada. Si bien esta forma de aproximar las estructuras reales mediante losas planas indefinidas puede parecer nuevamente grosera, sucede aquí algo parecido a lo expuesto anteriormente para la anomalía de Bouguer, y las estimaciones no resultan tan malas. Sin embargo, como el efecto de las masas más lejanas incorporadas ficticiamente por la losa indefinida es más importante sobre el potencial gravitatorio que sobre la atracción, la diferencia entre los cálculos exactos y los aproximados es mayor en el caso de las ondulaciones del geoide que en el caso de la gravedad. Remarquemos el hecho de que Haxby y Turcotte (1978) al hacer estas aproximaciones, resuelven la ondulación en términos de una función que depende únicamente de la altura de la estructura en estudio, además de las densidades y del espesor cortical normal asumidos como valores fijos; por ello estas aproximaciones resultan unidimensionales. Además son aproximaciones válidas únicamente para estructuras compensadas, ya sea considerando la hipótesis de Airy o la de Pratt.

Así como las aproximaciones en una dimensión nos permiten evaluar las ondulaciones del geoide de estructuras compensadas en forma expeditiva, existen aproximaciones en dos dimensiones. Dado un perfil de altitudes de una estructura y suponiendo que la misma se extiende infinitamente en el sentido transversal al perfil, las ondulaciones del geoide pueden obtenerse en forma aproximada mediante el cálculo del potencial de cuerpos rectangulares infinitos en esa dirección aplicando nuevamente la fórmula de Bruns (1). Para trabajar en forma exacta, la estructura y su masa compensadora se deben dividir en cuerpos tridimensionales sencillos (por ejemplo paralelepípedos), obteniendo el potencial total a partir de la integración exacta en tres dimensiones del potencial de dichos cuerpos. Finalmente, y como en los casos uni y bidimensionales, la ondulación del geoide se obtiene desde (1).

Ya hemos mencionado que tradicionalmente los análisis isostáticos se han realizado con las anomalías isostáticas; en forma reciente se empezaron a tener en cuenta las ondulaciones del geoide para este tipo de estudios (Introcaso et al. 2000, Cornaglia e Introcaso 2004, Crovetto e Introcaso 2004). Las ondulaciones del geoide generadas por una estructura teórica isostáticamente compensada pueden compararse con las ondulaciones del geoide observadas sobre la estructura real (en longitudes de onda compatibles con su ancho), y de esta forma disponer de otra vía de análisis isostático.

En este trabajo presentamos una evaluación de los alcances y limitaciones de las aproximaciones en una y dos dimensiones para el cálculo de las ondulaciones del geoide considerando estructuras compensadas, comparando sus resultados con los valores que surgen del cálculo exacto en tres dimensiones. Así podremos evaluar la aplicabilidad de estos caminos alternativos que nos permitirán hacer los análisis isostáticos en forma más expeditiva.

Mecanismo de compensación isostática

La isostasia estudia el equilibrio de la corteza terrestre. Cuando la corteza se eleva respecto del nivel medio del mar, como por ejemplo en el caso de un rasgo montañoso, debe existir algún tipo de mecanismo que compense este exceso de masa. De igual modo en las cuencas, tanto oceánicas como sedimentarias, algo debe contrarrestar el defecto de masa generado por el relleno de agua o sedimentos.

Existen diversas hipótesis isostáticas, siendo las más antiguas las debidas a Airy (1855) y Pratt (1855). En sus trabajos, ambos autores asumen que el equilibrio de la corteza se logra en forma local gracias a variaciones del espesor cortical y de la densidad litosférica respectivamente. Posteriormente, Vening Meinesz (1939) propuso la hipótesis flexural, según la cual la capa externa se comporta como una losa elástica que flexiona bajo la aplicación de una carga, dando lugar a una compensación regional (Watts 2001). Centraremos nuestro estudio en las tradicionales hipótesis de Airy y de Pratt (también denominada hipótesis térmica) ya que estos modelos clásicos son los considerados en el trabajo original de Haxby y Turcotte (1978) sobre aproximaciones unidimensionales para el cálculo del geoide; cualquier otro modelo puede evaluarse en forma similar al que aquí se presenta. Además, como la hipótesis de Airy que constituye un caso extremo del sistema flexural, proporciona la máxima deflexión cortical esperada, y todos los demás casos quedan acotados por ella.

En su hipótesis, Airy propone que la corteza se divide en bloques adyacentes de igual densidad, que se encuentran flotando en el manto en perfecto equilibrio hidrostático (Fig. 2). Para lograr dicho equilibrio los bloques que sobresalen del nivel medio del mar poseen una raíz compensadora que se hunde desplazando al manto (Fig. 2). En el caso de cuencas, para que exista equilibrio hidrostático el manto debe surgir desplazando a la corteza de su posición original, generando antirraíces (Fig. 2). En el caso de bloques topográficos elevados, el equilibrio hidrostático presupone la existencia de una raíz cortical cuyo espesor D R es igual a:

       (2)

donde h representa la altura del bloque sobre el nivel de referencia, r_t corresponde a la densidad de la topografía, r_ci a la densidad de la corteza inferior y r_m a la densidad del manto superior. Esta raíz se extiende por debajo de la corteza de espesor normal T_N (Fig. 2). En el caso de cuencas, la antirraíz D R' debe tener un espesor igual a:

     (3)

donde h' representa la profundidad de la cuenca, r_s corresponde a la densidad de los sedimentos (o agua más sedimentos en el caso de cuencas oceánicas), r_cs es la densidad de la corteza superior, r_ci es la densidad de la corteza inferior y r_m es la densidad del manto superior.

Figura 2: Bloques topográficos y cuencas (sedimentarias u oceánicas) en la hipótesis de Airy. r_t es la densidad de la topografía, r_cs es la densidad de la corteza superior, r_ci es la densidad de la corteza inferior, r_m es la densidad del manto superior, r_s es la densidad del relleno de la cuenca (sedimentos o agua y sedimentos), T_N representa el espesor normal de la corteza, h representa la altura en topografías elevadas, h' representa la profundidad en las cuencas, DR es el espesor de la raíz, y DR' es el espesor de la antirraíz.

La hipótesis de Pratt (o hipótesis térmica), establece que la compensación se produce a nivel litosférico en lugar de a nivel cortical, mediante bloques adyacentes de diferentes densidades (Fig. 3). Según esta hipótesis, todos los bloques producen la misma presión sobre una superficie denominada superficie de compensación. Las densidades dependen de las alturas de los bloques y de la profundidad de compensación adoptada (Fig. 3). Los bloques elevados sobre el nivel del mar deben tener una densidad r _{bloque 1} inferior a la densidad media de la litosfera, dada por:

     (4)

donde H representa la profundidad de la superficie de compensación (generalmente una profundidad de 100 km que es el espesor aproximado de la litosfera), h es la altura del bloque por sobre el nivel del mar y r _lit es la densidad media de la litosfera (Fig. 3). Los bloques por debajo de las cuencas (oceánicas o sedimentarias), deben tener una densidad r _{bloque 2} mayor a la media de la litosfera, dada por la expresión:

     (5)

h' simboliza aquí la profundidad de la cuenca, r _s es la densidad del relleno sedimentario (o del agua más sedimentos para casos oceánicos), r _lit es la densidad media de la litosfera y H es la profundidad de la superficie de compensación.

Figura 3: Bloques topográficos y cuencas (sedimentarias u oceánicas) en la hipótesis de Pratt. r _lit es la densidad de la litosfera normal, r _s es la densidad del relleno de la cuenca (sedimentos o agua y sedimentos), r _{bloque 1} es la densidad de la columna vertical correspondiente a un alto topográfico, r _{bloque 2} es la densidad de la columna vertical debajo de una cuenca, H es la profundidad de la superficie de compensación, h representa la altura en topografías elevadas y h' representa la profundidad en las cuencas.

Fórmulas exactas para el cálculo de las ondulaciones del geoide en tres dimensiones

El cálculo de las ondulaciones del geoide de una estructura compensada se hace a partir del cálculo de los potenciales gravitatorios de la masa topográfica (o bien del relleno de la cuenca) y de la masa compensadora, utilizándose la fórmula de Bruns (1). Una forma simple de realizar el cálculo de los potenciales es dividir a cada masa en un conjunto de paralelepípedos rectos, y calcular el potencial como la suma de las contribuciones de todos ellos. El potencial V de cada paralelepípedo en un punto P(x, y, z) puede ser calculado en forma exacta a través de la siguiente expresión (Guspí 1999):

     (6)

En esta expresión, Dx _i = x - x_i, Dy _i = y - y_i , Dz _i = z - z_i son las diferencias entre las coordenadas del punto y las caras del paralelepípedo (x₁, x₂, y₁, y₂, z₁, z₂), es la distancia entre el punto P(x, y, z) y cada uno de los ocho vértices del paralelepípedo, G es la constante de gravitación universal y es la densidad volumétrica de masa del paralelepípedo.

Una vez calculado el potencial perturbador total sobre el geoide (z = 0) como suma de los potenciales de las masas visibles y de las masas compensadoras (Fig. 2 y Fig. 3), se encuentra en forma exacta la ondulación isostática del geoide producida por toda la estructura usando la fórmula de Bruns (1).

Fórmulas aproximadas para el cálculo de las ondulaciones del geoide en dos dimensiones

Muchas veces se considera a la estructura en estudio como bidimensional. Es decir, se considera que la estructura se extiende infinitamente en la dirección perpendicular a un perfil. Esta aproximación es bastante adecuada en los casos de estructuras muy extendidas en una dirección. En la práctica, desde una sección central, una estructura bidimensional es aquella que tiene un largo de 3 a 5 veces su ancho.

El cálculo de las ondulaciones del geoide para estructuras de este estilo puede hacerse utilizando expresiones más simples (desaparece una dimensión) que las correspondientes a una estructura tridimensional. Nuevamente, dada una estructura compensada isostáticamente, los potenciales de la masa topográfica (o bien del relleno de la cuenca) y de la masa compensadora pueden obtenerse dividiendo a la estructura en rectángulos infinitos en dirección transversal a un perfil. El potencial V en un punto P(x, y, z) sobre el geoide (z = 0) de cada rectángulo infinito en dirección x puede integrarse como (Chapman 1979):

     (7)

donde y₁, y₂, z₁, z₂ son las coordenadas de las caras del rectángulo infinito, y la función H se define en la forma:

     (8)

Notemos que en (7) y (8) desaparece la variable x. Sumando todos los potenciales de los rectángulos que representan a las masas visibles y compensadoras, y utilizando la fórmula de Bruns (1), se obtiene la ondulación del geoide isostático que genera esta estructura bidimensional.

Fórmulas aproximadas de de Haxby y Turcotte para el cálculo de las ondulaciones del geoide en una dimensión

Las aproximaciones en una dimensión obtenidas por Haxby y Turcotte (1978) o Turcotte y Schubert (1982) para el cálculo del geoide isostático, se basan en la idea de losa plana indefinida introducida por Bouguer, e incluyen además el concepto de dipolo masivo (Introcaso 1999). Estas aproximaciones reemplazan a la masa topográfica (o al relleno de la cuenca), y a la masa compensadora por losas planas indefinidas. Las ondulaciones del geoide N que produce el conjunto dependen de la hipótesis isostática y de las densidades adoptadas, y resultan iguales a:

     (9)

donde T_N es el espesor normal de la corteza en la hipótesis de Airy; H es la profundidad de compensación en la hipótesis de Pratt; r_t, r_cs, r_ci, r_m, r_s y r_lit son las densidades de la topografía, de la corteza superior, de la corteza inferior, del manto, de los sedimentos (o del agua más sedimentos en casos oceánicos) y de la litosfera respectivamente; G es la constante de gravitación universal y g = 980 Gal es la gravedad normal asumida. En los casos de topografías elevadas h representa la altura y se considera positiva, y en los casos de cuencas h' representa la profundidad y también se considera positiva. Notemos que las expresiones (9) son independientes de x e y.

Estimación de los errores al utilizar las fórmulas aproximadas para el cálculo de las ondulaciones del Geoide

El objetivo del trabajo es evaluar los errores de las aproximaciones en una y dos dimensiones para el cálculo de las ondulaciones isostáticas del geoide generadas por estructuras elevadas y cuencas (sedimentarias u oceánicas), considerando las hipótesis isostáticas de Airy y de Pratt. Con el fin de lograr dicho objetivo, se propusieron modelos teóricos sencillos formados por dos paralelepípedos, uno representando la topografía (o al relleno de la cuenca), y el otro representando su masa compensadora. Se calcularon las ondulaciones del geoide del conjunto a través de las fórmulas exactas en tres dimensiones, y también a través de las aproximaciones en una y dos dimensiones. Los paralelepípedos tridimensionales se consideraron con alturas y anchos variables, manteniendo el largo igual al ancho (paralelepípedos de sección cuadrada). En todos los casos estudiados se calculó la ondulación del geoide en una estación E ubicada en el centro de la cara del paralelepípedo superior, sobre el geoide (z = 0) (Fig. 4).

Figura 4: a) Dos paralelepípedos tridimensionales, el superior representando la topografía o cuenca y el inferior la masa compensadora; b) Dos rectángulos bidimensionales (infinitos en una dirección), el superior representando la topografía o cuenca y el inferior la masa compensadora; c) Dos losas planas indefinidas (infinitas en dos direcciones), la superior representando la topografía o cuenca y la inferior la masa compensadora. Las flechas en (b) y (c) señalan la extensión al infinito y el punto E indica la ubicación de la estación de cálculo.

Considerando exactas las ondulaciones obtenidas con las expresiones tridimensionales, los errores relativos de las aproximaciones en una y dos dimensiones se definieron como:

     (10)

Topografías elevadas

Se calcularon las ondulaciones del geoide utilizando las fórmulas en una, dos y tres dimensiones para estructuras topográficas elevadas compensadas isostáticamente en las hipótesis de Airy y de Pratt. En la hipótesis de Airy, la densidad adoptada para el paralelepípedo topográfico fue r_t = 2,67 g/cm³, el espesor normal de la corteza fue adoptado como T_N = 33 km (Woollard 1962, Bullen 1963), y para el paralelepípedo raíz se adoptó una densidad igual al contraste entre la corteza inferior y el manto superior de Dr = r_ci - r_m = -0,4 g/cm³ (Introcaso et al. 1992). En el caso de la hipótesis de Pratt, se adoptó como densidad media de la litosfera normal r _lit = 3,1 gm/cm³ (Turcotte y Schubert 1982) y como profundidad de compensación H = 100 km.

En la figura 5 se pueden observar las ondulaciones del geoide obtenidas con las tres fórmulas (exacta y aproximadas) para un paralelepípedo de 2 km de altura en función del ancho (arista de la base), para ambas hipótesis isostáticas. Se ve claramente que la aproximación bidimensional se acerca bastante a los valores exactos, mientras que la unidimensional (constante, independiente del ancho) resulta excesiva. Las ondulaciones del geoide calculadas mediante las expresiones exactas en tres dimensiones y las aproximadas en una dimensión muestran discrepancias notables (Fig. 5), mientras que en el caso de la gravedad (Fig. 1), para estructuras de anchos mayores a 50 km los resultados de estas expresiones tienden a coincidir.

Figura 5: Ondulaciones isostáticas del geoide para estructuras topográficas elevadas paralelepípedas de 2 km de altura en función del ancho (igual al largo). En línea sólida, valores exactos (3D); en línea de trazos, aproximación en 2D; en línea de trazos y puntos, aproximación en 1D. a) Hipótesis de Airy y b) Hipótesis de Pratt.

En la figura 6 se muestran los errores (ecuación 10) de los valores obtenidos a partir de las aproximaciones en una y dos dimensiones respecto a los valores exactos en tres dimensiones, para cuerpos de distintas alturas y anchos, para ambas hipótesis. Las aproximaciones en una dimensión considerando tanto sistemas de Airy como sistemas de Pratt arrojan errores considerables para estructuras pequeñas (Figs. 6a y c). Los errores se incrementan con la altura, observándose para sistemas de Airy errores mayores al 20% para estructuras con un ancho menor a 200 km (Fig. 6a), mientras que para las mismas estructuras en sistemas de Pratt estos errores son mayores al 40% (Fig. 6c). Para estructuras con un ancho menor a 100 km, los errores pueden superar ampliamente el 100%, por lo cual se desaconseja totalmente la utilización de estas aproximaciones para ambas hipótesis isostáticas. Por otro lado, vemos que las aproximaciones en dos dimensiones tienen menor error que las anteriores (Figs. 6b y d). Para estas aproximaciones los errores son menores al 5% para estructuras con un ancho mayor a 400 km para ambos sistemas, mientras que están por encima del 10% para estructuras con un ancho menor a 200 km.

Figura 6: Errores (%) en el cálculo de las ondulaciones del geoide utilizando las aproximaciones en una y dos dimensiones respecto de los valores exactos en tres dimensiones para topografías elevadas en función de la altura y el ancho de la estructura tridimensional. a) Aproximación en 1D considerando la hipótesis de Airy (curvas cada 10%); b) Aproximación en 2D considerando la hipótesis de Airy (curvas cada 5%); c) Aproximación en 1D considerando la hipótesis de Pratt (curvas cada 10%); d) Aproximación en 2D considerando la hipótesis de Pratt (curvas cada 5%).

Cuencas sedimentarias

En forma similar se procedió para el caso de cuencas sedimentarias compensadas considerando ambas hipótesis. Para la hipótesis de Airy se asignó a la corteza superior una densidad de r_cs = 2,67 g/cm³, a los sedimentos una densidad de r_s = 2,27 g/cm³, el contraste de densidades entre el manto y la corteza inferior utilizado fue de Dr = r_m - r_ci = 0,4 g/cm³ y el espesor cortical asumido como normal fue de T_N = 33 km. Para la hipótesis de Pratt se adoptó como densidad media de la litosfera normal r _lit = 3,1 gm/cm³ , como densidad de los sedimentos r_s = 2,27 g/cm³ y como profundidad de compensación H = 100 km. Se estudiaron cuencas de distintas profundidades y anchos con sección cuadrada, para las cuales se calcularon las ondulaciones del geoide en forma exacta y mediante las dos aproximaciones.

En la figura 7 se observan las ondulaciones del geoide isostático para una cuenca de 2 km de profundidad en función del ancho (arista de la base) para ambas hipótesis isostáticas. Vemos aquí que ambas aproximaciones se acercan más al valor exacto que en el caso de topografías elevadas, siendo también más pequeños los valores absolutos de ondulación. En la figura 8 se muestran los errores (ecuación 10) de los valores obtenidos a partir de las aproximaciones en una y dos dimensiones respecto a los valores exactos en tres dimensiones. Vemos nuevamente que las aproximaciones en una dimensión presentan mayor error considerando sistemas de Pratt que utilizando sistemas de Airy (Figs. 8a y c). En sistemas de Airy, para cuencas de más de 350 km de ancho los errores son menores al 10% (Fig. 8a), mientras que en el caso de sistemas de Pratt para las mismas cuencas los errores son menores al 20% (Fig. 8c). Para cuencas menores a 100 km de ancho, en sistemas de Airy los errores son mayores al 40% mientras que en sistemas de Pratt son superiores al 80% (Figs. 8a y c). Otra característica importante de estas aproximaciones es que en ambos sistemas el error tiene muy poca dependencia con la profundidad de la cuenca, siendo el factor más influyente el ancho de la misma.

Figura 7: Ondulaciones isostáticas del geoide para cuencas sedimentarias paralelepípedas de 2 km de profundidad en función del ancho (igual al largo). En línea sólida, valores exactos (3D); en línea de trazos, aproximación en 2D; en línea de trazos y puntos, aproximación en 1D. a) Hipótesis de Airy y b) Hipótesis de Pratt.

Figura 8: Errores (%) en el cálculo de las ondulaciones del geoide utilizando las aproximaciones en una y dos dimensiones respecto de los valores exactos en tres dimensiones para cuencas sedimentarias en función de la profundidad y el ancho de la cuenca. a) Aproximación en 1D considerando la hipótesis de Airy (curvas cada 10%); b) Aproximación en 2D considerando la hipótesis de Airy (curvas cada 5%); c) Aproximación en 1D considerando la hipótesis de Pratt (curvas cada 10%); d) Aproximación en 2D considerando la hipótesis de Pratt (curvas cada 5%).

Las aproximaciones en dos dimensiones son también muy buenas en estos casos; para cuencas de más de 200 km de ancho los errores son menores al 5% en la hipótesis de Airy y menores al 10% en la hipótesis de Pratt (Figs. 8b y d). Para cuencas de menos de 100 km de ancho, los errores son mayores al 10% en sistemas de Airy (Fig. 8b) y mayores al 25% en sistemas Pratt (Fig. 8d). De igual forma, la influencia de la profundidad de la cuenca es escasa, controlando la variación del error el ancho de la misma.

Ejemplos reales

Para ejemplificar los resultados obtenidos se presentan dos casos reales, una cuenca sedimentaria y una estructura montañosa. Ambos casos se han analizado considerando a las estructuras compensadas según la hipótesis de Airy. Como hemos mencionado con anterioridad, los errores de las aproximaciones en el caso de estructuras compensadas según la hipótesis de Pratt son en general superiores a los errores de las aproximaciones de estructuras compensadas según la hipótesis de Airy, por lo que las conclusiones serán también válidas para dichas estructuras.

Cuenca de Beazley

La cuenca de Beazley se ubica en el centro-oeste de la provincia de San Luis (Fig. 9a). De figura romboidal, está delimitada al norte por la dorsal de San Pedro, al este por los macizos precámbricos Grande de San Luis y Charlone, al sur por la dorsal del cerro Varela y al oeste por el río Desaguadero y el eje del Gigante (Yrigoyen et al. 1989). La cubierta sedimentaria presenta hasta 4 km de potencia, localizándose el depocentro de la cuenca debajo de la salina del Bebedero, en una secuencia que presenta planos de biselamiento (Criado Roque et al. 1981). Los sedimentos encontrados son triásicos, cretácicos y terciarios, con columnas completas, con una densidad promedio de r_s = 2,35 g/cm³ obtenida a partir de perforaciones y velocidades sísmicas de refracción y reflexión (Manoni 1985, Martinez et al. 2001, Molinari 2004).

Figura 9: a) Mapa geológico esquemático de la provincia de San Luis y ubicación de la cuenca de Beazley (basado en Criado Roque et al. 1981); b) Isóbatas de basamento de la cuenca de Beazley en kilómetros (YPF); c) Ondulaciones del geoide obtenidas con fórmulas exactas en 3D suponiendo a la cuenca compensada según la hipótesis de Airy; d) Ondulaciones del geoide obtenidas con la fórmula aproximada en 2D suponiendo a la cuenca compensada según la hipótesis de Airy; e) Ondulaciones del geoide obtenidas con la fórmula aproximada 1D suponiendo a la cuenca compensada según la hipótesis de Airy (ondulaciones en metros).

Utilizando las isóbatas de basamento de la cuenca obtenidas por refracción sísmica en la zona por YPF (Fig. 9b), se construyó un modelo teórico suponiendo a la cuenca compensada isostáticamente en la hipótesis de Airy. Se adoptó como espesor cortical normal T_N = 33 km, una densidad para la corteza superior igual a r_cs = 2,67 g/cm³ y un contraste de densidades entre el manto y la corteza inferior de Dr = r_m - r_ci = 0,4 g/cm³ . En primer lugar, la cuenca y la masa compensadora se representaron mediante un conjunto de paralelepípedos rectos verticales, a partir de los cuales se calculó exactamente la ondulación del geoide generada por la estructura utilizando las fórmulas en tres dimensiones (Fig. 9c). Por otro lado, se utilizaron las expresiones aproximadas para una cuenca en una y dos dimensiones para estimar las ondulaciones del geoide (Figs. 9e y d). Obsérvese la similitud de las ondulaciones del geoide obtenidas mediante la aproximación en una dimensión (Fig. 9e) y las isóbatas de basamento de la cuenca (Fig. 9b), similitud debida a que esta aproximación utiliza como dato únicamente la profundidad de la cuenca. Comparando las ondulaciones obtenidas mediante las fórmulas aproximadas con las obtenidas mediante las expresiones exactas, encontramos errores muy significativos para esta estructura. La aproximación en dos dimensiones arroja un error medio del 14,5%, con valores extremos de hasta 71%. La aproximación en una dimensión presenta un error medio del 53,8%, con extremos de hasta 213%. Esto nos está indicando que para estructuras de corta longitud de onda (como la de esta cuenca), ambas aproximaciones son groseras, siendo su uso poco recomendable.

Andes bolivianos

Los Andes bolivianos ocupan una amplia zona del oeste del territorio boliviano, alcanzando altitudes de más de 4.000 m (Fig. 10a). Se dividen en cuatro unidades morfotectónicas paralelas: la Cordillera Occidental, el Altiplano, la Cordillera Oriental y las sierras Sub-andinas (Fig. 10b). Los antecedentes geofísicos indican que la zona se encuentra compensada isostáticamente según la hipótesis de Airy (Isacks 1988, Abriata e Introcaso 1990, Miranda e Introcaso 2000). Se consideró como zona de estudio la región limitada entre 69º y 62º de longitud oeste, y 14º y 22º de latitud sur (Crovetto e Introcaso 2005). Se utilizó el modelo digital de elevación GLOBE (Globe Task Team 1999), con una resolución de 1 km x 1 km como dato de entrada (Fig. 10c). Se propuso una estructura teórica perfectamente compensada según la hipótesis de Airy, considerando la densidad de la topografía como r_t = 2,67 g/cm³, el espesor cortical normal como T_N = 33 km y el contraste de densidades entre la corteza inferior y el manto superior como Dr = r_ci - r_m = -0,4 g/cm³.

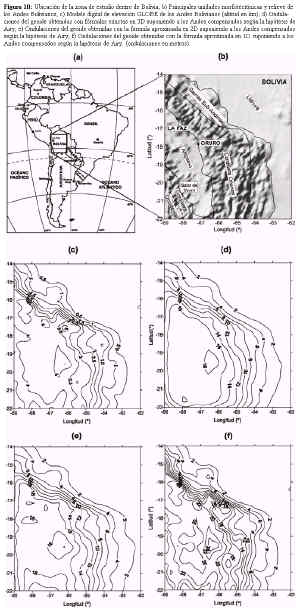
Figura 10: Ubicación de la zona de estudio dentro de Bolivia; b) Principales unidades morfotectónicas y relieve de los Andes Bolivianos; c) Modelo digital de elevación GLOBE de los Andes Bolivianos (altitud en km); d) Ondulaciones del geoide obtenidas con fórmulas exactas en 3D suponiendo a los Andes compensados según la hipótesis de Airy; e) Ondulaciones del geoide obtenidas con la fórmula aproximada en 2D suponiendo a los Andes compensados según la hipótesis de Airy; f) Ondulaciones del geoide obtenidas con la fórmula aproximada en 1D suponiendo a los Andes compensados según la hipótesis de Airy. (ondulaciones en metros).

Con estos datos, se calcularon las ondulaciones del geoide descomponiendo a la estructura y su raíz en paralelepípedos rectos verticales y utilizando las fórmulas exactas en tres dimensiones. También se usaron las aproximaciones en una y dos dimensiones para calcular las ondulaciones del geoide. En las figuras 10d, e y f se muestran los resultados obtenidos para cada caso. Se aprecia nuevamente que la aproximación en dos dimensiones (Fig. 10e) produce un geoide más cercano al geoide real (Fig. 10d), mientras que la aproximación en una dimensión (Fig. 10f) presenta mayores discrepancias. El valor medio de los errores son del 1% para la aproximación bidimensional y del 6% para la aproximación en una dimensión, con desvíos del 13% y 29% respectivamente. Estos resultados indican que para estructuras de longitud de onda similar a la estructura aquí analizada, ambas aproximaciones dan resultados razonables que pueden considerarse según el grado de precisión que requiera el estudio.

CONCLUSIONES

En este trabajo se mostró (a través de ejemplos teóricos y reales), que las aproximaciones en una y dos dimensiones que suelen utilizarse para el cálculo de las ondulaciones del geoide deben ser usadas con mucha precaución.

Cuando las estructuras son de corta longitud de onda (menores a 400 km de ancho), las aproximaciones en una dimensión propuestas por Haxby y Turcotte (1978) sobreestiman los resultados en más de un 10%, llegando en casos de estructuras muy pequeñas (100 km) a errores superiores al 100%. Estos errores son menores en el caso de cuencas que en el caso de topografías elevadas. Estas características se observan tanto para estructuras que obedecen la hipótesis de Airy como para aquellas que siguen el sistema de Pratt, aunque en este último caso los errores encontrados son siempre mayores. Los errores crecen cuando disminuye el ancho de la estructura analizada, por lo que debe tenerse especial cuidado al utilizar aproximaciones unidimensionales en estructuras angostas. Para estructuras de largas longitudes de onda (mayores a 500 km), pueden utilizarse como buenos estimadores de las ondulaciones reales, aunque se recomienda no perder de vista que son valores aproximados.

En el caso de las aproximaciones bidimensionales, las diferencias son apreciablemente menores. Los errores que se cometen son menores al considerar la hipótesis de Airy, siendo mayores para los casos de topografías elevadas que para cuencas (sedimentarias y oceánicas). Dichos errores disminuyen con el aumento del ancho y largo de la estructura tridimensional. Si bien esta aproximación en dos dimensiones presenta poco error respecto a los resultados exactos en tres dimensiones, no constituye una ventaja importante, ya que no representa gran ahorro en el tiempo de cálculo. Estas aproximaciones son prácticas cuando la información de la zona en estudio es un perfil, pero en caso de disponer de información en tres dimensiones, se recomienda el cálculo exacto.

Finalmente, los ejemplos reales analizados nos muestran cómo en estructuras pequeñas ambas aproximaciones sobreestiman los resultados, mientras que en estructuras de extensión significativa pueden ser utilizadas sin mayores precauciones.

AGRADECIMIENTOS

Carolina Crovetto desea agradecer a la Fundación Josefina Prats de Rosario y al CONICET por las ayudas económicas recibidas durante sus estudios de doctorado. Los autores desean agradecer los comentarios de los árbitros Claudia Prezzi y Augusto Rapallini, los cuales han contribuido sin duda a mejorar la claridad del manuscrito. Este trabajo fue parcialmente financiado por CONICET (PIP Nº 03056) y por la Agencia Nacional de Promoción Científica y Tecnológica (PICTR 2002-00166).

TRABAJOS CITADOS EN EL TEXTO

Abriata, J.C. e Introcaso, A. 1990. Contribución gravimétrica al estudio de la transecta ubicada al sur de Bolivia. Revista del Instituto Geográfico Militar 5(7): 8-19, Buenos Aires.         [ Links ]

Airy, G.B. 1855. On the computation of the effect of the attraction of mountainmasses, as disturbing the apparent astronomical latitude of stations of geodetic surveys. Philosophical Transactions of the Royal Society of London 145:101-104.         [ Links ]

Bullen, K. 1963. An introduction to the theory of seismology. Cambridge University Press, 381 p., Cambridge.         [ Links ]

Chapman, M. 1979. Techniques for interpretation of geoid anomalies. Journal of Geophysical Research 84(B8): 3793-3801.         [ Links ]

Cornaglia, L. e Introcaso, A. 2004. Exceso de gravedad en la sierra grande de San Luis obtenido a partir de ondulaciones del geoide. Estudio preliminar realizado sobre una sección transversal centrada aproximadamente en 32º 50' de latitud sur. Geoacta 29: 1-9, Buenos Aires.         [ Links ]

Criado Roque, P., Mombru, C, y Ramos, V. 1981. Estructura e interpretación tectónica. Geología de la Provincia de San Luis, 8º Congreso Geológico Argentino, Relatorio: 155-192, San Luis.         [ Links ]

Crovetto, C. e Introcaso, A. 2004. Indicadores isostáticos geóidicos. Un ejemplo para la Sierra de San Luis. Geoacta 29: 49- 54, Buenos Aires.         [ Links ]

Crovetto, C. e Introcaso, A. 2005. A modern gravimetric methodology applied to Bolivian Andes' study. 6^th International Symposium on Andean Geodynamics, Extended Abstracts: 198-201, Barcelona.         [ Links ]

GLOBE Task Team and others (Hastings, D., Dunbar, P., Elphingstone, G., Bootz, M., Murakami, H., Maruyama, H., Masaharu, H., Holland, P., Payne, J., Bryant, N., Logan, T., Muller, J.-P., Schreier, G., y MacDonald, J.) eds. 1999. The Global Land One-kilometer Base Elevation (GLOBE) Digital Elevation Model, Version 1.0. National Oceanic and Atmospheric Administration, National Geophysical Data Center, Boulder, Colorado, U.S.A.         [ Links ]

Guspí, F. 1999. Fórmulas compactas para el cálculo del potencial gravitatorio de prismas rectangulares. Contribuciones a la geodesia a fines del siglo XX. Homenaje a Oscar Parachú. UNR editora, 7:129-133, Rosario.         [ Links ]

Haxby, W. y Turcotte, D., 1978. On isostatic geoid anomalies. Journal of Geophysical Research 94(B4): 3876-3890.         [ Links ]

Heiskanen, W. y Moritz, H. 1967. Physical Geodesy. W. H. Freeman and Company, 364 p., San Francisco.         [ Links ]

Introcaso, A., Pacino, M.C. y Fraga, H. 1992. Gravity, isostasy and Andean crustal shortening between latitudes 30ºS and 35ºS. Tectonophysics 205: 31-48.         [ Links ]

Introcaso, A. 1999. Introducción a la inversión desde las ondulaciones del geoide. Contribuciones a la Geodesia en la Argentina de fines del Siglo XX. Homenaje a Oscar Parachú. UNR Editora, 8:135-164, Rosario.         [ Links ]

Introcaso, A., Pacino, M,C. y Guspí, F. 2000. The Andes of Argentina and Chile: Crustal configuration, isostasy, shortening and tectonic features from gravity data. Temas de Geociencia 5, UNR Editora, 31 p., Rosario.         [ Links ]

Isacks, B., 1988. Uplift of the Central Andes plateau and bending of the Bolivian orocline. Journal of Geophysical Research 93(B4): 3211-3231.         [ Links ]

Manoni, R. 1985. Geología del subsuelo de la Cuenca de Beazley. Boletín de Informaciones Petroleras, Tercera época, 2(4): 34-46.         [ Links ]

Martínez, P., Gímenez, M., Aguilera, D. e Introcaso, A. 2001. Subsidencia en las Cuencas Sedimentarias de Beazley y Salinas. 7^th International Congress of the Brazilian Geophysical Society: 824-827, Salvador de Bahía.         [ Links ]

Miranda, S. e Introcaso, A. 2000. Acortamientos corticales para los Andes Centrales Bolivianos a partir de datos de gravedad. 9º Congreso Geológico Chileno, Actas 2: 593-597, Puerto Varas.         [ Links ]

Molinari, R. 2004. Determinación del geoide (h-H) y evaluación preliminar del estado isostático para un perfil transversal a la cuenca de Beazley (San Luis, Argentina). Trabajo final de la carrera de Agrimensura. Facultad de Ciencias Exactas, Ingeniería y Agrimensura, Universidad Nacional de Rosario (inédito), 72 p., Rosario.         [ Links ]

Pratt, J.H. 1855. On the attraction of the Himalaya Mountains, and of the elevated regions beyond them, upon the plumb line in India. Philosophical Transactions of The Royal Society of London 145: 53-100.         [ Links ]

Turcotte, D. y Schubert, G. 1982. Geodynamics. Application of continuum physics to geological problems. John Wiley & Sons, 450 p., New York.         [ Links ]

Vening Meinesz, F.A. 1939. Tables fondamentales pour la réduction isostatique régionale. Bulletin Géodésique 63: 711- 776.         [ Links ]

Watts, A.B. 2001. Isostasy and Flexure of the Lithosphere. Cambridge University Press, 458p., Cambridge.         [ Links ]

Woollard, G. 1962. The relation of gravity anomalies to surface elevation, crustal structure and geology. University of Wisconsin, Geophysical Polar Research Center. Report 62-9, 292 p.         [ Links ]

Yrigoyen, M., Ortiz, A. y Manoni, R. 1989. Cuencas sedimentarias de San Luis. En Chebi, G.A. y Spalletti, L.A. (eds.) Cuencas Sedimentarias Argentinas, Serie de Correlación Geológica 6: 203-220, Tucumán.         [ Links ]

Recibido: 27 de junio, 2005
Aceptado: 20 de abril, 2006