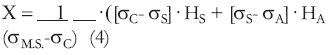Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Asociación Geológica Argentina
versión impresa ISSN 0004-4822versión On-line ISSN 1851-8249
Rev. Asoc. Geol. Argent. v.65 n.3 Buenos Aires nov. 2009
ARTÍCULOS
Análisis cortical de la cuenca Golfo de San Jorge utilizando anomalías de Bouguer y ondulaciones del geoide
Laura L. Cornaglia1,2, Francisco Ruiz1,2 y Antonio Introcaso2
1Instituto Geofísico Sismológico Volponi, Universidad Nacional de San Juan - CONICET - Grupo de Geofísica
2 IFIR, Universidad Nacional de Rosario - CONICET. Emails: cornagli@fceia.unr.edu.ar, fruiz@unsj-cuim.edu.ar, geofisic@fceia.unr.edu.ar
RESUMEN
Con la finalidad de evaluar características tales como tipo de corteza y estado isostático de la cuenca sedimentaria del Golfo de San Jorge, analizamos los valores observados de anomalías de Bouguer y de ondulaciones geoidales calculadas desde anomalías de aire libre por el método de fuentes equivalentes, comparándolos con las respuestas de un modelo de cuenca compensado hidrostáticamente determinado a partir de la masa topográfica de la zona y el relleno sedimentario de la cuenca. Por ambos caminos encontramos un exceso de masas que interpretamos como significativa antirraíz cortical y predice subsidencia para el futuro. Otras alternativas como por ejemplo la intrusión de densas masas intracorticales, no alteran las conclusiones.
Palabras clave: Cuenca; Anomalías; Gravedad; Ondulación; Geoide; Isostasia.
ABSTRACT: Crustal analysis of the San Jorge Basin based on Bouguer anomalies and geoid undulations. To evaluate crustal characteristics such as crust type and isostatic balance of the sedimentary San Jorge Gulf Basin, we analyzed observed Bouguer anomalies and geoid undulations calculated from free-air anomalies and equivalent sources, comparing them with the responses of a hydrostatic compensated basin model prepared using the topographic mass of the area and the basin sedimentary fill. In both cases we found an excess mass that we explained as a significant crustal anti-root that predicts subsidence in the future. Others alternatives as for example the emplacement of dense intracrustal masses, do not modified the conclusions.
Keywords: Basin; Anomalies; Gravity; Geoid; Undulations; Isostasy.
INTRODUCCIÓN
La cuenca sedimentaria del Golfo de San Jorge se localiza en la Patagonia, como parte de las provincias de Chubut y Santa Cruz. Se extiende sobre el mar epicontinental argentino y adquiere gran importancia económica por sus reservorios de petróleo; es de gran extensión superficial, estimándose su área en 170.000 km2 (Fig. 1). Martin (1954) fue el primero en destacar un máximo gravimétrico sobre la mayor potencia sedimentaria, explicando sin cuantificar que correspondía a un ajuste isostático imperfecto. Cesanelli y Lesta (1973) presentaron para la corteza superior sobre el meridiano 68°O y el paralelo 46°S, perfiles de reflexión y refracción sísmica, de gravedad y magnetismo, realizando una correlación del análisis geofísico con datos geológicos superficiales y subsuperficiales. Introcaso (1980) empleando dos secciones perpendiculares que atravesaban la cuenca, analizó los resultados gravimétricos continentales encontrando sobre el potente desarrollo sedimentario, nuevamente un máximo gravimétrico que aumentaba de forma considerable su valor al ser corregido por el efecto de los sedimentos. Analizando estas anomalías gravimétricas pudo inferir que "el techo de la masa anómala estaría dentro de la primera mitad de la corteza". Luego Introcaso et al. (1986) prepararon modelos geofísicos a partir de las anomalías de Bouguer corregidas por efectos de cortas longitudes de onda y del relleno sedimentario. La anomalía corregida encontrada, exhibió un positivo que fue asociado con atenuación cortical; a partir de estas respuestas gravimétricas se realizó una inversión encontrándose una antirraíz mayor a la esperada para un modelo compensado, indicando sobrecompensación isostática. Nuestro estudio involucra nuevos datos de gravedad y altimetría proveniente del modelo digital de elevación de terreno Etopo2. En el marco de la metodología tradicional, la gravedad observada fue comparada con valores gravitatorios teóricos correspondientes a un modelo de cuenca perfectamente compensado hidrostáticamente. Este modelo se determinó a partir de la geometría y relleno sedimentario de la cuenca y de la topografía de la zona. Centrando nuestra atención sobre el sector de mayor potencia sedimentaria, obtuvimos de la comparación realizada residuos positivos que no concuerdan con la respuesta gravitatoria esperable para el modelo asumido. Por el otro lado y desde una óptica moderna, calculamos valores de ondulación geoidal N a partir de anomalías de aire libre y la utilización de fuentes equivalentes. Estos valores provenientes de la observación de fueron cotejados con las ondulaciones teóricas del modelo. El resultado de esta nueva comparación exhibió también diferencias positivas. Así, a partir de lo obtenido por ambos caminos, inferimos una corteza sobrecompensada cuya interpretación isostática indica movilismo descendente para restablecer el equilibrio.
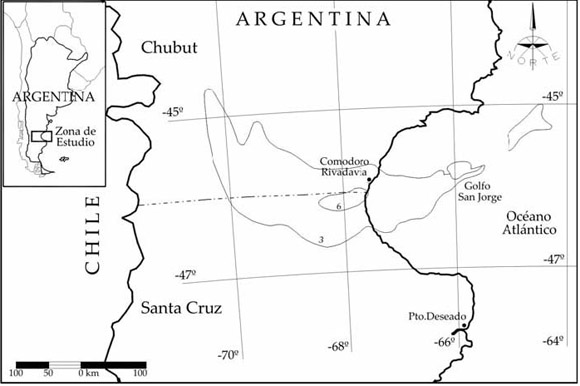
Figura 1: Cuenca sedimentaria del Golfo de San Jorge. La figura muestra sólo las isóbatas de basamento de profundidades 3 y 6 km.
LA CUENCA SEDIMENTARIA DEL GOLFO DE SAN JORGE
Strelkov et al. (2005) clasificaron a la cuenca sedimentaria del Golfo de San Jorge como de tipo intracratónica de génesis extensiva, desarrollada sobre una corteza eopaleozoica. Esta cuenca, de forma alargada en la dirección este-oeste, se desarrolla desde la faja plegada andina al oeste, y hasta el alto estructural al este en la plataforma del mar argentino, alojándose entre los macizos de Somuncura o Norpatagónico al norte y del Deseado al sur; la porción principal de la cuenca, al este de la sierra de San Bernardo, suele dividirse comúnmente en flanco norte, centro de la cuenca, flanco sur y zonas costa afuera (Baldi y Nevistic 1996, Sylwan 2001) (Fig. 2).
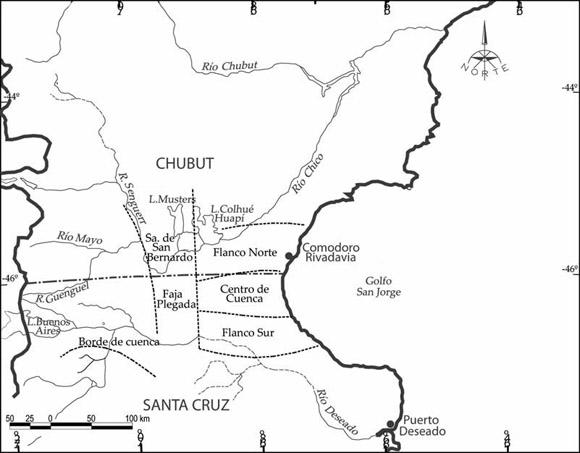
Figura 2: División de la porción principal de la cuenca del Golfo San Jorge. (Modificado de Homovc et al. 1993).
El origen de esta cuenca de acuerdo a Strelkov et al. (2005), se vincula con "una extensión litosférica generalizada desarrollada desde el Triásico en todo el margen oeste de Gondwana". La historia geológica de la cuenca según Baldi y Nevistic (1996) se divide en cuatro estadíos: (i) rift temprano, caracterizado por dos sucesos, el primero durante el Triásico Superior y Jurásico Inferior, anterior al desglose de Gondwana formándose una "serie de grábenes y hemigrábenes de gran extensión y baja integración" y el segundo, de subsidencia con la actividad volcánica; (ii) rift tardío, durante el Jurásico Superior y Cretácico Inferior, presentando una disminución en la actividad del fallamiento normal de manera que la cuenca muestra una progresiva integración debido a la gradual colmatación de las subcuencas vinculadas al rift temprano; (iii), hundimiento térmico temprano y por último (iv), hundimiento térmico tardío, desarrollado desde el Aptiano (Cretácico) hasta el Paleoceno (Terciario Inferior), ocasionando una subsidencia continua aunque de menor grado respecto al estadío anterior. Como consecuencia de la variación en el grado de deriva de la placa Sudamericana hacia el oeste, la cuenca "estuvo sujeta a eventos tectónicos compresionales y extensionales".
La estratigrafía de esta cuenca puede encontrarse en diversos trabajos; uno muy pormenorizado corresponde a Lesta et al. (1980). Diversos trabajos (Lesta et al. 1980, Introcaso 1980, Baldi y Nevistic 1996 y Strelkov et al. 2005) señalan que la columna estratigráfica comprende sedimentos jurásicos, cretácicos y terciarios, alcanzando hasta el Oligoceno a Mioceno. El paquete sedimentario tiene una profundidad de alrededor de 7.000 m en el centro de la cuenca (Baldi y Nevistic 1996).
DATOS UTILIZADOS
La base de datos que se ha utilizado en este trabajo involucra las isóbatas de basamento de la cuenca, anomalías gravimétricas de aire libre [AAL] y Bouguer [AB] y altimetría proveniente del modelo digital de elevación de terreno Etopo2.
La geometría de la cuenca se conformó a partir de las isóbatas de basamento que fueron extraídas de mapas tectónicos (para la zona continental, escala 1: 5.000.000), y geológicos (para la zona marina, escala 1: 5.000.000). Las curvas del sector oceánico provinieron del mapa geológico de la República Argentina (SEGEMAR 1996), mientras que las isóbatas del sector continental se extrajeron del Mapa Tectónico de América del Sur (Almeida et al. 1978). Una vez digitalizadas estas isóbatas, se procedió a su integración y posterior regularización con el fin de utilizarlas en el desarrollo de este trabajo que centró su estudio en el sector de mayor potencia sedimentaria continental de la cuenca.
La carta de anomalías de AAL (sector oceánico) y AB (sector continental) (Fig. 3) utilizada en este trabajo, fue elaborada a partir de la base de datos procesada por Green y Fairhead (1991). Los valores gravitatorios están referidos al sistema International Gravity Standardization Net 1971 (IGSN71). Los valores de las anomalías AB fueron obtenidos aplicando el valor de densidad media del granito (Torge 2001, entre otros) para la placa de Bouguer y correcciones de terreno. Cabe señalar que con la utilización de esta carta pudimos optimizar el procesamiento de los datos gravimétricos a través de la aplicación de expresiones de cálculo tridimensionales, a diferencia de lo realizado en trabajos anteriores en donde los datos se distribuían sobre secciones que atravesaban la cuenca; además éstos no contemplaron correcciones de terreno ni referencia a marco gravitatorios y geodésicos actuales.
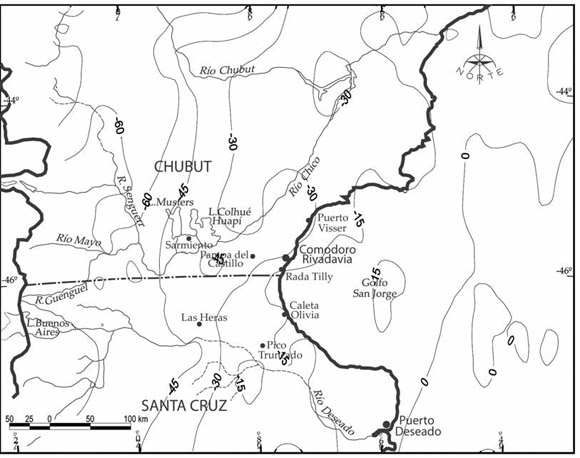
Figura 3: Carta de isoanómalas de AAL (sector oceánico) y AB (sector continental). Equidistancia 15 mGal.
La altimetría, para nada despreciable, fue tomada en consideración; así se utilizaron los valores altimétricos del modelo digital de elevación de terreno Etopo2 (National Geophysical Data Center NGCD, Etopo2: Bathymetry/Topography Data, US department of Comerce, Washington DC 2001) (Fig. 4) desarrollado en una serie de coeficientes armónicos esféricos hasta grado y orden 360 (Förste et al. 2007) y disponible en la web: http://icgem.gfz-potsdam.de/ICGEM/ICGEM.html, que corresponde al International Centre for Global Earth Models (ICGEM), uno de los seis centros del International Gravity Field Service (IGFS) de la International Association of Geodesy (IAG).
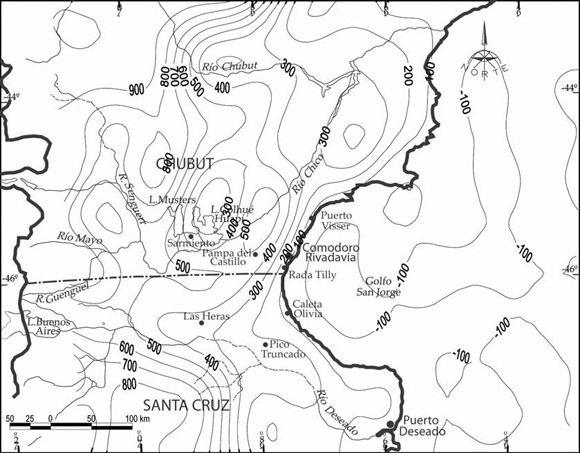
Figura 4: Valores altimétricos del modelo Etopo2. Equidistancia 100 metros.
MODELO TEÓRICO O DE COMPARACIÓN
La evaluación isostática exige construir un modelo de comparación perfectamente compensado. El modelo elegido fue calculado asumiendo una corteza inicialmente distensiva (Strelkov et al. 2005), sometida luego a pulsos de compresión menor tal como lo indica la topografía; compresión regional asociada con la orogenia andina (Baldi y Nevistic 1996).
Con la topografía y el relleno sedimentario conocidos se calcularon los espesores de la antirraíz compensadora a partir de ecuaciones (tanto para el sector continental como oceánico de la cuenca) que igualan presiones a 33 km de profundidad (espesor del Moho o base de una corteza estandarizada) (Fig. 5).
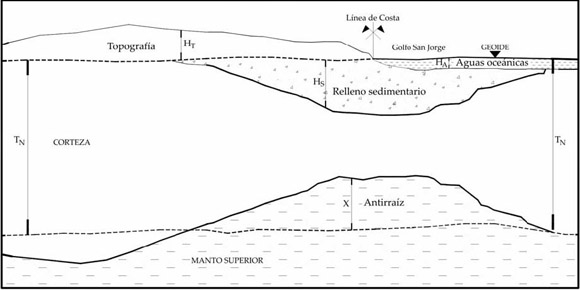
Figura 5: Modelo geofísico esquemático asumido para la cuenca.
(a) Sector continental:
HT· σT + HS· σS + (TN -[HS + X])· σC + Χ· σM.S. = TN· σC (1)
(b)Sector oceánico:
HA· σA + (HS - HA )· σS + (TN-[HS + X])· σC + Χ· σM.S. =TN· σC (2)
Donde σT es la densidad de la masa topográfica , σS es la densidad de los sedimentos, σC es la densidad de la corteza, σM.S. es la densidad del manto superior, σA es la densidad del agua, HT es la altura topográfica, HS es la profundidad de las isóbatas de basamento de la cuenca (relleno sedimentario), HA es la profundidad del fondo oceánico (batimetría), TN es el espesor 'normal' asumido para la corteza, y Χ es el espesor de la antirraíz compensadora. Despejando la incógnita Χ resulta:
(a)Sector continental:
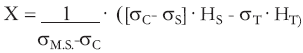 (3)
(3)
Con el fin de cuantificar las expresiones (3) y (4) hemos considerado: (a) Introcaso et al. (1986), utilizaron los valores de velocidades de sísmica de refracción del trabajo de Cesanelli y Lesta (1973) y aplicaron las relaciones de Nafe y Drake (1957) para calcular a partir de ellas la densidad del relleno sedimentario; el valor que obtuvieron fue el que adoptamos para este trabajo, es decir, σS=2,32 g· cm-3; (b) respecto a σCy σM.S. , aceptamos que sus valores promedio están entre (2,84 -2,93)g· cm-3 y 3,32 g· cm-3 respectivamente y asumimos σC=2,90 g· cm-3 y σM.S.=3,30 g· cm-3 (Introcaso 1997); (c) para σA y σT acordamos en utilizar σA=1,03 g· cm-3 (valor usual, Torge 2001, entre otros), y σT=2,70 g· cm-3 (valor medio asumido para el granito, Torge 2001, entre otros) y (d), la corteza 'normal' TN =33km (Bullen 1963).
Este modelo asumido para la cuenca establece un perfecto estado de compensación entre las masas anómalas topográficas y sedimentarias versus el espesor de la antirraíz.
Una vez asignados los valores numéricos de los parámetros en las ecuaciones (3) y (4) resulta:
(a)Sector continental:
 (5)
(5)
EFECTOS GRAVITATORIOS Y POTENCIALES TEÓRICOS O DE COMPARACIÓN
Obtenidas las profundidades x (Fig. 6), procedimos a calcular los efectos gravitatorios y potenciales del modelo. Para ello, se aplicaron fórmulas exactas tridimensionales una vez que las masas anómalas fueran aproximadas por un conjunto de paralelepípedos rectos homogéneos. Las expresiones de cálculo utilizadas para la gravedad y potencial gravitatorio fueron presentadas por Okabe (1979) y Guspí (1999) respectivamente, resultando para un punto Q (x, y, z) (Introcaso y Crovetto 2005):



Figura 6: Espesores de las antirraíces de las masas compensadoras del modelo asumido para la cuenca [ecuaciones (5) y (6)]. Equidistancia 1 km.
Donde gz(x, y, z) es la componente vertical de gravedad en el punto Q(x, y, z) ; T(x, y, z) es el potencial gravitatorio anómalo en el punto Q(x, y, z); dx, dy, dz, son las diferencias entre las caras del paralelepípedo (x1, x2, y1, y2, z1, z2) y las coordenadas del punto Q(x, y, z) con i=1,2; ![]() es la distancia entre el punto Q(x, y, z) y cada uno de los vértices del paralelepípedo; G es la constante de gravitación universal: G=6.67x108cm3· g-1· s-2; σ' es la densidad de la masa del paralelepípedo. Una vez obtenido T(x, y, z), la ondulación teórica o de comparación del geoide N(x, y) se obtuvo aplicando la fórmula de Bruns (Heiskanen y Moritz 1985, entre otros):
es la distancia entre el punto Q(x, y, z) y cada uno de los vértices del paralelepípedo; G es la constante de gravitación universal: G=6.67x108cm3· g-1· s-2; σ' es la densidad de la masa del paralelepípedo. Una vez obtenido T(x, y, z), la ondulación teórica o de comparación del geoide N(x, y) se obtuvo aplicando la fórmula de Bruns (Heiskanen y Moritz 1985, entre otros):
![]() (9)
(9)
Siendo γ la gravedad asumida comúnmente igual a 980 Gal.
Los cálculos se efectuaron aplicando el software desarrollado por Crovetto (2006) del Grupo de Geofísica del IFIR [CONICET-UNR].
ANOMALÍAS DE BOUGUER PARA EL ANÁLISIS ISOSTÁTICO
En el marco de la metodología tradicional,
el efecto gravitatorio del modelo EGSedim. representa la suma de los efectos gravitatorios del relleno sedimentario EGSedim (Fig. 7a), de la capa de agua EGC.A (Fig. 7b) y de las masas compensadoras EGM.Comp. (Fig. 7c). Es decir EGTeórico resulta (Fig. 7d):
EGTeórico=EGSedim.+EGC.A+EGM.Comp. (10)
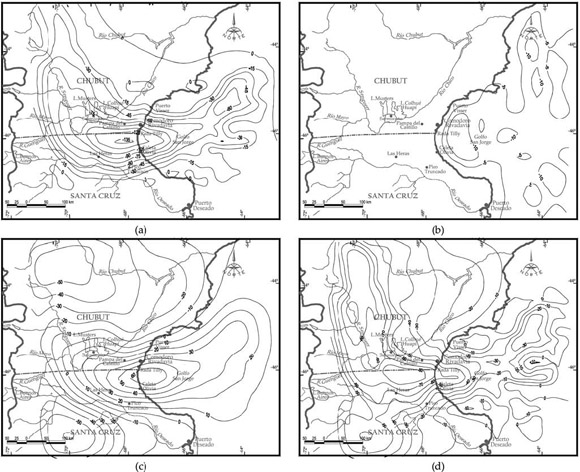
Figura 7: a) Efecto gravitatorio del relleno sedimentario de la cuenca EGSedim. Equidistancia 15 mGal.; b) Efecto gravitatorio de la capa de agua EGC.A. Equidistancia 5 mGal.; c) Efecto gravitatorio de las masas compensadoras EGM.Comp. Equidistancia 10 mGal.; d) Efecto gravitatorio total EGTeórico del modelo de comparación perfectamente compensado asumido para la cuenca. Equidistancia 10 mGal.
EGSedim. fue calculado en base a las isóbatas de basamento de Figura 1, asumiendo una densidad de σS = 2,32g· cm-3 para los sedimentos y una densidad diferencial con corteza: -0,58g· cm-3. EGC.A fue calculado asumiendo una densidad del agua σA= 1,03g· cm-3, manteniendo el valor 2,32g· cm3 para los sedimentos oceánicos; densidades diferenciales respectivas: -1,87g· cm-3 y −0,58g· cm-3 . EGM.Comp. fue calculado a partir de los espesores de la antirraíz de Figura 6 con una densidad de −3,30g· cm-3 para manto superior y densidad diferencial con corteza: +0,40g· cm-3.
ONDULACIONES DEL GEOIDE N PARA LA EVALUACIÓN ISOSTÁTICA
Desde que el potencial T (o la ondulación N) y la gravedad g se deducen uno del otro, nada impide intentar analizar el balance isostático a partir de N (Crovetto et al. 2007, Introcaso et al. 2002).
También aquí utilizaremos el modelo de comparación perfectamente compensado (véase Fig. 5) aunque ahora desde él calcularemos NTeórico como suma algebraica del total de efectos anómalos: topografía, sedimentos y antirraíz. En efecto, desde la óptica moderna, la ondulación teórica del modelo NTeórico implica el cálculo del potencial gravitatorio de las masas topográficas y con (8) y (9) el NTopog. (Fig. 8a). Análogamente, calculamos el NSedim. (Fig. 8b) y las ondulaciones de las masas compensadoras NM.Comp. (Fig. 8c). Es decir NTeórico resulta (Fig. 8d):
NTeórico = NTopog. + NSedim + NM.Comp. (11)
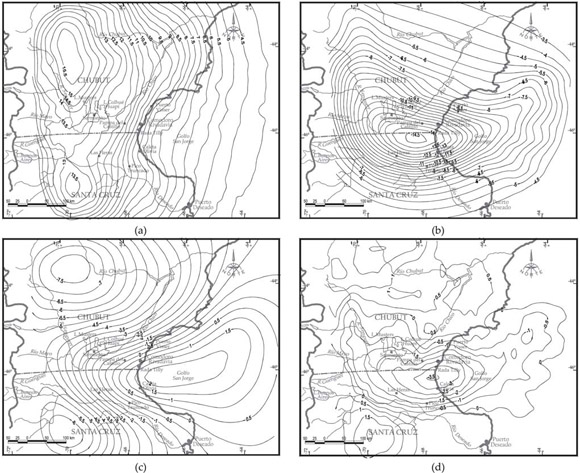
Figura 8: a) Ondulaciones geoidales de las masas topográficas y sector oceánico NTopog. Equidistancia 0,50 m; b) Efecto gravitatorio del relleno sedimentario de la cuenca NSedim. Equidistancia 0,50 m; c) Efecto gravitatorio de las masas compensadoras NM.Comp. Equidistancia 0,50 m; d) Ondulación NTeórico del modelo. Equidistancia 0,50 m.
CÁLCULO DE LAS ONDULACIONES DEL GEOIDE
A partir de las anomalías de Bouguer observadas ABObs (que insistimos contienen correcciones de terreno) (véase Fig. 3), obtuvimos las anomalías de Faye AF (Fig. 9), aplicando la clásica corrección de la placa de Bouguer:
AF= ABObs+ CB (12)
AF= ABObs+ 2π· G· s'T· HT (13)
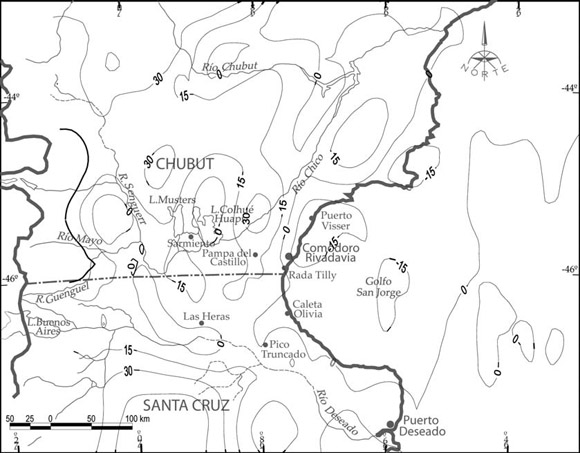
Figura 9: Anomalías AF obtenidas a partir de (13).
Equidistancia 15 mGal.
Donde CB es la corrección de la placa Bouguer, G es la constante de gravitación universal, HT es la altura topográfica (extraída del modelo digital de elevación de terreno) y σ' T es la densidad de la masa interpuesta entre el punto de cálculo y el geoide, asumida coincidente con la densidad media del granito (Torge 2001, entre otros). Para la construcción del geoide se empleó el método de fuentes equivalentes cuya descripción puede verse, entre otros, en Introcaso (2006) o Introcaso y Crovetto (2005). Los cálculos de N (Fig. 10) se efectuaron empleando el software desarrollado por Guspí et al. (2004), empleándose un factor de profundidad igual a 1,4 (Cordell 1992) y una estimación de precisión igual a 0,1 mGal (una mayor exigencia que la utilizada en Guspí et al. (2004)) para el ajuste de las anomalías de entrada. Una vez obtenida la intensidad de las fuentes, es posible calcular el potencial anómalo (Introcaso y Crovetto 2005):
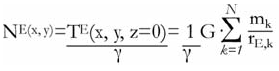 (9)
(9)
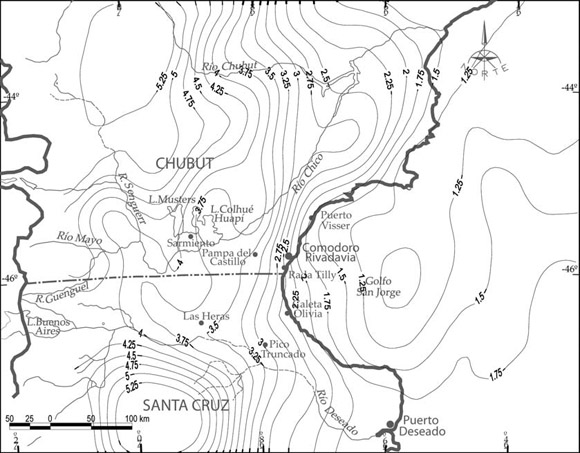
Figura 10: Ondulaciones geoidales calculadas NObservada a partir de las AF y fuentes equivalentes.
Donde NE es el valor de ondulación para la estación E, G es la constante de gravitación universal, g es el valor de gravedad asumido comúnmente igual a 980 Gal, mk es la masa calculada para la fuente ficticia k=ésima, rE,k es la distancia entre la masa puntual k=ésima y la estación E. Nuestro propósito fue aislar la ondulación local observada producida por la cuenca en estudio. Para ello fue necesario comparar ambas morfologías de NObservado y NTeórico.
Debido al carácter regular de NObservado decidimos asumirlo como ondulación regional sin modificaciones. Por otra parte, es sabido que el potencial está determinado a menos de una constante C (Trejo 1965, Introcaso y Crovetto 2005, entre otros). Esto nos permitió desplazar el NTeórico en un valor fijo (~2.40 m) buscando la coincidencia con NObservado.
COMPARACIÓN DE DATOS OBSERVADOS VS. VALORES TEÓRICOS O DE COMPARACIÓN
Los valores observados de las anomalías de Bouguer, ABObs (véase Fig. 3), sin ser corregidos por los efectos del relleno sedimentario ni afectados por procedimiento de filtrado alguno, fueron comparados con los valores gravitatorios del modelo de comparación EGTeórico (véase Fig. 8 (a), Ecuación 10). La diferencia numérica de los valores (Ecuación 15), que hemos denominado dgCuenca (Fig. 11) se efectuó sobre los datos regularizados de las ABObs y EG Teórico. Luego, empleando una sección que atraviesa la cuenca sobre su sector de mayor potencia sedimentaria continental en la dirección norte-sur (Fig. 12a), se muestran los órdenes de magnitud de cada uno de los valores involucrados como así también los resultados de la diferencia efectuada (Fig. 12b). Entonces:
dgCuenca =ABObs - EGTeórico (15)

Figura 11: Diferencia dgCuenca obtenidas a partir de la expresión (15). Equidistancia 10 mGal.
El perfil obtenido muestra residuos positivos que no coinciden con la respuesta gravitatoria esperable de acuerdo al modelo compensado asumido.
Con el mismo criterio se compararon las ondulaciones NObservado y NTeórico. (desplazado). Aplicando la Ecuación (16) se obtuvieron las diferencias correspondientes (Fig. 13). En la Figura 14 se observan las mismas sobre la sección elegida (véase Fig.12 (a)).
dNCuenca = NObservado y NTeórico (16)
Figura 12: a) Localización geográfica de la sección N-S; b) Perfil N-S. Eje sup.: anomalías ABObs y efecto EGTeórico; Eje del medio: diferencias dgCuenca; Eje inf.: basamento de la cuenca.

Figura 13: Diferencia dNCuenca obtenidas a partir de la expresión (16). Equidistancia 0,50 m.

Figura 14: Perfil N-S. Eje Sup.: ondulaciones NOvservado (línea continua) y NTeórico (desplazado) (línea punto y trazos); Eje del medio: diferencias dNCuenca; Eje inf.: basamento de la cuenca.
En este caso es posible nuevamente observar diferencias positivas que no representan la respuesta teórica del modelo adoptado.
BREVE DISCUSIÓN
Ambos resultados dgCuenca y dNCuenca exhiben positivos que en esta línea de trabajo hemos atribuído a un exceso de antirraíz aunque no se pueden descartar explicaciones alternativas como, por ejemplo, significativa intrusión intracortical de densas masas o combinación de ambas posibilidades.
Cualquier alternativa implica una significativa descompensación a partir de la cual podemos señalar una potencial subsidencia futura para restablecer el equilibrio. Esto reduciría la antirraíz y al mismo tiempo incrementaría el espesor sedimentario.
CONCLUSIONES
El procesamiento de datos para caracterizar la corteza que contiene a la cuenca sedimentaria del Golfo de San Jorge no fue sencillo. Con el fin de asegurar mayor consistencia para realizar las validaciones del modelo hemos empleado una doble metodología trabajando no sólo con valores de gravedad sino además con ondulaciones del geoide. Por los dos caminos encontramos nítidos excesos de masas por debajo de las proximidades del depocentro. Ellos indican que la compensación de masas es aún imperfecta. El modelo asumido indica la existencia de una antirraíz sobredimensionada que predice una futura subsidencia en busca del balance isostático. Otras alternativas tales como intrusión de masas intracorticales densas o combinación de éstas con exceso de antirraíz, no cambian la predicción de hundimiento cortical compensado.
AGRADECIMIENTOS
Este trabajo se desarrolló en el marco de delo asumido indica la existencia de una so de antirraíz, no cambian la predicción la beca posdoctoral interna de Laura Cornaglia otorgada por el Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) y fue parcialmente financiado por la Agencia Nacional de Promoción Científica y Tecnológica (PICT 200200166). Agradecemos las sugerencias de los Dres. Andrés Folguera y José Kostadinoff, árbitros del trabajo, quienes contribuyeron a mejorar el manuscrito original.
TRABAJOS CITADOS EN EL TEXTO
1. Almeida, F.F.M. de; Martin, F.C., Ferreira, E.O. y Furque, G. 1978. Tectonic map of South America. 1:5000000. Explanatory Note: Comission for the Geological Map of the World. DNPM/MME, Publ. DNPM/MME, 21 p., Brasilia. [ Links ]
2. Baldi, J.E. y Nevistic, V.A. 1996. Cuenca costa afuera del Golfo San Jorge. En Ramos, V.A. y Turic, M.A. (eds.) Geología y Recursos Naturales de la Plataforma Continental, 13° Congreso Geológico Argentino y 3° Congreso de Exploración de Hidrocarburos, Relatorio 10: 171-192. [ Links ]
3. Bullen, K. 1963. An introduction to the teory of seismology. Cambridge University Press, 381 p., Cambridge. [ Links ]
4. Cesanelli, M. y Lesta, P. 1973. Perfiles geofísicos prospectivos regionales en la Patagonia. Geoacta 6(2): 77-82. [ Links ]
5. Cordell, L. 1992. A scattered equivalent-source method for interpolation and griddind of potencial-field data in three dimensions. Geophysics 57: 629-636. [ Links ]
6. Crovetto, C., Novara, I. e Introcaso, A. 2007. A stretching model to explain the Salado basin (ARGENTINA). Boletín del Instituto de Fisiografía y Geología 77(1-2): 1-10, Rosario. [ Links ]
7. Förste, C., Schmidt, R., Stubenvoll, R., Flechtner, F., Meyer, U., König, R., Neumayer, H., Biancale, R., Lemoine, J.-M., Bruinsma, S., Loyer, S., Barthelmes, F., y Esselborn, S. 2007. The GeoForschungsZentrum Potsdam/Groupe de Recherche de Geodesie Spatiale satellite-only and combined gravity field models: EIGEN-GL04S1 and EIGEN-GL04C. Journal of Geodesy, DOI:10.1007/s00190-007-0183-8. [ Links ]
8. Green, C.M. y Fairhead, J.D. 1991. The South American Gravity Project. En Torge, W. (ed.) Recent Geodetic and Gravimetric Research in Latin America, Springer-Verlag. 215 p., Berlin. [ Links ]
9. Guspí, F. 1999. Fórmulas compactas para el cálculo del potencial gravitatorio de prismas rectangulares. Contribuciones a la geodesia a fines del siglo XX. Homenaje a Oscar Parachú. UNR Editora 7: 129-133, Rosario. [ Links ]
10. Guspí, F., Introcaso, A. e Introcaso, B. 2004. Gravity-enhanced representation of measured geoid undulations using equivalent sources. Geophysical Journal International (RAS) 158: 1-8. [ Links ]
11. Heiskanen, W. y Moritz, H. 1985. Geodesia Física. Instituto Geográfico Nacional. Instituto de Astronomía y Geodesia, 364 p., Madrid. [ Links ]
12. Homovc, J.F., Conforto, G.A. y Lafourcade, P.A. 1993. Faja plegada en el subsuelo de la cuenca del Golfo San Jorge ejemplo de inversión tectónica., 12° Congreso Geológico Argentino y 2° Congreso de Exploración de Hidrocarburos, Actas 3: 233-240, Mendoza. [ Links ]
13. Introcaso, A. 1980. Resultados gravimétricos sobre la cuenca del Golfo de San Jorge (Rep. Arg.). Geofísica Internacional 19(3): 221-238. [ Links ]
14. Introcaso, A. 1997. Gravimetría. UNR Editora, 355 p., Rosario. [ Links ]
15. Introcaso, A. 2006. Geodesia Física. Boletín del Instituto de Fisiografía y Geología. Volumen Especial 1, 128 p., Rosario. URL: http://www.fceia.unr.edu.ar/fisiografia. [ Links ]
16. Introcaso, A. y Crovetto, C. 2005. Introducción a la construcción del geoide. Temas de geociencia 12, UNR Editora, 56 p., Rosario. [ Links ]
17. Introcaso, A., Diez Rodriguez, A., Fraga, H., Nocioni, A., Gerster, R. y Pacino, M.C. 1986. Geophysical modelling procedures of sedimentary basins, (inédito), 26 p. [ Links ]
18. Introcaso, A., Guspí, G. e Introcaso, B. 2002. Interpretación del estado isostático de la Cuenca del Salado (Provincia de Buenos Aires) utilizando un geoide local obtenido mediante fuentes equivalentes a partir de las anomalías de aire libre. 15° Congreso Geológico Argentino, Actas Artículo 139, 6p., El Calafate. [ Links ]
19. Lesta, P., Ferello, R. y Chebli, G. 1980. Chubut Extraandino. Segundo Simposio de Geología Regional Argentina, Academia Nacional de Ciencias 2: 1307-1387, Córdoba. [ Links ]
20. Martin, R. 1954. Gravity Maxima corresponding with sedimentary basin. Geophysics 19: 89-94. [ Links ]
21. Nafe, J.E. y Drake, C.L. 1957. Variation with depth in shallow and deep water marine sediments of porosity, density and the velocities of compressional and shear waves. Geophysics 22(3): 523-552. [ Links ]
22. Okabe, M. 1979. Analytical expressions for gravity anomalies due to homogeneous polyhedral bodies and translations into magnetic anomalies. Geophysics 44(4): 730-741. [ Links ]
23. Sylwan, C. 2001. Geology de la Cuenca del Golfo San Jorge, Argentina. Journal of Iberian Geology 27: 123-157. [ Links ]
24. Strelkov, E., Clavijo, R., Suárez, F., Rodríguez, J., Basile, Y. y Sanagua, J. 2005. La cuenca del Golfo San Jorge. 6° Congreso de Exploración y Desarrollo de Hidrocarburos, Actas: 275-288, Mar del Plata. [ Links ]
25. Torge, W. 2001. Geodesy. Third Edition, Walter de Gruyter, 416 p., Berlin-New York. [ Links ]
26. Trejo, C. 1965. Análisis vectorial con teoría del potencial y aplicaciones. Editorial Kapelusz, 331 p., Buenos Aires. [ Links ]
Recibido: 31 de marzo, 2009
Aceptado: 22 de septiembre, 2009