Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.46 n.1 Bahía Blanca ene./jun. 2005
On the relationship between disjunctive relaxations and minors in packing and covering problems
V. Leoni* and G. Nasini†,
*Fundación Antorchas.
†Universidad Nacional de Rosario, Argentina
Abstract
In 2002, Aguilera et al. analyzed the performance of the disjunctive lift-and-project operator defined by Balas, Ceria and Cornuéjols on covering and packing polyhedra, in the context of blocking and antiblocking duality. Their results generalize Lovász's Perfect Graph Theorem and a theorem of Lehman on ideal clutters. This study motivated many authors to work on the same ideas, providing alternative proofs and analyzing the behaviour of other lift-and-project operators in the same context.
In this paper, we give a survey of the results in the subject and add some new results, showing that the key of the behaviour of the disjunctive operator on these particular classes of polyhedra is the strong relationship between disjunctive relaxations and original relaxations associated to some minors.
1. INTRODUCTION
Many problems in Combinatorial Optimization can be formulated as  linear programs, where the set
linear programs, where the set 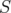 of feasible solutions may be seen as the set of integral solutions in a polyhedron
of feasible solutions may be seen as the set of integral solutions in a polyhedron 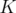 , i.e.
, i.e.  .
.
In spite of optimizing a linear function over 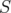 is equivalent to do it over
is equivalent to do it over

in the general case, the complete description of 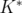 by linear inequalities is not known. Moreover, in most of the cases, even though a partial description is found, an exponential number of inequalities is involved.
by linear inequalities is not known. Moreover, in most of the cases, even though a partial description is found, an exponential number of inequalities is involved.
A polyhedron  will be called a relaxation of
will be called a relaxation of  if
if 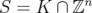 . Given two different relaxations
. Given two different relaxations 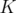 and
and 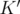 of
of 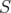 such that
such that 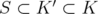 , the bound obtained by optimizing over
, the bound obtained by optimizing over 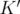 is tighter than the one obtained by optimizing over
is tighter than the one obtained by optimizing over 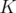 and we say that the relaxation
and we say that the relaxation 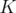 is weaker than
is weaker than 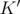 .
.
This fact motivates the definition of operators such that, applied on a relaxation 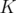 of
of 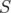 , in each step they obtain a new relaxation
, in each step they obtain a new relaxation 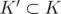 , arriving to
, arriving to 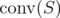 in a finite number of iterations.
in a finite number of iterations.
This is the case of the 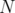 and
and 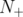 lift-and-project operators defined by Lovász and Schrijver [12] and the disjunctive operator (
lift-and-project operators defined by Lovász and Schrijver [12] and the disjunctive operator (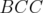 ) defined by Balas, Ceria and Cornuéjols [4].
) defined by Balas, Ceria and Cornuéjols [4].
In [1] and [2] the authors analyze the performance of the 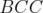 operator on covering and packing polyhedra in the context of blocking and antiblocking duality, respectively. Their results generalize Lovász's Perfect Graph Theorem and its analogous on ideal clutters, due to Lehman. These results motivated Gerards et al. [8] and more recently, Lipták and Tunçel [11], to give alternative proofs in the case of the generalization of Lovász's Perfect Graph Theorem. In the same way, Leoni and Nasini [10] exposed alternative and simpler proofs for the case of the generalization of Lehman's theorem. Lipták and Tunçel [11] started the analysis of the behaviour of the
operator on covering and packing polyhedra in the context of blocking and antiblocking duality, respectively. Their results generalize Lovász's Perfect Graph Theorem and its analogous on ideal clutters, due to Lehman. These results motivated Gerards et al. [8] and more recently, Lipták and Tunçel [11], to give alternative proofs in the case of the generalization of Lovász's Perfect Graph Theorem. In the same way, Leoni and Nasini [10] exposed alternative and simpler proofs for the case of the generalization of Lehman's theorem. Lipták and Tunçel [11] started the analysis of the behaviour of the 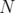 and
and 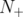 operators in the same context and, recently, Escalante et al. [6] completed this analysis, proving that similar generalizations do not exist for these operators.
operators in the same context and, recently, Escalante et al. [6] completed this analysis, proving that similar generalizations do not exist for these operators.
The aim of this paper is to show that the key of the behaviour of the disjunctive operator observed in [1] and [2] is the strong relationship between disjunctive relaxations and original relaxations associated to some particular minors. This relationship becomes clear from the characterization of the extreme points of these relaxations.
This idea was initiated by Nasini [13], working in the particular case of the clique relaxation 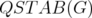 of the stable set polytope
of the stable set polytope 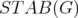 in a graph
in a graph 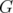 . Independently, Lipták and Tunçel [11] obtained the same result.
. Independently, Lipták and Tunçel [11] obtained the same result.
In Section 2, we provide the fundamental definitions that will be treated in the rest of the paper.
In Section 3, we summarize the results on the extreme points of the disjunctive relaxations for set covering and set packing polyhedra. Besides, we show that the results on 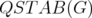 can be extended to more general relaxations of
can be extended to more general relaxations of 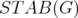 .
.
In Section 4, we summarize the results on the extreme points of the blocker of the disjunctive relaxations for set covering polyhedra. Looking for similar relationships in the context of set packing polyhedra, we show that the antiblocker of the disjunctive relaxations of 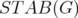 obtained from
obtained from 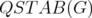 is also strongly related to the antiblocker of the clique relaxation associated to some particular subgraphs of the graph
is also strongly related to the antiblocker of the clique relaxation associated to some particular subgraphs of the graph 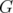 .
.
Finally, in Section 5 we summarize the results obtained in this work and present the conclusions.
2. DEFINITIONS AND PRELIMINARIES
The disjunctive operator defined by Balas, Ceria and Cornuéjols [4] can be applied on polyhedra ![n K ⊂ [0, 1]](/img/revistas/ruma/v46n1/1a0240x.png) . After a lift-and-project iteration of the operator on
. After a lift-and-project iteration of the operator on 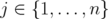 , they obtain
, they obtain
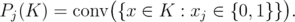
Applying iteratively the operator on a subset of indices 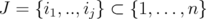 , they proved that
, they proved that
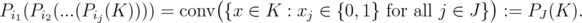
For any subset 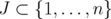 ,
, 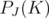 will be called a disjunctive relaxation of
will be called a disjunctive relaxation of 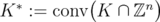 .
.
Clearly, 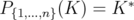 . This last property allows us to talk about the minimum number of iterations needed to find
. This last property allows us to talk about the minimum number of iterations needed to find 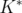 , which is called the disjunctive index of
, which is called the disjunctive index of 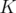 . It is also clear that
. It is also clear that  if and only if the disjunctive index of
if and only if the disjunctive index of 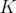 is equal to zero.
is equal to zero.
Given a graph 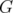 with
with 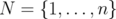 as set of nodes, let us recall that
as set of nodes, let us recall that 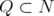 is a clique in
is a clique in 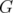 if in every pair in
if in every pair in 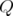 , its nodes are adjacent. Moreover,
, its nodes are adjacent. Moreover,  is a stable set in
is a stable set in 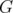 if in no pair of
if in no pair of 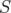 , its nodes are adjacent. Clearly, a clique in a graph
, its nodes are adjacent. Clearly, a clique in a graph 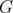 is a stable set in its complementary graph
is a stable set in its complementary graph 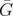 .
.
The stable set polytope 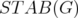 of
of 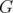 is the convex hull of the incidence vector of its stable sets. The clique relaxation
is the convex hull of the incidence vector of its stable sets. The clique relaxation 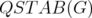 of
of 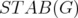 is defined as
is defined as
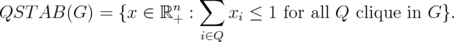
In [1], the authors study the behaviour of the disjunctive operator on polyhedra 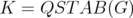 .
.
Following Lovász's Perfect Graph Theorem in [12], if a graph 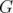 is perfect then its complementary graph
is perfect then its complementary graph 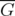 is also perfect. From the polyhedral characterization of perfect graphs given by Chvátal [5], i.e
is also perfect. From the polyhedral characterization of perfect graphs given by Chvátal [5], i.e 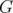 is perfect if and only if
is perfect if and only if  , we have that the disjunctive index of
, we have that the disjunctive index of 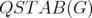 is zero if and only if the disjunctive index of
is zero if and only if the disjunctive index of 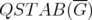 is zero. Moreover, it is known that if
is zero. Moreover, it is known that if 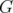 is minimally non perfect (mnp), then
is minimally non perfect (mnp), then 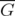 is also mnp and
is also mnp and 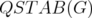 has only one fractional extreme point. It holds that if a graph
has only one fractional extreme point. It holds that if a graph 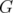 is
is 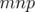 , the disjunctive indices of
, the disjunctive indices of 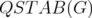 and
and 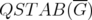 are both equal to one.
are both equal to one.
These well-known results have been generalized in [1] proving that
Theorem 1.
For any graph 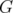 , the disjunctive indices of
, the disjunctive indices of 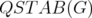 and
and 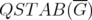 coincide.
coincide.
From this result, the disjunctive index of 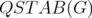 may be considered as a measure of the "imperfection" of
may be considered as a measure of the "imperfection" of 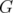 . In this sense, Theorem 1 shows that any graph is as "imperfect" as its complementary graph, generalizing Lovász's Perfect Graph Theorem. This result is proved in [1] as a consequence of the behaviour of the disjunctive relaxation on the context of antiblocker duality.
. In this sense, Theorem 1 shows that any graph is as "imperfect" as its complementary graph, generalizing Lovász's Perfect Graph Theorem. This result is proved in [1] as a consequence of the behaviour of the disjunctive relaxation on the context of antiblocker duality.
If 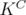 denotes the antiblocker of a polyhedron
denotes the antiblocker of a polyhedron 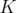 defined by
defined by
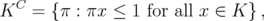
it is well known that
![C -- [QST AB(G)] = ST AB( G).](/img/revistas/ruma/v46n1/1a0290x.png)
The proof of Theorem 1 in [1] is a direct corollary of the following stronger result.
Theorem 2.
For any 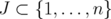 ,
, ![( ) P [P (QST AB(G))]C = [QST AB(G)]C = ST AB(G)- J J](/img/revistas/ruma/v46n1/1a0292x.png) .
.
Similar results have been obtained in [2], working on set covering polyhedra.
A clutter 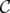 is a set of non-comparable subsets —called edges— of a set
is a set of non-comparable subsets —called edges— of a set 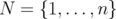 , called the vertex set.
, called the vertex set.
Given a clutter 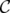 over
over 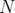 , the blocker of
, the blocker of 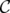 ,
, 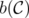 , is the clutter of minimal vertex covers of
, is the clutter of minimal vertex covers of 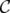 , i.e. minimal subsets
, i.e. minimal subsets 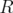 of
of 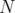 satisfying
satisfying
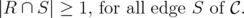
We will denote by 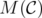 the
the  matrix (with entries 0 or 1) whose rows are the characteristic vectors of the edges of
matrix (with entries 0 or 1) whose rows are the characteristic vectors of the edges of  . Clearly,
. Clearly, 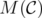 has no dominating rows.
has no dominating rows.
Given a clutter 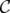 ,
, 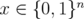 is the incidence vector of a vertex cover of
is the incidence vector of a vertex cover of 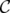 if and only if
if and only if 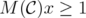 . The set covering polyhedron associated to
. The set covering polyhedron associated to 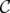 is defined as
is defined as
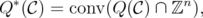
where 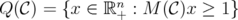 is called the original relaxation of
is called the original relaxation of 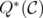 .
.
In this case, considering the blocker of a polyhedron 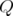 defined as
defined as
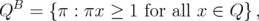
and the blocker 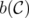 of a clutter
of a clutter 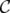 , it is well-known [7] that
, it is well-known [7] that
![Q *(C) = [Q(b(C))]B .](/img/revistas/ruma/v46n1/1a02119x.png)
In order to analyze the "disjunctive behaviour" over blocking polyhedra, the authors in [2] had to define an extension 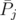 of the disjunctive operator, as
of the disjunctive operator, as
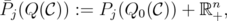
where ![n Q0(C) := Q(C) ∩ [0,1]](/img/revistas/ruma/v46n1/1a02122x.png) . They showed that
. They showed that 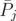 preserves the main properties of
preserves the main properties of 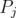 . In particular, for any
. In particular, for any 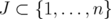 ,
,
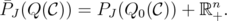
The disjunctive index is also well defined, since
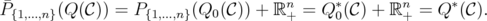
Ideal clutters, defined by Lehman, are those for which 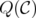 is integral, or equivalently, those for which the disjunctive index is zero.
is integral, or equivalently, those for which the disjunctive index is zero.
Lehman's theorem on ideal clutters [9] establishes that if a clutter is ideal then so is its blocker. In other words, Lehman's theorem says that the disjunctive index of 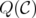 is zero if and only if the disjunctive index of
is zero if and only if the disjunctive index of 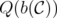 is zero. Moreover, it is known that if
is zero. Moreover, it is known that if 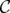 is minimally non ideal (
is minimally non ideal (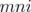 ), then
), then 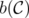 is also mni and
is also mni and 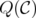 has only one fractional extreme point. It holds that if a clutter
has only one fractional extreme point. It holds that if a clutter 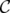 is
is 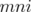 , the disjunctive indices of
, the disjunctive indices of 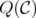 and
and 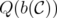 are both equal to
are both equal to 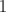 .
.
Lehman's theorem is generalized in [2] in the following sense:
Theorem 3. For any clutter 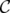 , the disjunctive indices of
, the disjunctive indices of 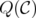 and
and 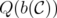 coincide.
coincide.
Once again, the disjunctive index of 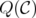 may be considered as a measure of the "non-idealness" of
may be considered as a measure of the "non-idealness" of 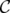 , and Theorem 3 shows that any clutter is as "non-ideal" as its blocker, generalizing Lehman's theorem.
, and Theorem 3 shows that any clutter is as "non-ideal" as its blocker, generalizing Lehman's theorem.
The proof of Theorem 3 in [2] is a direct corollary of the following stronger result (the analogous of Theorem 2) in the context of blocker duality.
Theorem 4. For any 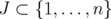 ,
, ![[ ]B B ¯PJ( P¯J (Q(C)) ) = [Q(C)] = Q *(b(C))](/img/revistas/ruma/v46n1/1a02146x.png) .
.
Proofs of Theorem 2 and Theorem 4 given respectively in [1] and [2] are based on the characterization of valid inequalities of the disjunctive relaxations. In those proofs and also in the alternative ones given in [8], the relationship between the disjunctives relaxations and some particular minors is not noticed.
3. DISJUNCTIVE RELAXATIONS, EXTREME POINTS AND MINORS
Let ![n K ⊂ [0,1]](/img/revistas/ruma/v46n1/1a02147x.png) be a polyhedron and consider for
be a polyhedron and consider for  ,
,
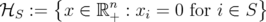
and
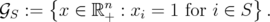
If 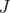 is a fixed subset of
is a fixed subset of 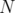 ,
,  and
and 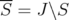 , let us define
, let us define
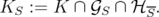
It is not hard to see [1] that
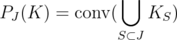
and, if 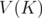 is the set of extreme points of
is the set of extreme points of 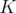 ,
,
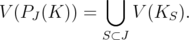
Given a graph 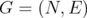 with
with 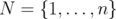 and considering
and considering 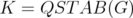 , it is clear that
, it is clear that 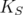 is not empty if and only if
is not empty if and only if 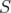 is a stable set in
is a stable set in 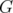 . Moreover, denoting by
. Moreover, denoting by 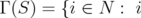 is adjacent to some
is adjacent to some 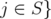 , if
, if 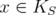 ,
,  for all
for all 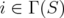 . Therefore, calling
. Therefore, calling  , we have
, we have
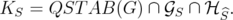
Given  , we write any
, we write any  as
as 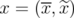 , with
, with 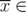
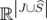 . Therefore, denoting by
. Therefore, denoting by 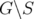 (respectively
(respectively 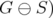 , the subgraph obtained from
, the subgraph obtained from 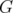 by the deletion (destruction) of nodes in
by the deletion (destruction) of nodes in 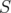 , the following lemma holds.
, the following lemma holds.
Lemma 5. Given 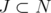 ,
,  and
and 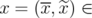
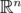 ,
,  is an extreme point of
is an extreme point of 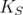 if and only if
if and only if 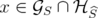 and
and 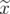 is an extreme point of
is an extreme point of 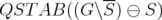 .
.
This lemma is the key of the proof in [13] of Theorem 6 below.
Theorem 6. [13] For any 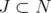 ,
, 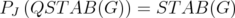 if and only if
if and only if 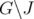 is perfect.
is perfect.
The generalization of Lovász's Perfect Graph Theorem given by Theorem 1 is a direct consequence of the previous theorem.
The "symmetry" of Theorem 1 and Theorem 3 can be also expressed by similar relationships between the extreme points of the disjunctive relaxations of the set covering polyhedron associated to a clutter 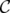 and those associated to some minors of
and those associated to some minors of 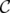 .
.
Given a clutter 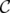 over
over 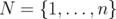 and
and 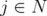 ,
, 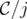 denotes the clutter obtained from
denotes the clutter obtained from 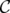 by the contraction of
by the contraction of 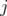 , i.e. the clutter defined over
, i.e. the clutter defined over 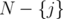 , whose edges are the minimal elements of
, whose edges are the minimal elements of 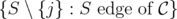 . Also,
. Also, 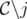 denotes the clutter obtained from
denotes the clutter obtained from 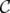 by the deletion of
by the deletion of 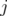 , i.e. the clutter defined over
, i.e. the clutter defined over 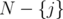 , whose edges are the edges of
, whose edges are the edges of 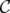 not containing
not containing 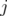 . Given two disjoints subsets
. Given two disjoints subsets 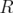 ,
, 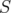 of
of 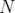 ,
, 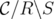 denotes the minor of
denotes the minor of 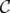 obtained by the contraction of nodes in
obtained by the contraction of nodes in 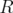 and deletion of nodes in
and deletion of nodes in 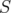 . It is known that
. It is known that  .
.
In this way, in [10] it is proved that
Theorem 7. [10] For any 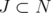 ,
, 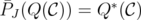 if and only if
if and only if 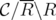 is ideal for every
is ideal for every  .
.
Let us notice that, meanwhile the integrality of 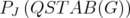 involves the perfection of only the subgraph induced by
involves the perfection of only the subgraph induced by 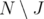 (see Theorem 6), the "symmetric" result for set covering polyhedra involves the idealness of many minors. In other words, in this case there is not a particular minor of
(see Theorem 6), the "symmetric" result for set covering polyhedra involves the idealness of many minors. In other words, in this case there is not a particular minor of 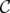 which guarantees the integrality of
which guarantees the integrality of 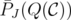 . This difference should be found in the characterization of the extreme points of the disjunctive relaxations of
. This difference should be found in the characterization of the extreme points of the disjunctive relaxations of 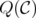 . We present here an scheme of the proof of Theorem 7 in [10].
. We present here an scheme of the proof of Theorem 7 in [10].
In the following, 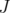 will be a fixed subset of
will be a fixed subset of 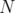 . For
. For 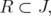 with
with 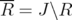 , let us consider the polyhedron
, let us consider the polyhedron
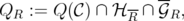
where
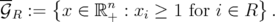
It can be easily seen that
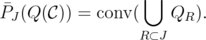
Then, every extreme point of 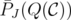 is an extreme point of
is an extreme point of 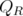 , for some
, for some  . Moreover, writing any
. Moreover, writing any  as
as 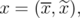 where
where 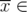
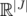 and denoting by
and denoting by 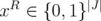 the characteristic vector of
the characteristic vector of  , we have
, we have
Lemma 8. Given 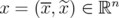 and
and  ,
,  is an extreme point of
is an extreme point of 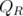 if and only if
if and only if  and
and 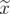 is an extreme point of
is an extreme point of 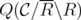 .
.
The difference with the "stable set case" appears noting that it is not true that for any  , every extreme point of
, every extreme point of 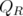 is an extreme point of
is an extreme point of 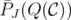 . However, it can be proved that
. However, it can be proved that
Lemma 9. [10] Let 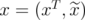 be an extreme point of
be an extreme point of 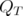 , for some
, for some  and
and 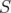 a minimal subset of
a minimal subset of 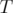 such that
such that 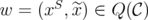 . Then,
. Then, 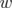 is an extreme point of
is an extreme point of 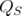 and also, an extreme point of
and also, an extreme point of 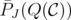 .
.
Now, we derive Theorem 7, the "symmetric" of Theorem 6:
Proof. (of Theorem 7)
Suppose that for some  ,
, 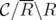 is not ideal, i.e. that
is not ideal, i.e. that 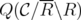 has some fractional extreme point
has some fractional extreme point 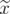 . Then,
. Then, 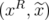 is a fractional extreme point of
is a fractional extreme point of 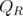 . From Lemma 9, there exists
. From Lemma 9, there exists  such that
such that 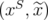 is a fractional extreme point of
is a fractional extreme point of 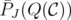 , and then
, and then 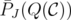 is not integral. Therefore,
is not integral. Therefore, 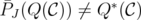 .
.
To see the converse, if 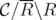 is ideal for every
is ideal for every  , from Lemma 8 follows that
, from Lemma 8 follows that 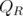 is an integral polyhedron for every
is an integral polyhedron for every  . Therefore,
. Therefore, 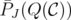 is also integral.
is also integral.
Now we come back to Theorem 6. Let us observe that, in other words, this theorem states that for any graph 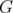 , the disjunctive index of
, the disjunctive index of 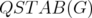 is the minimum number of nodes that it is necessary to delete in
is the minimum number of nodes that it is necessary to delete in 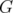 in order to obtain a perfect graph.
in order to obtain a perfect graph.
A similar result have been found in [3], working on the matching polytope in a graph. Let us recall that a matching in a graph 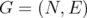 is a subset of edges where any two of them are incident to a same node of
is a subset of edges where any two of them are incident to a same node of 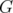 . The matching polytope
. The matching polytope 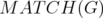 is defined as the convex hull of the incidence vector of the matchings in
is defined as the convex hull of the incidence vector of the matchings in 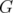 . The natural original relaxation of
. The natural original relaxation of 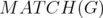 is
is
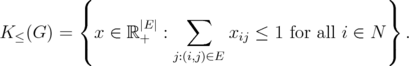
It is known that 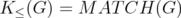 if and only if
if and only if 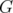 is bipartite. In [3], it is proved that the disjunctive index of
is bipartite. In [3], it is proved that the disjunctive index of 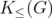 is the minimum number of edges that must be taken off from
is the minimum number of edges that must be taken off from 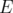 in order to obtain a bipartite graph.
in order to obtain a bipartite graph.
This fact does not seem to be surprising if we recall that the matching polytope of a graph 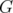 is exactly the stable set polytope of the line graph
is exactly the stable set polytope of the line graph 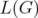 of
of 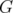 . However, it cannot be seen as a particular case of Theorem 6 because the relaxation
. However, it cannot be seen as a particular case of Theorem 6 because the relaxation 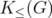 of
of 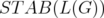 is, in general, weaker than
is, in general, weaker than 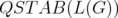 .
.
In a more general context, in a set packing problem we are given a clutter 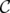 over a set
over a set 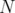 and optimize over
and optimize over 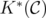 , the convex hull of
, the convex hull of  vectors in
vectors in 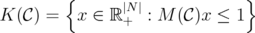 .
.
If we consider the associated graph 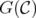 of
of 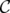 defined by a set of nodes equal to
defined by a set of nodes equal to 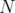 , the vertex set of
, the vertex set of 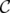 , and where two nodes in
, and where two nodes in 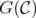 are adjacent if there exists an edge of
are adjacent if there exists an edge of 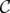 that contains both of them, it is not hard to see that
that contains both of them, it is not hard to see that 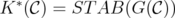 and
and 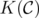 is a relaxation, weaker than
is a relaxation, weaker than 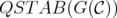 .
.
When 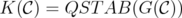 we say that the clutter is conformal. For this family of clutters we have the results on the disjunctive relaxations presented in Section 2.
we say that the clutter is conformal. For this family of clutters we have the results on the disjunctive relaxations presented in Section 2.
The rest of this section is devoted to generalize Theorem 6 for other families of clutters. We are looking for families of clutters C where, for any 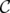 in C, the disjunctive index of the relaxation
in C, the disjunctive index of the relaxation 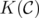 coincides with the minimum number of nodes we must delete from
coincides with the minimum number of nodes we must delete from 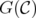 in order to obtain a graph
in order to obtain a graph 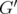 , such that
, such that 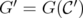 for some
for some 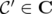 and
and 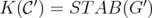 .
.
Given a family C of clutters and a graph 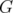 , let us say that
, let us say that 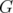 is a C-graph if
is a C-graph if 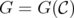 for some
for some 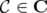 .
.
We need a consistent definition for the family we are looking for. For this purpose, we have to impose some conditions.
Definition 10. A family of clutters C is hereditary if it satisfies the following conditions:- if
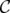 and
and 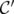 are in C and
are in C and  , then
, then  ;
; - if
 and
and  is a vertex of
is a vertex of 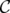 , then
, then 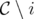 is in C.
is in C.
Definition 11. Given an hereditary family of clutters C and 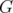 a C-graph such that
a C-graph such that 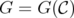 with
with  ,
, 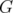 is C-perfect if and only
is C-perfect if and only 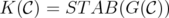 .
.
Condition 1 in Definition 10 implies that C-perfection in Definition 11 is well defined. Besides, it is not hard to see that  . Then, Condition 2 implies that any node induced subgraph of a C-graph is a C-graph, and moreover, any node induce subgraph of a C-perfect graph is C-perfect.
. Then, Condition 2 implies that any node induced subgraph of a C-graph is a C-graph, and moreover, any node induce subgraph of a C-perfect graph is C-perfect.
According to Definition 11, when C is the family of conformal clutters, a C-perfect graph is a perfect graph. Also, when C is the family of clutters with at most two vertices in each edge, for any clutter 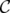 in C we have,
in C we have,
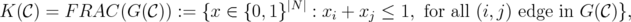
and it is known that C-perfect graphs are bipartite graphs.
This definition also includes 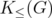 as a relaxation of
as a relaxation of  . In this case, the elements of C have vertex set equal to the set of edges of a graph
. In this case, the elements of C have vertex set equal to the set of edges of a graph 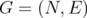 , and the edges are the subsets of
, and the edges are the subsets of 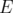 incident in
incident in 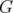 to a node in
to a node in 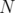 . Besides,
. Besides,  and
and  . It is known that
. It is known that 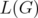 is C-perfect if and only if
is C-perfect if and only if 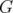 is bipartite.
is bipartite.
Now, the generalization of Theorem 6 will be formulated as
Theorem 12. If 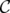 belongs to an hereditary family of clutters C and
belongs to an hereditary family of clutters C and 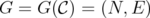 , for any
, for any 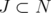 ,
,  if and only if
if and only if 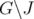 is C-perfect.
is C-perfect.
To prove Theorem 12, it only remains to recall that
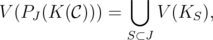
where 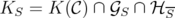 and notice that again,
and notice that again, 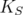 is not empty if and only if
is not empty if and only if 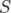 is a stable set in
is a stable set in 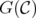 . Moreover, if
. Moreover, if 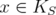 ,
,  for all
for all 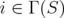 in
in 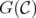 . Therefore, calling
. Therefore, calling  , we have
, we have
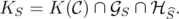
It is not difficult to see that 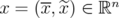 with
with 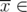
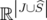 is an extreme point of
is an extreme point of 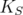 if
if 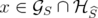 and
and 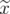 is an extreme point of
is an extreme point of 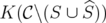 . Moreover,
. Moreover, 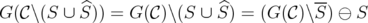 .
.
Proof. (of Theorem 12)
Clearly, 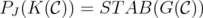 if and only
if and only 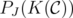 is an integral polyhedron. Equivalently, from the previous observations,
is an integral polyhedron. Equivalently, from the previous observations, 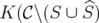 has to be integral, for any
has to be integral, for any 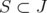 . Equivalently,
. Equivalently, 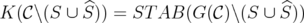 . Finally,
. Finally, 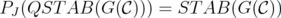 if and only if
if and only if 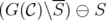 is C-perfect for all
is C-perfect for all 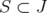 . Since
. Since 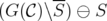 is a node induced subgraph of
is a node induced subgraph of 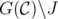 , the result follows.
, the result follows.
Now, for any graph 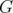 , the results for
, the results for 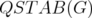 and
and 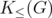 may be seen as particular cases of the previous theorem. We also have that the disjunctive index of
may be seen as particular cases of the previous theorem. We also have that the disjunctive index of 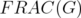 is the minimum number of nodes we must delete from
is the minimum number of nodes we must delete from 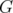 in order to obtain a bipartite graph.
in order to obtain a bipartite graph.
4. DISJUNCTIVE RELAXATIONS IN THE CONTEXT OF POLYHEDRAL DUALITY
The relationship between extreme points and minors has been also found in the context of "polyhedral duality" for set covering polyhedra [10]. The extreme points of the blocker of a disjunctive relaxation are characterized in the following theorem:
Theorem 13. [10] Let 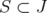 and
and 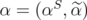 . Then,
. Then, ![[ ]B α ∈ ¯PJ (Q(C))](/img/revistas/ruma/v46n1/1a02390x.png) if and only if
if and only if ![α^∈ [Q(C ∕S\S)]B](/img/revistas/ruma/v46n1/1a02391x.png) . Moreover,
. Moreover, 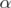 is an extreme point of
is an extreme point of ![[¯P (Q(C))]B J](/img/revistas/ruma/v46n1/1a02393x.png) if and only if
if and only if 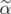 is an extreme point of
is an extreme point of ![[ --]B Q(C ∕S\ S)](/img/revistas/ruma/v46n1/1a02395x.png) .
.
Theorem 4 easily follows from the previous result.
In this section, we will find similar relationships between the antiblocker of a disjunctive relaxation of 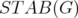 and some particular subgraphs of a graph
and some particular subgraphs of a graph  .
.
In the following, 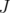 will be denote a fixed subset of
will be denote a fixed subset of 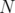 . Let
. Let 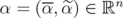 with
with  and
and ![α ∈ [ST AB(G)]C ∩ GS ∩ HS--](/img/revistas/ruma/v46n1/1a02402x.png) for some
for some  .
.
From the observations made by Gerards, Maróti and Schrijver in [8], we know that if  and
and 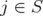 (
(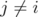 ), then
), then 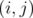 is an edge of
is an edge of 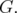 In particular, since
In particular, since  for all
for all  ;
; 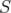 is a clique in
is a clique in 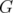 . Moreover, if
. Moreover, if 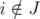 and
and  , then
, then  is a node of
is a node of  .
.
Now, let 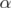 be an extreme point of
be an extreme point of ![[PJ (QST AB(G))]C ∩ GS ∩ HS--](/img/revistas/ruma/v46n1/1a02418x.png) , for some
, for some  and
and 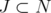 . Since
. Since ![[P (QST AB(G))]C ⊂ [ST AB(G)]C J](/img/revistas/ruma/v46n1/1a02421x.png) ,
, ![α ∈ [ST AB(G)]C ∩ G ∩ H -- S S](/img/revistas/ruma/v46n1/1a02422x.png) . Then, we have
. Then, we have ![C ^α ∈ [QST AB(G \J)]](/img/revistas/ruma/v46n1/1a02423x.png) and
and  when
when  is not a node of
is not a node of  In the following theorem, we prove that the converse also holds, i.e.
In the following theorem, we prove that the converse also holds, i.e.
Theorem 14. Let ![-- α = (α, ^α) ∈ [ST AB(G)]C ∩ GS ∩ HS--](/img/revistas/ruma/v46n1/1a02427x.png) . If
. If 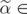
![[QST AB(G \J )]C](/img/revistas/ruma/v46n1/1a02429x.png)
and  when
when  is not a node of
is not a node of  then
then ![C α ∈ [PJ (QST AB(G))]](/img/revistas/ruma/v46n1/1a02433x.png) . Moreover, if
. Moreover, if 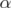 is an extreme point of
is an extreme point of ![C [PJ (QST AB(G))]](/img/revistas/ruma/v46n1/1a02435x.png) then
then 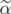 is an extreme point of
is an extreme point of ![C [QST AB(G \J)]](/img/revistas/ruma/v46n1/1a02437x.png) .
.
Proof. Let 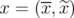 be an extreme point of
be an extreme point of 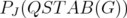 with
with 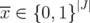 and
and 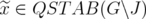 . Let us define
. Let us define 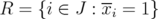 . We need to show that
. We need to show that 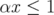 . Since
. Since 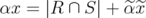 , clearly
, clearly 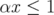 if
if 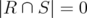 . If
. If 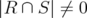 , then
, then 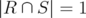 and it only remains to prove that
and it only remains to prove that 
Let 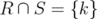 and
and 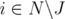 with
with  . Since
. Since 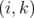 is an edge of
is an edge of 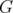 ,
, 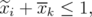 obtaining that
obtaining that  .
.
For the second part, let us assume that 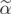 is a convex combination of two points
is a convex combination of two points 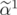 and
and 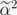 in
in ![[QST AB(G \J)]C](/img/revistas/ruma/v46n1/1a02460x.png) . Defining
. Defining 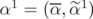 and
and 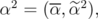 from the previous results we have
from the previous results we have ![αi ∈ [PJ (QST AB(G))]C](/img/revistas/ruma/v46n1/1a02463x.png) for
for 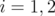 and
and 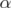 is a convex combination of
is a convex combination of 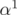 and
and 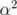 .
.
From this characterization follows an easy new alternative proof for Theorem 2.
Proof. (of Theorem 2)
Since ![-- C ST AB( G) ⊂ PJ ([PJ (QST AB(G))] )](/img/revistas/ruma/v46n1/1a02468x.png) , it suffices to prove that the polyhedron
, it suffices to prove that the polyhedron ![PJ ([PJ (QST AB(G))]C )](/img/revistas/ruma/v46n1/1a02469x.png) is integral. If
is integral. If 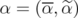 is any extreme point of it, then
is any extreme point of it, then 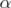 is an extreme point of
is an extreme point of ![[PJ (QST AB(G)]C](/img/revistas/ruma/v46n1/1a02472x.png) . Moreover,
. Moreover, ![α ∈ [ST AB(G)]C ∩ GS ∩ HS,-](/img/revistas/ruma/v46n1/1a02473x.png) for some
for some  From Theorem 14, we have that
From Theorem 14, we have that 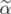 is an extreme point of
is an extreme point of ![C ----- [QST AB(G \J )] = ST AB( G \J )](/img/revistas/ruma/v46n1/1a02476x.png) and then,
and then, 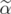 is integral.
is integral.
5. SUMMARY AND CONCLUSIONS
In order to make the symmetry of the results between the "packing" and "covering" cases clearer and to completely understand the relationship between the disjunctive relaxations and the original problem associated to some minors, let us summarize the results on the extreme points of the disjunctive relaxations and those of their "dual polyhedra".
Given a clutter 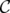 over
over 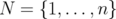 and
and 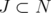 , let
, let
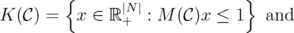
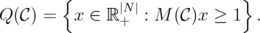
First, for the disjunctive relaxations, we have:
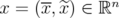 with
with 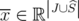 is an extreme point of
is an extreme point of 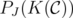 if and only if there exists
if and only if there exists 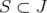 such that
such that 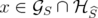 and
and 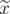 is an extreme point of
is an extreme point of 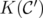 with
with 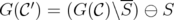 ;
; 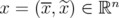 with
with  is an extreme point of
is an extreme point of 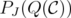 if and only if there exists
if and only if there exists 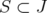 such that
such that 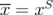 and
and 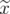 is an extreme point of
is an extreme point of 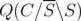 .
.
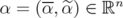 with
with  . We have:
. We have: - When
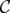 is the clutter of maximal cliques in a graph
is the clutter of maximal cliques in a graph 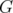 :
: 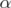 is an extreme point of
is an extreme point of ![[PJ(QST AB(G))]C](/img/revistas/ruma/v46n1/1a02503x.png) if and only if there exists
if and only if there exists  such that
such that 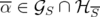 and
and 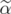 is an extreme point of
is an extreme point of ![C [QST AB(G \J)]](/img/revistas/ruma/v46n1/1a02507x.png) ;
; 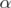 is an extreme point of
is an extreme point of ![[ ]B P¯J (Q(C))](/img/revistas/ruma/v46n1/1a02509x.png) if and only if there exists
if and only if there exists  such that
such that  and
and 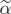 is an extreme point of
is an extreme point of ![[ --]B Q(C ∕S \S)](/img/revistas/ruma/v46n1/1a02513x.png) .
.
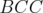 operator "preserves" the original combinatorial structure of the problem. The "negative" results obtained analyzing the behaviour of other lift-and-project operators in the same context ([11] and [6]) are due to the fact that the
operator "preserves" the original combinatorial structure of the problem. The "negative" results obtained analyzing the behaviour of other lift-and-project operators in the same context ([11] and [6]) are due to the fact that the 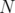 and
and 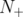 operators do not share this "combinatorial" property of the
operators do not share this "combinatorial" property of the 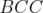 operator.
operator. References
[1] N. Aguilera, M. Escalante and G. Nasini. A Generalization of the Perfect Graph Theorem under the Disjunctive Index, Mathematics of Operations Research 27 (2002), pp. 460–469. [ Links ]
[2] N. Aguilera, M. Escalante and G. Nasini. The Disjunctive Procedure and Blocker Duality, Discrete Applied Mathematics 121/1-3 (2002), pp. 1–13. [ Links ]
[3] N. Aguilera, S. Bianchi and G. Nasini. Lift and Project Relaxations for the Matching and Related Polytopes, Discrete Applied Mathematics 134 (2004), pp. 193–212. [ Links ]
[4] E. Balas, G. Cornuéjols and S. Ceria. A Lift-and-Project Cutting Plane Algorithm for Mixed 0-1 programs, Mathematical Programming 58 (1993), pp. 295–324. [ Links ]
[5] V. Chvátal. On certain Polytopes Associated with Graphs, Journal of Combinatoriaal Theory Series B 18 (1975), pp. 138–154. [ Links ]
[6] M. Escalante, G. Nasini and M. Varaldo. Note on Lift-and- Project ranks and Antiblocking Duality, Electronic Notes on Discrete Mathematics 18 (2004), pp. 115–119. [ Links ]
[7] D. Fulkerson. Blocking and Antiblocking Pairs of Polyhedra, Mathematical Programming 1 (1971), pp. 168–194. [ Links ]
[8] A. Gerards, M. Maróti and A. Schrjiver. Note on : N. E. Aguilera, M. S. Escalante and G. L. Nasini, "A Generalization of the Perfect Graph Theorem under the Disjunctive Index", Mathematics of Operations Research 28 4 (2003), pp. 884–885. [ Links ]
[9] A. Lehman. On the With-Length Inequality, Mathematical Programming 17 (1979), pp. 403–417. [ Links ]
[10] V. Leoni and G. Nasini. Note on: N.E. Aguilera, M.S. Escalante, G.L. Nasini, "The disjunctive procedure and Blocker Duality", Discrete Applied Mathematics 150 (2005), pp. 251-255. [ Links ]
[11] L. Lipták and L. Tunçel. Lift-and-Project Ranks and Antiblocker Duality, Research Report: CORR 2003-16. [ Links ]
[12] L. Lovász and A. Schrijver. Cones of matrices and set-functions and 0-1 optimization, SIAM J. Optim. 1 (1991), pp. 166–190. [ Links ]
[13] G. Nasini. El índice de imperfección de un grafo y su complemento, Anales JAIIO-SIO 01 (2001), pp. 101–106. [ Links ]
V. Leoni
Departamento de Matemática
Facultad de Ciencias Exactas, Ingeniería y Agrimensura
Pellegrini 250
2000- Rosario, Argentina.
valeoni@fceia.unr.edu.ar
G. Nasini
Departamento de Matemática
Facultad de Ciencias Exactas, Ingeniería y Agrimensura
Pellegrini 250
2000- Rosario, Argentina.
nasini@fceia.unr.edu.ar
Recibido: 28 de junio de 2003
Aceptado: 15 de noviembre de 2005














