Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.46 n.1 Bahía Blanca ene./jun. 2005
The Bergman Kernel on Tube Domains
Ching-I Hsin,
Minghsin University of Science and Technology, Taiwan.
Abstract
Let 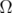 be a bounded strictly convex domain in
be a bounded strictly convex domain in 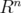 , and
, and 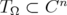 the tube domain over
the tube domain over 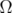 . In this paper, we show that the Bergman kernel of
. In this paper, we show that the Bergman kernel of 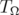 can be expressed easily by an integral formula.
can be expressed easily by an integral formula.
2000 Mathematics Subject Classification : 32A07, 32A25.
Key words and phrases. Bergman kernel; Tube domain.
1. Introduction
Let 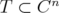 be a domain. The Bergman kernel (see for instance [4])
be a domain. The Bergman kernel (see for instance [4]) 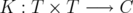 is one of the important holomorphic invariants associated to
is one of the important holomorphic invariants associated to 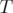 , but it is often difficult to compute
, but it is often difficult to compute 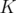 . We shall show that if
. We shall show that if 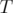 is a tube domain over a bounded strictly convex domain, then an easy computation leads quickly to its Bergman kernel.
is a tube domain over a bounded strictly convex domain, then an easy computation leads quickly to its Bergman kernel.
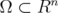 be a bounded strictly convex domain. We are interested in domains
be a bounded strictly convex domain. We are interested in domains  of the type
of the type 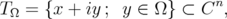 | (1.1) |
known as the tube domain over 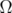 . Let
. Let 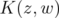 be the Bergman kernel of
be the Bergman kernel of 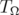 . The main result of this paper is as follows.
. The main result of this paper is as follows.
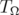 is given by
is given by 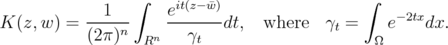 | (1.2) |
Given a function  on
on  , we shall say that
, we shall say that  reproduces
reproduces 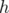 if
if
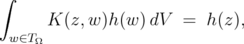 | (1.3) |
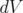 is the Lebesgue measure on
is the Lebesgue measure on 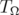 . Let
. Let 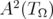 denote the Bergman space, namely the Hilbert space of all holomorphic functions
denote the Bergman space, namely the Hilbert space of all holomorphic functions 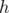 on
on 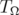 in which
in which 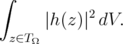 | (1.4) |
The Bergman kernel 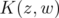 is uniquely characterized by the following three properties:
is uniquely characterized by the following three properties:
(i)  for all
for all 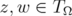 ;
;
(ii) 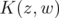 reproduces every element in
reproduces every element in  in the sense of (1.3);
in the sense of (1.3);
(iii) 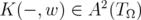 for all
for all 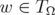 .
.
Our formulation of 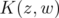 in (1.2) clearly satisfies condition (i). Therefore, to prove the theorem, we need to check conditions (ii) and (iii). This will be done by Propositions 2.4 and 2.5 in the next section.
in (1.2) clearly satisfies condition (i). Therefore, to prove the theorem, we need to check conditions (ii) and (iii). This will be done by Propositions 2.4 and 2.5 in the next section.
2. The Bergman kernel on tube domains
Let 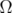 be a bounded strictly convex domain in
be a bounded strictly convex domain in 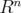 , and let
, and let 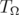 be the tube domain as defined in (1.1). Since
be the tube domain as defined in (1.1). Since 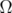 is strictly convex,
is strictly convex, 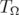 is strictly pseudoconvex.
is strictly pseudoconvex.
Let 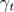 and
and 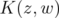 be defined as in (1.2). The Bergman space
be defined as in (1.2). The Bergman space 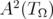 consists of holomorphic functions
consists of holomorphic functions  which satisfy (1.4). In this section, we show that
which satisfy (1.4). In this section, we show that  satisfies conditions (ii) and (iii) stated in the Introduction. Let
satisfies conditions (ii) and (iii) stated in the Introduction. Let 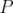 denote the polynomial functions, and we define
denote the polynomial functions, and we define
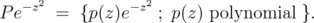
Lemma 2.1 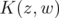 reproduces every element of
reproduces every element of 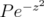 .
.
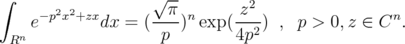 | (2.1) |
Here  denote the usual dot product. In deriving this identity, we observe that both sides of (2.1) are holomorphic in
denote the usual dot product. In deriving this identity, we observe that both sides of (2.1) are holomorphic in  . Therefore, it suffices to check that it holds on the totally real subspace
. Therefore, it suffices to check that it holds on the totally real subspace  . This can be obtained from standard integration tables ([3], 3.323
. This can be obtained from standard integration tables ([3], 3.323  2).
2).
Write 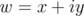 on
on 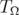 , where
, where 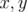 are variables on
are variables on 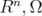 respectively. Then
respectively. Then
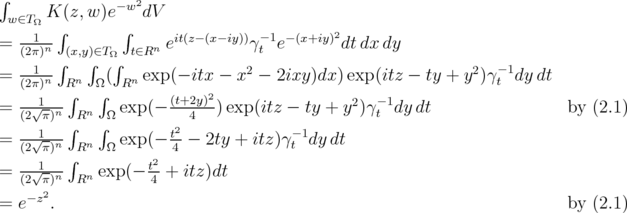
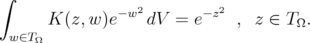 | (2.2) |
From (2.2), substitute  with
with  , where
, where  . This gives
. This gives
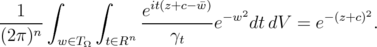
Changing the variable 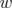 to
to  in LHS gives
in LHS gives
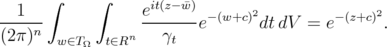
Apply 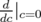 to both sides, we see that
to both sides, we see that 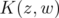 reproduces the function
reproduces the function 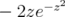 . We carry out the procedure
. We carry out the procedure 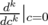 for
for 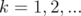 , and Lemma 2.1 follows.
, and Lemma 2.1 follows.
We plan to show that 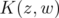 reproduces every element of
reproduces every element of 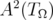 . In view of Lemma 2.1, this will follow if we can show that
. In view of Lemma 2.1, this will follow if we can show that 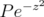 is a dense subset of the Hilbert space
is a dense subset of the Hilbert space 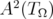 . This will be established by the next two lemmas. Our strategy is to convert the problem on
. This will be established by the next two lemmas. Our strategy is to convert the problem on 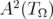 to another Hilbert space
to another Hilbert space 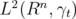 by Lemma 2.2, and obtain a result on
by Lemma 2.2, and obtain a result on 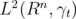 by Lemma 2.3. We then transfer this result back to
by Lemma 2.3. We then transfer this result back to 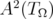 , by Proposition 2.4.
, by Proposition 2.4.
Let 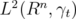 denote the Hilbert space of
denote the Hilbert space of 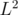 functions on
functions on 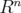 , with weight
, with weight 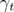 given in (1.2). Namely,
given in (1.2). Namely,
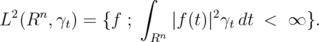
Lemma 2.2 (T. G. Genchev) The transformation
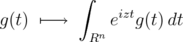 | (2.3) |
is an isometry from 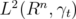 to
to 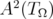 , preserving the Hilbert space norms.
, preserving the Hilbert space norms.
 , there exists
, there exists 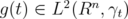 such that
such that 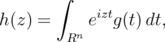 | (2.4) |
see [1],[2]. This means that the transformation in (2.3) is surjective. In order to see that (2.3) is well-defined, injective and preserves the norms, we shall prove that in (2.4),  .
.
Write 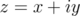 , and (2.4) gives
, and (2.4) gives
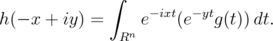
Thus for every fixed 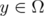 ,
, 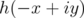 is the Fourier transform of
is the Fourier transform of 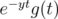 . By Plancherel's theorem,
. By Plancherel's theorem,
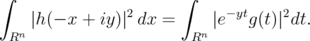
Apply 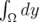 to both sides, we get
to both sides, we get
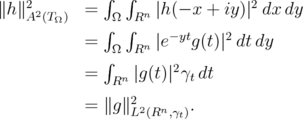
This proves Lemma 2.2. □
Next we define
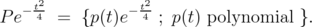
Lemma 2.3  is dense in the Hilbert space
is dense in the Hilbert space 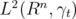 .
.
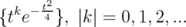 | (2.5) |
is a complete basis of 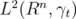 , and the lemma follows.
, and the lemma follows.
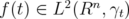 , and suppose that
, and suppose that 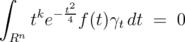 | (2.6) |
for all 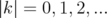 . It is easy to see that
. It is easy to see that 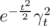 is bounded, so
is bounded, so
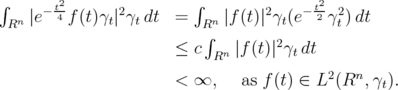
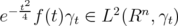 . Let
. Let 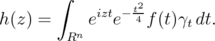 | (2.7) |
By Lemma 2.2, 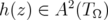 . We may assume that
. We may assume that 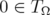 , and consider the power series expansion
, and consider the power series expansion
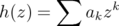
near  . Then
. Then
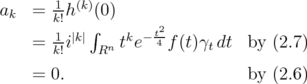
So 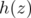 vanishes near
vanishes near  . However, since
. However, since 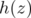 is holomorphic, it follows that
is holomorphic, it follows that  . By Lemma 2.2,
. By Lemma 2.2,
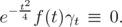
Since 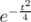 and
and 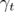 are always positive,
are always positive,

This shows that the functions in (2.5) form a complete basis of 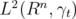 , and the lemma is proved. □
, and the lemma is proved. □
We combine Lemmas 2.1, 2.2 and 2.3 to show that:
Proposition 2.4 The function 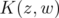 of (1.2) reproduces every element of
of (1.2) reproduces every element of 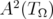 .
.
Proof: We claim that 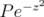 is dense in
is dense in 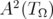 . Identity (2.1) implies that
. Identity (2.1) implies that
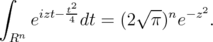
Applying 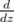 repeatedly to both sides, we see that if
repeatedly to both sides, we see that if 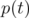 is a polynomial, then
is a polynomial, then
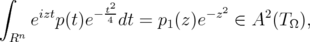
for another polynomial 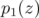 . Namely, the isometry in Lemma 2.2 sends every
. Namely, the isometry in Lemma 2.2 sends every
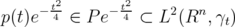
to some
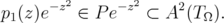
By Lemma 2.3, 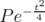 is dense in
is dense in 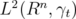 . Hence
. Hence 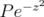 is dense in
is dense in 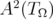 as claimed.
as claimed.
By Lemma 2.1, 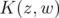 reproduces every element of
reproduces every element of 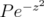 . Therefore, since
. Therefore, since 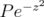 is dense in
is dense in 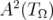 , it follows that
, it follows that 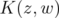 reproduces every element of
reproduces every element of 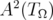 . □
. □
With this result, condition (ii) of 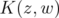 stated in the Introduction is verified. Therefore, to prove the theorem, it remains only to check condition (iii). This is done by the following proposition.
stated in the Introduction is verified. Therefore, to prove the theorem, it remains only to check condition (iii). This is done by the following proposition.
Proposition 2.5 For each fixed 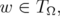
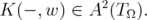
Proof: Fix 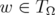 , and consider
, and consider  . For any fixed
. For any fixed 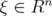 , formula (1.2) satisfies
, formula (1.2) satisfies
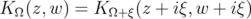
for all 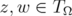 . Further,
. Further, 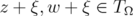 and
and 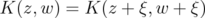 . Therefore, without loss of generality, we may assume that
. Therefore, without loss of generality, we may assume that 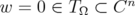 in the statement of this proposition. We want to show that
in the statement of this proposition. We want to show that 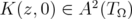 . But
. But
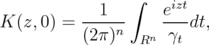
and with Lemma 2.2, we get
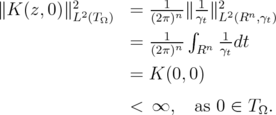
We have shown that, for each 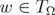 ,
, 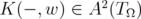 .
.
This result verifies condition (iii) of the Introduction, and the theorem follows.
References
[1] T. G. Genchev, Integral representations for functions holomorphic in tube domains, C. R. Acad. Bulgare Sci. 37 (1984), 717-720. [ Links ]
[2] T. G. Genchev, Paley-Wiener type theorems for functions in Bergman spaces over tube domains, J. Math. Anal. and Appl. 118 (1986), 496-501. [ Links ]
[3] I. S. Gradshteyn, I. M. Ryzhik, Table of Integrals, Series and Products, Academic Press, (1980). [ Links ]
[4] S. Krantz, Function Theory of Several Complex Variables, 2ed. Wadsworth & Brooks/Cole, Pacific Grove 1992. [ Links ]
Ching-I Hsin
Division of Natural Science,
Minghsin University of Science and Technology.
Hsinchu County 304, Taiwan.
hsin@must.edu.tw
Recibido: 6 de mayo de 2004
Aceptado: 28 de marzo de 2005














