Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932versão On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.46 n.1 Bahía Blanca jan./jun. 2005
Some operator inequalities for unitarily invariant norms*†
Cristina Cano, Irene Mosconi‡ and Demetrio Stojanoff§
‡ Partially supported by Universidad Nac. del Comahue
§ Partially supported CONICET (PIP 4463/96), UNLP 11 X350 and ANPCYT (PICT03-09521)
Abstract:
Let 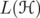 be the algebra of bounded operators on a complex separable Hilbert space
be the algebra of bounded operators on a complex separable Hilbert space 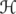 . Let
. Let 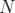 be a unitarily invariant norm defined on a norm ideal
be a unitarily invariant norm defined on a norm ideal 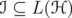 . Given two positive invertible operators
. Given two positive invertible operators 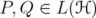 and
and ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a0614x.png) , we show that
, we show that 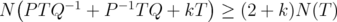 ,
, 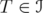 . This extends Zhang's inequality for matrices. We prove that this inequality is equivalent to two particular cases of itself, namely
. This extends Zhang's inequality for matrices. We prove that this inequality is equivalent to two particular cases of itself, namely  and
and 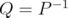 . We also characterize those numbers
. We also characterize those numbers 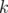 such that the map
such that the map 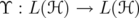 given by
given by 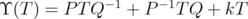 is invertible, and we estimate the induced norm of
is invertible, and we estimate the induced norm of  acting on the norm ideal
acting on the norm ideal 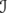 . We compute sharp constants for the involved inequalities in several particular cases.
. We compute sharp constants for the involved inequalities in several particular cases.
Keywords and phrases: Positive matrices; Inequalities; Unitarily invariant norm.
AMS Subject Classification: Primary 47A30, 47B15.
1. INTRODUCTION
Let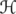 be a Hilbert space and denote by
be a Hilbert space and denote by 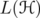 the algebra of bounded linear operators on
the algebra of bounded linear operators on 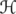 . In 1990, Corach-Porta-Recht [6] show that, for every invertible selfadjoint operator
. In 1990, Corach-Porta-Recht [6] show that, for every invertible selfadjoint operator 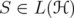 and for every
and for every 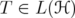 , it holds that
, it holds that 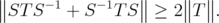 | (1) |
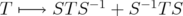 for not necessarily selfadjoint
for not necessarily selfadjoint 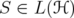 . In 2001, Seddik, [15] proved that, for
. In 2001, Seddik, [15] proved that, for 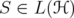 invertible and positive,
invertible and positive, 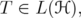 and
and 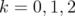 ,
, 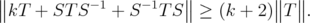 | (2) |
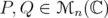 ,
, 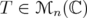 , and
, and ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a0640x.png) , then
, then 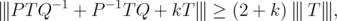 | (3) |
for every unitarily invariant norm  on
on 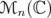 .
.
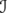 of
of 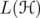 (see Remark 2.1 or Simon's book [17]). We show that, for every unitarily invariant norm
(see Remark 2.1 or Simon's book [17]). We show that, for every unitarily invariant norm  , the following inequalities are equivalent, for every
, the following inequalities are equivalent, for every ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a0647x.png) :
: 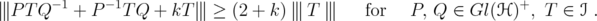 | (4) |
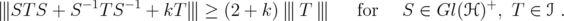 | (5) |
 | (6) |
We give a proof of inequality (6), using a technical result about unitarily invariant norms, which allows us to obtain a reduction to the matricial case. In this case, we use a result of Bhatia and Parthasarathy [4], and some properties of the Hadamard product of matrices. This result was previously proved for  in [2], for not necessarily positive
in [2], for not necessarily positive 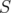 ,
, 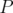 and
and 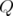 . We study the operators associated to the three mentioned inequalities, and their restriction as operators on the norm ideal
. We study the operators associated to the three mentioned inequalities, and their restriction as operators on the norm ideal 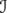 . We compute their spectra and, in some cases, their reduced minimum moduli (also called conorms). The rest of the paper deals with the estimation of sharp constants for inequality (5), with respect to the usual norm of
. We compute their spectra and, in some cases, their reduced minimum moduli (also called conorms). The rest of the paper deals with the estimation of sharp constants for inequality (5), with respect to the usual norm of 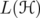 . We get the optimal constant, if one restricts to operators
. We get the optimal constant, if one restricts to operators 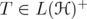 . Using the notion of Hadamard index for positive matrices, studied in [7], we compute, for a fixed
. Using the notion of Hadamard index for positive matrices, studied in [7], we compute, for a fixed  , the constant
, the constant
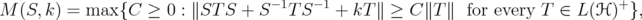
for  (see Proposition 5.6). Finally, we give some partial results for
(see Proposition 5.6). Finally, we give some partial results for 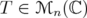 , in lower dimensions, showing numerical estimates of sharp constants. For
, in lower dimensions, showing numerical estimates of sharp constants. For 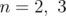 and
and  , we characterize the best intervals
, we characterize the best intervals 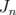 such that the inequality (6) holds in
such that the inequality (6) holds in 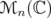 for every
for every 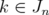 .
.
In section 2, we fix several notations and state some preliminary results. We expose with some detail the theory of unitarily invariant norms defined on norm ideals of 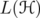 , proving some technical results in this area. In section 3, we show the equivalence of the mentioned inequalities and we give the proof of (6). In section 4, we study the associated operators. In section 5, we describe the theory of Hadamard index, and we use it to obtain a description of the constant
, proving some technical results in this area. In section 3, we show the equivalence of the mentioned inequalities and we give the proof of (6). In section 4, we study the associated operators. In section 5, we describe the theory of Hadamard index, and we use it to obtain a description of the constant 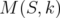 . In section 6 we study the case of matrices of lower dimensions.
. In section 6 we study the case of matrices of lower dimensions.
We wish to acknowledge Prof. G. Corach who shared with us fruitful discussions concerning these matters.
2. PRELIMINARIES
Let 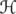 be a separable Hilbert space, and
be a separable Hilbert space, and 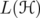 be the algebra of bounded linear operators on
be the algebra of bounded linear operators on 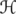 . We denote
. We denote 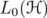 the ideal of compact operators,
the ideal of compact operators, 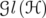 the group of invertible operators,
the group of invertible operators, 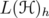 the set of hermitian operators,
the set of hermitian operators, 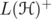 the set of positive definite operators,
the set of positive definite operators, 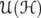 the unitary group, and
the unitary group, and 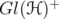 the set of invertible positive definite operators.
the set of invertible positive definite operators.
Given an operator 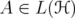 ,
, 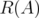 denotes the range of
denotes the range of 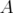 ,
, 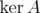 the nullspace of
the nullspace of 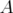 ,
, 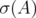 the spectrum of
the spectrum of 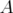 ,
, 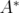 the adjoint of
the adjoint of 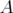 ,
, 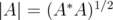 the modulus of
the modulus of 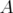 ,
, 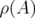 the spectral radius of
the spectral radius of 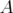 , and
, and  the spectral norm of
the spectral norm of 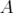 . Given a closed subspace
. Given a closed subspace  of
of  , we denote by
, we denote by 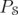 the orthogonal projection onto
the orthogonal projection onto 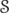 .
.
When  , we shall identify
, we shall identify 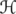 with
with  ,
, 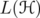 with
with 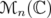 , and we use the following notations:
, and we use the following notations: 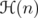 for
for 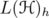 ,
, 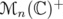 for
for 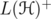 ,
, 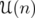 for
for 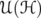 , and
, and 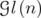 for
for 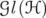 . A norm
. A norm  in
in 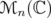 is called unitarily invariant if
is called unitarily invariant if  for every
for every 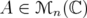 and
and 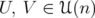 .
.
Remark 2.1. The notion of unitarily invariant norms can be defined also for operators on Hilbert spaces. We give some basic definitions (see Simon's book [17]): Let 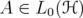 . Then also
. Then also 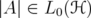 . We denote by
. We denote by 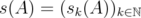 , the sequence of eigenvalues of
, the sequence of eigenvalues of  , taken in non increasing order and with multiplicity. If
, taken in non increasing order and with multiplicity. If 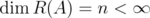 , we take
, we take 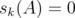 for
for 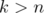 . The numbers
. The numbers 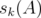 are called the singular values of
are called the singular values of 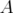 .
.
Denote by 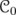 the set of complex sequences which converge to zero. Consider
the set of complex sequences which converge to zero. Consider 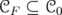 the set of sequences with finite non zero entries. For
the set of sequences with finite non zero entries. For 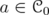 , denote
, denote 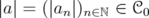 . A gauge symmetric function (or symmetric norm) is a map
. A gauge symmetric function (or symmetric norm) is a map 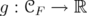 which satisfy the following properties:
which satisfy the following properties:
• 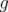 is a norm on
is a norm on 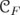 ,
,
•  for every
for every 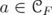 ,
,
•and 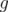 is invariant under permutations. We say that
is invariant under permutations. We say that 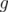 is normalized if
is normalized if 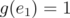 . For
. For 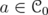 , define
, define
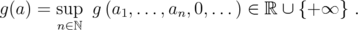
A unitarily invariant norm in 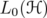 is a map
is a map  given by
given by 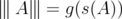 ,
, 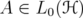 , where
, where 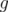 is a symmetric norm. The set
is a symmetric norm. The set
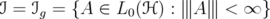
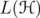 , called the norm ideal associated to
, called the norm ideal associated to  . Then
. Then  is a Banach space, and the following properties hold:
is a Banach space, and the following properties hold: - If
 , then
, then  , and
, and 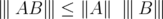 for every
for every 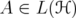 .
. - If
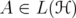 has finite rank, then
has finite rank, then 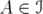 , because
, because 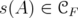 .
. - If
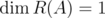 , then
, then 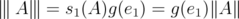 .
. - Given
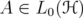 and
and 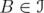 such that
such that 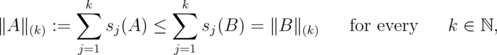
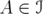 and
and  .
. - For every
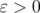 and
and  , there exists a finite rank operator
, there exists a finite rank operator 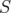 such that
such that 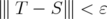 .
.
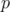 -norms
-norms 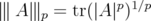 , for
, for 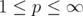 , and the Ky-Fan norms
, and the Ky-Fan norms 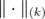 ,
,  . The usual norm, which coincides with
. The usual norm, which coincides with 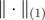 and
and 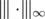 when restricted to
when restricted to 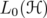 , is also unitarily invariant.
, is also unitarily invariant. 
Proposition 2.2. Let 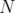 be an unitarily invariant norm on an ideal
be an unitarily invariant norm on an ideal 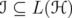 . Let
. Let 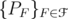 be a increasing net of projections in
be a increasing net of projections in 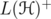 which converges strongly to the identity (i.e.,
which converges strongly to the identity (i.e., 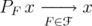 for every
for every 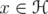 ). Then
). Then
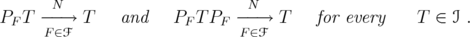
Proof. By Remark 2.1, for every 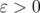 , there exists a finite rank operator
, there exists a finite rank operator 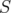 such that
such that  . For every
. For every 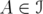 and every projection
and every projection 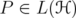 , it holds that
, it holds that 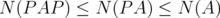 . In particular,
. In particular, 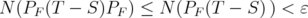 for every
for every 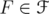 . Hence, we can assume that
. Hence, we can assume that 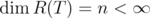 . Given
. Given 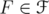 , denote
, denote 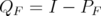 . Since
. Since 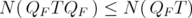 and
and
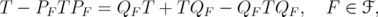
it suffices to prove that 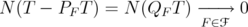 . Fix
. Fix 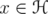 . Note that
. Note that 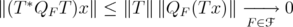 . Therefore
. Therefore
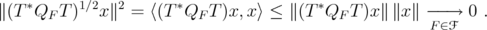
This implies that 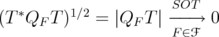 , and all these operators act on the fixed finite dimensional subspace
, and all these operators act on the fixed finite dimensional subspace 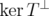 , where the convergence of operators in every norm (included
, where the convergence of operators in every norm (included 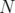 ) is equivalent to the SOT (or strong) convergence.
) is equivalent to the SOT (or strong) convergence.
 be a unitarily invariant norm defined on a norm ideal
be a unitarily invariant norm defined on a norm ideal 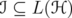 . The space
. The space 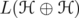 can be identified with the algebra of block
can be identified with the algebra of block 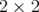 matrices with entries in
matrices with entries in 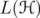 , denoted by
, denoted by 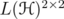 . Denote by
. Denote by 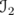 the ideal of
the ideal of 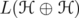 associated with the same norm
associated with the same norm  (i.e., by using the same symmetric norm
(i.e., by using the same symmetric norm 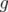 ). Then, the following properties hold
). Then, the following properties hold - Let
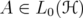 , and define
, and define 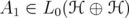 as any of the following matrices
as any of the following matrices
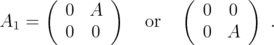
Then ,
,  , and
, and 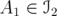 if and only if
if and only if 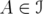 .
. - Under the mentioned identification,
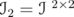 .
. 
![A = [aij],B = [bij] ∈ Mn( ℂ)](/img/revistas/ruma/v46n1/1a06226x.png) denote by
denote by  the Hadamard product
the Hadamard product ![[aijbij]](/img/revistas/ruma/v46n1/1a06228x.png) . Every
. Every 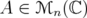 defines a linear map
defines a linear map 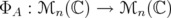 given by
given by 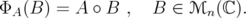 | (7) |
 on
on 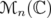 , it induces a norm of the linear map
, it induces a norm of the linear map 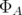 by means of
by means of 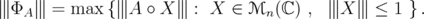 | (8) |
The following result collects two classical results of Schur about Hadamard (or Schur) products of positive matrices (see [16]), and a generalization of the second one for unitarily invariant norms, proved by Ando in [1, Proposition 7.7] .
Proposition 2.4 (Schur). Let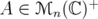 and
and 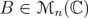 . Then
. Then - If
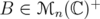 then also
then also 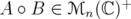 .
. - Denote by
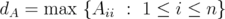 . Then
. Then
for every unitarily invariant norm
(9)  on
on 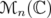 .
. 
 and
and  be an unitarily invariant norm on an ideal
be an unitarily invariant norm on an ideal 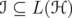 . Then the following inequalities are equivalent:
. Then the following inequalities are equivalent:  , for every
, for every 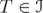 and
and 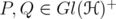 .
. 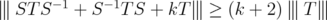 , for every
, for every 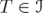 and
and 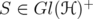 .
. 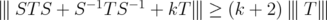 , for every
, for every 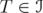 and
and 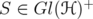 .
.
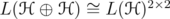 . For
. For 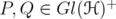 and
and 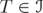 , define the operators
, define the operators
![[ ] [ ] S1 = P 0 and T1 = 0 T ∈ I2 . 0 Q 0 0](/img/revistas/ruma/v46n1/1a06260x.png)
Then
![[ ] -1 - 1 0 P T Q- 1 + P -1T Q + kT S1T1S 1 + S1 T1S1 + kT1 = 0 0 .](/img/revistas/ruma/v46n1/1a06261x.png)
Therefore, as  for every
for every 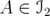 , then
, then
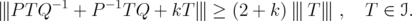
This shows  . The same arguments using
. The same arguments using ![[ ] S1 = P 0-1 0 Q](/img/revistas/ruma/v46n1/1a06266x.png) show
show  . □
. □
Remark 3.2. As said in the Introduction, the inequality 2 of Theorem 3.1 was proved, for the usual norm, by Corach-Porta-Recht in [6] with  (and
(and 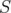 not necessarily positive), and by Ameur Seddik in [15] with
not necessarily positive), and by Ameur Seddik in [15] with  . The inequality 1 of Theorem 3.1 was proved, in the finite dimensional case, by X. Zhan in [18], for
. The inequality 1 of Theorem 3.1 was proved, in the finite dimensional case, by X. Zhan in [18], for ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06271x.png) . In the rest of this section, we give a proof of inequality 2 of Theorem 3.1 for
. In the rest of this section, we give a proof of inequality 2 of Theorem 3.1 for ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06272x.png) in the general setting.
in the general setting.
Lemma 3.3. Let 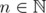 ,
,  and
and ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06275x.png) . Let
. Let 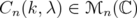 be given by
be given by
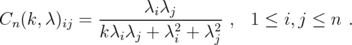
Then 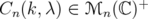 for every
for every 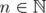 .
.
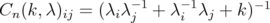 . These numbers are well defined because
. These numbers are well defined because  for every
for every  and
and 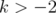 . Bhatia and Parthasarathy [4] proved that, for
. Bhatia and Parthasarathy [4] proved that, for 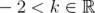 and
and 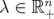 , the matrix
, the matrix 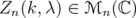 with entries
with entries 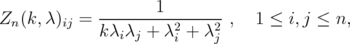 | (10) |
satisfies 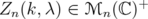 for every
for every 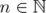 and
and 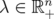 if and only if
if and only if ![k ∈ (- 2,2].](/img/revistas/ruma/v46n1/1a06291x.png)
On the other hand, if 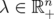 , then the matrix
, then the matrix 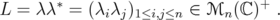 By Propposition 2.4,
By Propposition 2.4, 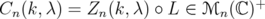 for every
for every ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06295x.png) . □
. □
Theorem 3.4. Let 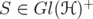 and
and ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06297x.png) . Then, for every unitarily invariant norm
. Then, for every unitarily invariant norm  on an ideal
on an ideal 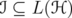 , and for every
, and for every  ,
,
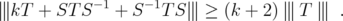
Proof. We follow the same steps as in [6]. By the spectral theorem, we can suppose that 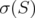 is finite, since
is finite, since 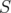 can be approximated in norm by operators
can be approximated in norm by operators 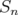 such that each
such that each 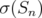 is finite. We can suppose also that
is finite. We can suppose also that 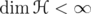 , by choosing an adequate net of finite rank projections
, by choosing an adequate net of finite rank projections 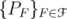 which converges strongly to the identity and replacing
which converges strongly to the identity and replacing 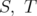 by
by 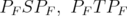 . Indeed, the net may be chosen in such a way that
. Indeed, the net may be chosen in such a way that  and
and 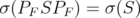 for every
for every 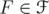 . Note that, by Proposition 2.2,
. Note that, by Proposition 2.2, 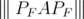 converges to
converges to 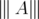 for every
for every  .
.
 is diagonal by a unitary change of basis in
is diagonal by a unitary change of basis in 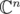 . Take
. Take 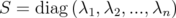 . Then
. Then 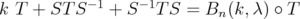 , where
, where 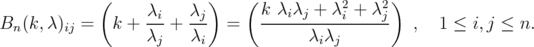 | (11) |
Since 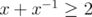 for every
for every  ,
, 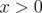 , it follows that, if
, it follows that, if 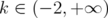 , then
, then 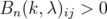 for every
for every 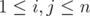 . Consider the matrix
. Consider the matrix 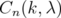 given by
given by  . Hence, in order to prove inequality (6) for every
. Hence, in order to prove inequality (6) for every 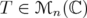 , it suffices to show that
, it suffices to show that  for
for 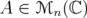 and
and ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06332x.png) . By Lemma 3.3,
. By Lemma 3.3, 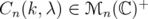 for every
for every ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06334x.png) . Finally, note that
. Finally, note that  ,
, 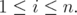 Therefore, inequality (6) holds by Eq. (9) in Proposition 2.4. □
Therefore, inequality (6) holds by Eq. (9) in Proposition 2.4. □
As a consequence of this result and Theorem 3.1, we get an infinite dimensional version, for every unitarily invariant norm, of Zhang inequality:
Corollary 3.5. Let 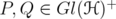 and
and ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06338x.png) . Then, for every unitarily invariant norm
. Then, for every unitarily invariant norm  on an ideal
on an ideal 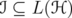 , and for every
, and for every  ,
,
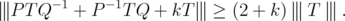
Corollary 3.6. Let 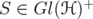 and
and ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06344x.png) . Then, for every unitarily invariant norm
. Then, for every unitarily invariant norm  on an ideal
on an ideal 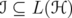 , and for every
, and for every  ,
,
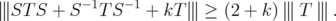
4. THE ASSOCIATED OPERATORS
In this section we study the operators associated with the inequalities proved in the previous section. Given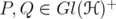 and
and 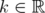 , we consider the bounded operator
, we consider the bounded operator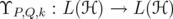 associated with inequality (4):
associated with inequality (4): 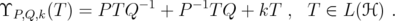 | (12) |
Hence, for every unitarily invariant norm  defined on an ideal
defined on an ideal 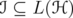 , inequality (4) means that
, inequality (4) means that 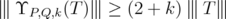 for
for  ,
, 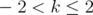 . Given
. Given 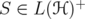 and
and 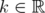 , define the operators
, define the operators 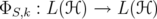 and
and 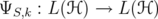 associated with inequalities (6) and (5):
associated with inequalities (6) and (5):  and
and 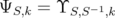 . In this section we characterize, for fixed
. In this section we characterize, for fixed 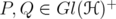 , those
, those  such that
such that 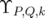 is invertible. In some cases we estimate, for a given norm on some ideal of
is invertible. In some cases we estimate, for a given norm on some ideal of 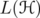 , the induced norms of their inverses.
, the induced norms of their inverses.
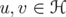 . Denote by
. Denote by 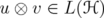 the operator given by
the operator given by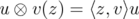 ,
, 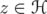 . It is clear that
. It is clear that  . Hence
. Hence 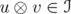 for every norm ideal induced by a unitarily invariant norm
for every norm ideal induced by a unitarily invariant norm  . The following properties are easy to see:
. The following properties are easy to see: 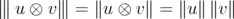 .
. - The map
 is sesqui linear.
is sesqui linear. - If
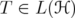 , then
, then  and
and  .
. 
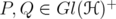 . Denote by
. Denote by  . Then
. Then
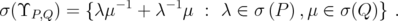
Moreover, 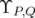 has the same spectrum, if it is considered as acting on any norm ideal
has the same spectrum, if it is considered as acting on any norm ideal 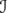 associated with a unitarily invariant norm.
associated with a unitarily invariant norm.
Proof. Fix the norm ideal 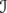 and consider the restriction
and consider the restriction 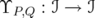 . Let
. Let 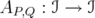 be given by
be given by  ,
, 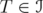 . Note that
. Note that 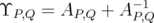 . Therefore, by the known properties of the Riesz functional calculus for operators on Banach spaces (in this case, the Banach space is
. Therefore, by the known properties of the Riesz functional calculus for operators on Banach spaces (in this case, the Banach space is 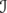 and the map is
and the map is 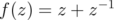 ), it suffices to show that
), it suffices to show that 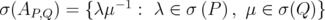 .
.
Given 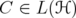 , denote by
, denote by 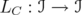 (resp.
(resp. 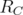 ) the operator given by
) the operator given by 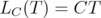 (resp.
(resp. 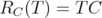 ),
),  . By Remark 2.1, these operators are bounded. If
. By Remark 2.1, these operators are bounded. If 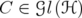 , then
, then 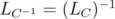 , and similarly for
, and similarly for 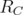 . Hence
. Hence 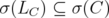 and
and 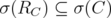 . Note that
. Note that 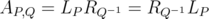 . Therefore
. Therefore
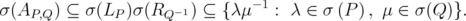
Given 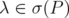 ,
, 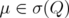 and
and 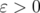 , let
, let 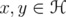 be unit vectors such that
be unit vectors such that 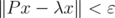 and
and 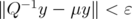 . Such vectors exist because
. Such vectors exist because  and
and 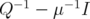 are selfadjoint operators. Consider the rank one operator
are selfadjoint operators. Consider the rank one operator 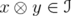 . Then, by Remark 4.1,
. Then, by Remark 4.1, 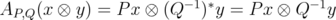 . Hence
. Hence
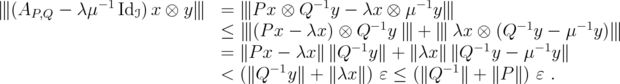
Therefore 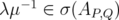 , because
, because  . This shows that
. This shows that 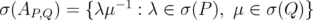 , and the proof is complete. □
, and the proof is complete. □
Corollary 4.3. Let 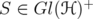 and
and 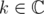 . Then
. Then 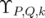 is invertible if and only if
is invertible if and only if 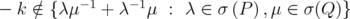 .
.
Proof. Just note that 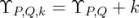 Id
Id . Then apply Proposition 4.2. □
. Then apply Proposition 4.2. □
Remark 4.4. Let  be a unitarily invariant norm defined on a norm ideal
be a unitarily invariant norm defined on a norm ideal 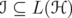 . By Remark 2.1,
. By Remark 2.1, 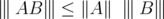 for
for 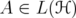 and
and 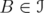 . Given a linear operator
. Given a linear operator 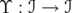 , we denote by
, we denote by 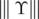 the induced norm:
the induced norm:

By a standard 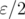 argument and using the continuity of "taking inverse", one can show that, for
argument and using the continuity of "taking inverse", one can show that, for ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06437x.png) fixed, the map
fixed, the map 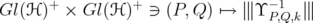 is continuous.
is continuous. 
Proposition 4.5. Let 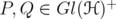 and
and ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06441x.png) . Let
. Let  be a unitarily invariant norm defined on a norm ideal
be a unitarily invariant norm defined on a norm ideal 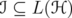 . Then
. Then 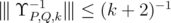 . Moreover, if
. Moreover, if 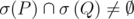 , then
, then  .
.
Proof. The inequality follows from Corollary 3.5. Suppose that 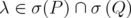 is an eigenvalue for both
is an eigenvalue for both 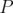 and
and 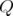 . Let
. Let 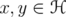 be unit vectors such that
be unit vectors such that  and
and  . Consider
. Consider 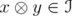 . Then, since
. Then, since  and
and  , it is easy to see that
, it is easy to see that  . Hence,
. Hence, 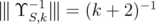 in this case. An easy consequence of spectral theory is that every
in this case. An easy consequence of spectral theory is that every 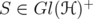 such that
such that 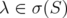 can be arbitrarily approximated by positive invertible operators such that
can be arbitrarily approximated by positive invertible operators such that 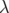 is a isolated point of their spectra, hence an eigenvalue. Applying this, jointly for
is a isolated point of their spectra, hence an eigenvalue. Applying this, jointly for 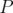 and
and 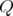 , for some
, for some 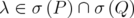 , and using the fact that the map
, and using the fact that the map  is continuous, the proof is completed. □
is continuous, the proof is completed. □
Corollary 4.6. Let 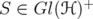 and
and ![k ∈ (- 2,2]](/img/revistas/ruma/v46n1/1a06466x.png) . Let
. Let  be a unitarily invariant norm defined on a norm ideal
be a unitarily invariant norm defined on a norm ideal 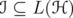 . Then
. Then 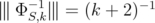 . If there exists
. If there exists 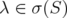 such that also
such that also 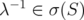 , then also
, then also 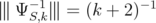 .
.
Proof. The first case follows applying Proposition 4.5 with 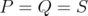 . Note that the hypothesis
. Note that the hypothesis 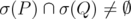 becomes obvious. For the second, take
becomes obvious. For the second, take  and
and 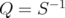 . Note that
. Note that 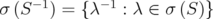 . □
. □
Remark 4.7. The Forbenius norm  works on the ideal of Hilbert Schmit operators, which is a Hilbert space with this norm. In this case, the operator
works on the ideal of Hilbert Schmit operators, which is a Hilbert space with this norm. In this case, the operator 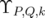 defined in Eq. (12) is positive, so that
defined in Eq. (12) is positive, so that 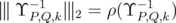 . Therefore, Proposition 4.2 gives the sharp constant for inequality (4) for this norm. Observe that
. Therefore, Proposition 4.2 gives the sharp constant for inequality (4) for this norm. Observe that 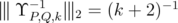 if and only if
if and only if 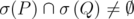 .
. 
5. SHARP CONSTANTS AND HADAMARD INDEX
Preliminary results. In this subsection, we shall give a brief exposition of the definitions and results of the theory of Hadamard index, which we shall use in the rest of the section. All the results are taken from [7].
Denote by 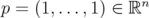 and
and 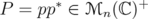 , the matrix with all its entries equal to
, the matrix with all its entries equal to 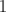 . Given
. Given 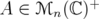 and
and 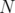 a norm on
a norm on 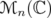 , we define the
, we define the 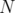 -index of
-index of 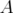 by
by
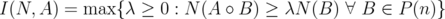
and the minimal index of 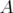 by
by
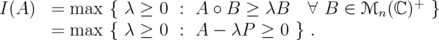
The index relative to the spectral norm on 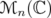 will be denoted by
will be denoted by 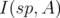 , and the index relative to the 2-norm
, and the index relative to the 2-norm 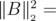 tr
tr  ,
, 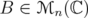 , is denoted by
, is denoted by 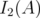 .
.
Proposition 5.1. Let 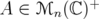 . Then
. Then 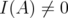 if and only if
if and only if 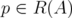 .
. 
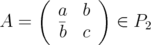 , then
, then 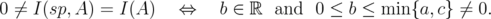 | (13) |
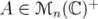 with nonnegative entries such that all
with nonnegative entries such that all 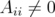 . Then the following conditions are equivalent:
. Then the following conditions are equivalent: - There exist
 with nonnegative entries such that
with nonnegative entries such that 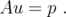
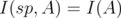 .
. 
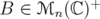 such that
such that 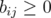 for all
for all  . Then there exists a subset
. Then there exists a subset 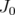 of
of 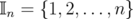 such that
such that 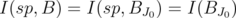 . Therefore
. Therefore 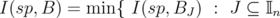 and
and 

Let 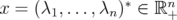 ,
, 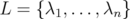 and
and  . We consider
. We consider
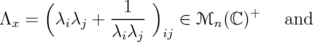
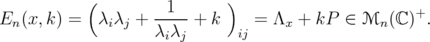 | (14) |
Proposition 5.4. Let 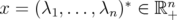 ,
, 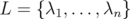 . Consider the matrix
. Consider the matrix 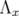 defined before. Then
defined before. Then 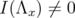 if and only
if and only 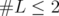 . More precisely,
. More precisely,
- If
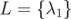 (i.e. #L = 1), then
(i.e. #L = 1), then 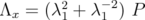 and
and 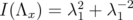 .
. - If
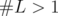 , then the image of
, then the image of 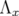 is the subspace generated by the vectors
is the subspace generated by the vectors 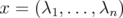 and
and 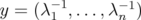 .
. - If
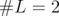 , say
, say 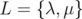 , denote
, denote 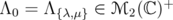 . Then
. Then 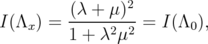
(15) - If
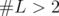 then
then 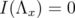 , because
, because 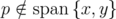 .
. 
 operators
operators 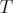 . Remark 5.5. Proposition 5.4 says that, in most cases (i.e.
. Remark 5.5. Proposition 5.4 says that, in most cases (i.e. 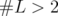 ),
), 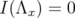 . On the other hand, in order to apply index theory for the matrix
. On the other hand, in order to apply index theory for the matrix  , we need that
, we need that 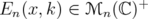 . Since
. Since 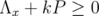 if and only if
if and only if 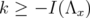 (by the definition of the minimal index), we can only consider the case
(by the definition of the minimal index), we can only consider the case  , in general. In this case, it is easy to check that
, in general. In this case, it is easy to check that  | (16) |
Hence, applying Proposition 5.4, we get formulas for 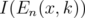 in any case.
in any case. 
We shall compute 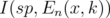 using Theorem 5.3. Hence, we shall use the principal minors of
using Theorem 5.3. Hence, we shall use the principal minors of 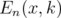 , which are matrices of the same type. Let
, which are matrices of the same type. Let 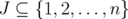 ,
, 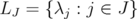 and
and 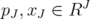 the induced vectors. Then
the induced vectors. Then
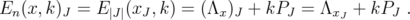
Claim: If 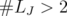 then,
then, 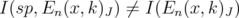 .
.
Indeed, by Proposition 5.4, 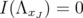 , because
, because 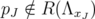 . Note that every
. Note that every 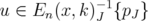 must satisfy
must satisfy 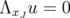 , because
, because 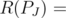 span
span 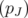 . By Proposition 5.4,
. By Proposition 5.4, 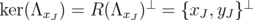 , where
, where 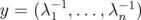 . As all entries of
. As all entries of 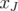 are strictly positive, if
are strictly positive, if 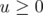 and
and 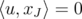 , then
, then  . Therefore, the Claim follows from Theorem 5.2.
. Therefore, the Claim follows from Theorem 5.2.
Hence, if 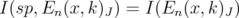 , then
, then 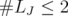 . If
. If 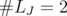 , let
, let 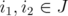 such that
such that 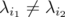 . By Theorem 5.2 there exists a vector
. By Theorem 5.2 there exists a vector 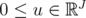 such that
such that 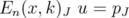 . Let
. Let 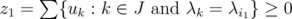 and
and 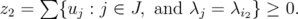 Easy computations show that, if we denote
Easy computations show that, if we denote 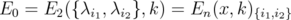 , then
, then 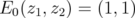 and, by Theorem 5.2,
and, by Theorem 5.2, 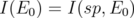 . Moreover, by equations (15) and (16),
. Moreover, by equations (15) and (16),
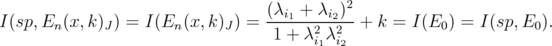
Therefore, in order to compute 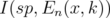 using Theorem 5.3, we have to consider only the diagonal entries of
using Theorem 5.3, we have to consider only the diagonal entries of 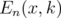 and some of its principal minors of size
and some of its principal minors of size 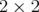 . If
. If 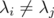 and
and 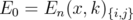 then, by equations (13) and (16),
then, by equations (13) and (16),
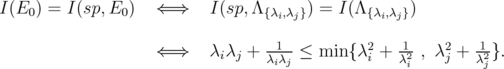
 , this is equivalent to
, this is equivalent to 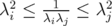 , which implies that
, which implies that 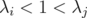 . So, by Theorem 5.3,
. So, by Theorem 5.3,  | (17) |
where 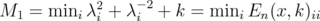 and
and
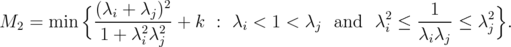
Now we can characterize the sharp constant for inequality (5), if we consider only  operators
operators  .
.
Proposition 5.6. Given 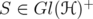 and
and  , denote by
, denote by 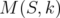 the greatest number such that
the greatest number such that 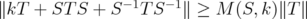 for every
for every 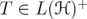 . Then
. Then 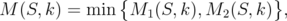 where
where 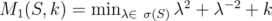 and
and
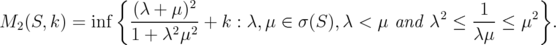
In particular, if  , then
, then 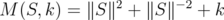 .
.
Proof. We shall use the same steps as in the proof of Theorem 3.4 (and [6]). By the spectral theorem, we can suppose that 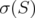 is finite, since
is finite, since 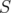 can be approximated in norm by operators
can be approximated in norm by operators 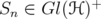 such that
such that 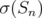 is a finite subset of
is a finite subset of 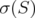 ,
, 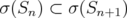 for all
for all 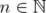 and
and 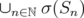 is dense in
is dense in 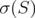 . So
. So 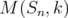 (and
(and 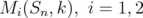 ) converge to
) converge to 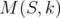 (resp.
(resp. 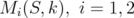 ).
).
We can also suppose that 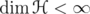 , by choosing an adequate net of finite rank projections
, by choosing an adequate net of finite rank projections 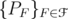 which converges strongly to the identity and replacing
which converges strongly to the identity and replacing 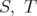 by
by 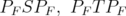 . Indeed, the net may be chosen in such a way that
. Indeed, the net may be chosen in such a way that  and
and 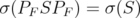 for all
for all 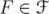 . Note that for every
. Note that for every 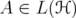 ,
, 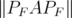 converges to
converges to  .
.
Finally, we can suppose that 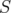 is diagonal by a unitary change of basis in
is diagonal by a unitary change of basis in 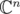 . In this case, if
. In this case, if  are the eigenvalues of
are the eigenvalues of 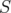 (with multiplicity) and
(with multiplicity) and 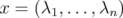 , then
, then 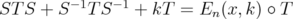 . Note that all our reductions (unitary equivalences and compressions) preserve the fact that
. Note that all our reductions (unitary equivalences and compressions) preserve the fact that 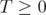 . Now the statement follows from formula (17). If
. Now the statement follows from formula (17). If  then
then  , since
, since 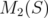 is the infimum of the empty set. Note that
is the infimum of the empty set. Note that 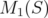 is attained at
is attained at  , because the map
, because the map 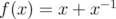 is decreasing on
is decreasing on ![(0, 1]](/img/revistas/ruma/v46n1/1a06652x.png) . □
. □
6. NUMERICAL RESULTS
Let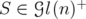 and
and 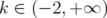 . Denote by
. Denote by 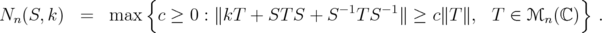 Corollary 3.6 says that, if
Corollary 3.6 says that, if 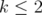 , then
, then 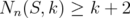 for every
for every 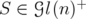 . On the other hand, Corollary 4.6 says that, if there exists
. On the other hand, Corollary 4.6 says that, if there exists 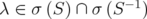 , then
, then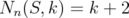 . In this section we search conditions for
. In this section we search conditions for 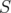 which assure that
which assure that . As in the proof of Theorem 3.4, we can assume that
. As in the proof of Theorem 3.4, we can assume that 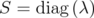 for some
for some 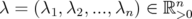 . In this case, we have that
. In this case, we have that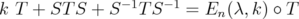 , where
, where 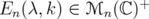 is the matrix defined in Eq. (14). Consider the matrix
is the matrix defined in Eq. (14). Consider the matrix 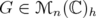 with entries
with entries 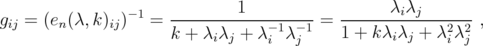 | (18) |
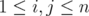 . Then, for
. Then, for 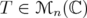 ,
, 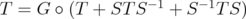 . Denote by
. Denote by 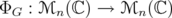 the map given by
the map given by  , for
, for 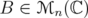 . We conclude that
. We conclude that 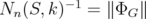 .
.
Remark 6.1. There exists an extensive bibliography concerning methods for computing the norm of a Hadamard multiplier like 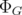 . The oldest result in this direction is Schur Theorem (Proposition 2.4) for the positive case. We have applied this result in the proof of Theorem 3.4, but it is not useful in this case, because
. The oldest result in this direction is Schur Theorem (Proposition 2.4) for the positive case. We have applied this result in the proof of Theorem 3.4, but it is not useful in this case, because 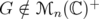 . The most general result is 1983's Haagerup theorem [10], which gives a complete characterization, but it is not effective. There exist also several fast algorithms (see, for example, [9]) which allow to make numerical experimentation for this problem. For example, we have observed that the behavior of the map
. The most general result is 1983's Haagerup theorem [10], which gives a complete characterization, but it is not effective. There exist also several fast algorithms (see, for example, [9]) which allow to make numerical experimentation for this problem. For example, we have observed that the behavior of the map 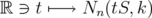 , for any fixed
, for any fixed 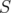 , is chaotic. But, as a great number of examples suggest, it seems that
, is chaotic. But, as a great number of examples suggest, it seems that  if and only if
if and only if 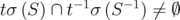 . Note that these cases are exactly those considered in Corollary 4.6.
. Note that these cases are exactly those considered in Corollary 4.6. 
Cowen and others [8] and [9] proved the following result for hermitian matrices:
Theorem 6.2. Let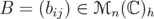 such that
such that 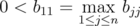 . Suppose that
. Suppose that 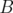 has rank two, or that
has rank two, or that 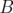 has one positive eigenvalue and
has one positive eigenvalue and  non positive eigenvalues. Then the following conditions are equivalent:
non positive eigenvalues. Then the following conditions are equivalent:  .
. - If
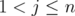 and
and 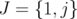 , then
, then 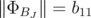 .
. - For
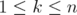 , it holds that
, it holds that  .
. 
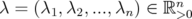 satisfies
satisfies 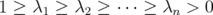 or
or 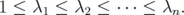 Since that map
Since that map 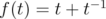 is increasing on
is increasing on  and it is decreasing on
and it is decreasing on 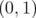 , it follows that the matrix
, it follows that the matrix 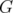 of Eq. (18) satisfies
of Eq. (18) satisfies 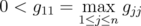 . This suggests that we could apply Theorem 6.2 for our problem. Unfortunately, for
. This suggests that we could apply Theorem 6.2 for our problem. Unfortunately, for 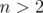 ,
, 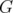 has rank greater than two, and it can have more that one positive eigenvalue. We prove the following result:
has rank greater than two, and it can have more that one positive eigenvalue. We prove the following result: Proposition 6.3. Let 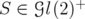 . Suppose that
. Suppose that 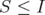 , or
, or 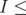 S. Then
S. Then
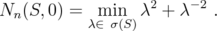
Proof. Suppose that 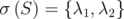 with
with 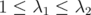 or
or 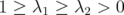 . Let
. Let 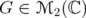 as in equation (18), for
as in equation (18), for  . Then
. Then 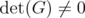 . Hence, since
. Hence, since  , can apply Theorem 6.2. Then, in order to prove that
, can apply Theorem 6.2. Then, in order to prove that  , it suffices to verify the inequality
, it suffices to verify the inequality 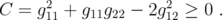 Note that
Note that
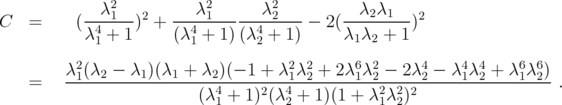
Straightforward computations with 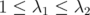 show that
show that 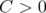 , since the polynomial
, since the polynomial 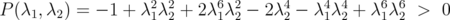 in this case. A similar analysis shows that still
in this case. A similar analysis shows that still 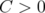 for
for 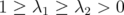 . The result follows by applying Theorem 6.2. □
. The result follows by applying Theorem 6.2. □
It was proved by Kwong (see [13]) that, if 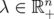 , then the matrix
, then the matrix 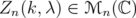 defined in Eq. (10), is positive semidefinite in the following cases:
defined in Eq. (10), is positive semidefinite in the following cases:  and
and 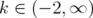 ,
,  and
and 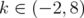 , and
, and  and
and 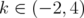 . Therefore, by the proof of Theorem 3.4, inequality (6) holds in
. Therefore, by the proof of Theorem 3.4, inequality (6) holds in 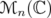 in these cases, for every unitarily invariant norm. Note that the proof Theorem 3.1 does not give similar estimates for the inequalities (4) and (5), because one needs to duplicate dimensions.
in these cases, for every unitarily invariant norm. Note that the proof Theorem 3.1 does not give similar estimates for the inequalities (4) and (5), because one needs to duplicate dimensions.
A numerical approach suggests that these intervals are optimal, both for the positivity of the matrix 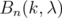 , defined in Eq. (11), and for inequality (6). In the case of
, defined in Eq. (11), and for inequality (6). In the case of 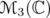 , if
, if 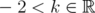 and
and 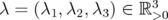 then, using symbolic computation with the software Mathematica, one obtains a kind of "proof" of the fact that
then, using symbolic computation with the software Mathematica, one obtains a kind of "proof" of the fact that 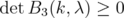 for every
for every  if and only if
if and only if 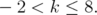 The
The 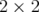 principal sub matrices of
principal sub matrices of 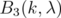 have the form
have the form 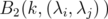 , and they live in
, and they live in 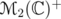 for every
for every 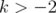 . Therefore,
. Therefore,
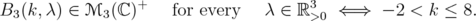
Likewise, for the 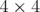 matrix case, it suffices to study
matrix case, it suffices to study 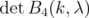 , for
, for 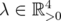 , and one obtains similar results.
, and one obtains similar results.
Denote by 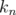 the maximum number
the maximum number  such that inequality (6) holds in
such that inequality (6) holds in 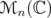 for the spectral norm. By the preceding comments, and the proof of Theorem 3.4,
for the spectral norm. By the preceding comments, and the proof of Theorem 3.4,

Computer experimentation using the softwares Mathematica and Matlab suggests that, also in this case,  ,
,  , and
, and  , for
, for 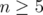 . In other words, inequality (6) holds for
. In other words, inequality (6) holds for 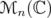 in the same intervals as it holds that
in the same intervals as it holds that 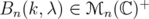 for every
for every  .
.
References
[1] T. Ando, Majorization and inequalities in matrix theory, Linear Algebra Appl. 199: 17-67, 1994. [ Links ]
[2] E. Andruchow, G. Corach and D. Stojanoff, Geometric operator inequalities, Linear Algebra Appl. 258: 295-310, 1997. [ Links ]
[3] R. Bhatia, and CH. Davis, More matrix forms of the Arithmetic-Geometric mean inequality, SIAM J. Matrix Anal. Appl. 14: 132-136, 1993. [ Links ]
[4] R. Bhatia and K. R. Parthasarathy, Positive definite functions and operator inequalities, Bull. London Math. Soc. 32: 214-228, 2000. [ Links ]
[5] R. Bhatia, Matrix Analysis, Springer-Verlag, New York, 1997. [ Links ]
[6] G. Corach, H. Porta and L. Recht, An operator inequality, Linear Algebra Appl. 142: 153-158, 1990. [ Links ]
[7] G. Corach and D. Stojanoff, Index of Hadamard multiplication by positive matrices II, Linear Algebra Appl. 332-334 (2001), 503-517. [ Links ]
[8] C. C. Cowen, K. E. Debro and P. D. Sepansky, Geometry and the norms of Hadamard multipliers, Linear Algebra Appl. 218: 239-249, 1995. [ Links ]
[9] C. C. Cowen, P. A. Ferguson, D. K. Jackman, E. A. Sexauer, C. Vogt y H. J. Woolf, Finding Norms of hadamard multipliers, Linear Algebra Appl. 247, 217-235 (1996). [ Links ]
[10] U. Haagerup, Decompositions of completely bounded maps on operator algebras, unpublished manuscript. [ Links ]
[11] F. Kittaneh, A note on the arithmetic-geometric inequality for matrices, Linear Algebra Appl. 171 (1992), 1-8. [ Links ]
[12] F. Kittaneh, On some operator inequalities, Linear Algebra Appl. 208/209:19-28, 1994. [ Links ]
[13] M.K. Kwong, On the definiteness of the solutions of certain matrix equations, Linear Algebra Appl. 108: 177-197, 1988. [ Links ]
[14] L. Livshits and S. C. Ong, On the invertibility properties of the map  and operator-norm inequalities, Linear Algebra Appl. 183: 117-129, 1993. [ Links ]
and operator-norm inequalities, Linear Algebra Appl. 183: 117-129, 1993. [ Links ]
[15] A. Seddik, Some results related to the Corach-Porta-Recht inequality, Proceedings of the American Mathematical Society, 129: 3009-3015, 2001. [ Links ]
[16] I. Schur, Bemerkungen zur theorie de beschränkten bilineareformen mit unendlich vielen veränderlichen, J. Reine Angew. Math. 140: 1-28, 1911. [ Links ]
[17] B. Simon, Trace ideals and their applications, London Mathematical Society Lecture Note Series, 35, Cambridge University Press, Cambridge-New York, 1979. [ Links ]
[18] X. Zhan, Inequalities for unitarily invariant norms, SIAM J. Matrix Anal. Appl. 20:466-470, 1999. [ Links ]
Cristina Cano
Depto. de Matemática,
FaEA-UNC,
Neuquén, Argentina.
cbcano@uncoma.edu.ar
Irene Mosconi
Depto. de Matemática,
FaEA-UNC,
Neuquén, Argentina.
imosconi@uncoma.edu.ar
Demetrio Stojanoff
Depto. de Matemática,
FCE-UNLP, La Plata, Argentina
and IAM-CONICET.
demetrio@mate.unlp.edu.ar
Recibido: 3 de junio de 2005
Aceptado: 21 de noviembre de 2005














