Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.46 n.2 Bahía Blanca jul./dic. 2005
Differential operators on smooth schemes and embedded singularities
Orlando Villamayor U.
En recuerdo de Angel Larrotonda
Abstract
Differential operators on smooth schemes have played a central role in the study of embedded desingularization.
J. Giraud provides an alternative approach to the form of induction used by Hironaka in his Desingularization Theorem (over fields of characteristic zero). In doing so, Giraud introduces technics based on differential operators. This result was important for the development of algorithms of desingularization in the late 80's (i.e. for constructive proofs of Hironaka's theorem).
More recently, differential operators appear in the work of J. Wlodarczyk ([35]), and also on the notes of J. Kollár ([25]).
The form of induction used in Hironaka's Desingularization Theorem, which is a form of elimination of one variable, is called maximal contact. Unfortunately it can only be formulated over fields of characteristic zero.
In this paper we report on an alternative approach to elimination of one variable, which makes use of higher differential operators. These results open the way to new invariants for singularities over fields of positive characteristic ([34]).
Key words and phrases. Resolution of singularities. Desingularization
2000 Mathematics subject classification. 14E15.
Contents
Part 1. Introduction.
1. Monoidal transformations and Hironaka's topology.
2. Integral closure of Rees algebras and a notion of equivalence.
3. On differential structures and Kollár's tuned ideals.
4. On differential structures and monoidal transformations.
5. Idealistic exponents versus basic objects.
6. Projection of differential structures and elimination of one variable.
References
Part 1. Introduction.
Let 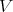 be a smooth scheme over a field
be a smooth scheme over a field 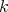 of characteristic zero, and let
of characteristic zero, and let 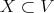 be a singular subscheme. Hironaka proves embedded desingularization of
be a singular subscheme. Hironaka proves embedded desingularization of 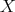 , considering as invariants the Hilbert-Samuel functions at the points of
, considering as invariants the Hilbert-Samuel functions at the points of 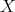 . His proof is based on the reduction of Hilbert Samuel functions by monoidal transformations ([22]).
. His proof is based on the reduction of Hilbert Samuel functions by monoidal transformations ([22]).
There is second theorem of Hironaka, used in his proof of reduction of Hilbert Samuel functions, which is called Log-resolution of ideals in smooth schemes. For this second theorem, which we discuss below, the invariant considered is the order of the ideal at the points of the smooth scheme.
In [17], both theorems are linked in a different way. In fact, if 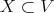 is defined by a sheaf of ideals
is defined by a sheaf of ideals  , then desingularization is proved by considering the order of the ideal
, then desingularization is proved by considering the order of the ideal 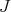 at points in
at points in 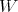 , and hence avoiding the use of Hilbert Samuel functions.
, and hence avoiding the use of Hilbert Samuel functions.
Let 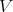 be a smooth scheme over a field
be a smooth scheme over a field 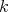 , and let
, and let 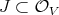 be a non-zero sheaf of ideals. Define a function
be a non-zero sheaf of ideals. Define a function
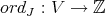
where 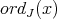 denotes the order of
denotes the order of  at the local regular ring
at the local regular ring 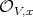 . Let
. Let  denote the biggest value achieved by this function (the biggest order of
denote the biggest value achieved by this function (the biggest order of  ). The pair
). The pair 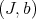 is the object of interest in Log principalization of ideals. There is a closed set attached to this pair in
is the object of interest in Log principalization of ideals. There is a closed set attached to this pair in 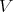 , namely the set of points where
, namely the set of points where 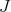 has order
has order 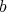 ; and there is also a notion of transformation of such pairs by blowing up suitable regular centers.
; and there is also a notion of transformation of such pairs by blowing up suitable regular centers.
We will attach to 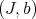 a graded subring of
a graded subring of ![OV [W ]](/img/revistas/ruma/v46n2/2a0123x.png) (sheaf of polynomial rings), namely a graded algebra (Rees algebra) of the form
(sheaf of polynomial rings), namely a graded algebra (Rees algebra) of the form
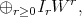
defined uniquely in terms of 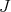 and
and 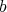 .
.
Actually the Rees algebras that we will consider are closely related to Kollárs notion of tuned ideals.
We will show that there is a closed set in 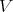 naturally attached to such Rees algebra, and also a notion of transformation. Of course the interest here is on the case of smooth schemes over fields of positive characteristic, where a weak form of elimination of one variable is discussed.
naturally attached to such Rees algebra, and also a notion of transformation. Of course the interest here is on the case of smooth schemes over fields of positive characteristic, where a weak form of elimination of one variable is discussed.
For any non-negative integer  the sheaf of
the sheaf of 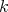 -linear differential operators, say
-linear differential operators, say 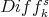 , is coherent and locally free over
, is coherent and locally free over 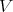 .
.
There is a natural identification, say 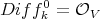 , and for each
, and for each  there is a natural inclusions
there is a natural inclusions 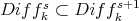 .
.
If  is an affine open set in
is an affine open set in  , each
, each 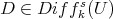 is a differential operator:
is a differential operator: 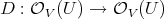 . We define an extension of a sheaf of ideals
. We define an extension of a sheaf of ideals 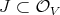 , say
, say 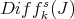 , so that over the affine open set
, so that over the affine open set 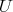 ,
, 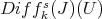 is the extension of
is the extension of 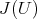 defined by adding all elements
defined by adding all elements 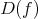 , for all
, for all 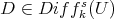 and
and 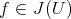 .
.
So 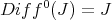 , and
, and 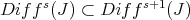 as sheaves of ideals in
as sheaves of ideals in 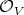 . Let
. Let 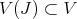 be the closed set defined by
be the closed set defined by 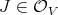 . So
. So
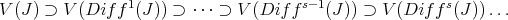
It is simple to check that the order of the ideal at the local regular ring 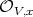 is
is 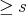 if and only if
if and only if 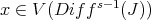 .
.
The previous observations say that 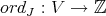 is an upper-semi-continuous function, and that the highest order of
is an upper-semi-continuous function, and that the highest order of 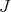 (at points
(at points 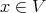 ) is
) is 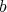 , if
, if 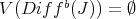 and
and 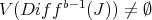 . Let
. Let
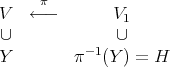
denote the blow up of 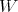 at a smooth irreducible sub-scheme
at a smooth irreducible sub-scheme  , and
, and 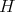 is the exceptional hypersurface. If
is the exceptional hypersurface. If 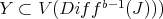 we say that
we say that 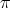 is
is 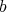 -permissible. In such case
-permissible. In such case
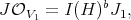
where 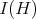 is the sheaf of functions vanishing along the exceptional hypersurface
is the sheaf of functions vanishing along the exceptional hypersurface 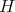 .
.
If  is
is 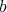 -permissible,
-permissible,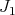 has at most order
has at most order 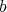 at points of
at points of 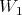 (i.e. that
(i.e. that 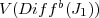
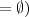 . If, in addition,
. If, in addition, 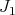 has no point of order
has no point of order 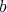 , then we say that
, then we say that 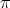 defines a
defines a 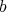 -simplification of
-simplification of 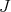 .
.
If 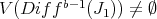 , let
, let 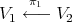 denote the monoidal transformation with center
denote the monoidal transformation with center 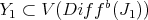 . We say that
. We say that 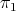 is
is 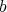 -permissible, and set
-permissible, and set
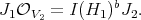
It turns out that 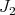 has at most points of order
has at most points of order 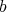 . If it does, define a
. If it does, define a 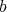 -permissible transformation at some smooth irreducible center
-permissible transformation at some smooth irreducible center 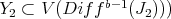 .
.
For 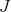 and
and 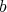 as before, we define, by iteration, a
as before, we define, by iteration, a 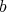 -permissible sequence
-permissible sequence
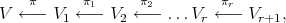
and a factorization 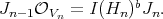
Let 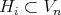 denote the strict transform of exceptional hypersurface
denote the strict transform of exceptional hypersurface 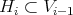 . Note that:
. Note that:
1)  are the irreducible components of the exceptional locus of
are the irreducible components of the exceptional locus of 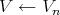 .
.
2) The total transform of 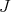 relates to
relates to 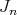 by an expression of the form
by an expression of the form
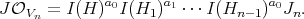
We say that this 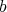 -permissible sequence defines a
-permissible sequence defines a 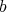 -simplication of
-simplication of 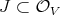 if
if 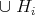 has normal crossings, and
has normal crossings, and 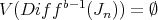 (i.e.
(i.e. 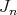 has order at most
has order at most  at
at 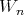 ).
).
When 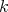 is a field of characteristic zero, and
is a field of characteristic zero, and 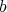 is the highest order of a sheaf of ideals
is the highest order of a sheaf of ideals 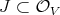 , Hironaka proves that there is a
, Hironaka proves that there is a 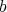 -simplification. Furthermore, taking this as starting point, he indicates how to achieve resolution of singularities.
-simplification. Furthermore, taking this as starting point, he indicates how to achieve resolution of singularities.
Hironaka's theorem of resolution of singularities is existential, precisely because his proof of 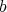 -simplification is existential.
-simplification is existential.
The achievement of constructive resolution of singularities was to provide an algorithm. So given 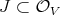 and
and 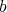 as before, as input, the algorithm defines a
as before, as input, the algorithm defines a 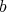 -simplification.
-simplification.
An advantage of a constructive proof of resolution of singularities, over the original existential proof, is that constructive resolutions are equivariant, they provide resolution en étale topology, they are compatible with change of base field etc. (see [32]).
Another advantage of the algorithm of 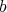 -simplification, already mentioned above, is that it simplifies the proof of desingularization ([17]).
-simplification, already mentioned above, is that it simplifies the proof of desingularization ([17]).
The key point for 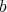 -simplification, already used in Hironaka's proof, is a form of induction. In fact, Hironaka proves
-simplification, already used in Hironaka's proof, is a form of induction. In fact, Hironaka proves 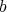 -simplification, by induction on the dimension of the ambient space
-simplification, by induction on the dimension of the ambient space 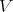 . To simplify matters, assume that
. To simplify matters, assume that 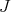 is locally principal, and let
is locally principal, and let 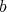 denote the highest order of
denote the highest order of 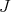 along points in
along points in 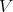 , which is now smooth over a field of characteristic zero. Let
, which is now smooth over a field of characteristic zero. Let
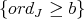
denote the closed set 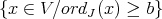 (or say
(or say  ).
).
Fix a closed point 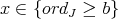 , and a regular system of parameters
, and a regular system of parameters 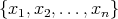 at
at 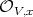 . For any
. For any 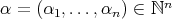 , set
, set  , and
, and
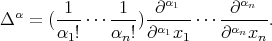
If  is locally generated by
is locally generated by 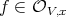 , then
, then 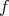 has order
has order 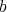 at
at 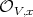 , and
, and
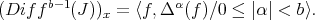
The key point is that, the order of 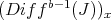 at
at 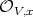 is one. This holds when
is one. This holds when 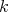 is a field of characteristic zero.
is a field of characteristic zero.
Recall that  locally at
locally at 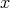 . One way to check that
. One way to check that 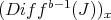 has order one at
has order one at 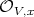 , is to check this at the completion
, is to check this at the completion 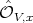 , say
, say ![R = k′[[x1,..,xn]]](/img/revistas/ruma/v46n2/2a01153x.png) . We may choose the system of parameters so that, for a suitable unit
. We may choose the system of parameters so that, for a suitable unit 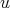 :
:
![u.f = f1 = Zb + a1Zb -1 + ⋅⋅⋅ + ab ∈ S[Z]](/img/revistas/ruma/v46n2/2a01155x.png)
![S = k[[x1,..,xn-1]]](/img/revistas/ruma/v46n2/2a01156x.png) , and
, and 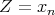 .
.
As 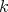 is a field of characteristic zero,
is a field of characteristic zero, ![S[Z] = S[Z1]](/img/revistas/ruma/v46n2/2a01159x.png) , where
, where 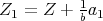 , and
, and
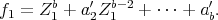
Then:
A) 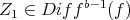 (in fact
(in fact 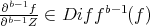 ). In particular the ideal
). In particular the ideal 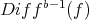 has order one at
has order one at 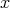 , and the closed set
, and the closed set 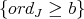 is locally included in a smooth scheme of dimension
is locally included in a smooth scheme of dimension  .
.
B)(Elimination.) 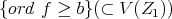 can be described as
can be described as

C) (Stability of elimination.) Both A), and the description in B), are preserved by any 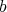 -permissible sequence of transformations.
-permissible sequence of transformations.
We will not go into details of A), B) and C). But let us point out the elimination of one variable in (B). In fact the closed set 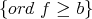 defined in terms of
defined in terms of 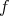 , is also described as
, is also described as 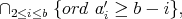 where now the
where now the 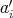 involve one variable less.
involve one variable less.
As indicated above, A),B), and C), together, conform the essential reason and argument in resolution of singularities in characteristic zero. They rely entirely on the hypothesis of characteristic zero. For instance A) does not hold over fields of positive characteristic; so there is no way to formulate this form of induction over arbitrary fields.
The objective of these notes is to report on an entirely different approach to induction, which can at least be formulated over arbitrary fields.
Suppose, for simplicity, that 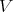 is affine, that
is affine, that 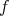 is global in
is global in 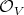 , and that
, and that 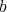 is the highest order of
is the highest order of 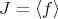 . We reformulate the study
. We reformulate the study 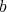 -sequences of transformations over
-sequences of transformations over 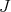 . In doing so we replace
. In doing so we replace 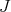 by a graded ring subring of
by a graded ring subring of ![OV [W ]](/img/revistas/ruma/v46n2/2a01183x.png) . In this case we consider the subring
. In this case we consider the subring
. V V](/img/revistas/ruma/v46n2/2a01184x.png)
In general, if 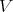 is affine, we define a Rees algebra as a subring of
is affine, we define a Rees algebra as a subring of ![OV [W ]](/img/revistas/ruma/v46n2/2a01186x.png) generated by a finite set, say
generated by a finite set, say
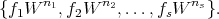
These subrings can also be expressed as 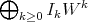 ,
, 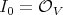 , and each
, and each 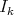 is an ideal. We say that
is an ideal. We say that 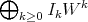 has differential structure, say Diff-structure, if
has differential structure, say Diff-structure, if 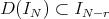 for
for 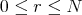 , and
, and 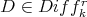 .
.
Diff-structures appear in [23] and [24](see 4.2), and they are closely related to the notion of tuned ideals introduced by J Kollár.
It is easy to show that any Rees algebra spans a smallest Diff-structure containing it. Diff-structures are known to have important geometric properties, which make them objects of particular interest. In this paper we report on a characteristic free form of eliminationdefined for Diff-structures (see (B) above).
We also study here a natural compatibility of monoidal transforms and Diff-structures. This is done via Taylor development in positive characteristic (see also [33]). So it makes sense to formulate stability of elimination (see (C) above) over arbitrary fields. Here results are stronger over fields of characteristic zero, where they provide an alternative approach to induction in desingularization theorems.
New invariants for singularities arise, in positive characteristic, when studying this form of elimination in the setting of Diff-structures.
1. Monoidal transformations and Hironaka's topology.
Fix a smooth scheme  over a field
over a field 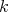 , an ideal
, an ideal 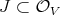 , and a positive integer
, and a positive integer 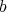 . Hironaka attaches to these data, say
. Hironaka attaches to these data, say 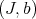 , a closed set, say
, a closed set, say
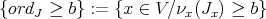
where 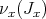 denote the order of
denote the order of 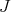 at the local regular ring
at the local regular ring 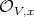 .
.
Given 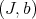 and
and 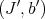 , then
, then
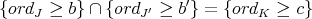
where 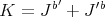 , and
, and 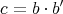 . Set formally
. Set formally 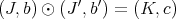 .
.
There is also a notion of permissible transformation on these data 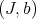 . Let
. Let 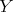 be a smooth subscheme in
be a smooth subscheme in 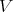 , included in the closed
, included in the closed 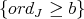 , and let
, and let
|
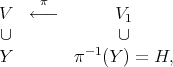 | (1.0.1) |
be the blow up of 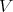 at a smooth sub-scheme
at a smooth sub-scheme 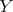 . Note that
. Note that
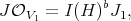
where 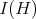 is the sheaf of functions vanishing along the exceptional hypersurface
is the sheaf of functions vanishing along the exceptional hypersurface 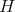 .
.
We call 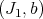 the transform of
the transform of 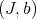 by the permissible monoidal transformation.
by the permissible monoidal transformation.
If  is permissible for both
is permissible for both 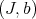 and
and 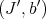 , then it is permissible for
, then it is permissible for 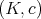 . Moreover, if
. Moreover, if 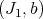 ,
, 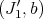 , and
, and 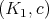 denote the transforms, then
denote the transforms, then 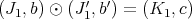 .
.
We now define a Rees algebra over 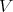 to be a graded noetherian subring of
to be a graded noetherian subring of ![OV [W ]](/img/revistas/ruma/v46n2/2a01231x.png) , say:
, say:
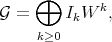
where 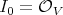 and each
and each 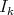 is a sheaf of ideals. And we assume that at any affine open set
is a sheaf of ideals. And we assume that at any affine open set 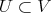 , there is a finite set
, there is a finite set
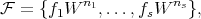
 and
and 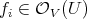 , so that the restriction of
, so that the restriction of 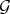 to
to 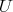 is
is
[W ]). V 1 s V](/img/revistas/ruma/v46n2/2a01241x.png)
To a Rees algebra 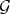 we attach a closed set:
we attach a closed set:
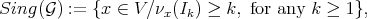
where 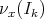 denotes the order of the ideal
denotes the order of the ideal 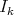 at the local regular ring
at the local regular ring 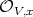 .
.
Remark 1.1. Rees algebras are related to Rees rings. A Rees algebra is a Rees ring if, given any affine open set  , and
, and 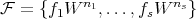 as above, all degrees
as above, all degrees 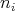 are one.
are one.
In general Rees algebras are integral closures of Rees rings in a suitable sense. In fact, if 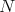 is a positive integer divisible by all
is a positive integer divisible by all 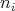 , it is easy to check that
, it is easy to check that
![n1 ns r OV (U )[f1W ,...,fsW ] = ⊕r≥0IrW (⊂ OV (U )[W ]),](/img/revistas/ruma/v46n2/2a01252x.png)
is integral over the Rees sub-ring [W N])](/img/revistas/ruma/v46n2/2a01253x.png) .
.
Proposition 1.2. Given an affine open  , and
, and 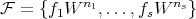 as above,
as above,
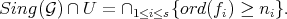
Proof. It is clear that 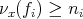 for
for 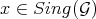 ,
, 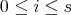 . So
. So
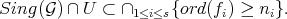
On the other hand, for any index  ,
, 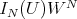 is generated by elements of the form
is generated by elements of the form 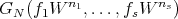 , where
, where ![GN (Y1,...,Ys) ∈ OU [Y1,...,Ys]](/img/revistas/ruma/v46n2/2a01264x.png) is weighted homogeneous of degree
is weighted homogeneous of degree 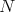 , provided each
, provided each 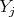 has weight
has weight 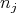 . The reverse inclusion is now clear. □
. The reverse inclusion is now clear. □
A monoidal transformation (1.0.1) is said to be permissible for 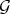 if
if 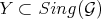 . In such case, for each index
. In such case, for each index 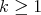 , there is a sheaf of ideals, say
, there is a sheaf of ideals, say 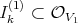 , so that
, so that
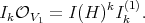
One can easily check that
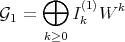
is a Rees algebra over 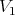 , which we call the transform of
, which we call the transform of 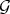 .
.
Let 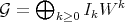 be a Rees algebra on
be a Rees algebra on 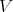 ,
, 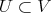 an affine open set, and let
an affine open set, and let 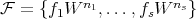 be such that the restriction of
be such that the restriction of 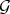 to
to 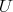 is
is
[W ]).](/img/revistas/ruma/v46n2/2a01282x.png)
Proposition 1.3. Let 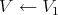 be a permissible transformation of
be a permissible transformation of 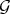 . There is an open covering of
. There is an open covering of 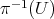 by affine sets
by affine sets 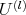 , so that:
, so that:
1) 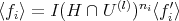 for suitable
for suitable 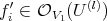 .
.
2) The restriction of 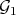 to
to 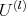 is
is
)[W ]). 1 1 s 1](/img/revistas/ruma/v46n2/2a01291x.png)
Proof. 1) follows from Prop 1.2. For 2) argue as in the proof of Prop 1.2, by using the fact that each ideal 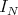 is generated by weighted homogeneous polynomials on the element of
is generated by weighted homogeneous polynomials on the element of 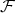 .
.
Given two Rees algebras over 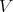 , say
, say 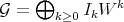 and
and 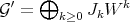 , set
, set 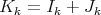 in
in 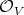 , and define:
, and define:
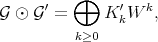
as the subalgebra of ![O [W ] V](/img/revistas/ruma/v46n2/2a01300x.png) generated by
generated by 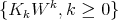 .
.
One can check that:
1) 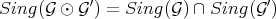 . In particular, if
. In particular, if  in (1.0.1) is permissible for
in (1.0.1) is permissible for  , it is also permissible for
, it is also permissible for 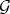 and for
and for 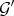 .
.
2) Set 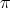 as in 1), and let
as in 1), and let 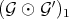 ,
, 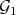 , and
, and 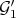 denote the transforms at
denote the transforms at  . Then:
. Then:
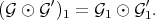
2. Integral closure of Rees algebras and a notion of equivalence.
We say that two Rees algebras over 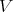 , say
, say 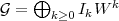 and
and 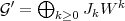 , are equivalent, if both have the same integral closure in
, are equivalent, if both have the same integral closure in ![OV [W ]](/img/revistas/ruma/v46n2/2a01316x.png) .
.
If 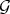 and
and 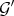 are equivalent, then:
are equivalent, then:
1) 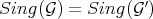 . In particular,
. In particular, 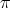 in (1.0.1) is permissible for
in (1.0.1) is permissible for 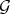 if and only if it is so for
if and only if it is so for 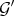 .
.
2) Set 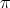 as in 1), and let
as in 1), and let 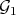 and
and 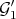 denote the transforms at
denote the transforms at 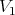 . Then
. Then 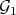 and
and 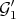 are equivalent over
are equivalent over 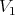 .
.
This shows that equivalent Rees algebras define the same closed sets, and the same holds after any sequence of permissible transformations.
Given a smooth scheme 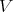 , and
, and 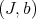 as in 1, we consider the Rees algebra generated over
as in 1, we consider the Rees algebra generated over 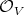 by
by 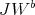 (as graded subring of
(as graded subring of ![OV [W ]](/img/revistas/ruma/v46n2/2a01334x.png) ).
).
Proposition 2.1. If 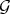 and
and 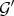 are the Rees algebras corresponding to Hironaka's pairs
are the Rees algebras corresponding to Hironaka's pairs 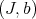 and
and 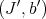 , then
, then  is equivalent to the Rees algebra assigned to
is equivalent to the Rees algebra assigned to  .
.
Proof. Fix an affine open set 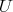 in
in 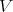 ,
, 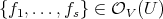 generators of
generators of 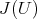 , and
, and 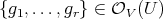 generators of
generators of 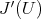 . Then:
. Then:
i) The restriction of 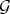 to
to 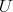 is
is
[W ]).](/img/revistas/ruma/v46n2/2a01349x.png)
ii) The restriction of 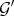 is
is
[W ]).](/img/revistas/ruma/v46n2/2a01351x.png)
iii) The restriction of  to
to 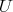 is
is
[W ]).](/img/revistas/ruma/v46n2/2a01354x.png)
iv) The restriction of the Rees algebra assigned to  is generated by
is generated by
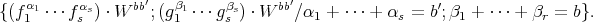
One can finally check that both algebras in (iii) and (iv) have the same integral closure in ![OV (U )[W ]](/img/revistas/ruma/v46n2/2a01357x.png) .□
.□
3. On differential structures and Kollár's tuned ideals.
Here 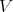 is smooth over a field
is smooth over a field 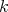 , so for each non-negative integer
, so for each non-negative integer  there is a locally free sheaf of differential operators of order
there is a locally free sheaf of differential operators of order  , say
, say 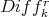 .
.
Definition 3.1. We say that a Rees algebra 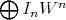 is a Diff-structure relative to the field
is a Diff-structure relative to the field 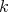 , if:
, if:
i) 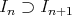 .
.
ii) There is open covering of 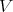 by affine open sets
by affine open sets 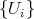 , and for any
, and for any 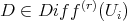 , and any
, and any 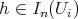 , then
, then 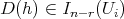 provided
provided 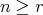 .
.
Given a sheaf of ideals 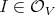 there is a natural definition of an extension, say
there is a natural definition of an extension, say 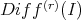 (see Introduction). Note that (ii) can be reformulated by
(see Introduction). Note that (ii) can be reformulated by
ii') 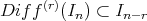 for each
for each 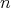 , and
, and 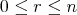 .
.
Fix a closed point 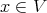 , and a regular system of parameters
, and a regular system of parameters  at
at 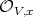 . The residue field, say
. The residue field, say 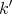 is a finite extension of
is a finite extension of 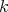 , and the completion
, and the completion ![ˆ ′ OV,x = k[[x1,...,xn]].](/img/revistas/ruma/v46n2/2a01382x.png)
The Taylor development is the continuous 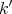 -linear ring homomorphism:
-linear ring homomorphism:
![T ay : k′[[x1,...,xn]] → k′[[x1,...,xn,T1,...,Tn]]](/img/revistas/ruma/v46n2/2a01384x.png)
that map 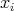 to
to  ,
, 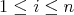 . So for
. So for ![f ∈ k ′[[x1, ...,xn]]](/img/revistas/ruma/v46n2/2a01388x.png) ,
, 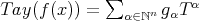 , with
, with ![g ∈ k ′[[x ,...,x ]] α 1 n](/img/revistas/ruma/v46n2/2a01390x.png) .
.
Define, for each 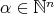 ,
, 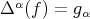 . It turns out that
. It turns out that
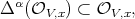
and that 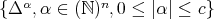 generate the
generate the 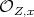 -module
-module 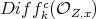 (i.e. generate
(i.e. generate 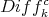 locally at
locally at 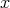 ).
).
Theorem 3.2. For any Rees algebra 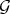 over a smooth scheme
over a smooth scheme 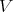 , there is a Diff-structure, say
, there is a Diff-structure, say 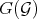 such that:
such that:
i) 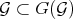 .
.
ii) If 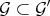 and
and 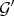 is a Diff-structure, then
is a Diff-structure, then 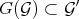 .
.
Furthermore, if 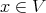 is a closed point, and
is a closed point, and  is a regular system of parameters at
is a regular system of parameters at 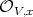 , and
, and 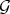 is locally generated by
is locally generated by
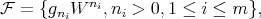
then
|
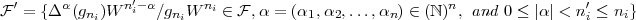 | (3.2.1) |
generates 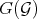 locally at
locally at 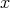 .
.
Remark 3.3. The local description in the Theorem shows that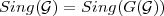 .
.
In fact, as 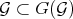 , it is clear that
, it is clear that 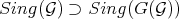 . For the converse note that if
. For the converse note that if 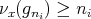 , then
, then 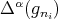 has order at least
has order at least  at the local ring
at the local ring 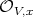 .
.
3.4. In general 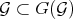 , and equality holds if
, and equality holds if 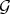 is already a Diff-structure.
is already a Diff-structure.
Let 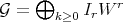 be a Diff-structure, in particular it is integral over a Rees subring, say
be a Diff-structure, in particular it is integral over a Rees subring, say ![O [I W N] V N](/img/revistas/ruma/v46n2/2a01424x.png) for suitable
for suitable 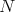 (see 1.1). These ideals
(see 1.1). These ideals 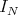 are called tuned ideals in [25], page 45.
are called tuned ideals in [25], page 45.
The previous Theorem defines an operator 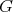 that extends Rees algebras into Diff-structures. Another natural operator we have considered on Rees algebras it that defined by taking normalization. The next Theorem relates both notions of extensions.
that extends Rees algebras into Diff-structures. Another natural operator we have considered on Rees algebras it that defined by taking normalization. The next Theorem relates both notions of extensions.
Theorem 3.5. Let 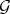 and
and 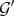 be equivalent Rees algebras on a smooth scheme
be equivalent Rees algebras on a smooth scheme 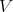 , then
, then 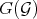 and
and 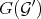 are also equivalent (in the sense of 2).
are also equivalent (in the sense of 2).
(see Th 6.12 [33]).
Definition 3.6. Fix 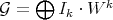 , a Rees algebra on
, a Rees algebra on 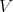 , and let
, and let  be a morphism of smooth schemes. We define the total transform of
be a morphism of smooth schemes. We define the total transform of 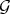 to be
to be
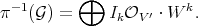
Namely the Rees algebra defined by the total transforms of the ideals 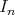 ,
, 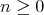 .
.
Theorem 3.7. Let  be a morphism of smooth schemes, then:
be a morphism of smooth schemes, then:
i) if 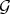 is a Diff-structure on
is a Diff-structure on 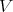 , the total transform
, the total transform 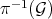 is a Diff-structure on
is a Diff-structure on 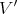 .
.
ii)  .
.
(See Th 5.4 [33])
4. On differential structures and monoidal transformations.
Let us briefly recall some previous results, where now 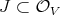 be the sheaf of ideals defining a hypersurface
be the sheaf of ideals defining a hypersurface 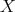 in the smooth scheme
in the smooth scheme 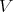 .
.
So 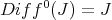 , and for each positive integer
, and for each positive integer  there is an inclusion
there is an inclusion 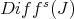
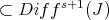 as sheaves of ideals in
as sheaves of ideals in 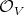 , and hence
, and hence 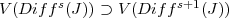 .
.
Recall that 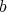 is the highest multiplicity at points of
is the highest multiplicity at points of 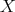 , if and only if
, if and only if 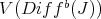
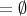 and
and 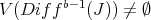 (i.e. if and only if
(i.e. if and only if 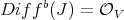 and
and 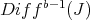 is a proper sheaf of ideals).
is a proper sheaf of ideals).
The closed set of interest is the set of 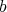 -fold points of
-fold points of 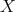 (i.e.
(i.e. 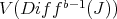 ). Consider now a
). Consider now a 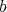 -permissible transformation, say
-permissible transformation, say
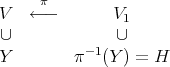
(i.e. the blow up of 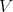 at a smooth sub-scheme
at a smooth sub-scheme 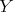 ). In such case
). In such case
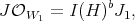
where 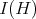 is the sheaf of functions vanishing along the exceptional hypersurface
is the sheaf of functions vanishing along the exceptional hypersurface 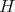 .
.
In this case 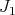 is the sheaf of ideals defining a hypersurface
is the sheaf of ideals defining a hypersurface 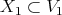 , which is the strict transform of the hypersurface
, which is the strict transform of the hypersurface 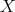 .
.
It is not hard to check that 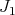 has at most order
has at most order 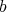 at points of
at points of 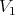 (i.e. that
(i.e. that 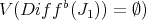 . If, in addition,
. If, in addition, 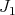 has no point of order
has no point of order 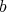 , then we say that
, then we say that 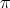 defines a
defines a 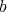 -simplification of
-simplification of 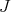 . At any rate, the closed set of interest is the set of
. At any rate, the closed set of interest is the set of 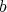 -fold points
-fold points 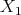 .
.
If 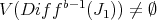 , let
, let 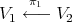 denote the monoidal transformation with center
denote the monoidal transformation with center 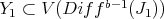 . So
. So 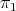 is
is 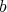 - permissible, and set
- permissible, and set
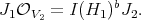
So again 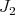 has at most points of order
has at most points of order 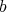 , and if it does, define a
, and if it does, define a 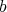 -permissible transformation at some smooth center
-permissible transformation at some smooth center 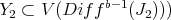 .
.
So for 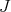 and
and 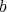 as before, we define, by iteration, a
as before, we define, by iteration, a 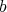 -permissible sequence
-permissible sequence
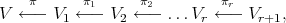
and a factorization 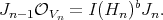 Where
Where 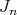 is the sheaf of ideals defining a hypersurface
is the sheaf of ideals defining a hypersurface 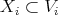 , which is the strict transform of
, which is the strict transform of 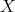 .
.
From the point of view of resolution it is clear that our interest is to define a 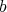 -permissible sequence so that
-permissible sequence so that 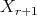 has no
has no 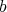 -fold points.
-fold points.
We say that a 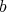 -permissible sequence defines a
-permissible sequence defines a 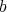 -simplication of
-simplication of 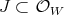 if the jacobian of
if the jacobian of 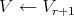 has normal crossings, and
has normal crossings, and 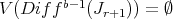 (i.e. if
(i.e. if 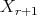 has at most points of multiplicity
has at most points of multiplicity  ).
).
Hironaka attaches to the original data 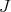 and
and 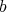 the pair
the pair 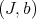 . The closed set assigned to this pair in
. The closed set assigned to this pair in 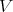 is
is 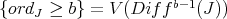 . In our case, the
. In our case, the 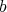 -fold points of the hypersurface
-fold points of the hypersurface 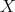 .
.
We attached to the original data a Rees algebra (up to integral closure), namely ![G = OV [JW b]](/img/revistas/ruma/v46n2/2a01521x.png) . And to this Rees algebra a closed set in
. And to this Rees algebra a closed set in 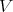 , namely
, namely 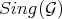 , which is again
, which is again 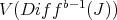 .
.
Moreover, we extended 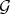 to a Diff-structure
to a Diff-structure 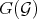 , and
, and 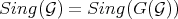 (Th. 3.2).
(Th. 3.2).
Let us focus on the 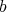 -permissible transformation
-permissible transformation 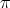 . The transform of Hironaka's pair is the pair
. The transform of Hironaka's pair is the pair 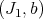 . The transformation
. The transformation 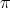 is also permissible for both
is also permissible for both 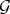 and
and 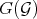 , defining transforms of Rees algebras, say
, defining transforms of Rees algebras, say 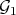 and
and 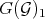 on
on 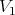 .
.
Note that, in our setting, 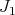 is the ideal defining defining
is the ideal defining defining 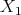 , which is the strict transform of
, which is the strict transform of 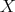 . The closed set assigned to
. The closed set assigned to 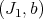 is the set of
is the set of 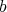 -fold points of
-fold points of 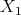 . On the other hand,
. On the other hand, ![G = O [J W b] 1 V1 1](/img/revistas/ruma/v46n2/2a01543x.png) , is such that
, is such that 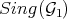 is again the set of
is again the set of 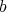 -fold points
-fold points 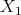 . A similar relation holds between pairs
. A similar relation holds between pairs 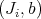 and the Rees algebras
and the Rees algebras 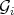 (transform of
(transform of 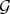 ), for any
), for any 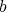 -permissible sequence.
-permissible sequence.
The natural question is on how do the successive transforms of 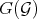 relate to the transforms of
relate to the transforms of 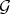 . The following theorem will address this question (see Th 7.6 [33]). It proves that the
. The following theorem will address this question (see Th 7.6 [33]). It proves that the 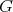 -operator on Rees algebras is, in a natural way, compatible with transformation.
-operator on Rees algebras is, in a natural way, compatible with transformation.
Theorem 4.1. (J. Giraud) Let 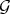 be a Rees algebra on a smooth scheme
be a Rees algebra on a smooth scheme 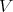 , and let
, and let  be a permissible (moniodal) transformation for
be a permissible (moniodal) transformation for 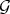 . Let
. Let 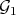 and
and 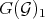 denote the transforms of
denote the transforms of 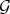 and
and 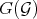 . Then:
. Then:
1) 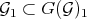 .
.
2) 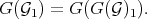
4.2. Hironaka considers the notion of Diff-structures in [23] and also in [24]. In this last paper he provides an interesting geometric interpretation of the elements of the integral closure of a Diff-structure, say 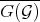 , which we briefly discuss below.
, which we briefly discuss below.
Recall that given an ideal 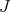 in a smooth scheme
in a smooth scheme 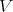 , and a positive integer
, and a positive integer 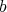 , Hironaka defines a pair
, Hironaka defines a pair 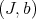 (actually a closely related notion of idealistic exponent). As mentioned in Section 1, there is a closed set in
(actually a closely related notion of idealistic exponent). As mentioned in Section 1, there is a closed set in 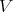 attached to the pair, and also a notion of permissible transforms of pairs.
attached to the pair, and also a notion of permissible transforms of pairs.
We have assign a Rees algebra to 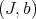 , say
, say ![b G = OV [J W ]](/img/revistas/ruma/v46n2/2a01571x.png) ; and a closed set to
; and a closed set to 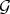 , namely
, namely 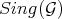 . We have also defined transformations of of Rees algebras, in accordance to transformations of pairs.
. We have also defined transformations of of Rees algebras, in accordance to transformations of pairs.
Here we have discussed integral closure of Rees algebras, and also a 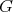 -operator on Rees algebras, as two different manners to extend a Rees algebra.
-operator on Rees algebras, as two different manners to extend a Rees algebra.
These two forms of extension of Rees algebras have a very particular geometric property. In fact, both extended algebras define the same closed set, and hence both admit the same transformations. Furthermore, the closed set defined by the transform of 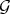 by a sequence of transformation, is the same closed set defined by the transform of the integral closure of
by a sequence of transformation, is the same closed set defined by the transform of the integral closure of 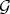 . Theorem 4.1 asserts that the same holds for the transform of
. Theorem 4.1 asserts that the same holds for the transform of 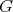 -extension of
-extension of 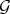 .
.
So given 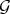 , it is quite natural to iterate both operators, by taking successively integral closure and Diff-structures, to obtain larger and larger extensions of
, it is quite natural to iterate both operators, by taking successively integral closure and Diff-structures, to obtain larger and larger extensions of 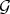 with this geometric property.
with this geometric property.
The result of Hironaka in [24] says that the 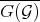 is the biggest extension of
is the biggest extension of 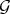 with this property. Namely that
with this property. Namely that 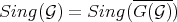 , and that the same equality of singular locus holds after any sequence of transformations. Theorem 4.1 can also be proved using this geometric characterization of
, and that the same equality of singular locus holds after any sequence of transformations. Theorem 4.1 can also be proved using this geometric characterization of 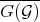 . The approach in [33] is different, and does not make use the concept of infinitely near singular point, but rather on technics that will also be useful for [34].
. The approach in [33] is different, and does not make use the concept of infinitely near singular point, but rather on technics that will also be useful for [34].
5. Idealistic exponents versus basic objects.
Recall that two ideals, say 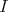 and
and 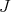 , in a normal domain
, in a normal domain 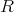 have the same integral closure if they are equal for any extension to a valuation ring (i.e. if
have the same integral closure if they are equal for any extension to a valuation ring (i.e. if 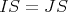 for any ring homomorphism
for any ring homomorphism  on a valuation ring
on a valuation ring 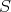 ). The notion extends naturally to sheaves of ideals.
). The notion extends naturally to sheaves of ideals.
Hironaka considers the following equivalence on pairs 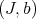 and
and 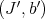 over a smooth scheme
over a smooth scheme 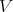 .
.
Definition 5.1. The pairs 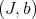 and
and 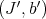 are idealistic equivalent on
are idealistic equivalent on 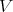 if
if 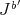 and
and 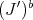 have the same integral closure.
have the same integral closure.
Proposition 5.2. Let 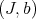 and
and 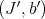 be idealistic equivalent. Then:
be idealistic equivalent. Then:
1) 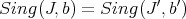 .
.
Note, in particular, that any monoidal transform 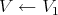 on a center
on a center 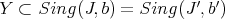 defines transforms, say
defines transforms, say 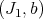 and
and 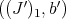 on
on 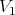 .
.
2)The pairs 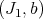 and
and 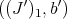 are idealistic equivalent on
are idealistic equivalent on 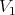 .
.
If two pairs 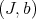 and
and 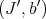 be idealistic equivalent over
be idealistic equivalent over 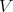 , the same holds for the restrictions to any open subset of
, the same holds for the restrictions to any open subset of 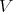 , and also for restrictions in the sense of etale topology, and even for smooth topology (i.e. pull-backs by smooth morphisms
, and also for restrictions in the sense of etale topology, and even for smooth topology (i.e. pull-backs by smooth morphisms  ).
).
Note that if 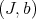 and
and 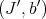 are idealistic equivalent, the they define the same closed set on
are idealistic equivalent, the they define the same closed set on 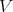 (i.e.
(i.e. 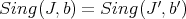 ), and the same holds for monoidal transformations, pull-backs by smooth schemes, and hence by concatenation of both kinds of transformations. When this last condition holds on the singular locus of two pairs we say that they define the same close sets.
), and the same holds for monoidal transformations, pull-backs by smooth schemes, and hence by concatenation of both kinds of transformations. When this last condition holds on the singular locus of two pairs we say that they define the same close sets.
Definition 5.3. Two pairs 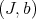 and
and 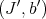 are basically equivalent on
are basically equivalent on 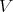 , if the define the same close sets.
, if the define the same close sets.
The proposition says that if two pairs are idealistic equivalent over 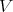 , then they are basically equivalent.
, then they are basically equivalent.
An idealistic exponent, as defined by Hironaka in [23], is an equivalence class of pairs in the sense of idealistic equivalence. Whereas the notion of equivalence among basic objects (see [31] or [32]) is the second one. In fact, the key point for constructive desingularization was to define an algorithm of resolutions of pairs 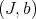 , so that two basically equivalent pairs undergo exactly the same resolution.
, so that two basically equivalent pairs undergo exactly the same resolution.
5.4. There are two notions of equivalence on the context of Rees algebras over 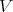 . The first, already formulated in Section 2:
. The first, already formulated in Section 2:
Definition 5.5. Two Rees algebras over 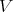 , say
, say 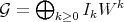 and
and 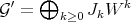 , are integrally equivalent, if both have the same integral closure.
, are integrally equivalent, if both have the same integral closure.
Proposition 5.6. Let 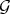 and
and 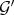 be two integrally equivalent Rees algebras over
be two integrally equivalent Rees algebras over 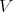 Then:
Then:
1) 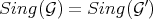 .
.
Note, in particular, that any monoidal transform 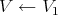 on a center
on a center 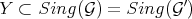 defines transforms, say
defines transforms, say 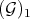 and
and 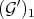 on
on 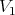 .
.
2) and
and 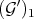 are integrally equivalent on
are integrally equivalent on 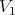 .
.
If 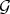 and
and 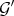 are integrally equivalent on
are integrally equivalent on 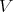 , the same holds for any open restriction, and also for pull-backs by smooth morphisms
, the same holds for any open restriction, and also for pull-backs by smooth morphisms  .
.
On the other hand, as 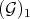 and
and 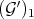 are integrally equivalent, the they define the same closed set on
are integrally equivalent, the they define the same closed set on 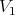 (the same singular locus), and the same holds for further monoidal transformations, pull-backs by smooth schemes, and concatenations of both kinds of transformations.
(the same singular locus), and the same holds for further monoidal transformations, pull-backs by smooth schemes, and concatenations of both kinds of transformations.
When this condition holds on the singular locus of two Rees algebras over 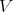 , we say that they define the same close sets.
, we say that they define the same close sets.
Definition 5.7. Two Rees algebras over 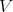 , say
, say 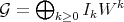 and
and 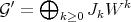 , are basically equivalent, if both define the same closed sets.
, are basically equivalent, if both define the same closed sets.
The previous Proposition asserts that if 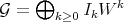 and
and 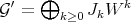 are integrally equivalent, then they are basically equivalent.
are integrally equivalent, then they are basically equivalent.
5.8. We assign to a pair 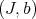 over a smooth scheme
over a smooth scheme 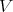 the Rees algebra, say:
the Rees algebra, say:
![G = O [JbW b], (J,b) V](/img/revistas/ruma/v46n2/2a01655x.png)
which is a graded subalgebra in ![OV [W ]](/img/revistas/ruma/v46n2/2a01656x.png) .
.
Proposition 5.9. 1) Two pairs 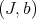 and
and 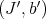 are idealistically equivalent over a smooth scheme
are idealistically equivalent over a smooth scheme  , if and only if the Rees algebras
, if and only if the Rees algebras 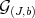 and
and 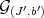 are integrally equivalent.
are integrally equivalent.
2) Two pairs 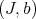 and
and 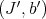 are basically equivalent over
are basically equivalent over 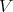 , if and only if the Rees algebras
, if and only if the Rees algebras 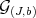 and
and 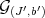 are basically equivalent.
are basically equivalent.
6. Projection of differential structures and elimination of one variable.
6.1. The notion of Rees algebra 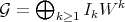 parallels that of idealistic exponents in [23], and the notion of singular locus
parallels that of idealistic exponents in [23], and the notion of singular locus 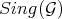 , is the natural analog for that defined for idealistic exponents.
, is the natural analog for that defined for idealistic exponents.
We finally introduce a function, again a natural analog to that defined for idealistic exponents. Fix 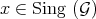 . Given
. Given 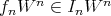 , set
, set
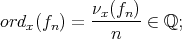
called the order of 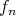 (weighted by
(weighted by 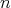 ), where
), where 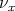 denotes the order at the local regular ring
denotes the order at the local regular ring 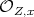 . As
. As 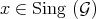 it follows that
it follows that 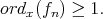 We also define
We also define
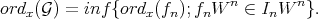
So, in general 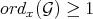 for any
for any 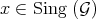 .
.
Proposition 6.2. 1) If 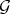 is a Rees algebra generated over
is a Rees algebra generated over  by
by 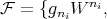
 , then
, then
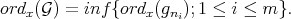
And if 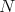 is any common multiple of all
is any common multiple of all 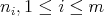 , then
, then 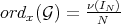 .
.
2) If 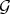 and
and 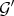 are graded structures with the same integral closure (e.g. if
are graded structures with the same integral closure (e.g. if 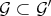 is a finite extension), then, for any
is a finite extension), then, for any 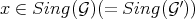
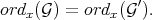
3) Set 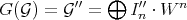 (the extension of
(the extension of 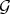 to a differential structure), then for any
to a differential structure), then for any 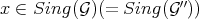 .
.
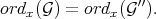
6.3. Let 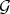 be a Rees algebra, and fix a closed point
be a Rees algebra, and fix a closed point 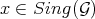 . We assume that at a affine open neighborhood of the point, say
. We assume that at a affine open neighborhood of the point, say  , there is a finite set
, there is a finite set 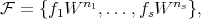
 and
and 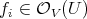 , so that the restriction of
, so that the restriction of 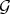 to
to 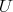 is
is
[W ]).](/img/revistas/ruma/v46n2/2a01706x.png)
Let
![⊕ k Gx = Ik ⋅ W (⊂ OV,x[W ])](/img/revistas/ruma/v46n2/2a01707x.png)
be the localization of 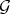 at
at 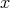 . As
. As 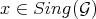 , the order of
, the order of 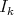 at
at 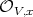 is at least
is at least 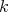 . We say that
. We say that 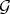 is simple at the singular point
is simple at the singular point 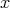 , if for some positive index
, if for some positive index 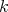 ,
, 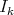 has order
has order 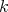 . This amounts to saying that
. This amounts to saying that 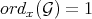 ; or equivalently, that for some
; or equivalently, that for some 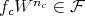 , the element
, the element 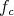 has order
has order 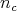 at
at 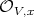 .
.
Recall that 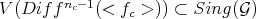 locally at
locally at 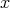 .
.
We may choose the system of parameters  at
at 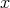 , so that at the completion
, so that at the completion 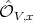 , say
, say ![′ R = k [[x1, ..,xn]]](/img/revistas/ruma/v46n2/2a01729x.png) :
:
![nc nc-1 u.fc = Z + a1Z + ⋅⋅⋅ + anc ∈ S[Z]](/img/revistas/ruma/v46n2/2a01730x.png)
![S = k[[x1,..,xn -1]]](/img/revistas/ruma/v46n2/2a01731x.png) , and
, and 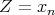 ; where
; where 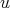 is a unit of
is a unit of 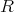 .
.
A similar result holds at a suitable étale neighborhood of 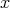 . We may assume that
. We may assume that 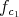 is a monic polynomial of degree
is a monic polynomial of degree 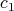 in
in ![S[Z]](/img/revistas/ruma/v46n2/2a01738x.png) , and of order
, and of order 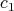 in
in ![S[Z] ⊂ R <MS,Z>](/img/revistas/ruma/v46n2/2a01740x.png) , where
, where 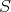 is regular.
is regular.
Let  be a smooth morphism defined at an étale neighborhood of
be a smooth morphism defined at an étale neighborhood of 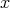 , where
, where 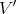 is smooth, dim
is smooth, dim 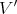 =dim
=dim 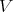 -1. We say that
-1. We say that 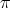 is transversal to
is transversal to 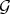 at
at 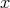 , if the previous setting holds for
, if the previous setting holds for 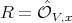 ,
, 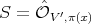 ; and for some
; and for some 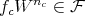 , where
, where 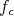 has order
has order 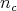 at
at 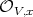 .
.
In these conditions, a transversal morphism 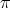 , induces a finite morphism
, induces a finite morphism
![π-: Spec(S[Z] ∕〈f (Z)〉) → Spec(S) 〉. c1](/img/revistas/ruma/v46n2/2a01757x.png)
Here we view ![H = Spec(S[Z] ∕〈fc1(Z)〉)](/img/revistas/ruma/v46n2/2a01758x.png) as a hypersurface in
as a hypersurface in 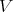 , and locally at
, and locally at 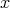 ,
, 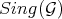 is included in the
is included in the 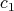 -fold points of this hypersurface. So
-fold points of this hypersurface. So
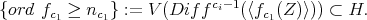
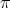 is one to one over a closed subset of
is one to one over a closed subset of 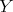 , namely on the image of the
, namely on the image of the 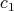 -fold points. Set
-fold points. Set |
![- Spec(S[Z] ∕ < f (Z) >) -π→ Spec(S) c1 ∪ 1 to 1 ∪ {ord fc1 ≥ nc1} -→ π({ord fc1 ≥ nc1})](/img/revistas/ruma/v46n2/2a01767x.png) | (6.3.1) |
Since 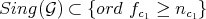 ,
, 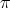 induces a one to one map, say
induces a one to one map, say
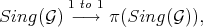
for any transversal morphism ![π : Spec(S[Z]) → Spec(S)](/img/revistas/ruma/v46n2/2a01771x.png) .
.
Theorem 6.4. Let 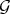 be a Diff-structure over a smooth scheme
be a Diff-structure over a smooth scheme 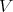 , and
, and 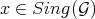 a closed point which we assume to be simple. Let
a closed point which we assume to be simple. Let 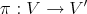 be a smooth morphism defined at an étale neighborhood of
be a smooth morphism defined at an étale neighborhood of 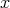 , where
, where 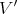 is smooth, dim
is smooth, dim 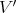 =dim
=dim 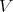 -1. Assume that
-1. Assume that 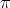 is transversal at
is transversal at 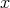 . Then:
. Then:
1) At a suitable neighborhood of 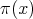 , there is a Rees algebra
, there is a Rees algebra 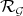 over the smooth scheme
over the smooth scheme 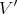 , so that
, so that 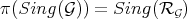 .
.
2) The morphism 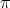 induces a one-to-one map from
induces a one-to-one map from 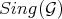 to
to 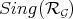 . Furthermore, setting
. Furthermore, setting 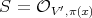 , and
, and ![S[Z]](/img/revistas/ruma/v46n2/2a01790x.png) as before, then the one-to-one map is that described above.
as before, then the one-to-one map is that described above.
The formulation of the theorem is independent of the choice of 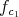 of order
of order 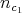 at
at 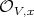 . However given a finite morphisms as that in (6.3.1), and a smooth center
. However given a finite morphisms as that in (6.3.1), and a smooth center 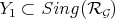 , there is a unique and smooth center
, there is a unique and smooth center 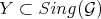 mapping isomorphically to
mapping isomorphically to 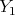 via
via 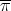 (and hence via
(and hence via 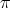 ). Set
). Set 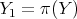 .
.
So both 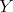 in
in 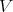 , and
, and 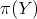 in
in 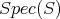 , are regular centers.
, are regular centers.
Let now 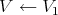 , and
, and 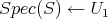 , denote the monoidal transformations at
, denote the monoidal transformations at 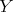 and
and 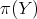 respectively; and let
respectively; and let 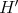 denote the strict transform of
denote the strict transform of 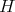 . The hypersurface
. The hypersurface 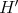 has at most points of multiplicity
has at most points of multiplicity 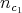 . Let
. Let 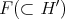 denotes the closed set of points of multiplicity
denotes the closed set of points of multiplicity 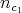 . After replacing
. After replacing 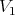 by a suitable neighborhood of
by a suitable neighborhood of 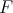 , we may assume that there is a finite morphism, say
, we may assume that there is a finite morphism, say  , compatible with
, compatible with 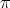 .
.
As the regular center 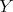 was chosen in
was chosen in 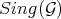 , then a weighted transform, say
, then a weighted transform, say
![⊕ G1 = I(n1) ⋅ W k(⊂ OV1[W ])](/img/revistas/ruma/v46n2/2a01820x.png)
is defined, and 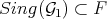 . So locally at a point
. So locally at a point 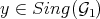 there is a finite morphism
there is a finite morphism
![π′ : Spec(S ′[Z]∕〈f′ (Z)〉) → U1, c1](/img/revistas/ruma/v46n2/2a01823x.png)
where 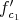 is a strict transform of
is a strict transform of 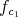 . Let
. Let 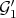 be the Diff-structure generated by
be the Diff-structure generated by 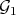 . According to the previous Theorem, locally at
. According to the previous Theorem, locally at 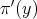 there is an elimination algebra, say
there is an elimination algebra, say
![R ′⊂ O ′ [W ]. G1 U1,π(y)](/img/revistas/ruma/v46n2/2a01829x.png)
On the other hand, 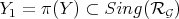 , so there is also a weighted transform
, so there is also a weighted transform
![(RG)1 ⊂ OU1[W ].](/img/revistas/ruma/v46n2/2a01831x.png)
The question now is to relate the Rees algebra 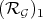 with
with 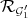 , locally at the point
, locally at the point 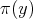 .
.
Proposition 6.5. With the setting as above:
1) There is a natural inclusion 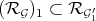 .
.
2) Over fields of characteristic zero both 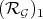 and
and 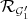 define the same Diff-structure, up to integral closure.
define the same Diff-structure, up to integral closure.
Here 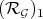 is the transform of
is the transform of  by one monoidal transformation. If we could guarantee that
by one monoidal transformation. If we could guarantee that 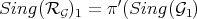 , we could identify the singular locus of
, we could identify the singular locus of 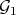 (i.e. of
(i.e. of 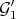 ) with the singular locus of the transform of
) with the singular locus of the transform of 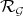 . If furthermore, this link between
. If furthermore, this link between 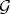 and
and 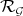 is preserved by any sequence of monoidal transformations, then we have achieved a way of representing the singular locus of
is preserved by any sequence of monoidal transformations, then we have achieved a way of representing the singular locus of 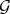 which is stable by monoidal transformations.
which is stable by monoidal transformations.
Part 2) in the previous Proposition ensures that this is the case over fields of characteristic zero, providing an alternative form of stability of elimination (see (C) in Introduction). This is not the case over fields of positive characteristic, but it is the starting point for new invariants in that context.
References
[1] S.S. Abhyankar, Good points of a Hypersurface, Adv. in Math. 68 (1988) 87-256. [ Links ]
[2] D. Abramovich and A.J. de Jong, 'Smoothness, semistability and toroidal geometry', Journal of Algebraic Geometry 6 (1997) 789-801. [ Links ]
[3] D. Abramovich and J. Wang, 'Equivariant resolution of singularities in characteristic 0', Mathematical Research Letters 4 (1997) 427-433. [ Links ]
[4] J.M. Aroca, H. Hironaka and J.L. Vicente, 'The theory of maximal contact', Mem. Mat. Ins. Jorge Juan (Madrid) 29 (1975). [ Links ]
[5] M. Artin. 'Algebraic approximation of structures over complete local rings', Pub. Math. I.H.E.S. 36 (1969) 23-58. [ Links ]
[6] E. Bierstone and P. Milman, 'Canonical desingularization in characteristic zero by blowing-up the maxima strata of a local invariant', Inv. Math. 128 (1997) 207-302. [ Links ]
[7] E. Bierstone and P. Milman, 'Desingularization algorithms I. Role of exceptional divisors'. Mosc. Math. J. 3 (2003), no3, 751-805, 1197. MR2078560 [ Links ]
[8] G. Bodnár and J. Schicho 'A Computer Program for the Resolution of Singularities', Resolution of singularities. A research book in tribute of Oscar Zariski (eds H. Hauser, J. Lipman, F. Oort, A. Quirós), Progr. Math. 181 (Birkhäuser, Basel, 2000) pp.231-238. [ Links ]
[9] G. Bodnár and J. Schicho, 'Automated resolution of singularities for hypersurfaces', J. Symbolic Comput. (4) 30 (2000) 401-428. [ Links ]
[10] F. Bogomolov and T. Pantev, 'Weak Hironaka Theorem', Mathematical Research Letters 3 (1996) 299-307. [ Links ]
[11] A. Bravo and O. Villamayor, 'Strengthening a Theorem of Embedded Desingularization,' Math. Res. Letters 8 (2001) 1-11. [ Links ]
[12] A. Bravo and O. Villamayor, 'A Strengthening of resolution of singularities in characteristic zero'. Proc. London Math. Soc. (3) 86 (2003) 327-357. [ Links ]
[13] S. Encinas and H. Hauser, 'Strong Resolution of Singularities'. Comment. Math. Helv. 77 2002, no. 4, 821-845. [ Links ]
[14] S. Encinas, A. Nobile and O. Villamayor, 'On algorithmic Equiresolution and stratification of Hilbert schemes'. Proc. London Math. Soc. (3) 86 (2003) 607-648. [ Links ]
[15] S. Encinas and O. Villamayor, 'Good points and constructive resolution of singularities', Acta Math. 181:1 (1998) 109-158. [ Links ]
[16] S. Encinas and O. Villamayor, 'A Course on Constructive Desingularization and Equivariance', Resolution of Singularities. A research textbook in tribute to Oscar Zariski (eds H. Hauser, J. Lipman, F. Oort, A. Quirós), Progr. in Math. 181 (Birkhäuser, Basel, 2000) pp. 147-227. [ Links ]
[17] S. Encinas and O. Villamayor, 'A new proof of desingularization over fields of characteristic zero'. Rev. Mat. Iberoamericana 19 (2003), no.2, 339-353. [ Links ]
[18] J. Giraud, 'Sur la theorie du contact maximal', Math. Zeit., 137 (1972), 285-310. [ Links ]
[19] J. Giraud. 'Contact maximal en caractéristique positive', Ann. Scien. de l'Ec. Norm. Sup. 4ème série, 8 (1975) 201-234. [ Links ]
[20] H. Hauser, Excellent surfaces and Their Taut Resolution in Resolution of Singularities. A research textbook in tribute to Oscar Zariski, Eds. H. Hauser, J. Lipman, F. Oort, A. Quirós. Progress in Math. vol 181, Birkhäuser 2000. [ Links ]
[21] H. Hauser, 'The Hironaka Theorem on Resolution of Singularities'(or: A proof we always wanted to understand), Bull. Amer. Math. Soc. (N.S.)40 (2003), no. 3,323-403. [ Links ]
[22] H. Hironaka, 'Resolution of singularities of an algebraic variety over a field of characteristic zero I-II', Ann. Math., 79 (1964) 109-326. [ Links ]
[23] H. Hironaka, 'Idealistic exponent of a singularity', Algebraic Geometry, The John Hopkins centennial lectures, Baltimore, John Hopkins University Press (1977), 52-125. [ Links ]
[24] H. Hironaka, 'Theory of infinitely near singular points', Journal Korean Math. Soc. 40 (2003), No.5, pp. 901-920 [ Links ]
[25] J. Kollár, 'Resolution of Singularities- Seattle Lecture' arXiv:math.AG/ 0508332 v1 17 Aug 2005. [ Links ]
[26] J. Lipman, 'Introduction to Resolution of Singularities', Proc. Symp. in Pure Math. 29 (1975) pp. 187-230. [ Links ]
[27] J. Lipman, 'Equisingularity and Simultaneous Resolution of Singularities', Resolution of Singularities. A research textbook in tribute to Oscar Zariski, (eds H. Hauser, J. Lipman, F. Oort and A. Quirós), Progr. in Math. 181, (Birkhäuser, Basel, 2000) pp. 485-505. [ Links ]
[28] K. Matsuki, 'Notes on the inductive algorithm of resolution of singularities'. Preprint. arXiv:math.math.AG/0103120 [ Links ]
[29] H. Matsumura. 'Commutative algebra', Mathematics Lecture Note Series, 56, Benjamin/Cummings Publishing Company, Inc., 2nd ed. edition, 1980. [ Links ]
[30] T. Oda, 'Infinitely very near singular points', Complex analytic singularities, Adv. Studies in Pure Math. 8 (North-Holland, 1987) pp. 363-404. [ Links ]
[31] O. Villamayor, 'Constructiveness of Hironaka's resolution', Ann. Scient. Ec. Norm. Sup. 4e serie 22 (1989) 1-32. [ Links ]
[32] O. Villamayor, 'Patching local uniformizations', Ann. Scient. Ec. Norm. Sup., 25 (1992), 629-677. [ Links ]
[33] O. Villamayor, 'Rees algebras on smooth schemes: integral closure and higher differential operators'. ArXiv:math. AG/0606795. [ Links ]
[34] O. Villamayor, 'Hypersurface singularities in positive characteristic.' ArXiv:math.AG/0606796. [ Links ]
[35] J. Wlodarczyk, 'Simple Hironaka resolution in characteristic zero', to appear (2005). [ Links ]
[36] B. Youssin, 'Newton Polyhedra without coordinates', Mem. Amer. Math. Soc. 433 (1990), 1-74,75-99. [ Links ]
Orlando Villamayor U.
Dpto. Matemáticas,
Facultad de Ciencias,
Universidad Autónoma de Madrid,
Canto Blanco 28049 Madrid, Spain
villamayor@uam.es
Recibido: 26 de diciembre de 2005
Aceptado: 7 de agosto de 2006














