Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.46 n.2 Bahía Blanca jul./dic. 2005
The left part and the Auslander-Reiten components of an artin algebra
Ibrahim Assem, Juan Ángel Cappa, María Inés Platzeck and Sonia Trepode
Dedicated to the memory of Ángel Rafael Larotonda
This paper was completed during a visit of the first author to the Universidad Nacional del Sur in Bahía Blanca (Argentina). He would like to thank María Inés Platzeck and María Julia Redondo, as well as all members of the argentinian group, for their invitation and warm hospitality. He also acknowledges partial support from NSERC of Canada. The other three authors gratefully acknowledge partial support from Universidad Nacional del Sur and CONICET of Argentina, and the fourth from ANPCyT of Argentina. The second author has a fellowship from CONICET, and the third and the fourth are researchers from CONICET.
Abstract. The left part 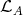 of the module category of an artin algebra
of the module category of an artin algebra 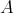 consists of all indecomposables whose predecessors have projective dimension at most one. In this paper, we study the Auslander-Reiten components of
consists of all indecomposables whose predecessors have projective dimension at most one. In this paper, we study the Auslander-Reiten components of 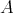 (and of its left support
(and of its left support 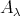 ) which intersect
) which intersect 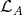 and also the class
and also the class 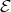 of the indecomposable Ext-injectives in the addditive subcategory add
of the indecomposable Ext-injectives in the addditive subcategory add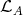 generated by
generated by 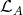 .
.
Key words and phrases. artin algebras, Auslander-Reiten quivers, sections, left and right supported algebras
2000 Mathematics Subject Classification. 16G70, 16G20, 16E10
INTRODUCTION
Let 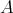 be an artin algebra and mod
be an artin algebra and mod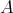 denote the category of finitely generated right
denote the category of finitely generated right 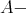 modules. The class
modules. The class 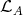 , called the left part of mod
, called the left part of mod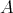 , is the full subcategory of mod
, is the full subcategory of mod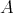 having as objects all indecomposable modules whose predecessors have projective dimension at most one. This class, introduced in [15], was heavily investigated and applied (see, for instance, the survey [4]).
having as objects all indecomposable modules whose predecessors have projective dimension at most one. This class, introduced in [15], was heavily investigated and applied (see, for instance, the survey [4]).
Our objective in this paper is to study the Auslander-Reiten components of an artin algebra which intersect the left part. Some information on these components was already obtained in [2, 3]. Here we are interested in the components which intersect the class 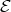 of the indecomposable Ext-injectives in the full additive subcategory add
of the indecomposable Ext-injectives in the full additive subcategory add 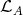 having as objects the direct sums of modules in
having as objects the direct sums of modules in 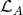 . We start by proving the following theorem.
. We start by proving the following theorem.
THEOREM (A). Let 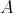 be an artin algebra, and
be an artin algebra, and 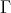 be a component of the Auslander-Reiten quiver of
be a component of the Auslander-Reiten quiver of 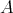 . If
. If 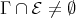 , then:
, then:
(a) Each 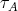 -orbit of
-orbit of 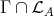 intersects
intersects 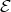 exactly once.
exactly once.
(b) The number of 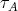 -orbits of
-orbits of 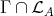 equals the number of modules in
equals the number of modules in  .
.
(c) 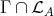 contains no module lying on a cycle between modules in
contains no module lying on a cycle between modules in 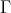 .
.
If, on the other hand, 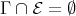 , then either
, then either 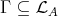 or else
or else 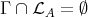 .
.
We recall that, by [3] (3.3), the class 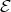 contains only finitely many non-isomorphic modules (hence only finitely many Auslander-Reiten components intersect
contains only finitely many non-isomorphic modules (hence only finitely many Auslander-Reiten components intersect 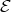 ).
).
As a consequence, we give a complete description of the Auslander-Reiten components lying entirely inside the left part.
We then try to describe the intersection of 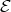 with a component
with a component 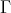 of the Auslander-Reiten quiver
of the Auslander-Reiten quiver 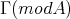 . We find that, in general,
. We find that, in general,  is not a section in
is not a section in 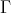 (in the sense of [20, 23]) but is very nearly one. This leads us to our second theorem, for which we recall that a component
(in the sense of [20, 23]) but is very nearly one. This leads us to our second theorem, for which we recall that a component 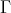 of
of 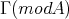 is called generalised standard if
is called generalised standard if 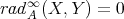 for all
for all 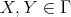 , see [23].
, see [23].
THEOREM (B). Let 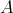 be an artin algebra and
be an artin algebra and 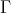 be a component of
be a component of 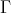 (mod
(mod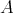 ) such that all projectives in
) such that all projectives in 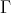 belong to
belong to 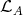 . If
. If 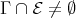 , then:
, then:
(a)  is a section in
is a section in 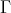 .
.
(b) 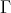 is generalised standard.
is generalised standard.
(c) 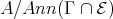 is a tilted algebra having
is a tilted algebra having 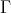 as a connecting component and
as a connecting component and  as a complete slice.
as a complete slice.
In particular, such a component 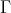 has only finitely many
has only finitely many 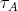 -orbits.
-orbits.
The situation is better if we look instead at the intersection of 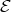 with the Auslander-Reiten components of the left support
with the Auslander-Reiten components of the left support 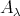 of
of 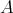 . We recall from [3, 24] that the left support
. We recall from [3, 24] that the left support 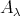 of
of 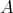 is the endomorphism algebra of the direct sum of the indecomposable projective
is the endomorphism algebra of the direct sum of the indecomposable projective 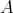 -modules lying in
-modules lying in 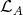 . It is shown in [3, 24] that every connected component of
. It is shown in [3, 24] that every connected component of 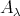 is a quasi-tilted algebra (in the sense of [15]). We prove the following theorem.
is a quasi-tilted algebra (in the sense of [15]). We prove the following theorem.
THEOREM (C). Let 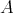 be an artin algebra and
be an artin algebra and 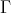 be a component of the Auslander-Reiten quiver of the left support
be a component of the Auslander-Reiten quiver of the left support 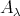 of
of 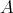 . If
. If 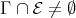 , then:
, then:
(a)  is a section in
is a section in 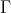 .
.
(b) 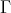 is directed, and generalised standard.
is directed, and generalised standard.
(c) 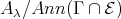 is a tilted algebra having
is a tilted algebra having 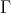 as a connecting component and
as a connecting component and  as a complete slice.
as a complete slice.
We then apply our results to the study of left supported algebras. We recall from [3] that an artin algebra 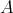 is left supported provided add
is left supported provided add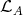 is contravariantly finite in mod
is contravariantly finite in mod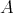 . Several classes of algebras are left supported, such as all representation-finite algebras, and all laura algebras which are not quasi-tilted (see [3, 4]). It is shown in [1] that an artin algebra
. Several classes of algebras are left supported, such as all representation-finite algebras, and all laura algebras which are not quasi-tilted (see [3, 4]). It is shown in [1] that an artin algebra 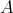 is left supported if and only if
is left supported if and only if 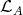 consists of all the predecessors of the modules in
consists of all the predecessors of the modules in 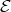 . We give here a proof of this fact which, in contrast to the homological nature of the proof in [1], uses our theorem and the full power of the Auslander-Reiten theory of quasi-tilted algebras. Our proof also yields a new characterisation: an algebra
. We give here a proof of this fact which, in contrast to the homological nature of the proof in [1], uses our theorem and the full power of the Auslander-Reiten theory of quasi-tilted algebras. Our proof also yields a new characterisation: an algebra 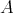 is left supported if and only if every projective
is left supported if and only if every projective 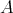 -module which belongs to
-module which belongs to 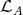 is a predecessor of
is a predecessor of 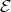 . We end the paper with a short proof of the theorem of D. Smith [25] (3.8) which characterises the left supported quasi-tilted algebras.
. We end the paper with a short proof of the theorem of D. Smith [25] (3.8) which characterises the left supported quasi-tilted algebras.
Clearly, the dual statements about the right part of the module category, also hold true. Here, we only concern ourselves with the left part, leaving the primal-dual translation to the reader.
We now describe the contents of the paper. After a brief preliminary section 1, the sections 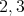 and
and 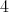 are respectively devoted to the proofs of our theorems (A), (B) and (C). In our final section
are respectively devoted to the proofs of our theorems (A), (B) and (C). In our final section  , we consider the applications to left supported algebras.
, we consider the applications to left supported algebras.
1.1. Notation. For a basic and connected artin algebra 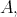 let mod
let mod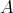 denote its category of finitely generated right modules and ind
denote its category of finitely generated right modules and ind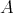 a full subcategory consisting of exactly one representative from each isomorphism class of indecomposable modules. We sometimes consider
a full subcategory consisting of exactly one representative from each isomorphism class of indecomposable modules. We sometimes consider 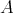 as a category, with objects a complete set
as a category, with objects a complete set  of primitive orthogonal idempotents, and where
of primitive orthogonal idempotents, and where 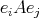 is the set of morphisms from
is the set of morphisms from 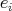 to
to 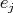 . An algebra
. An algebra 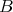 is a full subcategory of
is a full subcategory of 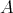 if there is an idempotent
if there is an idempotent 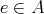 , which is a sum of some of the distinguished idempotents
, which is a sum of some of the distinguished idempotents 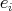 , such that
, such that 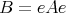 . It is convex in
. It is convex in 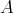 if, for any sequence
if, for any sequence 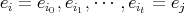 of objects of
of objects of 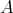 such that
such that 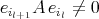 (with
(with 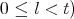 and
and 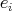 ,
, 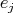 objects of
objects of 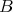 , all
, all 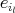 are in
are in 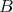 .
.
Given a full subcategory  of mod
of mod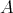 , we write
, we write 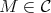 to indicate that
to indicate that 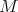 is an object in
is an object in  , and we denote by add
, and we denote by add the full subcategory with objects the direct sums of summands of modules in
the full subcategory with objects the direct sums of summands of modules in  . Given a module
. Given a module 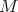 , we let pd
, we let pd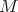 stand for its projective dimension. We also denote by
stand for its projective dimension. We also denote by 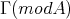 the Auslander-Reiten quiver of
the Auslander-Reiten quiver of 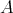 and by
and by 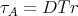 ,
, 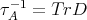 the Auslander-Reiten translations. For further notions or facts needed on mod
the Auslander-Reiten translations. For further notions or facts needed on mod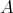 , we refer to [7, 22].
, we refer to [7, 22].
1.2. Paths. Let 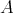 be an artin algebra and
be an artin algebra and 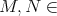 ind
ind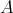 . A path
. A path 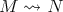 is a sequence
is a sequence
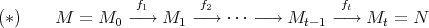
 are non-zero morphisms and the
are non-zero morphisms and the 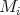 lie in ind
lie in ind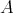 . We call
. We call 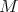 a predecessor of
a predecessor of 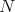 and
and 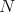 a successor of
a successor of 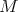 . A path from
. A path from 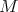 to
to 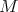 involving at least one non-isomorphism is a cycle. An indecomposable module
involving at least one non-isomorphism is a cycle. An indecomposable module  lying on no cycle is called directed . A path
lying on no cycle is called directed . A path  is called sectional if each
is called sectional if each  is irreducible and
is irreducible and 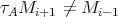 for all
for all 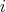 . A refinement of
. A refinement of  is a path
is a path 
 with
with 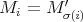 for all
for all 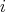 . A full subcategory
. A full subcategory  of ind
of ind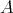 is convex if, for any path
is convex if, for any path  with
with 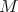 ,
, 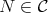 , all the
, all the 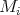 lie in
lie in  .
. 2. EXT-INJECTIVES IN THE LEFT PART.
2.1. Let 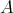 be an artin algebra. The left part
be an artin algebra. The left part 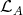 of mod
of mod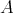 is the full subcategory of ind
is the full subcategory of ind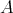 defined by
defined by
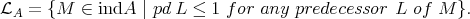
An indecomposable module 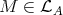 is called Ext-projective (or Ext-injective) in add
is called Ext-projective (or Ext-injective) in add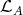 if Ext
if Ext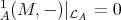 (or Ext
(or Ext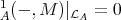 , respectively), see [9]. While the Ext-projectives in add
, respectively), see [9]. While the Ext-projectives in add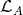 are the projective modules lying in
are the projective modules lying in 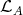 (see [3] (3.1)), the Ext-injectives are more interesting. Before stating their characterisations we recall that, by [9] (3.7),
(see [3] (3.1)), the Ext-injectives are more interesting. Before stating their characterisations we recall that, by [9] (3.7), 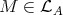 is Ext-injective in add
is Ext-injective in add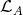 if and only if
if and only if 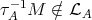 .
.
LEMMA [5] (3.2), [3] (3.1). Let 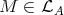 .
.
(a) The following are equivalent:
Hom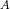
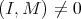 .
. 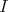 and a path
and a path 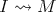 .
. 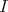 and a sectional path
and a sectional path 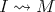 .
.
(b) The following conditions are equivalent for 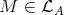 which does not satisfy conditions (a):
which does not satisfy conditions (a):
Hom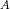
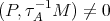 .
. 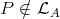 and a path
and a path 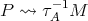 .
. 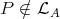 and a sectional path
and a sectional path 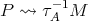 .
.
Letting 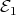 (or
(or 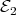 ) denote the set of all
) denote the set of all 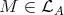 verifying (a) (or (b), respectively), and setting
verifying (a) (or (b), respectively), and setting 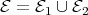 , then
, then 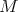 is Ext-injective in add
is Ext-injective in add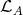 if and only if
if and only if 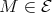 .
. 
2.2. The following lemma will also be useful.
LEMMA [3] (3.2) (3.4). (a) Any path of irreducible morphisms in 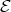 is sectional.
is sectional.
(b) Let 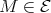 and
and 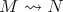 with
with 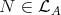 . Then this path can be refined to a sectional path and
. Then this path can be refined to a sectional path and 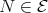 . In particular,
. In particular, 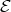 is convex in ind
is convex in ind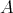 .
. 
2.3. The following immediate corollary will be useful in the proof of our theorem (A).
COROLLARY All modules in 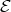 are directed.
are directed.
Proof. Assume 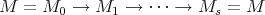 is a cycle in ind
is a cycle in ind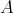 , with
, with 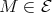 . By (2.2) above, such a cycle can be refined to a sectional cycle with all indecomposables lying in
. By (2.2) above, such a cycle can be refined to a sectional cycle with all indecomposables lying in 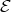 . Now compose two copies of this cycle to form a larger cycle in
. Now compose two copies of this cycle to form a larger cycle in 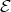 of irreducible morphisms. By (2.2), this cycle is also sectional, in contradiction to [11, 12] .
of irreducible morphisms. By (2.2), this cycle is also sectional, in contradiction to [11, 12] . 
2.4. THEOREM (A). Let 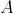 be an artin algebra, and
be an artin algebra, and 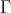 be a component of the Auslander-Reiten quiver of
be a component of the Auslander-Reiten quiver of 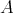 . If
. If 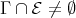 , then:
, then:
(a) Each 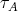 -orbit of
-orbit of 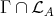 intersects
intersects 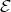 exactly once.
exactly once.
(b) The number of 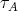 -orbits of
-orbits of 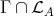 equals the number of modules in
equals the number of modules in  .
.
(c) 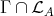 contains no module lying on a cycle between modules in
contains no module lying on a cycle between modules in 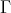 .
.
If, on the other hand, 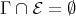 , then either
, then either 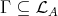 or else
or else 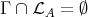 .
.
Proof. Assume first that 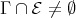 , that is, the component
, that is, the component 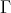 contains an Ext-injective in add
contains an Ext-injective in add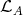 .
.
(a) If 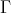 contains an injective module, then the statement follows from [3] (3.5). We may thus assume that
contains an injective module, then the statement follows from [3] (3.5). We may thus assume that 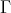 contains no injective. But then
contains no injective. But then 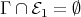 , and therefore
, and therefore 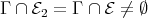 . Thus, by (2.1), there exist an indecomposable projective
. Thus, by (2.1), there exist an indecomposable projective 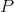 in
in 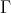 such that
such that 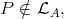 a module
a module 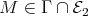 and a sectional path
and a sectional path 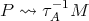 . Now let
. Now let 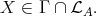 Since
Since 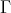 contains no injective, there exists
contains no injective, there exists 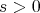 such that
such that 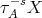 is a successor of
is a successor of 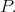 Hence
Hence 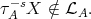 Since
Since 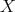 itself lies in
itself lies in 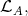 there exists
there exists  such that
such that 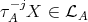 but
but 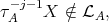 so that
so that 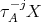 is Ext-injective in add
is Ext-injective in add 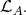 This shows that every
This shows that every 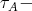 orbit of
orbit of 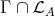 intersects
intersects 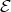 at least once.
at least once.
Furthermore, it intersects it only once: if 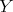 and
and 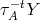 (with
(with  ) both belong to
) both belong to  then, by (2.2), all the modules on the path
then, by (2.2), all the modules on the path
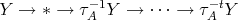
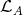 . In particular,
. In particular, 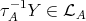 and this contradicts the Ext-injectivity of
and this contradicts the Ext-injectivity of 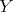 . This completes the proof of (a).
. This completes the proof of (a). (b) It follows from (a) that the number of 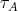 -orbits in
-orbits in 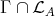 does not exceed the cardinality of
does not exceed the cardinality of  (note that by [3] (3.3), the cardinality of
(note that by [3] (3.3), the cardinality of 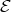 is finite and does not exceed the rank of the Grothendieck group
is finite and does not exceed the rank of the Grothendieck group 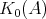 of
of 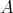 ). Since clearly, any element of
). Since clearly, any element of  belongs to exactly one
belongs to exactly one 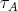 -orbit in
-orbit in 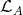 , this establishes (b).
, this establishes (b).
(c) Let 
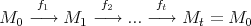
be a cycle with 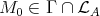 and all
and all 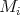 in
in 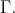 Clearly, all
Clearly, all 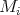 belong to
belong to 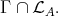 By (2.2) and (2.3), none of the
By (2.2) and (2.3), none of the 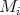 belongs to
belongs to 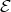 and none of the
and none of the  factors through an injective module. Indeed, if
factors through an injective module. Indeed, if  factors through the injective
factors through the injective 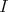 , then some indecomposable summand of
, then some indecomposable summand of 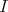 would belong to
would belong to 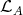 and thus
and thus 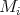 would lie in
would lie in 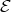 , contradicting (2.3). Then the cycle
, contradicting (2.3). Then the cycle  induces a cycle
induces a cycle 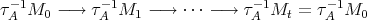 , and every module in this cycle belongs to
, and every module in this cycle belongs to 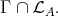 We can iterate this procedure and deduce that, for any
We can iterate this procedure and deduce that, for any 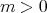 , the module
, the module 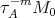 lies on a cycle in
lies on a cycle in 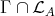 . However, as shown in (a), there exists
. However, as shown in (a), there exists 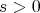 such that
such that 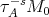 does not belong to
does not belong to 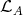 , and this contradiction proves (c).
, and this contradiction proves (c).
Now assume that the component 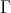 contains no Ext-injective, that is,
contains no Ext-injective, that is,  If
If 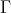 contains both a module in
contains both a module in 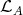 and a module which is not in
and a module which is not in 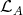 , then there exists an irreducible morphism
, then there exists an irreducible morphism  with
with 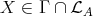 and
and 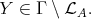 Since
Since 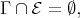 then
then 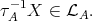 But this is a contradiction, because
But this is a contradiction, because 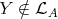 and Hom
and Hom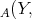
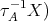
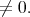 This shows that either
This shows that either 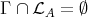 or
or 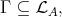 as required.
as required. 
We observe that part (c) of the theorem was already proven in [3] (1.5) under the additional hypothesis that 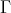 contains an injective module.
contains an injective module.
2.5. COROLLARY [3] (1.6). Let 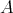 be a representation-finite artin algebra. Then
be a representation-finite artin algebra. Then 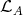 is directed.
is directed. 
2.6. We have a good description of the Auslander-Reiten components which completely lie in 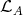 . We need to recall a definition. The endomorphism algebra
. We need to recall a definition. The endomorphism algebra 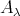 of the direct sum of all the projective modules lying in
of the direct sum of all the projective modules lying in 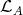 is called the left support of
is called the left support of 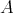 , see [3, 24]. Clearly,
, see [3, 24]. Clearly, 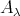 is (isomorphic to) a full convex subcategory of
is (isomorphic to) a full convex subcategory of 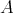 , closed under successors, and any
, closed under successors, and any 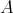 -module lying in
-module lying in 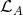 has a natural
has a natural 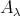 -module structure. It is shown in [3] (2.3), [24] (3.1) that
-module structure. It is shown in [3] (2.3), [24] (3.1) that 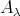 is a product of connected quasi-tilted algebras, and that
is a product of connected quasi-tilted algebras, and that 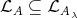 . The following corollary generalises [3] (5.5).
. The following corollary generalises [3] (5.5).
COROLLARY. Let 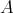 be a representation-infinite not hereditary artin algebra, and
be a representation-infinite not hereditary artin algebra, and 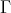 be a component of
be a component of 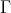 (mod
(mod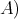 lying entirely in
lying entirely in  . Then
. Then 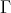 is one of the following: a postprojective component, a regular component (directed, stable tube or of type
is one of the following: a postprojective component, a regular component (directed, stable tube or of type 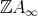 ), a semiregular tube without injectives, or a ray extension of
), a semiregular tube without injectives, or a ray extension of 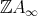 .
.
Proof. Indeed, the component 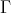 lies entirely in mod
lies entirely in mod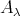 and thus is a component of
and thus is a component of 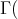 mod
mod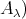 . Since
. Since 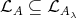 , then
, then 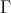 is a component of
is a component of 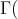 mod
mod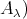 lying in the left part
lying in the left part 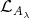 . The statement then follows from the well-known description of the Auslander-Reiten components of quasi-tilted algebras, as in [13, 18].
. The statement then follows from the well-known description of the Auslander-Reiten components of quasi-tilted algebras, as in [13, 18]. 
3. EXT-INJECTIVES AS SECTIONS IN 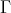 (mod
(mod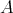 ).
).
3.1. We recall the following notion from [20, 23]. Let 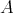 be an artin algebra and
be an artin algebra and 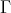 be a component of
be a component of 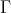 (mod
(mod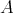 ). A full connected subquiver
). A full connected subquiver  of
of 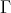 is called a section if it satisfies the following conditions:
is called a section if it satisfies the following conditions:
(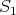 )
)  contains no oriented cycle.
contains no oriented cycle.
(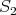 )
)  intersects each
intersects each 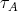 -orbit of
-orbit of 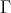 exactly once.
exactly once.
(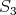 )
)  is convex in
is convex in 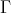 .
.
(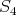 ) If
) If  is an arrow in
is an arrow in 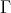 with
with 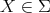 , then
, then 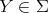 or
or 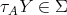 .
.
(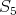 ) If
) If  is an arrow in
is an arrow in 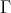 with
with 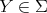 , then
, then 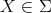 or
or 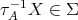 .
.
As we show next, the intersection of 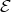 with a component of
with a component of 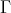 (mod
(mod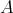 ) satisfies several of these conditions (but generally not all).
) satisfies several of these conditions (but generally not all).
PROPOSITION. Assume 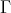 is a component of
is a component of 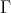 (mod
(mod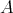 ) which intersects
) which intersects 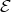 . Then
. Then  satisfies (
satisfies (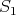 ), (
), (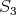 ), (
), (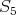 ) above, and the following conditions
) above, and the following conditions
( )
)  intersects each
intersects each 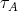 -orbit of
-orbit of 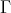 at most once.
at most once.
(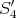 ) If
) If 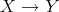 is an arrow in
is an arrow in 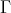 with
with 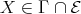 and
and 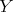 non-projective, then
non-projective, then 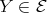 or
or 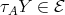 .
.
Proof. (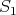 ) follows from Theorem (A) (c).
) follows from Theorem (A) (c).
( ) follows from Theorem (A) (a).
) follows from Theorem (A) (a).
(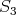 ) follows from (2.2).
) follows from (2.2).
(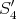 ) If
) If 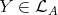 , then
, then 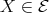 and (2.2) imply
and (2.2) imply 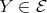 . Otherwise, since
. Otherwise, since 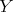 is non-projective, there exists an arrow
is non-projective, there exists an arrow 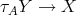 . Since
. Since 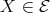 , then
, then 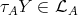 . Since
. Since 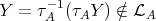 , we get
, we get 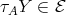 .
.
(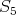 ) If
) If 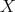 is injective then, since it lies in
is injective then, since it lies in 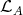 (because it precedes
(because it precedes 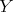 ), it belongs to
), it belongs to 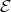 . So assume it is not and consider the arrow
. So assume it is not and consider the arrow 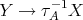 . If
. If 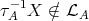 then, again,
then, again, 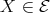 while, if
while, if 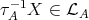 , then
, then 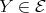 and (2.2) imply
and (2.2) imply 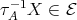 .
. 
3.2. EXAMPLE. Let 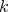 be a field and
be a field and 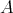 be the radical square zero
be the radical square zero 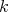 -algebra given by the quiver
-algebra given by the quiver
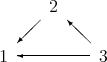
Here, 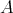 is representation finite and
is representation finite and 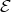 consists of the two indecomposable projectives
consists of the two indecomposable projectives 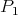 and
and 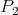 corresponding to the points
corresponding to the points  and
and 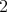 , respectively. Clearly,
, respectively. Clearly, 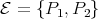 is not a section in
is not a section in 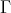 (mod
(mod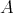 ) : indeed, there is an arrow
) : indeed, there is an arrow 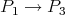 with
with 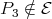 and, moreover,
and, moreover, 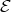 does not intersect each
does not intersect each 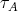 -orbit of
-orbit of 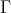 (mod
(mod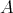 ).
).
3.3. We are now in a position to prove our second main theorem.
THEOREM (B). Let 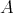 be an artin algebra and
be an artin algebra and 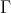 be a component of
be a component of 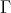 (mod
(mod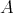 ) such that all projectives in
) such that all projectives in 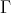 belong to
belong to 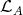 . If
. If 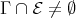 , then:
, then:
(a)  is a section in
is a section in 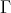 .
.
(b) 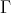 is generalised standard.
is generalised standard.
(c) 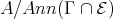 is a tilted algebra having
is a tilted algebra having 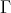 as a connecting component and
as a connecting component and  as a complete slice.
as a complete slice.
Proof.
(a) We start by observing that, if 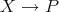 is an arrow in
is an arrow in 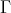 , with
, with 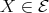 and
and 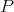 projective then, by hypothesis,
projective then, by hypothesis, 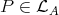 . Thus, (2.2) implies
. Thus, (2.2) implies 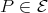 . This shows that (
. This shows that (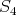 ) is satisfied. In view of the lemma, it suffices to show that
) is satisfied. In view of the lemma, it suffices to show that  cuts each
cuts each 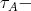 orbit of
orbit of 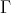 .
.
We claim that if 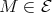 and
and 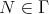 lie in two neighbouring orbits, then
lie in two neighbouring orbits, then 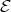 intersects the
intersects the 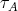 -orbit of
-orbit of 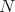 . This claim and induction imply the statement. We assume that
. This claim and induction imply the statement. We assume that 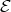 does not intersect the orbit of
does not intersect the orbit of 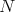 and try to reach a contradiction. There exist
and try to reach a contradiction. There exist 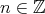 and an arrow
and an arrow 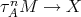 or
or 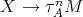 , with
, with 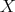 in the
in the 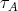 -orbit of
-orbit of 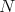 , where we may suppose, without loss of generality, that
, where we may suppose, without loss of generality, that  is minimal.
is minimal.
Suppose first that 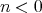 . If there exists an arrow
. If there exists an arrow 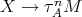 then there exists an arrow
then there exists an arrow 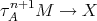 , a contradiction to the minimality of
, a contradiction to the minimality of  . If, on the other hand, there exists an arrow
. If, on the other hand, there exists an arrow 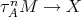 , then there is a path in
, then there is a path in 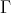 of the form
of the form 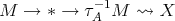 . Since
. Since 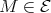 then
then 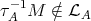 . Hence
. Hence 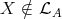 . In particular,
. In particular, 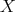 is not projective, so there exists an arrow
is not projective, so there exists an arrow 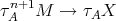 , contrary to the minimality of
, contrary to the minimality of  .
.
Suppose now that  . If there exists an arrow
. If there exists an arrow 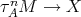 , then there exists an arrow
, then there exists an arrow 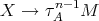 , a contradiction to the minimality of
, a contradiction to the minimality of  . If, on the other hand, there exists an arrow
. If, on the other hand, there exists an arrow 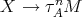 , then there is a path in
, then there is a path in 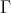 of the form
of the form 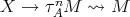 . Hence
. Hence 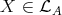 . In particular,
. In particular, 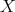 is not injective (otherwise,
is not injective (otherwise, 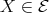 , a contradiction). Hence there exists an arrow
, a contradiction). Hence there exists an arrow 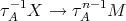 , contrary to the minimality of
, contrary to the minimality of  .
.
We have thus shown that necessarily  , that is, there is an arrow
, that is, there is an arrow  or
or  . If
. If  then, by (
then, by (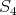 ),
), 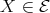 or
or 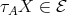 , in any case a contradiction. If
, in any case a contradiction. If  , then (3.1) yields
, then (3.1) yields 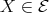 or
or 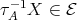 , again a contradiction in any case. This completes the proof of (a).
, again a contradiction in any case. This completes the proof of (a).
(b) By [23], Theorem 2, it suffices to show that for any 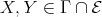 , we have Hom
, we have Hom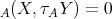 . But
. But 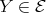 implies pd
implies pd . Therefore the Ext-injectivity of
. Therefore the Ext-injectivity of 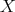 in add
in add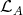 implies that
implies that
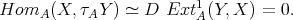
(c) This follows directly from [20] (2.2). 
3.4. EXAMPLE. Let 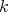 be a field and
be a field and 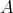 be the radical square zero algebra given by the quiver
be the radical square zero algebra given by the quiver
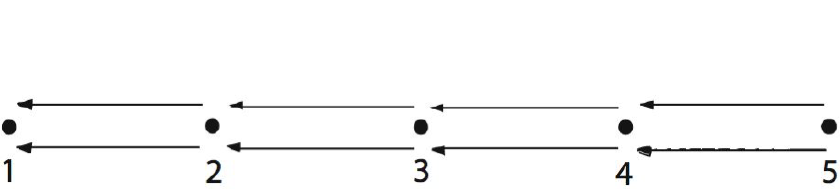
Let 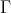 be the component containing the injective
be the component containing the injective 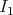 corresponding to the point
corresponding to the point  . Clearly,
. Clearly, 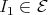 , so that
, so that 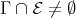 . On the other hand, the only projective lying in
. On the other hand, the only projective lying in 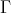 is
is 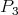 , and it belongs to
, and it belongs to 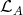 . Thus, the hypotheses of the theorem apply here. Note that
. Thus, the hypotheses of the theorem apply here. Note that 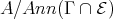 is equal to the left support
is equal to the left support 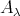 of
of 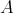 , that is, the full convex subcategory with objects
, that is, the full convex subcategory with objects 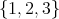 .
.
4. EXT-INJECTIVES AND THE LEFT SUPPORT
4.1. In this section we study the intersection of 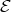 with the components of the Auslander-Reiten quiver of the left support
with the components of the Auslander-Reiten quiver of the left support 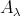 of the artin algebra
of the artin algebra 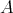 .
.
We observe first that if 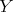 is an
is an 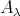 -module and
-module and 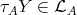 then
then 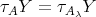 . In particular,
. In particular, 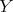 is not projective in mod
is not projective in mod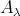 . Indeed, since mod
. Indeed, since mod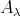 is closed under extensions in mod
is closed under extensions in mod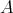 , then the inclusion
, then the inclusion 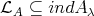 implies that the almost split sequence in mod
implies that the almost split sequence in mod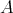 ending at
ending at 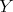 is entirely contained in mod
is entirely contained in mod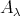 (See also [7], p. 187). Similarly, if
(See also [7], p. 187). Similarly, if 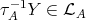 , then
, then 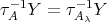 , and
, and 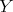 is not an injective
is not an injective 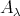 -module.
-module.
LEMMA. If an indecomposable injective 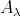 -module
-module 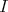 is a predecessor of
is a predecessor of 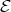 , then
, then 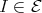 .
.
Proof. This is clear if 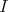 is an indecomposable injective
is an indecomposable injective 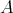 -module. So assume it is not. Since
-module. So assume it is not. Since 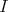 precedes
precedes 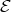 , then
, then 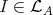 . By the above observation we obtain that
. By the above observation we obtain that 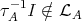 , because
, because 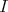 is
is 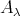 -injective. This proves that
-injective. This proves that 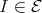 , as desired.
, as desired. 
4.2. The following is an easy consequence of (3.1) and the results in [3].
LEMMA. Let 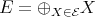 . Then
. Then 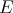 is a convex partial tilting
is a convex partial tilting 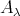 -module . In particular,
-module . In particular, 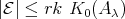 .
.
Proof. Indeed, since 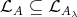 (see [3], (2.1)),
(see [3], (2.1)),  implies pd
implies pd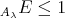 . Since Ext
. Since Ext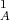
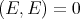 and
and 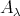 is a full convex subcategory of
is a full convex subcategory of 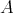 , we also have Ext
, we also have Ext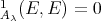 . Finally, the convexity of
. Finally, the convexity of 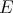 in ind
in ind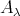 follows from its convexity in ind
follows from its convexity in ind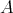 (see (2.2)).
(see (2.2)). 
4.3. THEOREM C. Let 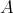 be an artin algebra and
be an artin algebra and 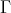 be a component of the Auslander-Reiten quiver of the left support
be a component of the Auslander-Reiten quiver of the left support 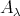 of
of 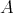 . If
. If 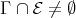 , then:
, then:
(a)  is a section in
is a section in 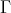 .
.
(b) 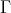 is directed, and generalised standard.
is directed, and generalised standard.
(c) 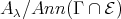 is a tilted algebra having
is a tilted algebra having 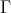 as a connecting component and
as a connecting component and  as a complete slice.
as a complete slice.
Proof. (a) In order to show that  is a section in
is a section in 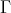 , we just have to check the conditions of the definition in (3.1). Clearly, (
, we just have to check the conditions of the definition in (3.1). Clearly, (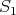 ) follows from (2.3) and the observation that any cycle in ind
) follows from (2.3) and the observation that any cycle in ind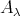 induces one in ind
induces one in ind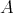 . Also, (
. Also, (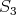 ) follows from (4.2). We start by proving (
) follows from (4.2). We start by proving (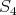 ) and (
) and (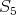 ).
).
(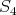 ) Assume
) Assume 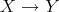 is an arrow in
is an arrow in 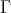 , with
, with 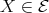 . If
. If 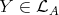 , then (2.2) implies
, then (2.2) implies 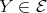 . Assume
. Assume 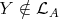 . Then, in particular,
. Then, in particular, 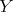 is not a projective
is not a projective 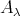 -module. Since
-module. Since 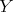 is an
is an 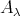 -module, it is not a projective
-module, it is not a projective 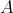 -module either, so there is an irreducible morphism
-module either, so there is an irreducible morphism 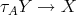 in mod
in mod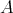 . Then
. Then 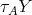 precedes
precedes 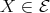 and therefore lies in
and therefore lies in 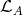 . Thus, as we observed in (4.1),
. Thus, as we observed in (4.1),  . Since
. Since 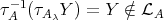 , we conclude that
, we conclude that 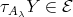 , as required.
, as required.
(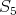 ) Assume
) Assume 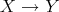 is an arrow in
is an arrow in 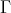 , with
, with 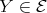 . If
. If 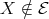 , then
, then 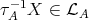 and, again by the observation in 4.1, we know that
and, again by the observation in 4.1, we know that 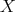 is not an injective
is not an injective 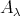 -module. Hence
-module. Hence 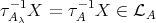 . Since there is an arrow
. Since there is an arrow 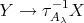 , we conclude that
, we conclude that 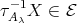 , as required.
, as required.
There remains to prove (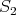 ), that is, that
), that is, that 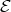 intersects each orbit of
intersects each orbit of 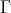 exactly once. We use the same technique as in the proof of Theorem (B). Clearly, the situation is different and so the arguments vary slightly.
exactly once. We use the same technique as in the proof of Theorem (B). Clearly, the situation is different and so the arguments vary slightly.
We start by proving that 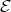 intersects each orbit of
intersects each orbit of 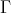 at least once. We claim that if
at least once. We claim that if 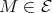 and
and 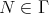 lie in two neighbouring orbits, then
lie in two neighbouring orbits, then 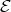 intersects the
intersects the 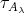 -orbit of
-orbit of 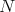 . This claim and induction imply the statement. We assume that
. This claim and induction imply the statement. We assume that 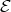 does not intersect the orbit of
does not intersect the orbit of 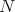 and try to reach a contradiction. There exist
and try to reach a contradiction. There exist 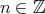 and an arrow
and an arrow 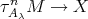 or
or 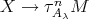 , with
, with 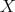 in the
in the 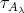 -orbit of
-orbit of 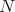 , where we may suppose, without loss of generality, that
, where we may suppose, without loss of generality, that  is minimal.
is minimal.
Suppose first that 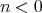 . If there exists an arrow
. If there exists an arrow 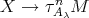 then there exists an arrow
then there exists an arrow 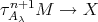 , a contradiction to the minimality of
, a contradiction to the minimality of  . If, on the other hand, there exists an arrow
. If, on the other hand, there exists an arrow 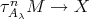 , then there is a path in
, then there is a path in  of the form
of the form 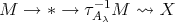 . Now,
. Now, 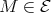 implies
implies 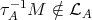 . By [7] p. 186, there exists an epimorphism
. By [7] p. 186, there exists an epimorphism  . Hence
. Hence 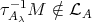 and so
and so 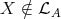 . In particular,
. In particular, 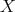 is not a projective
is not a projective 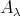 -module, so there exists an arrow
-module, so there exists an arrow 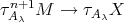 , contrary to the minimality of
, contrary to the minimality of  .
.
Suppose now that  . If there exists an arrow
. If there exists an arrow 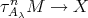 , then there exists an arrow
, then there exists an arrow 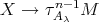 , a contradiction to the minimality of
, a contradiction to the minimality of  . If, on the other hand, there exists an arrow
. If, on the other hand, there exists an arrow 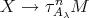 , then there is a path in
, then there is a path in 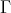 of the form
of the form 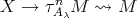 , hence
, hence 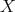 is a predecessor of
is a predecessor of 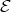 . Since
. Since 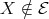 , by hypothesis, then we know by (4.1) that
, by hypothesis, then we know by (4.1) that  is not injective in mod
is not injective in mod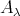 . Hence there exists an arrow
. Hence there exists an arrow 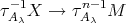 , contrary to the minimality of
, contrary to the minimality of  .
.
This shows that necessarily  , that is, there is an arrow
, that is, there is an arrow  or
or  . If
. If  then (
then (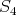 ) yields
) yields 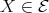 or
or 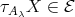 , in any case a contradiction. If
, in any case a contradiction. If  , then (
, then (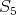 ) yields
) yields 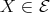 or
or 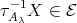 , again a contradiction in any case.
, again a contradiction in any case.
We proved that 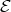 intersects each
intersects each 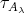 -orbit of
-orbit of 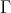 . Suppose now that
. Suppose now that 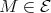 and
and 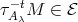 with
with  . Then the epimorphism
. Then the epimorphism  yields a path
yields a path 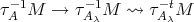 , so that
, so that 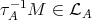 . This is a contradiction because
. This is a contradiction because 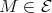 . Thus (a) is proven.
. Thus (a) is proven.
(b) Since, by [13], directed components of quasi-tilted algebras are postprojective, preinjective or connecting, thus always generalised standard (see [20, 23]), it suffices to show that 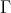 is directed. If this is not the case then, by [18] (4.3),
is directed. If this is not the case then, by [18] (4.3), 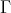 is a stable tube, of type
is a stable tube, of type 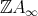 or obtained from one of these by finitely many ray or coray insertions.
or obtained from one of these by finitely many ray or coray insertions.
We first notice that by (2.3), any 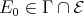 is directed in ind
is directed in ind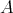 , hence in ind
, hence in ind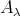 . In particular,
. In particular, 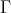 is neither a stable tube, nor of type
is neither a stable tube, nor of type 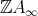 . Therefore
. Therefore 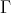 is obtained from one of these by ray or coray insertions.
is obtained from one of these by ray or coray insertions.
Assume first that 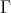 is an inserted tube or component of type
is an inserted tube or component of type 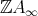 , and let
, and let 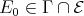 . We claim that
. We claim that 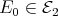 . Indeed, if this is not the case, then there exists an injective
. Indeed, if this is not the case, then there exists an injective 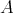 -module
-module 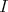 such that Hom
such that Hom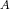
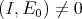 , by (2.1). However,
, by (2.1). However, 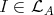 implies that
implies that 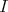 is an
is an 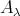 -module, so that
-module, so that 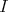 is an injective
is an injective 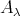 -module. But this is impossible because no injective
-module. But this is impossible because no injective 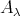 -module precedes an inserted tube or component of type
-module precedes an inserted tube or component of type 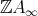 . This establishes our claim. Thus, there exists an indecomposable projective module
. This establishes our claim. Thus, there exists an indecomposable projective module 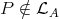 such that Hom
such that Hom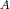
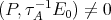 , by (2.1). On the other hand,
, by (2.1). On the other hand, 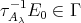 , therefore there exist a non-directed projective
, therefore there exist a non-directed projective 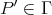 and a path
and a path 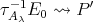 in
in 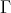 . This is clear if
. This is clear if 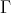 is an inserted tube, and follows from [10, 17] if
is an inserted tube, and follows from [10, 17] if 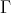 is an inserted component of type
is an inserted component of type 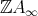 . Hence there exists a path
. Hence there exists a path  in ind
in ind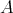 . Since
. Since 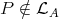 , then
, then 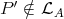 . However,
. However, 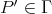 , hence
, hence 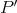 is a projective
is a projective 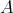 -module lying in
-module lying in 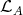 , a contradiction.
, a contradiction.
Assume next that 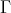 is a co-inserted tube or component of type
is a co-inserted tube or component of type 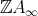 , and let
, and let 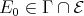 . Then, among the predecessors of
. Then, among the predecessors of  lies a cycle
lies a cycle 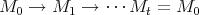 , with all
, with all 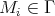 . Since all
. Since all 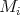 precede
precede  and, by hypothesis,
and, by hypothesis, 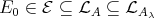 , then this cycle lies in
, then this cycle lies in 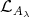 . This contradicts Theorem (A) (c) (also [3] (1.5) (b)).
. This contradicts Theorem (A) (c) (also [3] (1.5) (b)).
(c) This follows directly from [20] (2.2). 
4.4. EXAMPLE. It is important to underline that, while the components of 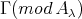 which cut
which cut 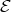 are directed, and even generalised standard, the same does not hold for the components of
are directed, and even generalised standard, the same does not hold for the components of 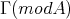 . Indeed, let
. Indeed, let 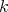 be a field and
be a field and 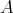 be given by the quiver
be given by the quiver
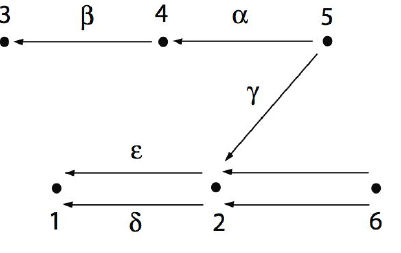
bound by 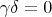 ,
,  and
and 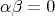 . Letting, as usual,
. Letting, as usual, 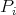 and
and 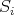 denote respectively the indecomposable projective and the simple modules corresponding to the point
denote respectively the indecomposable projective and the simple modules corresponding to the point 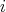 , we have an almost split sequence
, we have an almost split sequence  .
.
Moreover, rad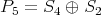 , where
, where 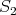 lies in a regular component of type
lies in a regular component of type 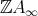 in the Auslander-Reiten quiver of the wild hereditary algebra
in the Auslander-Reiten quiver of the wild hereditary algebra 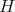 which is the full subcategory of
which is the full subcategory of 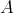 with objects the points
with objects the points  ,
, 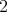 and
and 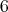 . Now, the projective
. Now, the projective 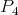 is also injective and lies in
is also injective and lies in 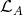 (because its unique proper predecessor is
(because its unique proper predecessor is 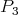 ), hence in
), hence in 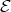 . Therefore, the component of
. Therefore, the component of 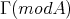 containing it is neither directed, nor generalised standard.
containing it is neither directed, nor generalised standard.
4.5. LEMMA. Let 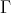 be a component of
be a component of  .
.
(a) If  is a non-connecting postprojective component, then
is a non-connecting postprojective component, then 
(b) If  is a non-connecting preinjective component, then
is a non-connecting preinjective component, then 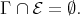
(c) If 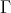 intersects
intersects 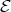 , then
, then 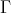 is connecting.
is connecting.
(d) If a connected component 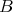 of
of 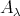 is not tilted, then
is not tilted, then 
Proof. (a) Assume that 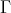 is a non-connecting postprojective component of
is a non-connecting postprojective component of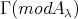 such that
such that 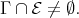 Let
Let 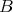 be the (unique) connected component of
be the (unique) connected component of 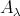 such that
such that 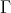 consists of
consists of 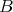 -modules. We claim that
-modules. We claim that 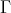 does not contain every indecomposable projective
does not contain every indecomposable projective 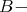 module. Indeed, if this is not the case, then the number of
module. Indeed, if this is not the case, then the number of 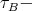 orbits in
orbits in 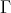 coincides with rk
coincides with rk 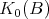 . By Theorem (C) (a),
. By Theorem (C) (a), 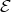 intersects each
intersects each 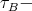 orbit of
orbit of 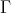 exactly once. Hence
exactly once. Hence  has rk
has rk 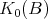 elements. From this and (4.2) we deduce that
elements. From this and (4.2) we deduce that 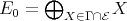 is a convex tilting
is a convex tilting 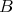 -module. By [6], (2.1),
-module. By [6], (2.1),  is a complete slice in mod
is a complete slice in mod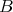 . But this is a contradiction, because
. But this is a contradiction, because 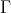 was assumed to be non-connecting. This establishes our claim.
was assumed to be non-connecting. This establishes our claim.
Now, let 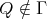 be an indecomposable projective
be an indecomposable projective 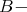 module. Since
module. Since 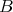 is a connected algebra, there exists a walk of projective
is a connected algebra, there exists a walk of projective 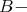 modules
modules  with
with 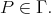 Thus there exists
Thus there exists 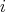 such that
such that 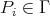 and
and 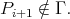 Since
Since 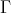 does not receive morphisms from other components of
does not receive morphisms from other components of 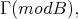 then Hom
then Hom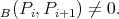 By [21] (2.1) there exists, for each
By [21] (2.1) there exists, for each 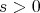 , a path
, a path

with  irreducible. Since
irreducible. Since  is as large as we want, and
is as large as we want, and 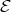 intersects each
intersects each 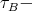 orbit of
orbit of 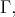 we may choose
we may choose  so that
so that 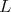 is a proper successor of
is a proper successor of  On the other hand,
On the other hand, 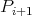 is a projective
is a projective 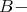 module, hence a projective
module, hence a projective 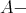 module lying in
module lying in 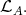 Thus
Thus 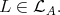 Since
Since 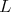 is a successor of
is a successor of 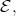 by (2.2),
by (2.2), 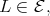 a contradiction which proves (a).
a contradiction which proves (a).
(b) Assume that 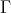 is a non-connecting preinjective component of
is a non-connecting preinjective component of 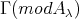 such that
such that 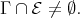 Using the same reasoning as in (a), there exist
Using the same reasoning as in (a), there exist 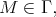 which is a proper predecessor of
which is a proper predecessor of  and an indecomposable injective
and an indecomposable injective 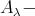 module
module 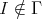 such that Hom
such that Hom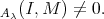 Since
Since 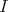 precedes
precedes 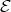 then, by (4.1),
then, by (4.1), 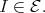 The convexity of
The convexity of 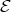 yields the contradiction
yields the contradiction 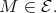 This establishes (b).
This establishes (b).
(c) It is shown in [3, 24] that every connected component of 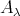 is quasi-tilted. By Theorem (C),
is quasi-tilted. By Theorem (C), 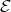 intersects only directed components of
intersects only directed components of 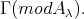 Furthermore, directed components of quasi-tilted algebras are necessarily postprojective, preinjective or connecting. Now the result follows from (a) and (b).
Furthermore, directed components of quasi-tilted algebras are necessarily postprojective, preinjective or connecting. Now the result follows from (a) and (b).
(d) Is a consequence of (c). 
4.6. PROPOSITION Let 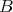 be a connected component of the left support
be a connected component of the left support 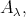 such that
such that  Then
Then 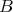 is a tilted algebra and
is a tilted algebra and 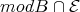 is a complete slice in
is a complete slice in 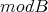 .
.
Proof. Let 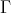 be a component of
be a component of 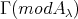 such that
such that 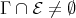 . By (c) of the previous lemma, we know that
. By (c) of the previous lemma, we know that 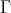 is a connecting component. Since, on the other hand,
is a connecting component. Since, on the other hand, 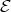 intersects each
intersects each 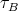 -orbit of
-orbit of 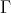 exactly once (by Theorem (C) (a)), we have
exactly once (by Theorem (C) (a)), we have 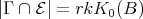 . But by (4.2),
. But by (4.2),  . Hence
. Hence 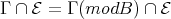 and the direct sum of the modules in
and the direct sum of the modules in 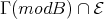 is a convex tilting
is a convex tilting 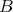 -module. The result then follows from [6](2.1).
-module. The result then follows from [6](2.1). 
Observe that if 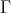 is a component of
is a component of 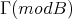 such that
such that 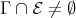 , then it follows from the proof of (4.6) that
, then it follows from the proof of (4.6) that  is a complete slice in mod
is a complete slice in mod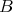 . Therefore, by [23],
. Therefore, by [23], 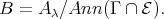
4.7. EXAMPLE. It is possible to have 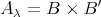 , and
, and 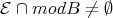 , while
, while 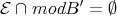 . Indeed, let
. Indeed, let 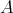 be given by the quiver
be given by the quiver

bound by 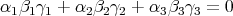 ,
, 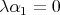 ,
, 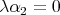 ,,
,, 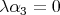 ,
, 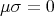 ,
, 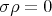 . Let
. Let 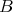 denote the (tilted) full subcategory of
denote the (tilted) full subcategory of 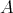 having as objects
having as objects 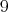 ,
, 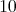 and
and 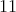 , and
, and 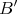 denote the (tubular) full subcategory of
denote the (tubular) full subcategory of 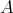 having as objects
having as objects  ,
, 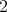 ,
, 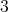 ,
, 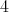 ,
,  ,
, 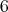 ,
, 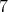 ,
,  . Then
. Then 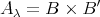 ,
, 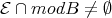 (it consists of the indecomposable modules
(it consists of the indecomposable modules 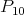 ,
, 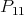 and
and 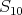 ) while
) while 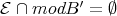 (because
(because 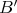 is a tubular algebra).
is a tubular algebra).
5.1. An artin algebra 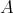 is left supported if add
is left supported if add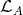 is contravariantly finite in mod
is contravariantly finite in mod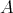 , in the sense of [8]. It is shown in [3] (5.1) that an artin algebra
, in the sense of [8]. It is shown in [3] (5.1) that an artin algebra 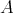 is left supported if and only if each connected component of
is left supported if and only if each connected component of 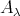 is tilted and the restriction of
is tilted and the restriction of 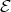 to this component is a complete slice. Several other characterisations of left supported algebras are given in [1, 3]. In particular, it is shown in [1] that
to this component is a complete slice. Several other characterisations of left supported algebras are given in [1, 3]. In particular, it is shown in [1] that 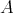 is left supported if and only if
is left supported if and only if 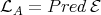 , where Pred
, where Pred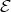 denotes the full subcategory of ind
denotes the full subcategory of ind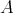 having as objects all the
having as objects all the 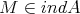 such that there exists
such that there exists 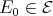 and a path
and a path 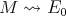 . Our objective in this section is to give another proof of this theorem, using the results above. Our proof also yields a new characterisation of left supported algebras.
. Our objective in this section is to give another proof of this theorem, using the results above. Our proof also yields a new characterisation of left supported algebras.
THEOREM. Let 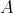 be an artin algebra. Then the following conditions are equivalent:
be an artin algebra. Then the following conditions are equivalent:
(a) 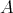 is left supported.
is left supported.
(b) 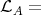 Pred
Pred 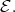
(c) Every projective 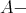 module which belongs to
module which belongs to 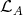 is a predecessor of
is a predecessor of 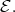
Proof. (a) implies (b). Assume that 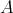 is left supported. By [3](4.2),
is left supported. By [3](4.2), 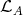 is cogenerated by the direct sum of the modules in
is cogenerated by the direct sum of the modules in 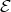 . In particular,
. In particular, 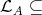 Pred
Pred 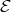 . Since the reverse inclusion is obvious, this completes the proof of (a) implies (b).
. Since the reverse inclusion is obvious, this completes the proof of (a) implies (b).
Clearly (b) implies (c). To prove that (c) implies (a) we assume that every projective 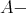 module which belongs to
module which belongs to 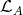 is a predecessor of
is a predecessor of 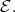 Let
Let 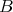 be a connected component of
be a connected component of 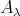 and
and 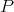 be an indecomposable projective
be an indecomposable projective 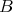 -module. Since
-module. Since 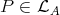 , there exist
, there exist 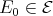 and a path
and a path 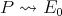 in
in 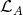 , hence in mod
, hence in mod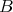 . Therefore, mod
. Therefore, mod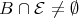 . By (4.6),
. By (4.6), 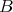 is a tilted algebra and
is a tilted algebra and 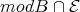 is a complete slice in
is a complete slice in 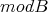 . Hence
. Hence 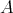 is left supported.
is left supported. 
5.2. We end this paper with a short proof of a result by D. Smith.
THEOREM.([25] (3.8)) Let 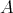 be a quasi-tilted algebra. Then
be a quasi-tilted algebra. Then 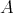 is left supported if and only if
is left supported if and only if 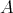 is tilted having a complete slice containing an injective module.
is tilted having a complete slice containing an injective module.
Proof. Since 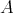 is quasi-tilted, then
is quasi-tilted, then  . Assume that
. Assume that 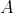 is left supported. Then
is left supported. Then 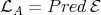 . By (5.1),
. By (5.1), 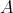 is tilted and
is tilted and 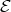 is a complete slice in
is a complete slice in 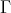 (mod
(mod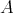 ). Furthermore, since
). Furthermore, since 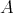 is quasi-tilted, then all projective
is quasi-tilted, then all projective 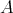 -modules lie in
-modules lie in 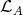 , so that
, so that  and
and 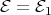 . Thus
. Thus 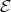 must contain an injective module.
must contain an injective module.
Conversely, if 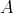 has a complete slice containing an injective, then there exists a complete slice
has a complete slice containing an injective, then there exists a complete slice  having all its sources injective. By (2.1),
having all its sources injective. By (2.1), 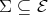 . Since
. Since 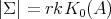 , it follows from [3] (3.3) that
, it follows from [3] (3.3) that 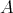 is left supported.
is left supported. 
1. I. Assem, J. A. Cappa, M. I. Platzeck and S. Trepode, Some characterisations of supported algebras, J. Pure Appl. Algebra. In Press. [ Links ]
2. I. Assem, F. U. Coelho, Two-sided gluings of tilted algebras, J. Algebra 269 (2003) 456-479. [ Links ]
3. I. Assem, F. U. Coelho, S. Trepode, The left and the right parts of a module category, J. Algebra 281 (2004) 518-534. [ Links ]
4. I. Assem, F. U. Coelho, M. Lanzilotta, D. Smith, S. Trepode, Algebras determined by their left and right parts, Proc. XV Coloquio Latinoamericano de Álgebra, Contemp. Math. 376 (2005) 13-47, Amer. Math. Soc. [ Links ]
5. I. Assem, M. Lanzilotta, M. J. Redondo, Laura skew group algebras, to appear. [ Links ]
6. I. Assem, M. I. Platzeck, S. Trepode, On the representation dimension of tilted and laura algebras, J. of Algebra. 283 (2005) 161-189. [ Links ]
7. M. Auslander, I. Reiten, S. O. Smalø, Representation Theory of Artin Algebras, Cambridge Studies in Advanced Mathematics 36, Cambridge Univ. Press, (1995). [ Links ]
8. M. Auslander, S. O. Smalø, Preprojective modules over artin algebras, J. Algebra 66 (1980) 61-122. [ Links ]
9. M. Auslander, S. O. Smalø, Almost split sequences in subcategories, J. Algebra 69 (1981) 426-454. [ Links ]
10. D. Baer, Wild hereditary artin algebras and linear methods, Manuscripta Math., 55 (1986) 69-82. [ Links ]
11. R. Bautista, S. O. Smalø, Non-existent cycles, Comm. Algebra, 11 (16) (1983) 1755-1767. [ Links ]
12. K. Bongartz, On a result of Bautista and Smalø on cycles, Comm. Algebra, 11 (18) (1983) 2123-2124. [ Links ]
13. F. U. Coelho, Directing components for quasi-tilted algebras, Coll. Math. 82 (1999), 271-275. [ Links ]
14. D. Happel, A characterization of hereditary categories with tilting object, Invent. Math. 144 (2001) 381-398. [ Links ]
15. D. Happel, I. Reiten, S. O. Smalø, Tilting in Abelian Categories and Quasitilted Algebras, Memoirs AMS 575 (1996). [ Links ]
16. O. Kerner, Tilting wild algebras, J. London Math. Soc. (2) 39 (1989), 29-47. [ Links ]
17. O. Kerner, Representation of wild quivers, Proc. Workshop UNAM, México 1994 CMS Conf. Proc. 19 (1996), 65-108. [ Links ]
18. H. Lenzing, A. Skowronski, Quasi-tilted algebras of canonical type, Coll. Math. 71 (2) (1996), 161-181. [ Links ]
19. S. Liu, The connected components of the Auslander-Reiten quiver of a tilted algebra, J. Algebra 161 (2) (1993) 505-523. [ Links ]
20. S. Liu, Tilted algebras and generalized standard Auslander-Reiten components, Arch. Math. 61 (1993) 12-19. [ Links ]
21. C. M. Ringel, Report on the Brauer-Thrall conjectures, Proc. ICRA II (Ottawa, 1979), Lecture Notes in Math. 831 (1980) 104-136, Springer-Verlag. [ Links ]
22. C. M. Ringel, Tame algebras and integral quadratic forms, Lecture Notes in Math. 1099 (1984), Springer-Verlag. [ Links ]
23. A. Skowronski, Generalized standard Auslander-Reiten components without oriented cycles, Osaka J. Math. 30 (1993) 515-529. [ Links ]
24. A. Skowronski, On artin algebras with almost all indecomposable modules of projective or injective dimension at most one, Central European J. Math. 1 (2003) 108-122. [ Links ]
25. D. Smith, On generalized standard Auslander-Reiten components having only finitely many non-directing modules, J. Algebra 279 (2004) 493-513. [ Links ]
Ibrahim Assem
Département de Mathématiques,
Faculté des Sciences,
Université de Sherbrooke,
Sherbrooke, Québec,
Canada, J1K 2R1
ibrahim.assem@usherbrooke.ca
Juan Ángel Cappa
Instituto de Matemática,
Universidad Nacional del Sur,
8000 Bahía Blanca, Argentina
jacappa@yahoo.com.ar
María Inés Platzeck
Instituto de Matemática,
Universidad Nacional del Sur,
8000 Bahía Blanca, Argentina
platzeck@uns.edu.ar
Sonia Trepode
Departamento de Matemática,
Facultad de Ciencias Exactas y Naturales,
Funes 3350,
Universidad Nacional de Mar del Plata,
7600 Mar del Plata, Argentina
strepode@mdp.edu.ar
Recibido: 26 de enero de 2006
Aceptado: 7 de agosto de 2006













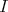 such that
such that 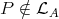 such that
such that 
