Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932On-line version ISSN 1669-9637
Rev. Unión Mat. Argent. vol.46 no.2 Bahía Blanca July/Dec. 2005
Moore-Penrose inverse and doubly commuting elements in C*-algebras
Enrico Boasso
This work is dedicated to the memory of Professor Angel R. Larotonda, Pucho for all who knew him.
This research was supported by UBACYT and CONICET
Abstract: In this work it is proved that the Moore-Penrose inverse of the product of 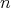 -doubly commuting regular
-doubly commuting regular 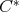 -algebra elements obeys the so-called reverse order law. Conversely, conditions regarding the reverse order law of the Moore-Penrose inverse are given in order to characterize when
-algebra elements obeys the so-called reverse order law. Conversely, conditions regarding the reverse order law of the Moore-Penrose inverse are given in order to characterize when 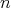 -regular elements doubly commute. Furthermore, applications of the main results of this article to normal
-regular elements doubly commute. Furthermore, applications of the main results of this article to normal 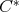 -algebra elements, to Hilbert space operators and to Calkin algebras will be considered.
-algebra elements, to Hilbert space operators and to Calkin algebras will be considered.
Key words and phrases. Generalized inverse, Moore-Penrose inverse, and doubly commuting elements in a 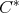 -algebra.
-algebra.
2000 Mathematics Subject Classification. 46L05, 47A
1. Introduction
Consider an unitary ring 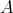 . An element
. An element 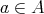 will be said regular if it has a generalized inverse in A, that is if there exists
will be said regular if it has a generalized inverse in A, that is if there exists 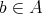 such that
such that
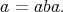
Note that if  is a regular element of
is a regular element of 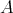 and
and 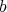 is a generalized inverse of
is a generalized inverse of  , then
, then 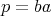 and
and  are idempotents of A, that is
are idempotents of A, that is 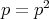 and
and 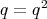 .
.
Given 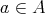 a regular element, a generalized inverse
a regular element, a generalized inverse 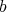 of
of  will be called normalized, if
will be called normalized, if 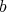 is regular and
is regular and  is a pseudo inverse of
is a pseudo inverse of 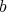 , equivalently if
, equivalently if

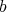 is a generalized inverse of
is a generalized inverse of  , then
, then 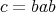 is a normalized pseudo inverse of
is a normalized pseudo inverse of  .
. Next suppose that  is a regular element and
is a regular element and 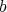 is a normalized generalized inverse of
is a normalized generalized inverse of  . In the presence of an involution
. In the presence of an involution 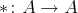 , it is possible to enquire if the idempotents
, it is possible to enquire if the idempotents 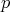 and
and 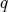 are self-adjoint, that is whether
are self-adjoint, that is whether 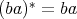 and
and 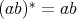 . In this case
. In this case 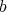 is called the Moore-Penrose inverse of
is called the Moore-Penrose inverse of  , see [16] where this concept was introduced.
, see [16] where this concept was introduced.
In [10] it was proved that each regular element  in a
in a 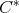 -algebra
-algebra 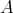 has a uniquely determined Moore-Penrose inverse. The Moore-Penrose inverse of
has a uniquely determined Moore-Penrose inverse. The Moore-Penrose inverse of 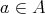 will be denote by
will be denote by 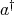 . Therefore, the Moore-Penrose inverse of a regular element
. Therefore, the Moore-Penrose inverse of a regular element 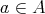 is the unique element that satisfy the following equations:
is the unique element that satisfy the following equations:
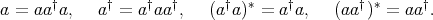
 has a Moore-Penrose inverse, then
has a Moore-Penrose inverse, then 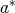 also has a Moore-Penrose inverse and
also has a Moore-Penrose inverse and

 is a regular element, then
is a regular element, then 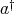 also is and
also is and
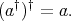
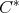 -algebras, see the works [10], [11], [14] and [16].
-algebras, see the works [10], [11], [14] and [16]. On the other hand, an 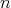 -tuple
-tuple 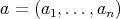 of elements in a
of elements in a 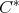 -algebra A will be called doubly commuting, if
-algebra A will be called doubly commuting, if  and
and 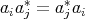 , for all
, for all 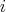 ,
, 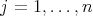 ,
, 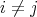 . For instance, necessary and sufficient for
. For instance, necessary and sufficient for 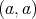 to be doubly commuting is that
to be doubly commuting is that  is a normal element in
is a normal element in 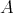 .
.
Doubly commuting operators have been studied in very different contexts, to mention only some of the most relevant works, see for example [1]-[4], [6]-[8] and [12]. In this article, doubly commuting tuples of regular 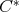 -algebra elements will be consider. The main objective of this work consists in the study of the relationship between such tuples and the Moore-Penrose inverse of the product of the elements in the tuple.
-algebra elements will be consider. The main objective of this work consists in the study of the relationship between such tuples and the Moore-Penrose inverse of the product of the elements in the tuple.
In fact, given an 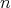 -tuple
-tuple 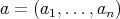 of regular elements in a
of regular elements in a 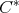 -algebra A, if the
-algebra A, if the 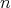 -tuple
-tuple  is doubly commuting, then
is doubly commuting, then 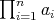 is regular and
is regular and
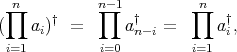
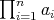 complies with the so-called reverse order law for the Moore-Penrose inverse. Moreover, if
complies with the so-called reverse order law for the Moore-Penrose inverse. Moreover, if  is such a tuple, then
is such a tuple, then 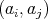 and
and 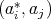 are doubly commuting pairs, where
are doubly commuting pairs, where 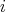 ,
, ![j ∈ [[1,n]]](/img/revistas/ruma/v46n2/2a0381x.png) ,
, 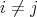 . Consequently,
. Consequently, 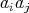 and
and 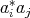 are regular and
are regular and

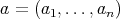 is an
is an 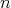 -tuple of regular elements in a
-tuple of regular elements in a 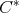 -algebra A such that the above identities are verified by
-algebra A such that the above identities are verified by 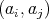 and
and 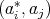 , for all
, for all 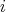 ,
, ![j ∈ [[1, n]]](/img/revistas/ruma/v46n2/2a0392x.png) ,
, 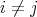 , then
, then  is a doubly commuting
is a doubly commuting 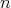 -tuple of elements in the
-tuple of elements in the 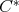 -algebra
-algebra 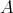 .
. It is worth noticing that this characterization consists in an extension to the objects under consideration of the sufficient conditon given by J.J. Koliha in [13; 2.13] for the product of two regular elements to be Moore-Penrose invertible.
In section 2 it will be proved the aforementioned characterization. In section three, on the other hand, some applications will be developed. In fact, three sorts of objects will be considered, namely, tuples of commuting regular normal 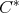 -algebra elements, tuples of doubly commuting regular Hilbert space operators, and tuples of almost doubly commuting regular Hilbert space operators (that is doubly commuting tuples of regular elements in Calkin algebras).
-algebra elements, tuples of doubly commuting regular Hilbert space operators, and tuples of almost doubly commuting regular Hilbert space operators (that is doubly commuting tuples of regular elements in Calkin algebras).
This article is dedicated to the memory of Professor Angel R. Larotonda, who unfortunately and unexpectedly died on January 2th 2005. Although it is not necessary to comment Professor Larotonda's work as mathematician, for his scientific publications consist in a set of achievements which speak for themselves, a few words about the man deserve to be said. The author knew Professor Larotonda for more than twenty years. During uncountable conversations shared with Professor Larotonda, this researcher always showed his condition of sensible, civilized and cultivated human being, three characteristics that seem to be far from being widespread in this time and in any time.
Acknowledgements. The author wishes to express his indebtedness to the organizers of this volume, especially to Professor G. Corach, for have invited the author to contribute with this homage.
2. Main Results
In this section the relationship between the Moore-Penrose inverse and doubly commuting tuples of regular 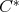 -algebra elements will be studied. In fact, the characterization described in the previous section will be proved. In first place, a property of doubly commuting tuples is discussed.
-algebra elements will be studied. In fact, the characterization described in the previous section will be proved. In first place, a property of doubly commuting tuples is discussed.
Remark 2.1. Let 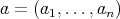 be an
be an 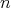 -tuple of elements of a
-tuple of elements of a 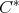 -algebra
-algebra 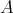 . Consider
. Consider ![π: [[1,n]] → [[1,n]]](/img/revistas/ruma/v46n2/2a03104x.png) a permutation, and define an
a permutation, and define an 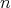 -tuple
-tuple 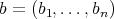 in such a way that
in such a way that 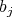 is either
is either 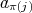 or
or 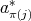 . Then, it is easy to prove that
. Then, it is easy to prove that  is doubly commuting if and only if
is doubly commuting if and only if 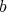 is.
is.
Furthermore, note that the following facts are equivalents:
i) 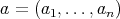 is a doubly commuting
is a doubly commuting 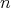 -tuple of elements of
-tuple of elements of 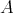 ,
,
ii) for each 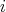 ,
, 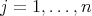 ,
, 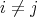 ,
, 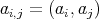 is a pair of doubly commuting elements of
is a pair of doubly commuting elements of 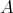 .
.
Proposition 2.2. Let 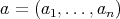 be an
be an 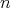 -tuple of regular elements in a
-tuple of regular elements in a 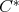 -algebra
-algebra 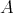 . Consider the
. Consider the 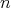 -tuple
-tuple 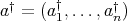 . Then,
. Then,  is doubly commuting if and only if
is doubly commuting if and only if 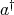 is.
is.
Proof. According to Remark 2.1, it is enough to prove that a pair of regular elements 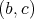 is doubly commuting if and only if
is doubly commuting if and only if 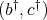 is.
is.
Suppose that 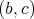 is a doubly commuting pair of regular elements of
is a doubly commuting pair of regular elements of 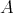 . Then, according to Theorem 5 of [10],
. Then, according to Theorem 5 of [10],
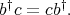
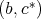 is a doubly commuting pair, it is clear that
is a doubly commuting pair, it is clear that
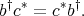
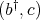 is a doubly commuting pair.
is a doubly commuting pair. However, according to Remark 2.1, 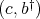 is a doubly commuting pair, and thanks to what has been proved,
is a doubly commuting pair, and thanks to what has been proved, 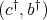 is a doubly commuting pair. Therefore, according again to Remark 2.1,
is a doubly commuting pair. Therefore, according again to Remark 2.1, 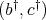 is a doubly commuting pair.
is a doubly commuting pair.
Conversely, if 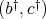 is a doubly commuting pair, since
is a doubly commuting pair, since 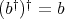 and
and 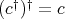 , according to the first part of the proof,
, according to the first part of the proof, 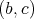 is a doubly commuting pair
is a doubly commuting pair 
Note that in [13] Theorem 5 of [10] was proved using the Drazin inverse, see [13; 2.12]. Therefore, Proposition 2.2 can also be derived using the Drazin inverse, see [13; 2.12] and [13; 2.13].
Remark 2.3. Let 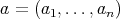 be an
be an 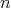 -tuple of regular elements in a
-tuple of regular elements in a 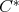 -algebra
-algebra 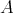 . Consider
. Consider ![π : [[1,n]] → [[1,n]]](/img/revistas/ruma/v46n2/2a03147x.png) a permutation, and define an
a permutation, and define an 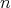 -tuple
-tuple 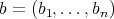 in the following way. Given
in the following way. Given 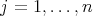 ,
, 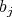 is either
is either 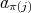 ,
, 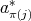 ,
, 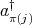 or
or 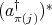 . Then, according to Remark 2.1 and to Proposition 2.2,
. Then, according to Remark 2.1 and to Proposition 2.2,  is doubly commuting if and only if
is doubly commuting if and only if 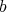 is.
is.
Furthermore, according to Remark 2.1 and to Proposition 2.2, the following facts are equivalent:
i)  is an
is an 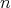 -tuple of doubly commuting regular elements of
-tuple of doubly commuting regular elements of 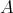 ,
,
ii) for each 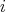 ,
, 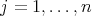 ,
, 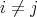 ,
, 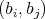 is a pair of doubly commuting regular elements of
is a pair of doubly commuting regular elements of 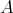 .
.
Next follows the first part of our characterization. In fact, in the following theorem it will be proved that the product of the elements in a doubly commuting tuple of regular elements satisfy the so-called reverse order law for the Moore-Penrose inverse.
Theorem 2.4. Let 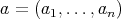 be an
be an 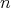 -tuple of doubly commuting regular elements of a
-tuple of doubly commuting regular elements of a 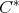 -algebra
-algebra  . Then,
. Then, 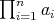 is regular and
is regular and
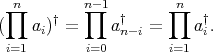
Proof. Consider 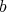 and
and  two regular elements of
two regular elements of 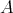 such that the pair
such that the pair 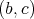 is doubly commuting. According to [13; 2.13],
is doubly commuting. According to [13; 2.13], 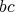 is regular and
is regular and
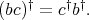
 a doubly commuting tuple of regular elements of
a doubly commuting tuple of regular elements of 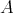 . Suppose that
. Suppose that 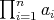 is regular and
is regular and

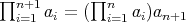 is regular and
is regular and
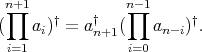
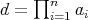 . According to Remark 2.1,
. According to Remark 2.1, 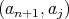 is a doubly commuting pair for
is a doubly commuting pair for 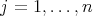 , which implies that
, which implies that 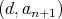 is a doubly commuting pair of regular elements. Therefore, according to the part of the theorem that has been proved,
is a doubly commuting pair of regular elements. Therefore, according to the part of the theorem that has been proved, 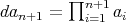 is regular, and
is regular, and
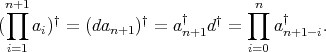
The last identity is a consequence of [13; 2.13] or Proposition 2.2. 
Remark 2.5. Let 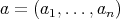 be an
be an 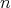 -tuple of doubly commuting regular elements in a
-tuple of doubly commuting regular elements in a 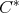 -algebra
-algebra 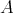 . Consider
. Consider ![π : [[1,n]] → [[1,n]]](/img/revistas/ruma/v46n2/2a03194x.png) a permutation and consider an
a permutation and consider an 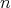 -tuple
-tuple 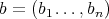 , where
, where 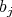 is either
is either 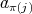 ,
, 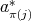 ,
, 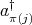 or
or 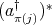 ,
, 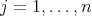 . Then,
. Then, 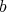 is an
is an 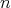 -tuple of doubly commuting regular elements of
-tuple of doubly commuting regular elements of 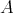 . Consequently, according to [13; 2.13] or Proposition 2.2 and to Theorem 2.4,
. Consequently, according to [13; 2.13] or Proposition 2.2 and to Theorem 2.4, 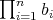 is regular and
is regular and
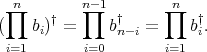
![π,σ : [[1,n]] → [[1,n]]](/img/revistas/ruma/v46n2/2a03208x.png) . Let
. Let ![τ : [[1,n]] → [[1,n]]](/img/revistas/ruma/v46n2/2a03209x.png) be the permutation
be the permutation 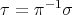 , that is
, that is  . Next associate to
. Next associate to 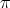 an
an 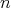 -tuple
-tuple 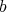 as in the previous paragraph. Then, it is possible to associate to
as in the previous paragraph. Then, it is possible to associate to  an
an 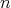 -tuple
-tuple  such that
such that 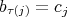 , for
, for 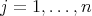 . Consequently, according to [13; 2.13] or Proposition 2.2 and to Theorem 2.4,
. Consequently, according to [13; 2.13] or Proposition 2.2 and to Theorem 2.4,
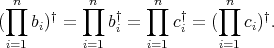
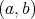 is a pair of doubly commuting regular elements of the
is a pair of doubly commuting regular elements of the 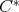 -algebra
-algebra 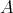 , the following identities hold.
, the following identities hold.
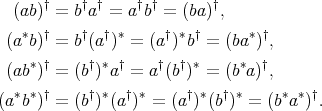
Consequently,
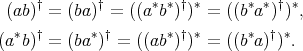
Finally, recall that according to Remark 2.1, 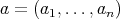 is a doubly commuting
is a doubly commuting 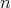 -tuple of regular elements of
-tuple of regular elements of 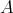 if and only if
if and only if 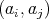 is a doubly commuting pair of regular elements of
is a doubly commuting pair of regular elements of 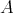 , for
, for 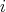 ,
, 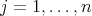 ,
, 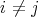 . Therefore, for each such pair the above identities hold.
. Therefore, for each such pair the above identities hold.
Next follows the converse of Theorem 2.4.
Theorem 2.6. Consider 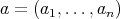 an
an 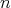 -tuple of regular elements in a
-tuple of regular elements in a 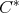 -algebra
-algebra 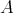 . Suppose that for all
. Suppose that for all 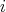 ,
, 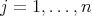 ,
, 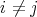 ,
, 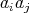 ,
, 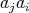 ,
, 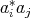 and
and 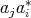 are regular and comply with the following identities:
are regular and comply with the following identities:

 is a doubly commuting
is a doubly commuting 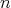 -tuple of regular elements of
-tuple of regular elements of 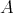 .
. Proof. According to Remark 2.1, it is enough to prove that 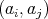 is doubly commuting for all
is doubly commuting for all 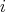 ,
, 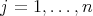 ,
, 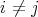 . However, since
. However, since 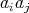 and
and 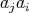 are regular and
are regular and  , it is clear that
, it is clear that  . Similarly,
. Similarly, 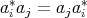 . Therefore,
. Therefore, 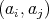 is a doubly commuting pair,
is a doubly commuting pair, 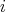 ,
, 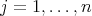 ,
, 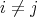 .
. 
Remark 2.7. In [13] sufficient conditions for a product to be Moore-Penrose inversible were given. Actually, thanks to the Theorem 2.6 it is now possible to state the following characterization. Let  and
and 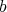 be two regular elements in a
be two regular elements in a 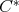 -algebra A. If
-algebra A. If 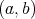 is a doubly commuting pair, then
is a doubly commuting pair, then 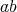 ,
, 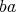 ,
, 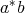 and
and 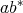 are regular and
are regular and

 and
and 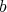 are two regular elements such that
are two regular elements such that 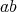 ,
, 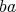 ,
, 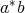 and
and 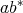 are regular and they comply with the above identities, then
are regular and they comply with the above identities, then 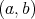 is a doubly commuting pair. Furthermore, in this case
is a doubly commuting pair. Furthermore, in this case 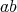 and
and 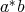 comply the reverse order law for the Moore-Penrose inverse.
comply the reverse order law for the Moore-Penrose inverse. 3. Some applications
In this section several applications of the main results of this work will be considered. In first place, commuting tuples of normal elements in a 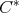 -algebra will be studied.
-algebra will be studied.
Remark 3.1. Let 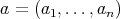 be a doubly commuting
be a doubly commuting 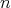 -tuple of elements in a
-tuple of elements in a 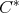 -algebra
-algebra 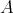 . Let
. Let 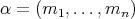 be an
be an 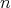 -tuple of nonnegative entire numbers and define the
-tuple of nonnegative entire numbers and define the 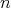 -tuple
-tuple
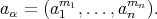
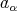 is a doubly commuting
is a doubly commuting 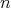 -tuple of elements of
-tuple of elements of 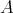 .
. On the other hand, if 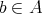 is a regular normal element of
is a regular normal element of 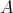 , then
, then 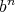 is regular and
is regular and  , for all
, for all 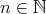 .
.
In fact, since 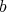 is regular,
is regular, 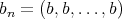 (
(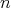 -times) is a doubly commuting
-times) is a doubly commuting 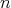 -tuple of regular elements of
-tuple of regular elements of 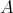 . Therefore, according to Theorem 2.4,
. Therefore, according to Theorem 2.4, 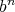 is regular and
is regular and  .
.
In the following theorem the characterization of the previous section will be applied to commuting tuples of regular normal elements. This result is an extension of [13; 2.14] to the case under consideration.
Theorem 3.2. Let 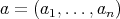 be a commuting
be a commuting 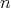 -tuple of regular normal elements in a
-tuple of regular normal elements in a 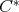 -algebra
-algebra 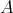 . Let
. Let 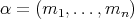 be an
be an 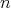 -tuple of nonnegative entire numbers. Then
-tuple of nonnegative entire numbers. Then 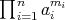 is regular and
is regular and
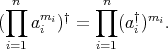
Proof. First of all recall that according to the Flugede-Putnam Theorem, [5; IX, 6.7] or [9; 9.6.7], 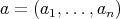 is a doubly commuting tuple.
is a doubly commuting tuple.
Next consider, as in Remark 3.1, the 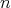 -tuple
-tuple
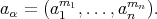
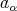 is a doubly commuting tuple of regular elements of
is a doubly commuting tuple of regular elements of 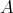 . Consequently, according to Theorem 2.4, Remark 2.5 and Remark 3.1 again, the proof of the Theorem is concluded.
. Consequently, according to Theorem 2.4, Remark 2.5 and Remark 3.1 again, the proof of the Theorem is concluded. 
Remark 3.3. Let 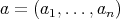 be a commuting
be a commuting 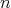 -tuple of regular normal elements in a
-tuple of regular normal elements in a 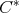 -algebra
-algebra 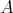 . Consider, as in Remark 2.3,
. Consider, as in Remark 2.3, ![π : [[1,n]] → [[1,n]]](/img/revistas/ruma/v46n2/2a03321x.png) a permutation, and define an
a permutation, and define an 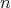 -tuple
-tuple 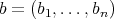 , where given
, where given 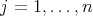 ,
, 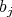 is either
is either 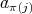 ,
, 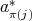 ,
, 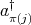 or
or 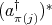 . Next consider the
. Next consider the 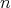 -tuple
-tuple 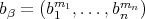 , where
, where 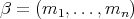 is an
is an 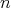 -tuple of nonnegative integers. Then, according to Proposition 2.2, Remark 3.1, Theorem 3.2 and Theorem 10 of [10],
-tuple of nonnegative integers. Then, according to Proposition 2.2, Remark 3.1, Theorem 3.2 and Theorem 10 of [10], 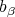 is an
is an 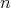 -tuple of doubly commuting regular normal elements of
-tuple of doubly commuting regular normal elements of 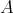 . Therefore, according to Theorem 3.2,
. Therefore, according to Theorem 3.2, 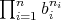 is regular and
is regular and
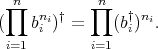
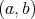 is a pair of commuting regular normal elements in a
is a pair of commuting regular normal elements in a 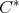 -algebra
-algebra 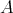 , then
, then
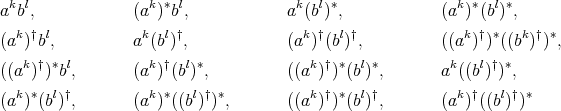
are regular elements of  , for
, for  and
and  . Furthermore, their Moore-Pensrose inverses can be calculated according to the first part of the present Remark.
. Furthermore, their Moore-Pensrose inverses can be calculated according to the first part of the present Remark.
Next the main results of the present work will be applied to 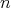 -tuples of regular Hilbert space operators.
-tuples of regular Hilbert space operators.
Let 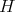 be a Hilbert space and consider
be a Hilbert space and consider 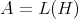 , the
, the 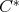 -algebra of all bounded and linear maps defined in
-algebra of all bounded and linear maps defined in 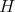 . Recall that
. Recall that 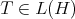 is regular as an operator if and only if
is regular as an operator if and only if 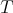 is a regular element of
is a regular element of 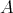 . Moreover, necessary and sufficient for
. Moreover, necessary and sufficient for 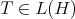 to be a regular operator is the fact that the range of
to be a regular operator is the fact that the range of 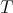 ,
, 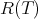 , is a closed subspace of
, is a closed subspace of 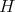 , see for example [9; 3.8]. Note that in this case the Moore-Penrose inverse can be described in a direct way.
, see for example [9; 3.8]. Note that in this case the Moore-Penrose inverse can be described in a direct way.
In fact, consider 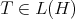 a bounded Hilbert space operator with closed range. Define
a bounded Hilbert space operator with closed range. Define 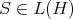 as follows:
as follows:
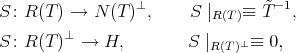
where 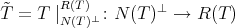 , that is the restriction to
, that is the restriction to 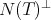 of
of 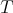 . Then, it is not diffuclt to prove that
. Then, it is not diffuclt to prove that
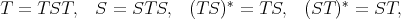
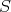 is the Moore-Penrose inverse of
is the Moore-Penrose inverse of 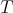 .
. On the other hand, an 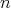 -tuple of continuous linear maps defined in
-tuple of continuous linear maps defined in 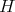 ,
, 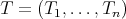 , is doubly commuting as operators if and only if it is doubly commuting as elements of
, is doubly commuting as operators if and only if it is doubly commuting as elements of 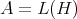 . In the following theorems the relationship between doubly commuting tuples of regular operators and the Moore-Penrose inverse will be studied.
. In the following theorems the relationship between doubly commuting tuples of regular operators and the Moore-Penrose inverse will be studied.
Theorem 3.4. Let 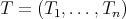 be an
be an 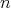 -tuple of regular Hilbert space operators. Then, if the
-tuple of regular Hilbert space operators. Then, if the 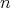 -tuple
-tuple 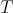 is doubly commuting,
is doubly commuting, 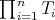 is a regular operator and
is a regular operator and
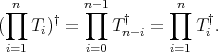
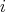 ,
, 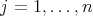 ,
, 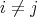 ,
, 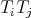 ,
, 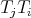 ,
, 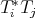 and
and 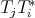 are regular operators which comply with the following identities:
are regular operators which comply with the following identities:

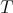 is a doubly commuting
is a doubly commuting 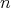 -tuple of regular Hilbert space operators.
-tuple of regular Hilbert space operators. Proof. It is a consequence of Theorems 2.4 and 2.6. 
Theorem 3.5. Let 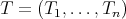 be an
be an 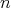 -tuple of commuting regular normal operators defined in a Hilbert space
-tuple of commuting regular normal operators defined in a Hilbert space 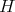 . Next consider the
. Next consider the 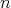 -tuple
-tuple 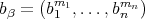 , where
, where 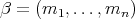 is an
is an 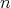 -tuple of nonnegative integers. Then,
-tuple of nonnegative integers. Then, 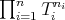 is regular and
is regular and
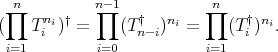
Proof. It is a consequence of Theorem 3.2. 
The last application of the results of the previous section concerns Calkin algebras.
Recall that if 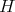 is a Hilbert space and
is a Hilbert space and 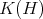 denotes the closed ideal of all compact operators defined in
denotes the closed ideal of all compact operators defined in 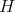 , then the Calkin algebra of
, then the Calkin algebra of 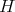 ,
, 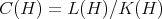 , is a
, is a 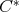 -algebra. Moreover, tha natural quotient map
-algebra. Moreover, tha natural quotient map 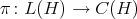 is a
is a 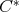 -algebra morphism, see [5; 4] or [15; 4.1.16].
-algebra morphism, see [5; 4] or [15; 4.1.16].
Furthermore, note that if 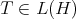 is a regular operator, then
is a regular operator, then 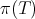 is a regular element of
is a regular element of 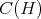 . In addition, it is not difficult to prove that if
. In addition, it is not difficult to prove that if 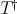 is the Moore-Penrose inverse of a regular operator
is the Moore-Penrose inverse of a regular operator 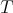 , then
, then  .
.
On the other hand, recall that an 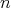 -tuple
-tuple 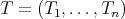 is said to be almost commuting (resp. almost doubly commuting), if
is said to be almost commuting (resp. almost doubly commuting), if 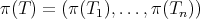 is a commuting tuple (resp. a doubly commuting tuple) in the
is a commuting tuple (resp. a doubly commuting tuple) in the 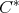 -algebra
-algebra 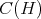 , that is if
, that is if  (resp.
(resp.  and
and  ) belong to
) belong to 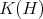 , for
, for 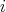 ,
, 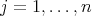 ,
, 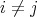 , see [6], [7] and [8]. In the following theorems the relationship between
, see [6], [7] and [8]. In the following theorems the relationship between 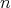 -tuples of almost doubly commuting regular operators and the Moore-Penrose inverse will be studied.
-tuples of almost doubly commuting regular operators and the Moore-Penrose inverse will be studied.
Theorem 3.6. Let 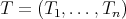 be an
be an 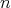 -tuple of regular operators defined in the Hilbert space
-tuple of regular operators defined in the Hilbert space 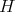 . Suppose that
. Suppose that 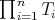 is regular. Then, if
is regular. Then, if 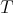 is an almost doubly commuting tuple of operators,
is an almost doubly commuting tuple of operators,
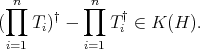
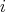 ,
, 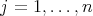 ,
, 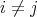 ,
, 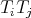 ,
, 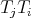 ,
, 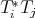 and
and 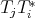 are regular operators such that
are regular operators such that

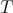 is an almost doubly commuting
is an almost doubly commuting 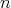 -tuple of regular Hilbert space operators.
-tuple of regular Hilbert space operators. Proof. It is a consequence of Theorem 3.4 and the above recalled facts regarding Calkin algebras. 
Theorem 3.7. Let 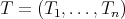 be an
be an 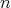 -tuple of almost commuting regular normal operators defined in a Hilbert space
-tuple of almost commuting regular normal operators defined in a Hilbert space 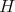 . Next consider the
. Next consider the 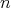 -tuple
-tuple 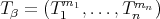 , where
, where 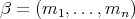 is an
is an 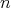 -tuple of nonnegative integers, and suppose that
-tuple of nonnegative integers, and suppose that 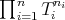 is regular . Then,
is regular . Then, 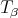 is an
is an 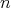 -tuple of almost doubly commuting regular operators defined in
-tuple of almost doubly commuting regular operators defined in 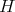 , and
, and
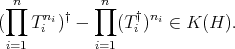
Proof. It is a consequence of Theorems 3.2, 3.5 and the recalled facts regarding Calkin algebras. 
Remark 3.8. It is worth noticing that Theorems 3.2 and 3.4-3.7 can be extended to other tuples of 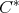 -algebra elements and of Hilbert space operators respectively in the same way that it was done in Remarks 2.3 and 2.5, that is considering permutations and new tuples defined by Moore-Penrose inverses and adjoints.
-algebra elements and of Hilbert space operators respectively in the same way that it was done in Remarks 2.3 and 2.5, that is considering permutations and new tuples defined by Moore-Penrose inverses and adjoints.
[1] E. Albrecht and M. Ptak, Invariant subspaces for doubly commuting contractions with rich Taylor spectrum, J. Operator Theory 40 (1998), 373-384. [ Links ]
[2] M. Cho, R. Curto, T. Huruya and W. Zelazko, Cartesian form of Putnam's inequality for doubly commuting hyponormal  -tuples, Indiana Univ. Math. J. 49 (2000), 1437-1448. [ Links ]
-tuples, Indiana Univ. Math. J. 49 (2000), 1437-1448. [ Links ]
[3] M. Cho and A. T. Dash, On the joint spectra of doubly commuting  -tuples of seminormal operators, Glasgow Math. J. 26 (1985), 47-50. [ Links ]
-tuples of seminormal operators, Glasgow Math. J. 26 (1985), 47-50. [ Links ]
[4] M. Cho, B. P. Duggal and W. Y. Lee, Putnam's inequality of doubly commuting  -tuples for log-hyponormal operators, Math. Proc. Royal Ir. Acad. Sect. A 100 A (2000), 163-169. [ Links ]
-tuples for log-hyponormal operators, Math. Proc. Royal Ir. Acad. Sect. A 100 A (2000), 163-169. [ Links ]
[5] J. B. Conway, A Course in Functional Analysis, Springer Verlag, New York, Berlin, Heidelberg, Tokio, 1985. [ Links ]
[6] R. Curto, On the connectedness of invertible  -tuples, Indiana Univ. Math. J. 29 (1980), 393-406. [ Links ]
-tuples, Indiana Univ. Math. J. 29 (1980), 393-406. [ Links ]
[7] R. Curto, Fredholm and invertible  -tuples of operators. The deformation problem, Trans. Amer. Math. Soc. 266 (1981), 129-159. [ Links ]
-tuples of operators. The deformation problem, Trans. Amer. Math. Soc. 266 (1981), 129-159. [ Links ]
[8] R. Curto, Spectral inclusion for doubly commuting subnormal  -tuples, Proc. Amer. Math. Soc. 83 (1981), 730-734. [ Links ]
-tuples, Proc. Amer. Math. Soc. 83 (1981), 730-734. [ Links ]
[9] R. Harte, Invertibility and Singularity for Bounded Linear Operators, Marcel Dekker, New York and Basel, 1988. [ Links ]
[10] R. Harte and M. Mbekhta, On generalized inverses in 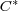 -algebras, Studia Math. 103 (1992), 71-77. [ Links ]
-algebras, Studia Math. 103 (1992), 71-77. [ Links ]
[11] R. Harte and M. Mbekhta, On generalized inverses in 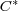 -algebras II, Studia Math. 106 (1993), 129-138. [ Links ]
-algebras II, Studia Math. 106 (1993), 129-138. [ Links ]
[12] I. H. Jeon, On joint essential spectra of doubly commuting  -tuples of
-tuples of 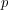 -hyponormal operators, Glasgow Math. J. 40 (1998), 353-358. [ Links ]
-hyponormal operators, Glasgow Math. J. 40 (1998), 353-358. [ Links ]
[13] J. J. Koliha, The Drazin and Moore-Penrose inverse in 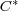 -algebras, Math. Proc. Royal Ir. Acad. Sect. A 99 A (1999) no. 1, 17-27. [ Links ]
-algebras, Math. Proc. Royal Ir. Acad. Sect. A 99 A (1999) no. 1, 17-27. [ Links ]
[14] M. Mbekhta, Conorme et inverse généralisé dans les 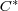 -algèbres, Canadian Math. Bull. 35 (1992), 512-522. [ Links ]
-algèbres, Canadian Math. Bull. 35 (1992), 512-522. [ Links ]
[15] G. J. Murphy, 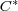 -Algebras and Operator Theory, Academic Press, Boston, (1990). [ Links ]
-Algebras and Operator Theory, Academic Press, Boston, (1990). [ Links ]
[16] R. Penrose, A generalized inverse for matrices, Proc. Cambridge Philos. Soc. 51 (1955), 406-413. [ Links ]
Enrico Boasso
Departamento de Matemática,
Facultad de Ciencias Exactas y Naturales,
Universidad de Buenos Aires,
Ciudad Universitaria - Pab. I,
(1428) Buenos Aires, Argentina.
eboasso@dm.uba.ar
Recibido: 17 de agosto de 2005
Aceptado: 7 de agosto de 2006














