Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932versão On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.46 n.2 Bahía Blanca jul./dez. 2005
Extending polynomials on Banach spaces—a survey
Ignacio Zalduendo
A la memoria de Pucho Larotonda, maestro y amigo
Throughout, 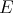 ,
, 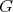 , and
, and 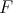 will be complex Banach spaces,
will be complex Banach spaces, 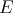 a subspace of
a subspace of 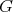 . The question which gave rise to the material reviewed here was first posed by Dineen [D1] in relation to holomorphic completeness and in the context of more general locally convex spaces. It is the following: when can a continuous homogeneous polynomial
. The question which gave rise to the material reviewed here was first posed by Dineen [D1] in relation to holomorphic completeness and in the context of more general locally convex spaces. It is the following: when can a continuous homogeneous polynomial 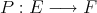 be extended to
be extended to 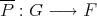 ? Several answers—none complete—have been given for varying hypotheses on the spaces and the polynomials involved, and several applications have appeared. We attempt here to unify the existing approaches to the problem, and to point out the common ingredients in the solutions.
? Several answers—none complete—have been given for varying hypotheses on the spaces and the polynomials involved, and several applications have appeared. We attempt here to unify the existing approaches to the problem, and to point out the common ingredients in the solutions.
It is clearly not possible in general to extend polynomials to larger spaces, in fact this is true even of linear functions: the identity  cannot be extended to
cannot be extended to  , for
, for  is non-complemented in
is non-complemented in 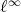 . When
. When 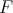 is the complex field and
is the complex field and 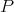 is linear there is of course the Hahn-Banach theorem, but we shall see that in the non-linear case, there are scalar-valued polynomials which cannot be extended.
is linear there is of course the Hahn-Banach theorem, but we shall see that in the non-linear case, there are scalar-valued polynomials which cannot be extended.
The positive results in this matter can be loosely grouped into two main categories: those providing linear extension morphisms by which all polynomials can be extended to some larger space, and Hahn-Banach type extensions applicable to some polynomials and extending those to all larger spaces. We concentrate on the first type of result in sections 1 and 2, and on the second type in section 3.
We restrict our attention to polynomials over Banach spaces, although many results have been obtained regarding the extension of holomorphic functions on Banach or other locally convex spaces ([Bol], [CM], [GGM2], [Kh1], [Kh2], [Mo2], [Mo3], [MV]). Also, many applications have appeared which we do not go into here: to holomorphic completeness [D1], to geodesics [DT], polarization constants [LR], reflexivity of spaces of polynomials [JPZ] [AD], the spectra of algebras of analytic functions over Banach spaces [ACG1] [AGGM], integral representation of analytic functions [PZ], and orthogonally additive polynomials ([BLLl], [PgV], [CLZ]).
In the first section we consider the Aron-Berner extension. We begin with the Arens product in a commutative Banach algebra, a very specific extension of a bilinear function, but nevertheless an extension in which some of the main points of more general extensions already appear, such as lack of symmetry and the notion of regularity. We then define and study the Aron-Berner extension, an extension of polynomials from a Banach space to its bidual. In the second section, we consider extensions from 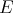 to
to 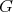 . Here all solutions stem from the existence of a continuous linear extension morphism for linear forms
. Here all solutions stem from the existence of a continuous linear extension morphism for linear forms  , a condition obviously stronger than Hahn-Banach, and not satisfied in all cases. Section 3 is devoted to Hahn-Banach type extensions. We are naturally drawn to 'linearization' of polynomials, and thus to preduals of spaces of polynomials. The space of 'extendible' polynomials is considered also.
, a condition obviously stronger than Hahn-Banach, and not satisfied in all cases. Section 3 is devoted to Hahn-Banach type extensions. We are naturally drawn to 'linearization' of polynomials, and thus to preduals of spaces of polynomials. The space of 'extendible' polynomials is considered also.
This survey has been brewing, on and off, for about a decade. It started out as a talk prepared for the Conference on Polynomials and Holomorphic Functions on Locally Convex Spaces, in University College Dublin in September of 1994, and then lay dormant for a couple of years until the Departamento de Análisis Matemático of the Universidad Complutense de Madrid invited the author to lecture on these topics in the winter of 1997, thus providing the oportunity for extensive rewriting. A first version appeared as a preprint [Z3] in the series Publicaciones del Departamento de Análisis Matemático of the Complutense. More recently, the author has lectured on these matters in a Seminar at the Universidad de Buenos Aires, and so had the oportunity to add more recent material —particularly to section 3— and make these notes up to date. It is a pleasure to thank my colleagues at UCD, UCM, and UBA for their interest and support. Also, many participants at the Conference in Dublin, and many of those present at the Madrid and Buenos Aires lectures have helped to mold these notes with their comments, their questions, and in more than a few cases, their answers. In this respect, it is a pleasure to acknowledge the contribution of J. M. Ansemil, R. Aron, F. Bombal, C. Boyd, D. Carando, V. Dimant, S. Dineen, J. A. Jaramillo, J. G. Llavona, A. Peris, A. Prieto, R. Ryan, S. Lassalle, and A. Tonge.
A word of caution. In writing these notes I have had in mind my students more than my colleagues. Thus, the result has been more an introduction than a survey. The experts will find some of their theorems missing, their proofs changed, their points of view distorted. The choice of material has been personal, and probably guided by aesthetic sense more than anything else. Also, in many places, the absence of a reference is not due to my originality, but to my ignorance.
Before going on to the first section of this paper, we succintly present the basic definitions and notation of the theory of polynomials on Banach spaces. For a truly comprehensive text, see [D4].
A 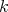 -homogeneous polynomial
-homogeneous polynomial 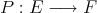 is a function which can be written as
is a function which can be written as 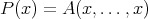 where
where 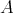 is a
is a 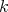 -linear function from
-linear function from  to
to 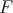 . When
. When 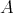 is symmetric, it can be recovered from the corresponding polynomial
is symmetric, it can be recovered from the corresponding polynomial 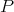 by any of several polarization formulas. Thus, there is a one-to-one correspondence between
by any of several polarization formulas. Thus, there is a one-to-one correspondence between 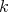 -homogeneous polynomials and symmetric
-homogeneous polynomials and symmetric 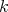 -linear functions.
-linear functions.
The 'uniform' norm of 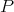 can be defined as
can be defined as
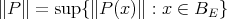
where 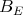 is the closed unit ball of
is the closed unit ball of 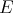 . Continuity of
. Continuity of 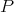 (and of the corresponding symmetric
(and of the corresponding symmetric 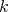 -linear function
-linear function 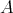 ) is equivalent to finiteness of
) is equivalent to finiteness of  . The space of
. The space of 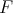 -valued continuous
-valued continuous 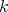 -homogeneous polynomials, with the uniform norm, is a Banach space which we will denote by
-homogeneous polynomials, with the uniform norm, is a Banach space which we will denote by 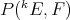 , or simply by
, or simply by 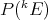 when
when 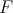 is the scalar field.
is the scalar field.
We will need to consider several more restricted classes of scalar-valued polynomials, each of which gives rise to a vector subspace of 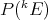 .
.
Surely the simplest kind of polynomials over a Banach space are the polynomials of finite type, those which may be written as 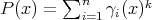 , where each
, where each  is a continuous linear form over
is a continuous linear form over 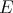 . Slightly larger is the class of nuclear polynomials, made up of those which may be represented (non-uniquely) as
. Slightly larger is the class of nuclear polynomials, made up of those which may be represented (non-uniquely) as  , with
, with 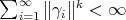 . These form a non-closed vector subspace of
. These form a non-closed vector subspace of 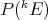 (although they do form a Banach space in the 'nuclear' norm, i.e. the infimum of
(although they do form a Banach space in the 'nuclear' norm, i.e. the infimum of 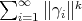 over all possible representations of
over all possible representations of 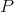 ). The closure of the space of nuclear (or also of the finite-type polynomials) in the uniform norm is the space of approximable polynomials. Larger still are the spaces of weakly continuous polynomials (those which are weakly continuous over all bounded subsets of
). The closure of the space of nuclear (or also of the finite-type polynomials) in the uniform norm is the space of approximable polynomials. Larger still are the spaces of weakly continuous polynomials (those which are weakly continuous over all bounded subsets of 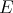 ) and weakly sequentially continuous polynomials. We thus have the chain of vector subspaces of
) and weakly sequentially continuous polynomials. We thus have the chain of vector subspaces of 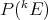
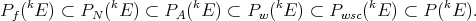
Reverse inclusions sometimes hold, highlighting the interplay between the study of polynomials and Banach space theory: if 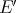 has the approximation property
has the approximation property 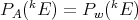 [AP], if
[AP], if 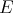 has the Dunford-Pettis property
has the Dunford-Pettis property 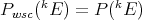 [Ry1], while
[Ry1], while  holds if and only if
holds if and only if 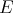 contains no copy of
contains no copy of 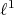 [FGLl]. Another important class of polynomials is that of integral polynomials: those which may be represented by a regular Borel measure
[FGLl]. Another important class of polynomials is that of integral polynomials: those which may be represented by a regular Borel measure 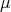 over the unit ball of
over the unit ball of 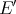 (considered with the weak
(considered with the weak topology) in the following way
topology) in the following way
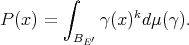
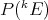 in the uniform norm. We have the inclusions
in the uniform norm. We have the inclusions 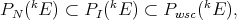
with 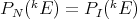 when
when  has the Radon-Nikodym property [A] (for example, if
has the Radon-Nikodym property [A] (for example, if 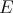 is reflexive).
is reflexive).
The only trivially extendible scalar-valued polynomials are the finite-type and the nuclear polynomials. These can be extended to any larger space by simply using the Hahn-Banach theorem to extend their component linear forms 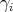 . We shall see that the integral polynomials are also extendible but that there are, in general, approximable polynomials which cannot be extended.
. We shall see that the integral polynomials are also extendible but that there are, in general, approximable polynomials which cannot be extended.
In 1951 R. Arens ([A1], [A2]) found a way of extending the product of a Banach algebra 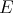 to its bidual
to its bidual 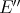 in such a way that this bidual became itself a Banach algebra. We restrict our presentation here to commutative Banach algebras
in such a way that this bidual became itself a Banach algebra. We restrict our presentation here to commutative Banach algebras 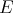 , for in the sequel we will be interested in polynomials, and thus in symmetric multilinear forms.
, for in the sequel we will be interested in polynomials, and thus in symmetric multilinear forms.
Suppose then that 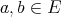 ,
, 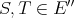 , and
, and 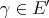 . The elements
. The elements 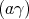 and
and 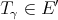 are defined by setting
are defined by setting
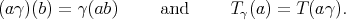
Now, given 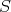 and
and 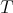 in the bidual of
in the bidual of 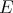 , define the product of
, define the product of 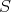 and
and 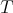 by
by
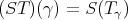
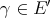 . It is easily seen that this product extends the product in
. It is easily seen that this product extends the product in 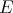 . Also, we observe the following two facts which will have analogues in the more general Aron-Berner extension.
. Also, we observe the following two facts which will have analogues in the more general Aron-Berner extension. i) The map 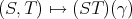 is weak
is weak -continuous of its first variable: Indeed, if
-continuous of its first variable: Indeed, if  is weak
is weak -converging to
-converging to 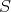 , then
, then  . ii) All elements of
. ii) All elements of 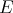 commute with all elements of
commute with all elements of 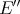 : Take
: Take 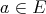 and
and 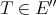 . Then for any
. Then for any 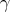
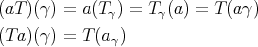
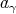 is just
is just 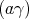 .
. In general, the map in i) is not continuous of the second variable, and the Arens product is not commutative. In fact we will see in the next section that these two properties are equivalent. To see that the product is not commutative, we present the following example [Z2] (see also [Re]).
Example 1.1.
Let 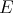 be the commutative Banach algebra
be the commutative Banach algebra 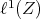 with the convolution product
with the convolution product
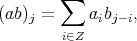
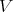 of
of 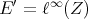
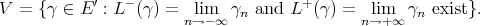
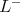 and
and 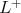 to elements
to elements 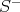 and
and 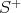 of
of 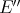 . These do not commute. To see this, take
. These do not commute. To see this, take 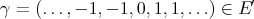 and observe that
and observe that 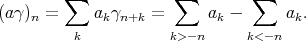
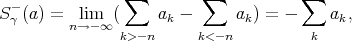
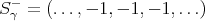 . Analogously
. Analogously 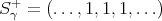 . Now
. Now 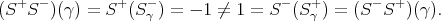
The process applied to the map  can be carried out on an arbitrary continuous bilinear function
can be carried out on an arbitrary continuous bilinear function
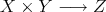
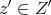 and
and 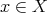 ; then we obtain an element of
; then we obtain an element of 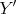 . This mapping is bilinear and continuous, producing
. This mapping is bilinear and continuous, producing 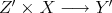 . If we repeat the process again we obtain
. If we repeat the process again we obtain 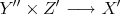 , and when repeated once more,
, and when repeated once more, 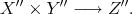
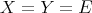 , a Banach space,
, a Banach space, 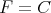 , and
, and 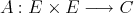 a symmetric bilinear form on
a symmetric bilinear form on 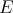 , the construction produces an extension of
, the construction produces an extension of 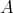 to
to 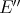 .
. The same extension can be defined in other ways. Here are two:
a) Say 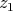 and
and 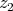 are elements of the bidual, and choose nets
are elements of the bidual, and choose nets 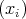 and
and  converging to
converging to 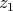 and
and 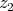 in the weak
in the weak topology of
topology of 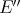 . Now put
. Now put
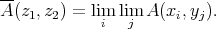
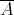 is not, in general, weak
is not, in general, weak -continuous in the second variable, but only in the first.
-continuous in the second variable, but only in the first. b) Define the associated symmetric linear map 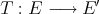 by
by 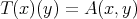 . Its bitranspose
. Its bitranspose 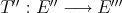 corresponds to a continuous bilinear extension of
corresponds to a continuous bilinear extension of 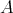
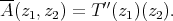
Similar constructions can be carried out for 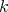 -linear forms. Note that in all cases there is a choice involved in the ordering (of the limits, of
-linear forms. Note that in all cases there is a choice involved in the ordering (of the limits, of 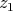 and
and 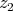 ). It turns out that even though
). It turns out that even though 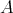 is symmetric, the extended form
is symmetric, the extended form 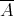 need not be symmetric. In fact one has the following equivalences, with
need not be symmetric. In fact one has the following equivalences, with 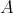 and
and 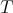 as above.
as above.
Proposition 1.2. ([DH], [Rp]) The following are equivalent:
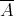 is symmetric.
is symmetric. 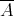 is separately weak
is separately weak -continuous in both variables.
-continuous in both variables. 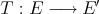 is weakly compact.
is weakly compact.
Proof. i) implies ii): 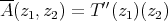 is always weak
is always weak -continuous in the first variable, for transpose maps are weak
-continuous in the first variable, for transpose maps are weak to weak
to weak -continuous. Thus symmetry implies weak
-continuous. Thus symmetry implies weak -continuity in the other variable as well.
-continuity in the other variable as well.
ii) implies iii): Fix any 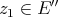 . Weak
. Weak -continuity of
-continuity of 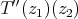 in the variable
in the variable 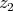 says that
says that 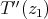 is actually in the canonical inclusion of
is actually in the canonical inclusion of 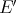 in
in 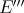 . Thus
. Thus 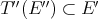 and
and  is weakly compact by Gantmacher's theorem [HP].
is weakly compact by Gantmacher's theorem [HP].
iii) implies i): We denote the canonical inclusion of  in
in 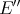 by
by 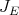 and that of
and that of 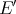 in
in 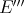 by
by 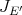 . First, note that since
. First, note that since 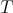 is symmetric,
is symmetric, 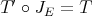 . Indeed, for any
. Indeed, for any  and
and 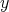 in
in 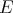 ,
,
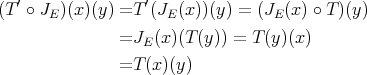
This in turn implies that for any  ,
, 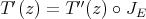 : for all
: for all 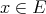 , we have
, we have
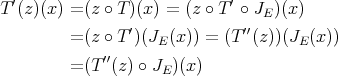
Thus, if 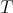 is weakly compact we obtain
is weakly compact we obtain 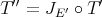 : Since
: Since 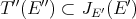 , and
, and  separates points of
separates points of  , we need only see that for
, we need only see that for 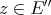 and
and 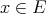 ,
, 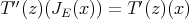 . But this is
. But this is 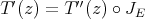 . Thus we have,
. Thus we have,
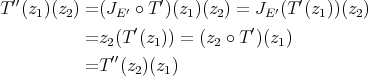
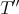 is symmetric. □
is symmetric. □ It is worth noting that elements of 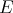 always commute with those of
always commute with those of 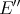 , even when
, even when 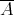 is not symmetric. Thus
is not symmetric. Thus 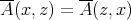 for any choice of
for any choice of 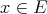 and
and 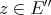 .
.
If the equivalent conditions in the proposition hold for all symmetric 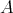 ,
, 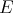 is said to be symmetrically regular, and if all (symmetric or otherwise) operators
is said to be symmetrically regular, and if all (symmetric or otherwise) operators  are weakly compact,
are weakly compact, 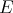 is regular. As Example 1.1 shows,
is regular. As Example 1.1 shows, 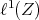 is not symmetrically regular (and hence not regular). The operator
is not symmetrically regular (and hence not regular). The operator 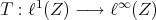 corresponding to Example 1.1 is given by
corresponding to Example 1.1 is given by
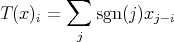
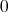 is taken as
is taken as 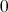 . It is easily seen that
. It is easily seen that 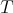 is not weakly compact: any subsequence of
is not weakly compact: any subsequence of 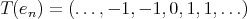 (with
(with 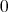 in
in  th place) which converges weakly does so to
th place) which converges weakly does so to 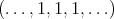 , but
, but 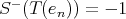 for all
for all 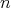 . So the image of the unit ball is not weakly sequentially compact.
. So the image of the unit ball is not weakly sequentially compact. Another example of such an operator  [ACG1] is given by
[ACG1] is given by
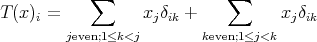
and yet another [Re] by
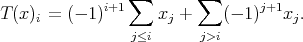
On the other hand, 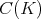 spaces are regular [GI], as are all
spaces are regular [GI], as are all 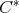 -algebras.
-algebras.
We continue with some results on symmetric regularity, as found in [AGGM].
Proposition 1.3. 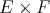 is regular if and only if all operators in
is regular if and only if all operators in 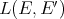 ,
, 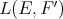 ,
, 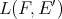 ,
, 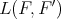 are weakly compact.
are weakly compact.
Proof. Just note that one may write 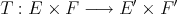 as
as
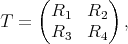
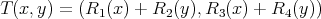 . □
. □ An immediate consequence is that 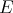 is regular if and only if
is regular if and only if 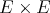 is regular. Also, if
is regular. Also, if 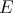 is non-reflexive,
is non-reflexive, 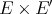 is non-regular.
is non-regular.
Proposition 1.4.
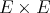 is symmetrically regular, then
is symmetrically regular, then 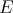 is regular.
is regular. 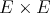 is regular if and only if it is symmetrically regular.
is regular if and only if it is symmetrically regular.
Proof. i) Take  , any continuous operator, and define
, any continuous operator, and define  by
by
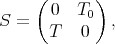
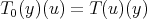 . Then
. Then 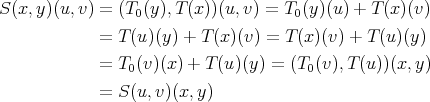
Thus 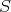 is symmetric, and therefore it, and
is symmetric, and therefore it, and 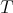 , are compact.
, are compact.
ii) This is now easy from part i) and the fact that 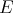 is regular if and only if
is regular if and only if 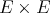 is. □
is. □
We now define the Aron-Berner extension of a continuous 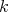 -homogeneous scalar-valued polynomial
-homogeneous scalar-valued polynomial 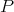 defined over the Banach space
defined over the Banach space 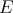 . We choose to give a degree-
. We choose to give a degree-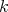 version of the first definition mentioned above, but note that the second is also easily adapted to this case. We first extend
version of the first definition mentioned above, but note that the second is also easily adapted to this case. We first extend 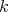 -linear forms:
-linear forms:
Given  and
and 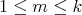 , define
, define

 . Here
. Here 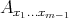 denotes the linear form obtained from
denotes the linear form obtained from  by fixing
by fixing  variables (note that by symmetry it does not matter where these variables are fixed). The map
variables (note that by symmetry it does not matter where these variables are fixed). The map  is linear, continuous and of norm
is linear, continuous and of norm  . Now, given
. Now, given 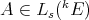 we may define the extended
we may define the extended 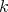 -linear form
-linear form 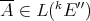 by
by 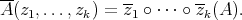
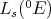 with the scalar field. The extended mapping
with the scalar field. The extended mapping 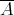 need not be symmetric. We have in fact
need not be symmetric. We have in fact 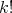 extensions, one for each choice of ordering in
extensions, one for each choice of ordering in  . Note however that for
. Note however that for 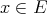 we do have
we do have  , and that
, and that 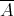 is weak
is weak -continuous in the first variable [Z1]. These properties are analogous to those of the Arens product.
-continuous in the first variable [Z1]. These properties are analogous to those of the Arens product. When 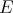 is symmetrically regular, variables in
is symmetrically regular, variables in 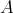 can be permuted in pairs even in the extensions of
can be permuted in pairs even in the extensions of 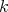 -linear forms, so that if
-linear forms, so that if 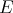 is symmetrically regular the extension of any symmetric
is symmetrically regular the extension of any symmetric 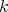 -linear form is itself symmetric.
-linear form is itself symmetric.
We define the Aron-Berner extension of 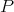 to the bidual
to the bidual 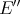 of
of 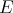 by setting
by setting
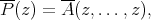
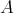 is the unique symmetric continuous
is the unique symmetric continuous 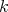 -linear form
-linear form 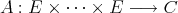 such that
such that 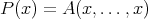 for every
for every 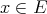 .
. It must be stressed that this extension is quite algebraic in nature. Indeed, the formal manipulations involved can be carried out with no regard to topology whatsoever. It is certainly not an extension by continuity, and 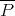 need not be weak
need not be weak -continuous (consider the polynomial
-continuous (consider the polynomial 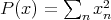 over
over 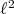 ).
).
However the Aron-Berner extension respects most of the usual classes of continuous polynomials, as we shall see below. Also, a relation with the weak -topology in
-topology in 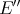 is present, though perhaps more subtly than one would expect, as the next two theorems show.
is present, though perhaps more subtly than one would expect, as the next two theorems show.
First, there is the following characterization of the Aron-Berner extension [Z1] in terms of first-order differentials.
Theorem 1.5. [Z1] If 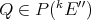 and
and 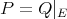 , then
, then  if and only if
if and only if
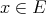 ,
, 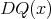 is weak
is weak -continuous, and
-continuous, and 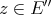 and
and 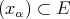 converging weak
converging weak to
to  ,
,  . □
. □
Condition b) is somewhat odd, but examples show that 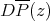 need not be weak
need not be weak -continuous for
-continuous for 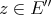 and that condition a) alone does not guarantee that
and that condition a) alone does not guarantee that 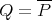 . Indeed, let
. Indeed, let 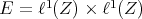 and
and 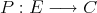 such that
such that 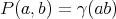 (with notation as in Example 1.1). Then the Aron-Berner extension of
(with notation as in Example 1.1). Then the Aron-Berner extension of 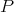 is
is  2](/img/revistas/ruma/v46n2/2a04315x.png) . However, since
. However, since 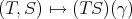 is not weak
is not weak -continuous in the second variable, choose
-continuous in the second variable, choose 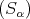 converging weak
converging weak to
to 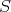 with
with 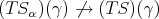 ; let
; let 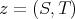 and
and 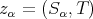 . Then
. Then  weak
weak , but
, but 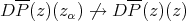 . Also, if
. Also, if 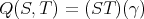 , then
, then 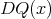 is weak
is weak -continuous for all
-continuous for all 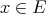 , but
, but 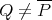 .
.
One consequence of the above characterization is the linearity of the Aron-Berner extension mapping  . Indeed,
. Indeed, 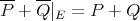 , and for all
, and for all 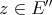 the differential
the differential 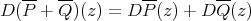 has the same continuity properties as each summand. The same holds for scalar multiples of
has the same continuity properties as each summand. The same holds for scalar multiples of 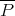 .
.
Thus, the Aron-Berner extension is a one-to-one linear map

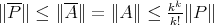 . However, more can be said. Davie and Gamelin have proved [DG] the following theorem which shows that in fact the Aron-Berner map is an isometry onto its image.
. However, more can be said. Davie and Gamelin have proved [DG] the following theorem which shows that in fact the Aron-Berner map is an isometry onto its image. Theorem 1.6.  . In fact, given
. In fact, given 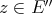 and a polynomial
and a polynomial 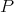 , there is a bounded net
, there is a bounded net 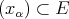 weak
weak -converging to
-converging to  and for which
and for which 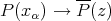 .
.
Proof. Let 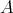 be the symmetric
be the symmetric 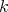 -linear form associated with
-linear form associated with 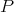 . Fix
. Fix  in the unit ball of
in the unit ball of 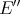 , and
, and 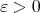 . For any natural number
. For any natural number 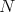 (to be fixed later) choose, using Goldstine's theorem, an element
(to be fixed later) choose, using Goldstine's theorem, an element 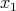 in the unit ball of
in the unit ball of 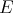 such that
such that
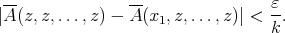
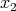 in the unit ball of
in the unit ball of 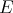 such that
such that 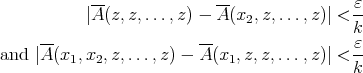
 in the unit ball of
in the unit ball of  such that whenever
such that whenever  , then
, then 
 , or (considering that
, or (considering that  is symmetric) for any
is symmetric) for any 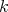 different indexes
different indexes 
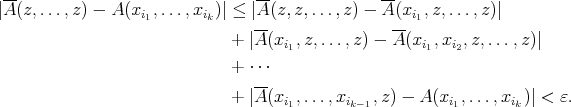
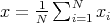 .
. 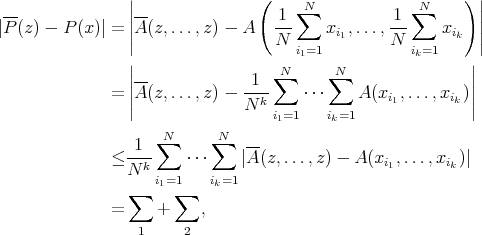
 , we have
, we have ![∑ ∑ ∑ + ≤ ɛ + 1 2 2 [ ] 1 ∑ ≤ ɛ + 2∥A ∥--k- number of terms in N 2 1 = ɛ + 2∥A ∥--k[N k - N (N - 1) ⋅⋅⋅(N - k + 1)] N( ) = ɛ + 2∥A ∥ 1 - N--N---1-⋅⋅⋅ N---k-+-1 N N N](/img/revistas/ruma/v46n2/2a04371x.png)
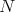 large; i.e. the larger the number of indexes
large; i.e. the larger the number of indexes  that one uses, the smaller the chance of having repeated indexes in a group of
that one uses, the smaller the chance of having repeated indexes in a group of 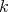 of them. Thus
of them. Thus 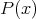 can be as close as
can be as close as 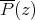 as required. □
as required. □ A polynomial 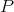 may in general admit many other norm-preserving extensions to
may in general admit many other norm-preserving extensions to 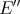 , but there are a few uniqueness results. For example, 2-homogeneous norm-attaining polynomials on
, but there are a few uniqueness results. For example, 2-homogeneous norm-attaining polynomials on  have unique norm-preserving extension to
have unique norm-preserving extension to  [ABC].
[ABC].
In view of the Davie-Gamelin theorem, one can consider the Aron-Berner extension as an inclusion map

A few comments on the preservation of the usual classes of polynomials through the Aron-Berner extension: Clearly finite type, nuclear, and approximable polynomials are preserved. Less clear but nevertheless true is the fact that integral polynomials over 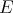 are mapped into integral polynomials over
are mapped into integral polynomials over 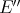 . We have:
. We have:
Theorem 1.7. [CZ1] The Aron-Berner extension of an integral polynomial over 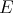 is an integral polynomial over
is an integral polynomial over 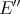 . Furthermore, if
. Furthermore, if 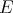 contains no copy of
contains no copy of 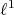 , and
, and 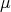 is a measure representing
is a measure representing 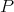 , then
, then
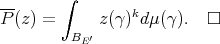
Note that this integral makes no sense if 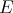 contains a copy of
contains a copy of 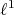 , for
, for  need not be a
need not be a 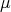 -measurable function over
-measurable function over 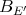 [H]. Also, an analogue of the Davie-Gamelin theorem holds: the integral norm of
[H]. Also, an analogue of the Davie-Gamelin theorem holds: the integral norm of 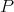 is the same as that of
is the same as that of 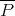 . The same holds for the class of extendible polynomials (which we will present in §3). De Moraes has proved:
. The same holds for the class of extendible polynomials (which we will present in §3). De Moraes has proved:
Theorem 1.8. [Mo1] The Aron-Berner extension of a weakly continuous polynomial over 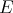 is a weakly continuous polynomial over
is a weakly continuous polynomial over 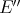 . □
. □
Another proof of this fact is possible through the characterization of weakly continuous polynomials as those which are continuous with respect to the seminorm
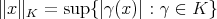
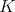 of
of 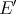 [ALRR], [T]. Indeed, it has been shown [AG], [CDDL] that for any particular
[ALRR], [T]. Indeed, it has been shown [AG], [CDDL] that for any particular 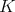 , such polynomials are preserved by the Aron-Berner extension.
, such polynomials are preserved by the Aron-Berner extension. The Aron-Berner extension does not, in general, preserve the class 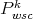 of weakly sequentially continuous polynomials, as the following example shows.
of weakly sequentially continuous polynomials, as the following example shows.
Example 1.9. Given any Banach space 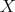 , consider the 2-homogeneous polynomial
, consider the 2-homogeneous polynomial 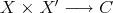 defined by
defined by  . It is easily seen that weak sequential continuity of this polynomial is equivalent to
. It is easily seen that weak sequential continuity of this polynomial is equivalent to 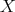 having the Dunford-Pettis property.
having the Dunford-Pettis property.
Now consider a Banach space 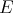 having the Dunford-Pettis property whose dual
having the Dunford-Pettis property whose dual 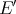 does not have it (say
does not have it (say 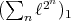 , [S]), and consider the weakly sequentially continuous polynomial
, [S]), and consider the weakly sequentially continuous polynomial
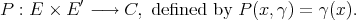
The Aron-Berner extension of this polynomial is
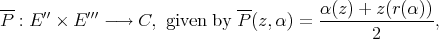
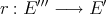 is the restriction mapping (i. e.,
is the restriction mapping (i. e., 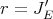 ). Thus if we restrict
). Thus if we restrict 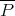 to the subspace
to the subspace  , we obtain the polynomial
, we obtain the polynomial 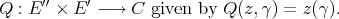
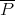 were weakly sequentially continuous,
were weakly sequentially continuous,  would be also, and hence
would be also, and hence 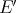 would have the Dunford-Pettis property, contradicting our assumption.
would have the Dunford-Pettis property, contradicting our assumption. A positive result in this matter is the following theorem of González and Gutiérrez (who actually prove a more general result).
Theorem 1.10. [GG] If 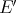 has the Dunford-Pettis property, then the Aron-Berner extension preserves weakly sequentially continuous polynomials. □
has the Dunford-Pettis property, then the Aron-Berner extension preserves weakly sequentially continuous polynomials. □
Through the Aron-Berner extension, polynomials defined on 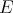 can be evaluated at points of
can be evaluated at points of 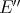 , and indeed at points of any even dual (
, and indeed at points of any even dual (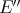 ,
, 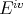 ,...) of
,...) of 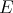 . It is natural to ask then if evaluations at such points constitute new evaluations or if, for example, given
. It is natural to ask then if evaluations at such points constitute new evaluations or if, for example, given 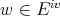 there is an element
there is an element 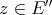 which polynomials
which polynomials 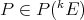 cannot distinguish from
cannot distinguish from  , that is
, that is 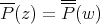 for all such
for all such 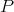 . Clearly, for
. Clearly, for  there is such an element of
there is such an element of 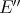 ; it is
; it is 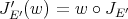 , where
, where 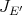 is the canonical inclusion of
is the canonical inclusion of 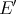 in its bidual
in its bidual 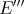 . The matter for
. The matter for 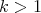 is far more interesting, and has been studied by Aron, Galindo, García and Maestre, who found the following.
is far more interesting, and has been studied by Aron, Galindo, García and Maestre, who found the following.
Theorem 1.11. [AGGM] Each evaluation at a point of 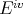 is in fact an evaluation at a point of
is in fact an evaluation at a point of 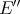 if and only if
if and only if 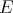 is symmetrically regular. □
is symmetrically regular. □
For 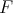 -valued polynomials
-valued polynomials 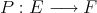 , the extension process described above produces an
, the extension process described above produces an 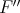 -valued polynomial
-valued polynomial 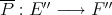 . It can be seen that if
. It can be seen that if 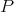 is weakly compact, then the image of
is weakly compact, then the image of 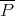 is in
is in 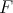 , although (unlike the linear case) the converse is not true. However, even in situations in which
, although (unlike the linear case) the converse is not true. However, even in situations in which 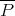 is
is 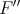 -valued, analogues of Theorem 1.5 and Theorem 1.6 hold [C1].
-valued, analogues of Theorem 1.5 and Theorem 1.6 hold [C1].
§2. Extension morphisms from 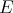 to
to 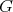
Several particular cases have been studied ([AB], [DT], [GGMM], [LR], [Z1]) of situations in which all polynomials defined over a Banach space 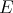 are extended to a certain larger Banach space
are extended to a certain larger Banach space 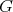 . In all these instances there turns out to be an extension morphism. We present in this section a unified version of the above mentioned results, and several formulations equivalent to the existence of an extension morphism for polynomials.
. In all these instances there turns out to be an extension morphism. We present in this section a unified version of the above mentioned results, and several formulations equivalent to the existence of an extension morphism for polynomials.
We shall need the following result of Aron and Schottenloher [AS].
Theorem 2.1. Let 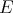 and
and 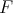 be arbitrary Banach spaces. Then
be arbitrary Banach spaces. Then 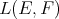 is isomorphic to a complemented subspace of
is isomorphic to a complemented subspace of 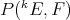 .
.
Proof. Fix 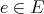 and
and 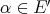 a norm-one linear functional such that
a norm-one linear functional such that 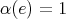 . Define the 'inclusion'
. Define the 'inclusion'  by
by 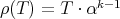 (the product is point-wise). Also, define the 'projection'
(the product is point-wise). Also, define the 'projection' 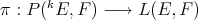 by
by  . Note that
. Note that 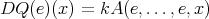 , where
, where 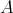 is the symmetric
is the symmetric 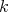 -linear operator associated to
-linear operator associated to  , and that if
, and that if 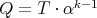 ,
,
![1 A(e,...,e, x) = --[T (e)α(e)⋅⋅⋅α(x) + ⋅⋅⋅ + α(e) ⋅⋅⋅T(e)α(x) + α(e) ⋅⋅⋅α(e)T (x)]. k](/img/revistas/ruma/v46n2/2a04473x.png)
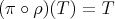 . Indeed, for any
. Indeed, for any 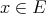 , we have
, we have 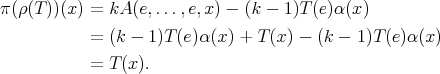
The existence of a linear extension mapping  is equivalent to the existence of a linear extension mapping
is equivalent to the existence of a linear extension mapping  . We have the following theorem. The 'if' part is a reformulation of results in [GGMM] and [Ni], the 'only if' part is due to A. Peris.
. We have the following theorem. The 'if' part is a reformulation of results in [GGMM] and [Ni], the 'only if' part is due to A. Peris.
Theorem 2.2. Let 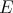 be a subspace of
be a subspace of 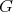 , and
, and 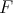 an arbitrary Banach space. Then there is an extension morphism
an arbitrary Banach space. Then there is an extension morphism 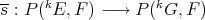 if and only if there is an extension morphism
if and only if there is an extension morphism 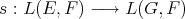
Proof. Suppose 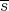 exists, and define
exists, and define 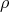 and
and 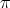 as in Theorem 2.1. Now let
as in Theorem 2.1. Now let 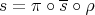 .
.  is continuous, linear, and for
is continuous, linear, and for 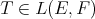 and
and 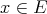 ,
, 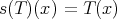 :
:
(x) - (k - 1)s(ρ(T ))(e)α(x) = D[ ρ(T)](e)(x) - (k - 1)ρ(T )(e)α(x) = T (x),](/img/revistas/ruma/v46n2/2a04492x.png)
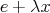 is in
is in 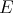 for any
for any 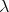 .
. Now suppose that  is given. We want to define
is given. We want to define 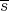 , and proceed as in the definition of the Aron-Berner extension. Given
, and proceed as in the definition of the Aron-Berner extension. Given 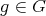 and
and 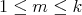 , define
, define
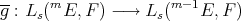
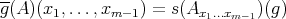 . Here
. Here 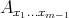 denotes the linear form obtained from
denotes the linear form obtained from 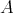 by fixing
by fixing  variables. Now, given
variables. Now, given 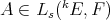 we may define the extended
we may define the extended 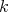 -linear function
-linear function 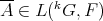 by
by 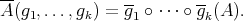
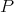 is a polynomial in
is a polynomial in 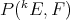 , and
, and 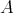 its associated symmetric
its associated symmetric 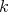 -linear function, set
-linear function, set 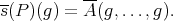
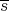 is a linear extension mapping from
is a linear extension mapping from 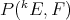 to
to 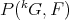 . □
. □ Note that the function 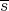 cannot be defined (even non-linearly) if
cannot be defined (even non-linearly) if  is not linear. Indeed, a non-linear
is not linear. Indeed, a non-linear  would induce a
would induce a 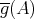 which would fail to be
which would fail to be 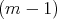 -linear in the above definition. Also, note that the constructions
-linear in the above definition. Also, note that the constructions  and
and 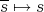 are not in general inverse of each other.
are not in general inverse of each other.
The fact that 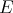 is a subspace of
is a subspace of 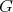 and
and  an extension map makes
an extension map makes 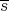 an extension map; however, the construction can be carried through for any continuous linear map
an extension map; however, the construction can be carried through for any continuous linear map 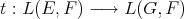 , giving rise to a continuous linear map
, giving rise to a continuous linear map

 need not be
need not be  . The following example is taken from [LZ].
. The following example is taken from [LZ]. Example 2.3. 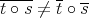 :
:
If  is a Banach space, consider (as in Example 1.9) the 2-homogeneous polynomial
is a Banach space, consider (as in Example 1.9) the 2-homogeneous polynomial  defined over
defined over 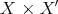 by
by 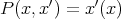 . Recall that the Aron-Berner extension of
. Recall that the Aron-Berner extension of 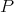 to
to  is
is
![-- P(x ′′,x′′′) = 1-[x ′′′(x′′) + x′′(ρ(x′′′))], 2](/img/revistas/ruma/v46n2/2a04539x.png)
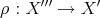 is the restriction (i.e., the transpose of the natural inclusion
is the restriction (i.e., the transpose of the natural inclusion 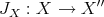 ). We will use the notation
). We will use the notation 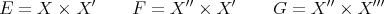

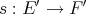 and
and 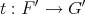 given by
given by 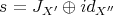 ,
,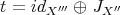 . Also, we denote
. Also, we denote 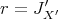 . We now check that
. We now check that 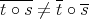 .
. First, calculate 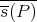 :
:
![----- iv ′′′ -- iv ′′′ 1- iv ′′′ ′′′ iv s(P )(x ,x ) = Q(x ,x ) = 2[x (x ) + x (r(x ))].](/img/revistas/ruma/v46n2/2a04551x.png)
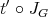 :
: 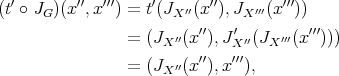
![----- (t ∘ s)(P)(x′′,x ′′′) = (s(P ) ∘ t′ ∘ JG)(x ′′,x′′′) ----- = s(P )(JX ′′(x′′),x′′′) 1 = --[JX ′′(x′′)(x′′′) + x′′′(r(JX′′(x′′)))] 2 = x′′′(x′′).](/img/revistas/ruma/v46n2/2a04554x.png)
![----- -- (t ∘ s)(P )(x ′′,x ′′′) = (P ∘ (t ∘ s)′ ∘ JG)(x ′′,x′′′) -- ′ ′ ′′ ′′′ = (P ∘ s)((t ∘ JG)(x ,x )) -- ′ ′′ ′′ ′′′ = (P ∘ s)(JX (x ),x ) = P (r(JX′′(x′′)),x′′′) -- ′′ ′′′ = P (x ,x ) 1 ′′′ ′′ ′′ ′′′ = --[x (x ) + x (ρ(x ))], 2](/img/revistas/ruma/v46n2/2a04555x.png)
 if and only if
if and only if 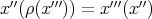 , but this only happens for reflexive
, but this only happens for reflexive 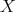 .
. We now provide some examples of situations in which a linear extension map exists for linear operators, and thus also for polynomials. We begin with the case of 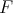 -valued polynomials in the first three examples, and continue with scalar-valued polynomials in the rest.
-valued polynomials in the first three examples, and continue with scalar-valued polynomials in the rest.
Example 2.4. (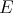 complemented in
complemented in 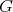 ):
):
This is clearly the simplest case for extension. If 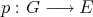 is a projector, any polynomial
is a projector, any polynomial  may be extended by setting
may be extended by setting 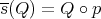 . This extension is a morphism and comes from
. This extension is a morphism and comes from 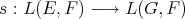
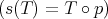 by the construction above.
by the construction above.
Example 2.5. ([Z1]):
If 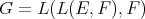 ,
, 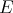 may be considered contained in
may be considered contained in 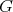 through the inclusion mapping
through the inclusion mapping  defined by
defined by 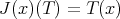 . In this case one may define
. In this case one may define 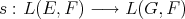 by
by 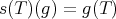 .
.
Example 2.6.
If there is a linear extension map for linear forms  , and
, and 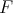 is complemented in its bidual (this happens, for example if
is complemented in its bidual (this happens, for example if 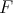 is a dual space), one may define
is a dual space), one may define 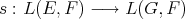 as follows. First define
as follows. First define 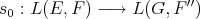 by
by 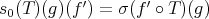 , and then
, and then  , where
, where  is the projection
is the projection  . If
. If  exists but
exists but 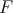 is not complemented in
is not complemented in 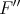 , one may define an extension morphism
, one may define an extension morphism 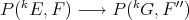 .
.
Example 2.7. (the Aron-Berner extension [AB]):
For 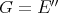 , the Aron-Berner extension comes from the extension morphism
, the Aron-Berner extension comes from the extension morphism  , the canonical inclusion of
, the canonical inclusion of 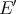 in its bidual.
in its bidual.
Example 2.8. (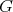 in an 'local' ultrapower of
in an 'local' ultrapower of 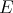 [DT], [LR]):
[DT], [LR]):
Suppose 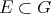 and
and 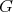 is finitely represented in
is finitely represented in 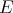 in the following sense: for each finite-dimensional subspace of
in the following sense: for each finite-dimensional subspace of 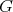 and each
and each 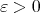 there is a isomorphism
there is a isomorphism 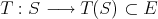 such that
such that 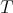 is the identity when restricted to
is the identity when restricted to  and
and 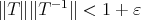 . In such a situation one can define a linear extension morphism
. In such a situation one can define a linear extension morphism  in the following way: Consider the indexing set
in the following way: Consider the indexing set 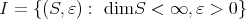 ordered by
ordered by 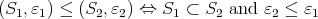 . The sets
. The sets 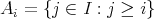 form a filter basis over
form a filter basis over 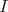 . Let
. Let  be any ultrafilter containing this basis. We have, for any
be any ultrafilter containing this basis. We have, for any 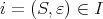 ,
,
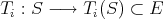
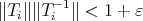 . For each
. For each 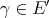 , define
, define 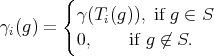
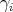 's are not linear,
's are not linear, 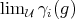 is, and we may define
is, and we may define 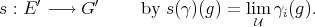
 is then a linear extension map, for if
is then a linear extension map, for if 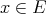 ,
, 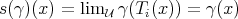 . This induces an extension morphism
. This induces an extension morphism 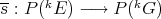 , which is the extension
, which is the extension  in [LR] and [DT].
in [LR] and [DT]. We now give more conditions equivalent to the existence of a linear extension morphism  (and therefore equivalent to the existence of a linear extension morphism for polynomials). Other conditions may be found in [CGJ1] and in [D4, Prop. 6.18]. The implication ii)
(and therefore equivalent to the existence of a linear extension morphism for polynomials). Other conditions may be found in [CGJ1] and in [D4, Prop. 6.18]. The implication ii)  iii) is taken from [D3]. First, some definitions:
iii) is taken from [D3]. First, some definitions:
We say 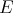 is finitely complemented in
is finitely complemented in 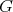 , if there is a constant
, if there is a constant  such that for all finite-dimensional subspaces
such that for all finite-dimensional subspaces 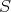 of
of 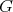 , there is a projector
, there is a projector 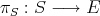 such that
such that 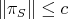 , and
, and 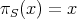 for
for 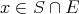 .
.
If 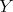 is a subspace of
is a subspace of  we shall say, following Dineen [D3], that
we shall say, following Dineen [D3], that 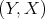 has the polynomial extension property if for all
has the polynomial extension property if for all 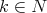 , each polynomial
, each polynomial 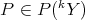 extends to a polynomial
extends to a polynomial 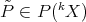 . Note that it is not required that these extensions define a linear morphism.
. Note that it is not required that these extensions define a linear morphism. 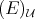 denotes the ultrapower of
denotes the ultrapower of 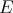 corresponding to the ultrafilter
corresponding to the ultrafilter  .
.
Theorem 2.9. Let 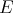 be a subspace of
be a subspace of 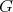 . Then the following are equivalent.
. Then the following are equivalent.
 .
. 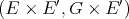 has the polynomial extension property.
has the polynomial extension property. 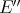 is complemented in
is complemented in  .
. 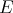 is finitely complemented in
is finitely complemented in 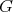 .
.  and a continuous linear function
and a continuous linear function  such that
such that 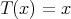 for
for 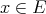 .
.
Proof. i) implies ii): Consider  the dual of
the dual of 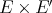 and
and 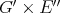 the dual of
the dual of 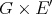 in the usual way. Then
in the usual way. Then

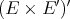 to
to 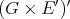 . Thus by the preceding theorem (with
. Thus by the preceding theorem (with 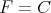 ) every
) every 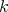 -homogeneous polynomial over
-homogeneous polynomial over 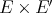 extends to a
extends to a 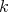 -homogeneous polynomial over
-homogeneous polynomial over  .
. ii) implies iii): Define 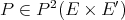 by
by 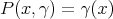 . There is, by ii), a polynomial
. There is, by ii), a polynomial 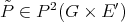 which extends
which extends 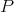 . This polynomial extends by Aron-Berner to a polynomial
. This polynomial extends by Aron-Berner to a polynomial 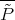 over
over 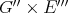 . We consider
. We consider  its restriction to
its restriction to  . Now if
. Now if 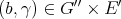 , let
, let
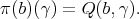
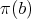 is an element of
is an element of 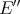 , and
, and 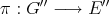 is continuous and linear. Now if
is continuous and linear. Now if 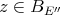 and
and 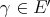 , the weak
, the weak -closure of
-closure of 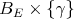 contains
contains 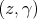 . Using the Davie-Gamelin theorem, construct a net
. Using the Davie-Gamelin theorem, construct a net  weak
weak -converging to
-converging to  and such that
and such that  . Then
. Then 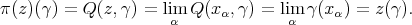
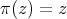 , and
, and 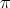 is a projection of
is a projection of 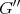 onto
onto 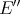 .
. iii) implies iv): If  is a projector, take
is a projector, take 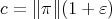 . For any finite-dimensional subspace
. For any finite-dimensional subspace  of
of  ,
,  is a finite-dimensional subspace of
is a finite-dimensional subspace of 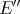 . By the local reflexivity principle [De] there is a linear operator
. By the local reflexivity principle [De] there is a linear operator
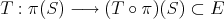
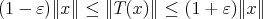 for
for 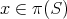 , and if
, and if 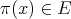 ,
, 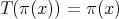 . Then
. Then 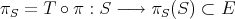 has norm
has norm  , and for
, and for 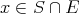 we have
we have 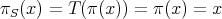 .
. iv) implies v): Consider the indexing set

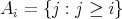 and
and  be an ultrafilter on
be an ultrafilter on 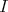 containing the
containing the 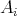 's. For each
's. For each 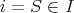 we have a projector
we have a projector 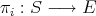 of norm not exceeding
of norm not exceeding  . Define for each
. Define for each 
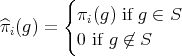
 be defined as
be defined as ![T (g) = [(^πi(g))]](/img/revistas/ruma/v46n2/2a04717x.png) (the class of the family
(the class of the family 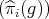 in the ultraproduct
in the ultraproduct 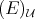 ).
). 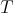 is linear -though the
is linear -though the 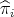 's are not- and
's are not- and 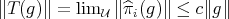 . Now if
. Now if 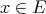 , for all
, for all 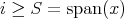 ,
, 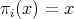 , so
, so ![T (x) = [(^πi(x))] = [(x)]](/img/revistas/ruma/v46n2/2a04726x.png) .
. v) implies i): First define 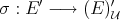 as
as ![σ(γ)([(xi)]) = limU γ(xi)](/img/revistas/ruma/v46n2/2a04728x.png) . Now set
. Now set 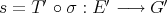 . This is a linear extension morphism. Indeed, for all
. This is a linear extension morphism. Indeed, for all 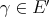 and
and 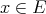 , we have
, we have
![′ s(γ)(x) = (T ∘ σ)(γ)(x) = (σ(γ) ∘ T)(x) = σ(γ)[(x)] = lim γ(x) U = γ(x).](/img/revistas/ruma/v46n2/2a04732x.png)
Some comments are in order. First, in iii) of the theorem we consider the bitranspose 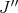 of the inclusion
of the inclusion  to be the natural inclusion map of
to be the natural inclusion map of 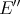 in
in 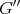 . This may, in some cases, be misleading. Consider for example the canonical inclusion
. This may, in some cases, be misleading. Consider for example the canonical inclusion 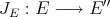 . Then it is easily checked that the inclusion
. Then it is easily checked that the inclusion 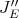 is not the canonical one
is not the canonical one 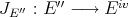 : indeed, let
: indeed, let 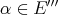 be non-zero, but such that
be non-zero, but such that 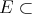 Ker
Ker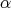 , and take
, and take 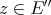 such that
such that 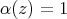 . Then
. Then
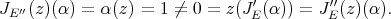
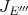 and
and 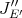 produce different extension morphisms
produce different extension morphisms 
Note ([CGJ1], [Ka]) also that from the point of view of homological algebra, while complementation of 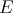 in
in  is the splitting of the sequence
is the splitting of the sequence
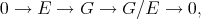
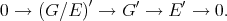
Note also that one could write a 'norm sensitive' version of the theorem, putting ' norm preserving',
norm preserving', 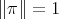 ,
, 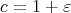 for any
for any  , and
, and 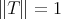 .
.
We close this section with an application of the procedure 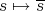 of Theorem 2.2. In [DD] Díaz and Dineen prove that if Banach spaces
of Theorem 2.2. In [DD] Díaz and Dineen prove that if Banach spaces 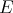 ,
, 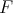 have isomorphic duals, and
have isomorphic duals, and 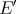 has the Schur property and the approximation property, then
has the Schur property and the approximation property, then 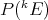 and
and 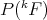 are isomorphic, i.e.: with the above hypotheses, the dual space
are isomorphic, i.e.: with the above hypotheses, the dual space 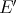 determines the space of polynomials
determines the space of polynomials 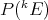 . If
. If 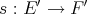 is an isomorphism, it seems natural to look into the map
is an isomorphism, it seems natural to look into the map 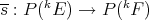 . As mentioned after Theorem 2.2, in general
. As mentioned after Theorem 2.2, in general 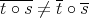 . However, in the presence of Arens regularity, the procedure is sufficiently well-behaved to produce the following result (proved independently in [CCG] and [LZ]).
. However, in the presence of Arens regularity, the procedure is sufficiently well-behaved to produce the following result (proved independently in [CCG] and [LZ]).
Theorem 2.10. If 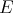 and
and 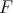 are symmetrically Arens-regular, and
are symmetrically Arens-regular, and 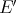 and
and 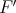 are isomorphic (resp. isometric), then for any
are isomorphic (resp. isometric), then for any 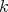 ,
, 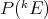 and
and 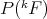 are isomorphic (resp. isometric). □
are isomorphic (resp. isometric). □
§3. Hahn-Banach type extensions
We now address the problem of when a continuous 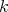 -homogeneous scalar-valued polynomial
-homogeneous scalar-valued polynomial 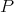 can be extended to any larger Banach space, regardless of whether other polynomials over the same space can be so extended and whether such extensions supply linear morphisms or not.
can be extended to any larger Banach space, regardless of whether other polynomials over the same space can be so extended and whether such extensions supply linear morphisms or not.
Following Kirwan and Ryan [KR], we shall say 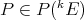 is extendible if it can be extended to a continuous polynomial over any Banach space
is extendible if it can be extended to a continuous polynomial over any Banach space 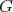 containing
containing 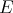 as a subspace, and denote by
as a subspace, and denote by 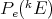 the space of all such polynomials. We start with some immediate comments on extendible polynomials.
the space of all such polynomials. We start with some immediate comments on extendible polynomials.
Remark 3.1.
All extendible polynomials are weakly sequentially continuous. Indeed, consider 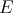 a subspace of
a subspace of 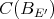 (the space of continuous functions over the closed unit ball of
(the space of continuous functions over the closed unit ball of 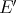 with the weak
with the weak topology), through the mapping
topology), through the mapping 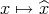 where
where 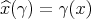 . If
. If  is an extendible polynomial over
is an extendible polynomial over  , it extends to a polynomial
, it extends to a polynomial 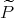 over
over 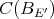 . Since
. Since 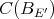 has the Dunford-Pettis property, every polynomial defined on it is weakly sequentially continuous [Ry1] and this forces
has the Dunford-Pettis property, every polynomial defined on it is weakly sequentially continuous [Ry1] and this forces 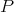 to be weakly sequentially continuous as well.
to be weakly sequentially continuous as well.
Remark 3.2.
If 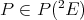 is extendible, and
is extendible, and 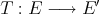 is the symmetric linear operator associated to
is the symmetric linear operator associated to 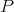 , then
, then 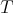 is weakly compact: Call
is weakly compact: Call 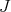 the inclusion of
the inclusion of 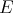 in
in 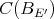 defined above, and let
defined above, and let 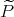 be an extension of
be an extension of 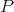 . This means that
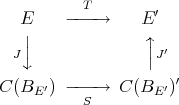
. This means that 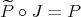 , or equivalently, that there is a symmetric linear operator
, or equivalently, that there is a symmetric linear operator  such that the following diagram commutes
such that the following diagram commutes
 is symmetrically regular,
is symmetrically regular, 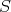 is weakly compact, and since
is weakly compact, and since 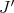 is weak-to-weak continuous,
is weak-to-weak continuous, 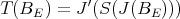 is weakly precompact. Thus
is weakly precompact. Thus 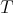 is weakly compact.
is weakly compact. Remark 3.3.
From [KR]: If 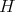 is a Hilbert space, and
is a Hilbert space, and 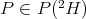 , then
, then 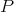 is extendible if and only if
is extendible if and only if 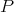 is nuclear: Suppose first that
is nuclear: Suppose first that 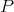 is extendible and, much as in the previous example, consider
is extendible and, much as in the previous example, consider 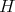 contained in
contained in 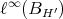 . On extending
. On extending 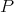 one obtains the diagram
one obtains the diagram
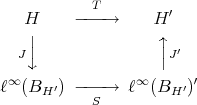
 is an
is an  -space,
-space,  and
and 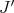 are 2-summing, and so
are 2-summing, and so  is nuclear. Then
is nuclear. Then 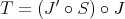 is nuclear, and so is
is nuclear, and so is  . The other implication is trivial, for all nuclear polynomials on any space are extendible.
. The other implication is trivial, for all nuclear polynomials on any space are extendible. We may now present a few concrete examples of non-extendible scalar-valued polynomials.
1) 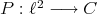 , given by
, given by 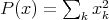 cannot be extendible, for it is not weakly sequentially continuous: the unit basis in
cannot be extendible, for it is not weakly sequentially continuous: the unit basis in 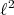 tends weakly to
tends weakly to 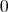 , but
, but 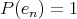 for any
for any 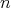 (also,
(also, 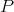 is not nuclear).
is not nuclear).
2) 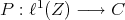 , given by
, given by 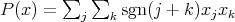 is not extendible. This is the polynomial corresponding to the non-weakly compact operator given in Example 1.1, so it cannot be extendible.
is not extendible. This is the polynomial corresponding to the non-weakly compact operator given in Example 1.1, so it cannot be extendible.
3) 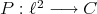 , given by
, given by 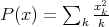 is not extendible, for it is not nuclear (and
is not extendible, for it is not nuclear (and 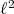 is a Hilbert space).
is a Hilbert space). 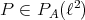 ; thus there are approximable polynomials which are not extendible.
; thus there are approximable polynomials which are not extendible.
There are, in general, many non-extendible scalar valued polynomials on a Banach space. There are some classes of polynomials, however, which are always extendible. All finite-type and all nuclear polynomials can be extended by simply applying the Hahn-Banach theorem to their component linear forms. It is also true that all integral polynomials over a Banach space are extendible [CZ1].
A problem related to the non-extendibility of polynomials and considered by P. Mazet in [Ma2] is the following: find the smallest constant  such that for any hyperplane
such that for any hyperplane 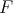 in
in 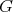 every 2-homogeneous polynomial
every 2-homogeneous polynomial 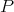 on
on 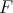 can be extended to
can be extended to 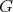 with the norm of the extension not exceeding
with the norm of the extension not exceeding 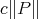 . Clearly
. Clearly  must be larger than one, for otherwise using a transfinite induction argument every
must be larger than one, for otherwise using a transfinite induction argument every 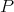 would be extendible. Mazet finds the following bounds.
would be extendible. Mazet finds the following bounds.
Theorem 3.4. For real spaces,  . For complex spaces,
. For complex spaces, 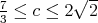 . □
. □
One way of extending polynomials defined on 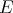 to
to 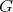 would be to identify each with a linear form, and then apply the Hahn-Banach theorem to this linear form. Thus, we are interested in representing spaces of polynomials as dual spaces: say
would be to identify each with a linear form, and then apply the Hahn-Banach theorem to this linear form. Thus, we are interested in representing spaces of polynomials as dual spaces: say 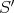 is algebraically isomorphic to a subspace
is algebraically isomorphic to a subspace  of
of 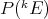 , and that
, and that 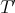 is algebraically isomorphic to a subspace
is algebraically isomorphic to a subspace 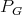 of
of 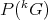 , and that there is an linear inyection
, and that there is an linear inyection  . Then if
. Then if 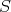 is topologically a subspace of
is topologically a subspace of 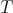 , each
, each 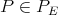 (considered as a linear form over
(considered as a linear form over 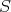 ) may be extended by Hahn-Banach to
) may be extended by Hahn-Banach to 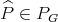 . In fact, any given polynomial
. In fact, any given polynomial 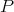 will be extendible to
will be extendible to 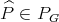 if and only if, as a linear functional on
if and only if, as a linear functional on 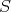 it is continuous for the topology induced on
it is continuous for the topology induced on 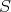 by
by 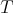 .
.
There have been several constructions of preduals of spaces of polynomials, and indeed, of spaces of holomorphic functions. In fact, the constructions usually produce more than just preduals. They produce solutions to the following problem: given a space of scalar-valued functions 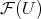 on the set
on the set 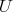 , can one construct a space
, can one construct a space 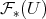 and a function
and a function  of the same type as those of
of the same type as those of 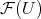 factoring all functions of
factoring all functions of 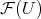 and identifying each with a continuous linear form
and identifying each with a continuous linear form 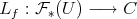 ? That is,
? That is,
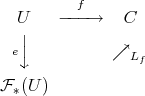
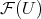 algebraically and topologically with the dual of
algebraically and topologically with the dual of 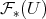 , and indeed, the space of
, and indeed, the space of 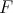 -valued functions
-valued functions 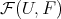 with the continuous linear operators
with the continuous linear operators 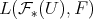 . The existence of such a 'linearization' is strictly stronger than the mere existence of a predual.
. The existence of such a 'linearization' is strictly stronger than the mere existence of a predual. Constructions of this type have been obtained for spaces of continuous homogeneous polynomials by R. Ryan [Ry2] through the use of symmetric tensor products. In the holomorphic setting, linearizations have been constructed for holomorphic functions by P. Mazet [Ma1] and J. Mujica and L. Nachbin [MN], for bounded holomorphic functions by J. Mujica [M2], and for holomorphic functions of bounded type by P. Galindo, D. García and M. Maestre [GGM1] and Mujica [M3] (see also [Boy]). A more abstract approach produces linearizations for a wide class of function spaces [CZ2].
We restrict our attention here to preduals of spaces of polynomials. Given 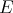 , let us denote by
, let us denote by 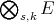 the vector space of symmetric
the vector space of symmetric 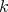 -fold tensor products of elements of
-fold tensor products of elements of 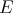 . Its algebraic dual
. Its algebraic dual 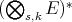 is the space of all (not necesarily continuous)
is the space of all (not necesarily continuous) 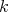 -homogeneous polynomials over
-homogeneous polynomials over 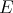 . Furthermore, if
. Furthermore, if 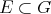 , there is a linear injection
, there is a linear injection  . By requiring more or less stringent continuity conditions of the elements of
. By requiring more or less stringent continuity conditions of the elements of 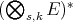 one may obtain all classes of polynomials over
one may obtain all classes of polynomials over 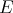 , in fact the following result holds [CZ1].
, in fact the following result holds [CZ1].
Proposition 3.5. If 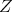 is any subspace of
is any subspace of 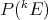 containing the finite type polynomials,
containing the finite type polynomials, 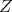 is (algebraically) isomorphic to
is (algebraically) isomorphic to 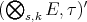 , where
, where  is a Hausdorff locally convex topology on
is a Hausdorff locally convex topology on 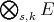 . □
. □
Note that C. Boyd and R. Ryan have proved that not all such subspaces of 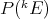 are dual Banach spaces [BoyR]. We illustrate the proposition above by presenting a few of the classical polynomial spaces as duals of
are dual Banach spaces [BoyR]. We illustrate the proposition above by presenting a few of the classical polynomial spaces as duals of 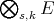 with the topologies indicated. We denote a typical element
with the topologies indicated. We denote a typical element  of
of 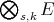 as a finite sum
as a finite sum 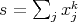 , where the
, where the 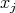 's are elements of
's are elements of 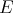 (this representation is not unique).
(this representation is not unique).
a) 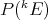 is isometrically the dual of
is isometrically the dual of 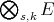 when this space is endowed with the projective tensor norm [Ry2],
when this space is endowed with the projective tensor norm [Ry2], 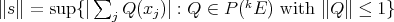 .
.
b) 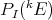 is isometrically the dual of
is isometrically the dual of 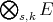 , when endowed with the following norm (equivalent to the injective tensor norm):
, when endowed with the following norm (equivalent to the injective tensor norm):
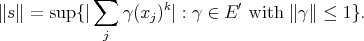
c) 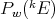 is algebraically the dual of
is algebraically the dual of 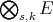 when endowed with the following locally convex topology [CZ1]. Consider, for each compact subset
when endowed with the following locally convex topology [CZ1]. Consider, for each compact subset 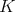 of
of 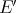 , the following seminorm on
, the following seminorm on 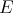 :
: 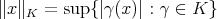 , and define the seminorm
, and define the seminorm 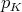 on
on 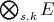 by
by 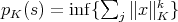 , where the infimum ranges over all possible representations of
, where the infimum ranges over all possible representations of  . If
. If 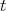 is the topology induced by all such seminorms, we obtain an algebraic isomorphism
is the topology induced by all such seminorms, we obtain an algebraic isomorphism 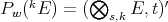 .
.
For more on tensor products of Banach spaces see [DF] and [Ry3].
We now review some results of Carando, Dimant, Kirwan, Pérez-García, Ryan, and Sevilla regarding the space 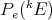 of all extendible polynomials over
of all extendible polynomials over 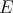 . As a set, we have seen that
. As a set, we have seen that 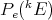 is contained in the space of weakly sequentially continuous polynomials, and that it contains the space of integral polynomials, but not in general the approximable polynomials. Kirwan and Ryan have proved the following.
is contained in the space of weakly sequentially continuous polynomials, and that it contains the space of integral polynomials, but not in general the approximable polynomials. Kirwan and Ryan have proved the following.
Theorem 3.6. Let 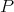 be an extendible polynomial. There is then a constant
be an extendible polynomial. There is then a constant  such that for any Banach space
such that for any Banach space 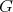 containing
containing 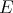 , some extension of
, some extension of 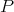 to
to 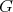 has norm not larger than
has norm not larger than  . □
. □
In their proof they construct a Banach space which is an 'amalgamation' of all those which contain 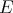 , and extend
, and extend 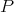 to this large space. It is therefore possible to define a norm on
to this large space. It is therefore possible to define a norm on 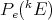 by setting
by setting
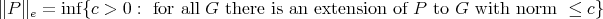
This norm is larger than the usual norm in 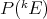 , and is equivalent to it if and only if every polynomial is extendible. Also,
, and is equivalent to it if and only if every polynomial is extendible. Also, 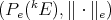 is complete, and a predual of it is obtained by putting in
is complete, and a predual of it is obtained by putting in 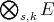 the norm
the norm
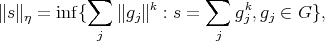
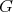 's range over all Banach spaces containing
's range over all Banach spaces containing 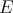 as a subspace.
as a subspace. In [C1], Carando takes a different approach to obtain a predual of 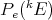 . Starting with the inclusion
. Starting with the inclusion  defined in Remark 3.1, he considers
defined in Remark 3.1, he considers
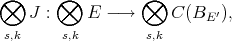
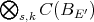 the projective norm, and then considering in
the projective norm, and then considering in 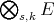 the norm induced by this map.
the norm induced by this map. Apart from the map 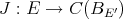 , another inclusion which has proved useful in the study of extendible polynomials is
, another inclusion which has proved useful in the study of extendible polynomials is
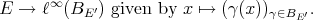
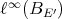 has the metric extension property [DF], that is, given a linear map
has the metric extension property [DF], that is, given a linear map 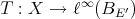 and
and 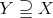 ,
, 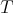 admits a norm-preserving extension to
admits a norm-preserving extension to 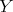 . The following results are adapted from [C1] and [CGJ1].
. The following results are adapted from [C1] and [CGJ1]. Theorem 3.7. Let 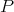 be a scalar-valued
be a scalar-valued 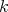 -homogeneous polynomial over
-homogeneous polynomial over 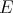 . Then the following are equivalent:
. Then the following are equivalent:
a) 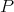 is extendible.
is extendible.
b) 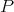 extends to
extends to 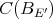 .
.
b') For some compact set 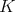 , there is a linear operator
, there is a linear operator  , and
, and 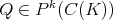 such that
such that 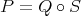 .
.
c) 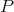 extends to
extends to 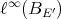 .
.
c') For some set 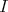 , there is a linear operator
, there is a linear operator  , and
, and 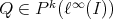 such that
such that 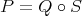 . □
. □
In [CGJ1] the authors study extendibility of bilinear forms, and obtain, among other results:
Theorem 3.8. Let 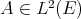 . Then the following are equivalent.
. Then the following are equivalent.
a) 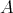 is extedible.
is extedible.
b) There exists an 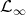 -space and operators
-space and operators 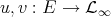 and
and 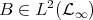 such that
such that 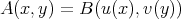 .
.
c) There exists a Hilbert space 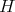 and two 2-summing operators
and two 2-summing operators 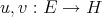 such that
such that 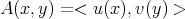 . □
. □
Results similar to those of Theorem 3.6 for vector-valued polynomials can be found in [C1]. There the following results for a 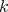 -homogeneous polynomial
-homogeneous polynomial 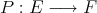 are obtained.
are obtained.
Theorem 3.9.  is extendible if and only if
is extendible if and only if  extends to
extends to 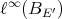 . If
. If 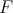 is complemented in its bidual,
is complemented in its bidual, 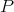 is extendible if and only if
is extendible if and only if 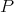 extends to
extends to 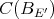 . □
. □
An immediate corollary of b') above is
Corollary 3.10. If 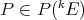 is extendible, and
is extendible, and 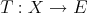 linear, then
linear, then  is extendible and
is extendible and 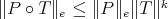 . □
. □
Thus, any restriction of an extendible polynomial is extendible. Also, if 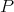 is extendible, so is its Aron-Berner extension. By c), and the fact that
is extendible, so is its Aron-Berner extension. By c), and the fact that 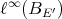 has the metric extension property, the norm of any extension of
has the metric extension property, the norm of any extension of 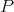 to any space can be bounded by the norm of any extension of
to any space can be bounded by the norm of any extension of 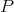 to
to 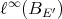 . Thus the 'extendible' norm
. Thus the 'extendible' norm  defined above can also be expressed as
defined above can also be expressed as
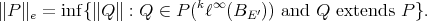
In [P] Pisier gave a counterexample to a well-known conjecture of Grothendieck [G] regarding the non-existence of non-nuclear locally convex spaces 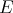 and
and 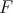 such that the injective and projective tensor norms coincide on the tensor product
such that the injective and projective tensor norms coincide on the tensor product  . Pisier constructed a Banach space
. Pisier constructed a Banach space 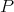 such that
such that  . Thus, over Pisier's space all 2-homogeneous polynomials are integral. The situation is very different for polynomials of degree higher than 2. Indeed, [Pg] has shown that any infinite-dimensional Banach space admits extendible non-integral polynomials of any degree higher that 3, and in [CD] Carando and Dimant close the gap by proving the same for any degree higher than 2. Their construction makes use of finite-dimensional estimates of Boas [Boa].
. Thus, over Pisier's space all 2-homogeneous polynomials are integral. The situation is very different for polynomials of degree higher than 2. Indeed, [Pg] has shown that any infinite-dimensional Banach space admits extendible non-integral polynomials of any degree higher that 3, and in [CD] Carando and Dimant close the gap by proving the same for any degree higher than 2. Their construction makes use of finite-dimensional estimates of Boas [Boa].
Any space of cotype 2 (this includes 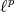 spaces for
spaces for 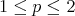 ) can be embedded in Pisier's space [P]. Thus if
) can be embedded in Pisier's space [P]. Thus if 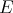 has cotype 2, all extendible 2-homogenesous polynomials over
has cotype 2, all extendible 2-homogenesous polynomials over 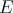 are integral. Indeed, an extension to Pisier's space will be integral, and thus also the original polynomial ([CGJ1], [C2]).
are integral. Indeed, an extension to Pisier's space will be integral, and thus also the original polynomial ([CGJ1], [C2]).
Regarding extendible polynomials on 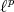 spaces, Carando, Dimant and Sevilla [C2] [CDS] have constructed on all
spaces, Carando, Dimant and Sevilla [C2] [CDS] have constructed on all 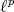 spaces with
spaces with  extendible polynomials which are not integral.
extendible polynomials which are not integral.
Polynomials of degree two and bilinear forms have attracted particular attention in recent years. In [CGJ2] a homological approach is applied to the problem of extendibility of bilinear forms from 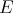 to
to 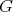 . Considerations of pushout and pullback diagrams produce the results:
. Considerations of pushout and pullback diagrams produce the results:
Proposition 3.11. If for all 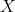 the sequences
the sequences
 extend to
extend to  . If for all
. If for all 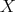 the sequences
the sequences 
 extend to
extend to  . □
. □ Since some of these properties are known when  is an
is an 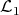 -space, the authors concentrate on these and produce the following:
-space, the authors concentrate on these and produce the following:
Theorem 3.12. If  is an
is an 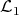 -space and
-space and 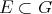 , the following are equivalent.
, the following are equivalent.
a) All bilinear forms on 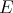 extend to
extend to 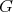 .
.
b) All exact sequences 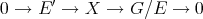 split.
split.
c) All exact sequences  split.
split.
[A] Alencar, R., Multilinear mappings of nuclear and integral type, Proc. Amer. Math. Soc. 94 (1) (1985), 33-38.
[A1] Arens, R., The adjoint of a bilinear operation, Proc. Amer. Math. Soc. 2 (1951), 839-848.
[A2] Arens, R., Operations induced in function classes, Monatsh. Math. 55 (1951), 1-19.
[AB] Aron, R. and Berner, P., A Hahn-Banach extension theorem for analytic mappings, Bull. Soc. Math. France 106 (1) (1978), 3-24.
[ABC] Aron, R., Boyd, C. and Choi, Y. S., Unique Hahn-Banach theorems for spaces of homogeneous polynomials, J. Aust. Math. Soc. 70 (3) (2001), 387-400.
[ACG1] Aron, R., Cole, B., and Gamelin, T., Spectra of algebras of analytic functions on a Banach space, J. Reine Angew. Math. 415 (1991), 51-93.
[ACG2] Aron, R., Cole, B., and Gamelin, T., Weak-star continuous analytic functions, Canad. Jour. Math. 47 (4) (1995), 673-683.
[AD] Aron, R. and Dineen, S., Q-reflexive Banach spaces, Rocky Mountain Jour. Math. 27(4) (1997), 1009-1025.
[AG] Aron, R. and Galindo, P., Weakly compact multilinear mappings, Proc. Edinburgh Math. Soc. 40 (1997), 181-192.
[AGGM] Aron, R., Galindo, P., García, D., and Maestre, M., Regularity and algebras of analytic functions in infinite dimensions, Trans. Amer. Math. Soc. 348 (2) (1996), 543-559.
[AHV] Aron, R., Hervés, C. and Valdivia, M., Weakly continuous mappings on Banach spaces, Jour. Funct. Anal. 52 (2) (1983), 189-204.
[ALRR] Aron, R., Lindström, M., Ruess, W. and Ryan, R., Uniform factorization for compact sets of operators, Proc. Amer. Math. Soc. 127(4) (1999), 1119-1125.
[AP] Aron, R. and Prolla, J., Polynomial approximation of differentiable functions on Banach spaces, Jour. Reine Angew. Math. 313 (1980), 195-216.
[AS] Aron, R. and Schottenloher, M., Compact holomorphic mappings on Banach spaces and the approximation property, Jour. Funct. Anal. 21 (1) (1976), 7-30.
[Ba] Barroso, J., Introduction to holomorphy North-Holland Math. Studies, 106, 1985.
[BLLl] Benyamini, Y., Lassalle, S. and Llavona, J. L. G., Homogeneous orthogonally-additive polynomials on Banach lattices, Bull. London Math. Soc. 38(3) (2006), 459-469.
[Boa] Boas, H. P., Majorant series, J. Korean Math. Soc. 37(2) (2000), 321-337.
[Bol] Boland, P., Holomorphic functions on nuclear spaces, Trans. Amer. Math. Soc. 209 (1975), 275-281.
[Boy] Boyd, C., Montel and reflexive preduals of spaces of holomorphic functions on Fréchet spaces, Studia Math. 107(3) (1993), 305-315.
[BoyR] Boyd, C. and Ryan, R., Geometric theory of spaces of integral polynomials and symmetric tensor products, J. Funct. Anal. 179(1) (2001), 18-42.
[CCG] Cabello Sánchez, F., Castillo, J. M. F. and García, R., Polynomials on dual-isomorphic spaces Ark. Mat. 38 (2000), 37-44.
[C1] Carando, D., Extendible polynomials on Banach spaces, J. Math. Anal. Appl. 233(1) (1999), 359-372.
[C2] Carando, D., Extendibility of polynomials and analytic functions on 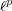 , Studia Math. 145(1) (2001), 67-73.
, Studia Math. 145(1) (2001), 67-73.
[CD] Carando, D. and Dimant, V., Extension of polynomials and John's theorem for symmetric tensor products to appear in Proc. of the Amer. Math. Soc.
[CDDL] Carando, D., Dimant, V., Duarte, B. and Lassalle, S., 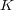 -bounded polynomials, Math. Proc. Royal Irish Acad. 98A(2) (1998), 159-171.
-bounded polynomials, Math. Proc. Royal Irish Acad. 98A(2) (1998), 159-171.
[CDS] Carando, D., Dimant, V. and Sevilla, P., Limit orders and multilinear forms on 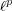 spaces, Publ. RIMS 42 (2006), 507-522.
spaces, Publ. RIMS 42 (2006), 507-522.
[CLZ] Carando, D., Lassalle, S. and Zalduendo, I., Orthogonally additive polynomials over 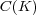 are measures -a short proof to appear in Int. Eq. and Oper. Theory.
are measures -a short proof to appear in Int. Eq. and Oper. Theory.
[CZ1] Carando, D. and Zalduendo, I., A Hahn-Banach theorem for integral polynomials, Proc. Amer. Math. Soc. 127 (1999), 241-250.
[CZ2] Carando, D. and Zalduendo, I., Linearization of functions, Math. Ann. 328 (2004), 683-700.
[CGJ1] Castillo, J. M. F., García, R. and Jaramillo, J. A., Extension of bilinear forms on Banach spaces, Proc. Amer. Math. Soc. 129(12) (2001), 3647-3656.
[CGJ2] Castillo, J. M. F., García, R. and Jaramillo, J. A., Extension of bilinear forms from subspaces of 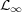 -spaces, Ann. Acad. Sci. Fenn. 27 (2002), 91-96.
-spaces, Ann. Acad. Sci. Fenn. 27 (2002), 91-96.
[CM] Colombeau, J. F. and Mujica, J., Holomorphic and differentiable mappings of uniform bounded type, North-Holland Math. Studies 71 (1982), 179-200.
[DG] Davie, A. and Gamelin, T., A theorem on polynomial-star approximation Proc. Amer. Math. Soc. 106 (2) (1989), 351-356.
[De] Dean, D., The equation  and the principle of local reflexivity, Proc. Amer Math. Soc. 40 (1973), 146-148.
and the principle of local reflexivity, Proc. Amer Math. Soc. 40 (1973), 146-148.
[DF] Defant, A. and Floret, K., Tensor norms and operator ideals, North-Holland, Amsterdam, 1993.
[DD] Díaz, J. C. and Dineen, S., Polynomials on stable spaces, Ark. Mat. 36 (1998) 87-96.
[D1] Dineen, S., Holomorphically complete locally convex topological vector spaces, LNM 332 (1973), 77-111.
[D2] Dineen, S., Complex analysis in locally convex spaces, North-Holland Math. Studies, 57, 1981.
[D3] Dineen, S., Quasinormable spaces of holomorphic functions Note Mat. 13 (1) (1993), 155-195.
[D4] Dineen, S., Complex analysis on infinite dimensional spaces, Springer-Verlag, London, 1999.
[DT] Dineen, S. and Timoney, R., Complex geodesics on convex domains, North-Holland Math. Studies 170 (1992), 333-365.
[DH] Duncan, J. and Hosseiniun, S., The second dual of a Banach algebra Proc. Royal Soc. Edinb. A84 (1979), 309-325.
[FGLl] Ferrera, J., Gómez, J. and Llavona, J., On completion of spaces of weakly continuous functions, Bull. London Math. Soc. 15 (1983), 260-264.
[GGM1] Galindo, P., García, D. and Maestre, M., Holomorphic mappings of bounded type, J. Math. Anal. Appl. 166(1) (1992), 236-246.
[GGM2] Galindo, P., García, D. and Maestre, M., Entire functions of bounded type on Fréchet spaces, Math. Nachr. 161 (1993), 185-198.
[GGMM] Galindo, P., García, D., Maestre, M., and Mujica, J., Extensions of multilinear mappings on Banach spaces, Studia Math. 108 (1) (1994), 55-76.
[GI] Godefroy, G. and Iochum, B., Arens-regularity of Banach algebras and geometry of Banach spaces, Jour. Funct. Anal. 80 (1988), 47-59.
[GG] González, M. and Gutiérrez, J., When every polynomial is unconditionally converging, Arch. Math. 63 (2) (1994), 145-151.
[G] Grothendieck, A. Résumé de la théorie métrique des produits tensoriels topologiques, Bol. Soc. Mat. Sao Paulo 8 (1956), 83-110.
[GJLl] Gutiérrez, J., Jaramillo, J. and Llavona, J., Polynomials and geometry of Banach spaces, Extracta Math. 10 (2) (1995), 79-114.
[H] Haydon, R., Some more characterizations of Banach spaces containing 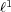 , Math. Proc. Cambridge Phil. Soc. 80 (2) (1976), 269-276.
, Math. Proc. Cambridge Phil. Soc. 80 (2) (1976), 269-276.
[HP] Hille, E. and Phillips, R., Functional analysis and semigroups, Amer. Math. Soc., Providence, RI, 1974.
[IL] Iochum, B. and Loupias, G., Arens regularity and local reflexivity principle for Banach algebras, Math. Ann. 284 (1) (1989), 23-40.
[JPZ] Jaramillo, J., Prieto, A. and Zalduendo, I., The bidual of the space of polynomials on a Banach space, Math. Proc. Cambridge Phil. Soc. 122 (1997), 457-471.
[Ka] Kalton, N., Locally complemented subspaces and 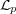 -spaces for
-spaces for 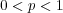 , Math. Nachr. 115 (1984), 71-97.
, Math. Nachr. 115 (1984), 71-97.
[Kh1] Khue, N. V., On the extension of holomorphic maps on locally convex space, Ann. Polon. Math. 43(3) (1983), 267-282.
[Kh2] Khue, N. V., On the extension of holomorphic functions on locally convex spaces with values in Fréchet spaces, Ann. Polon. Math. 44(2) (1984), 163-175.
[KR] Kirwan, P. and Ryan, R., Extendibility of homogeneous polynomials on Banach spaces, Proc. Amer. Math. Soc. 126(4) (1998), 1023-1029.
[LZ] Lassalle, S. and Zalduendo, I., To what extent does the dual Banach space 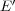 determine the polynomials over
determine the polynomials over 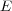 ?, Ark. Mat. 38 (2000), 343-354.
?, Ark. Mat. 38 (2000), 343-354.
[LR] Lindström, M. and Ryan, R., Applications of ultraproducts to infinite-dimensional holomorphy, Math. Scand. 71 (2) (1992), 229-242.
[Ma1] Mazet, P., Analytic sets in locally convex spaces, North-Holland Mathematics Studies 89 (1984).
[Ma2] Mazet, P., A Hahn-Banach theorem for quadratic forms, Math. Proc. of the Royal Irish Ac. 100A(2) (2000), 177-182.
[MV] Meise, R. and Vogt, D., Extension of entire functions on nuclear locally convex spaces, Proc. Amer. Math. Soc. 92 (4) (1984), 494-500.
[Mo1] Moraes, L., The Hahn-Banach extension theorem for some spaces of n-homogeneous polynomials, North-Holland Math. Studies 90 (1984), 265-274.
[Mo2] Moraes, L., A Hahn-Banach extension theorem for some holomorphic functions, North-Holland Math. Studies 125 (1986), 205-220.
[Mo3] Moraes, L., Extension of holomorphic mappings from 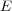 to
to 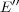 , Proc. Amer. Math. Soc. 118 (2) (1993), 455-461.
, Proc. Amer. Math. Soc. 118 (2) (1993), 455-461.
[M1] Mujica, J., Complex analysis in Banach spaces, North-Holland Math. Studies, 120, Amsterdam, 1986.
[M2] Mujica, J., Linearization of bounded holomorphic mappings on Banach spaces, Trans. Amer. Math. Soc. 324 (1991), 867-887.
[M3] Mujica, J., Linearization of holomorphic mappings of bounded type, Progress in Functional Analysis (1992), North-Holland, Amsterdam, 149-162.
[MN] Mujica, J. and Nachbin, L., Linearization of holomorphic mappings on locally convex spaces, J. Math. Pures Appl. 71 (1992), 543-560.
[N] Nachbin, L., Topology on spaces of holomorphic mappings, Springer-Verlag, New York, 1969.
[Ni] Nicodemi, O., Homomorphisms of algebras of germs of holomorphic functions, LNM 843 (1981), 534-546.
[Pg] Pérez-García, D., A counterexample using 4-linear forms, Bull. Aust. Math. Soc. 70(3) (2004), 469-473.
[PgV] Pérez-García, D. and Villanueva, I., Orthogonally additive polynomials on spaces of continuous functions, J. Math. Anal. Appl. 306(1) (2005), 97-105.
[PZ] Pinasco, D. and Zalduendo, I., Integral representation of holomorphic functions on Banach spaces, J. Math. Anal. Appl. 308 (2005), 159-174.
[P] Pisier, G., Counterexamples to a conjecture of Grothendieck, Acta Math. 151 (1983), 181-208.
[Re] Rennison, J., A note on the extension of associative products, Proc. Amer. Math. Soc. 17 (6) (1966), 1375-1377.
[Rp] Rodríguez Palacios, A., A note on Arens regularity, Quart. Jour. Math. Oxford Ser. 2 38 (149) (1987), 91-93.
[Ry1] Ryan, R., Dunford-Pettis properties, Bull. Acad. Polon. Sci. 27 (1979), 373-379.
[Ry2] Ryan, R., Applications of topological tensor products to infinite dimensional holomorphy, Ph. D. thesis, University College, Dublin, 1980.
[Ry3] Ryan, R., Introduction to tensor products of Banach spaces, Springer-Verlag, London, 2002.
[S] Stegall, C., Duals of certain spaces with the Dunford-Pettis property, Notices Amer. Math. Soc. 19 (7) (1972), A799.
[T] Toma, E., Aplicaçoes holomorfas e polinomios  -continuos, Ph. D. thesis, Universidade Federal do Rio de Janeiro, Rio de Janeiro, 1993.
-continuos, Ph. D. thesis, Universidade Federal do Rio de Janeiro, Rio de Janeiro, 1993.
[Z1] Zalduendo, I., A canonical extension for analytic functions on Banach spaces, Trans. Amer. Math. Soc. 320 (2) (1990), 747-763.
[Z2] Zalduendo, I., A simple example of a non-commutative Arens product, Publ. Mat. 35 (2) (1991), 475-477.
[Z3] Zalduendo, I., Extending polynomials-a survey, Publicaciones del Departamento de Análisis Matemático - Universidad Complutense de Madrid secc. 1, Num. 41 (1998).
Ignacio Zalduendo
Departamento de Matemática,
Universidad Torcuato Di Tella,
Miñones 2177 (C1428ATG),
Buenos Aires, Argentina
nacho@utdt.edu
Recibido: 12 de setiembre de 2005
Aceptado: 7 de agosto de 2006














