Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.46 n.2 Bahía Blanca jul./dic. 2005
Infinitely many minimal curves joining arbitrarily close points in a homogeneous space of the unitary group of a C*-algebra
Esteban Andruchow, Luis E. Mata-Lorenzo, Lázaro Recht, Alberto Mendoza and Alejandro Varela
Dedicated to the memory of Ángel Rafael Larotonda (Pucho).
Abstract: We give an example of a homogeneous space of the unitary group of a C*-algebra which presents a remarkable phenomenon, in its natural Finsler metric there are infinitely many minimal curves joining arbitrarily close points.
In this paper, we give an example of a homogeneous space of the unitary group of a C -algebra which presents a remarkable phenomenon. Namely, in its natural Finsler metric there are infinitely many minimal curves joining arbitrarily close points. More precisely the homogeneous space will be called
-algebra which presents a remarkable phenomenon. Namely, in its natural Finsler metric there are infinitely many minimal curves joining arbitrarily close points. More precisely the homogeneous space will be called  . The unitary group
. The unitary group  of a C
of a C -algebra
-algebra  acts transitively on the left on
acts transitively on the left on  . The action is denoted by
. The action is denoted by  , for
, for 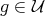 and
and 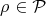 . The isotropy
. The isotropy 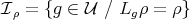 will be the unitary group of a
will be the unitary group of a 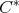 -subalgebra
-subalgebra 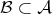 . The Finsler norm in
. The Finsler norm in 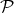 is naturally defined by
is naturally defined by 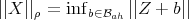 , for
, for 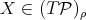 where
where 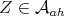 projects to
projects to 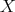 in the quotient
in the quotient 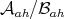 which is identified to the tangent space
which is identified to the tangent space 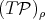 . These definitions and notation are borrowed from [1].
. These definitions and notation are borrowed from [1].
This work is part of a forthcoming paper by the same authors which will contain additional results about minimal vectors. We call an element 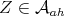 minimal vector if
minimal vector if 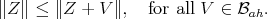
In [1] the following theorem is proven.
Theorem 2.1. Let 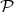 be a homogeneous space of the unitary group of a C
be a homogeneous space of the unitary group of a C -algebra
-algebra 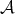 . Consider
. Consider 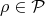 and
and 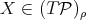 . Suppose that there exists
. Suppose that there exists 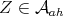 which is a minimal vector i.e.
which is a minimal vector i.e. 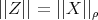 . Then the oneparameter curve
. Then the oneparameter curve 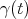 given by
given by 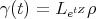 has minimal length in the class of all curves in
has minimal length in the class of all curves in 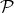 joining
joining 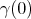 to
to 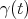 for each
for each 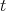 with
with 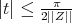 .
.
We will use the following notation. Let 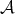 be a unital C
be a unital C -algebra, and
-algebra, and 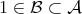 a C
a C -subalgebra. Denote
-subalgebra. Denote 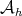 and
and 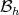 (resp.
(resp. 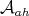 and
and 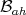 ) the sets of selfadjoint (resp. anti-hermitian) elements of
) the sets of selfadjoint (resp. anti-hermitian) elements of 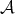 and
and  . Let
. Let 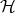 be a Hilbert space,
be a Hilbert space, 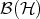 the algebra of bounded operators acting on
the algebra of bounded operators acting on 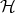 , and
, and 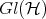 the group of invertible operators.
the group of invertible operators.
We call an element 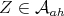 a minimal vector if
a minimal vector if
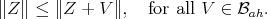
Note that since for any operator, 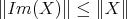 , it follows that
, it follows that 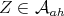 is minimal if and only if
is minimal if and only if
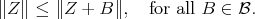
In view of the purpose of this paper stated in the introduction and the previous theorem, to look for minimal curves we have to find minimal vectors and therefore the following theorem is relevant.
Theorem 2.2. An element 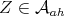 is minimal if and only if there exists a representation
is minimal if and only if there exists a representation 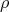 of
of 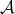 in a Hilbert space
in a Hilbert space 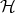 and a unit vector
and a unit vector 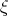 such that
such that
Proof. The if part is trivial. Suppose that there exist 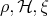 as above. Then if
as above. Then if 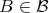 ,
,
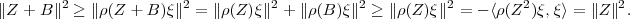
Suppose now that 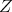 is minimal. Denote by
is minimal. Denote by 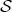 the closed (real) linear span of
the closed (real) linear span of 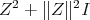 and the operators of the form
and the operators of the form 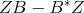 for all possible
for all possible  . Note that
. Note that 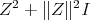 is positive and
is positive and 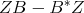 is selfadjoint, i.e.
is selfadjoint, i.e. 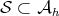 .
.
Denote by  the cone of positive and invertible elements of
the cone of positive and invertible elements of  . We claim that the minimality condition implies that
. We claim that the minimality condition implies that 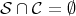 . Indeed, otherwise, since
. Indeed, otherwise, since  is open, there would exist
is open, there would exist 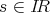 and
and 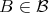 such that
such that
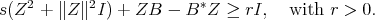
We may suppose that  , so that dividing by
, so that dividing by  we get that for given
we get that for given 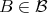 ,
, 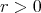 ,
,
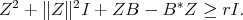
(2.1)
Also note that 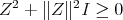 , then for
, then for 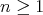 ,
,
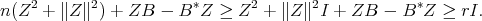
Or equivalently, dividing by 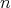 ,
,
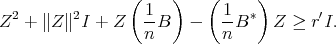
In other words, one can find 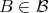 with arbitrarily small norm such that inequality 2.1 holds.
with arbitrarily small norm such that inequality 2.1 holds.
This inequality clearly implies that
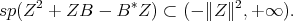
On the other hand, since 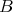 can be chosen with arbitrarily small norm, and
can be chosen with arbitrarily small norm, and 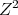 is non positive, it is clear that one can choose
is non positive, it is clear that one can choose 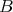 in order that
in order that 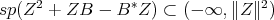 . Therefore there exists
. Therefore there exists 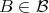 such that
such that 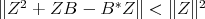 . Let us show that this contradicts the minimality of
. Let us show that this contradicts the minimality of 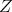 , and thus proves our claim. Indeed, this is stated in lemma 5.3 of [1]:
, and thus proves our claim. Indeed, this is stated in lemma 5.3 of [1]:
Lemma 2.3. If 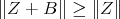 for all
for all 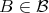 , then also
, then also 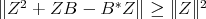 .
.
We include its proof. Consider for  ,
, 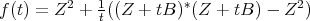 . Note that
. Note that  . Otherwise
. Otherwise  and then the convex combination
and then the convex combination 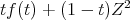 has norm strictly smaller than
has norm strictly smaller than 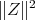 for
for 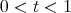 . Note that
. Note that
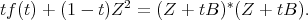
That is 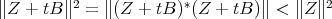 , which contradicts the hypothesis, and the lemma is proven, as well as our claim.
, which contradicts the hypothesis, and the lemma is proven, as well as our claim.
We have that 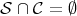 , with
, with 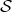 a closed (real) linear submanifold of
a closed (real) linear submanifold of 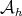 and
and  open and convex in
open and convex in 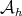 . By the Hahn-Banach theorem, there exists a bounded linear functional
. By the Hahn-Banach theorem, there exists a bounded linear functional 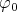 in
in 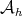 such that
such that
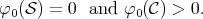
The functional 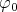 has a unique selfadjoint extension to
has a unique selfadjoint extension to 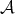 , let
, let 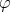 be the normalization of this functional. Then clearly
be the normalization of this functional. Then clearly 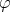 is a state which vanishes on
is a state which vanishes on  . Let
. Let 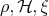 be the GNS triple associated to this state. Note that since
be the GNS triple associated to this state. Note that since 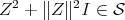 ,
, 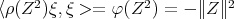 , and therefore, by the equality part in the Cauchy-Schwartz inequality, it follows that
, and therefore, by the equality part in the Cauchy-Schwartz inequality, it follows that
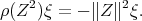
Moreover,  . Since
. Since 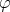 is selfadjoint, this means
is selfadjoint, this means 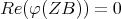 for all
for all 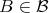 . Putting
. Putting 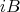 in the place of
in the place of 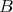 , one has that in fact
, one has that in fact 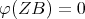 for all
for all 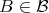 . Then,
. Then,
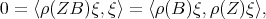
which concludes the proof. 
3. Infinitely many minimal curves joining arbitrarily close points
In this example the homogeneous space 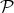 is the flag manifold of 4-tuples of mutually orthogonal lines in
is the flag manifold of 4-tuples of mutually orthogonal lines in 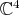 (1-dimensional complex subspaces). The group of unitary operators in
(1-dimensional complex subspaces). The group of unitary operators in 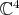 acts on the left in
acts on the left in 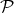 by sending each complex line to its image by the unitary operator (thus preserving the orthogonality of the new 4-tuple complex lines). Consider the canonical flag
by sending each complex line to its image by the unitary operator (thus preserving the orthogonality of the new 4-tuple complex lines). Consider the canonical flag 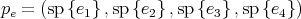 where
where 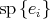 is the complex line spanned by the canonical vector
is the complex line spanned by the canonical vector 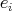 in
in 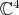 . The isotropy of the canonical flag
. The isotropy of the canonical flag  is the subgroup of 'diagonal' unitary operators.
is the subgroup of 'diagonal' unitary operators.
We consider now the submanifold 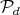 of
of 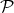 given by
given by
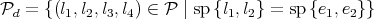
Notice that 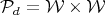 where
where 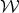 is the flag manifold of couples of mutually orthogonal 1-dimensional complex lines in
is the flag manifold of couples of mutually orthogonal 1-dimensional complex lines in  . Notice also that an ordered pair of mutually orthogonal 1-dimensional complex lines in
. Notice also that an ordered pair of mutually orthogonal 1-dimensional complex lines in  is totally determined by the first complex line of the pair, hence
is totally determined by the first complex line of the pair, hence 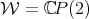 . Furthermore
. Furthermore 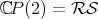 , the Riemann Sphere, hence
, the Riemann Sphere, hence 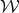 =
=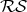 .
.
The minimal curves presented in this example shall be constructed in 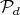 . For a better geometrical view of those curves we shall identify
. For a better geometrical view of those curves we shall identify 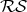 , via stereographic projection, with the unit sphere
, via stereographic projection, with the unit sphere  in
in 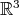 , hence we shall make the identification
, hence we shall make the identification  .
.
3.1. A description of the minimal curves. Let 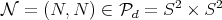 be the point whose coordinates are both the North Pole,
be the point whose coordinates are both the North Pole, 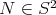 . Let
. Let 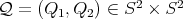 be any point of
be any point of 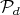 such that
such that 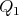 has higher latitude than
has higher latitude than 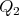 in
in 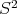 (
(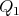 is closer to
is closer to 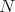 than
than 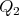 ).
).
We will fix  so that so that 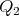 is above the equator line (and is above the equator line (and 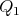 is even higher) and present a family of minimal curves is even higher) and present a family of minimal curves ![Γ β(t) = (γ1,β(t),γ2(t)), for t ∈ [0,1]](/img/revistas/ruma/v46n2/2a07179x.png) , all joining , all joining 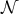 to to  . .
|
 |
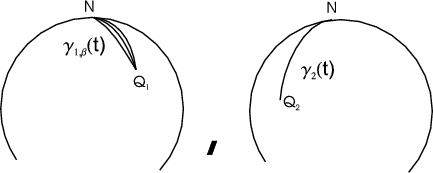 |  |
3.2. A precise description of the minimal curves. To present the curves drawn above we give a more manageable description of 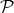 . We consider the unitary subgroup
. We consider the unitary subgroup 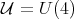 of the
of the 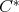 -algebra
-algebra 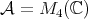 of
of 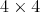 complex matrices, and denote with
complex matrices, and denote with  the subalgebra of diagonal matrices in
the subalgebra of diagonal matrices in 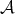 . The homogeneous space
. The homogeneous space 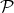 is given by the quotient
is given by the quotient 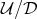 , where
, where 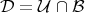 is the subgroup of the diagonal unitary matrices. The group
is the subgroup of the diagonal unitary matrices. The group  acts on
acts on 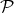 (on the left). The tangent space at 1 (the identity class) is the subspace of anti-hermitian matrices in
(on the left). The tangent space at 1 (the identity class) is the subspace of anti-hermitian matrices in 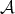 with zeroes on the diagonal.
with zeroes on the diagonal.
We construct 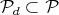 as follows. First consider the subgroup
as follows. First consider the subgroup 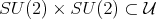 of special unitary matrices build with two,
of special unitary matrices build with two, 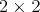 , blocks on the diagonal. We set
, blocks on the diagonal. We set 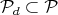 as the quotient of
as the quotient of 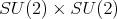 by the subgroup
by the subgroup 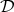 of diagonal special unitary matrices. This submanifold is in itself a product of two copies of the quotient
of diagonal special unitary matrices. This submanifold is in itself a product of two copies of the quotient 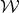 of
of 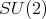 by the subgroup of diagonal matrices in
by the subgroup of diagonal matrices in 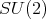 . For the relations among the different groups here mentioned we suggest [2]. We write
. For the relations among the different groups here mentioned we suggest [2]. We write 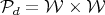 and a point of
and a point of 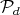 is a class (in a quotient) which in itself has two components which are also classes. We shall use the notation
is a class (in a quotient) which in itself has two components which are also classes. We shall use the notation ![[U ] = ([u1],[u2]) ∈ Pd = W × W](/img/revistas/ruma/v46n2/2a07220x.png) .
.
The minimal curves starting at 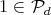 are of the form
are of the form ![[ ] γ(t) = etZ](/img/revistas/ruma/v46n2/2a07222x.png) where the matrices
where the matrices 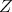 are anti-hermitian matrices with zero trace in
are anti-hermitian matrices with zero trace in 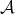 built with two blocks of anti-hermitian
built with two blocks of anti-hermitian 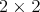 matrices on the diagonal (each one with zero trace).
matrices on the diagonal (each one with zero trace).
The minimality of the curves is granted by 2.1 for the matrices 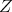 shall be minimal vectors according to theorem 2.2. In fact, we shall consider
shall be minimal vectors according to theorem 2.2. In fact, we shall consider 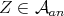 of the form
of the form
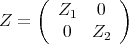
where 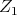 and
and 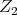 are anti-hermitian
are anti-hermitian 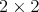 matrices of the form
matrices of the form
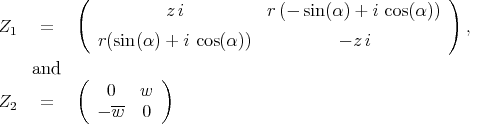
(3.2)
(3.3)
where 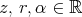 , and
, and 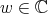 .
.
The minimality of these matrices 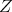 is assured in the case where
is assured in the case where 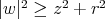 . In such case,
. In such case, 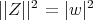 and, in relation to theorem 2.2, just consider the operator representation
and, in relation to theorem 2.2, just consider the operator representation 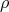 of the
of the 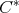 -algebra
-algebra 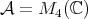 on
on 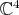 , together with the unit vector
, together with the unit vector 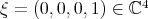 .
.
3.2.1. The two components of the curves in  . The curve
. The curve ![γ(t) = [etZ]= ([etZ1],](/img/revistas/ruma/v46n2/2a07244x.png)
![[etZ2])](/img/revistas/ruma/v46n2/2a07245x.png) in
in  has two components (in
has two components (in  ).
).
We shall regard the Riemann Sphere  as the complex plane
as the complex plane  with the point "
with the point "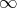 " added. Consider a matrix
" added. Consider a matrix 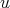 in
in 
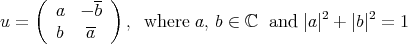
We consider the mapping 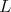 from
from 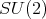 to
to 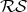 is given by
is given by
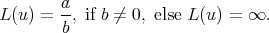
It is clear that this mapping induces an explicit diffeomorphism from the quotient of 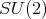 by its diagonal matrices to the Riemann Sphere
by its diagonal matrices to the Riemann Sphere 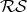 .
.
Consider the unit sphere 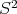 in
in 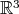 , and let the equatorial plane,
, and let the equatorial plane,  , represent the "finite" part of the Riemann Sphere
, represent the "finite" part of the Riemann Sphere 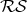 . We set
. We set 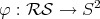 to be the stereographic projection given as by:
to be the stereographic projection given as by:
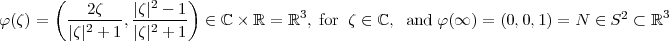
Notice that in the class 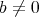 , if
, if 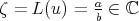 , then
, then 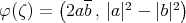 . If
. If  , then
, then 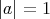 , hence
, hence 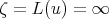 , then
, then 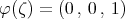 .
.
Via a composition of two maps, we define the diffeomorphism 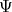 from
from 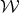 onto
onto 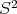 : for
: for ![[( - )] a - b [u] = b a- ∈ W](/img/revistas/ruma/v46n2/2a07276x.png) we set,
we set,
![( - ) ( - ) Ψ([u]) = φ (L(u)) = 2a b, ∣a∣2 - ∣b∣2 = 2ab, 1 - 2∣b∣2 ∈ S2](/img/revistas/ruma/v46n2/2a07277x.png)
Considering the curve 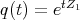 in
in 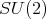 with
with 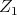 as in (3.2) above, and setting
as in (3.2) above, and setting 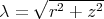 , it can be verified that
, it can be verified that 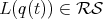 is given by,
is given by,
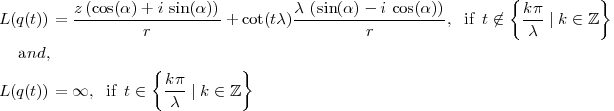
(3.4)
(3.5)
Notice then that 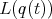 parametrizes a straight line
parametrizes a straight line 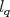 in
in 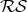 . Hence the curve
. Hence the curve
![Ψ([q(t)]) = φ(L(q(t)))](/img/revistas/ruma/v46n2/2a07287x.png)
is an arc of a circle in 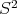 (not necessarily a great circle) contained in the plane in
(not necessarily a great circle) contained in the plane in 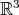 that contains both the line
that contains both the line 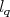 , in the equatorial plane, and the North Pole
, in the equatorial plane, and the North Pole 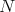 , in
, in  . It can be verified that this plane has unit normal vectors given by:
. It can be verified that this plane has unit normal vectors given by:
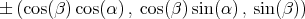
where 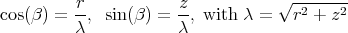 .
.
3.2.2. Some observations on the curves ![Ψ ([etZ1])](/img/revistas/ruma/v46n2/2a07295x.png) and
and ![Ψ ([etZ2])](/img/revistas/ruma/v46n2/2a07296x.png) in
in  . Let
. Let ![( ) γ1,β(t) = Ψ [etZ1]](/img/revistas/ruma/v46n2/2a07298x.png) , where
, where 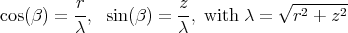 , and let
, and let ![γ (t) = Ψ ([etZ2]) 2](/img/revistas/ruma/v46n2/2a07300x.png)
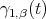 runs over a great circle in
runs over a great circle in  if and only if
if and only if 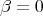 (equivalently
(equivalently  ).
). 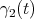 runs over a great circle in
runs over a great circle in  (
(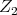 has parameter
has parameter  ).
). 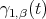 varies continuously with the parameter
varies continuously with the parameter 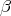 .
. 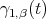 starts at
starts at 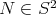 and returns to that point exactly for
and returns to that point exactly for 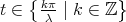 .
. 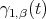 has constant speed
has constant speed 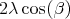 in
in  .
. 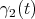 has constant speed
has constant speed 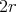 in
in  .
.
3.2.3. The curves ![Γ (t) = (Ψ ([etZ1]), Ψ ([etZ2])) β](/img/revistas/ruma/v46n2/2a07320x.png) in
in 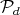 . Lets give explicit values of the "parameters"
. Lets give explicit values of the "parameters" 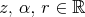 and
and 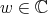 that define
that define 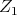 and
and 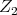 (according to formulas (3.2) and (3.3)), so that for
(according to formulas (3.2) and (3.3)), so that for ![t ∈ [0,1]](/img/revistas/ruma/v46n2/2a07326x.png) , the curves
, the curves ![( ) γ1,β(t) = Ψ [etZ1]](/img/revistas/ruma/v46n2/2a07327x.png) and
and ![( ) γ2(t) = Ψ [etZ2]](/img/revistas/ruma/v46n2/2a07328x.png) join the point
join the point 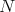 to
to 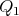 and
and 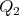 respectively.
respectively.
Suppose that the distances from 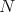 to
to 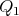 and
and 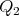 in
in  are
are 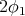 and
and 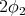 respectively (with
respectively (with  ).
).
By means of some rotation of the sphere 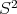 we may suppose that
we may suppose that 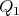 is in the plane generated by
is in the plane generated by  and
and 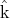 , as in figure 1 below, and we have,
, as in figure 1 below, and we have, 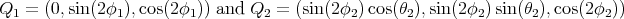 .
.
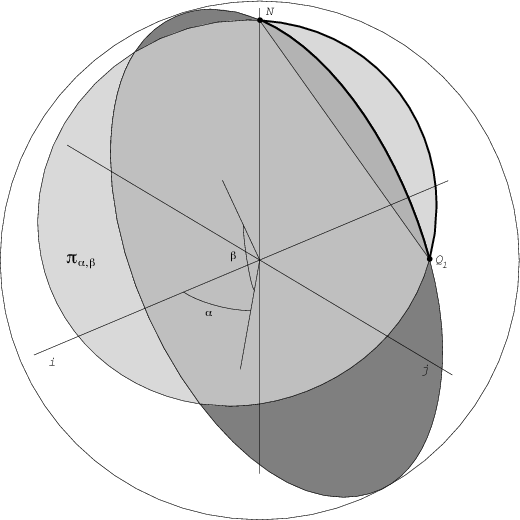
Figure 1: We suppose that 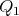 is in the plane generated by
is in the plane generated by  and
and 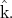
For 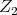 we set
we set 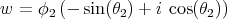 so that
so that ![( Z2) γ2(1) = Ψ [e ] = Q2](/img/revistas/ruma/v46n2/2a07350x.png) .
.
We have to choose the values 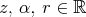 and
and 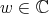 that define
that define 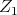 . This is equivalent to chose
. This is equivalent to chose 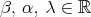 via the change of variables given by the equations
via the change of variables given by the equations
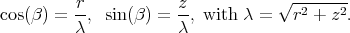
The parameters 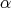 and
and 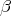 are shown in figure 1, with the only restriction that the vector
are shown in figure 1, with the only restriction that the vector
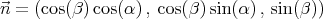
is orthogonal to a plane 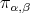 that contains
that contains 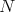 and
and 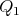 .
.
The parameter 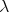 is determined after choosing
is determined after choosing 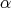 and
and 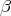 so that the short arc joining
so that the short arc joining 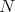 and
and 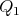 , in the intersection of the plane
, in the intersection of the plane 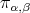 with the sphere
with the sphere 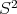 as in figure 1, has length
as in figure 1, has length 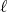 equal to
equal to 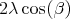 , from where the value of
, from where the value of 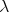 is drawn.
is drawn.
[1] Durán, C. E., Mata-Lorenzo, L. E. and Recht, L., Metric geometry in homogeneous spaces of the unitary group of a C -algebra: Part I-minimal curves, Adv. Math. 184 No. 2 (2004), 342-366. [ Links ]
-algebra: Part I-minimal curves, Adv. Math. 184 No. 2 (2004), 342-366. [ Links ]
[2] Whittaker, E. T. "A Treatise on the Analytical Dynamics of Particles and Rigid Bodies", Cambridge University Press, London 1988. [ Links ]
Esteban Andruchow
Instituto de Ciencias,
Universidad Nacional de Gral. Sarmiento,
J. M. Gutierrez (1613) Los Polvorines, Argentina
eandruch@ungs.edu.ar
Luis E. Mata-Lorenzo
Universidad Simón Bolívar, Apartado 89000,
Caracas 1080A, Venezuela
lmata@usb.ve
Lázaro Recht
Universidad Simón Bolívar, Apartado 89000,
Caracas 1080A, Venezuela, and
Instituto Argentino de Matemática, CONICET, Argentina
recht@usb.ve
Alberto Mendoza
Universidad Simón Bolívar, Apartado 89000,
Caracas 1080A, Venezuela
jacob@usb.ve
Alejandro Varela
Instituto de Ciencias,
Universidad Nacional de Gral. Sarmiento,
J. M. Gutierrez (1613) Los Polvorines, Argentina
avarela@ungs.edu.ar
Recibido: 23 de marzo de 2006
Aceptado: 7 de agosto de 2006













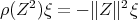 .
. 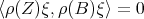 for all
for all 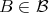 .
.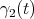 in
in 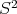 will trace the smaller arc of the great circle that contains
will trace the smaller arc of the great circle that contains 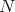 and
and 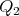 .
. 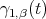 will vary continuously with the parameter
will vary continuously with the parameter 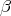 .
. 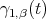 will parametrize the smaller arc of some circle in
will parametrize the smaller arc of some circle in 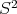 that joins
that joins 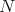 to
to 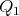 ; the arcs will not be great circles but for
; the arcs will not be great circles but for 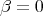 .
.
