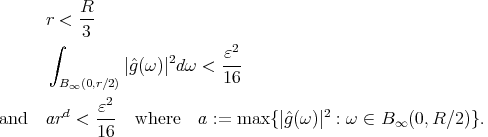Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.46 n.2 Bahía Blanca jul./dic. 2005
Geometric Methods in Wavelet Theory
C. Cabrelli and U. Molter
To the memory of our teacher and colleague Pucho Larotonda, who taught us much more than Mathematics.
The authors are partially supported by Grants: PICT 15033, CONICET, PIP 5650, UBACyT X058 and X108
Abstract: In this paper we present an overview of how geometric methods can be successfully used to solve problems in Analysis. We will focus on self-similar objects and use their structure to construct frames, Riesz bases and wavelet bases in 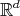 with a single generator function. Further, we show that the generating functions for these systems are dense in
with a single generator function. Further, we show that the generating functions for these systems are dense in  .
.
Key words and phrases. Self-Similarity, Wavelets, Affine Systems, Wavelet Sets, Riesz basis wavelets
2000 Mathematics Subject Classification. Primary: 42C40, Secondary: 42C30
In this article we review some geometric methods that have proven to be very successful in different contexts and we show their application to wavelet construction (sections 5 and 6).
We describe the notion of self-similarity as developed by Hutchinson [Hut81] and its characterization in terms of contraction mappings in general metric spaces. We show that when these results are applied to affine functions in the euclidean space using a fixed expanding matrix, they can produce a self-similar tiling of the space. In other words, given an expansive matrix  and an admissible lattice
and an admissible lattice  , it is in general the case that there exists a self-similar set associated to
, it is in general the case that there exists a self-similar set associated to 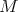 that tiles the plane by
that tiles the plane by 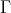 -translates.
-translates.
Tilings by lattice translates are associated to local Fourier orthonormal bases, which leads to the notion of spectral sets and to the "Fuglede Conjecture", as we describe in section 4.
When the property of tiling by 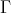 -translates is linked to the self-similarity of the tile by an expansive matrix, a beautiful construction of wavelet bases is obtained. This is the theory of wavelet sets (section 5).
-translates is linked to the self-similarity of the tile by an expansive matrix, a beautiful construction of wavelet bases is obtained. This is the theory of wavelet sets (section 5).
Finally, a careful choice of the expanding matrix and the lattice in the wavelet set construction, allows to approximate any function in 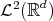 by a generator of a Riesz wavelet system. We develop this density result in section 6.
by a generator of a Riesz wavelet system. We develop this density result in section 6.
Throughout this section the concept of self-similarity in a very general way will play a fundamental role. In 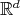 , a similarity is a function of the type
, a similarity is a function of the type 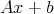 where
where 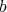 is a point in
is a point in 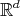 and
and 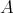 is a
is a 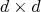 isotropic matrix, i.e. all eigenvalues have the same magnitude. The name reflects the fact that this transformation copies objects into similar objects, just smaller, bigger or simply translated or rotated, depending on the matrix
isotropic matrix, i.e. all eigenvalues have the same magnitude. The name reflects the fact that this transformation copies objects into similar objects, just smaller, bigger or simply translated or rotated, depending on the matrix 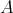 and the point
and the point 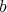 .
.
In this sense, an object could be called self-similar if you can write it as the finite union of copies of itself, i.e.
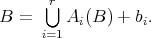
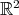 (see Figure 1).
(see Figure 1).
Figure 1: Self-Similar square
Not so trivial, but still simple, is the well known middle third Cantor set, which we will denote by 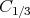 . If you look at the Cantor set, you realize, that you can write it as the union of two shrunken copies of itself, one in the
. If you look at the Cantor set, you realize, that you can write it as the union of two shrunken copies of itself, one in the ![[0, 1] 3](/img/revistas/ruma/v46n2/2a0821x.png) interval and the other one in the
interval and the other one in the ![[2 ,1] 3](/img/revistas/ruma/v46n2/2a0822x.png) interval.
interval.
Both examples are examples of compact sets in 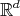 . They also share the property, that they are the (almost) disjoint union of smaller copies of themselves. This allows to virtually see the self-similarity.
. They also share the property, that they are the (almost) disjoint union of smaller copies of themselves. This allows to virtually see the self-similarity.
We will also be interested in self-similar functions, or measures. Self-similar objects are interesting for us, since the self-similarity allows us to recover information of the whole object by looking only at some part, since one can think that the properties are "translated" into each part. Therefore self-similar objects may be easier to study than "arbitrary" objects. This is one of the reasons why we are interested in finding and characterizing self-similar objects. The fact that they are simple to describe and in many cases they are dense, in the sense that they approximate arbitrary objects, makes this characterization extremely useful.
One of the main tools to construct self-similar objects, will be by resort to the fixed point theorem or Banach contraction principle. Since we will try to apply it to very different scenarios, we will state it here in its most general way. The proof can be found in may textbooks, such as [Rud64].
Theorem 2.1 (Generalized Banach Contraction Principle). Let 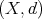 be a complete metric space, and let
be a complete metric space, and let  be a function such that there exists a metric
be a function such that there exists a metric 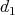 which is equivalent to
which is equivalent to 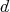 , for which there exist
, for which there exist 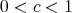 , and
, and  such that for all
such that for all 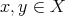
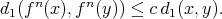
(2.1)
Then there exists a unique point 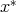 in
in 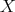 , such that
, such that 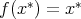 .
.
2.1. The space of compact sets in 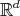 . To describe the setting for the theory, we start defining an appropriate structure for the space of non-empty compact sets in
. To describe the setting for the theory, we start defining an appropriate structure for the space of non-empty compact sets in 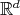 . Precisely, we define
. Precisely, we define 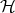 by
by 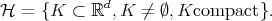
(2.2)
We want to transform 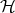 into a metric space, and therefore we need to define an appropriate metric on
into a metric space, and therefore we need to define an appropriate metric on 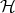 . We would like that this metric takes the similarity of the shapes into account. For example, a point
. We would like that this metric takes the similarity of the shapes into account. For example, a point 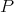 and a segment
and a segment 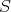 should not be close with the appropriate distance.
should not be close with the appropriate distance.
One distance that performs this task in a reasonable way, is the so-called Hausdorff distance.
Definition 2.2. Let 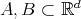 be non-empty compact sets, then the Hausdorff distance between
be non-empty compact sets, then the Hausdorff distance between 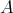 and
and 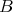 is
is 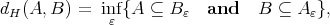
(2.3)
The following Theorem is straightforward (see for example [Hut81].
Theorem 2.3. The space 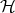 of all non-empty compact subsets of
of all non-empty compact subsets of 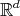 equipped with the Hausdorff distance is a complete metric space.
equipped with the Hausdorff distance is a complete metric space.
3. Attractors and self-similar sets
The following theorem, due to Hutchinson ([Hut81]), is a key result in the theory of self-similar sets and provides a simple way to construct them.
Theorem 3.1. Let  be
be 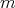 contraction-mappings in
contraction-mappings in 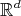 , with contraction factors
, with contraction factors 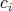 . There exists a unique non-empty compact set
. There exists a unique non-empty compact set 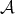 satisfying
satisfying
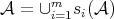
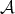 is self-similar with respect to
is self-similar with respect to  ). Furthermore, if
). Furthermore, if 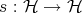 is the map defined by
is the map defined by 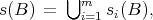 for each compact set
for each compact set 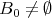 , the sequence
, the sequence 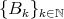 given by
given by 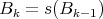 converges to
converges to 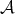 in
in  .
. Proof. The proof is immediate noting that
Examples of Self-Similar Sets:
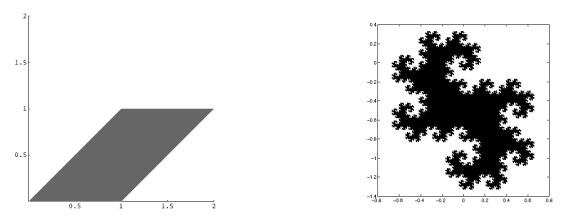
Figure 2: Self-Similar parallelogram and twin dragon attractors
Focusing on the application we have in mind, we will look at a particular case of Theorem 3.1 which is satisfied by all our examples so far.
For this, let  be a full rank lattice, i.e.
be a full rank lattice, i.e. 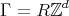 with
with 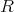 any invertible matrix. Let
any invertible matrix. Let  be a set of generators for the lattice
be a set of generators for the lattice  , i.e., independent vectors such that
, i.e., independent vectors such that

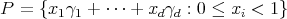
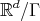 . A matrix
. A matrix  is said to be expansive, if all the eigenvalues have absolute value bigger than
is said to be expansive, if all the eigenvalues have absolute value bigger than  . If
. If  is expansive, and
is expansive, and 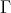 is a lattice such that
is a lattice such that 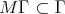 , a set of representatives of the quotient
, a set of representatives of the quotient 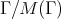 is called a full set of digits for that lattice. Note that, since
is called a full set of digits for that lattice. Note that, since 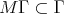 ,
, 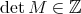 . A full set of digits always has
. A full set of digits always has 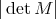 elements. We have the following result.
elements. We have the following result. Proposition 3.2. Let 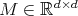 be an expansive matrix and let
be an expansive matrix and let 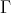 be a lattice such that
be a lattice such that 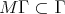 ,
, 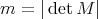 , and
, and 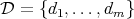 be a full set of digits. There always exists a non-empty compact set
be a full set of digits. There always exists a non-empty compact set 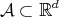 satisfying
satisfying 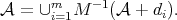
(3.1)
The following properties of 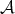 will be useful [Ban91], cf. also [GM92]. For a general description see also [CHM04]. If
will be useful [Ban91], cf. also [GM92]. For a general description see also [CHM04]. If 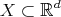 , we will denote by
, we will denote by 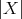 the
the 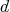 -dimensional Lebesgue measure of
-dimensional Lebesgue measure of 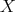 .
.
Lemma 3.3. Let 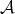 be as in (3.1). Then the following statements hold.
be as in (3.1). Then the following statements hold.
In other words, part (c) above says that if 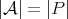 , then
, then 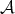 is a tile in the sense that the
is a tile in the sense that the 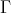 -translates
-translates 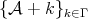 cover
cover 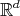 with overlaps of measure zero.
with overlaps of measure zero.
A long-standing open problem was the question of whether for each dilation matrix 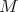 there exists a full set of digits
there exists a full set of digits 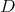 such that the corresponding attractor
such that the corresponding attractor 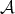 is a tile. Lagarias and Wang proved that this is the case if
is a tile. Lagarias and Wang proved that this is the case if 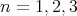 or if
or if 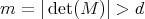 [LW95], [LW96], [LW97]. Potiopa [Pot97] however showed that if
[LW95], [LW96], [LW97]. Potiopa [Pot97] however showed that if  and
and
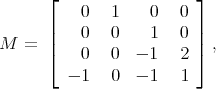
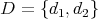 such that the unique self similar set
such that the unique self similar set 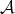 associated to
associated to 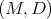 i.e.
i.e. 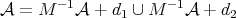 is a tile, cf. [LW99]. Note that this matrix
is a tile, cf. [LW99]. Note that this matrix 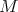 has determinant
has determinant 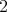 .
. Let  a measurable set such that
a measurable set such that 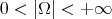 . The set
. The set 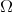 is called a spectral set if there exists a discrete set
is called a spectral set if there exists a discrete set 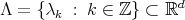 such that the set of exponential functions
such that the set of exponential functions 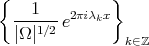
(4.1)
is an orthonormal basis of 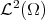 . In this case,
. In this case, 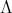 is called the spectrum of
is called the spectrum of 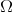 . Many results on spectral sets can be found in the work of Jörgensen et. al ([JP91, JP92, JP98a, JP98b, JP99, BJR99]), Wang ([Wan02, PW01]) and others.
. Many results on spectral sets can be found in the work of Jörgensen et. al ([JP91, JP92, JP98a, JP98b, JP99, BJR99]), Wang ([Wan02, PW01]) and others.
In 1974 Fuglede ([Fug74]) proved the following theorem.
Theorem 4.1. 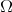 is a spectral set with spectrum
is a spectral set with spectrum 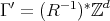 if and only if
if and only if 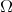 tiles
tiles 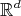 by translations on
by translations on 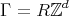 (the dual lattice of
(the dual lattice of 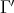 ).
).
He further conjectured that his theorem was still true, if one removes the condition that the spectrum of 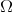 has to be a lattice. Terence Tao ([Tao04]) proved in 2003, that - at least for dimension
has to be a lattice. Terence Tao ([Tao04]) proved in 2003, that - at least for dimension 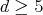 - this is false.
- this is false.
However, Fuglede's Theorem allows us to add an additional equivalence to item (c) of Lemma 3.3 above:
Proposition 4.2. Let  be an expansive matrix and
be an expansive matrix and 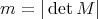 . Let
. Let  be a lattice such that
be a lattice such that  and let
and let  be a full set of digits. We have
be a full set of digits. We have 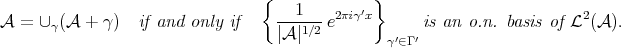
(4.2)
5. Minimal supported (in frequency) wavelets
For a lattice  , an expansive matrix
, an expansive matrix  such that
such that 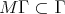 ,
, 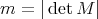 , and
, and 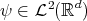 we consider the set
we consider the set 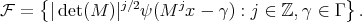
(5.1)
The question we are addressing now, is for which 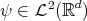 ,
, 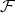 is an orthonormal basis for
is an orthonormal basis for 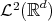 . Such a function will be called a wavelet.
. Such a function will be called a wavelet.
The following Theorem, whose proof is straightforward, characterizes those wavelets whose Fourier transform has support with smallest possible measure.
Theorem 5.1. Let 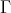 and
and 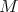 be as before, and let
be as before, and let 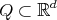 be such that
be such that
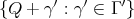 tiles
tiles 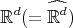 (i.e.
(i.e.  is a tile for
is a tile for 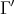 , the dual lattice of
, the dual lattice of 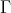 )
) 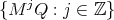 tiles
tiles 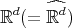 , i.e.
, i.e. 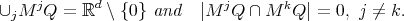
Then if 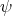 is such that
is such that 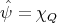 we have
we have
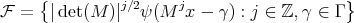
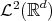 .
. 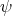 is called a Minimal Supported in Frequency wavelet (MSFW).
is called a Minimal Supported in Frequency wavelet (MSFW). 5.1. Construction of  . Therefore, in order to obtain MSFW, we need to construct a set
. Therefore, in order to obtain MSFW, we need to construct a set  that satisfies the conditions above. Sets of this type are called wavelet sets and have been studied by many groups of researchers ([BL01, BMM99, BS02, BS04, DLS97, DLS98, ILP98, SW98, Wan02, Zak96]. We will illustrate the construction given by Benedetto [BL01, BS02, BS04] for a particular case, which will be useful in the next section.
that satisfies the conditions above. Sets of this type are called wavelet sets and have been studied by many groups of researchers ([BL01, BMM99, BS02, BS04, DLS97, DLS98, ILP98, SW98, Wan02, Zak96]. We will illustrate the construction given by Benedetto [BL01, BS02, BS04] for a particular case, which will be useful in the next section.
Assume that 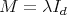 with
with  and that
and that 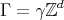 , for
, for 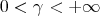 . (The choice of
. (The choice of 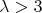 is only to simplify the construction.) Set
is only to simplify the construction.) Set ![γ d - 1 γd Q0 = [0,2] \ M [0, 2]](/img/revistas/ruma/v46n2/2a08197x.png) (see Figure 3).
(see Figure 3).

Figure 3: The annulus tiles by dilations by
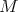 but not by
but not by 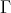 translates
translates This set tiles by dilation by 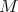 , but not by
, but not by 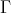 -translates. We need to fill the hole.
-translates. We need to fill the hole.
We define 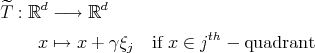
where 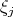 is the vertex of the cube
is the vertex of the cube ![[- 1,1]d](/img/revistas/ruma/v46n2/2a08205x.png) that lies in the
that lies in the 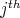 -quadrant.
-quadrant.
It will be convenient to use the notation 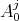 for the intersection of the set
for the intersection of the set 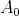 with the
with the 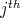 -quadrant. With this notation, note that
-quadrant. With this notation, note that 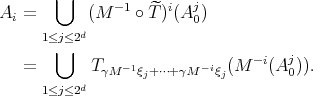
(5.4)
Here 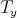 denotes the usual translation by
denotes the usual translation by 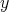 in
in 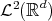 . Therefore we have that
. Therefore we have that 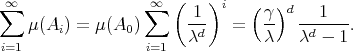
(5.5)
Figure 4:
 tiles by dilations by
tiles by dilations by 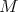 and by
and by 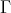 translates
translates Observe that:
This fact allows us to conclude that:
which allows us to rewrite 
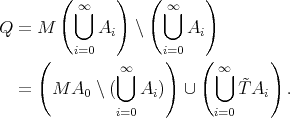
This shows that  is in fact
is in fact 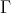 -congruent to
-congruent to ![[0, γ]d 2](/img/revistas/ruma/v46n2/2a08240x.png) .
.
Therefore, using Fuglede's Theorem (Theorem 4.1) we have that
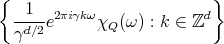
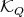 , and using that
, and using that 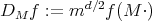 is a unitary operator, we conclude that
is a unitary operator, we conclude that 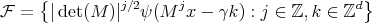
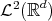 .
. In this section we will outline, how we can use the construction of the previous section, to answer an open question posed by D. Larson. For details, we refer the reader to [CM06].
The question we are going to address now is the following:
Given 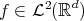 , and
, and 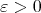 , does there exist a function
, does there exist a function 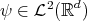 , an expansive matrix
, an expansive matrix 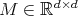 , and a lattice
, and a lattice 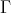 , such that
, such that
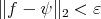 and
and 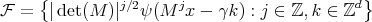 is a Riesz basis for
is a Riesz basis for 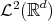 ?
?
Here we are relaxing the condition of being an orthonormal basis, to the Riesz basis condition.
We recall that a set 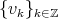 is a Riesz basis for a Hilbert space
is a Riesz basis for a Hilbert space 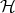 , if it is complete in
, if it is complete in 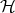 and there exist constants
and there exist constants 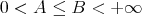 , such that for every
, such that for every 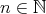 and every finite sequence of scalars
and every finite sequence of scalars 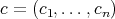 ,
,
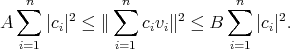
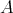 and
and 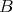 are called Riesz basis bounds.
are called Riesz basis bounds. In order to show, how the previous results can be used to give a positive answer to this question, we need the following result.
Lemma 6.1. Let 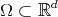 be a set of finite measure. If
be a set of finite measure. If 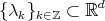 satisfies that
satisfies that 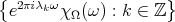 is a Riesz basis for
is a Riesz basis for 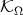 with bounds
with bounds 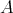 and
and 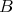 and
and 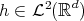 satisfies that
satisfies that 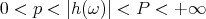 then
then 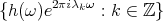
is a Riesz basis for 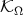 , with Riesz bounds
, with Riesz bounds 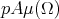 and
and 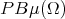 .
.
If  is an invertible matrix and
is an invertible matrix and 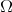 satisfies that
satisfies that 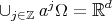 up to a set of zero measure, with the union being almost disjoint, and
up to a set of zero measure, with the union being almost disjoint, and 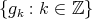 is a Riesz basis for
is a Riesz basis for 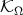 , then
, then 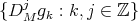
is a Riesz basis for 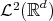 with the same bounds. (Here
with the same bounds. (Here 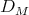 is the dilation operator defined in the previous section.)
is the dilation operator defined in the previous section.)
Proof. The first assertion is immediate, and the second one follows from the fact that the dilation is a unitary operator in 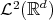 . □
. □
In view of this Lemma, if we are given a function in 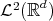 , we need to find the right lattice and the appropriate dilation matrix. For this we proceed in the following way:
, we need to find the right lattice and the appropriate dilation matrix. For this we proceed in the following way:
Let now
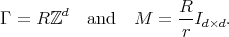
 , we have that
, we have that 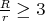 and we are therefore in the previously described situation.
and we are therefore in the previously described situation. We define the set  as in (5.6), and for
as in (5.6), and for 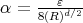 , the function
, the function  by
by
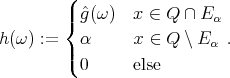
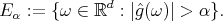 |
Then the function 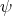 , with
, with 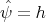 satisfies that
satisfies that
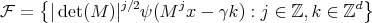
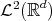 (see [CM06] for the details of the proof).
(see [CM06] for the details of the proof). We thank Gustavo Corach for inviting us to be part of this volume in memory of our fond colleague Pucho Larotonda.
[Ban91] C. Bandt, Self-similar sets. V. Integer matrices and fractal tilings of 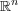 , Proc. Amer. Math. Soc. 112 (1991), 549-562. [ Links ]
, Proc. Amer. Math. Soc. 112 (1991), 549-562. [ Links ]
[BJR99] Ola Bratteli, Palle E. T. Jørgensen, and Derek W. Robinson, Spectral asymptotics of periodic elliptic operators, Math. Z. 232 (1999), no. 4, 621-650. [ Links ]
[BL01] J. J. Benedetto and M. Leon, The construction of single wavelets in d-dimensions, J. Geometric Analysis (2001), 1-15. [ Links ]
[BMM99] Lawrence W. Baggett, Herbert A. Medina, and Kathy D. Merrill, Generalized multi-resolution analyses and a construction procedure for all wavelet sets in 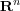 , J. Fourier Anal. Appl. 5 (1999), no. 6, 563-573. [ Links ]
, J. Fourier Anal. Appl. 5 (1999), no. 6, 563-573. [ Links ]
[BS02] John J. Benedetto and Songkiat Sumetkijakan, A fractal set constructed from a class of wavelet sets, Inverse problems, image analysis, and medical imaging (New Orleans, LA, 2001), Contemp. Math., vol. 313, Amer. Math. Soc., Providence, RI, 2002, pp. 19-35. [ Links ]
[BS04] J. J. Benedetto and S. Sumetkijakan, Tight frames and geometric properties of wavelet sets, preprint, 2004. [ Links ]
[CHM04] C. Cabrelli, C. Heil, and U. Molter, Self-Similarity and Multiwavelets in Higher Dimensions, Memoirs of the American Mathematical Society, vol. 170, American Mathematical Society, Providence, RI, USA, 2004. [ Links ]
[CM06] C. Cabrelli and U. Molter, Density of the set of generators of wavelet systems, Constructive Approximation. To appear, 2006. (arXiv math. CA/0509321). [ Links ]
[DLS97] Xingde Dai, David R. Larson, and Darrin M. Speegle, Wavelet sets in 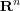 , J. Fourier Anal. Appl. 3 (1997), no. 4, 451-456. MR 98m:42048 [ Links ]
, J. Fourier Anal. Appl. 3 (1997), no. 4, 451-456. MR 98m:42048 [ Links ]
[DLS98] _________ , Wavelet sets in 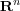 . II, Wavelets, multiwavelets, and their applications (San Diego, CA, 1997), Amer. Math. Soc., Providence, RI, 1998, pp. 15-40. MR 99d:42054 [ Links ]
. II, Wavelets, multiwavelets, and their applications (San Diego, CA, 1997), Amer. Math. Soc., Providence, RI, 1998, pp. 15-40. MR 99d:42054 [ Links ]
[Fug74] Bent Fuglede, Commuting self-adjoint partial differential operators and a group theoretic problem, J. Functional Analysis 16 (1974), 101-121. MR MR0470754 (57 #10500) [ Links ]
[GM92] K. Gröchenig and W. R. Madych, Multiresolution analysis, Haar bases, and self-similar tilings of 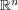 , IEEE Trans. Inform. Theory 38 (1992), 556-568. [ Links ]
, IEEE Trans. Inform. Theory 38 (1992), 556-568. [ Links ]
[Hut81] J. Hutchinson, Fractals and self-similarity, Indiana Univ. Math. J. 30 (1981), 713-747. [ Links ]
[ILP98] Eugen J. Ionascu, David R. Larson, and Carl M. Pearcy, On wavelet sets, J. Fourier Anal. Appl. 4 (1998), no. 6, 711-721. [ Links ]
[JP91] Palle E. T. Jorgensen and Steen Pedersen, An algebraic spectral problem for 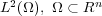 , C. R. Acad. Sci. Paris Sér. I Math. 312 (1991), no. 7, 495-498. [ Links ]
, C. R. Acad. Sci. Paris Sér. I Math. 312 (1991), no. 7, 495-498. [ Links ]
[JP92] P. E. T. Jorgensen and S. Pedersen, Spectral theory for borel sets in  of finite measure, J. Funct. Anal. 107 (1992), 72-104. [ Links ]
of finite measure, J. Funct. Anal. 107 (1992), 72-104. [ Links ]
[JP98a] Palle E. T. Jorgensen and Steen Pedersen, Dense analytic subspaces in fractal 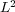 -spaces, J. Anal. Math. 75 (1998), 185-228. [ Links ]
-spaces, J. Anal. Math. 75 (1998), 185-228. [ Links ]
[JP98b] _________ , Local harmonic analysis for domains in  of finite measure, Analysis and topology, World Sci. Publishing, River Edge, NJ, 1998, pp. 377-410. [ Links ]
of finite measure, Analysis and topology, World Sci. Publishing, River Edge, NJ, 1998, pp. 377-410. [ Links ]
[JP99] _________ , Spectral pairs in Cartesian coordinates, J. Fourier Anal. Appl. 5 (1999), no. 4, 285-302. [ Links ]
[LW95] J. C. Lagarias and Y. Wang, Haar type orthonormal wavelet bases in 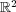 , J. Fourier Anal. Appl. 2 (1995), 1-14. [ Links ]
, J. Fourier Anal. Appl. 2 (1995), 1-14. [ Links ]
[LW96] _________ , Haar bases for 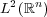 and algebraic number theory, J. Number Theory 57 (1996), 181-197. [ Links ]
and algebraic number theory, J. Number Theory 57 (1996), 181-197. [ Links ]
[LW97] _________ , Integral self-affine tiles in 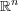 . II. Lattice tilings, J. Fourier Anal. Appl. 3 (1997), 83-102. [ Links ]
. II. Lattice tilings, J. Fourier Anal. Appl. 3 (1997), 83-102. [ Links ]
[LW99] _________ , Corrigendum and addendum to: Haar bases for 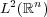 and algebraic number theory, J. Number Theory 76 (1999), 330-336. [ Links ]
and algebraic number theory, J. Number Theory 76 (1999), 330-336. [ Links ]
[Pot97] A. Potiopa, A problem of Lagarias and Wang, Master's Thesis, Siedlce University, Siedlce, Poland (Polish), 1997. [ Links ]
[PW01] Steen Pedersen and Yang Wang, Universal spectra, universal tiling sets and the spectral set conjecture, Math. Scand. 88 (2001), no. 2, 246-256. [ Links ]
[Rud64] Walter Rudin, Principles of mathematical analysis, Second edition, McGraw-Hill, New York, 1964. MR MR0166310 (29 #3587) [ Links ]
[SW98] Paolo M. Soardi and David Weiland, Single wavelets in n-dimensions, J. Fourier Anal. Appl. 4 (1998), no. 3, 299-315. [ Links ]
[Tao04] Terence Tao, Fuglede's conjecture is false in 5 and higher dimensions, Math. Res. Lett. 11 (2004), no. 2-3, 251-258. MR MR2067470 [ Links ]
[Wan02] Yang Wang, Wavelets, tiling, and spectral sets, Duke Math. J. 114 (2002), no. 1, 43-57. [ Links ]
[Zak96] Victor Zakharov, Nonseparable multidimensional Littlewood-Paley like wavelet bases, Preprint, 1996. [ Links ]
Carlos Cabrelli
Departamento de Matemática,
Facultad de Ciencias Exactas y Naturales,
Universidad de Buenos Aires,
Ciudad Universitaria, Pabellón I,
1428 Capital Federal, ARGENTINA
and CONICET, Argentina
cabrelli@dm.uba.ar
Ursula M. Molter
Departamento de Matemática,
Facultad de Ciencias Exactas y Naturales,
Universidad de Buenos Aires,
Ciudad Universitaria, Pabellón I,
1428 Capital Federal, ARGENTINA
and CONICET, Argentina
umolter@dm.uba.ar
Recibido: 27 de marzo de 2006
Aceptado: 7 de agosto de 2006













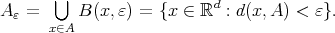
![1 1 1 s1(x) = 2x s2(x) = 2x + 2 A = [0,1]](/img/revistas/ruma/v46n2/2a0869x.png)

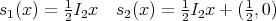
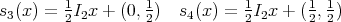
![A = [0, 1] × [0,1]](/img/revistas/ruma/v46n2/2a0875x.png) (see Figure
(see Figure 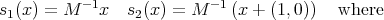
![[ ] [ ] 1 1 1 - 1 M = 1 - 1 or M = 1 1](/img/revistas/ruma/v46n2/2a0877x.png) In this case, the attractors
In this case, the attractors 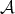 are shown in Figure
are shown in Figure 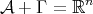 .
. 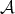 has nonempty interior,
has nonempty interior, 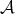 is the closure of
is the closure of 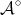 , and
, and 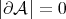 .
.  for all
for all 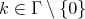 if and only if
if and only if 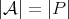 . In this case,
. In this case, 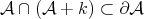 for each
for each 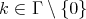 .
. 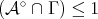 .
.![-1 γ-d --γ--d A0 = M [0,2 ] = [0,(2λ) ]](/img/revistas/ruma/v46n2/2a08207x.png)
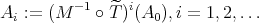
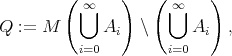
 tiles
tiles 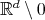 by dilations by
by dilations by 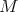 .
.  tiles
tiles 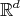 by translations on
by translations on 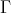 . For this, we first note that if
. For this, we first note that if 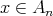 then
then 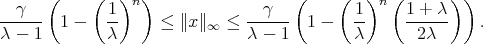
![Ai ⊂ ([0, γ2]d \ A0),](/img/revistas/ruma/v46n2/2a08232x.png) for
for  ,
, 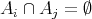 if
if 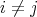 ,
,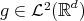 , such that
, such that 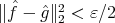 and
and 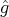 is continuous.
is continuous. 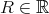 such that
such that 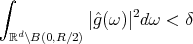
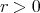 small enough such that:
small enough such that: