Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.47 n.1 Bahía Blanca ene./jun. 2006
Aroldo Kaplan
Transparencies of the talk given at egeo2005 (La Falda, Junio de 2005), slightly edited
SUBMATH:
Subriemannian Geometry, Subelliptic Operators, Subanalytic Varieties, Subsymplectic Geometry.
Only eventually (not originally) related.
Motivations: PDE, Control Theory, non-holonomic systems, ...
Subriemannian Geometry:
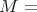 smooth or analytic manifold
smooth or analytic manifold
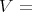 distribution on
distribution on 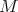 (subbundle of
(subbundle of 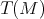 , smooth or analytic)
, smooth or analytic)
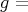 inner product on
inner product on 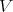 , smooth or analytic
, smooth or analytic
A submanifold 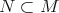 is horizontal if
is horizontal if 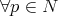
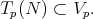
 Must think that moving along non-horizontal directions is forbidden. Analogy with Parking Problem.
Must think that moving along non-horizontal directions is forbidden. Analogy with Parking Problem.
 Whatever the
Whatever the 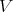 ,
,  always horizontal curves: integral curves of vector fields in
always horizontal curves: integral curves of vector fields in  .
.
 Maximal horizontal submanifolds? 2nd. half of talk.
Maximal horizontal submanifolds? 2nd. half of talk.
 Horizontal curves
Horizontal curves ![γ : [a,b] → M](/img/revistas/ruma/v47n1/1a0116x.png) have
have
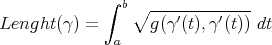
Carnot-Carathéodory "distance" on  :
:
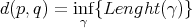
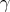 horizontal,
horizontal, 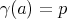 ,
, 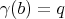 ,
, 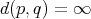
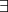 no such curve.
no such curve.
 Main problems since
Main problems since 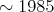 :
:
Regularity of 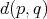
Recovering 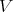 from
from 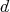 (Gromov)
(Gromov)
Admissible domains for Bdy. Value Problems for
Subelliptic Operators
Defined by regularity condition: 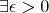 :
:
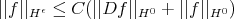
True for elliptic 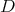 , where
, where  , wherefrom
, wherefrom
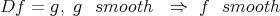
(def. of hypoelliptic).
But false for 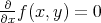 ! (take
! (take 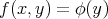 arbitrary).
arbitrary).
Important special case: sublaplacians

 vector fields on a manifold
vector fields on a manifold 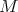
 Classical: if
Classical: if 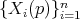 is a basis of
is a basis of 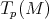
 , then
, then  elliptic. This implies Existence, Uniqueness and Regularity for
elliptic. This implies Existence, Uniqueness and Regularity for
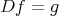
 Relation with previous situation:
Relation with previous situation:
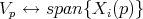
 Kohn's sublaplacian in
Kohn's sublaplacian in  (bdy. value of the Bargmann laplacian of the 3-ball in
(bdy. value of the Bargmann laplacian of the 3-ball in  ):
):
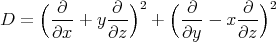
not elliptic, degenerates along  -axis. Still, hypoelliptic, even analytically so:
-axis. Still, hypoelliptic, even analytically so:
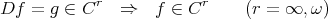
Ultimate reason: 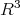 is spanned by
is spanned by
![∂ ∂ ∂ ∂ ∂ X = ---+ y --, Y = ---- x ---, [X, Y] = - 2--- ∂x ∂z ∂y ∂z ∂z](/img/revistas/ruma/v47n1/1a0155x.png)
Remark: Kohn's sublaplacian can be viewed as the boundary value of the laplacian of the 3-ball in 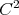 , with its Bargmann metric.
, with its Bargmann metric.
Classes of distributions
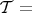 tangent sheaf of
tangent sheaf of 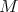 (germs of vector fields)
(germs of vector fields)
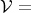 subsheaf of fields
subsheaf of fields 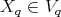 .
.
Filtration of 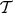 generated by
generated by 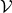 :
:
![W1 = V W2 = V + [V, V] W3 = V + [V, V] + [V, [V, V ]] .. .](/img/revistas/ruma/v47n1/1a0163x.png)
 V Involutive:
V Involutive: 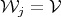
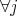 (
(![[V, V ] ⊂ V](/img/revistas/ruma/v47n1/1a0168x.png) ).
).
 V Outvolutive, bracket-generating, fat:
V Outvolutive, bracket-generating, fat: 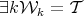
Recall Involutive case:
 Frobenius: Involutive
Frobenius: Involutive  completely integrable:
completely integrable:
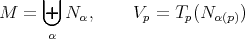
with the leaves 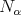 maximal.
maximal.
Involutive subriemannian geometry? Not very interesting: each 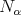 is riemannian.
is riemannian. 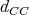 distance between leaves is
distance between leaves is 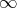 .
. 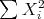 is far from regular. Still, Lie algebras of vector fields are fundamental in Control. If
is far from regular. Still, Lie algebras of vector fields are fundamental in Control. If 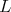 is such, then
is such, then 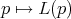 not a distribution: dim
not a distribution: dim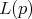 may jump. It is a "Distribution with singularities", but involutive, so one can ask
may jump. It is a "Distribution with singularities", but involutive, so one can ask
 Is every point of
Is every point of 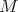 contained in a unique maximal integral submanifold of
contained in a unique maximal integral submanifold of 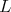 ?
?
Answer: NO for smooth, YES for analytic.
(Hermann-Nagano Theorem). This is why real analyticity - and, eventually, subanalyticity - eventually come in [S].
Outvolutive distributions
 Example:
Example: 
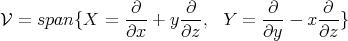
![∂-- [X, Y ] = - 2 ∂z ∕∈ V](/img/revistas/ruma/v47n1/1a0189x.png)
so ![X, Y, [X, Y ],](/img/revistas/ruma/v47n1/1a0190x.png) span
span 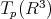 everywhere.
everywhere.
From now on,  will be outvolutive.
will be outvolutive.
THEOREMS. Assume  can be connected with smooth arcs.
can be connected with smooth arcs.
 Chow (anti-Frobenius). Any two points can be joined by a smooth horizontal curve.
Chow (anti-Frobenius). Any two points can be joined by a smooth horizontal curve.
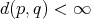 for any subriemannian structure on
for any subriemannian structure on 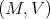 .
.
 Regularity of
Regularity of 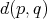 is critical. For example, unless
is critical. For example, unless 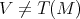 , the function
, the function 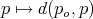 is not continuously differentiable in any punctured neighborhood of
is not continuously differentiable in any punctured neighborhood of 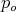 !
!
Instead,
 Agrachev:
Agrachev:
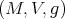 analytic
analytic 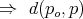 subanalytic
subanalytic
i.e., 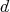 -balls are subanalytic.
-balls are subanalytic.
Subanalytic sets: locally projections of semianalytic. Equivalently, locally of the form
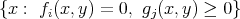
with 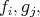 real analytic.
real analytic.
Lojasiewicz, Sussmann, ...
As to subellipticity,
 Hormander:
Hormander:
If  is a local basis of
is a local basis of 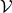 , then
, then 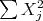 is hypoelliptic
is hypoelliptic
Horizontal Submanifolds


 many horizontal curves. Higher dimension?
many horizontal curves. Higher dimension?
Integral objects of non-integrable things are likely interesting. Also occur spontaneously in minimal surfaces, Jets of Maps, Control, ... But are hard to find, no general pattern.
Models:
Carnot Groups
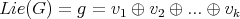
satisfying
![[v1,vj] = vj+1](/img/revistas/ruma/v47n1/1a01117x.png)
Canonical distribution on 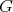 :
:
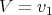
 Origin: Gromov's Theorems on growth of discrete groups
Origin: Gromov's Theorems on growth of discrete groups
 Not just examples: any outvolutive distribution filters
Not just examples: any outvolutive distribution filters  . The associated graded
. The associated graded
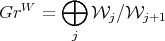
is a sheaf of Carnot algebras.
 How many? Even step 2
How many? Even step 2
![g = v ⊕ z z = [v, v]](/img/revistas/ruma/v47n1/1a01125x.png)
no classification is possible for 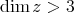 . (Bernstein-Gelfand-Ponomarev-Gabriel-Coxeter-Dynkin Diagram has
. (Bernstein-Gelfand-Ponomarev-Gabriel-Coxeter-Dynkin Diagram has 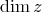 edges joining 2 vertices)
edges joining 2 vertices)
Models of models?
Groups of Heisenberg type
But "as role models go, they are hard to emulate": only Carnot groups with abundant domains admissible for the Dirichlet problem and/or explicit fundamental solutions for 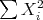 , weakly convex gauge ...
, weakly convex gauge ...
 Definition:
Definition: 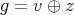 with inner products such that
with inner products such that
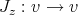
defined by
![′ ′ (Jzu,u )v = (z,[u,u ])z](/img/revistas/ruma/v47n1/1a01132x.png)
satisfies
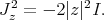
Equivalently: 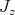 defines unitary representation of Cliff(
defines unitary representation of Cliff( ) on
) on  .
.
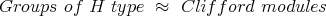
Parametrized by 2 or 3 natural numbers
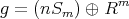
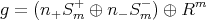
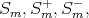 spinor spaces.
spinor spaces.
 Analogy with symplectic.
Analogy with symplectic.
 History: fundamental solution for
History: fundamental solution for 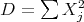 :
:
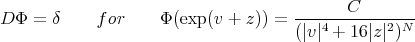
Since then keep yielding interesting riemannian examples (K., Willmore-Damek-Ricci, Selberg-Lauret, Gordon, Szabo, ... ).

 is largest. As to subriemannian:
is largest. As to subriemannian:
"Manifolds of Heisenberg type are to subriemannian Geometry, as Euclidean spaces, or symmetric spaces, are to riemannian geometry"
 The search for maximal horizontal submanifolds in groups of Heisenberg type is joint work with Levstein, Saal, Tiraboschi.
The search for maximal horizontal submanifolds in groups of Heisenberg type is joint work with Levstein, Saal, Tiraboschi.
 In any Carnot group, for any horizontal submanifold
In any Carnot group, for any horizontal submanifold 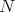 and any point
and any point 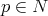 , there exists a unique horizontal subgroup
, there exists a unique horizontal subgroup 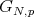 such that
such that
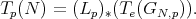
Any horizontal subgroup is abelian.
Hope to find all the latter. The following points to other reasons
![M aximal isotropic subspaces of (v,[ , ]) U](/img/revistas/ruma/v47n1/1a01153x.png)
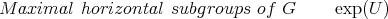
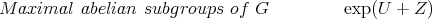
 Classical examples to keep in mind:
Classical examples to keep in mind:
On the 3-dimensional Heisenberg group, the distribution is 2-dimensional and the maximal horizontal submanifolds are 1-dimensional. But too many. Subgroups then.
On the 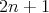 dimensional Heisenberg, the distribution is 2n-dimensional and the maximal horizontal submanifolds are n-dimensional. Distinguished class:
dimensional Heisenberg, the distribution is 2n-dimensional and the maximal horizontal submanifolds are n-dimensional. Distinguished class: 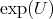 with
with 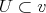 totally isotropic in the usual sense.
totally isotropic in the usual sense.
 In general, maximal possible dimension is
In general, maximal possible dimension is  : "Lagrangian" subspaces. Not always achieved.
: "Lagrangian" subspaces. Not always achieved. 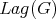 is a variety. Have a description (to be presented by Levstein in Colonia).
is a variety. Have a description (to be presented by Levstein in Colonia).
 Relation with Schroedinger Representations (?), Deligne's "Reality and the Heisenberg group".
Relation with Schroedinger Representations (?), Deligne's "Reality and the Heisenberg group".
SOME CONCLUSIONS
 Sometimes
Sometimes 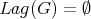
 Sometimes any two Lagragians are conjugate by an automorphism of
Sometimes any two Lagragians are conjugate by an automorphism of 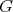 , sometimes not.
, sometimes not.
 Sometimes
Sometimes 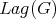 is a group. For example, if
is a group. For example, if  mod
mod 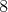 and
and
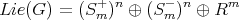
then
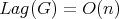
 Always
Always 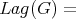 finite
finite  of
of  -orbits, of the form
-orbits, of the form  , with
, with  reductive
reductive
 NEXT: Maximal, but dim
NEXT: Maximal, but dim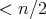 ?
?
Examples! In  Quaternionic 7-dimensional or Octonionic 15-dimensional Heisenberg there are no horizontal submanifolds of dimension
Quaternionic 7-dimensional or Octonionic 15-dimensional Heisenberg there are no horizontal submanifolds of dimension  . The distribution has dimension 4 and 8, respectively.
. The distribution has dimension 4 and 8, respectively.
Bibliography
A good starting point for geometers is R. Montgomery's review of Gromov's book. The following references were chosen specifically for the talk, but they and their bibliography are representative
R. Montgomery A tour of subriemannian geometries, their geodesics and applications, A.M.S. Mathematical Surveys and Monographs, 2002 [ Links ]
Gromov Carnot-Carathéodory spaces seen from within, in Subriemannian Geometry, Progr. Math., 144, Bikhauser (1996). Review by R. Montgomery in MathSciNet 2000f:53034 [ Links ]
Capogna - Garofalo - Nhieu, Properties of harmonic measures in the Dirichlet problem for nilpotent Lie groups of Heisenberg type, American Journal of Mathematics 124, 2 (2002) [ Links ]
Danielli - Garofalo - Nhieu, Notions of convexity in Carnot groups, Comm. in Analysis and Geom., 11-2 (2003) [ Links ]
M. Christ, A remark on sums of squares of complex vector fields, math.CV/0503506 [ Links ]
Kaplan Fundamental solutions for a class of hypoelliptic operators associated with composition of quadratic forms, Trans. A.M.S. 258 (1980) [ Links ]
Agrachev - Gauthier On the subanalyticity of CC distances, Annales de l'Institut Henri Poincaré; Analyse non-linéare 18, No. 3, (2001), Review by Sussmann in MathSciNet 2002h:93031 [ Links ]
Sussmann, Why real analyticity is important in Control Theory, Perspectives in control theory, Birkhuser (1990) [ Links ]
Citti - Sarti A cortical based model of perceptual completion in the roto-translation space, Workshop on Second Order Subelliptic Equations and Applications, Cortona, June 2003 [ Links ]
Aroldo Kaplan
FaMAF-CIEM, Universidad Nacional de Córdoba,
Córdoba 5000, Argentina
kaplan@mate.uncor.edu
Recibido: 30 de septiembre de 2005
Aceptado: 27 de septiembre de 2006














