Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932versão On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.47 n.1 Bahía Blanca jan./jun. 2006
Riemannian G-manifolds as Euclidean submanifolds
Ruy Tojeiro
Abstract: We survey on some recent developments on the study of Riemannian G-manifolds as Euclidean submanifolds.
2000 Mathematics Subject Classification. 53 A07, 53 C40, 53 C42
Key words and phrases. Riemannian G-manifolds, rotation hypersurfaces, polar actions, rigidity of hypersurfaces, warped products
Let 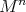 be a complete Riemannian manifold of dimension
be a complete Riemannian manifold of dimension 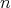 acted on by a connected closed subgroup
acted on by a connected closed subgroup 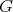 of its isometry group
of its isometry group 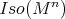 . We refer to
. We refer to 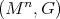 , or simply to
, or simply to 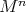 for short, as a Riemannian
for short, as a Riemannian 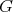 -manifold. The codimension of a maximal dimensional
-manifold. The codimension of a maximal dimensional 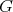 -orbit is called the
-orbit is called the 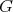 -cohomogeneity of
-cohomogeneity of 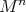 . In particular,
. In particular, 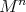 is
is 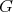 -homogeneous if it has
-homogeneous if it has 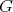 -cohomogeneity zero, that is, if
-cohomogeneity zero, that is, if 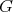 acts transitively on
acts transitively on 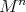 .
.
Riemannian 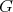 -manifolds have been extensively studied from various points of view. In particular, those of low cohomogeneity have been used as a rich source of examples of Riemannian manifolds whose metrics have several important geometric properties, including metrics of positive sectional curvatures, Einstein and Ricci-flat metrics, and metrics with exceptional holonomy groups.
-manifolds have been extensively studied from various points of view. In particular, those of low cohomogeneity have been used as a rich source of examples of Riemannian manifolds whose metrics have several important geometric properties, including metrics of positive sectional curvatures, Einstein and Ricci-flat metrics, and metrics with exceptional holonomy groups.
An interesting and natural problem is to study Riemannian 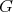 -manifolds as submanifolds of Euclidean space
-manifolds as submanifolds of Euclidean space 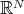 . These include submanifolds that are invariant by the action of a closed subgroup of the isometry group of
. These include submanifolds that are invariant by the action of a closed subgroup of the isometry group of 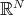 . By a result of Moore [Mo], every compact homogeneous Riemannian manifold
. By a result of Moore [Mo], every compact homogeneous Riemannian manifold 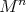 can be realized in this way, namely,
can be realized in this way, namely, 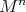 admits an isometric embedding into some Euclidean space that is equivariant with respect to its full isometry group. On the other hand, a theorem of Kobayashi [Ko] states that an isometric immersion
admits an isometric embedding into some Euclidean space that is equivariant with respect to its full isometry group. On the other hand, a theorem of Kobayashi [Ko] states that an isometric immersion 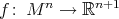 ,
, 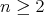 , of a compact homogeneous Riemannian manifold must be equivariant with respect to the full isometry group of
, of a compact homogeneous Riemannian manifold must be equivariant with respect to the full isometry group of 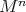 , thus implying
, thus implying 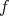 to be an embedding of
to be an embedding of 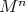 as a round hypersphere of
as a round hypersphere of 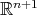 .
.
The aim of this paper is to survey on some recent developments on this problem, mostly for the case of Riemannian 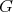 -manifolds as Euclidean hypersurfaces.
-manifolds as Euclidean hypersurfaces.
The study of Riemannian 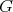 -manifolds as Euclidean submanifolds was initiated by the following result of Kobayashi [Ko] for compact homogeneous hypersurfaces.
-manifolds as Euclidean submanifolds was initiated by the following result of Kobayashi [Ko] for compact homogeneous hypersurfaces.
Theorem 1. Let 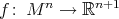 be an isometric immersion of a compact homogeneous Riemannian manifold. Then
be an isometric immersion of a compact homogeneous Riemannian manifold. Then 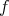 embeds
embeds 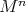 as a round sphere.
as a round sphere.
The main step in the proof of Kobayashi's theorem is to show that 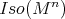 can be realized as a group of extrinsic isometries of Euclidean space, i.e., that there exists a Lie-group homomorphism
can be realized as a group of extrinsic isometries of Euclidean space, i.e., that there exists a Lie-group homomorphism 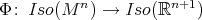 with respect to which
with respect to which 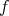 is equivariant, in the sense that
is equivariant, in the sense that 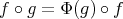 for all
for all 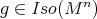 . As in several subsequent results, this is accomplished by establishing the rigidity of
. As in several subsequent results, this is accomplished by establishing the rigidity of 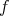 . Recall that an isometric immersion
. Recall that an isometric immersion 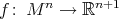 is rigid if any other isometric immersion
is rigid if any other isometric immersion 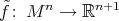 differs from
differs from 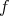 by a rigid motion of
by a rigid motion of 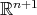 . Under the assumptions of Kobayashi's theorem, one can start by using the well-known fact that any compact Euclidean hypersurface has a point with strictly positive sectional curvatures (and hence with nonvanishing principal curvatures) and then use the homogeneity of
. Under the assumptions of Kobayashi's theorem, one can start by using the well-known fact that any compact Euclidean hypersurface has a point with strictly positive sectional curvatures (and hence with nonvanishing principal curvatures) and then use the homogeneity of 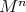 to conclude that this must hold everywhere on
to conclude that this must hold everywhere on 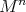 . For
. For 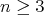 , the local rigidity theorem of Cartan-Beez-Killing can thus be applied: a Euclidean hypersurface of dimension
, the local rigidity theorem of Cartan-Beez-Killing can thus be applied: a Euclidean hypersurface of dimension 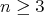 is rigid whenever it has at least three nonzero principal curvatures everywhere. Applying this result to the pair of isometric immersions
is rigid whenever it has at least three nonzero principal curvatures everywhere. Applying this result to the pair of isometric immersions 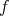 and
and  , for each fixed
, for each fixed 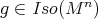 , one gets a rigid motion
, one gets a rigid motion 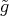 such that
such that 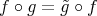 . Once we have this, it is not difficult to prove that the correspondence
. Once we have this, it is not difficult to prove that the correspondence  defines a Lie-group homomorphism
defines a Lie-group homomorphism 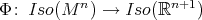 such that
such that 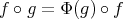 for all
for all 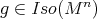 . Moreover, the subgroup
. Moreover, the subgroup 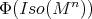 of
of 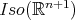 being compact, it has a fixed point by a well-known result of Cartan. This implies that
being compact, it has a fixed point by a well-known result of Cartan. This implies that 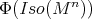 is contained in (a conjugacy class of) the orthogonal group
is contained in (a conjugacy class of) the orthogonal group 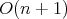 . Since the image
. Since the image 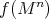 lies in a
lies in a 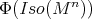 -orbit, it must be a round hypersphere of
-orbit, it must be a round hypersphere of 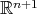 . Finally, that
. Finally, that 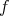 is an embedding follows by a standard covering map argument.
is an embedding follows by a standard covering map argument.
The extension of Kobayashi's theorem to the noncompact case came soon afterwards with the contribution by Nagano and Takahashi [NT], who proved that if 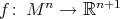 is an isometric immersion of a homogeneous Riemannian manifold then
is an isometric immersion of a homogeneous Riemannian manifold then 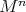 is isometric to
is isometric to 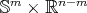 ,
, 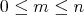 , provided that the rank
, provided that the rank 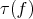 of the second fundamental form of
of the second fundamental form of 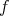 is different from
is different from 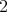 at some point. Moreover,
at some point. Moreover, 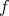 splits as
splits as 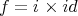 if
if 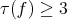 at some (and hence at any) point of
at some (and hence at any) point of 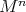 , where
, where 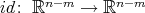 is the identity map and
is the identity map and  ,
, 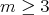 , is an umbilical inclusion, and otherwise it is a cylinder over a plane curve. The restriction on
, is an umbilical inclusion, and otherwise it is a cylinder over a plane curve. The restriction on 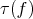 was later removed by Harle [Ha], as a consequence of a more general result on complete Euclidean hypersurfaces with constant scalar curvature. A simpler proof of Harle's theorem making use of the Gauss parameterization of hypersurfaces whose second fundamental forms have constant rank was subsequently given by Dajczer-Gromoll [DG
was later removed by Harle [Ha], as a consequence of a more general result on complete Euclidean hypersurfaces with constant scalar curvature. A simpler proof of Harle's theorem making use of the Gauss parameterization of hypersurfaces whose second fundamental forms have constant rank was subsequently given by Dajczer-Gromoll [DG ].
].
3. Homogeneous submanifolds of codimension two
Non-equivariant isometric immersions 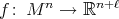 ,
,  , of homogeneous Riemannian manifolds can be easily constructed by taking, for instance, a composition
, of homogeneous Riemannian manifolds can be easily constructed by taking, for instance, a composition 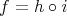 of an umbilical inclusion
of an umbilical inclusion  with an isometric immersion
with an isometric immersion  of an open subset
of an open subset 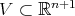 containing
containing  . This indicates that classifying homogeneous Euclidean submanifolds of higher codimension should be much harder than in the hypersurface case. Nevertheless, for compact submanifolds of dimension
. This indicates that classifying homogeneous Euclidean submanifolds of higher codimension should be much harder than in the hypersurface case. Nevertheless, for compact submanifolds of dimension 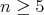 and codimension two this was accomplished by Castro-Noronha [CN]:
and codimension two this was accomplished by Castro-Noronha [CN]:
Theorem 2. Let 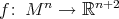 ,
, 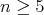 , be an isometric immersion of a compact homogeneous Riemannian manifold. Then one of the following possibilities holds:
, be an isometric immersion of a compact homogeneous Riemannian manifold. Then one of the following possibilities holds:
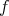 is equivariant with respect to an orthogonal representation
is equivariant with respect to an orthogonal representation 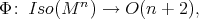
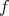 is a homogeneous isoparametric hypersurface of
is a homogeneous isoparametric hypersurface of 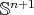 ;
;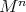 is isometric to
is isometric to 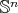 ;
;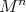 is isometrically covered by
is isometrically covered by 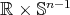 .
.
The authors have actually been able to obtain the same conclusion by assuming, instead of compactness of 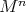 , that
, that 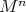 has at least one point where the index of relative nullity of
has at least one point where the index of relative nullity of 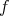 , that is, the dimension of the kernel of its second fundamental form, is not greater than
, that is, the dimension of the kernel of its second fundamental form, is not greater than  .
.
The main tool in the proof is a rigidity result for Euclidean submanifolds due to do Carmo-Dajczer [dCD], which implies that a Euclidean 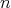 -dimensional submanifold of dimension
-dimensional submanifold of dimension 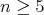 and codimension two is rigid whenever its index of relative nullity is everywhere less than or equal to
and codimension two is rigid whenever its index of relative nullity is everywhere less than or equal to  and there are at least three nonzero principal curvatures in every normal direction. Using this result, the authors prove that a compact homogeneous Euclidean submanifold of codimension two is rigid if it has at least one point where the index of relative nullity is not greater than
and there are at least three nonzero principal curvatures in every normal direction. Using this result, the authors prove that a compact homogeneous Euclidean submanifold of codimension two is rigid if it has at least one point where the index of relative nullity is not greater than  , unless at every point one can find an orthonormal basis
, unless at every point one can find an orthonormal basis 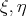 of the normal space at that point such that the shape operators
of the normal space at that point such that the shape operators 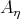 and
and 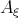 satisfy
satisfy 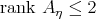 and
and 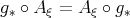 for every intrinsic isometry
for every intrinsic isometry 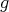 of the submanifold. Rigidity forces the submanifold to be extrinsically homogeneous, as previously discussed, giving the first possibility in the statement. The proof proceeds by considering separately the cases in which the rank of
of the submanifold. Rigidity forces the submanifold to be extrinsically homogeneous, as previously discussed, giving the first possibility in the statement. The proof proceeds by considering separately the cases in which the rank of 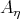 is either
is either  or
or 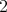 . The former leads to the two remaining possibilities in the statement, whereas in the most delicate case where
. The former leads to the two remaining possibilities in the statement, whereas in the most delicate case where 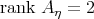 it is shown that the submanifold is an extrinsic product
it is shown that the submanifold is an extrinsic product 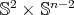 .
.
As far as we know, it remains an open problem to determine the cases in which a homogeneous Euclidean submanifold of codimension greater than two can fail to be extrinsically homogeneous. In the next sections we go back to the case of 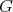 -hypersurfaces, but allow the intrinsic
-hypersurfaces, but allow the intrinsic 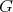 -action to be no longer transitive.
-action to be no longer transitive.
4. Complete 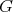 -hypersurfaces of cohomogeneity one
-hypersurfaces of cohomogeneity one
In this section we discuss Riemannian 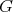 -manifolds of cohomogeneity one isometrically immersed in Euclidean space as hypersurfaces. We start with the simplest examples:
-manifolds of cohomogeneity one isometrically immersed in Euclidean space as hypersurfaces. We start with the simplest examples:
4.1. Hypersurfaces of revolution. Consider a curve 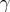 that is either contained in the interior of a half-space
that is either contained in the interior of a half-space 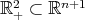 or meets its boundary
or meets its boundary 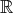 orthogonally. Now let the subgroup
orthogonally. Now let the subgroup 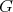 of
of 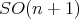 that fixes
that fixes 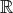 act on
act on 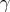 . This gives rise to a
. This gives rise to a 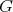 -invariant hypersurface
-invariant hypersurface 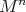 of
of 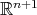 , called a hypersurface of revolution with
, called a hypersurface of revolution with 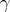 as profile. The group
as profile. The group 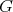 acts on
acts on 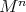 with one-codimensional round spheres as principal orbits. In particular, they are umbilical submanifolds of
with one-codimensional round spheres as principal orbits. In particular, they are umbilical submanifolds of 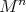 , i.e., at any point their principal curvatures coincide. It was shown by Podestá-Spiro [PS] that this property characterizes hypersurfaces of revolution among compact hypersurfaces of cohomogeneity one with dimension
, i.e., at any point their principal curvatures coincide. It was shown by Podestá-Spiro [PS] that this property characterizes hypersurfaces of revolution among compact hypersurfaces of cohomogeneity one with dimension 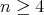 :
:
Theorem 3. Let 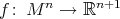 ,
, 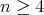 , be an isometric immersion of a compact Riemannian manifold. Assume that a closed connected subgroup
, be an isometric immersion of a compact Riemannian manifold. Assume that a closed connected subgroup 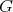 of
of 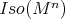 acts on
acts on 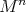 with cohomogeneity one. If the
with cohomogeneity one. If the 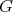 -principal orbits are umbilical in
-principal orbits are umbilical in 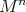 then
then 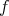 is a hypersurface of revolution.
is a hypersurface of revolution.
For any manifold 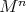 of
of 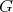 -cohomogeneity one, and any open interval
-cohomogeneity one, and any open interval 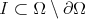 in the interior of the orbit space
in the interior of the orbit space 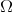 (which is diffeomorphic to either
(which is diffeomorphic to either 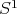 ,
, 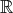 ,
, ![[0,1]](/img/revistas/ruma/v47n1/1a08155x.png) or
or 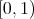 ), the inverse image
), the inverse image 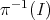 by the quotient map is
by the quotient map is 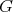 -equivariantly diffeomorphic to
-equivariantly diffeomorphic to 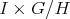 , where
, where 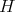 denotes an isotropy subgroup of principal type (see, e.g., [AA]). One of the main ingredients in Podestá-Spiro's proof of Theorem 3 is the observation that umbilicity of the principal orbits implies the metric induced on
denotes an isotropy subgroup of principal type (see, e.g., [AA]). One of the main ingredients in Podestá-Spiro's proof of Theorem 3 is the observation that umbilicity of the principal orbits implies the metric induced on 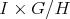 by this diffeomorphism to be a warped product metric
by this diffeomorphism to be a warped product metric  .
.
The assumption of umbilicity of the principal orbits in Podestá-Spiro's theorem has been weakened in subsequent developments. Namely, still in the compact case the same conclusion was obtained by assuming, instead, that  and all
and all 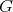 -principal orbits have constant sectional curvature [AMN], and that
-principal orbits have constant sectional curvature [AMN], and that  and all
and all 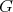 -principal orbits have positive sectional curvatures [CN].
-principal orbits have positive sectional curvatures [CN].
The noncompact case of Podestá-Spiro's result was studied by Mercuri-Seixas in [MS]. Here, even for cohomogeneity one isometric actions of compact Lie groups it is easy to construct non-rotational examples. For instance, consider the standard action of 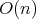 on
on 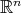 and isometrically immerse
and isometrically immerse 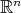 into
into 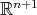 as a cylinder over a plane curve. Moreover, asking the hypersurface not to be everywhere flat is not enough, as pointed out in [MS]. For actions of compact groups, the right assumption turns out to be that no connected component of the flat part of the hypersurface be unbounded. The case of complete noncompact cohomogeneity one hypersurfaces under the action of a closed and noncompact Lie group (with umbilical principal orbits) was also considered in [MS].
as a cylinder over a plane curve. Moreover, asking the hypersurface not to be everywhere flat is not enough, as pointed out in [MS]. For actions of compact groups, the right assumption turns out to be that no connected component of the flat part of the hypersurface be unbounded. The case of complete noncompact cohomogeneity one hypersurfaces under the action of a closed and noncompact Lie group (with umbilical principal orbits) was also considered in [MS].
4.2. Standard examples. More general examples of Euclidean 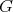 -hypersurfaces of cohomogeneity one, with
-hypersurfaces of cohomogeneity one, with 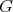 compact and connected, are produced as follows. Start with a cohomogeneity two closed connected subgroup
compact and connected, are produced as follows. Start with a cohomogeneity two closed connected subgroup 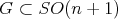 , so that the orbit space
, so that the orbit space 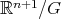 is a two dimensional manifold, possibly with boundary. Now consider the hypersurface
is a two dimensional manifold, possibly with boundary. Now consider the hypersurface 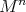 of
of 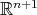 given by the inverse image under the canonical projection onto
given by the inverse image under the canonical projection onto 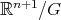 of a curve that is either contained in the interior of
of a curve that is either contained in the interior of 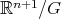 or meets its boundary orthogonally. We call
or meets its boundary orthogonally. We call 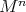 a standard example.
a standard example.
The natural question that emerges is whether, under reasonable global assumptions, the standard examples comprise all Euclidean hypersurfaces of cohomogeneity one. The answer is given by the following result of [MPST]:
Theorem 4. Let 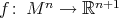 be an isometric immersion of a complete Riemannian manifold acted on with cohomogeneity one by a compact connected subgroup of
be an isometric immersion of a complete Riemannian manifold acted on with cohomogeneity one by a compact connected subgroup of 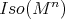 . If either
. If either  and
and 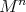 is compact, or if
is compact, or if  and the connected components of the flat part of
and the connected components of the flat part of 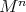 are bounded, then
are bounded, then 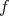 is either rigid or a hypersurface of revolution. In particular, it is a standard example.
is either rigid or a hypersurface of revolution. In particular, it is a standard example.
The proof of Theorem 4 relies on a global rigidity result due to Sacksteder [Sa], which states that a compact Euclidean hypersurface 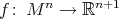 of dimension
of dimension  is rigid whenever the subset of totally geodesic points of
is rigid whenever the subset of totally geodesic points of 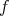 does not disconnect
does not disconnect 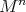 . In fact, the arguments in an unpublished proof of Sacksteder's theorem due to Ferus actually show more than the preceding statement. Namely, if
. In fact, the arguments in an unpublished proof of Sacksteder's theorem due to Ferus actually show more than the preceding statement. Namely, if 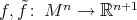 are isometric immersions of a complete Riemannian manifold of dimension
are isometric immersions of a complete Riemannian manifold of dimension 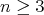 such that there exists no complete leaf of dimension
such that there exists no complete leaf of dimension  or
or  of the relative nullity distribution of
of the relative nullity distribution of 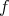 , then it is shown that their second fundamental forms are related by
, then it is shown that their second fundamental forms are related by 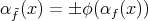 at every
at every 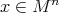 , where
, where 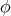 is a vector bundle isometry between the normal bundles of
is a vector bundle isometry between the normal bundles of 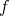 and
and 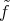 . This allows one to prove the following general result [MPST], [MT]:
. This allows one to prove the following general result [MPST], [MT]:
Theorem 5. Let 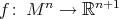 ,
,  , be a complete hypersurface. Assume that there exists no complete leaf of relative nullity of
, be a complete hypersurface. Assume that there exists no complete leaf of relative nullity of 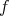 of dimension
of dimension  or
or  . Then there exists a Lie-group homomorphism
. Then there exists a Lie-group homomorphism 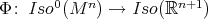 of the identity component of
of the identity component of 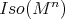 into
into 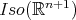 such that
such that 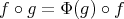 for all
for all 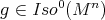 .
.
Notice that Theorem 5 easily implies the results of Kobayashi and, more generally, of Nagano-Takahashi mentioned in Section  . Namely, if
. Namely, if 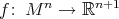 is an isometric immersion of a homogeneous Riemannian manifold such that
is an isometric immersion of a homogeneous Riemannian manifold such that 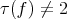 at some point, then either
at some point, then either 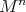 is flat, and hence
is flat, and hence 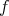 is a cylinder over a plane curve by a well-known theorem of Hartman-Nirenberg, or
is a cylinder over a plane curve by a well-known theorem of Hartman-Nirenberg, or 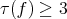 and Theorem 5 applies: it follows that
and Theorem 5 applies: it follows that 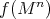 is an orbit of a cohomogeneity one subgroup of
is an orbit of a cohomogeneity one subgroup of 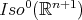 , in which case
, in which case 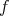 is an isoparametric hypersurface of
is an isoparametric hypersurface of 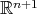 , whence an extrinsic product
, whence an extrinsic product 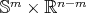 ,
, 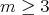 .
.
The proof of Theorem 5 is simple enough to be included here in almost full detail: given 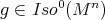 , let
, let 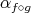 denote the second fundamental form of
denote the second fundamental form of  . On one hand, using that
. On one hand, using that 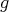 is an isometry we have
is an isometry we have
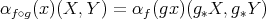
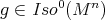 ,
, 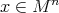 and
and 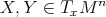 . In particular, this implies that the map
. In particular, this implies that the map 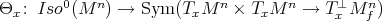 into the vector space of symmetric bilinear maps of
into the vector space of symmetric bilinear maps of 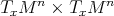 into
into 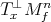 , given by
, given by 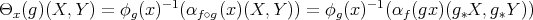
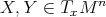 , is continuous. On the other hand, by the preceding remarks on Sacksteder's theorem, either
, is continuous. On the other hand, by the preceding remarks on Sacksteder's theorem, either 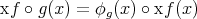 or
or 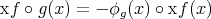 , where
, where 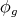 is a vector bundle isometry between
is a vector bundle isometry between 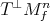 and
and 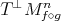 . Thus
. Thus 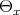 is a continuous map taking values in
is a continuous map taking values in 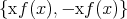 , whence must be constant by the connectedness of
, whence must be constant by the connectedness of 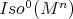 . Since
. Since 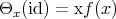 , it follows that
, it follows that 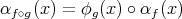 for every
for every 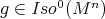 and
and 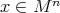 . By the Fundamental Theorem of Hypersurfaces, for each
. By the Fundamental Theorem of Hypersurfaces, for each 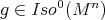 there exists
there exists 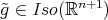 such that
such that  . It now follows from standard arguments that
. It now follows from standard arguments that  defines a Lie-group homomorphism
defines a Lie-group homomorphism 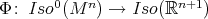 , whose image must lie in
, whose image must lie in 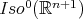 because it is connected.
because it is connected. As a consequence of Theorem 5, if 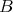 denotes the set of totally geodesic points of
denotes the set of totally geodesic points of 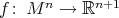 as in the statement, then
as in the statement, then
 | (1) |
Before we sketch a proof of this assertion, we first observe that it already implies the conclusion of Theorem 4 in the compact case. Namely, if 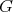 is a compact connected subgroup of
is a compact connected subgroup of 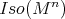 acting with cohomogeneity one, then (1) and Sacksteder's theorem imply that
acting with cohomogeneity one, then (1) and Sacksteder's theorem imply that 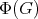 has a fixed vector
has a fixed vector  , hence every orbit of
, hence every orbit of 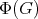 through a point not in the line spanned by
through a point not in the line spanned by  is a hypersphere of an affine hyperplane orthogonal to
is a hypersphere of an affine hyperplane orthogonal to  . Thus
. Thus 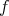 is a hypersurface of revolution. If
is a hypersurface of revolution. If 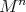 is not compact, one still has to consider the case in which
is not compact, one still has to consider the case in which 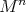 carries a complete leaf of relative nullity of
carries a complete leaf of relative nullity of 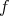 of dimension
of dimension  . Here a key rôle is played by the results of [CN], applied to the orbits of
. Here a key rôle is played by the results of [CN], applied to the orbits of 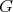 as compact homogeneous submanifolds of
as compact homogeneous submanifolds of 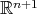 with codimension two. In this case
with codimension two. In this case 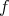 turns out to be an extrinsic product
turns out to be an extrinsic product 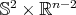 , hence rigid, with products
, hence rigid, with products 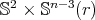 as the
as the 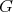 -principal orbits.
-principal orbits.
Now, to prove (1) one first uses the equivariance of 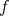 in order to show that
in order to show that 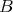 is invariant under
is invariant under 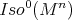 . It then follows that the orbit of
. It then follows that the orbit of 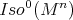 through a point
through a point 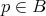 is a connected subset of totally geodesic points, whence must be contained in a hyperplane
is a connected subset of totally geodesic points, whence must be contained in a hyperplane 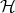 that is tangent to
that is tangent to 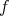 along it by a lemma of [DG
along it by a lemma of [DG ]. Therefore, a unit vector
]. Therefore, a unit vector  orthogonal to
orthogonal to 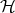 spans
spans 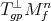 for every
for every 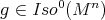 . Since
. Since 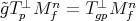 for every
for every 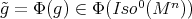 , because
, because 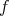 is equivariant with respect to
is equivariant with respect to 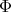 , the connectedness of
, the connectedness of 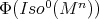 implies that it must fix
implies that it must fix  .
.
5. Compact locally polar 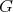 -hypersurfaces
-hypersurfaces
An isometric action of a compact Lie group 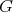 on a Riemannian manifold
on a Riemannian manifold 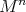 is said to be locally polar if the distribution of normal spaces to principal orbits on the regular part of
is said to be locally polar if the distribution of normal spaces to principal orbits on the regular part of 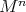 is integrable. Then
is integrable. Then 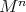 is called a locally polar Riemannian
is called a locally polar Riemannian 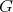 -manifold. For instance, any isometric action of cohomogeneity one is locally polar. It was shown by Heintze-Liu-Olmos [HLO], answering a question posed by Palais-Terng [PT], that for any complete locally polar Riemannian
-manifold. For instance, any isometric action of cohomogeneity one is locally polar. It was shown by Heintze-Liu-Olmos [HLO], answering a question posed by Palais-Terng [PT], that for any complete locally polar Riemannian 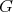 -manifold there exists a connected complete immersed submanifold
-manifold there exists a connected complete immersed submanifold  of
of 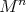 that intersects orthogonally all
that intersects orthogonally all 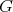 -orbits. Such a submanifold is called a section, and it is always a totally geodesic submanifold of
-orbits. Such a submanifold is called a section, and it is always a totally geodesic submanifold of 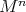 . The action is said to be polar if there exists a closed and embedded section. Clearly, for orthogonal representations there is no distinction between polar and locally polar actions, for in this case sections are just affine subspaces. Polar orthogonal representations have been classified by Dadok [D]. As a consequence of his classification, he obtained that every polar representation is orbit equivalent to (i.e., has the same orbits as) the isotropy representation of a semi-simple symmetric space.
. The action is said to be polar if there exists a closed and embedded section. Clearly, for orthogonal representations there is no distinction between polar and locally polar actions, for in this case sections are just affine subspaces. Polar orthogonal representations have been classified by Dadok [D]. As a consequence of his classification, he obtained that every polar representation is orbit equivalent to (i.e., has the same orbits as) the isotropy representation of a semi-simple symmetric space.
It was shown in [BCO] (see Proposition 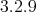 ) that if a closed subgroup of
) that if a closed subgroup of 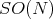 acts polarly on
acts polarly on 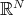 and leaves invariant a submanifold
and leaves invariant a submanifold 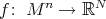 , then its restricted action on
, then its restricted action on 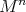 is locally polar. It is not true, however, that every locally polar action on a Euclidean submanifold arises in this way, even assuming it to be compact. For instance, consider a compact submanifold
is locally polar. It is not true, however, that every locally polar action on a Euclidean submanifold arises in this way, even assuming it to be compact. For instance, consider a compact submanifold 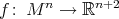 that is invariant under the action of one of the closed subgroups
that is invariant under the action of one of the closed subgroups 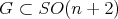 that act non-polarly on
that act non-polarly on 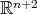 with cohomogeneity three. Then the induced action of
with cohomogeneity three. Then the induced action of 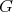 on
on 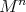 has cohomogeneity one, whence is locally polar. Nevertheless, for compact hypersurfaces of dimension
has cohomogeneity one, whence is locally polar. Nevertheless, for compact hypersurfaces of dimension 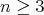 it was shown in [MT] that this is indeed the case.
it was shown in [MT] that this is indeed the case.
Theorem 6. Let 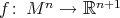 ,
, 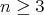 , be an isometric immersion of a compact Riemannian manifold. Assume that a closed connected subgroup
, be an isometric immersion of a compact Riemannian manifold. Assume that a closed connected subgroup 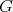 of
of 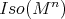 acts locally polarly on
acts locally polarly on 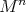 with cohomogeneity
with cohomogeneity 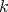 . Then there exists an orthogonal representation
. Then there exists an orthogonal representation 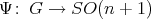 such that
such that 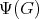 acts polarly on
acts polarly on 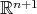 with cohomogeneity
with cohomogeneity  and
and 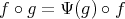 for every
for every 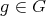 .
.
For the proof of Theorem 6, one starts by recalling that 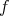 is equivariant with respect to a Lie-group homomorphism
is equivariant with respect to a Lie-group homomorphism 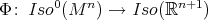 by Theorem 5, which here must actually be an orthogonal representation of
by Theorem 5, which here must actually be an orthogonal representation of 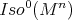 as a closed subgroup of
as a closed subgroup of 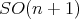 by the compactness and connectedness of
by the compactness and connectedness of 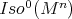 . Thus, it suffices to prove that
. Thus, it suffices to prove that 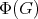 acts polarly on
acts polarly on 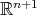 and set
and set 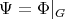 . For that, the idea is to make use of a result of Palais-Terng [PT], according to which an orthogonal representation in
. For that, the idea is to make use of a result of Palais-Terng [PT], according to which an orthogonal representation in 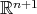 of a compact Lie group
of a compact Lie group 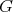 is polar whenever it has an orbit that is an isoparametric submanifold
is polar whenever it has an orbit that is an isoparametric submanifold 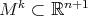 and, in addition, either
and, in addition, either 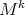 is full (i.e., not contained in any affine subspace) or, if otherwise,
is full (i.e., not contained in any affine subspace) or, if otherwise, 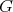 acts trivially on the orthogonal complement of the linear span of
acts trivially on the orthogonal complement of the linear span of 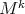 . Recall that a submanifold
. Recall that a submanifold 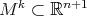 is isoparametric if it has flat normal bundle and the principal curvatures with respect to every parallel normal vector field along any curve in
is isoparametric if it has flat normal bundle and the principal curvatures with respect to every parallel normal vector field along any curve in 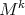 are constant (with constant multiplicities). The proof then consists of proving that these conditions are satisfied by the action of
are constant (with constant multiplicities). The proof then consists of proving that these conditions are satisfied by the action of 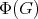 , for which the main tool is to use that principal orbits of locally polar isometric actions are characterized by the fact that equivariant normal vector fields are parallel with respect to the normal connection.
, for which the main tool is to use that principal orbits of locally polar isometric actions are characterized by the fact that equivariant normal vector fields are parallel with respect to the normal connection.
The simplest examples of hypersurfaces 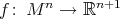 that are invariant by a polar action on
that are invariant by a polar action on 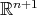 of a closed subgroup of
of a closed subgroup of 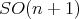 are the hypersurfaces of revolution (with possibly higher dimensional profiles), which are produced by the action on a hypersurface
are the hypersurfaces of revolution (with possibly higher dimensional profiles), which are produced by the action on a hypersurface 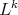 (possibly with boundary) of a half-space of
(possibly with boundary) of a half-space of 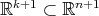 , disjoint to the boundary
, disjoint to the boundary 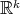 or orthogonal to it, of a closed subgroup
or orthogonal to it, of a closed subgroup 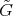 of
of 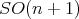 that fixes
that fixes 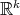 and acts transitively on the hyperspheres of the orthogonal complement
and acts transitively on the hyperspheres of the orthogonal complement 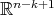 of
of 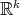 . The following result of [MT] gives several sufficient conditions for a compact Euclidean hypersurface as in Theorem 6 to be a hypersurface of revolution.
. The following result of [MT] gives several sufficient conditions for a compact Euclidean hypersurface as in Theorem 6 to be a hypersurface of revolution.
Corollary 7. Let 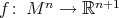 ,
,  , be an isometric immersion of a compact Riemannian manifold. Assume that a closed connected subgroup
, be an isometric immersion of a compact Riemannian manifold. Assume that a closed connected subgroup 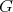 of
of 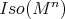 acts locally polarly on
acts locally polarly on 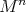 with cohomogeneity
with cohomogeneity 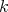 . Then any of the following additional conditions implies that
. Then any of the following additional conditions implies that 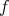 is a hypersurface of revolution:
is a hypersurface of revolution:
- there exists a totally geodesic (in
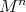 )
) 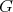 -principal orbit;
-principal orbit; 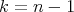 ;
;- the
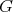 -principal orbits are umbilical in
-principal orbits are umbilical in 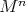 ;
; - there exists a
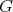 -principal orbit with nonzero constant sectional curvatures;
-principal orbit with nonzero constant sectional curvatures; - there exists a
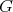 -principal orbit with positive sectional curvatures.
-principal orbit with positive sectional curvatures.
Moreover, in this case 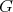 is isomorphic to one of the closed subgroups of
is isomorphic to one of the closed subgroups of  that act transitively on
that act transitively on 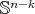 .
.
For the case of hypersurfaces of cohomogeneity  , the same conclusion was also derived in the noncompact case in [MPST] under the assumptions of Theorem 4. Another sufficient condition obtained in [MPST] for a hypersurface of
, the same conclusion was also derived in the noncompact case in [MPST] under the assumptions of Theorem 4. Another sufficient condition obtained in [MPST] for a hypersurface of 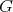 -cohomogeneity one and dimension
-cohomogeneity one and dimension 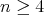 as in Theorem 4 to be a hypersurface of revolution is that some principal
as in Theorem 4 to be a hypersurface of revolution is that some principal 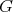 -orbit be homeomorphic to a sphere. This was accomplished by combining Theorem 4 and the fact that an isoparametric hypersurface of the sphere of dimension
-orbit be homeomorphic to a sphere. This was accomplished by combining Theorem 4 and the fact that an isoparametric hypersurface of the sphere of dimension 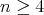 can not have a sphere as its universal covering, unless it is a round sphere. The proof of the latter uses several of the known restrictions on the number
can not have a sphere as its universal covering, unless it is a round sphere. The proof of the latter uses several of the known restrictions on the number 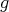 of principal curvatures of isoparametric hypersurfaces and on their multiplicities in order to show that the only possibility allowed for an isoparametric hypersurface of dimension
of principal curvatures of isoparametric hypersurfaces and on their multiplicities in order to show that the only possibility allowed for an isoparametric hypersurface of dimension 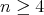 covered by a sphere is that
covered by a sphere is that  .
.
For the proof of Corollary 7, since one already knows from Theorem 6 that there exists an orthogonal representation 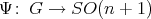 such that
such that 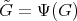 acts polarly on
acts polarly on 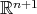 and
and 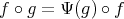 for every
for every 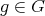 , it suffices to show that any of the conditions in the statement implies that
, it suffices to show that any of the conditions in the statement implies that
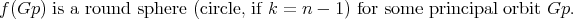 | (2) |
Indeed, since 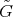 acts polarly on
acts polarly on 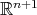 it fixes the subspace orthogonal to the linear span of
it fixes the subspace orthogonal to the linear span of 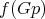 , and hence
, and hence 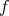 is a hypersurface of revolution. Moreover, a standard covering map argument shows that
is a hypersurface of revolution. Moreover, a standard covering map argument shows that 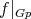 must be an embedding if
must be an embedding if 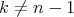 . Thus, if
. Thus, if 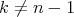 and
and 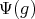 is the identity for some
is the identity for some 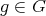 then it follows from
then it follows from 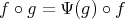 and the injectivity of
and the injectivity of 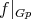 that
that 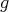 must fix any point of
must fix any point of 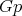 . Since
. Since 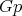 is a principal orbit, this easily implies that
is a principal orbit, this easily implies that 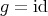 , and hence that
, and hence that 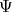 is an isomorphism of
is an isomorphism of 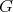 onto
onto 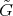 .
.
Now, to prove (2) one uses the fact that 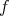 immerses
immerses 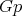 as an isoparametric submanifold, since
as an isoparametric submanifold, since 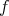 is equivariant with respect to
is equivariant with respect to 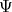 and principal orbits of polar representations are isoparametric submanifolds [PT]. If some principal
and principal orbits of polar representations are isoparametric submanifolds [PT]. If some principal 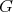 -orbit is totally geodesic, then the first normal spaces of
-orbit is totally geodesic, then the first normal spaces of 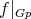 in
in 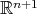 , that is, the subspaces of the normal spaces spanned by the image of its second fundamental form, are one-dimensional. Since for isoparametric submanifolds the first normal spaces always form a parallel subbundle of the normal bundle with respect to the normal connection, a standard reduction of codimension result implies that
, that is, the subspaces of the normal spaces spanned by the image of its second fundamental form, are one-dimensional. Since for isoparametric submanifolds the first normal spaces always form a parallel subbundle of the normal bundle with respect to the normal connection, a standard reduction of codimension result implies that 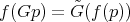 is contained as a hypersurface in some affine hyperplane
is contained as a hypersurface in some affine hyperplane 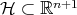 , and thus is a round hypersphere of
, and thus is a round hypersphere of 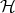 (a circle if
(a circle if 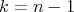 ). Conditions
). Conditions 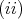 an
an 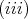 both imply
both imply 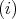 . In fact, if
. In fact, if 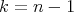 then the principal orbit of maximal length must be a geodesic. Similarly, if all principal orbits are umbilical in
then the principal orbit of maximal length must be a geodesic. Similarly, if all principal orbits are umbilical in 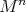 then the one of maximal volume is both minimal and umbilical, whence totally geodesic. Finally, one can show that an isoparametric submanifold that has either constant and nonzero or positive sectional curvatures must be a round sphere, which yields the statement under the remaining conditions
then the one of maximal volume is both minimal and umbilical, whence totally geodesic. Finally, one can show that an isoparametric submanifold that has either constant and nonzero or positive sectional curvatures must be a round sphere, which yields the statement under the remaining conditions  and
and 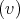 , respectively.
, respectively.
Corollary 7 and the results of [MPST] for cohomogeneity one hypersurfaces mentioned after it generalize and give simpler proofs of Podestá-Spiro's theorem and some of its extensions described in Section  . Further extensions have been recently obtained in [Mou], where the case of complete Euclidean hypersurfaces of dimension
. Further extensions have been recently obtained in [Mou], where the case of complete Euclidean hypersurfaces of dimension 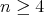 acted on locally polarly with umbilical principal orbits of codimension
acted on locally polarly with umbilical principal orbits of codimension 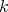 by a closed connected subgroup
by a closed connected subgroup 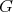 of its isometry group was considered. In case
of its isometry group was considered. In case 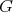 is compact and
is compact and  the hypersurface was shown to be of revolution if the connected components of the flat part of the hypersurface are bounded. If
the hypersurface was shown to be of revolution if the connected components of the flat part of the hypersurface are bounded. If 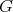 is not compact, the hypersurface is not everywhere flat and, for a given section
is not compact, the hypersurface is not everywhere flat and, for a given section  , the connected components of the subset of
, the connected components of the subset of  formed by flat points of the hypersurface are assumed to be bounded, it was shown that the hypersurface is either an extrinsic product
formed by flat points of the hypersurface are assumed to be bounded, it was shown that the hypersurface is either an extrinsic product 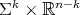 , the principal orbits being the fibers
, the principal orbits being the fibers 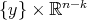 ,
, 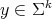 , or an extrinsic product
, or an extrinsic product  ,
,  , in which case the principal orbits are the fibers
, in which case the principal orbits are the fibers 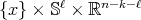 ,
, 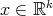 . For
. For  these results reduce to the ones in [MS] referred to at the end of Section
these results reduce to the ones in [MS] referred to at the end of Section  .
.
In part 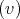 of Corollary 7, it was shown in [MT] that weakening the assumption to non-negativity of the sectional curvatures of some principal
of Corollary 7, it was shown in [MT] that weakening the assumption to non-negativity of the sectional curvatures of some principal 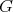 -orbit implies
-orbit implies 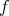 to be a multi-rotational hypersurface in the sense of [DN]:
to be a multi-rotational hypersurface in the sense of [DN]:
Corollary 8. Under the assumptions of Theorem 6, suppose further that there exists a 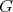 -principal orbit
-principal orbit 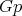 with nonnegative sectional curvatures. Then there exist an orthogonal decomposition
with nonnegative sectional curvatures. Then there exist an orthogonal decomposition 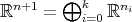 into
into 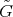 -invariant subspaces, where
-invariant subspaces, where 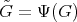 , and connected Lie subgroups
, and connected Lie subgroups  of
of 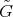 such that
such that 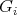 acts on
acts on 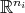 , the action being transitive on
, the action being transitive on 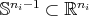 , and the action of
, and the action of 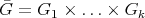 on
on 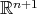 given by
given by
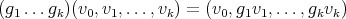
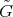 . In particular, if
. In particular, if 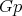 is flat then
is flat then  and
and 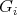 is isomorphic to
is isomorphic to 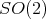 for
for 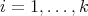 .
. Corollary 7 was used in [MT] to study a problem that is seemingly unrelated to isometric actions. Let 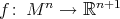 be a hypersurface of revolution as described in the paragraph preceding Corollary 7. Then the open and dense subset of
be a hypersurface of revolution as described in the paragraph preceding Corollary 7. Then the open and dense subset of 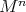 that is mapped by
that is mapped by 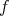 onto the complement of the axis
onto the complement of the axis 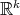 is isometric to the warped product
is isometric to the warped product 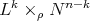 , where
, where 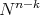 is the orbit of some fixed point
is the orbit of some fixed point 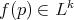 under the action of
under the action of 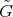 , and the warping function
, and the warping function 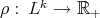 is a constant multiple of the distance to
is a constant multiple of the distance to 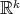 . Recall that a warped product
. Recall that a warped product 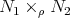 of Riemannian manifolds
of Riemannian manifolds 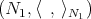 and
and 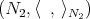 with warping function
with warping function 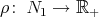 is the product manifold
is the product manifold 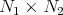 endowed with the metric
endowed with the metric 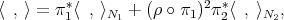 where
where 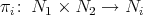 ,
, 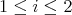 , denote the canonical projections. The problem is then to determine whether hypersurfaces of revolution are characterized by their intrinsic warped product structure. For compact Euclidean hypersurfaces of dimension
, denote the canonical projections. The problem is then to determine whether hypersurfaces of revolution are characterized by their intrinsic warped product structure. For compact Euclidean hypersurfaces of dimension 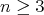 this was answered affirmatively in [MT]:
this was answered affirmatively in [MT]:
Theorem 9. Let 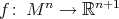 ,
, 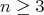 , be a compact hypersurface. If there exists an isometry onto an open and dense subset
, be a compact hypersurface. If there exists an isometry onto an open and dense subset  of a warped product
of a warped product 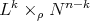 with
with 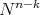 connected and complete (in particular if
connected and complete (in particular if 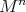 is isometric to a warped product
is isometric to a warped product 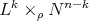 with
with 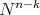 connected) then
connected) then 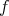 is a hypersurface of revolution.
is a hypersurface of revolution.
Theorem 9 can be seen as a global version in the hypersurface case of the local classification in [DT] of isometric immersions in codimension  of warped products
of warped products 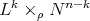 ,
, 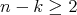 , into Euclidean space. It follows from the results of [DT] that an isometric immersion
, into Euclidean space. It follows from the results of [DT] that an isometric immersion 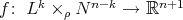 ,
, 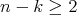 , of a warped product with no flat points is either a hypersurface of revolution or an extrinsic product
, of a warped product with no flat points is either a hypersurface of revolution or an extrinsic product 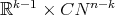 , where
, where 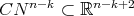 denotes the cone over a hypersurface
denotes the cone over a hypersurface 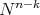 of
of 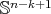 .
.
Acknowledgment. This survey is a slightly extended version of a talk given at the "II Encuentro de Geometria Diferencial" held in La Falda (Argentina) on June 2005. The author would like to take the opportunity to thank Carlos Olmos and the other colleagues from the Mathematics Department of the Universidad Nacional de Cordoba for the hospitality during his stay in La Falda and for the invitation to contribute with this paper.
[AA] ALEKSEEVSKI, A. V., ALEKSEEVSKI, D. V.: Riemannian G-manifold with one dimensional orbit space. Ann. Global Anal. Geom. 11 (1993), 197-211. [ Links ]
[AMN] ASPERTI, A.C., MERCURI, F., NORONHA, M.H.: Cohomogeneity one manifolds and hypersurfaces of revolution. Bolletino U.M.I. 11-B (1997), 199-215. [ Links ]
[BCO] BERNDT, J., CONSOLE, S., OLMOS, C.: Submanifolds and Holonomy, CRC/Chapman and Hall Research Notes Series in Math. 434 (2003), Boca Ratton. [ Links ]
[dCD] DO CARMO, M., DAJCZER, M.: A rigidity theorem for higher codimensions. Math. Ann. 274 (1986), 577-583. [ Links ]
[CN] CASTRO, H., NORONHA, M. H.: Homogeneous submanifolds in codimension two. Geom. Dedicata 78 (1999), 111-120. [ Links ]
[D] DADOK, J.: Polar coordinates induced by actions of compact Lie groups. Trans. Amer. Math. Soc. 288 (1985), 125-137. [ Links ]
[Da] DAJCZER, M. et al.: Submanifolds and isometric immersions. Matematics Lecture Series 13, Publish or Perish Inc., Houston-Texas, 1990. [ Links ]
[DG1] DAJCZER, M., GROMOLL, D.: Rigidity of complete Euclidean hypersurfaces. J.Diff. Geom. 31 (1990), 401-416. [ Links ]
[DG2] DAJCZER, M., GROMOLL, D.: Gauss parametrizations and rigidity aspects of submanifolds. J.Diff. Geom. 22 (1985), 1-12. [ Links ]
[DT] DAJCZER, M., TOJEIRO, R.: Isometric immersions in codimension two of warped products into space forms. Illinois J. Math. 48 (3) (2004), 711-746. [ Links ]
[DN] DILLEN, F., NÖLKER, S.: Semi-parallel submanifolds, multi-rotation surfaces and the helix-property. J. Reine Angew. Math. 435 (1993), 33-63. [ Links ]
[Ha] HARLE, C.: Rigidity of hypersurfaces with constant scalar curvature. J.Diff. Geom. 5 (1971), 85-111. [ Links ]
[HLO] HEINTZE, E., LIU, X., OLMOS, C.: Isoparametric submanifolds and a Chevalley-type restriction theorem. Integrable systems, geometry and topology, 151-190, AMS/IP Stud. Adv. Math. 36, Amer. Math. Soc., Providence, RI, 2006. [ Links ]
[Ko] KOBAYASHI, S.: Compact homogeneous hypersurfaces. Trans. Amer. Math. Soc. 88 (1958), 137-143. [ Links ]
[MPST] MERCURI, F., PODESTÀ, F., SEIXAS, J. A., TOJEIRO, R.: Cohomogeneity one hypersurfaces of Euclidean spaces. Comment. Math. Helv. 81 (2) (2006), 471-479. [ Links ]
[MS] MERCURI, F., SEIXAS, J. A.: Hypersurfaces of cohomogeneity one and hypersurfaces of revolution. Diff. Geom. Appl. 20(2) (2004), 255-239. [ Links ]
[Mo] MOORE, J. D.: Equivariant embeddings of Riemannian homogeneous spaces, Indiana Univ. Math. J. 25 (1976), 271-279. [ Links ]
[Mou] MOUTINHO, I.: G-variedades Riemannianas como hipersuperfícies de formas espaciais, Phd thesis, Universidade Federal de São Carlos, 2005. [ Links ]
[MT] MOUTINHO, I., TOJEIRO, R.: Polar actions on compact Euclidean hypersurfaces. Preprint. [ Links ]
[NT] NAGANO, T., TAKAHASHI, T.: Homogeneous hypersurfaces in Euclidean spaces. J. Math. Soc. Japan 12 (1960), 1-7. [ Links ]
[PT] PALAIS, R., TERNG, C.-L.: A general theory of canonical forms. Trans. Amer. Math. Soc. 300 (1987), 771-789. [ Links ]
[PS] PODESTÀ, F., SPIRO, A.: Cohomogeneity one manifolds and hypersurfaces of Euclidean space. Ann. Global Anal. Geom. 13 (1995), 169-184. [ Links ]
[Sa] SACKSTEDER, R.: The rigidity of hypersurfaces, J. of Math. Mech. 11 (1962), 929-939. [ Links ]
Ruy Tojeiro
Universidade Federal de São Carlos
13565-905-São Carlos, Brazil
tojeiro@dm.ufscar.br
Recibido: 7 de setiembre de 2005
Aceptado: 29 de agosto de 2006