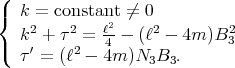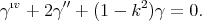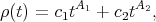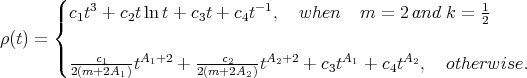Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932versão On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.47 n.2 Bahía Blanca jul./dez. 2006
A short survey on biharmonic maps between Riemannian manifolds
S. Montaldo and C. Oniciuc
2000 Mathematics Subject Classification. 58E20.
Key words and phrases. Harmonic and biharmonic maps.
The first author was supported by Regione Autonoma Sardegna (Italy). The second author was supported by a CNR-NATO (Italy) fellowship, and by the Grant At, 73/2005, CNCSIS (Romania)
Let 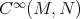 be the space of smooth maps
be the space of smooth maps 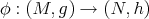 between two Riemannian manifolds. A map
between two Riemannian manifolds. A map 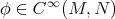 is called harmonic if it is a critical point of the energy functional
is called harmonic if it is a critical point of the energy functional
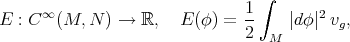
and is characterized by the vanishing of the first tension field 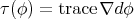 . In the same vein, if we denote by
. In the same vein, if we denote by 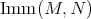 the space of Riemannian immersions in
the space of Riemannian immersions in 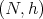 , then a Riemannian immersion
, then a Riemannian immersion 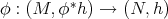 is called minimal if it is a critical point of the volume functional
is called minimal if it is a critical point of the volume functional
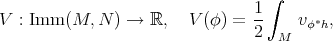
and the corresponding Euler-Lagrange equation is  , where
, where 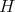 is the mean curvature vector field.
is the mean curvature vector field.
If 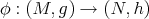 is a Riemannian immersion, then it is a critical point of the bienergy in
is a Riemannian immersion, then it is a critical point of the bienergy in 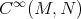 if and only if it is a minimal immersion [26]. Thus, in order to study minimal immersions one can look at harmonic Riemannian immersions.
if and only if it is a minimal immersion [26]. Thus, in order to study minimal immersions one can look at harmonic Riemannian immersions.
A natural generalization of harmonic maps and minimal immersions can be given by considering the functionals obtained integrating the square of the norm of the tension field or of the mean curvature vector field, respectively. More precisely:
- biharmonic maps are the critical points of the bienergy functional
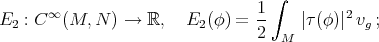
- Willmore immersions are the critical points of the Willmore functional
where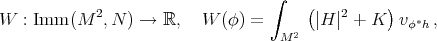
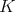 is the sectional curvature of
is the sectional curvature of  restricted to the image of
restricted to the image of  .
.
While the above variational problems are natural generalizations of harmonic maps and minimal immersions, biharmonic Riemannian immersions do not recover Willmore immersions, even when the ambient space is 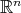 . Therefore, the two generalizations give rise to different variational problems.
. Therefore, the two generalizations give rise to different variational problems.
In a different setting, in [19], B.Y. Chen defined biharmonic submanifolds 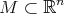 of the Euclidean space as those with harmonic mean curvature vector field, that is
of the Euclidean space as those with harmonic mean curvature vector field, that is 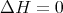 , where
, where  is the rough Laplacian. If we apply the definition of biharmonic maps to Riemannian immersions into the Euclidean space we recover Chen's notion of biharmonic submanifolds. Thus biharmonic Riemannian immersions can also be thought as a generalization of Chen's biharmonic submanifolds.
is the rough Laplacian. If we apply the definition of biharmonic maps to Riemannian immersions into the Euclidean space we recover Chen's notion of biharmonic submanifolds. Thus biharmonic Riemannian immersions can also be thought as a generalization of Chen's biharmonic submanifolds.
In the last decade there has been a growing interest in the theory of biharmonic maps which can be divided in two main research directions. On the one side, the differential geometric aspect has driven attention to the construction of examples and classification results; this is the face of biharmonic maps we shall try to report. The other side is the analytic aspect from the point of view of PDE: biharmonic maps are solutions of a fourth order strongly elliptic semilinear PDE. We shall not report on this aspect and we refer the reader to [18, 35, 36, 55, 56, 57] and the references therein.
The differential geometric aspect of biharmonic submanifolds was also studied in the semi-Riemannian case. We shall not discuss this case, although it is very rich in examples, and we refer the reader to [20] and the references therein.
We mention some other reasons that should encourage the study of biharmonic maps.
- The theory of biharmonic functions is an old and rich subject: they have been studied since 1862 by Maxwell and Airy to describe a mathematical model of elasticity; the theory of polyharmonic functions was later on developed, for example, by E. Almansi, T. Levi-Civita and M. Nicolescu. Recently, biharmonic functions on Riemannian manifolds were studied by R. Caddeo and L. Vanhecke [10, 17], L. Sario et al. [52], and others.
- The identity map of a Riemannian manifold is trivially a harmonic map, but in most cases is not stable (local minimum), for example consider
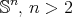 . In contrast, the identity map, as a biharmonic map, is always stable, in fact an absolute minimum of the energy.
. In contrast, the identity map, as a biharmonic map, is always stable, in fact an absolute minimum of the energy. - Harmonic maps do not always exists, for instance, J. Eells and J.C. Wood showed in [27] that there exists no harmonic map from
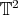 to
to  (whatever the metrics chosen) in the homotopy class of Brower degree
(whatever the metrics chosen) in the homotopy class of Brower degree 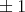 . We expect biharmonic maps to succeed where harmonic maps have failed.
. We expect biharmonic maps to succeed where harmonic maps have failed.
In this short survey we try to report on the theory of biharmonic maps between Riemannian manifolds, conscious that we might have not included all known results in the literature.
Table of Contents
2. The biharmonic equation
3. Non-existence results
3.1. Riemannian immersions
3.2. Submanifolds of 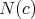
3.3. Riemannian submersions
4. Biharmonic Riemannian immersions
4.1. Biharmonic curves on surfaces
4.2. Biharmonic curves of the Heisenberg group 
4.3. The biharmonic submanifolds of 
4.4. Biharmonic submanifolds of 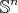
4.5. Biharmonic submanifolds in Sasakian space forms
5. Biharmonic Riemannian submersions
6. Biharmonic maps between Euclidean spaces
7. Biharmonic maps and conformal changes
7.1. Conformal change on the domain
7.2. Conformal change on the codomain
8. Biharmonic morphisms
9. The second variation of biharmonic maps
Acknowledgements. The first author wishes to thank the organizers of the "II Workshop in Differential Geometry - Córdoba - June 2005" for their exquisite hospitality and the opportunity of presenting a lecture. The second author wishes to thank Renzo Caddeo and the Dipartimento di Matematica e Informatica, Università di Cagliari, for hospitality during the preparation of this paper.
Let 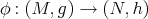 be a smooth map, then, for a compact subset
be a smooth map, then, for a compact subset 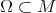 , the energy of
, the energy of 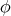 is defined by
is defined by
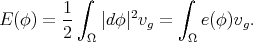
Critical points of the energy, for any compact subset 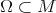 , are called harmonic maps and the corresponding Euler-Lagrange equation is
, are called harmonic maps and the corresponding Euler-Lagrange equation is
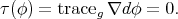
The equation 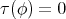 is called the harmonic equation and, in local coordinates
is called the harmonic equation and, in local coordinates  on
on 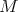 and
and 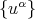 on
on 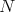 , takes the familiar form
, takes the familiar form
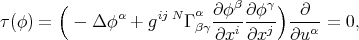
where 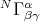 are the Christoffel symbols of
are the Christoffel symbols of 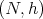 and
and 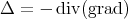 is the Beltrami-Laplace operator on
is the Beltrami-Laplace operator on 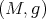 .
.
A smooth map 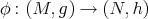 is biharmonic if it is a critical point, for any compact subset
is biharmonic if it is a critical point, for any compact subset 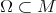 , of the bienergy functional
, of the bienergy functional
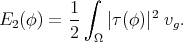
We will now derive the biharmonic equation, that is the Euler-Lagrange equation associated to the bienergy. For simplicity of exposition we will perform the calculation for smooth maps 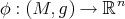 , defined by
, defined by 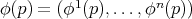 , with
, with 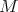 compact. In this case we have
compact. In this case we have
| (2.1) |
To compute the corresponding Euler-Lagrange equation, let 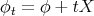 be a one-parameter smooth variation of
be a one-parameter smooth variation of 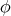 in the direction of a vector field
in the direction of a vector field 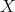 on
on 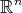 and denote with
and denote with  the operator
the operator 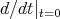 . We have
. We have
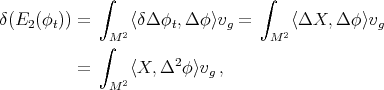
where in the last equality we have used that  is self-adjoint. Since
is self-adjoint. Since 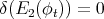 , for any vector field
, for any vector field 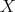 , we conclude that
, we conclude that 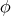 is biharmonic if and only if
is biharmonic if and only if
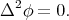
Moreover, if 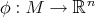 is a Riemannian immersion, then, using Beltrami equation
is a Riemannian immersion, then, using Beltrami equation  , we have that
, we have that 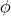 is biharmonic if and only if
is biharmonic if and only if
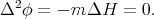
Therefore, as mentioned in the introduction, we recover Chen's definition of biharmonic submanifolds in 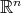 .
.
For a smooth map 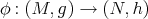 the Euler-Lagrange equation associated to the bienergy becomes more complicated and, as one would expect, it involves the curvature of the codomain. More precisely, a smooth map
the Euler-Lagrange equation associated to the bienergy becomes more complicated and, as one would expect, it involves the curvature of the codomain. More precisely, a smooth map 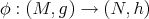 is biharmonic if it satisfies the following biharmonic equation
is biharmonic if it satisfies the following biharmonic equation
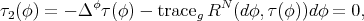
where 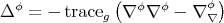 is the rough Laplacian on sections of
is the rough Laplacian on sections of 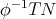 and
and ![RN (X, Y ) = [∇X ,∇Y ] - ∇ [X,Y]](/img/revistas/ruma/v47n2/2a0280x.png) is the curvature operator on
is the curvature operator on 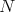 .
.
From the expression of the bitension field 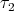 it is clear that a harmonic map (
it is clear that a harmonic map ( ) is automatically a biharmonic map, in fact a minimum of the bienergy.
) is automatically a biharmonic map, in fact a minimum of the bienergy.
We call a non-harmonic biharmonic map a proper biharmonic map.
As we have just seen, a harmonic map is biharmonic, so a basic question in the theory is to understand under what conditions the converse is true. A first general answer to this problem, proved by G.Y. Jiang, is
Theorem 3.1 ([33, 34]). Let 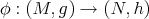 be a smooth map. If
be a smooth map. If 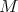 is compact, orientable and
is compact, orientable and 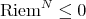 , then
, then 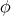 is biharmonic if and only if it is harmonic.
is biharmonic if and only if it is harmonic.
Jiang's theorem is a direct application of the Weitzenböck formula. In fact, if 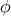 is biharmonic, the Weitzenböck formula and
is biharmonic, the Weitzenböck formula and 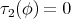 give
give
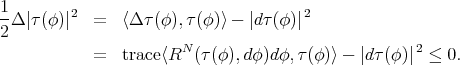
Then, since 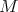 is compact, by the maximal principle, we find that
is compact, by the maximal principle, we find that 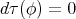 . Now using the identity
. Now using the identity
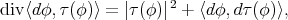
we deduce that 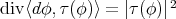 and, after integration, we conclude.
and, after integration, we conclude.
3.1. Riemannian immersions. If 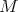 is not compact, then the above argument can be used with the extra assumption that
is not compact, then the above argument can be used with the extra assumption that 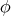 is a Riemannian immersion and that the norm of
is a Riemannian immersion and that the norm of 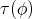 is constant, as was shown by C. Oniciuc in
is constant, as was shown by C. Oniciuc in
Theorem 3.2 ([44]). Let 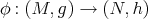 be a Riemannian immersion. If
be a Riemannian immersion. If 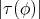 is constant and
is constant and 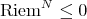 , then
, then 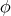 is biharmonic if and only if it is minimal.
is biharmonic if and only if it is minimal.
The curvature condition in Theorems 3.1 and 3.2 can be weakened in the case of codimension one, that is 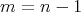 . We have
. We have
Theorem 3.3 ([44]). Let 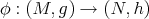 be a Riemannian immersion with
be a Riemannian immersion with 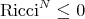 and
and 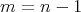 .
.
- If
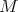 is compact and orientable, then
is compact and orientable, then 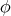 is biharmonic if and only if it is minimal.
is biharmonic if and only if it is minimal. - If
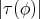 is constant, then
is constant, then 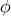 is biharmonic if and only if it is minimal.
is biharmonic if and only if it is minimal.
3.2. Submanifolds of 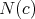 . Let
. Let 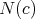 be a manifold with constant sectional curvature
be a manifold with constant sectional curvature  ,
, 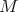 a submanifold of
a submanifold of 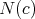 and denote by
and denote by 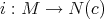 the canonical inclusion. In this case the tension and bitension fields assume the following form
the canonical inclusion. In this case the tension and bitension fields assume the following form
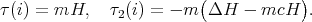
If  , there are strong restrictions on the existence of proper biharmonic submanifolds in
, there are strong restrictions on the existence of proper biharmonic submanifolds in 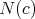 . If
. If 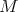 is compact, then there exists no proper biharmonic Riemannian immersion from
is compact, then there exists no proper biharmonic Riemannian immersion from 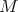 into
into 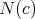 . In fact, from Theorem 3.1,
. In fact, from Theorem 3.1, 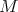 should be minimal. If
should be minimal. If 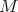 is not compact and
is not compact and 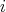 is a proper biharmonic map then, from Theorem 3.2,
is a proper biharmonic map then, from Theorem 3.2, 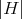 cannot be constant.
cannot be constant.
If 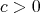 , as we shall see in Sections 4.3 and 4.4, we do have examples of compact proper biharmonic submanifolds.
, as we shall see in Sections 4.3 and 4.4, we do have examples of compact proper biharmonic submanifolds.
The main tool in the study of biharmonic submanifolds of 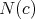 is the decomposition of the bitension field in its tangential and normal components. Then, asking that both components are identically zero, we conclude that the canonical inclusion
is the decomposition of the bitension field in its tangential and normal components. Then, asking that both components are identically zero, we conclude that the canonical inclusion 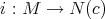 is biharmonic if and only if
is biharmonic if and only if
|
| (3.1) |
where 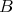 is the second fundamental form of
is the second fundamental form of 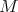 in
in 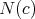 ,
, 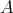 the shape operator,
the shape operator, 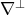 the normal connection and
the normal connection and 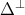 the Laplacian in the normal bundle of
the Laplacian in the normal bundle of 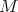 .
.
Equation (3.1) was used by B.Y. Chen, for  , and by R. Caddeo, S. Montaldo and C. Oniciuc, for
, and by R. Caddeo, S. Montaldo and C. Oniciuc, for 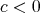 , to prove that in the case of biharmonic surfaces in
, to prove that in the case of biharmonic surfaces in 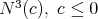 , the mean curvature must be constant, thus
, the mean curvature must be constant, thus
Theorem 3.4 ([19, 21, 12]). Let 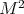 be a surface of
be a surface of 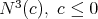 . Then
. Then 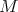 is biharmonic if and only if it is minimal.
is biharmonic if and only if it is minimal.
For higher dimensional cases it is not known whether there exist proper biharmonic submanifolds of 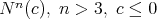 , although, for
, although, for 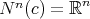 , partial results have been obtained. For instance:
, partial results have been obtained. For instance:
- Every biharmonic curve of
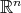 is an open part of a straight line [24].
is an open part of a straight line [24]. - Every biharmonic submanifold of finite type in
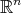 is minimal [24].
is minimal [24]. - There exists no proper biharmonic hypersurface of
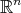 with at most two principal curvatures [24].
with at most two principal curvatures [24]. - Let
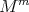 be a pseudo-umbilical submanifold of
be a pseudo-umbilical submanifold of 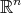 . If
. If 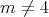 , then
, then 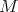 is biharmonic if and only if minimal [24].
is biharmonic if and only if minimal [24]. - Let
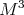 be a hypersurface of
be a hypersurface of 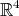 . Then
. Then 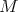 is biharmonic if and only if minimal [30].
is biharmonic if and only if minimal [30]. - Any submanifold of
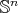 cannot be biharmonic in
cannot be biharmonic in 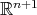 [19].
[19]. - Let
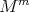 be a pseudo-umbilical submanifold of
be a pseudo-umbilical submanifold of 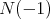 . If
. If 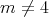 , then
, then 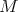 is biharmonic if and only if minimal
is biharmonic if and only if minimal [12].
[12].
All these results suggested the following
Generalized Chen's Conjecture: Biharmonic submanifolds of a manifold 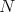 with
with 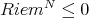 are minimal.
are minimal.
3.3. Riemannian submersions. Let 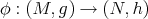 be a Riemannian submersion with basic tension field. Then the bitension field, computed in [44], is
be a Riemannian submersion with basic tension field. Then the bitension field, computed in [44], is
|
| (3.2) |
Using this formula we find some non-existence results which are, in some sense, dual to those for Riemannian immersions. They can be stated as follows:
Proposition 3.5 ([44]). A biharmonic Riemannian submersion 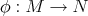 with basic tension field is harmonic in the following cases:
with basic tension field is harmonic in the following cases:
- if
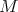 is compact, orientable and
is compact, orientable and 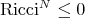 ;
; - if
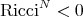 and
and 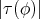 is constant;
is constant; - if
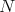 is compact and
is compact and 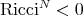 .
.
4. Biharmonic Riemannian immersions
In this section we report on the known examples of proper biharmonic Riemannian immersions. Of course, the first and easiest examples can be found looking at differentiable curves in a Riemannian manifold. This is the first class we shall describe.
Let  be a curve parametrized by arc length from an open interval
be a curve parametrized by arc length from an open interval 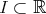 to a Riemannian manifold. In this case the tension field becomes
to a Riemannian manifold. In this case the tension field becomes 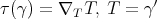 , and the biharmonic equation reduces to
, and the biharmonic equation reduces to
|
| (4.1) |
To describe geometrically Equation (4.1) let us recall the definition of the Frenet frame.
Definition 4.1 (See, for example, [37]). The Frenet frame 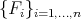 associated to a curve
associated to a curve 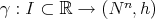 , parametrized by arc length, is the orthonormalisation of the
, parametrized by arc length, is the orthonormalisation of the  -uple
-uple 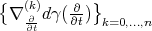 , described by:
, described by:
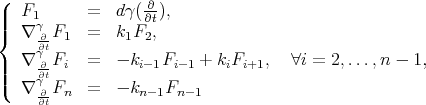
where the functions 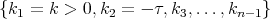 are called the curvatures of
are called the curvatures of 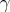 and
and 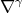 is the connection on the pull-back bundle
is the connection on the pull-back bundle 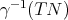 . Note that
. Note that 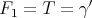 is the unit tangent vector field along the curve.
is the unit tangent vector field along the curve.
We point out that when the dimension of 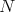 is
is 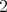 , the first curvature
, the first curvature 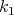 is replaced by the signed curvature.
is replaced by the signed curvature.
Using the Frenet frame, we get that a curve is proper (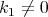 ) biharmonic if and only if
) biharmonic if and only if
|
| (4.2) |
4.1. Biharmonic curves on surfaces. Let 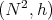 be an oriented surface and let
be an oriented surface and let 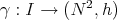 be a differentiable curve parametrized by arc length. Then Equation (4.2) reduces to
be a differentiable curve parametrized by arc length. Then Equation (4.2) reduces to
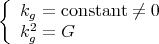
where 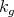 is the curvature (with sign) of
is the curvature (with sign) of 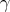 and
and 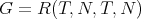 is the Gauss curvature of the surface.
is the Gauss curvature of the surface.
As an immediate consequence we have:
Proposition 4.2 ([14]). Let 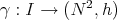 be a proper biharmonic curve on an oriented surface
be a proper biharmonic curve on an oriented surface 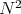 . Then, along
. Then, along 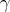 , the Gauss curvature must be constant, positive and equal to the square of the geodesic curvature of
, the Gauss curvature must be constant, positive and equal to the square of the geodesic curvature of 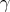 . Therefore, if
. Therefore, if 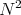 has non-positive Gauss curvature, any biharmonic curve is a geodesic of
has non-positive Gauss curvature, any biharmonic curve is a geodesic of 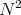 .
.
Proposition 4.2 gives a positive answer to the generalized Chen's conjecture.
Now, let 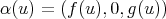 be a curve in the
be a curve in the 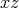 -plane and consider the surface of revolution, obtained by rotating this curve about the
-plane and consider the surface of revolution, obtained by rotating this curve about the  -axis, with the standard parametrization
-axis, with the standard parametrization
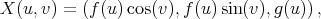
where  is the rotation angle. Assuming that
is the rotation angle. Assuming that 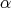 is parametrized by arc length, we have
is parametrized by arc length, we have
Proposition 4.3 ([14]). A parallel 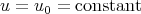 is biharmonic if and only if
is biharmonic if and only if 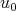 satisfies the equation
satisfies the equation
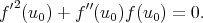
Example 4.4 (Torus). On a torus of revolution with its standard parametrization
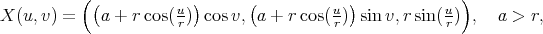
the biharmonic parallels are
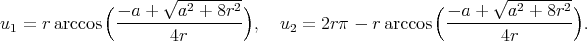
Example 4.5 (Sphere). There is a geometric way to understand the behaviour of biharmonic curves on a sphere. In fact, the torsion  and curvature
and curvature 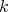 (without sign) of
(without sign) of 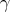 , seen in the ambient space
, seen in the ambient space 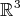 , satisfy
, satisfy 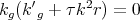 . From this we see that
. From this we see that 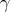 is a proper biharmonic curve if and only if
is a proper biharmonic curve if and only if  and
and 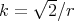 , i.e.
, i.e. 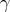 is the circle of radius
is the circle of radius 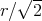 .
.
For more examples see [14, 15].
4.2. Biharmonic curves of the Heisenberg group  . The Heisenberg group
. The Heisenberg group  can be seen as the Euclidean space
can be seen as the Euclidean space 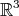 endowed with the multiplication
endowed with the multiplication
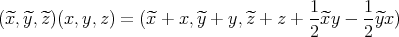
and with the left-invariant Riemannian metric 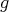 given by
given by
|
| (4.3) |
Let  be a differentiable curve parametrized by arc length. Then, from (4.2),
be a differentiable curve parametrized by arc length. Then, from (4.2), 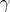 is a proper biharmonic curve if and only if
is a proper biharmonic curve if and only if
|
| (4.4) |
where 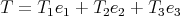 ,
, 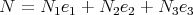 , and
, and 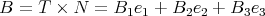 . Here
. Here 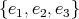 is the left-invariant orthonormal basis with respect to the metric (4.3).
is the left-invariant orthonormal basis with respect to the metric (4.3).
By analogy with curves in 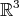 , we use the name helix for a curve in a Riemannian manifold having both geodesic curvature and geodesic torsion constant.
, we use the name helix for a curve in a Riemannian manifold having both geodesic curvature and geodesic torsion constant.
Using System (4.4), in [16], R. Caddeo, C. Oniciuc and P. Piu showed that a proper biharmonic curve in  is a helix and gave their explicit parametrizations, as shown in the following
is a helix and gave their explicit parametrizations, as shown in the following
Theorem 4.6 ([16]). The parametric equations of all proper biharmonic curves 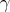 of
of  are
are
|
| (4.5) |
where 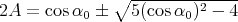 ,
, ![√ - √- α ∈ (0,arccos 2-5] ∪ [arccos(- 2-5),π ) 0 5 5](/img/revistas/ruma/v47n2/2a02253x.png) and
and 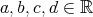 .
.
Geometrically, proper biharmonic curves in  can be obtained as the intersection of a minimal helicoid with a round cylinder. Moreover, they are geodesic of this round cylinder.
can be obtained as the intersection of a minimal helicoid with a round cylinder. Moreover, they are geodesic of this round cylinder.
The above method can be extended to study biharmonic curves in Cartan-Vranceanu three-manifolds (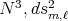 ), where
), where 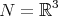 if
if 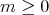 ,
, 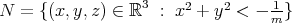 if
if 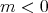 , and the Riemannian metric
, and the Riemannian metric 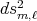 is defined by
is defined by
|
| (4.6) |
This two-parameter family of metrics reduces to the Heisenberg metric for 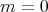 and
and  . The system for proper biharmonic curves corresponding to the metric
. The system for proper biharmonic curves corresponding to the metric 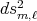 can be obtained by using the same techniques, and turns out to be
can be obtained by using the same techniques, and turns out to be
|
| (4.7) |
System 4.7 also implies that the proper biharmonic curves of 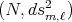 are helices [13]. The explicit parametrization of proper biharmonic curves of
are helices [13]. The explicit parametrization of proper biharmonic curves of 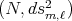 was given in [23], for
was given in [23], for  , and in [13] in general.
, and in [13] in general.
We point out that biharmonic curves were studied in other spaces which are generalizations of the above cases. For example:
- In [28], D. Fetcu studied biharmonic curves in the
 dimensional Heisenberg group
dimensional Heisenberg group 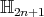 and obtained two families of proper biharmonic curves.
and obtained two families of proper biharmonic curves. - A. Balmuş studied, in [6], the biharmonic curves on Berger spheres
 , obtaining their explicit parametric equations.
, obtaining their explicit parametric equations.
4.3. The biharmonic submanifolds of  . In [11] the authors give a complete classification of the proper biharmonic submanifolds of
. In [11] the authors give a complete classification of the proper biharmonic submanifolds of  .
.
Using System(4.2) it was first proved that the proper biharmonic curves 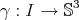 are the helices with
are the helices with 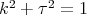 . If we look at
. If we look at 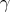 as a curve in
as a curve in 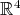 , the biharmonic condition can be expressed as
, the biharmonic condition can be expressed as
|
| (4.8) |
Now, by integration of (4.8), we obtain
Theorem 4.7 ([11],[8]). Let 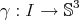 be a curve parametrized by arc length. Then it is proper biharmonic if and only if it is either the circle of radius
be a curve parametrized by arc length. Then it is proper biharmonic if and only if it is either the circle of radius 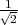 , or a geodesic of the Clifford torus
, or a geodesic of the Clifford torus 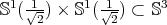 with slope different from
with slope different from 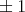 .
.
As to proper biharmonic surfaces 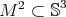 of the three-dimensional sphere, one can first prove that Equation (3.1) implies the following
of the three-dimensional sphere, one can first prove that Equation (3.1) implies the following
Theorem 4.8 ([11]). Let 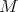 be a surface of
be a surface of  . Then it is proper biharmonic if and only if
. Then it is proper biharmonic if and only if 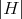 is constant and
is constant and 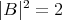 .
.
The classification of constant mean curvature surfaces in  with
with 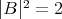 is known, in fact we have
is known, in fact we have
Theorem 4.9 ([11],[31]). Let 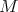 be a surface of
be a surface of  with constant mean curvature and
with constant mean curvature and 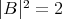 .
.
- If
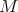 is not compact, then locally it is a piece of either a hypersphere
is not compact, then locally it is a piece of either a hypersphere 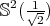 or a torus
or a torus 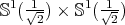 .
. - If
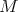 is compact and orientable, then it is either
is compact and orientable, then it is either 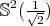 or
or 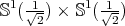 .
.
Now, since the Clifford torus 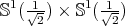 is minimal in
is minimal in  , we can state:
, we can state:
Theorem 4.10 ([11]). Let 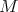 be a proper biharmonic surface of
be a proper biharmonic surface of  .
.
- If
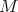 is not compact, then it is locally a piece of
is not compact, then it is locally a piece of 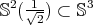 .
. - If
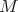 is compact and orientable, then it is
is compact and orientable, then it is 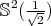 .
.
4.4. Biharmonic submanifolds of 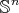 . We start describing some basic examples of proper biharmonic submanifolds of
. We start describing some basic examples of proper biharmonic submanifolds of 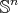 .
.
Let  ,
, 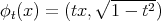 ,
, ![t ∈ [0,1]](/img/revistas/ruma/v47n2/2a02314x.png) . Up to a homothetic transformation,
. Up to a homothetic transformation, 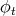 is the canonical inclusion of the hypersphere
is the canonical inclusion of the hypersphere 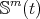 in
in 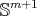 . A simple calculation shows that
. A simple calculation shows that 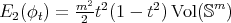 . Derivating
. Derivating  with respect to
with respect to  we find that
we find that 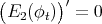 if and only if
if and only if 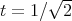 .
.
This simple argument shows that 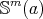 is a good candidate for proper biharmonic submanifold of
is a good candidate for proper biharmonic submanifold of 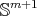 if
if 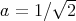 . It is not difficult to show that, indeed, the bitension field of
. It is not difficult to show that, indeed, the bitension field of 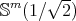 is zero, proving that it is the only proper biharmonic hypersphere of
is zero, proving that it is the only proper biharmonic hypersphere of 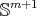 .
.
To explain the next example we first note that, from (3.1), we have
Proposition 4.11. Let 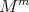 be a non-minimal hypersurface of
be a non-minimal hypersurface of 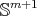 with parallel mean curvature, i.e. the norm of
with parallel mean curvature, i.e. the norm of 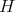 is constant. Then
is constant. Then 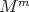 is a proper biharmonic submanifold if and only if
is a proper biharmonic submanifold if and only if 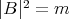 .
.
Let 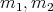 be two positive integers such that
be two positive integers such that 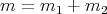 , and let
, and let 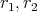 be two positive real numbers such that
be two positive real numbers such that 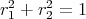 . Then the generalized Clifford torus
. Then the generalized Clifford torus 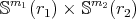 is a hypersurface of
is a hypersurface of 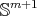 . A simple calculation shows that
. A simple calculation shows that
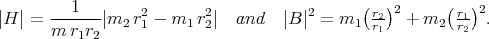
We thus have
- If
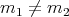 , then
, then 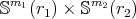 is a proper biharmonic submanifold of
is a proper biharmonic submanifold of 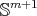 if and only if
if and only if 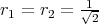 .
. - If
 , then the following statements are equivalent:
, then the following statements are equivalent: 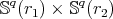 is a biharmonic submanifold of
is a biharmonic submanifold of 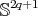
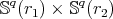 is a minimal submanifold of
is a minimal submanifold of 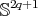
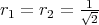 .
.
The submanifolds 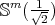 and the generalized Clifford torus are the only known examples of proper biharmonic hypersurfaces of
and the generalized Clifford torus are the only known examples of proper biharmonic hypersurfaces of 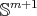 . As we have seen in Theorem 4.10, for
. As we have seen in Theorem 4.10, for  , the hypersphere
, the hypersphere 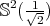 is the only one.
is the only one.
Open problem: classify all proper biharmonic hypersurfaces of 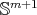 .
.
The situation seems much richer if the codimension is greater than one. We shall present a construction of proper biharmonic submanifolds in 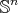 . Let
. Let 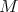 be a submanifold of
be a submanifold of 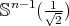 . Then
. Then 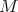 can be seen as a submanifold of
can be seen as a submanifold of 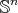 and we have
and we have
Theorem 4.13 ([12],[42]). Assume that 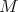 is a submanifold of
is a submanifold of 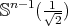 . Then
. Then 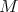 is a proper biharmonic submanifold of
is a proper biharmonic submanifold of 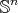 if and only if it is minimal in
if and only if it is minimal in 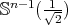 .
.
Theorem 4.13 is a useful tool to construct examples of proper biharmonic submanifolds. For instance, using a well known result of H.B. Lawson [38], we have
Theorem 4.14 ([12]). There exist closed orientable embedded proper biharmonic surfaces of arbitrary genus in  .
.
This shows the existence of an abundance of proper biharmonic surfaces in  , in contrast with the case of
, in contrast with the case of  .
.
The biharmonic submanifolds that we have produced so far are all pseudo-umbilical, i.e. 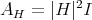 . We now want to give examples of biharmonic submanifolds of
. We now want to give examples of biharmonic submanifolds of 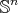 that are not of this type.
that are not of this type.
With this aim, let 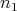 ,
, 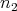 be two positive integers such that
be two positive integers such that 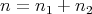 , and let
, and let 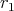 ,
, 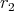 be two positive real numbers such that
be two positive real numbers such that 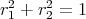 . Let
. Let 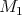 be a minimal submanifold of
be a minimal submanifold of 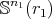 , of dimension
, of dimension 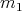 , with
, with 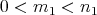 , and let
, and let 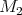 be a minimal submanifold of
be a minimal submanifold of 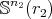 , of dimension
, of dimension 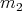 , with
, with 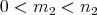 . We have:
. We have:
Theorem 4.15 ([12]). The manifold 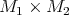 is a proper biharmonic submanifold of
is a proper biharmonic submanifold of 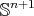 if and only if
if and only if 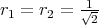 and
and 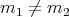 .
.
If 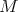 is a submanifold of
is a submanifold of 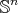 with
with 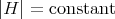 , then it is possible to give a partial classification. In fact we have
, then it is possible to give a partial classification. In fact we have
Theorem 4.16 ([48]). Let 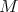 be a submanifold of
be a submanifold of 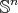 such that
such that 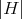 is constant.
is constant.
- If
 , then
, then 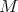 is never biharmonic.
is never biharmonic. - If
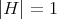 , then
, then 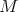 is biharmonic if and only if it is pseudo-umbilical and
is biharmonic if and only if it is pseudo-umbilical and 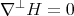 , i.e.
, i.e. 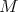 is a minimal submanifold of
is a minimal submanifold of 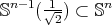 .
.
As an immediate consequence we have
Corollary 4.17 ([48]). If 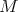 is a compact orientable hypersurface of
is a compact orientable hypersurface of 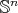 with
with 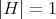 , then
, then 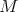 is proper biharmonic if and only if
is proper biharmonic if and only if 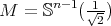 .
.
Another partial classification for compact hypersurfaces in 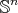 was given in [22], in terms of the length of the second fundamental form and of the sign of the sectional curvature.
was given in [22], in terms of the length of the second fundamental form and of the sign of the sectional curvature.
We end this section presenting two classes of proper biharmonic curves of 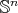
Proposition 4.18 ([12]).
- The circles
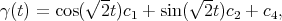 where
where 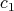 ,
, 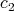 ,
, 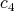 are constant orthogonal vectors of
are constant orthogonal vectors of 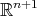 with
with 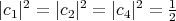 , are proper biharmonic curves of
, are proper biharmonic curves of 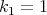 .
. - The curves
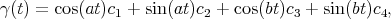 where
where 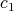 ,
, 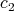 ,
, 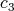 ,
, 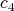 are constant orthogonal vectors of
are constant orthogonal vectors of 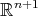 with
with 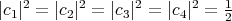 , and
, and 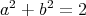 ,
, 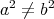 , are proper biharmonic of
, are proper biharmonic of 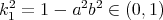 .
.
4.5. Biharmonic submanifolds in Sasakian space forms. A "generalization" of Riemannian manifolds with constant sectional curvature is that of Sasakian space forms. First, recall that 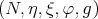 is a contact Riemannian manifold if:
is a contact Riemannian manifold if:  is a
is a  -dimensional manifold;
-dimensional manifold; 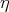 is an one-form satisfying
is an one-form satisfying 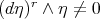 ;
; 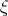 is the vector field defined by
is the vector field defined by 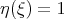 and
and 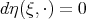 ;
; 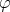 is an endomorphism field;
is an endomorphism field; 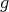 is a Riemannian metric on
is a Riemannian metric on 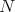 such that,
such that, 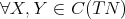 ,
,
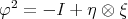
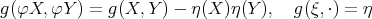
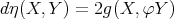 .
.
A contact Riemannian manifold 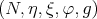 is a Sasaki manifold if
is a Sasaki manifold if
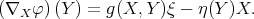
If the sectional curvature is constant on all 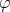 -invariant tangent
-invariant tangent 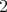 -planes of
-planes of 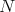 , then
, then 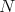 is called of constant holomorphic sectional curvature. Moreover, if a Sasaki manifold
is called of constant holomorphic sectional curvature. Moreover, if a Sasaki manifold 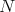 is connected, complete and of constant holomorphic sectional curvature, then it is called a Sasakian space form. We have the following classification.
is connected, complete and of constant holomorphic sectional curvature, then it is called a Sasakian space form. We have the following classification.
Theorem 4.19 ([9]). A simply connected three-dimensional Sasakian space form is isomorphic to one of the following:
- the special unitary group
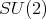
- the Heisenberg group

- the universal covering group of
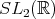 .
.
In particular, a simply connected three-dimensional Sasakian space form of constant holomorphic sectional curvature  is isometric to
is isometric to  .
.
In [32], J. Inoguchi classified proper biharmonic Legendre curves and Hopf cylinders in three-dimensional Sasakian space forms. To state Inoguchi results we recall that:
- a curve
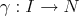 parametrized by arc length is Legendre if
parametrized by arc length is Legendre if 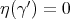 ;
; - a Hopf cylinder is
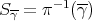 , where
, where 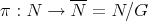 is the projection of
is the projection of 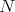 onto the orbit space
onto the orbit space 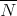 determined by the action of the one-parameter group of isometries generated by
determined by the action of the one-parameter group of isometries generated by 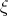 , when the action is simply transitive.
, when the action is simply transitive.
Theorem 4.20 ([32]). Let 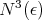 be a Sasakian space form of constant holomorphic sectional curvature
be a Sasakian space form of constant holomorphic sectional curvature  and
and 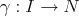 a biharmonic Legendre curve parametrized by arclength.
a biharmonic Legendre curve parametrized by arclength.
- If
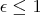 , then
, then 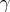 is a Legendre geodesic.
is a Legendre geodesic. - If
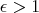 , then
, then 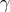 is a Legendre geodesic or a Legendre helix of curvature
is a Legendre geodesic or a Legendre helix of curvature 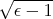 .
.
Theorem 4.21 ([32]). Let 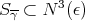 be a biharmonic Hopf cylinder in a Sasakian space form.
be a biharmonic Hopf cylinder in a Sasakian space form.
- If
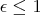 , then
, then 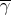 is a geodesic.
is a geodesic. - If
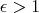 , then
, then 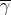 is a geodesic or a Riemannian circle of curvature
is a geodesic or a Riemannian circle of curvature 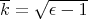 .
.
In particular, there exist proper biharmonic Hopf cylinders in Sasakian space forms of holomorphic sectional curvature greater than  .
.
T. Sasahara classified, in [53], proper biharmonic Legendre surfaces in Sasakian space forms and, in the case when the ambient space is the unit  -dimensional sphere
-dimensional sphere  , he obtained their explicit representations.
, he obtained their explicit representations.
Theorem 4.22 ([53]). Let 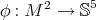 be a proper biharmonic Legendre immersion. Then the position vector field
be a proper biharmonic Legendre immersion. Then the position vector field 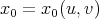 of
of 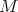 in
in 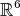 is given by:
is given by:
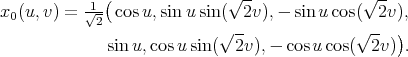
Other results on biharmonic Legendre curves and biharmonic anti-invariant surfaces in Sasakian space forms and  -manifolds were obtained in [1, 2].
-manifolds were obtained in [1, 2].
5. Biharmonic Riemannian submersions
In this section we discuss some examples of proper biharmonic Riemannian submersions. From the expression of the bitension field (3.2) we have immediately the following
Theorem 5.1 ([44]). Let 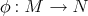 be a Riemannian submersion with basic, non-zero, tension field. Then
be a Riemannian submersion with basic, non-zero, tension field. Then 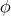 is proper biharmonic if:
is proper biharmonic if:
 ;
;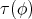 is a unit Killing vector field on
is a unit Killing vector field on 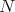 .
.
Theorem 5.1 was used in [44] to construct examples of proper biharmonic Riemannian submersions. These examples are projections 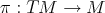 from the tangent bundle of a Riemannian manifold endowed with a "Sasaki type" metric. Indeed, let
from the tangent bundle of a Riemannian manifold endowed with a "Sasaki type" metric. Indeed, let 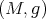 be an
be an 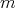 -dimensional Riemannian manifold and let
-dimensional Riemannian manifold and let 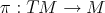 be its tangent bundle. We denote by
be its tangent bundle. We denote by 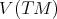 the vertical distribution on
the vertical distribution on 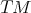 defined by
defined by 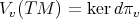 ,
, 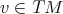 . We consider a nonlinear connection on
. We consider a nonlinear connection on 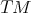 defined by the distribution
defined by the distribution 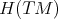 on
on 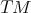 , complementary to
, complementary to 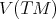 , i.e.
, i.e. 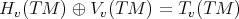 ,
, 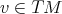 . For any induced local chart
. For any induced local chart 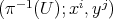 on
on 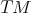 we have a local adapted frame in
we have a local adapted frame in 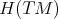 defined by the local vector fields
defined by the local vector fields
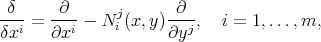
where the local functions 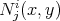 are the connection coefficients of the nonlinear connection defined by
are the connection coefficients of the nonlinear connection defined by 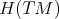 . If we endow
. If we endow 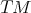 with the Riemannian metric
with the Riemannian metric 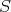 defined by
defined by
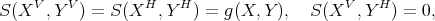
then the canonical projection 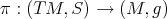 is a Riemannian submersion. (For more details on the metrics on the tangent bundle see, for example, [49].) The biharmonicity of the map
is a Riemannian submersion. (For more details on the metrics on the tangent bundle see, for example, [49].) The biharmonicity of the map 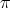 depends on the choice of the connection coefficients
depends on the choice of the connection coefficients 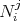 . For suitable choices we have:
. For suitable choices we have:
Proposition 5.2 ([44]).
- Let
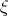 be an unit Killing vector field and let
be an unit Killing vector field and let 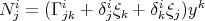 be a projective change of the Levi-Civita connection
be a projective change of the Levi-Civita connection  on
on 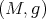 . Then
. Then 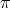 is a proper biharmonic map.
is a proper biharmonic map. - Let
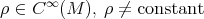 , be an affine function and let
, be an affine function and let 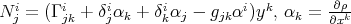 , be a conformal change of the connection
, be a conformal change of the connection  . Then
. Then 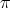 is a proper biharmonic map.
is a proper biharmonic map.
Another important class of biharmonic Riemannian submersions was described in [7] and it is descried as follows. Let 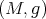 and
and 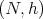 be Riemannian manifolds and denote by
be Riemannian manifolds and denote by 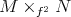 their warped product with respect to a positive function on
their warped product with respect to a positive function on 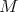 , then the projection
, then the projection 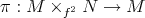 is a Riemannian submersion with
is a Riemannian submersion with 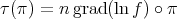 . When
. When 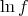 is affine,
is affine, 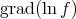 is Killing of constant norm, hence
is Killing of constant norm, hence 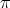 is biharmonic.
is biharmonic.
6. Biharmonic maps between Euclidean spaces
Let 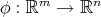 ,
,  be a smooth map. Then, the bitension field assumes the simple expression
be a smooth map. Then, the bitension field assumes the simple expression 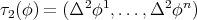 . Thus, a map
. Thus, a map 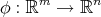 is biharmonic if and only if its component functions are biharmonic.
is biharmonic if and only if its component functions are biharmonic.
If we want proper solutions defined everywhere, then we can take polynomial solutions of degree three. If we look for maps which are not defined everywhere, then there are interesting classes of examples. One of these can be described as follows.
A smooth map 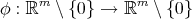 is axially symmetric if there exist a map
is axially symmetric if there exist a map 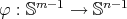 and a function
and a function 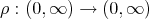 such that, for
such that, for 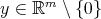 ,
,
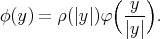
Assume that the map 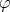 is not constant. An axially symmetric map
is not constant. An axially symmetric map 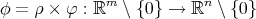 is harmonic if and only if
is harmonic if and only if 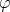 is an eigenmap of eigenvalue
is an eigenmap of eigenvalue 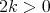 (see [25] for the definition of eigenmaps) and
(see [25] for the definition of eigenmaps) and
|
| (6.1) |
where 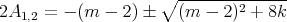 and
and 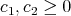 with
with 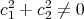 .
.
The biharmonicity of axially symmetric maps 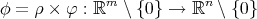 was discussed in [7], where the authors give the following classification.
was discussed in [7], where the authors give the following classification.
Theorem 6.1 ([7]). Let 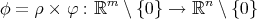 be an axially symmetric map and assume that
be an axially symmetric map and assume that 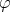 is an eigenmap of eigenvalue
is an eigenmap of eigenvalue 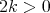 .
.
- If
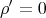 , then
, then - for
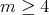 ,
, 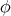 can not be biharmonic.
can not be biharmonic. - for
 ,
, 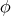 is proper biharmonic if and only if
is proper biharmonic if and only if 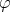 is an eigenmap of homogeneous degree
is an eigenmap of homogeneous degree  .
. - for
 ,
, 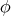 is proper biharmonic if and only if
is proper biharmonic if and only if 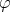 is an eigenmap of homogeneous degree
is an eigenmap of homogeneous degree  .
.
- for
- If
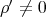 , then
, then 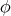 is proper biharmonic if and only if
is proper biharmonic if and only if (6.2) where
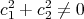 and
and 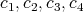 arbitrary such that
arbitrary such that 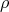 takes values in
takes values in 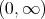 .
.
Example 6.2. An important class of axially symmetric diffeomorphisms of 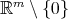 is given by
is given by
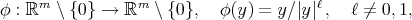
which, for  , provides the well known Kelvin transformation. For these maps,
, provides the well known Kelvin transformation. For these maps, 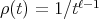 and
and 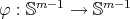 is the identity map. An easy computation shows that
is the identity map. An easy computation shows that 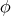 is harmonic if and only if
is harmonic if and only if 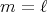 .
.
Using (6.2) it follows that 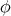 is proper biharmonic if and only if
is proper biharmonic if and only if 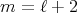 . For
. For  this result was first obtained in [3].
this result was first obtained in [3].
We also note that the proper biharmonic map 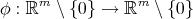 ,
, 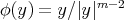 , is harmonic with respect to the conformal metric on the domain given by
, is harmonic with respect to the conformal metric on the domain given by 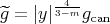 . This property is similar to that of the Kelvin transformation proved by B. Fuglede in [29].
. This property is similar to that of the Kelvin transformation proved by B. Fuglede in [29].
7. Biharmonic maps and conformal changes
7.1. Conformal change on the domain. Let 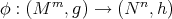 be a harmonic map. Consider a conformal change of the domain metric, i.e.
be a harmonic map. Consider a conformal change of the domain metric, i.e. 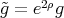 for some smooth function
for some smooth function 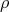 .
.
If 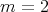 , from the conformal invariance of the energy, the map
, from the conformal invariance of the energy, the map 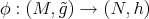 remains harmonic. If
remains harmonic. If 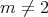 , then
, then 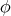 does not remain, necessarily, harmonic. Therefore, it is reasonable to seek under what conditions on the function
does not remain, necessarily, harmonic. Therefore, it is reasonable to seek under what conditions on the function 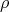 the map
the map 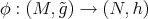 is biharmonic.
is biharmonic.
This problem was attacked in [3], where P. Baird and D. Kamissoko first proved the following general result.
Proposition 7.1 ([3]). Let 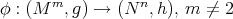 , be a harmonic map. Let
, be a harmonic map. Let 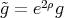 be a metric conformally equivalent to
be a metric conformally equivalent to 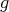 . Then
. Then 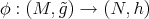 is biharmonic if and only if
is biharmonic if and only if
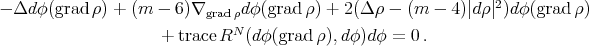
If 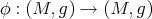 is the identity map
is the identity map  , we call a conformally equivalent metric
, we call a conformally equivalent metric 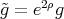 , for which
, for which  becomes biharmonic, a biharmonic metric with respect to
becomes biharmonic, a biharmonic metric with respect to 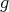 .
.
Applying the maximum principle we have
Theorem 7.2 ([3]). Let 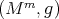 ,
, 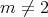 , be a compact manifold of negative Ricci curvature. Then there is no biharmonic metric conformally related to
, be a compact manifold of negative Ricci curvature. Then there is no biharmonic metric conformally related to 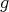 other than a constant multiple of
other than a constant multiple of 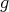 .
.
There is a surprising connection between biharmonic metrics and isoparametric functions. We recall that a smooth function 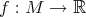 is called isoparametric if, for each
is called isoparametric if, for each 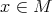 where
where 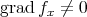 , there are real functions
, there are real functions 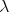 and
and  such that
such that

on some neighbourhood of 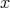 . The above mentioned link is provided by the following
. The above mentioned link is provided by the following
Theorem 7.3 ([3]). Let 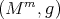 ,
, 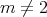 , be an Einstein manifold. Let
, be an Einstein manifold. Let 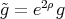 be a biharmonic metric conformally equivalent to
be a biharmonic metric conformally equivalent to 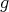 . Then the function
. Then the function 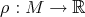 is isoparametric.
is isoparametric.
Conversely, let 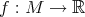 be an isoparametric function, then away from critical points of
be an isoparametric function, then away from critical points of 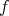 , there is a reparametrization
, there is a reparametrization 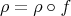 such that
such that 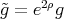 is a biharmonic metric.
is a biharmonic metric.
7.2. Conformal change on the codomain. Let 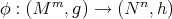 be a harmonic map. Consider the "dual problem", i.e. a conformal change
be a harmonic map. Consider the "dual problem", i.e. a conformal change 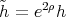 of the codomain metric. In this case the analogous of Proposition 7.1 is more complicated and we shall review only on some special situations.
of the codomain metric. In this case the analogous of Proposition 7.1 is more complicated and we shall review only on some special situations.
If 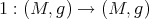 is the identity map, then it is proved, in [5], that
is the identity map, then it is proved, in [5], that 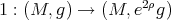 is biharmonic if and only if
is biharmonic if and only if
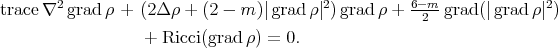
This equation was used in [5] to prove similar results to Theorem 7.3, for the conformal change of the metric on the codomain.
In a similar setting, in [46, 47], C. Oniciuc constructed new examples of biharmonic maps deforming the metric on a sphere. More precisely, let 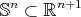 be the
be the 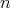 -dimensional sphere endowed with the conformal modified metric
-dimensional sphere endowed with the conformal modified metric 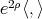 , where
, where 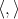 is the canonical metric on
is the canonical metric on 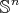 and
and  . Let
. Let  be the equatorial sphere of
be the equatorial sphere of 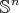 . Then the inclusion
. Then the inclusion 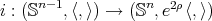 is a proper biharmonic map.
is a proper biharmonic map.
This result was generalized in
Theorem 7.4 ([46, 47]). Let 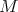 be a minimal submanifold of
be a minimal submanifold of 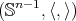 . Then
. Then 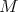 is a proper biharmonic submanifold of
is a proper biharmonic submanifold of 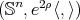 .
.
Observe that even a geodesic  will not remain harmonic after a conformal change of the metric on
will not remain harmonic after a conformal change of the metric on 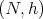 , unless the conformal factor is constant. As to biharmonicity of
, unless the conformal factor is constant. As to biharmonicity of 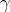 we have the following.
we have the following.
Theorem 7.5 ([39]). Let 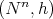 be a Riemannian manifold. Fix a point
be a Riemannian manifold. Fix a point 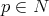 and let
and let 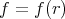 be a non-constant function, depending only on the geodesic distance
be a non-constant function, depending only on the geodesic distance  from
from 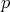 , which is a solution of the following ODE:
, which is a solution of the following ODE:
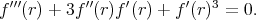
Then any geodesic  such that
such that 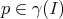 becomes a proper biharmonic curve
becomes a proper biharmonic curve 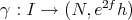 .
.
For example, take 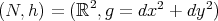 and
and 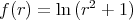 , where
, where 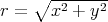 is the distance from the origin. Then any straight line on the flat
is the distance from the origin. Then any straight line on the flat 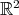 turns to a biharmonic curve on
turns to a biharmonic curve on 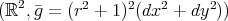 , which is the metric, in local isothermal coordinates, of the Enneper minimal surface.
, which is the metric, in local isothermal coordinates, of the Enneper minimal surface.
In analogy with the case of harmonic morphisms (see [4]) the definition of biharmonic morphisms can be formulated as follows.
Definition 8.1. A map 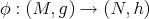 is a biharmonic morphism if for any biharmonic function
is a biharmonic morphism if for any biharmonic function 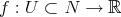 , its pull-back by
, its pull-back by 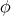 ,
, 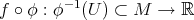 , is a biharmonic function.
, is a biharmonic function.
In [40] E. Loubeau and Y.-L. Ou gave the characterization of the biharmonic morphisms showing that a map is a biharmonic morphism if and only if it is a horizontally weakly conformal biharmonic map and its dilation satisfies a certain technical condition.
A more direct characterization is
Theorem 8.2 ([50, 40]). A map 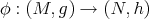 is a biharmonic morphism if and only if there exists a function
is a biharmonic morphism if and only if there exists a function 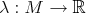 such that
such that
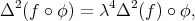
for all functions 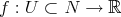 .
.
If 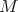 is compact, the notion of biharmonic morphisms becomes trivial, in fact we have
is compact, the notion of biharmonic morphisms becomes trivial, in fact we have
Theorem 8.3 ([40]). Let 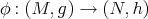 be a non-constant map. If
be a non-constant map. If 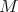 is compact, then
is compact, then 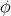 is a biharmonic morphism if and only if it is a harmonic morphism of constant dilation, hence a homothetic submersion with minimal fibers.
is a biharmonic morphism if and only if it is a harmonic morphism of constant dilation, hence a homothetic submersion with minimal fibers.
In [51], Y.-L. Ou, using the theory of 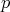 -harmonic morphisms, proved the following properties.
-harmonic morphisms, proved the following properties.
Theorem 8.4 ([51]). The radial projection 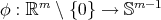 ,
, 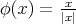 , is a biharmonic morphism if and only if
, is a biharmonic morphism if and only if  .
.
Theorem 8.5 ([51]). The projection 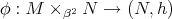 ,
, 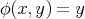 , of a warped product onto its second factor is a biharmonic morphism if and only if
, of a warped product onto its second factor is a biharmonic morphism if and only if 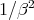 is a harmonic function on
is a harmonic function on 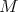 .
.
In the case of polynomial biharmonic morphisms between Euclidean spaces there is a full classification.
Theorem 8.6 ([51]). Let 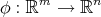 be a polynomial biharmonic morphism, i.e. a biharmonic morphism whose component functions are polynomials, with
be a polynomial biharmonic morphism, i.e. a biharmonic morphism whose component functions are polynomials, with 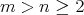 . Then
. Then 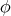 is an orthogonal projection followed by a homothety.
is an orthogonal projection followed by a homothety.
9. The second variation of biharmonic maps
The second variation formula for the bienergy functional  was obtained, in a general setting, by G.Y. Jiang in [34]. For biharmonic maps in Euclidean spheres, the second variation formula takes a simpler expression.
was obtained, in a general setting, by G.Y. Jiang in [34]. For biharmonic maps in Euclidean spheres, the second variation formula takes a simpler expression.
Theorem 9.1 ([45]). Let 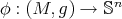 be a biharmonic map. Then the Hessian of the bienergy
be a biharmonic map. Then the Hessian of the bienergy  at
at 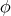 is given by
is given by
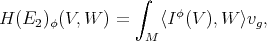
where
Although the expression of the operator 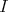 is rather complicated, in some particular cases it becomes easy to study.
is rather complicated, in some particular cases it becomes easy to study.
In the instance when 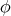 is the identity map of
is the identity map of 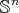 ,
, 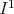 has the expression
has the expression
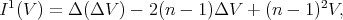
and we can immediately deduce
Theorem 9.2 ([45]). The identity map 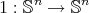 is biharmonic stable and
is biharmonic stable and
- if
 , then
, then 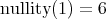 ;
; - if
 , then
, then 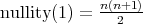 .
.
A large class of biharmonic maps for which it is possible to study the Hessian is obtained using the following generalization of Theorem 4.13.
Theorem 9.3 ([42]). Let 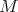 be an orientable compact manifold and
be an orientable compact manifold and 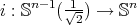 the canonical inclusion. If
the canonical inclusion. If 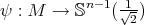 is a non-constant map, then
is a non-constant map, then 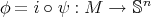 is proper biharmonic if and only if
is proper biharmonic if and only if 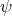 is harmonic and
is harmonic and  is constant.
is constant.
Remark 9.4. All the biharmonic maps constructed using Theorem 9.3 are unstable. To see this, let 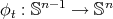 ,
, 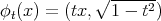 ,
, ![t ∈ [0,1]](/img/revistas/ruma/v47n2/2a02715x.png) , the map defined in Section 4.4. Then
, the map defined in Section 4.4. Then
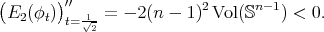
Thus the problem is to describe qualitatively their index and nullity.
Theorem 9.5 ([41]). Let 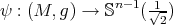 be a minimal immersion. The nullity of the biharmonic map
be a minimal immersion. The nullity of the biharmonic map 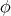 is bounded from below by the dimension of
is bounded from below by the dimension of 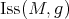 .
.
When 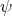 is the identity map of
is the identity map of 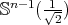 we have
we have
Theorem 9.6 ([41],[8]). The biharmonic index of the canonical inclusion 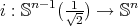 is exactly
is exactly  , and its nullity is
, and its nullity is 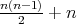 .
.
Proposition 9.7 ([43]). Let  be a minimal immersion,
be a minimal immersion, 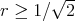 . Then
. Then
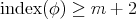 if either
if either 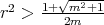 , or
, or 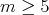 and
and 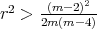 ;
;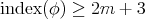 if
if 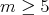 and
and 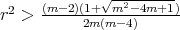 .
.
When 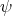 is the minimal generalized Veronese map we get
is the minimal generalized Veronese map we get
Corollary 9.8 ([41]). The biharmonic map derived from the generalized Veronese map 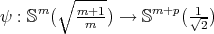 ,
, 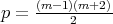 , has index at least
, has index at least  , when
, when  , and at least
, and at least 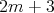 , when
, when  .
.
In Theorem 9.6 and Proposition 9.7 the map 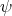 was a minimal immersion. We shall consider now the case of harmonic Riemannian submersions, and choose for
was a minimal immersion. We shall consider now the case of harmonic Riemannian submersions, and choose for 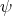 the Hopf map.
the Hopf map.
Theorem 9.9 ([42]). The index of the biharmonic map 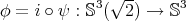 is at least
is at least 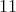 , while its nullity is bounded from below by
, while its nullity is bounded from below by 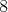 .
.
We note that, for the above results, the authors described explicitly the spaces where 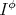 is negative definite or vanishes.
is negative definite or vanishes.
For the case of surfaces in Sasakian space forms, T. Sasahara, considering a variational vector field parallel to 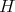 , gave a sufficient condition for proper biharmonic Legendre submanifolds into an arbitrary Sasakian space form to be unstable. This condition is expressed in terms of the mean curvature vector field and of the second fundamental form of the submanifold. In particular
, gave a sufficient condition for proper biharmonic Legendre submanifolds into an arbitrary Sasakian space form to be unstable. This condition is expressed in terms of the mean curvature vector field and of the second fundamental form of the submanifold. In particular
Theorem 9.10 ([54]). The biharmonic Legendre curves and surfaces in Sasakian space forms are unstable.
[1] K. Arslan, R. Ezentas, C. Murathan, T. Sasahara. Biharmonic anti-invariant submanifolds in Sasakian space forms. Beitrage Algebra Geom., to appear. [ Links ]
[2] K. Arslan, R. Ezentas, C. Murathan, T. Sasahara. Biharmonic submanifolds in 3-dimensional 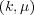 -manifolds. Internat. J. Math. Math. Sci., 22 (2005), 3575-3586. [ Links ]
-manifolds. Internat. J. Math. Math. Sci., 22 (2005), 3575-3586. [ Links ]
[3] P. Baird, D. Kamissoko. On constructing biharmonic maps and metrics. Ann. Global Anal. Geom. 23 (2003), 65-75. [ Links ]
[4] P. Baird, J.C. Wood. Harmonic Morphisms between Riemannian Manifolds. Oxford Science Publications, 2003. [ Links ]
[5] A. Balmuş. Biharmonic properties and conformal changes. An. Stiint. Univ. Al.I. Cuza Iasi Mat. (N.S.) 50 (2004), 361-372. [ Links ]
[6] A. Balmuş. On the biharmonic curves of the Euclidian and Berger 3-dimensional spheres. Sci. Ann. Univ. Agric. Sci. Vet. Med. 47 (2004), 87-96. [ Links ]
[7] A. Balmuş, S. Montaldo, C. Oniciuc. Biharmonic maps between warped product manifolds, J. Geom. Phys. 57 (2007), 449-466. [ Links ]
[8] A. Balmuş, C. Oniciuc. Some remarks on the biharmonic submanifolds of  and their stability. An. Stiint. Univ. Al.I. Cuza Iasi, Mat. (N.S), 51 (2005), 171-190. [ Links ]
and their stability. An. Stiint. Univ. Al.I. Cuza Iasi, Mat. (N.S), 51 (2005), 171-190. [ Links ]
[9] J. Berndt, F. Tricerri, L. Vanhecke. Generalized Heisenberg groups and Damek-Ricci harmonic spaces. Lecture Notes in Mathematics, 1598. Springer-Verlag, Berlin, 1995. [ Links ]
[10] R. Caddeo. Riemannian manifolds on which the distance function is biharmonic. Rend. Sem. Mat. Univ. Politec. Torino, 40 (1982), 93-101. [ Links ]
[11] R. Caddeo, S. Montaldo, C. Oniciuc. Biharmonic submanifolds of 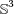 . Int. J. Math., 12 (2001), 867-876. [ Links ]
. Int. J. Math., 12 (2001), 867-876. [ Links ]
[12] R. Caddeo, S. Montaldo, C. Oniciuc. Biharmonic submanifolds in spheres. Israel J. Math., 130 (2002), 109-123. [ Links ]
[13] R. Caddeo, S. Montaldo, C. Oniciuc, P. Piu. The classification of biharmonic curves of Cartan-Vranceanu 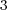 -dimensional spaces. Modern trends in geometry and topology, Cluj Univ. Press, Cluj-Napoca (2006), 121-131. [ Links ]
-dimensional spaces. Modern trends in geometry and topology, Cluj Univ. Press, Cluj-Napoca (2006), 121-131. [ Links ]
[14] R. Caddeo, S. Montaldo, P. Piu. Biharmonic curves on a surface. Rend. Mat. Appl., 21 (2001), 143-157. [ Links ]
[15] R. Caddeo, S. Montaldo, P. Piu. On Biharmonic Maps. Contemporary Mathematics, 288 (2001), 286-290. [ Links ]
[16] R. Caddeo, C. Oniciuc, P. Piu. Explicit formulas for non-geodesic biharmonic curves of the Heisenberg group. Rend. Sem. Mat. Univ. Politec. Torino, 62 (2004), 265-278. [ Links ]
[17] R. Caddeo, L. Vanhecke. Does " on a Riemannian manifold" imply flatness? Period. Math. Hungar., 17 (1986), 109-117. [ Links ]
on a Riemannian manifold" imply flatness? Period. Math. Hungar., 17 (1986), 109-117. [ Links ]
[18] S.-Y. A. Chang, L. Wang, P.C. Yang. A regularity theory of biharmonic maps. Comm. Pure Appl. Math., 52 (1999), 1113-1137. [ Links ]
[19] B.-Y. Chen. Some open problems and conjectures on submanifolds of finite type. Soochow J. Math., 17 (1991), 169-188. [ Links ]
[20] B.-Y. Chen. A report on submanifolds of finite type. Soochow J. Math., 22 (1996), 117-337. [ Links ]
[21] B.-Y. Chen, S. Ishikawa. Biharmonic pseudo-Riemannian submanifolds in pseudo-Euclidean spaces. Kyushu J. Math., 52 (1998), 167-185. [ Links ]
[22] J.H. Chen. Compact 2-harmonic hypersurfaces in 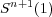 . Acta Math. Sinica, 36 (1993), 341-347. [ Links ]
. Acta Math. Sinica, 36 (1993), 341-347. [ Links ]
[23] J.T. Cho, J. Inoguchi, J.-E. Lee. Biharmonic curves in 3-dimensional Saskian space forms. Ann. Mat. Pura Appl., to appear. [ Links ]
[24] I. Dimitric. Submanifolds of 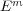 with harmonic mean curvature vector. Bull. Inst. Math. Acad. Sinica, 20 (1992), 53-65. [ Links ]
with harmonic mean curvature vector. Bull. Inst. Math. Acad. Sinica, 20 (1992), 53-65. [ Links ]
[25] J. Eells, A. Ratto. Harmonic Maps and Minimal Immersions with Symmetries. Princeton University Press, 1993. [ Links ]
[26] J. Eells, J.H. Sampson. Harmonic mappings of Riemannian manifolds. Amer. J. Math., 86 (1964), 109-160. [ Links ]
[27] J. Eells, J.C. Wood. Restrictions on harmonic maps of surfaces. Topology, 15 (1976), 263-266. [ Links ]
[28] D. Fetcu. Biharmonic curves in the generalized Heisenberg group. Beiträge Algebra Geom., 46 (2005), 513-521. [ Links ]
[29] B. Fuglede. Harmonic morphisms between Riemannian manifolds. Ann. Inst. Fourier (Grenoble) 28 (1978), 107-144. [ Links ]
[30] T. Hasanis, T. Vlachos. Hypersurfaces in 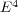 with harmonic mean curvature vector field. Math. Nachr., 172 (1995), 145-169. [ Links ]
with harmonic mean curvature vector field. Math. Nachr., 172 (1995), 145-169. [ Links ]
[31] Z.H. Hou. Hypersurfaces in a sphere with constant mean curvature. Proc. Amer. Math. Soc. 125 (1997), 1193-1196. [ Links ]
[32] J. Inoguchi. Submanifolds with harmonic mean curvature in contact 3-manifolds. Colloq. Math., 100 (2004), 163-179 . [ Links ]
[33] G.Y. Jiang. 2-harmonic isometric immersions between Riemannian manifolds. Chinese Ann. Math. Ser. A, 7 (1986), 130-144. [ Links ]
[34] G.Y. Jiang. 2-harmonic maps and their first and second variational formulas. Chinese Ann. Math. Ser. A, 7 (1986), 389-402. [ Links ]
[35] T. Lamm. Heat flow for extrinsic biharmonic maps with small initial energy. Ann. Global. Anal. Geom., 26 (2004), 369-384. [ Links ]
[36] T. Lamm. Biharmonic map heat flow into manifolds of nonpositive curvature. Calc. Var., 22 (2005), 421-445. [ Links ]
[37] D. Laugwitz. Differential and Riemannian geometry. Academic Press, 1965. [ Links ]
[38] H.B. Lawson. Complete minimal surfaces in 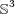 . Ann. of Math., 92 (1970), 335-374. [ Links ]
. Ann. of Math., 92 (1970), 335-374. [ Links ]
[39] E. Loubeau, S. Montaldo. Biminimal immersions in space forms. arXiv:math.DG/0405320. [ Links ]
[40] E. Loubeau, Y.-L. Ou. The characterization of biharmonic morphisms. Differential Geometry and its Applications (Opava, 2001), Math. Publ., 3 (2001), 31-41. [ Links ]
[41] E. Loubeau, C. Oniciuc. The index of biharmonic maps in spheres. Compositio Math., 141 (2005), 729-745. [ Links ]
[42] E. Loubeau, C. Oniciuc. On the biharmonic and harmonic indices of the Hopf map. Trans. Amer. Math. Soc., to appear. [ Links ]
[43] E. Loubeau, C. Oniciuc. The stability of biharmonic maps. preprint. [ Links ]
[44] C. Oniciuc. Biharmonic maps between Riemannian manifolds. An. Stiint. Univ. Al.I. Cuza Iasi Mat. (N.S.), 48 (2002), 237-248. [ Links ]
[45] C. Oniciuc. On the second variation formula for biharmonic maps to a sphere. Publ. Math. Debrecen, 61 (2002), 613-622. [ Links ]
[46] C. Oniciuc. New examples of biharmonic maps in spheres. Colloq. Math., 97(2003), 131-139. [ Links ]
[47] C. Oniciuc. Biharmonic maps in spheres and conformal changes. Recent advances in geometry and topology, Cluj Univ. Press, Cluj-Napoca, 2004, 279-282. [ Links ]
[48] C. Oniciuc. Tangency and Harmonicity Properties. PhD Thesis, Geometry Balkan Press 2003, http://vectron.mathem.pub.ro [ Links ]
[49] V. Oproiu. Some classes of natural almost Hermitian structures on the tangent bundles. Publ. Math. Debrecen, 62 (2003), 561-576. [ Links ]
[50] Y.-L. Ou. Biharmonic morphisms between Riemannian manifolds. Geometry and topology of submanifolds, X (Beijing/Berlin, 1999), 231-239. [ Links ]
[51] Y.-L. Ou. p-harmonic morphisms, biharmonic morphisms, and nonharmonic biharmonic maps. J. Geom. Phys., 56 (2006), 358-374. [ Links ]
[52] L. Sario, M. Nakai, C. Wang, L. Chung. Classification theory of Riemannian manifolds. Harmonic, quasiharmonic and biharmonic functions. Lecture Notes in Mathematics, Vol. 605. Springer-Verlag, Berlin-New York, 1977. [ Links ]
[53] T. Sasahara. Legendre surfaces in Sasakian space forms whose mean curvature vectors are eigenvectors. Publ. Math. Debrecen, 67 (2005) 285-303. [ Links ]
[54] T. Sasahara. Stability of biharmonic Legendrian submanifolds in Sasakian space forms. Canadian Math. Bulletin, to appear. [ Links ]
[55] P. Strzelecki. On biharmonic maps and their generalizations. Calc. Var., 18 (2003), 401-432. [ Links ]
[56] C. Wang. Biharmonic maps from 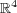 into a Riemannian manifold. Math. Z., 247 (2004), 65-87. [ Links ]
into a Riemannian manifold. Math. Z., 247 (2004), 65-87. [ Links ]
[57] C. Wang. Remarks on biharmonic maps into spheres. Calc. Var., 21 (2004), 221-242. [ Links ]
S. Montaldo Università degli Studi di Cagliari
Dipartimento di Matematica
Via Ospedale 72
09124 Cagliari, Italy
montaldo@unica.it
C. Oniciuc
Faculty of Mathematics
"Al.I. Cuza" University of Iasi
Bd. Carol I no. 11
700506 Iasi, Romania
oniciucc@uaic.ro
Recibido: 2 de noviembre de 2005
Aceptado: 29 de agosto de 2006













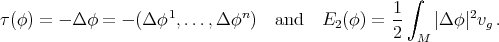
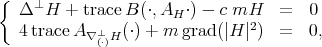
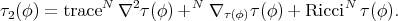
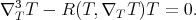
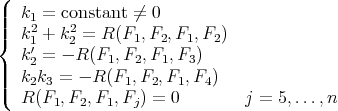
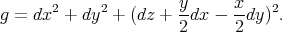
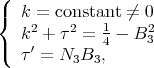
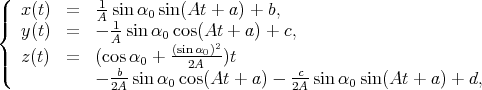
![( ) 2 ----dx2-+-dy2---- ℓ----ydx---xdy---- 2 dsm,ℓ = [1 + m (x2 + y2)]2 + dz + 2 [1 + m (x2 + y2)] , ℓ,m ∈ ℝ.](/img/revistas/ruma/v47n2/2a02262x.png)