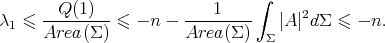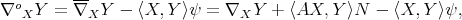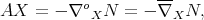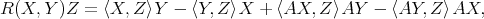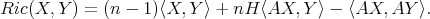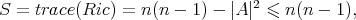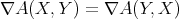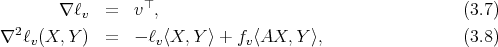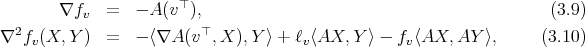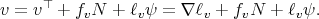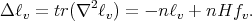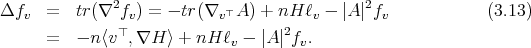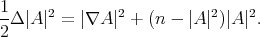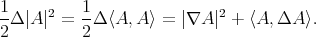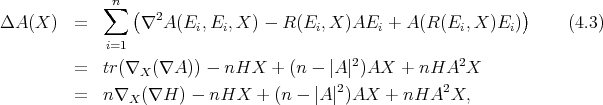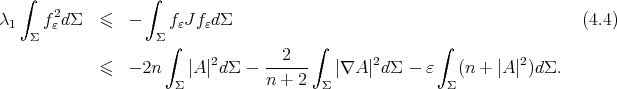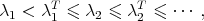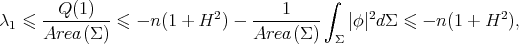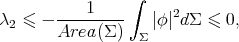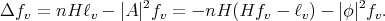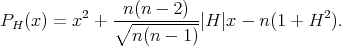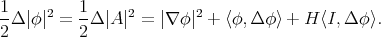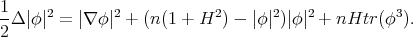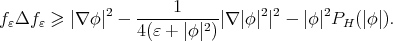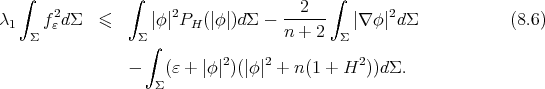Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.47 n.2 Bahía Blanca jul./dic. 2006
On the stability index of minimal and constant mean curvature hypersurfaces in spheres
Luis J. Alías
Abstract: The study of minimal and, more generally, constant mean curvature hypersurfaces in Riemannian space forms is a classical topic in differential geometry. As is well known, minimal hypersurfaces are critical points of the variational problem of minimizing area. Similarly, hypersurfaces with constant mean curvature are also solutions to that variational problem, when restricted to volume-preserving variations. In this paper we review about the stability index of both minimal and constant mean curvature hypersurfaces in Euclidean spheres, including some recent progress by the author, jointly with some of his collaborators. One of our main objectives on writing this paper has been to make it comprehensible for a wide audience, trying to be as self-contained as possible.
2000 Mathematics Subject Classification. Primary 53C42; Secondary 53A10
The author was partially supported by MEC/FEDER project no. MTM2004-04934-C04-02, F. Séneca project no. 00625/PI/04, and F. Séneca grant 01798/EE/05, Spain
1. Stability and index of minimal hypersurfaces
Let us consider 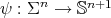 an orientable hypersurface immersed into the unit Euclidean sphere
an orientable hypersurface immersed into the unit Euclidean sphere 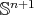 . We will denote by
. We will denote by  the shape operator of
the shape operator of  with respect to a globally defined normal unit vector field
with respect to a globally defined normal unit vector field 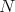 . That is,
. That is, 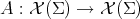 is the endomorphism determined by
is the endomorphism determined by
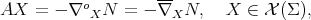
where  and
and 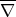 denote, respectively, the Levi-Civita connections on
denote, respectively, the Levi-Civita connections on 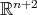 and
and 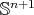 . As is well known,
. As is well known, 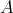 defines a symmetric endomorphism on
defines a symmetric endomorphism on 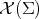 whose eigenvalues
whose eigenvalues  are usually referred to as the principal curvatures of the hypersurface. The mean curvature of
are usually referred to as the principal curvatures of the hypersurface. The mean curvature of  is then defined as
is then defined as
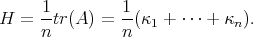
Throughout this paper, we will assume that  is compact. Every smooth function
is compact. Every smooth function 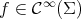 induces a normal variation
induces a normal variation  of the original immersion
of the original immersion 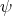 , given by
, given by
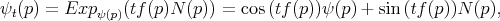
where Exp denotes the exponential map in 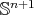 . Since
. Since  is compact and
is compact and 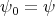 is an immersion, there exists
is an immersion, there exists 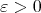 such that every
such that every 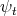 is also an immersion, for
is also an immersion, for 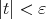 . Then we can consider the area function
. Then we can consider the area function 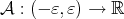 which assigns to each
which assigns to each 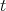 the
the 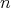 -dimensional area of
-dimensional area of  with respect to the metric induced on
with respect to the metric induced on  by the immersion
by the immersion 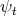 . That is,
. That is,
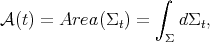
where 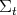 stands for the manifold
stands for the manifold  endowed with the metric induced by
endowed with the metric induced by 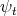 from the Euclidean metric on
from the Euclidean metric on 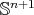 , and
, and 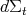 is the
is the 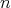 -dimensional area element of that metric on
-dimensional area element of that metric on  . The first variation formula for the area [16, Chapter I, Theorem 4] establishes that
. The first variation formula for the area [16, Chapter I, Theorem 4] establishes that
|
| (1.1) |
As a consequence,  is a minimal hypersurface (that is,
is a minimal hypersurface (that is,  on
on  ) if and only if
) if and only if 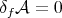 for every smooth function
for every smooth function 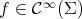 . In other words, minimal hypersurfaces are characterized as critical points of the area functional.
. In other words, minimal hypersurfaces are characterized as critical points of the area functional.
The stability operator of this variational problem is given by the second variation formula for the area [16, Chapter I, Theorem 32], which in our case is written as follows
|
| (1.2) |
Here  , where
, where  stands for the Laplacian operator of
stands for the Laplacian operator of  and
and 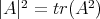 is the square of the norm of the shape operator. The operator
is the square of the norm of the shape operator. The operator 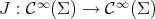 is called the Jacobi (or stability) operator of the minimal hypersurface
is called the Jacobi (or stability) operator of the minimal hypersurface  . The Jacobi operator
. The Jacobi operator 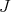 belongs to a class of operators which are usually referred to as Schrödinger operators, that is, operators of the form
belongs to a class of operators which are usually referred to as Schrödinger operators, that is, operators of the form  , where
, where 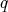 is any continuous function on
is any continuous function on  . As is well known, the spectrum of
. As is well known, the spectrum of 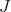
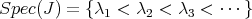
consists of an increasing sequence of eigenvalues 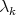 with finite multiplicities
with finite multiplicities 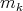 and such that
and such that 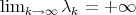 . Moreover, the first eigenvalue is simple (
. Moreover, the first eigenvalue is simple (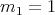 ) and it satisfies the following min-max characterization
) and it satisfies the following min-max characterization
|
| (1.3) |
Observe that with our criterion, a real number 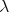 is an eigenvalue of
is an eigenvalue of 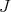 if and only if
if and only if 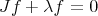 for some smooth function
for some smooth function 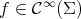 ,
, 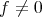 .
.
The Jacobi operator induces the quadratic form 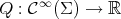 acting on the space of smooth functions on
acting on the space of smooth functions on  by
by
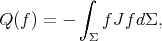
and the index of a minimal hypersurface  , denoted by
, denoted by 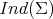 , is defined as the maximum dimension of any subspace
, is defined as the maximum dimension of any subspace 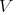 of
of 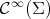 on which
on which  is negative definite. That is,
is negative definite. That is,
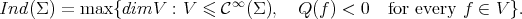
Equivalently, 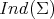 is the number of negative eigenvalues of
is the number of negative eigenvalues of 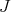 (counted with multiplicity), which is necessarily finite and it is given by
(counted with multiplicity), which is necessarily finite and it is given by
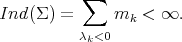
A minimal hypersurface would be said to be stable if 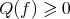 for every
for every 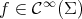 . Equivalently, in terms of the index, stability would mean that
. Equivalently, in terms of the index, stability would mean that 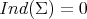 .
.
Intuitively, 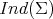 measures the number of independent directions in which the hypersurface fails to minimize area. To see it, observe that if
measures the number of independent directions in which the hypersurface fails to minimize area. To see it, observe that if 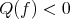 for some
for some 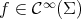 , then
, then 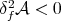 and therefore
and therefore  for small values of
for small values of 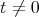 , in the normal variation of
, in the normal variation of  induced by
induced by 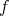 . That means that the minimal hypersurface
. That means that the minimal hypersurface  , while a critical point of the area functional, is not a local minimum. For minimal hypersurfaces in
, while a critical point of the area functional, is not a local minimum. For minimal hypersurfaces in 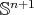 this is always the case. In fact, taking the constant function
this is always the case. In fact, taking the constant function 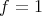 one has
one has
|
| (1.4) |
In particular, every compact minimal hypersurface in 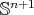 is unstable.
is unstable.
2. Minimal hypersurfaces with low index
We have just seen that there exists no compact stable minimal hypersurface in 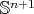 . Equivalently,
. Equivalently, 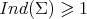 for every compact minimal hypersurface in the sphere. In [22, Theorem 5.1.1], Simons characterized the totally geodesic equators
for every compact minimal hypersurface in the sphere. In [22, Theorem 5.1.1], Simons characterized the totally geodesic equators 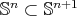 as the only compact minimal hypersurfaces in
as the only compact minimal hypersurfaces in 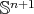 with
with 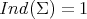 . Later on, Urbano [23] when
. Later on, Urbano [23] when  , and El Soufi [11] for general
, and El Soufi [11] for general 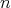 (see also [20, Lemma 3.1]), proved that if
(see also [20, Lemma 3.1]), proved that if  is not a totally geodesic equator, then not only must be
is not a totally geodesic equator, then not only must be 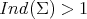 but in fact it must hold
but in fact it must hold
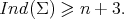
Therefore, we have the following result.
Theorem 1. Let 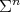 be a compact orientable minimal hypersurface immersed into the Euclidean sphere
be a compact orientable minimal hypersurface immersed into the Euclidean sphere 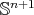 . Then
. Then
- either
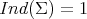 (and
(and  is a totally geodesic equator
is a totally geodesic equator 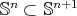 ),
), - or
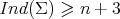 .
.
On the other hand, apart from the totally geodesic equators, which are obtained as intersections of 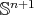 with linear hyperplanes of
with linear hyperplanes of 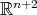 , the easiest minimal hypersurfaces in
, the easiest minimal hypersurfaces in 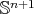 are the minimal Clifford tori. They are obtained by considering the standard immersions
are the minimal Clifford tori. They are obtained by considering the standard immersions 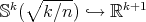 and
and 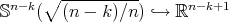 , for a given integer
, for a given integer  , and taking the product immersion
, and taking the product immersion 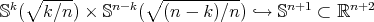 . As we will see in the next section, all minimal Clifford tori have
. As we will see in the next section, all minimal Clifford tori have 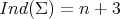 . For that reason, it has been conjectured for a long time that minimal Clifford tori are the only compact minimal hypersurfaces in
. For that reason, it has been conjectured for a long time that minimal Clifford tori are the only compact minimal hypersurfaces in 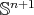 with
with 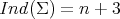 , changing Theorem 1 into the following conjecture.
, changing Theorem 1 into the following conjecture.
Conjecture 2. Let 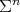 be a compact orientable minimal hypersurface immersed into the Euclidean sphere
be a compact orientable minimal hypersurface immersed into the Euclidean sphere 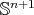 . Then
. Then
- either
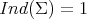 (and
(and  is a totally geodesic equator
is a totally geodesic equator 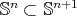 ),
), - or
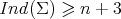 , with equality if and only if
, with equality if and only if  is a minimal Clifford torus
is a minimal Clifford torus 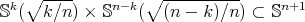 .
.
In [23], Urbano showed that the conjecture is true when  . See also next section for some other partial answers to Conjecture 2 in the general
. See also next section for some other partial answers to Conjecture 2 in the general 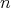 -dimensional case.
-dimensional case.
On the other hand, using also the constant function  as a test function in (1.3) to estimate
as a test function in (1.3) to estimate 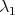 , from (1.4) one finds that
, from (1.4) one finds that
|
| (2.1) |
Moreover, equality 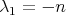 holds if and only if
holds if and only if 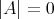 on
on  , that is, if and only if
, that is, if and only if  is a totally geodesic equator
is a totally geodesic equator 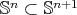 . In [22, Lemma 6.1.7] Simons proved that when
. In [22, Lemma 6.1.7] Simons proved that when  is not a totally geodesic equator, then not only must be
is not a totally geodesic equator, then not only must be 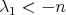 but in fact it must hold
but in fact it must hold
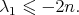
Later on, Wu [24] was able to characterize the case in which equality 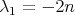 holds, by showing that equality holds if and only if
holds, by showing that equality holds if and only if  is a minimal Clifford torus. More recently, Perdomo [21] has considered again this problem, giving a new proof of that spectral characterization of minimal Clifford tori by the first stability eigenvalue. Summing up, we have the following result.
is a minimal Clifford torus. More recently, Perdomo [21] has considered again this problem, giving a new proof of that spectral characterization of minimal Clifford tori by the first stability eigenvalue. Summing up, we have the following result.
Theorem 3. Let 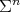 be a compact orientable minimal hypersurface immersed into the Euclidean sphere
be a compact orientable minimal hypersurface immersed into the Euclidean sphere 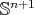 , and let
, and let 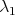 stand for the first eigenvalue of its Jacobi operator. Then
stand for the first eigenvalue of its Jacobi operator. Then
- either
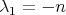 (and
(and  is a totally geodesic equator
is a totally geodesic equator 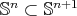 ),
), - or
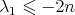 , with equality if and only if
, with equality if and only if  is a minimal Clifford torus
is a minimal Clifford torus 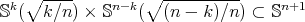 .
.
3. Proof of Theorem 1 and some partial answers to Conjecture 2
Before giving the proof of Theorem 1, we will fix some notation and establish some basic formulae which will be useful throughout this paper. Let us consider 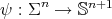 an orientable hypersurface immersed into the unit Euclidean sphere
an orientable hypersurface immersed into the unit Euclidean sphere 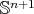 , with normal unit vector field
, with normal unit vector field 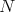 . If
. If  denotes the Levi-Civita connection on
denotes the Levi-Civita connection on  , then the Gauss and Weingarten formulae for the immersion
, then the Gauss and Weingarten formulae for the immersion 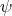 are given by
are given by
|
| (3.1) |
and
|
| (3.2) |
for every tangent vector fields 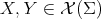 .
.
As is well known, the curvature tensor 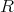 of the hypersurface
of the hypersurface  is described in terms of
is described in terms of 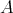 by the Gauss equation of
by the Gauss equation of  , which can be written as
, which can be written as
|
| (3.3) |
for 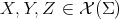 . Observe that our criterion for the definition of the curvature is
. Observe that our criterion for the definition of the curvature is
![R (X, Y )Z = ∇ [X,Y]Z - [∇X ,∇Y ]Z.](/img/revistas/ruma/v47n2/2a04171x.png)
As a consequence of (3.3), the Ricci curvature of  is given by
is given by
|
| (3.4) |
It follows from here that the scalar curvature of every minimal hypersurface in 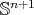 satisfies
satisfies
|
| (3.5) |
with equality only at points where  is totally geodesic. As a consequence, the only minimal hypersurfaces in
is totally geodesic. As a consequence, the only minimal hypersurfaces in 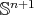 which are isometric to a unit round sphere are the totally geodesic equators. On the other hand, the Codazzi equation of
which are isometric to a unit round sphere are the totally geodesic equators. On the other hand, the Codazzi equation of  is given by
is given by
|
| (3.6) |
for every tangent vector fields 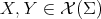 , where
, where 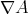 denotes the covariant differential of
denotes the covariant differential of 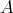 ,
,
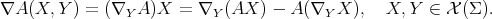
For a fixed arbitrary vector 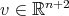 , we will consider the functions
, we will consider the functions 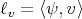 and
and 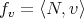 defined on
defined on  . Observe that
. Observe that 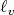 and
and 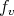 are, respectively, the coordinates of the immersion
are, respectively, the coordinates of the immersion 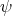 and the Gauss map
and the Gauss map 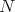 . A standard computation, using Gauss (3.1) and Weingarten (3.2) formulae, shows that the gradient and the hessian of the functions
. A standard computation, using Gauss (3.1) and Weingarten (3.2) formulae, shows that the gradient and the hessian of the functions 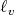 and
and 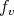 are given by
are given by
for every tangent vector fields 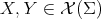 . Here
. Here 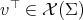 denotes the tangential component of
denotes the tangential component of  along the immersion
along the immersion 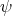 , that is,
, that is,
|
| (3.11) |
Equation (3.8) directly yields
|
| (3.12) |
On the other hand, using Codazzi equation (3.6) in (3.10) we also get
Here we are using the fact that trace commutes with the covariant derivative, which yields
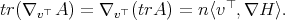
Now we are ready to prove Theorem 1.
Proof of Theorem 1. We already know from our previous discussions that 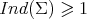 for every compact minimal hypersurface in
for every compact minimal hypersurface in 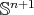 . Moreover, if
. Moreover, if  is a totally geodesic equator in
is a totally geodesic equator in 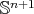 , then the Jacobi operator reduces to
, then the Jacobi operator reduces to  , where
, where  is the Laplacian operator on the unit sphere
is the Laplacian operator on the unit sphere 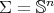 . In particular, the eigenvalues of
. In particular, the eigenvalues of 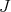 are given by
are given by 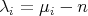 , where
, where 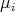 denotes the
denotes the 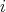 -th eigenvalue of the Laplacian on
-th eigenvalue of the Laplacian on 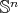 , with the same multiplicity. Then,
, with the same multiplicity. Then, 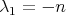 with multiplicity 1 and
with multiplicity 1 and  . In particular,
. In particular, 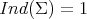 for a totally geodesic equator of the sphere.
for a totally geodesic equator of the sphere.
Therefore, it remains to show that, if  is not a totally geodesic equator, then
is not a totally geodesic equator, then 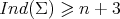 . When
. When  is not totally geodesic, we already know from the estimate (2.1) that
is not totally geodesic, we already know from the estimate (2.1) that 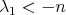 with multiplicity
with multiplicity 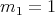 . Therefore, we will prove that
. Therefore, we will prove that 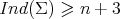 by showing that
by showing that  is also another negative eigenvalue of
is also another negative eigenvalue of 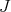 with multiplicity at least
with multiplicity at least  . Since
. Since  , equation (3.13) implies that
, equation (3.13) implies that 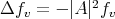 , and then
, and then
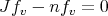
for every 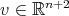 . Thus, whenever
. Thus, whenever 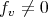 , the functions
, the functions 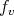 are eigenfunctions of
are eigenfunctions of 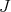 with negative eigenvalue
with negative eigenvalue  . We claim that if
. We claim that if  is not totally geodesic in
is not totally geodesic in 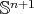 , then the dimension of the linear subspace
, then the dimension of the linear subspace 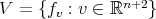 is
is  . If our claim is true, then the multiplicity of
. If our claim is true, then the multiplicity of  as an eigenvalue of
as an eigenvalue of 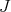 will be at least
will be at least  and this will finish the proof of the theorem.
and this will finish the proof of the theorem.
To show our claim, we will follow the ideas of Urbano in [23] for the case  . Obviously,
. Obviously,  . If
. If 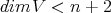 , then there exists a unit vector
, then there exists a unit vector 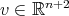 such that
such that 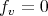 on
on  . From (3.8), that implies that
. From (3.8), that implies that 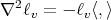 . Moreover, by (3.11) we also have
. Moreover, by (3.11) we also have
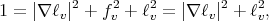
which in particular implies that the function 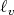 cannot be constant on
cannot be constant on  . Then a classical result by Obata [18, Theorem A] implies that
. Then a classical result by Obata [18, Theorem A] implies that  is isometric to a unit round sphere. But we have already seen as a consequence of Gauss equation (3.3) that the only minimal hypersurfaces in
is isometric to a unit round sphere. But we have already seen as a consequence of Gauss equation (3.3) that the only minimal hypersurfaces in 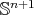 which are isometric to a unit round sphere are the totally geodesic equators. Thus, if
which are isometric to a unit round sphere are the totally geodesic equators. Thus, if  is not totally geodesic we have
is not totally geodesic we have  , as claimed. We also refer the reader to [20, Lemma 3.1] for an alternative proof of our claim, using a more geometric argument. □
, as claimed. We also refer the reader to [20, Lemma 3.1] for an alternative proof of our claim, using a more geometric argument. □
Let us consider now a minimal Clifford torus 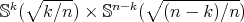 in
in 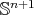 . At a point
. At a point 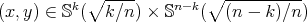 , the vector field
, the vector field
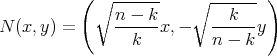
defines a normal unit vector at the point 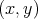 . With respect to this orientation, its principal curvatures are given by
. With respect to this orientation, its principal curvatures are given by
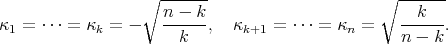
Then, every minimal Clifford torus has 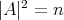 . In particular, its Jacobi operator reduces to
. In particular, its Jacobi operator reduces to  , where
, where  is the Laplacian on the product manifold
is the Laplacian on the product manifold 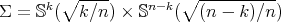 , and the eigenvalues of
, and the eigenvalues of 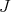 are given by
are given by 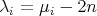 , where
, where 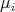 are the eigenvalues of
are the eigenvalues of  . Therefore, the index of
. Therefore, the index of  reduces to the number of eigenvalues of
reduces to the number of eigenvalues of  (counted with multiplicity) which are strictly less than
(counted with multiplicity) which are strictly less than 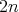 .
.
To compute it, simply recall that if 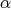 is an eigenvalue of the Laplacian on a Riemannian manifold
is an eigenvalue of the Laplacian on a Riemannian manifold 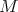 with multiplicity
with multiplicity 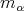 and
and 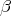 is an eigenvalue of the Laplacian on a Riemannian manifold
is an eigenvalue of the Laplacian on a Riemannian manifold 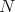 with multiplicity
with multiplicity 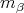 , then
, then 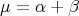 is an eigenvalue of the Laplacian on the product manifold
is an eigenvalue of the Laplacian on the product manifold 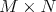 , and the multiplicity of
, and the multiplicity of 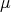 is the sum of the products
is the sum of the products 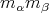 for all the possible values of
for all the possible values of 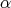 and
and 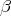 satisfying
satisfying 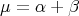 [8]. In our case, the eigenvalues of the Laplacian on
[8]. In our case, the eigenvalues of the Laplacian on 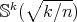 are given by
are given by
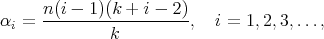
with multiplicities
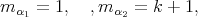
and
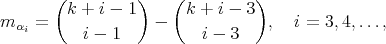
and the eigenvalues of the Laplacian on 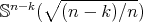 are given by
are given by
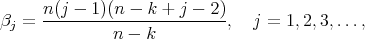
with multiplicities
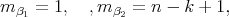
and
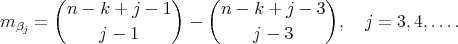
It easily follows from here that 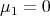 with multiplicity 1,
with multiplicity 1, 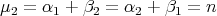 with multiplicity
with multiplicity  and
and  . Therefore, all minimal Clifford tori in
. Therefore, all minimal Clifford tori in 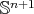 have
have 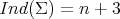 , which supports Conjecture 2.
, which supports Conjecture 2.
In [23] Urbano obtained the following characterization of minimal Clifford tori in  , solving Conjecture 2 when
, solving Conjecture 2 when  .
.
Theorem 4. Let 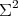 be a compact orientable minimal surface immersed into
be a compact orientable minimal surface immersed into  , which is not a totally geodesic equator. Then
, which is not a totally geodesic equator. Then 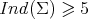 , with equality if and only if
, with equality if and only if 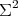 is a minimal Clifford torus
is a minimal Clifford torus 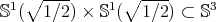 .
.
Later on, Guadalupe, Brasil Jr. and Delgado [14] showed that the conjecture is true for every dimension 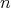 , under the additional hypothesis that
, under the additional hypothesis that  has constant scalar curvature, obtaining the following result.
has constant scalar curvature, obtaining the following result.
Theorem 5. Let 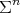 be a compact orientable minimal hypersurface immersed into
be a compact orientable minimal hypersurface immersed into 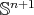 , which is not a totally geodesic equator. Assume that
, which is not a totally geodesic equator. Assume that  has constant scalar curvature. Then
has constant scalar curvature. Then 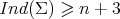 , with equality if and only if
, with equality if and only if 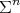 is a minimal Clifford torus
is a minimal Clifford torus 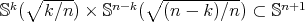 .
.
More recently, Perdomo [20] has showed that the conjecture is also true for every dimension 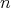 with an additional assumption about the symmetries of
with an additional assumption about the symmetries of  , and, in particular, the conjecture is true for minimal hypersurfaces with antipodal symmetry.
, and, in particular, the conjecture is true for minimal hypersurfaces with antipodal symmetry.
The proof of Theorem 3 makes use of a celebrated formula for the Laplacian of the function 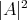 on
on  , which was established by Simons in [22]. Specifically, for the case of minimal hypersurfaces in
, which was established by Simons in [22]. Specifically, for the case of minimal hypersurfaces in 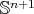 , Simons formula reads as follows,
, Simons formula reads as follows,
|
| (4.1) |
To give a proof of (4.1), let us introduce the following standard notation. Let 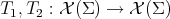 be two self-adjoint operators. Then
be two self-adjoint operators. Then
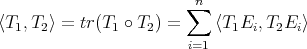
and
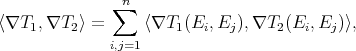
where  is a local orthonormal frame on
is a local orthonormal frame on  . Recall that, in our notation,
. Recall that, in our notation,
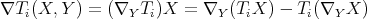
for 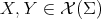 . On the other hand, the rough Laplacian of an operator
. On the other hand, the rough Laplacian of an operator 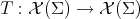 is defined as the operator
is defined as the operator 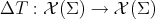 given by
given by
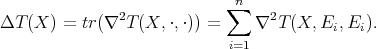
Recall again that in our notation, 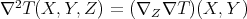 .
.
Consider now  an orientable hypersurface immersed in
an orientable hypersurface immersed in 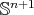 , which in principle we do not assume to be minimal. A standard tensor computation implies
, which in principle we do not assume to be minimal. A standard tensor computation implies
|
| (4.2) |
By the Codazzi equation (3.6), we know that 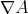 is symmetric and, hence,
is symmetric and, hence, 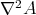 is also symmetric in its two first variables,
is also symmetric in its two first variables,
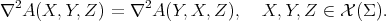
Regarding to the symmetries of 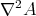 in the other variables, it is not difficult to see that
in the other variables, it is not difficult to see that
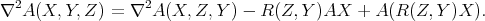
Thus, using the Gauss equation (3.3) we conclude from here that
where we have used the facts that trace commutes with 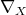 and that
and that 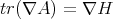 . In particular, if
. In particular, if  is a minimal hypersurface in
is a minimal hypersurface in 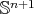 we conclude that
we conclude that
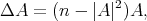
which jointly with (4.2) implies (4.1).
As a first application of Simons formula (4.1), we have the following result.
Theorem 6. Let  be a compact orientable minimal hypersurface immersed into the Euclidean sphere
be a compact orientable minimal hypersurface immersed into the Euclidean sphere 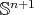 , and assume that
, and assume that  on
on  . Then
. Then
- either
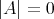 (and
(and  is a totally geodesic equator
is a totally geodesic equator 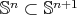 ),
), - or
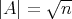 and
and  is a minimal Clifford torus.
is a minimal Clifford torus.
Part (i) and the sharp bound given in (ii) are due to Simons [22, Corollary 5.3.2]. On the other hand, the characterization of minimal Clifford tori given in (ii), which is local, was obtained independent and simultaneously by Chern, do Carmo and Kobayashi [10] and Lawson [15].
Proof of Theorem 6. Integrating (4.1) on  , and using Stokes' theorem and the hypothesis
, and using Stokes' theorem and the hypothesis 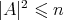 , we obtain that
, we obtain that
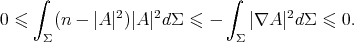
Therefore 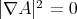 on
on  , and either
, and either 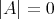 (and
(and  is totally geodesic) or
is totally geodesic) or 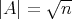 . This proves part (i) of the theorem and the first statement of part (ii). If
. This proves part (i) of the theorem and the first statement of part (ii). If 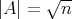 , then a local argument using the fact that
, then a local argument using the fact that 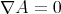 implies that
implies that  has exactly two constant principal curvatures
has exactly two constant principal curvatures
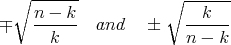
with multiplicities  and
and 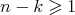 , respectively (for the details, see [10] or the proof of [15, Lemma 1]). In other words,
, respectively (for the details, see [10] or the proof of [15, Lemma 1]). In other words,  is a minimal isoparametric hypersurface of
is a minimal isoparametric hypersurface of 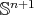 with two distinct principal curvatures, and from a classical result by Cartan [9],
with two distinct principal curvatures, and from a classical result by Cartan [9],  must be a minimal Clifford tori. Actually, in [9] Cartan showed that an isoparametric hypersurface of
must be a minimal Clifford tori. Actually, in [9] Cartan showed that an isoparametric hypersurface of 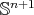 with two distinct principal curvatures must be an open piece of a standard product
with two distinct principal curvatures must be an open piece of a standard product 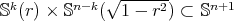 with
with 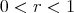 , but
, but  being minimal it must be
being minimal it must be 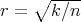 . □
. □
The proof of Theorem 3 below makes use also of the following auxiliary result, which can be found in [7] (see also [24, Lemma 1]).
Lemma 7. Let 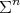 be a Riemannian manifold, and consider
be a Riemannian manifold, and consider 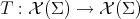 a symmetric tensor on
a symmetric tensor on  such that
such that 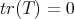 and its covariant differential
and its covariant differential 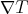 is symmetric. Then
is symmetric. Then
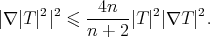
Proof of Theorem 3. We already know from (2.1) that  with equality if and only if
with equality if and only if  is a totally geodesic equator. Then, assume that
is a totally geodesic equator. Then, assume that  is not totally geodesic and consider, for every
is not totally geodesic and consider, for every  , the positive smooth function
, the positive smooth function 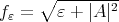 . We will use
. We will use 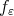 as a test function to estimate
as a test function to estimate 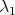 in (1.3). Observe that
in (1.3). Observe that
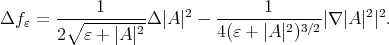
Therefore, using Simons formula (4.1) we obtain
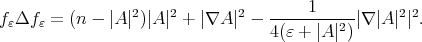
On the other hand, Lemma 7 applied to 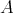 yields
yields
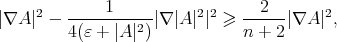
so that
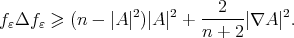
Then,
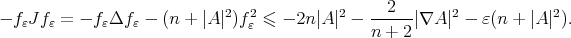
Therefore, using 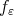 as a test function in (1.3), we get
as a test function in (1.3), we get
Since  is not totally geodesic, then
is not totally geodesic, then
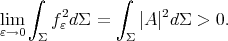
Now, letting 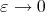 in (4.4) we conclude from here that
in (4.4) we conclude from here that
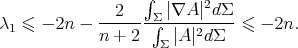
Moreover, if 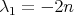 then
then 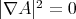 on
on  , and Lemma 7 implies that
, and Lemma 7 implies that 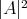 is a positive constant. Thus
is a positive constant. Thus  , where
, where 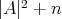 is a constant, and the first eigenvalue of
is a constant, and the first eigenvalue of 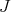 is simply the constant
is simply the constant 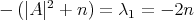 . Therefore,
. Therefore, 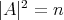 and by Theorem 6 we conclude that
and by Theorem 6 we conclude that  must be a minimal Clifford torus. □
must be a minimal Clifford torus. □
In [21], Perdomo gave another proof of the characterization of minimal Clifford tori by the equality 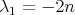 . His proof is based on a maximum principle, and it works as follows. Let us assume that
. His proof is based on a maximum principle, and it works as follows. Let us assume that 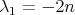 . In particular, by (2.1) we know that
. In particular, by (2.1) we know that  is not totally geodesic. Let
is not totally geodesic. Let 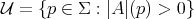 be the (non-empty) open subset of non-geodesic points of
be the (non-empty) open subset of non-geodesic points of  . The function
. The function  is smooth on
is smooth on  . Writing
. Writing 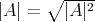 and using Simons formula (4.1), we obtain that
and using Simons formula (4.1), we obtain that
|
| (4.5) |
on  . By Lemma 7 we also have
. By Lemma 7 we also have
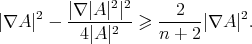
Therefore, using this into (4.5) we obtain
|
| (4.6) |
on  . Moreover, if equality
. Moreover, if equality 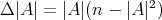 holds at a point
holds at a point 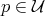 , then
, then 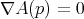 .
.
As is well known, the first eigenvalue 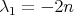 is simple, and its eigenspace is generated by a positive smooth function
is simple, and its eigenspace is generated by a positive smooth function 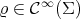 . Then
. Then 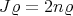 or, equivalently,
or, equivalently,
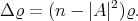
Observe that
|
| (4.7) |
Consider the smooth function 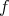 defined on
defined on  by
by 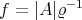 . A straightforward computation using (4.6) and (4.7) yields
. A straightforward computation using (4.6) and (4.7) yields
|
| (4.8) |
Summing up,
|
| (4.9) |
where 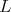 is the differential operator on
is the differential operator on  given by
given by 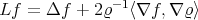 . Let
. Let 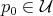 be a point where the function
be a point where the function 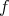 attains its (positive) maximum on
attains its (positive) maximum on  , and let
, and let 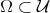 be a region around
be a region around  on which
on which 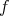 is greater than some positive constant. Since the maximum of
is greater than some positive constant. Since the maximum of 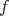 in
in 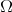 is attained in the interior of
is attained in the interior of 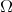 , by (4.9) and the maximum principle applied to
, by (4.9) and the maximum principle applied to 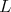 we deduce that
we deduce that 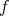 is constant on
is constant on 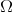 . Since
. Since  is connected, we conclude that
is connected, we conclude that 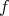 is a positive constant on the whole
is a positive constant on the whole  . Therefore, equality trivially holds in (4.9). That means that the inequality in (4.8) must be an equality, but this happens if and only if equality happens in (4.6), which implies that
. Therefore, equality trivially holds in (4.9). That means that the inequality in (4.8) must be an equality, but this happens if and only if equality happens in (4.6), which implies that 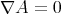 on
on  . Then, by Lemma 7 we know that
. Then, by Lemma 7 we know that  is a positive constant, and since
is a positive constant, and since 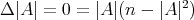 , we obtain that
, we obtain that 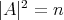 . Then Theorem 6 implies that
. Then Theorem 6 implies that  must be a minimal Clifford torus. This finishes Perdomo's proof.
must be a minimal Clifford torus. This finishes Perdomo's proof.
5. Stability and index of constant mean curvature hypersurfaces
Let 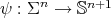 be a compact orientable hypersurface immersed into the unit Euclidean sphere. As another consequence of the first variation formula for the area (1.1), we have that
be a compact orientable hypersurface immersed into the unit Euclidean sphere. As another consequence of the first variation formula for the area (1.1), we have that  has constant mean curvature (not necessarily zero) if and only if
has constant mean curvature (not necessarily zero) if and only if 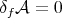 for every smooth function
for every smooth function 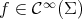 satisfying the additional condition
satisfying the additional condition 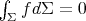 . To see it, assume that
. To see it, assume that 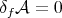 for every
for every 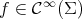 satisfying
satisfying 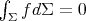 , and write
, and write 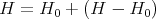 , where
, where
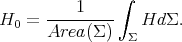
Since 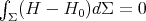 , then
, then
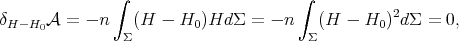
but this implies that 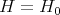 is constant on
is constant on  .
.
Geometrically, the additional condition 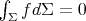 means that the variations under consideration preserve a certain volume function. In fact, if
means that the variations under consideration preserve a certain volume function. In fact, if 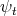 is the normal variation induced by a smooth function
is the normal variation induced by a smooth function 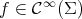 , then the volume function is the function
, then the volume function is the function 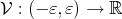 defined by
defined by
![∫ V (t) = Ψ *(dV ), [0,t]× Σ](/img/revistas/ruma/v47n2/2a04481x.png)
where 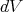 denotes the
denotes the  -dimensional volume element of
-dimensional volume element of 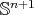 and
and 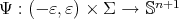 is the variation of
is the variation of 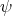 ,
, 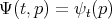 . Then, the first variation of
. Then, the first variation of 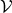 is given by
is given by
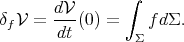
We refer the reader to [5, 6] for the details. A variation is said to be volume-preserving if 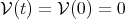 for all
for all 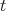 . As shown by Barbosa, do Carmo and Eschenburg in [6, Lemma 2.2], given a smooth function
. As shown by Barbosa, do Carmo and Eschenburg in [6, Lemma 2.2], given a smooth function 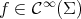 with
with 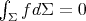 , there exists a volume-preserving normal variation whose variation vector field is
, there exists a volume-preserving normal variation whose variation vector field is 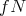 . As a consequence,
. As a consequence,  has constant mean curvature (not necessarily zero) if and only if
has constant mean curvature (not necessarily zero) if and only if 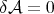 for every volume-preserving variation of
for every volume-preserving variation of  . In other words, constant mean curvature hypersurfaces are characterized as critical points of the area functional when restricted to volume-preserving variations.
. In other words, constant mean curvature hypersurfaces are characterized as critical points of the area functional when restricted to volume-preserving variations.
As in the case of minimal hypersurfaces, the stability operator of this variational problem is given by the second variation formula of the area (1.2), and similarly the corresponding quadratic form is also given by
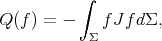
with Jacobi operator  . However, in contrast to the case of minimal hypersurfaces, in the case of hypersurfaces with constant mean curvature one can consider two different eigenvalue problems: the usual Dirichlet problem, associated with the quadratic form
. However, in contrast to the case of minimal hypersurfaces, in the case of hypersurfaces with constant mean curvature one can consider two different eigenvalue problems: the usual Dirichlet problem, associated with the quadratic form  acting on the whole space of smooth functions on
acting on the whole space of smooth functions on  , and the so called twisted Dirichlet problem, associated with the same quadratic form
, and the so called twisted Dirichlet problem, associated with the same quadratic form  , but restricted to the subspace of smooth functions
, but restricted to the subspace of smooth functions 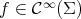 satisfying the additional condition
satisfying the additional condition 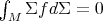 .
.
Similarly, there are two different notions of stability and index, the strong stability and strong index, denoted by 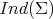 and associated to the usual Dirichlet problem, and the weak stability and weak index, denoted by
and associated to the usual Dirichlet problem, and the weak stability and weak index, denoted by 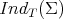 and associated to the twisted Dirichlet problem. Thus, the strong index is simply
and associated to the twisted Dirichlet problem. Thus, the strong index is simply
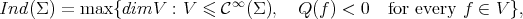
and  is called strongly stable if and only if
is called strongly stable if and only if 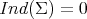 . On the other hand, the weak index is
. On the other hand, the weak index is
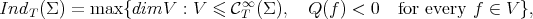
where
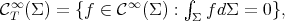
and  is called weakly stable if and only if
is called weakly stable if and only if 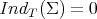 . From a geometrical point of view, the weak index is more natural than the strong index. However, from an analytical point of view, the strong index is more natural and easier to use.
. From a geometrical point of view, the weak index is more natural than the strong index. However, from an analytical point of view, the strong index is more natural and easier to use.
In [4], Barbosa and Bérard studied in depth the twisted Dirichlet problem, comparing the eigenvalues of this problem with the eigenvalues of the usual Dirichlet problem. For instance, it easily follows from the min-max principle that both spectra are interwined by
|
| (5.1) |
where
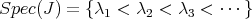
is the usual spectrum of 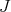 and
and

is its twisted spectrum.
When dealing with constant mean curvature hypersurfaces, instead of the second fundamental form 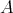 , it is more convenient to work with the so called traceless second fundamental form, which is given by
, it is more convenient to work with the so called traceless second fundamental form, which is given by 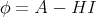 , where
, where 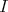 denotes the identity operator on
denotes the identity operator on 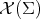 . Observe that
. Observe that
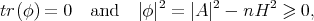
with equality if and only if  is totally umbilical. For that reason
is totally umbilical. For that reason 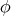 is also called the total umbilicity tensor of
is also called the total umbilicity tensor of  . In terms of
. In terms of 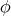 , the Jacobi operator is given by
, the Jacobi operator is given by
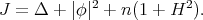
Using again the constant function 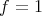 as a test function for estimating
as a test function for estimating 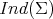 one has
one has
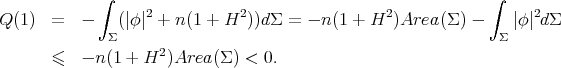
In particular, 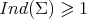 for every constant mean curvature hypersurface in
for every constant mean curvature hypersurface in 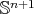 , which means that there is no strongly stable constant mean curvature hypersurface in
, which means that there is no strongly stable constant mean curvature hypersurface in 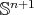 . It also follows from here that
. It also follows from here that
|
| (5.2) |
with equality 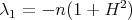 if and only if
if and only if  is a totally umbilical round sphere
is a totally umbilical round sphere 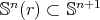 . Observe that, in general,
. Observe that, in general, 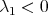 contributes to
contributes to 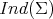 but not to
but not to 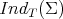 because its eigenspace is generated by a positive smooth function
because its eigenspace is generated by a positive smooth function 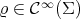 which does not satisfy the additional condition
which does not satisfy the additional condition 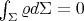 . On the other hand, in [13, Theorem 2.1], El Soufi and Ilias derived a sharp upper bound for the second eigenvalue of a Scrödinger operator of the form
. On the other hand, in [13, Theorem 2.1], El Soufi and Ilias derived a sharp upper bound for the second eigenvalue of a Scrödinger operator of the form  of a compact submanifold
of a compact submanifold 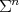 of a Riemannian space form, in terms of the total mean curvature of
of a Riemannian space form, in terms of the total mean curvature of  and the mean value of the potential
and the mean value of the potential 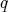 . In particular, for the Jacobi operator of a constant mean curvature hypersurface in
. In particular, for the Jacobi operator of a constant mean curvature hypersurface in 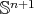 , their estimate yields
, their estimate yields
|
| (5.3) |
with equality  if and only if
if and only if  is totally umbilical. See also [12] for another interesting bound for the second eigenvalue of a Scrödinger operator, and its applications to the study of minimal and constant mean curvature hypersurfaces.
is totally umbilical. See also [12] for another interesting bound for the second eigenvalue of a Scrödinger operator, and its applications to the study of minimal and constant mean curvature hypersurfaces.
6. Weakly stable constant mean curvature hypersurfaces
We have just shown that there is no compact strongly stable constant mean curvature hypersurface in 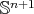 . In contrast to this, Barbosa, do Carmo and Eschenburg [6, Theorem 1.2] characterized the totally umbilical round spheres
. In contrast to this, Barbosa, do Carmo and Eschenburg [6, Theorem 1.2] characterized the totally umbilical round spheres 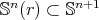 as the only compact weakly stable constant mean curvature hypersurfaces in
as the only compact weakly stable constant mean curvature hypersurfaces in 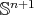 .
.
Theorem 8. Let 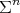 be a compact orientable constant mean curvature hypersurface immersed into the unit Euclidean sphere
be a compact orientable constant mean curvature hypersurface immersed into the unit Euclidean sphere 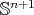 . Then
. Then  is weakly stable if and only if
is weakly stable if and only if  is a totally umbilical round sphere
is a totally umbilical round sphere  .
.
Proof. If  is a totally umbilical round sphere
is a totally umbilical round sphere 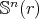 in
in 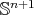 with radius
with radius 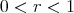 , then
, then 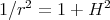 and the Jacobi operator reduces to
and the Jacobi operator reduces to 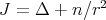 . Therefore, the eigenvalues of
. Therefore, the eigenvalues of 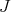 are given by
are given by 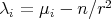 , where
, where 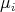 is the
is the 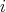 -th eigenvalue of the Laplacian operator on
-th eigenvalue of the Laplacian operator on 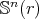 , with the same multiplicity. In particular,
, with the same multiplicity. In particular, 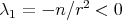 with multiplicity 1 and its associated eigenfunctions are the constant functions. Therefore, since all the other eigenfunctions of
with multiplicity 1 and its associated eigenfunctions are the constant functions. Therefore, since all the other eigenfunctions of 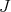 (for the usual Dirichlet problem) are orthogonal to the constant functions, they do satisfy the additional condition
(for the usual Dirichlet problem) are orthogonal to the constant functions, they do satisfy the additional condition 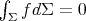 . Thus, in this case we have
. Thus, in this case we have 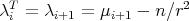 for every
for every  . Since
. Since 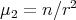 , it follows from here that
, it follows from here that 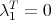 and
and  is weakly stable.
is weakly stable.
Conversely, assume that  is a compact orientable hypersurface with constant mean curvature in
is a compact orientable hypersurface with constant mean curvature in 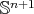 which is weakly stable. This means that
which is weakly stable. This means that
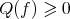
for every smooth function 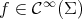 with
with 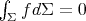 . As in the proof of Theorem 1, we will work with the functions
. As in the proof of Theorem 1, we will work with the functions 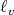 and
and 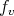 , where
, where 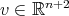 is a fixed arbitrary vector. Since
is a fixed arbitrary vector. Since 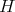 is constant, writing
is constant, writing 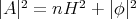 equation (3.13) becomes
equation (3.13) becomes
|
| (6.1) |
Let us consider the function 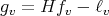 . From (3.12) we have that
. From (3.12) we have that  , so that
, so that 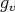 trivially satisfies the condition
trivially satisfies the condition 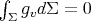 . Using (3.12) and (6.1), we easily get
. Using (3.12) and (6.1), we easily get
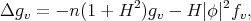
and then

Therefore, we have that
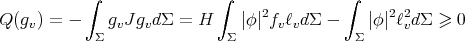
for every fixed arbitrary vector 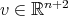 . Let us choose
. Let us choose 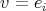 as an element of the standard orthonormal basis of
as an element of the standard orthonormal basis of 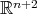 ,
, 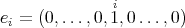 . Then
. Then
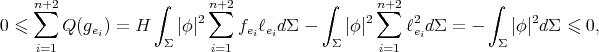
because of
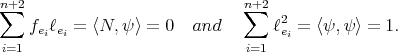
But this implies that 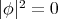 on
on  , and it must be totally umbilical. □
, and it must be totally umbilical. □
It is worth pointing out that Theorem 8 can be seen also as a consequence of the estimate (5.3), jointly with the interwining (5.1) of the two spectra of 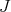 . In fact, if
. In fact, if  is weakly stable, then we have
is weakly stable, then we have
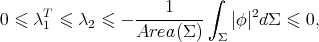
which implies again that 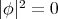 and
and  must be totally umbilical.
must be totally umbilical.
7. Constant mean curvature hypersurfaces with low index
Apart from the totally umbilical spheres, the easiest constant mean curvature hypersurfaces in 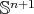 are the constant mean curvature Clifford tori. They are obtained by considering the standard immersions
are the constant mean curvature Clifford tori. They are obtained by considering the standard immersions 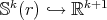 and
and 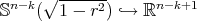 , for a given radius
, for a given radius 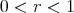 and integer
and integer  , and taking the product immersion
, and taking the product immersion 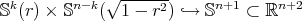 . Its principal curvatures are given by
. Its principal curvatures are given by
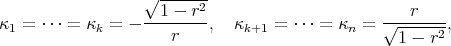
and its constant mean curvature 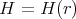 is given by
is given by
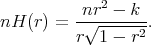
In particular, 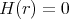 precisely when
precisely when 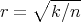 , which corresponds to the minimal Clifford torus.
, which corresponds to the minimal Clifford torus.
For the constant mean curvature Clifford tori, one has

and the Jacobi operator reduces to 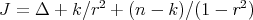 , where
, where  is the Laplacian operator on the product manifold
is the Laplacian operator on the product manifold 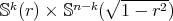 . In particular, the eigenvalues of
. In particular, the eigenvalues of 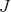 are given by
are given by 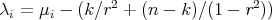 , where
, where  are the eigenvalues of
are the eigenvalues of  , and they have the same multiplicity. Thus,
, and they have the same multiplicity. Thus,  with multiplicity 1 and its associated eigenfunctions are the constant functions. Moreover, since all the rest of eigenfunctions of
with multiplicity 1 and its associated eigenfunctions are the constant functions. Moreover, since all the rest of eigenfunctions of 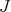 (for the usual Dirichlet problem) are orthogonal to the constant functions, they do satisfy the additional condition
(for the usual Dirichlet problem) are orthogonal to the constant functions, they do satisfy the additional condition 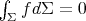 . Thus, similarly to the case of totally umbilical round spheres, we have
. Thus, similarly to the case of totally umbilical round spheres, we have 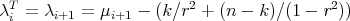 for every
for every  , and
, and 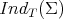 reduces to the number of positive eigenvalues of the Laplacian operator (counted with multiplicity) which are strictly less than
reduces to the number of positive eigenvalues of the Laplacian operator (counted with multiplicity) which are strictly less than 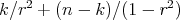 . This yields that
. This yields that 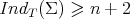 for every constant mean curvature Clifford torus, and
for every constant mean curvature Clifford torus, and 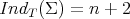 precisely when
precisely when  (for the details, see [3, Section 3]). Observe that, in particular, this happens when
(for the details, see [3, Section 3]). Observe that, in particular, this happens when 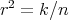 , so that, the minimal Clifford tori satisfy
, so that, the minimal Clifford tori satisfy 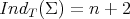 when regarded as constant mean curvature hypersurfaces.
when regarded as constant mean curvature hypersurfaces.
Motivated by this value of 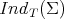 , in [3] Alías, Brasil and Perdomo have recently obtained the following result, which extends Theorem 1 (under the additional hypothesis of constant scalar curvature) and Theorem 5 to the case of constant mean curvature hypersurfaces.
, in [3] Alías, Brasil and Perdomo have recently obtained the following result, which extends Theorem 1 (under the additional hypothesis of constant scalar curvature) and Theorem 5 to the case of constant mean curvature hypersurfaces.
Theorem 9. Let 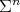 be a compact orientable hypersurface immersed into the Euclidean sphere
be a compact orientable hypersurface immersed into the Euclidean sphere 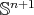 with constant mean curvature. Assume that
with constant mean curvature. Assume that  has constant scalar curvature. Then
has constant scalar curvature. Then
- either
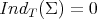 (and
(and  is a totally umbilic sphere in
is a totally umbilic sphere in 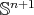 ), or
), or 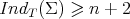 , with equality if and only if
, with equality if and only if  is a constant mean curvature Clifford torus
is a constant mean curvature Clifford torus 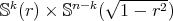 with radius
with radius 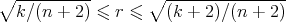 .
.
As observed in [3], the value of the index of the constant mean curvature Clifford tori 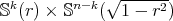 converges to infinity as
converges to infinity as  converges either to 0 or 1. For that reason, in contrast to the case of minimal Clifford tori, it is not possible, in general, to find a characterization of all constant mean curvature Clifford tori in terms of their index.
converges either to 0 or 1. For that reason, in contrast to the case of minimal Clifford tori, it is not possible, in general, to find a characterization of all constant mean curvature Clifford tori in terms of their index.
Proof. We already know from Theorem 8 that 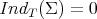 for the totally umbilical round spheres, whereas
for the totally umbilical round spheres, whereas 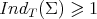 for the rest of compact constant mean curvature hypersurfaces in
for the rest of compact constant mean curvature hypersurfaces in 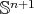 , without any additional hypothesis. Then, first we need to show that, if the scalar curvature of
, without any additional hypothesis. Then, first we need to show that, if the scalar curvature of  is constant (or equivalently,
is constant (or equivalently, 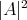 is constant; see equation (3.5)), then
is constant; see equation (3.5)), then 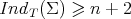 for every compact constant mean curvature hypersurface in
for every compact constant mean curvature hypersurface in 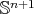 which is not totally umbilical. That is, we need to find a subspace
which is not totally umbilical. That is, we need to find a subspace 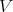 of
of 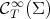 with
with  on which
on which  is negative definite.
is negative definite.
As in the proof of Theorem 8, we will consider the functions 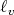 and
and 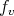 , where
, where 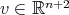 is a fixed arbitrary vector. When
is a fixed arbitrary vector. When 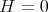 , we can take
, we can take 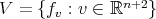 . In fact, since
. In fact, since  and
and 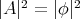 is a positive constant, then (6.1) implies that the functions
is a positive constant, then (6.1) implies that the functions 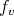 are eigenfunctions of
are eigenfunctions of 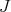 with negative eigenvalue
with negative eigenvalue  and that they also satisfy the condition
and that they also satisfy the condition 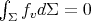 . Moreover, we have also seen in the proof of Theorem 1 that, when
. Moreover, we have also seen in the proof of Theorem 1 that, when  is minimal and not totally geodesic, then
is minimal and not totally geodesic, then  .
.
Therefore, in what follows we assume that 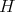 is a non-zero constant. In that case, we take
is a non-zero constant. In that case, we take 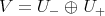 where
where
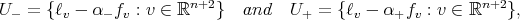
and 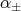 are the two different real roots of the quadratic equation
are the two different real roots of the quadratic equation
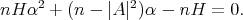
That is,
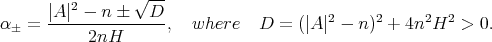
Using (3.12) and (6.1), it is not difficult to see that 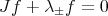 for every
for every 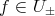 , where
, where
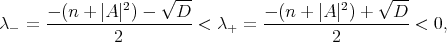
and that they also satisfy the condition 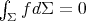 . Therefore
. Therefore
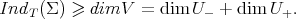
It remains to estimate  . Taking into account that
. Taking into account that 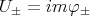 , where
, where 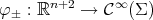 is the linear map given by
is the linear map given by 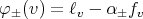 , we deduce that
, we deduce that
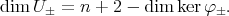
On the other hand, using that 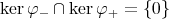 we also have
we also have
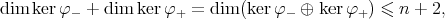
which implies
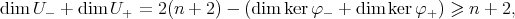
and therefore 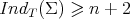 . We refer the reader to [3, Section 4] for further details about this proof.
. We refer the reader to [3, Section 4] for further details about this proof.
Moreover, if 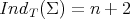 then
then 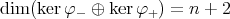 which means that
which means that 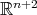 splits as direct sum of the two subspaces
splits as direct sum of the two subspaces 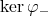 and
and 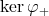 . Then, at any point
. Then, at any point  the tangent space
the tangent space 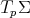 splits also as a direct sum of two subspaces
splits also as a direct sum of two subspaces
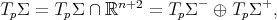
where 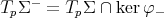 and
and 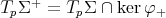 . Using that
. Using that  is not totally umbilical, and equations (3.7) and (3.9), we can see that, at each point
is not totally umbilical, and equations (3.7) and (3.9), we can see that, at each point 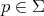 ,
, 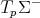 and
and 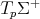 are subspaces of principal directions of
are subspaces of principal directions of 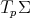 with constant principal curvatures
with constant principal curvatures 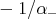 and
and 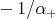 , respectively (see [3, Section 4] for the details). As a consequence,
, respectively (see [3, Section 4] for the details). As a consequence,  is a compact isoparametric hypersurface of
is a compact isoparametric hypersurface of 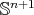 with two distinct principal curvatures, and from the well known rigidity result by Cartan [9] we conclude that
with two distinct principal curvatures, and from the well known rigidity result by Cartan [9] we conclude that  is a standard product of the form
is a standard product of the form 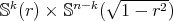 with radius
with radius 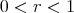 . Finally, from our previous discussion about the values of
. Finally, from our previous discussion about the values of 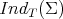 for those hypersurfaces, we conclude that it must be
for those hypersurfaces, we conclude that it must be 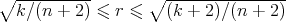 . □
. □
8. A sharp estimate for the first eigenvalue of the Jacobi operator
As we already know from (5.2), the first eigenvalue of the Jacobi operator of a compact hypersurface  with constant mean curvature
with constant mean curvature 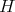 in
in 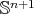 satisfies
satisfies
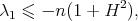
with equality if and only if  is a totally umbilical round sphere. As an extension of Theorem 3 to the case of constant mean curvature, Alías, Barros and Brasil in [2] have recently proved that when
is a totally umbilical round sphere. As an extension of Theorem 3 to the case of constant mean curvature, Alías, Barros and Brasil in [2] have recently proved that when  is not totally umbilical, then not only must be
is not totally umbilical, then not only must be 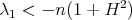 but it fact it must hold
but it fact it must hold
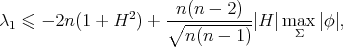
where 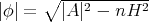 is the norm of the total umbilicity tensor of
is the norm of the total umbilicity tensor of  . Moreover, they were also able to characterize the case where equality holds, obtaining the following extension of Theorem 1.
. Moreover, they were also able to characterize the case where equality holds, obtaining the following extension of Theorem 1.
Theorem 10. Let 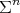 be a compact orientable hypersurface immersed into the Euclidean sphere
be a compact orientable hypersurface immersed into the Euclidean sphere 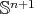 with constant mean curvature
with constant mean curvature 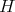 , and let
, and let 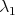 stand for the first eigenvalue of its Jacobi operator. Then
stand for the first eigenvalue of its Jacobi operator. Then
- either
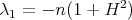 (and
(and  is a totally umbilic sphere in
is a totally umbilic sphere in 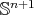 ), or
), or 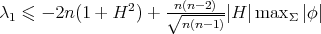 , with equality if and only if
, with equality if and only if  and
and  is a minimal Clifford torus
is a minimal Clifford torus 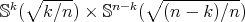 , with
, with  ;
;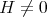 ,
,  , and
, and 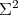 is a constant mean curvature Clifford torus
is a constant mean curvature Clifford torus 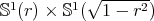 with
with 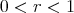 ,
, 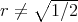 ;
;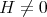 ,
,  , and
, and 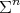 is a constant mean curvature Clifford torus
is a constant mean curvature Clifford torus 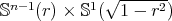 with
with 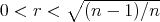 .
.
For the proof of Theorem 10, we will need the following result due to Alencar and do Carmo, which extends Theorem 6 to the case of constant mean curvature hypersurfaces.
Theorem 11. Let 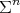 be a compact orientable hypersurface immersed into the Euclidean sphere
be a compact orientable hypersurface immersed into the Euclidean sphere 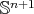 with constant mean curvature
with constant mean curvature 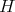 , and assume that
, and assume that  , where
, where
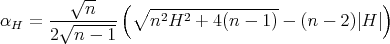
is the positive root of the polynomial
|
| (8.1) |
Then
- either
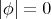 (and
(and  is a totally umbilic sphere in
is a totally umbilic sphere in 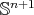 ), or
), or 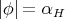 and
and  and
and  is a minimal Clifford torus
is a minimal Clifford torus 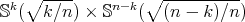 , with
, with  ;
;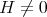 ,
,  , and
, and 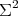 is a constant mean curvature Clifford torus
is a constant mean curvature Clifford torus 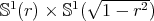 with
with 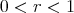 ,
, 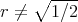 ;
;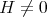 ,
,  , and
, and 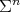 is a constant mean curvature Clifford torus
is a constant mean curvature Clifford torus 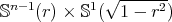 with
with 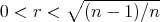 .
.
The proofs of Theorem 10 and Theorem 11 make use of an extension of Simons formula (4.1) for the case of hypersurfaces with constant mean curvature, which is due to Nomizu and Smyth [17]. To see it, consider 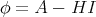 the total umbilicity tensor and recall that
the total umbilicity tensor and recall that 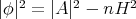 . Since we are assuming now that
. Since we are assuming now that 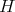 is constant, we have that
is constant, we have that  and
and  , and (4.2) can be written in terms of
, and (4.2) can be written in terms of 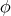 as follows
as follows
|
| (8.2) |
Moreover, by (4.3) we also have
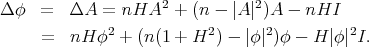
Then, taking into account that 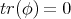 , (8.2) becomes
, (8.2) becomes
|
| (8.3) |
As a first application of equation (8.3), we may give the proof of Theorem 11. For the proof, we will also need the following auxiliary result, known as Okumura lemma, which can be found in [19] and [1, Lemma 2.6].
Lemma 12. Let  be real numbers such that
be real numbers such that 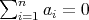 . Then
. Then
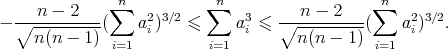
Moreover, equality holds in the right-hand (respectively, left-hand) side if and only if  of the
of the 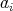 's are nonpositive (respectively, nonnegative) and equal.
's are nonpositive (respectively, nonnegative) and equal.
Proof of Theorem 11. Since 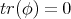 , we may use Lemma 12 to estimate
, we may use Lemma 12 to estimate 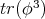 as follows
as follows
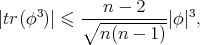
and then
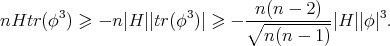
Using this in (8.3), we find 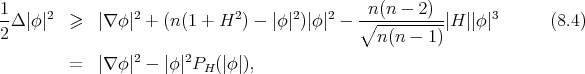 where
where 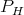 is given by (8.1). That is,
is given by (8.1). That is,
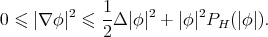
Integrating this inequality on  , and using Stokes' theorem and the hypothesis
, and using Stokes' theorem and the hypothesis  , we find that
, we find that
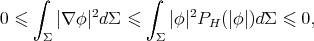
because of 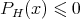 when
when ![x ∈ [0,αH ]](/img/revistas/ruma/v47n2/2a04805x.png) . Therefore,
. Therefore, 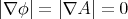 on
on  , and either
, and either 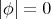 (and
(and  is totally umbilical) or
is totally umbilical) or 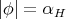 . This proves part (i) of Theorem 11 and the first statement of part (ii). If
. This proves part (i) of Theorem 11 and the first statement of part (ii). If  , then
, then 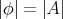 ,
, 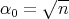 and part (ii)(a) just follows from (ii) in Theorem 6. If
and part (ii)(a) just follows from (ii) in Theorem 6. If 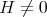 and
and 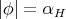 , then a local argument using the facts that
, then a local argument using the facts that 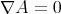 and that equality holds in the right-hand side of Lemma 12 implies that
and that equality holds in the right-hand side of Lemma 12 implies that  has exactly two constant principal curvatures, with multiplicities
has exactly two constant principal curvatures, with multiplicities 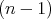 and 1. Then, by Cartan's result on isoparametric hypersurfaces of the sphere [9] we conclude that
and 1. Then, by Cartan's result on isoparametric hypersurfaces of the sphere [9] we conclude that  must be a constant mean curvature Clifford torus of the form
must be a constant mean curvature Clifford torus of the form 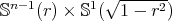 with
with 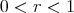 and
and 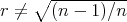 , since we are assuming
, since we are assuming 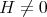 . Finally,to identify which constant mean curvature Clifford tori do appear, a direct computation shows that when
. Finally,to identify which constant mean curvature Clifford tori do appear, a direct computation shows that when  we have
we have 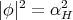 for all of them, but when
for all of them, but when  we have
we have
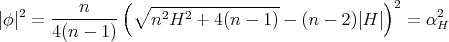
when 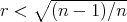 , and
, and
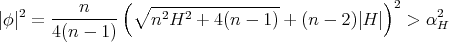
when 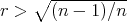 (for the details see [1, p. 1227] or [2, p. 878]) □
(for the details see [1, p. 1227] or [2, p. 878]) □
Now we are ready to prove Theorem 10.
Proof of Theorem 10. We already know that 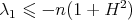 with equality if and only if
with equality if and only if  is totally umbilical, which proves part (i). Then we may assume that
is totally umbilical, which proves part (i). Then we may assume that  is not totally umbilical and consider, for every
is not totally umbilical and consider, for every 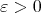 , the positive smooth function
, the positive smooth function 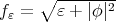 . As in the proof of Theorem 3, we will use
. As in the proof of Theorem 3, we will use 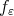 as a test function to estimate
as a test function to estimate 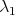 in (1.3). We observe that
in (1.3). We observe that
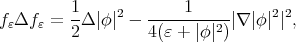
which using (8.4) yields
|
| (8.5) |
From Lemma 7 applied to 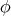 , we also have
, we also have
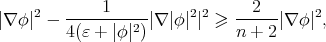
which jointly with (8.5) gives
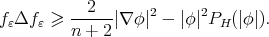
Then,
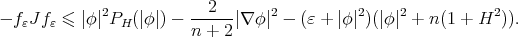
Therefore, using 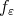 as a test function in (1.3), we get
as a test function in (1.3), we get
Since  is not totally umbilical, then
is not totally umbilical, then
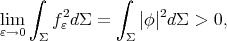
and letting  in (8.6) we conclude that
in (8.6) we conclude that
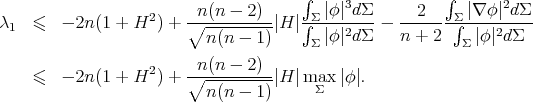
This proves the first statement of part (ii). Moreover, if
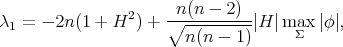
then 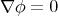 on
on  and by Lemma 7 we know that
and by Lemma 7 we know that 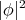 is a positive constant. Thus
is a positive constant. Thus 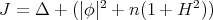 , where
, where 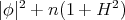 is a constant, and the first eigenvalue of
is a constant, and the first eigenvalue of 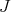 is simply the constant
is simply the constant
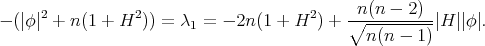
That is,  and
and 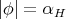 , and by Theorem 11 we know that it must hold either (a), (b) or (c). Conversely, we already know from Theorem 3 that
, and by Theorem 11 we know that it must hold either (a), (b) or (c). Conversely, we already know from Theorem 3 that 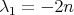 for all minimal Clifford tori in
for all minimal Clifford tori in 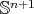 , and it is not difficult to see that
, and it is not difficult to see that 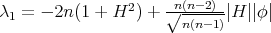 for the constant mean curvature Clifford tori in (b) and (c). See [2] for the details. □
for the constant mean curvature Clifford tori in (b) and (c). See [2] for the details. □
Finally, it is worth pointing out that Perdomo's technique in [21] also works here to characterize the equality case. For the details about this claim, see [2, Section 4].
This work was written while the author was visiting the Institut des Hautes Études Scientifiques (IHÉS) in Bures-sur-Yvette, France. He thanks IHÉS for its hospitality and support.
1. H. Alencar and M. do Carmo, Hypersurfaces with constant mean curvature in spheres, Proc. Amer. Math. Soc. 120 (1994), 1223-1229. [ Links ]
2. L.J. Alías, A. Barros and A. Brasil Jr., A spectral characterization of the H(r)-torus by the first stability eigenvalue, Proc. Amer. Math. Soc. 133 (2005), no. 3, 875-884. [ Links ]
3. L.J. Alías, A. Brasil Jr. and O. Perdomo, On the stability index of hypersurfaces with constant mean curvature in spheres, to appear in Proc. Amer. Math. Soc.. [ Links ]
4. J.L. Barbosa and P. Bérard, Eigenvalue and "twisted" eigenvalue problems. Applications to CMC surfaces, J. Math. Pures Appl. (9) 79 (2000), 427-450. [ Links ]
5. J.L. Barbosa and M. do Carmo, Stability of hypersurfaces with constant mean curvature, Math. Z. 185 (1984), 339-353. [ Links ]
6. J.L. Barbosa, M. do Carmo and J. Eschenburg, Stability of hypersurfaces with constant mean curvature in Riemannian manifolds, Math. Z. 197 (1988), 123-138. [ Links ]
7. A. Barros, A. Brasil Jr. and L.A.M. Sousa Jr., A new characterization of submanifolds with parallel mean curvature vector in 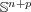 , Kodai. Math. J. 27 (2004), 45-56. [ Links ]
, Kodai. Math. J. 27 (2004), 45-56. [ Links ]
8. M. Berger, P. Gauduchon, and E. Mazet, Le spectre d'une variété riemannienne. Lecture Notes in Mathematics, Vol. 194 Springer-Verlag, Berlin-New York 1971. [ Links ]
9. E. Cartan, Familles de surfaces isoparamétriques dans les espaces à courbure constante, Annali di Mat. 17 (1938), 177-191. [ Links ]
10. S.S. Chern,M. do Carmo, and S. Kobayashi, Minimal submanifolds of a sphere with second fundamental form of constant length. 1970 Functional Analysis and Related Fields (Proc. Conf. for M. Stone, Univ. Chicago, Chicago, Ill., 1968) pp. 59-75 Springer, New York. [ Links ]
11. A. El Soufi, Applications harmoniques, immersions minimales et transformations conformes de la sphére, Compositio Math. 85 (1993), 281-298. [ Links ]
12. A. El Soufi and S. Ilias, Majoration de la seconde valeur propre d'un opérateur de Schrödinger sur une variété compacte et applications, J. Funct. Anal. 103 (1992), 294-316. [ Links ]
13. A. El Soufi and S. Ilias, Second eigenvalue of Schrödinger operators and mean curvature, Comm. Math. Phys. 208 (2000), 761-770. [ Links ]
14. I. Guadalupe, A. Brasil Jr., and J.A. Delgado, A characterization of the Clifford torus. Rend. Circ. Mat. Palermo (2) 48 (1999), 537-540. [ Links ]
15. H.B. Lawson Jr., Local rigidity theorems for minimal hypersurfaces, Ann. of Math. (2) 89 (1969), 187-197. [ Links ]
16. H.B. Lawson Jr., Lectures on minimal submanifolds. Vol. I. Second edition. Mathematics Lecture Series, 9. Publish or Perish, Inc., Wilmington, Del., 1980. [ Links ]
17. K. Nomizu and B. Smyth, A formula of Simons' type and hypersurfaces with constant mean curvature, J. Differential Geometry 3 (1969), 367-377. [ Links ]
18. M. Obata, Certain conditions for a Riemannian manifold to be iosometric with a sphere, J. Math. Soc. Japan 14 (1962), 333-340. [ Links ]
19. M. Okumura, Hypersurfaces and a pinching problem on the second fundamental tensor, Amer. J. Math. 96 (1974), 207-213. [ Links ]
20. O. Perdomo, Low index minimal hypersurfaces of spheres, Asian J. Math. 5 (2001), 741-749. [ Links ]
21. O. Perdomo, First stability eigenvalue characterization of Clifford hypersurfaces, Proc. Amer. Math. Soc. 130 (2002), 3379-3384 [ Links ]
22. J. Simons, Minimal varieties in Riemannian manifolds, Ann. of Math. (2), 88 (1968) 62-105. [ Links ]
23. F. Urbano, Minimal surfaces with low index in the three-dimensional sphere, Proc. Amer. Math. Soc. 108 (1990), 989-992. [ Links ]
24. C. Wu, New characterizations of the Clifford tori and the Veronese surface, Arch. Math. (Basel), 61 (1993), 277-284. [ Links ]
Luis J. Alías
Departamento de Matemáticas,
Universidad de Murcia,
E-30100 Espinardo, Murcia, Spain
ljalias@um.es
Recibido: 14 de diciembre de 2005 Aceptado: 29 de agosto de 2006