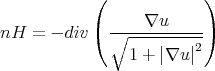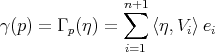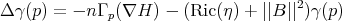Hypersurfaces with constant mean curvature

Susana Fornari

Resume of the Conference presented in the II Encuentro de Geometría Diferencial La Falda, Sierras de Córdoba, Argentina, June 6-11, 2005.

Abstract: The hypersurfaces with constant mean curvature (cmc) are studied under different aspects:

1- As critical Points of a Variational Problem.
2- As solutions of a Dirichlet Problem.
3- Under the point of view of harmonicity of the Gauss map.

We explain, in a short wave, the principal technical and some results obtained in each aspects.

1. Hypersurfaces of cmc as critical points of a Variational Problem.

An isometric immersion with constant mean curvature is a critical point of the area functional for variations preserving volume.

When the critical point is a local minimum, 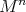is called stable. In particular, the stable hypersurfaces, when compact, bound isoparametric domains (frontier with area minima for a given fixed volume).

In 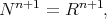or 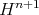the unique compact and stable hypersurfaces with cmc. are the geodesic spheres [B-dC-E, 1984], [Heintze, 1988].

In 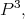the real projective space of dim 3, the compact stable surfaces are embedded, have genus 0 or 1, geodesic sphere or flat torus, respectively. Ritoré-Ros, 1992, [R-R]. In this paper, the authors give the isoperimetrical profile of these surfaces.

In the torus 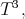the stable compact surfaces 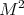immersed with cmc are not classified. Partial results are known (see [F-R1] and references):

  - the genus 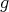of 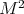must be

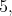  - if or then

  - if 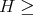some constant 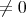(depending on the radius of the Torus) then the stable surface with cmc 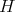is embedded and or

  - It is known a stable surface with genus 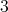and

Here 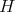 denotes the mean curvature of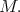

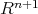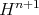The stable non compact hypersurface with cmc. are also studied. In they are hyperplanes In and 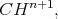the horospheres and tubes with sufficiently large radius around totally geodesic cod 2 -submanifolds are cmc stable hypersurfaces.

2. Constant Mean Curvature hypersurfaces as Solutions of a Dirichlet Problem.

It is known that if 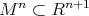is the graph of a differentiable functio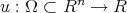n then

where denotes the gradient in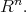

Therefore, the existence of a graph with constant mean curvature is equivalent to assure the existence of the solution of a Dirichlet problem:

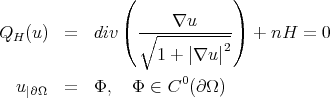
In this case, 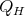is a quasi linear elliptic operator of second order and it satisfies the Maximum Principle.

For limited domains, with appropriate conditions in the mean curvature of the boundary, the Dirichlet problem above has a unique solution (Serrin, 1969) [S].

For not limited domains 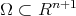the existence of solutions depends on the construction of appropriate barriers (Perron's method).

In and 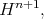it is possible to define the "graph" of a real function whose domain is a region 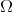contained in a totally geodesic submanifold of dim 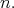The Dirichlet problem is similar to the above problem, but the operator 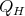can be quite complicated.

These graphs have been recently studied, some references are: Guio- Sá Earp, 2005 [G-S], Fornari, Lira, Ripoll, 2002 [F,L,R], Dajczer -Ripoll, preprint [D-R], Alias-Dajczer, preprint [A-D].

3. Constant Mean Curvature hypersurface and harmonicity of the Gauss map.

Given a complete surface 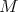 in 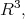 it is well known that:

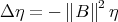
where 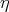is the unit normal to a surface, 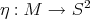,  is the Laplacian of  and  is the norm of the second fundamental of .

The above equation has been used to obtain many important results, one of them, due to Hoffman, Osserman and Shoen, 1982, [H-O-S] said:

"If  closed hemisphere of 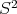 then 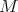 is a plane or a right circular cylinder"

or equivalently

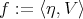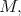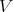
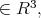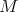"If the function   does not change sign on for same fixed vector   then  is invariant by a one parameter subgroup of translations of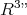

In a joint work with Espirito-Santo, Frensel  and Ripoll, [ES-F-F-R], 2003, we obtain similar results for hypersurfaces 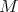 immersed with cmc  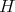on a Lie group with bi-invariant metric. Later on, in 2005, with J. Ripoll, [F-R,2] we extend this result for hypersurfaces  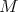immersed with cmc  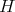on a -dimensional Riemannian manifold :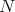

Consider the functi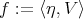on   on 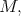 where 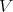 is a Killing field of 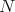. We prove that:

Using this result, similarly to those in 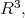we prove 

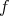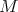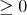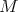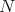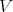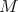"if  does not change sign on  and   then  is invariant by the one parameter subgroup of isometries of  determined by  or  is umbilic".

As consequence of this result we obtain a stability criterion for cmc surfaces in a manifold of dim 3:

"Let 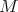 be a surface of constant mean curvature  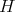(not necessarily complete) in  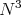with 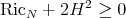 and let  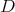be a domain in  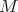such tha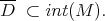t  Let 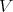 be a Killing vector field on  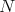and assume that  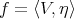has a sign o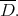n  Then 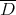 is stable".

It follows that any radial or horizontal cmc graph in the half space model for the hyperbolic 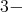space is stable.

If the manifold 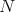 admits linearly independ Killing vector fields at each point, it is possible to define a normal Killing translation map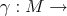  

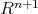
This map is a natural extension of the Gauss map of a hypersurface in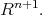

We obtain:

Using this formula we prove the following results:

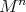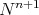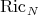
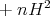
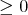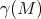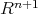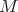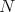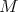Let  be a compact riemannian manifold immersed with cmc in a riemannian manifold  with   . If  is contained in a half space of  then  is invariant by a one parameter subgroup of isometries of  or  is umbilic.

In particular, it arises in this context a natural and interesting extension of a conjecture of  M. P. do Carmo which asserts that the Gauss image of a complete cmc surface in 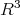 which is not a plane nor a cylinder contains a neighborhood of some equator of the sphere:

Conjecture (An extension of a conjecture of M. P. do Carmo):

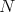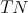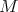Let be a dimensional Killing parallelizable riemannian manifold and let be a Killing basis of . Let be a complete constant mean curvature hypersurface immersed in 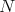and let be the normal Killing translation map associated to 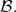If 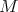is not invariant by a Killing field generated (over the real numbers) by 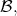then the radial projection of 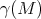on the unit sphere covers a neighborhood of some equator of the sphere.

References

[A-D]    Alias, L; Dajczer, M, "Geodesic normal graphs of constant mean curvature" preprint.        [ Links ]

[D-R]    Dajczer, M; Ripoll, J: "An extension of a Theorem of Serrin to graphs in warped products", preprint.        [ Links ]

[ES-F-F-R]    Espirito-Santo, N.; Fornari, S., Frensel K.; Ripoll, J. "Constant mean curvature hypersurfaces in a Lie group with a bi-invariant metric"; Manuscripta Mathematica 111-4 (2003), 459-470.        [ Links ]

[F-L-R]    Fornari, S.; Lira, J.; Ripoll, J; "Geodesic Graphs with constant mean curvature in Spheres"; Geometria Dedicata 90, (2002), 201-216.        [ Links ]

[F-R,1]    Fornari, S., Ripoll, J; "Stability of compact hypersurfaces with constant mean curvature", Indiana J. Math., vol 43, no 1 (1994), 367-380.        [ Links ]

[F-R,2]    Fornari, S., Ripoll, J; "Killing fields, generalized Gauss map and constant mean curvature hypersurfaces"; Illinois J. Math. 48-4 (2005), 1385-1403.        [ Links ]

[G-S]    Earp, R. S.; Guio, E. M. "Existence and non-existence for a mean curvature equation in hyperbolic space" Communications On Pure And Applied Analysis, USA, v. 4, n. 3, (2005), p. 549-568,        [ Links ]

[H-O-S]    Hoffman D.; Osserman R.; Schoen R.: "On the Gauss map of complete constant mean curvature surfaces in 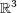and 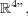Comm. Math. Helv. 57, (1982), 519 - 531.        [ Links ]

[R-R]    Ritoré M., Ros A.,  "Stable constant mean curvature tori and the isoperimetric problem in three space forms", Comm. Math. Helv. vol. 67, N. 2, (1992}        [ Links ]

[S]    Serrin, J. "The problem of Dirichlet for quasilinear elliptic differential equations with many independent variables". Philos. Trans. Royal Soc. London Ser. A, 264 (1969), 413-496.        [ Links ]

Susana Fornari
Departamento de Matemática - UFMG
Belo Horizonte, Brasil.
sfornari@mat.ufmg.br

Recibido: 1 de septiembre de 2005
Aceptado: 17 de septiembre de 2006