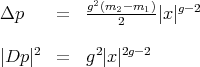Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932versão On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.47 n.2 Bahía Blanca jul./dez. 2006
Hipervariedades mínimas algebraicas en Sn
Oscar Mario Perdomo and Héber Mesa P.
Abstract: En este artículo se discutirá la existencia de hipervariedades compactas mínimas en la esfera 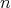 -dimensional
-dimensional 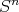 que se pueden escribir como la hipersuperficie de nivel de un polinomio homogéneo de grado
que se pueden escribir como la hipersuperficie de nivel de un polinomio homogéneo de grado 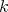 . Es decir estamos interesados en hipervariedades mínimas de la forma
. Es decir estamos interesados en hipervariedades mínimas de la forma 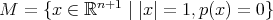 para algún polinomio homogéneo irreducible
para algún polinomio homogéneo irreducible 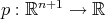 .
.
Sea 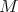 una variedad
una variedad  dimensional compacta y sin frontera, orientable, y
dimensional compacta y sin frontera, orientable, y 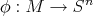 una inmersión. Para todo
una inmersión. Para todo 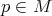 existe una vecindad
existe una vecindad 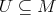 que contiene a
que contiene a 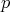 tal que
tal que 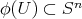 es difeomorfa a
es difeomorfa a  . Identificaremos
. Identificaremos  con
con 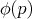 ,
, 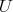 con
con 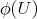 y cada vector
y cada vector 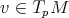 con
con 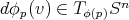 . Denotaremos por
. Denotaremos por 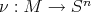 una aplicación de Gauss sobre
una aplicación de Gauss sobre 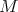 , es decir,
, es decir,  satisface que
satisface que 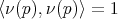 ,
, 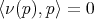 y
y 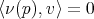 para todo
para todo 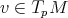 . Así, para todo
. Así, para todo 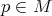 se tiene que
se tiene que 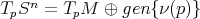 . Es posible demostrar que para esta aplicación se tiene que
. Es posible demostrar que para esta aplicación se tiene que 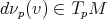 para todo vector
para todo vector 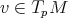 . Definimos el operador de forma
. Definimos el operador de forma 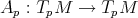 como
como 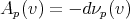 . No es difícil demostrar que
. No es difícil demostrar que 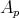 es una aplicación lineal autoadjunta, esto es
es una aplicación lineal autoadjunta, esto es 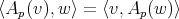 para todo par de vectores
para todo par de vectores 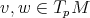 ; esto garantiza la existencia de
; esto garantiza la existencia de  vectores
vectores 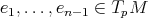 ortogonales y
ortogonales y  números reales
números reales 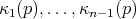 tales que
tales que 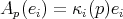 para
para  . Estos valores propios de
. Estos valores propios de 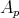 son conocidos como curvaturas principales de
son conocidos como curvaturas principales de 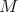 en
en 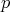 . La curvatura media
. La curvatura media 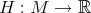 se define en cada punto como el promedio de las curvaturas principales, esto es
se define en cada punto como el promedio de las curvaturas principales, esto es 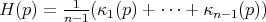 .
. 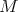 es llamada mínima si la curvatura media es idénticamente cero y es llamada totalmente geodésica si las curvaturas principales en cada punto de
es llamada mínima si la curvatura media es idénticamente cero y es llamada totalmente geodésica si las curvaturas principales en cada punto de 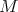 son cero. Diremos que una hipervariedad
son cero. Diremos que una hipervariedad 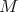 en
en 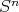 es algebraica si existe un polinomio homogéneo irreducible
es algebraica si existe un polinomio homogéneo irreducible 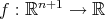 tal que
tal que 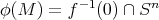 . Si el grado de
. Si el grado de 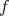 es
es 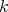 diremos que
diremos que 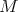 es algebraica de grado
es algebraica de grado 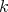 . En el caso en que
. En el caso en que  para todo
para todo 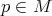 podemos definir una aplicación de Gauss
podemos definir una aplicación de Gauss  en cada punto
en cada punto 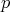 como
como 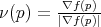 , y ya que
, y ya que 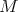 es la preimagen de un valor regular de una función diferenciable, entonces
es la preimagen de un valor regular de una función diferenciable, entonces 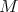 se encuentra encajada en
se encuentra encajada en 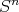 .
.
A la hora de buscar ejemplos de hipervariedades en 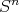 que sean mínimas y algebraicas podemos ver el problema desde dos perspectivas diferentes, considerar el conjunto de polinomios homogéneos y determinar cuáles de ellos reproducen variedades mínimas, o determinar cuáles de los ejemplos conocidos de variedades mínimas en
que sean mínimas y algebraicas podemos ver el problema desde dos perspectivas diferentes, considerar el conjunto de polinomios homogéneos y determinar cuáles de ellos reproducen variedades mínimas, o determinar cuáles de los ejemplos conocidos de variedades mínimas en 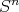 pueden ser modelados por algún polinomio homogéneo.
pueden ser modelados por algún polinomio homogéneo.
A continuación mostraremos algunos ejemplos conocidos de hipervariedades mínimas 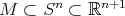 que se pueden escribir como la preimagen de cero de algún polinomio homogéneo irreducible.
que se pueden escribir como la preimagen de cero de algún polinomio homogéneo irreducible.
1.1. Ecuadores. Uno de los ejemplos más sencillos son los ecuadores, los cuales son de la forma 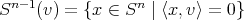 donde
donde 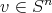 . En este caso la aplicación de Gauss se puede definir por
. En este caso la aplicación de Gauss se puede definir por 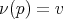 , dado que
, dado que  es constante, entonces
es constante, entonces 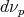 es idénticamente cero, igualmente el operador de forma. Claramente las curvaturas principales son cero en cada punto, y así,
es idénticamente cero, igualmente el operador de forma. Claramente las curvaturas principales son cero en cada punto, y así, 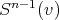 es totalmente geodésica y por tanto mínima. Si consideramos el polinomio homogéneo
es totalmente geodésica y por tanto mínima. Si consideramos el polinomio homogéneo 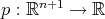 definido por
definido por 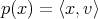 , entonces
, entonces 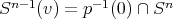 , lo que nos indica que
, lo que nos indica que 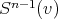 es algebraica. Esto prueba que los ecuadores son algebraicos de grado 1. Recíprocamente es fácil verificar que si
es algebraica. Esto prueba que los ecuadores son algebraicos de grado 1. Recíprocamente es fácil verificar que si 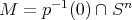 , donde
, donde  es un polinomio homogéneo de grado 1, entonces
es un polinomio homogéneo de grado 1, entonces  es un ecuador. Luego estos son los únicos ejemplos de hipervariedades mínimas algebraicas de grado 1.
es un ecuador. Luego estos son los únicos ejemplos de hipervariedades mínimas algebraicas de grado 1.
1.2. Variedades de Clifford. Sean  enteros tales que
enteros tales que 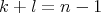 con
con 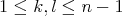 , definimos
, definimos 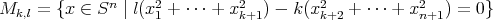 . No es difícil ver que
. No es difícil ver que 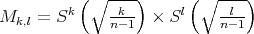 , donde
, donde 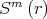 es la esfera
es la esfera 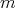 -dimensional en
-dimensional en 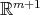 con centro en el origen y radio
con centro en el origen y radio  . Se puede demostrar que las curvaturas principales son constantes y están dadas por
. Se puede demostrar que las curvaturas principales son constantes y están dadas por 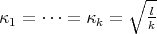 y
y 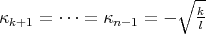 . Fácilmente se comprueba que
. Fácilmente se comprueba que 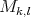 es mínima. Diremos que una hipervariedad
es mínima. Diremos que una hipervariedad 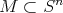 es Clifford si se puede obtener por un movimiento rígido de
es Clifford si se puede obtener por un movimiento rígido de 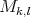 . Note que
. Note que 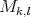 también es algebraica pues
también es algebraica pues 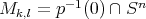 , donde
, donde 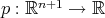 es el polinomio homogéneo
es el polinomio homogéneo 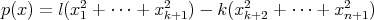 .
.
En el caso en que 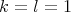 tenemos la superficie mínima algebraica
tenemos la superficie mínima algebraica 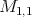 en
en 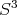 ; esta superficie es llamada toro de Clifford y va a ser de gran importancia ya que aparece en otras familias de superficies mínimas algebraicas en
; esta superficie es llamada toro de Clifford y va a ser de gran importancia ya que aparece en otras familias de superficies mínimas algebraicas en 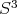 .
.
1.3. Variedades isoparamétricas. Una hipervariedad es llamada isoparamétrica si sus curvaturas principales son constantes, es decir, no dependen del punto en la variedad donde se determinan. Como hemos visto en los ejemplos anteriores, los ecuadores y las hipervariedades de Clifford son ejemplos de hipervariedades isoparamétricas en 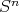 . Un teorema importante en el estudio de estas hipervariedades afirma que solo existen como máximo dos posibilidades para las multiplicidades de las curvaturas principales, las cuales se denotan
. Un teorema importante en el estudio de estas hipervariedades afirma que solo existen como máximo dos posibilidades para las multiplicidades de las curvaturas principales, las cuales se denotan 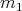 y
y 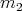 [7]. En 1980 Munzner demostró que toda hipervariedad isoparamétrica con
[7]. En 1980 Munzner demostró que toda hipervariedad isoparamétrica con 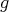 curvaturas principales distintas es algebraica de grado
curvaturas principales distintas es algebraica de grado 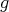 . Más aún, él probó que un polinomio homogéneo
. Más aún, él probó que un polinomio homogéneo 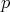 de grado
de grado 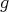 determina una hipervariedad isoparamétrica, si y solo si
determina una hipervariedad isoparamétrica, si y solo si 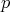 satisface las siguientes ecuaciones
satisface las siguientes ecuaciones
|
| (1) |
Un año más tarde, Munzner determinó los posibles valores de 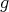 para los cuales existen hipervariedades isoparamétricas, específicamente demostró que el grado de un polinomio que es solución de (1) solo puede ser
para los cuales existen hipervariedades isoparamétricas, específicamente demostró que el grado de un polinomio que es solución de (1) solo puede ser 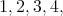 ó
ó 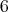 .
.
Todo polinomio homogéneo 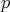 solución de
solución de 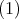 tiene la propiedad de que para todo
tiene la propiedad de que para todo 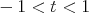 la hipervariedad
la hipervariedad 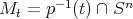 es suave e isoparamétrica, además la curvatura media de
es suave e isoparamétrica, además la curvatura media de 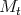 varía de forma monótona entre
varía de forma monótona entre 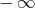 y
y 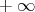 cuando
cuando 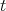 varía entre
varía entre 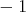 y
y  ; luego existe un
; luego existe un 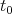 tal que la curvatura media de
tal que la curvatura media de 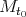 es cero, es decir
es cero, es decir 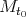 es mínima. Se sabe que para
es mínima. Se sabe que para 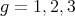 estas hipervariedades mínimas e isoparamétricas están caracterizadas: para
estas hipervariedades mínimas e isoparamétricas están caracterizadas: para  son los ecuadores y para
son los ecuadores y para  las variedades de Clifford; para
las variedades de Clifford; para 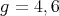 hay algunos ejemplos pero no se han caracterizado.
hay algunos ejemplos pero no se han caracterizado.
1.4. Ejemplos no encajados. En [1] Lawson demuestra que para el polinomio homogéneo 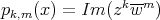 se tiene que
se tiene que 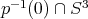 es mínima, donde
es mínima, donde 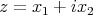 y
y 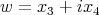 . Note que estos ejemplos muestran la existencia de superficies mínimas algebraicas de cualquier grado en
. Note que estos ejemplos muestran la existencia de superficies mínimas algebraicas de cualquier grado en 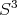 . Para el caso en que
. Para el caso en que  y
y  se tiene que
se tiene que 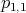 determina el toro de Clifford; se puede verificar que este es el único ejemplo de esta familia que está encajado.
determina el toro de Clifford; se puede verificar que este es el único ejemplo de esta familia que está encajado.
Ejemplos de hipervariedades mínimas en 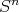 son escasos. En 1970, Lawson construyó una gran familia de superficies mínimas y compactas en
son escasos. En 1970, Lawson construyó una gran familia de superficies mínimas y compactas en 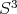 , [1]. Estos ejemplos mostraron que toda superficie compacta, excepto el espacio proyectivo, se puede inmersar en
, [1]. Estos ejemplos mostraron que toda superficie compacta, excepto el espacio proyectivo, se puede inmersar en 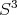 de manera mínima. Más aún, toda superficie compacta y orientable se puede encajar en
de manera mínima. Más aún, toda superficie compacta y orientable se puede encajar en 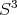 . Lawson dividió esta gran familia de superficies en varias subfamilias. En esta sección describiremos una de estas familias y abordaremos la pregunta sobre si estas superficies son o no algebraicas.
. Lawson dividió esta gran familia de superficies en varias subfamilias. En esta sección describiremos una de estas familias y abordaremos la pregunta sobre si estas superficies son o no algebraicas.
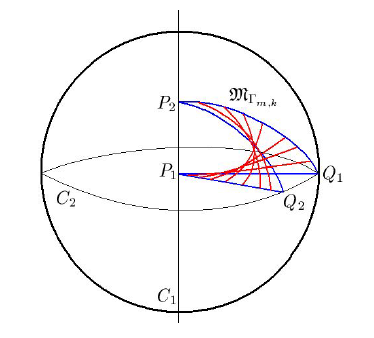
2.1. Superficies 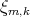 . Consideremos las circunferencias
. Consideremos las circunferencias 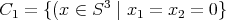 y
y 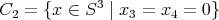 . Para cada par de enteros no negativos
. Para cada par de enteros no negativos 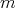 y
y 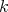 tomemos puntos
tomemos puntos 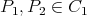 y
y 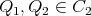 tales que la distancia en
tales que la distancia en 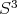 entre
entre 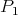 y
y 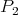 sea
sea 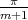 y la distancia en
y la distancia en 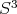 entre
entre 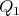 y
y 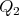 sea
sea 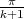 . Construyamos el polígono
. Construyamos el polígono 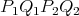 tal que sus lados sean segmentos de geodésica y dos vértices son unidos a través del segmento de geodésica más corto entre ellos. Denotaremos a este polígono geodésico
tal que sus lados sean segmentos de geodésica y dos vértices son unidos a través del segmento de geodésica más corto entre ellos. Denotaremos a este polígono geodésico 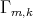 . Consideraremos
. Consideraremos 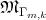 la superficie en
la superficie en 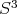 solución al problema de Plateau asociada a esta curva cerrada, entonces
solución al problema de Plateau asociada a esta curva cerrada, entonces 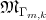 es mínima y
es mínima y 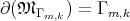 . La geodésica que pasa por
. La geodésica que pasa por 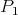 y
y 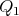 la notaremos
la notaremos 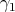 , la que pasa por
, la que pasa por 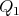 y
y 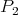 la notaremos
la notaremos 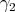 , y análogamente denotamos
, y análogamente denotamos 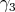 y
y 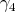 . Note que toda geodésica en
. Note que toda geodésica en 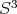 , cuando es vista como un subconjunto de
, cuando es vista como un subconjunto de 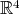 , está contenida en un plano 2 dimensional que pasa por el origen. Es fácil verificar que
, está contenida en un plano 2 dimensional que pasa por el origen. Es fácil verificar que 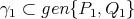 ,
, 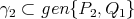 ,
, 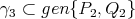 y
y 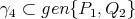 . A cada geodésica
. A cada geodésica 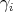 asociaremos una isometría
asociaremos una isometría 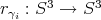 que consiste en una reflexión sobre el plano donde la geodésica
que consiste en una reflexión sobre el plano donde la geodésica 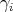 se encuentra. La primera simetría
se encuentra. La primera simetría  se determina como sigue
se determina como sigue 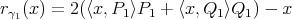 ; las demás se definen de manera análoga. Denotaremos
; las demás se definen de manera análoga. Denotaremos 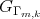 el grupo generado por las simetrías asociadas a cada geodésica, esto es
el grupo generado por las simetrías asociadas a cada geodésica, esto es 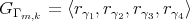 . Sea
. Sea 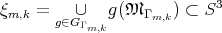 ; se demuestra que esta es una superficie mínima, orientable, compacta y sin frontera de género
; se demuestra que esta es una superficie mínima, orientable, compacta y sin frontera de género 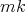 . Acerca de la algebraicidad de estas superficies, se tiene que
. Acerca de la algebraicidad de estas superficies, se tiene que 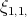 es el toro de Clifford y por tanto una superficie algebraica. Lawson en [1] conjetura que
es el toro de Clifford y por tanto una superficie algebraica. Lawson en [1] conjetura que 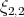 no es algebraica, la conjetura aún sigue abierta. Nosotros demostramos que si
no es algebraica, la conjetura aún sigue abierta. Nosotros demostramos que si 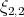 es algebraica, entonces su grado debe ser impar mayor o igual a
es algebraica, entonces su grado debe ser impar mayor o igual a  .
.
Figura 1: Región fundamental
Para cada polinomio 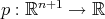 de grado
de grado 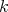 definimos
definimos 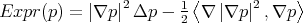 . Note que
. Note que 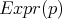 es un polinomio homogéneo de grado
es un polinomio homogéneo de grado  . Es conocido que si
. Es conocido que si 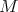 es algebraica y mínima, entonces el polinomio irreducible
es algebraica y mínima, entonces el polinomio irreducible 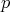 que determina a
que determina a 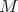 satisface que
satisface que 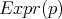 se anula en
se anula en  , [1]. Polinomios que satisfacen esta propiedad serán llamados polinomios que satisfacen la condición de minimalidad. En general no es cierto que todo polinomio que satisface la condición de minimalidad determina una hipersuperficie mínima. Por ejemplo, el polinomio
, [1]. Polinomios que satisfacen esta propiedad serán llamados polinomios que satisfacen la condición de minimalidad. En general no es cierto que todo polinomio que satisface la condición de minimalidad determina una hipersuperficie mínima. Por ejemplo, el polinomio 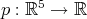 definido por
definido por 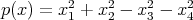 satisface la condición de minimalidad, pero el conjunto
satisface la condición de minimalidad, pero el conjunto 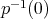 no es la imagen de una inmersión ya que
no es la imagen de una inmersión ya que 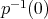 tiene una singularidad en
tiene una singularidad en 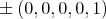 .
.
Note que el problema de hallar estos polinomios no es algebraico ni de ecuaciones diferenciales parciales, por que se requiere que 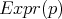 se anule en el conjunto
se anule en el conjunto 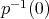 donde
donde 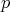 es desconocido.
es desconocido.
En el caso en que 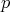 divida a
divida a 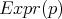 , es decir, si
, es decir, si 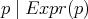 , claramente se tiene que
, claramente se tiene que 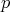 satisface la condición de minimalidad, pero no sabemos si es cierto que si esta condición se cumple entonces
satisface la condición de minimalidad, pero no sabemos si es cierto que si esta condición se cumple entonces 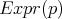 deba ser un múltiplo de
deba ser un múltiplo de 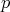 . Observamos que si en lugar de estar trabajando con polinomios sobre los reales, estuviésemos trabajando con polinomios sobre los complejos, entonces el teorema de los ceros de Hilbert garantizaría que el polinomio
. Observamos que si en lugar de estar trabajando con polinomios sobre los reales, estuviésemos trabajando con polinomios sobre los complejos, entonces el teorema de los ceros de Hilbert garantizaría que el polinomio 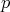 debería dividir al polinomio
debería dividir al polinomio 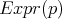 . Es decir, si se tuviese un teorema de los ceros de Hilbert para polinomios sobre los reales, entonces, el problema de hallar hipervariedades mínimas en
. Es decir, si se tuviese un teorema de los ceros de Hilbert para polinomios sobre los reales, entonces, el problema de hallar hipervariedades mínimas en 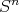 sería un problema algebraico, un problema que se reduce a resolver un sistema de ecuaciones. Algunos ejemplos sencillos de polinomios
sería un problema algebraico, un problema que se reduce a resolver un sistema de ecuaciones. Algunos ejemplos sencillos de polinomios 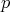 y
y 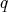 de variable real, donde
de variable real, donde 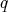 se anula en todos los puntos donde se anula
se anula en todos los puntos donde se anula  , pero
, pero 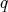 no es un múltiplo de
no es un múltiplo de 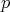 , ocurren porque
, ocurren porque 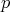 tiene "pocos ceros reales" en el sentido de que el conjunto
tiene "pocos ceros reales" en el sentido de que el conjunto 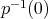 está contenido en una variedad de dimensión menor que
está contenido en una variedad de dimensión menor que 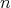 y no determina una subvariedad
y no determina una subvariedad 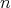 -dimensional, como ocurre en general.
-dimensional, como ocurre en general.
Por esta razón esperamos que si exigimos al polinomio 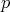 anularse en una variedad
anularse en una variedad 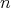 -dimensional entonces se tenga una versión del teorema de los ceros de Hilbert en
-dimensional entonces se tenga una versión del teorema de los ceros de Hilbert en 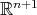 . Propondremos la siguiente conjetura:
. Propondremos la siguiente conjetura:
Conjetura: Si 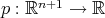 es un polinomio homogéneo tal que
es un polinomio homogéneo tal que 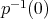 es una hipervariedad mínima, entonces
es una hipervariedad mínima, entonces 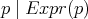 .
.
En el caso en que el grado de 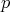 sea uno o dos, dado que se conocen las hipervariedades mínimas en cada caso, se puede demostrar que la conjetura es cierta. Más aún, los polinomios que determinan hipervariedades isoparamétricas de grado 3 satisfacen la conjetura. Esto se demuestra usando la ecuación (1) de la sección 1.3 y el hecho de que en este caso
sea uno o dos, dado que se conocen las hipervariedades mínimas en cada caso, se puede demostrar que la conjetura es cierta. Más aún, los polinomios que determinan hipervariedades isoparamétricas de grado 3 satisfacen la conjetura. Esto se demuestra usando la ecuación (1) de la sección 1.3 y el hecho de que en este caso  , [7].
, [7].
Si la conjetura fuese probada, el problema de determinar hipervariedades mínimas en 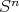 se convertiría en un problema algebraico. Si denotamos por
se convertiría en un problema algebraico. Si denotamos por 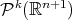 al espacio de polinomios homogéneos de grado
al espacio de polinomios homogéneos de grado 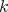 en
en 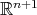 , podemos considerar la función
, podemos considerar la función 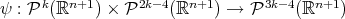 definida por
definida por 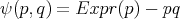 , y entonces estaríamos interesados en encontrar los ceros
, y entonces estaríamos interesados en encontrar los ceros 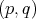 de este operador con
de este operador con 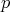 irreducible, ya que éstos determinarían los posibles ejemplos de hipervariedades mínimas algebraicas.
irreducible, ya que éstos determinarían los posibles ejemplos de hipervariedades mínimas algebraicas.
4. Resultados e ideas de la demostración
En esta sección se discutirán algunos resultados parciales obtenidos. Como se puede apreciar después de pensar un poco en el problema de encontrar polinomios que satisfacen la condición de minimalidad, la dificultad de este problema aumenta a medida que el grado del polinomio y la dimensión de la esfera aumentan. El primer caso interesante es el caso de los polinomios de grado 3 en 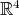 , es decir, superficies algebraicas en
, es decir, superficies algebraicas en 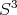 . Este caso lo resolvimos completamente, y demostramos que no existen superficies algebraicas de grado 3 que estén encajadas; luego demostramos que la únicas que están inmersas son los ejemplos de Lawson de grado 3 discutidos en la sección 1.4. Desde el punto de vista algebraico se ha demostrado que los únicos polinomios irreducibles en el espacio 20 dimensional de polinomios homogéneos de grado 3 en
. Este caso lo resolvimos completamente, y demostramos que no existen superficies algebraicas de grado 3 que estén encajadas; luego demostramos que la únicas que están inmersas son los ejemplos de Lawson de grado 3 discutidos en la sección 1.4. Desde el punto de vista algebraico se ha demostrado que los únicos polinomios irreducibles en el espacio 20 dimensional de polinomios homogéneos de grado 3 en 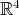 que satisfacen la condición de minimalidad son los obtenidos por el polinomio
que satisfacen la condición de minimalidad son los obtenidos por el polinomio 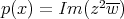 , donde
, donde 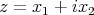 y
y 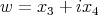 , salvo un cambio ortogonal de coordenadas. El siguiente caso en orden de dificultad es el de polinomios de grado 4 en
, salvo un cambio ortogonal de coordenadas. El siguiente caso en orden de dificultad es el de polinomios de grado 4 en 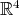 . La dificultad en este caso aumenta considerablemente ya que la dimensión del espacio de polinomios homogéneos en
. La dificultad en este caso aumenta considerablemente ya que la dimensión del espacio de polinomios homogéneos en 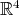 cambia de 20 a 35 cuando el grado de los polinomios cambia de 3 a 4. En general, la dimensión del espacio
cambia de 20 a 35 cuando el grado de los polinomios cambia de 3 a 4. En general, la dimensión del espacio 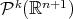 es
es 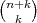 . Nosotros consideramos el caso de los polinomios de grado 4 en
. Nosotros consideramos el caso de los polinomios de grado 4 en 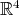 y demostramos que ninguno de estos polinomios determinaba una de las superficies
y demostramos que ninguno de estos polinomios determinaba una de las superficies 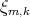 , es decir, demostramos que ninguna superficie de esta familia de ejemplos de Lawson es analítica de grado 4.
, es decir, demostramos que ninguna superficie de esta familia de ejemplos de Lawson es analítica de grado 4.
Una observación importante en este estudio de hipervariedades algebraicas es que todas ellas tienen simetría antipodal, esto se debe a que si 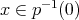 entonces
entonces 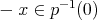 . Concentrándonos por un momento en superficies algebraicas regulares
. Concentrándonos por un momento en superficies algebraicas regulares 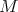 en
en 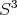 , es decir, superficies tales que
, es decir, superficies tales que 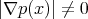 para todo
para todo 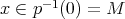 , podemos notar que
, podemos notar que 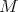 es una superficie encajada en
es una superficie encajada en 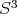 y por lo tanto orientable. Si identificamos cada punto con su antipodal en
y por lo tanto orientable. Si identificamos cada punto con su antipodal en 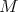 obtenemos una superficie
obtenemos una superficie 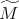 compacta y encajada en
compacta y encajada en 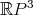 , donde para cada
, donde para cada 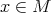 se tiene que
se tiene que ![^ [x] = {x,- x} ∈ M](/img/revistas/ruma/v47n2/2a06271x.png) . Acerca de superficies encajadas en
. Acerca de superficies encajadas en 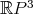 se tiene el siguiente teorema.
se tiene el siguiente teorema.
Teorema 1 [6]. Sea 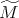 una superficie no orientable y compacta.
una superficie no orientable y compacta. 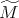 se puede encajar en
se puede encajar en 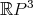 si y sólo si la característica de Euler de
si y sólo si la característica de Euler de 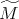 es impar.
es impar.
Resolvamos ahora la pregunta ¿cuándo la superficie 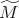 es orientable? Note que
es orientable? Note que ![T ℝP 3 = T S2 ∐ T S2 ∕~ [x] x -x](/img/revistas/ruma/v47n2/2a06278x.png) , donde identificamos cada vector
, donde identificamos cada vector 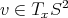 con
con 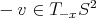 y
y  representa la operación unión disjunta de conjuntos. Dado que
representa la operación unión disjunta de conjuntos. Dado que 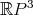 es orientable, entonces
es orientable, entonces 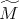 es orientable si y sólo si existe un campo vectorial normal
es orientable si y sólo si existe un campo vectorial normal  . Si el grado del polinomio
. Si el grado del polinomio 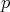 que determina a
que determina a 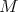 es par, entonces
es par, entonces 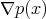 es impar y
es impar y ![[ ∇p(x)] ^ν([x]) = |∇p(x)|](/img/revistas/ruma/v47n2/2a06288x.png) está bien definido y por tanto
está bien definido y por tanto 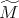 es orientable. Análogamente si el grado de
es orientable. Análogamente si el grado de 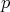 es impar, entonces
es impar, entonces 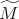 no es orientable. Note que usando el teorema anterior y el hecho de que la característica de Euler de toda superficie compacta sin frontera y orientable es par, se demuestra que la característica de Euler de
no es orientable. Note que usando el teorema anterior y el hecho de que la característica de Euler de toda superficie compacta sin frontera y orientable es par, se demuestra que la característica de Euler de 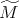 es impar si y sólo si el grado de
es impar si y sólo si el grado de 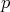 es impar.
es impar.
A continuación enunciaremos los resultados obtenidos por los autores en esta línea. Aunque no presentaremos las demostraciones correspondientes, daremos algunos puntos claves de su desarrollo.
Teniendo en cuenta que 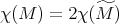 , entonces del Teorema 1 y las observaciones hechas acerca de la orientabilidad de
, entonces del Teorema 1 y las observaciones hechas acerca de la orientabilidad de 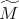 , deducimos información sobre la superficie
, deducimos información sobre la superficie 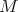 en términos de su característica de Euler según la paridad del grado del polinomio homogéneo
en términos de su característica de Euler según la paridad del grado del polinomio homogéneo 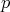 que la determina.
que la determina.
Resultado 1 [3]. Sea 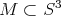 una superficie algebraica regular.
una superficie algebraica regular. 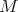 es de grado par si y sólo si la característica de Euler de
es de grado par si y sólo si la característica de Euler de 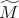 es par.
es par.
La demostración se obtiene directamente del Teorema 1 y de las observaciones hechas arriba.
Resultado 2 [4]. No existen superficies mínimas algebraicas encajadas de grado tres en 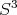 .
.
La demostración de este resultado consiste en considerar un polinomio general 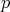 de grado 3 en
de grado 3 en 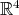 y suponer que este satisface la condición de minimalidad. Luego, sin pérdida de generalidad, se hacen algunas consideraciones sobre el polinomio, correspondientes al hecho de suponer que el punto
y suponer que este satisface la condición de minimalidad. Luego, sin pérdida de generalidad, se hacen algunas consideraciones sobre el polinomio, correspondientes al hecho de suponer que el punto 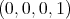 es un punto de la variedad, y que el espacio tangente en
es un punto de la variedad, y que el espacio tangente en 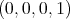 es el espacio
es el espacio 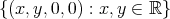 . Estas consideraciones brindan algunas ecuaciones sobre los coeficientes de
. Estas consideraciones brindan algunas ecuaciones sobre los coeficientes de  , en particular algunos de estos coeficientes se anulan, disminuyendo el número de variables a considerar. Una vez hecha esta reducción se determinan algunas soluciones de la ecuación
, en particular algunos de estos coeficientes se anulan, disminuyendo el número de variables a considerar. Una vez hecha esta reducción se determinan algunas soluciones de la ecuación 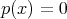 en términos de sus coeficientes, un problema difícil, pues el polinomio es general; en realidad estamos encontrando puntos sobre la superficie
en términos de sus coeficientes, un problema difícil, pues el polinomio es general; en realidad estamos encontrando puntos sobre la superficie 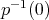 . Estas soluciones también satisfacen la ecuación
. Estas soluciones también satisfacen la ecuación 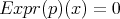 dada la condición de minimalidad, y esto nos brinda nuevas ecuaciones sobre los coeficientes de
dada la condición de minimalidad, y esto nos brinda nuevas ecuaciones sobre los coeficientes de 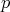 . Ahora se desea encontrar suficientes ecuaciones sobre estos coeficientes como para determinar el polinomio
. Ahora se desea encontrar suficientes ecuaciones sobre estos coeficientes como para determinar el polinomio 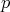 ó llegar a una contradicción con la existencia de dicho polinomio. Un paso clave en la demostración de este teorema fue utilizar el hecho de que la superficie no puede ser topológicamente un toro por el Teorema 1, y por lo tanto, las curvaturas principales deben anularse en algún punto [1].
ó llegar a una contradicción con la existencia de dicho polinomio. Un paso clave en la demostración de este teorema fue utilizar el hecho de que la superficie no puede ser topológicamente un toro por el Teorema 1, y por lo tanto, las curvaturas principales deben anularse en algún punto [1].
Resultado 3 [5]. Salvo un cambio de coordenadas, la única superficie mínima e inmersa en 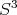 que es algebraica de orden 3, es la dada por el polinomio
que es algebraica de orden 3, es la dada por el polinomio 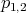 de la sección 1.4.
de la sección 1.4.
La demostración de este teorema es análoga a la anterior pero algunas ecuaciones sobre los coeficientes del polinomio 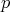 que determina la superficie mínima se hacen usando los siguientes dos lemas:
que determina la superficie mínima se hacen usando los siguientes dos lemas:
Lema 1 [5]. Si 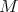 esta inmersa de manera mínima en
esta inmersa de manera mínima en 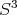 y para algún subespacio tres dimensional
y para algún subespacio tres dimensional 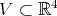 se tiene que
se tiene que  es una circunferencia de radio 1, entonces
es una circunferencia de radio 1, entonces 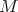 debe ser un ecuador.
debe ser un ecuador.
Lema 2 [5]. Todo polinomio de grado 3 en 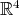 que satisface la condición de minimalidad debe anularse en un subespacio dos dimensional.
que satisface la condición de minimalidad debe anularse en un subespacio dos dimensional.
Resultado 4 [3]. Ninguno de los ejemplos de Lawson 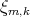 con suma de índices impar es algebraico. Aún más, no tienen simetría antipodal.
con suma de índices impar es algebraico. Aún más, no tienen simetría antipodal.
Para la demostración de este teorema se realizó una división de la esfera 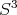 en subconjuntos que denominamos cuadrantes generalizados, y determinamos cuáles de estos cuadrantes eran ocupados por la superficie
en subconjuntos que denominamos cuadrantes generalizados, y determinamos cuáles de estos cuadrantes eran ocupados por la superficie 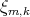 estudiando la acción del grupo
estudiando la acción del grupo 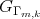 sobre esta familia de cuadrantes. Demostramos que en el caso en que
sobre esta familia de cuadrantes. Demostramos que en el caso en que  es impar, la superficie ocupaba un cuadrante, pero no el cuadrante antipodal, concluyendo así que la superficie no puede tener simetría antipodal.
es impar, la superficie ocupaba un cuadrante, pero no el cuadrante antipodal, concluyendo así que la superficie no puede tener simetría antipodal.
Resultado 5 [3]. Si 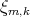 es una superficie algebraica regular, entonces
es una superficie algebraica regular, entonces 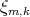 es de grado impar si y solo si
es de grado impar si y solo si 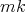 es par. En particular ninguno de los ejemplos de Lawson
es par. En particular ninguno de los ejemplos de Lawson 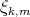 con
con 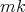 par, es algebraico de grado par.
par, es algebraico de grado par.
En el caso de que la superficie 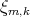 sea algebraica de grado par se concluye por el Resultado 1 que la superficie
sea algebraica de grado par se concluye por el Resultado 1 que la superficie 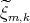 tiene característica de Euler par. Dado que la característica de Euler de
tiene característica de Euler par. Dado que la característica de Euler de 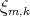 es
es 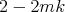 , entonces
, entonces 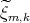 tiene característica de Euler
tiene característica de Euler 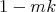 , y por lo tanto
, y por lo tanto 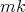 es impar. Análogamente el resultado se tiene cuando suponemos que
es impar. Análogamente el resultado se tiene cuando suponemos que 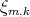 es de grado impar.
es de grado impar.
Resultado 6 [3]. Si la superficie 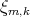 es algebraica de grado
es algebraica de grado 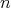 , entonces
, entonces 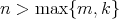 .
.
Note que si un polinomio en 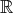 tiene muchas raíces, entonces su grado debe ser al menos igual al número de raíces; para la demostración de este resultado razonamos de manera análoga. Suponemos que existe un polinomio
tiene muchas raíces, entonces su grado debe ser al menos igual al número de raíces; para la demostración de este resultado razonamos de manera análoga. Suponemos que existe un polinomio 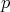 de grado
de grado 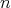 tal que
tal que 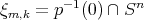 y demostramos que este polinomio se anula en un conjunto de planos, lo que permite una escritura del polinomio
y demostramos que este polinomio se anula en un conjunto de planos, lo que permite una escritura del polinomio 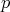 que da la condición buscada sobre el grado de
que da la condición buscada sobre el grado de 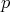 . Esto se deriva del siguiente lema:
. Esto se deriva del siguiente lema:
Lema 3 [3]. Sean  tales que para todo
tales que para todo 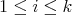 ,
, 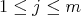 se tiene
se tiene 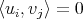 y para
y para 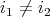 ,
, 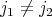 cada par de vectores
cada par de vectores 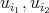 y
y 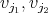 son linealmente independientes. Si
son linealmente independientes. Si 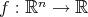 es un polinomio que se anula en los conjuntos
es un polinomio que se anula en los conjuntos 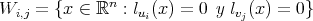 , entonces existen polinomios
, entonces existen polinomios  tales que
tales que 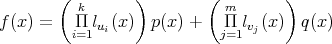 , donde
, donde 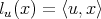 .
.
Resultado 7 [3]. Ninguno de los ejemplos de Lawson 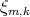 es algebraico de grado cuatro.
es algebraico de grado cuatro.
La demostración de este teorema se obtiene aplicando algunos de los resultados anteriores y usando algunas ideas de la demostración del Resultado 2. Note que el Resultado 6 implica que las únicas posibles superficies algebraicas de grado 4 son 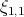 ,
, 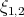 ,
, 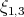 ,
, 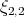 ,
, 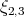 ,
, 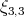 . El Resultado 5 garantiza que
. El Resultado 5 garantiza que 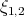 ,
, 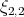 ,
, 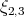 no lo son y
no lo son y 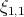 es el toro de Clifford. Para demostrar que
es el toro de Clifford. Para demostrar que 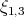 y
y 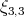 tampoco son algebraicas de grado 4, se supone la existencia de un polinomio homogéneo
tampoco son algebraicas de grado 4, se supone la existencia de un polinomio homogéneo 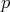 tal que satisface la condición de minimalidad y
tal que satisface la condición de minimalidad y 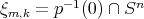 . Dado que se conocen algunos puntos de la superficie podemos encontrar ecuaciones para los coeficientes de
. Dado que se conocen algunos puntos de la superficie podemos encontrar ecuaciones para los coeficientes de 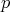 usando la ecuación
usando la ecuación 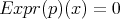 y así se llega a una contradicción.
y así se llega a una contradicción.
[1] Lawson, H. Complete minimal surfaces in 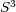 . Ann. of Math. (2) 92 1970 335-374. [ Links ]
. Ann. of Math. (2) 92 1970 335-374. [ Links ]
[2] Munzner, H. Isoparametrische Hyperflachen in Spharen (geometrischer Teil), Math. Ann. 251, (1980) pp 57-71. [ Links ]
[3] Mesa, H. Superficies mínimas algebraicas de grado cuatro en 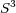 . Tesis de Maestría, Universidad del Valle, 2005. [ Links ]
. Tesis de Maestría, Universidad del Valle, 2005. [ Links ]
[4] Perdomo, O. Non-existence of regular algebraic surfaces of spheres of degree 3. Aceptado para publicación en The Journal of Geometry. [ Links ]
[5] Perdomo, O. Characterization of minimal algebraic surfaces of the sphere with degree 3. En preparación. [ Links ]
[6] Perdomo, O. nonembeddability of the Klein bottle in 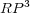 and Lawson's conjecture. Rev. Acad. Colombiana Cienc. Exact. Fís. Natur. 29 (2005), no. 110, 149-154. [ Links ]
and Lawson's conjecture. Rev. Acad. Colombiana Cienc. Exact. Fís. Natur. 29 (2005), no. 110, 149-154. [ Links ]
[7] Solomon, B. The harmonic analisys of cubic isoparametric minimal hypersurfaces I: dimensions 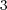 and
and 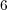 . Amer. J. Math. 112 (1990), no. 2, 157-203
. Amer. J. Math. 112 (1990), no. 2, 157-203
Oscar Mario Perdomo
Universidad del Valle,
Cali - Colombia
iosperdom@univalle.edu.co
Héber Mesa P.
Universidad del Valle,
Cali - Colombia
hebermes@univalle.edu.co
Recibido: 26 de enero de 2006
Aceptado: 7 de agosto de 2006