Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.47 n.2 Bahía Blanca jul./dic. 2006
Einstein metrics on flag manifolds
Evandro C. F. dos Santos* and Caio J. C. Negreiros**
*Partially supported by FUNCAP
**Partialy supported by CNPq grant 303695/2005-6 and Fapesp grant 02/10246-2
Abstract: In this survey we describe new invariant Einstein metrics on flag manifolds. Following closely San Martin-Negreiros's paper [26] we state results relating Kähler, (1,2)-symplectic and Einstein structures on flags. For the proofs see [11] and [10].
2000 Mathematics Subject Classification. 53C55; 58D17; 53C25; 22F30.
Key words and phrases. Flag manifolds, Einstein metrics, Semi-simple Lie groups.
We recall that a Riemannian metric  on a manifold
on a manifold 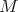 is called Einstein if
is called Einstein if 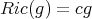 for some constant
for some constant  . As we know Einstein metrics form a special class of metrics on a given manifold (see [4]). In this note we announce properties of these metrics and new examples of Einstein metrics on flag manifolds as described in [11] and [10].
. As we know Einstein metrics form a special class of metrics on a given manifold (see [4]). In this note we announce properties of these metrics and new examples of Einstein metrics on flag manifolds as described in [11] and [10].
With this purpose in mind, we consider  as being a complex semi-simple Lie algebra and
as being a complex semi-simple Lie algebra and  a simple root system for
a simple root system for  . If
. If 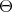 is an arbitrary subset of
is an arbitrary subset of  ,
,  denotes the roots spanned by
denotes the roots spanned by  . We have
. We have
| | (1) |
where  is a Cartan subalgebra of
is a Cartan subalgebra of  and
and  is the root space associated to the root
is the root space associated to the root  . Let
. Let
|
| (2) |
the canonical parabolic subalgebra determined by  . Hence
. Hence
|
| (3) |
 is called a flag manifold, where
is called a flag manifold, where  has the Lie algebra
has the Lie algebra  and
and 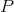 is the normalizer of
is the normalizer of 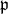 in
in 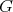 . Each manifold
. Each manifold  has a very rich complex geometry, containing families of invariant Hermitian structures denoted by
has a very rich complex geometry, containing families of invariant Hermitian structures denoted by  .
.
The case  for
for  , i.e., the full flag manifold is nowadays well understood. Starting with the work of Borel (cf. [7]), the classification of all invariant Hermitian structures is known and it was derived in [26].
, i.e., the full flag manifold is nowadays well understood. Starting with the work of Borel (cf. [7]), the classification of all invariant Hermitian structures is known and it was derived in [26].
On the other hand, the case  for
for 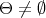 is much less known so far. Some partial results are derived in [27] and [28].
is much less known so far. Some partial results are derived in [27] and [28].
We now describe the contents of this survey. In the first two sections we discuss all the invariant Hermitian structures on  and the associated Einstein system of equations. In Section 3 we present new invariant Einstein metrics on generalized flag manifolds of type
and the associated Einstein system of equations. In Section 3 we present new invariant Einstein metrics on generalized flag manifolds of type  We suggest Besse's book [4] as a reference for Einstein manifolds.
We suggest Besse's book [4] as a reference for Einstein manifolds.
In Section 4 we state the classification of all invariant Einstein metrics on 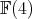 and state some partial results relating Kähler, (1,2)-symplectic and Einstein structures on
and state some partial results relating Kähler, (1,2)-symplectic and Einstein structures on  .
.
For a very stimulating article see [1].
All manifolds and maps between them will be assumed to be  in this survey.
in this survey.
We would like to thank to FAEP-UNICAMP and FAPESP (grant 02/10246-2) for the financial support.
1. General results on the invariant Hermitian geometry of flag manifolds
We denote by  the Cartan-Killing form of
the Cartan-Killing form of 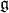 , and we fix a Weyl basis
, and we fix a Weyl basis  for
for  . We define the compact real form of
. We define the compact real form of  , as the real subalgebra
, as the real subalgebra
|
|
where  and
and  .
.
Let  be the origin of
be the origin of  .
.  is identified with
is identified with
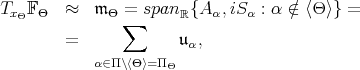
where 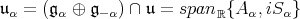 . Complexifying
. Complexifying 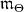 we obtain
we obtain  , which can be identified with
, which can be identified with
|
| (4) |
A  -invariant almost complex structure
-invariant almost complex structure  on
on 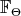 , is completely determined by a collection of numbers
, is completely determined by a collection of numbers  ,
,  .
.
A  -invariant Riemannian metric
-invariant Riemannian metric  on
on  is completely characterized by the following inner product
is completely characterized by the following inner product  on
on 
|
| (5) |
where  is definite-positive with respect to the Cartan-Killing form. On each irreducible component of
is definite-positive with respect to the Cartan-Killing form. On each irreducible component of  ,
, 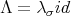 with
with  .
.
Consider 
 the conjugation of
the conjugation of  relatively to
relatively to 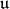 . Hence,
. Hence,  is a Hermitian form on
is a Hermitian form on 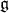 , that originates a
, that originates a  -invariant Hermitian form on
-invariant Hermitian form on  .
.
If 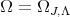 denotes the corresponding Kähler form then
denotes the corresponding Kähler form then
|
| (6) |
We recall that a almost-Hermitian manifold is said  -symplectic if
-symplectic if  when one of the vectors
when one of the vectors  ,
, 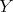 ,
,  is of type
is of type  , and the other two are of type
, and the other two are of type  . If
. If  is integrable and
is integrable and  , we say
, we say  is a Kähler manifold.
is a Kähler manifold.
2. Ricci tensor and the Einstein system of equations
We now consider  a
a  -orthogonal basis adapted to a decomposition of
-orthogonal basis adapted to a decomposition of  In other words,
In other words,  for some
for some  and
and  if
if  with
with  Define, as in [29],
Define, as in [29],
|
| (7) |
that is,
|
| (8) |
where in the second equation we take all indices  with
with  Notice that
Notice that ![[ ] k i j](/img/revistas/ruma/v47n2/2a07103x.png) is independent of orthonormal frame chosen for
is independent of orthonormal frame chosen for  and
and ![∑ [eα,eβ ] = γ A γαβ](/img/revistas/ruma/v47n2/2a07105x.png)

![[ k ] i j =](/img/revistas/ruma/v47n2/2a07107x.png)
![[ k ] [ j ] j i = k i](/img/revistas/ruma/v47n2/2a07108x.png)
Furthermore, if  is an element of Weyl´s group then
is an element of Weyl´s group then
|
| (9) |
The following result is due to Wang-Ziller [29] (see also [2]):
Lemma 2.1. The components  of the Ricci tensor of an
of the Ricci tensor of an 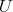 -invariant metric on
-invariant metric on  are given by:
are given by:
|
| (10) |
where 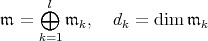 .
.
More generally, Arvanitoyeorgos proved in [3] the following result
Proposition 2.2. The Ricci tensor of an invariant metric  on a flag manifold
on a flag manifold  is given by
is given by

We have the following non-homogeneous version of this equation

With each solution we associate the Einstein constant, which is defined as the value of the Ricci tensor  when
when  is re-normalized to have unit volume.
is re-normalized to have unit volume.
Using the Einstein system of equations described above, we describe now the known and new Einstein metrics on 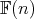 as in [11] and [10].
as in [11] and [10].
a) The normal metric. We notice this metric is not Kähler.
b) Kähler-Einstein metrics
On the flag manifold  (
( , up to permutation there is a unique integrable structure
, up to permutation there is a unique integrable structure  , and associated with it a unique (up to scaling) Kähler-Einstein metric (which corresponds to the choice
, and associated with it a unique (up to scaling) Kähler-Einstein metric (which corresponds to the choice  according to Matsushima [19] or [4]):
according to Matsushima [19] or [4]):

Thus, counting in the symmetry of this metric, we have 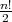 Kähler-Einstein metrics on
Kähler-Einstein metrics on  .
.
c) The Arvanitoyeorgos metrics
Arvanitoyeorgos ([3]) considers for all ![s ∈ [1,n]](/img/revistas/ruma/v47n2/2a07130x.png) metrics in
metrics in  (
( ) satisfying
) satisfying
 (
(  ),
),  otherwise
otherwise
The Einstein system is reduced to the equations in 
 whose solution is
whose solution is  and
and  . Counting permutations, we get
. Counting permutations, we get  Arvanitoyeorgos metrics whose Einstein constant is seen to be
Arvanitoyeorgos metrics whose Einstein constant is seen to be

d) The Sakane-Senda metrics
Sakane and Senda in [25] consider metrics in  (
( ) satisfying
) satisfying
 (
(  or
or  ),
),  otherwise
otherwise
Again, the the Einstein system is reduced to two equations in 
 whose solution is
whose solution is  and
and  .
.
e) A new family
If  we find another solution in
we find another solution in  , for
, for  and
and  .
.
f) Two new families
On  (
(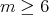 ) we consider
) we consider
 (
( 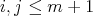 or
or  ),
), 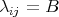 otherwise
otherwise
There are two families as solution of the Einstein system. The Einstein constants for these two families are, respectively,

g) A new metric
Still assuming the same pattern, with  , we find on
, we find on 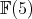 the invariant Einstein metric with
the invariant Einstein metric with  and
and  . The Einstein constant of this metric is
. The Einstein constant of this metric is 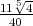 .
.
We define the class 
 .
.
A complete classification of the Einstein metrics for 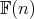
 is completely unknown. It is not even know if the number of such metrics is finite (the Bohn-Wang-Ziller conjecture).
is completely unknown. It is not even know if the number of such metrics is finite (the Bohn-Wang-Ziller conjecture).
In [11] and [10] we use the procedure described above in order to obtain new Einstein metrics on non-maximal A -type manifolds. Our notation will be
-type manifolds. Our notation will be  where
where  represents block-matrices of size
represents block-matrices of size 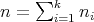 . All the entries in each block are equal, so that the metric is completely expressed by a reduced
. All the entries in each block are equal, so that the metric is completely expressed by a reduced 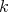

 matrix, which we denote by
matrix, which we denote by  .
.
Theorem 3.1. a) On  The set of restrictions
The set of restrictions  produce two invariant non-Kähler Einstein. On the other hand the restrictions
produce two invariant non-Kähler Einstein. On the other hand the restrictions 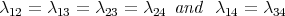 do not produce any solution.
do not produce any solution.
b) On  i.e.
i.e.  (
( ) we look for a
) we look for a 

 reduced matrix
reduced matrix 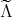 with
with
 (
( ),
),  otherwise
otherwise
In this way we can produce two non-Kähler Einstein metrics.
c) On  with
with  the invariant metric represented by the
the invariant metric represented by the 

 matrix
matrix 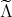 is Einstein if, and only if, the same matrix represents an Einstein metric on
is Einstein if, and only if, the same matrix represents an Einstein metric on  .
.
4. Results on the classification of Einstein metrics on 
Gray and Hervella in [13] gave a complete classification of triples  into sixteen classes for arbitrary almost Hermitian manifolds. San Martin-Negreiros discussed in [26] the case where
into sixteen classes for arbitrary almost Hermitian manifolds. San Martin-Negreiros discussed in [26] the case where  is a maximal flag manifold. They have proved that the invariant almost Hermitian structures on maximal flag manifolds can be divided only in three classes, namely
is a maximal flag manifold. They have proved that the invariant almost Hermitian structures on maximal flag manifolds can be divided only in three classes, namely


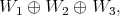 where the class
where the class  contains any invariant almost Hermitian structures.
contains any invariant almost Hermitian structures.
In [26] it is proved that an invariant pair 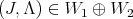 if and only if for all
if and only if for all  -triple of roots
-triple of roots 
|
| (11) |
The next lemma characterizes the Hermitian structures belonging to  (see [26]) for more details.
(see [26]) for more details.
Lemma 4.1. A necessary and sufficient condition for an invariant pair  to be in
to be in  is
is  -triple
-triple  .
.
In [11] or [10] the following result is proved:
Theorem 4.2. If 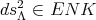 for
for  , then this metric belongs to
, then this metric belongs to  .
.
This result leads us to conjecture that any invariant Einstein non-Kähler metric on  is in
is in  . One result supporting this conjecture is
. One result supporting this conjecture is
Theorem 4.3. The space  admits (up to scaling) precisely 3 classes of invariant Einstein metrics: The Kähler-Einstein [7], the 4 Arvanitoyeorgos's class [3], and the class of the normal metric [30].
admits (up to scaling) precisely 3 classes of invariant Einstein metrics: The Kähler-Einstein [7], the 4 Arvanitoyeorgos's class [3], and the class of the normal metric [30].
[1] V. I. Arnold, Symplectization, Complexification and Mathematical Trinities, Fields Institute Communications, 24 (1999), 23-36. [ Links ]
[2] A. Arvanitoyeorgos, Invariant Einstein metrics on generalized flag manifolds, PhD thesis, Rochester University,1991. [ Links ]
[3] A. Arvanitoyeorgos, New invariant Einstein metrics on generalized flag manifolds, Trans. Amer. math.Soc., 337(1993), 981-995. [ Links ]
[4] A. Besse, Einstein Manifolds, Springer Verlag, 1987 [ Links ]
[5] C. Böhm, M. Wang and W. Ziller, A variational approach for compact homogeneous Einstein manifolds, Geometric and Functional Analysis 4 Vol.14, (2004) 681-733. [ Links ]
[6] M. Bordemann, M. Forger and H. Romer, Homogeneous Kähler manifolds:Paving the way towards supersymmetric sigma-models, Commun. Math. Physics,102, (1986), 605-647. [ Links ]
[7] A. Borel, Kählerian coset spaces of semi-simple Lie groups, Proc. Nat. Acad. Sci. USA 40 (1954), 1147-1151. [ Links ]
[8] É. Cartan, Sur les domaines bornés homogènes de l'espace des n variables complexes, Abhandl. Math. Sem. Hamburg, 11 (1935), 116-162 [ Links ]
[9] N. Cohen, C. J. C. Negreiros, M. Paredes, S. Pinzón, L. A. B. San Martin, f-structures on the classical flag manifold which admit (1,2)-symplectic metrics. Tôhoku Math. J. 57(2) (2005), 262-271. [ Links ]
[10] N. Cohen, E. C. F. dos Santos and C. J. C. Negreiros, Properties of Einstein metrics on flag manifolds, Preprint. State University of Campinas, 2005. [ Links ]
[11] Evandro C. F. dos Santos,Métricas de Einstein em varedades bandeira, PhD thesis. State University of Campinas, 2005. [ Links ]
[12] Evandro C. F. dos Santos, Caio J. C. Negreiros and Sofia Pinzòn, (1,2)-symplectic submanifols of a flag manifold, Preprint. State University of Campinas, 2005. [ Links ]
[13] A. Gray and L. M. Hervella, The sixteen classes of almost Hermitian manifolds and their linear invariants, Ann. Mat. Pura Appl. 123 (1980), 35-58. [ Links ]
[14] M.A.Guest, Geometry of maps between generalized flag manifolds, J. Differential Geometry, 25 (1987), 223-247 [ Links ]
[15] S. Helgason, Differential Geometry, Lie Groups and Symmetric Spaces, Academic Press, 1978. [ Links ]
[16] D.Hilbert, Die Grundlagen der Physik,Nachr. Akad. Wiss. Gött. 395-407 (1915). Reprinted in Math. Ann., 92 (1924),1-32. [ Links ]
[17] M. Kimura, Homogeneous Einstein Metrics on Certain Kähler C-spaces, Advanced Studies in Pure Mathematics. 18-I, 1990. Recent topics in Differential and analytic Geometry (1986), 303-320. [ Links ]
[18] S. Kobayashi and K. Nomizu, Foundations of differential geometry, Interscience Publishers, vol.2 (1969). [ Links ]
[19] Y. Matsushima, Remarks on Kähler-Einstein Manifolds, Nagoya Math. Journal 46, (1972), 161-173. [ Links ]
[20] J. Milnor, Curvatures of left invariant metrics on Lie groups, Adv. in Mathematics 21, (1976), 293-329. [ Links ]
[21] X. Mo and C. J. C. Negreiros, (1,2)-Symplectic structures on flag manifolds, Tohoku Math. J. 52 (2000), 271-282. [ Links ]
[22] Y. Mutö, On Einstein metrics, Journal of Differential geometry, 9 (1974), 521-530. [ Links ]
[23] M. Paredes, Aspectos da geometria complexa das variedades bandeira, Tese de Doutorado, Universidade Estadual de Campinas,2000. [ Links ]
[24] S. Pinzòn, Variedades bandeira,estruturas-f e mètricas (1,2)-simplèticas, Tese de Doutorado, Universidade Estadual de Campinas, 2003. [ Links ]
[25] Y. Sakane, Homogeneous Einstein metrics on flag manifolds, Lobatchevskii Journal of Mathematics, vol.4, (1999), 71-87. [ Links ]
[26] Luiz A. B. San Martin and Caio J. C. Negreiros, Invariant almost Hermitian structures on flag manifolds, Advances in Math., 178 (2003), 277-310. [ Links ]
[27] Luiz. A. B. San Martin and Rita. C. J. Silva, Invariant nearly-Kähler structures, preprint, State University of Campinas (2003). [ Links ]
[28] Rita de Cássia de J. Silva, Estruturas quase Hermitianas invariantes em espaços homogêneos de grupos semi-simples, Ph.D. thesis, State University of Campinas, 2003. [ Links ]
[29] M. Wang and W. Ziller, Existence and Non-Existence of Homogeneous Einstein Metrics, Invent. math., 84, (1986), 177-194. [ Links ]
[30] M. Wang and W. Ziller, On normal homogeneous Einstein metrics, Ann. Sci. Ecole norm. Sup.18 (1985), 563-633. [ Links ]
Evandro C. F. dos Santos
Department of Mathematics
Universidade Regional do Cariri
Av. Leão Sampaio s/n Km 4
Juazeiro do Norte-Ce
Cep 63040-000 - Brazil
evandrocfsantos@gmail.com
Caio J. C. Negreiros
Departament of Mathematics - IMECC - Unicamp
PO Box 6065 - Campinas - Brazil
caione@ime.unicamp.br
Recibido: 20 de octubre de 2005
Aceptado: 15 de noviembre de 2006













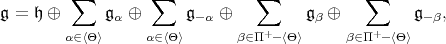





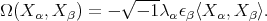
![γ A αβ = ([eα,eβ],eγ),](/img/revistas/ruma/v47n2/2a0799x.png)
![[ k ] ∑ γ 2 i j (A αβ) =](/img/revistas/ruma/v47n2/2a07100x.png)
![[ w (γ) ] [ γ ] w(α) w (β) = α β](/img/revistas/ruma/v47n2/2a07110x.png)
![∑l [ k ] ∑l [ j ] r = -1--+ -1-- -λk-- i j - --1- -λk-- k i (k = 1,⋅⋅⋅ ,l), k 2λk 4dk λiλj 2dk λiλj i,j=1 i,j=1](/img/revistas/ruma/v47n2/2a07114x.png)


