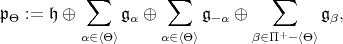Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.47 n.2 Bahía Blanca jul./dic. 2006
Stability of holomorphic-horizontal maps and Einstein metrics on flag manifolds
Caio J. C. Negreiros
Partialy supported by CNPq grant 303695/2005-6 and Fapesp grant 02/10246-2
Abstract: In this note we announce several results concerning the stability of certain families of harmonic maps that we call holomorphic-horizontal frames, with respect to families of invariant Hermitian structures on flag manifolds. Special emphasis is given to the Einstein case. See [23] for additional detail and the proofs of the results mentioned in this survey.
Let  be a complex semi-simple Lie algebra and
be a complex semi-simple Lie algebra and  a simple root system for
a simple root system for  . If
. If  is an arbitrary subset of
is an arbitrary subset of  ,
,  denotes the roots spanned by
denotes the roots spanned by  . We have
. We have
|
| (1) |
where  is a Cartan subalgebra of
is a Cartan subalgebra of  and,
and,  is the root space associated to the root
is the root space associated to the root  .
.
Let
|
| (2) |
the canonical parabolic subalgebra determined by 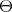 . Thus,
. Thus,
|
| (3) |
The flag manifold is defined as  , where
, where 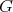 has Lie algebra
has Lie algebra 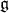 and
and  is the normalizer of
is the normalizer of  in
in 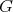 .
.
 for
for 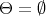 , is called the full flag manifold and is denoted by
, is called the full flag manifold and is denoted by  . This case is nowadays well understood. Starting with the work of Borel (cf. [3]), the classification of all invariant Hermitian structures is known and it was described in [25].
. This case is nowadays well understood. Starting with the work of Borel (cf. [3]), the classification of all invariant Hermitian structures is known and it was described in [25].
The main purpose for this note is to announce some results discussing the stability phenomenon for the energy functional for to a special class of maps 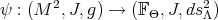 , called holomorphic-horizontal frames. The energy functional is taken with respect to several families of invariant Hermitian structures on
, called holomorphic-horizontal frames. The energy functional is taken with respect to several families of invariant Hermitian structures on 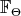 . These maps are deeply connected with the study of harmonic/minimal surfaces in
. These maps are deeply connected with the study of harmonic/minimal surfaces in 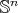 ,
,  ,
, 
 , Twistor Theory and so on (cf. [27], [8], [4], [15]).
, Twistor Theory and so on (cf. [27], [8], [4], [15]).
The layout of the paper is as follows. In the first two sections, we state general results on the invariant Hermitian geometry of  , and state the holomorphic and harmonic map equations. We give in this note, examples of families holomorphic-horizontal frames only in the
, and state the holomorphic and harmonic map equations. We give in this note, examples of families holomorphic-horizontal frames only in the  case, but in [23] we also discuss the cases
case, but in [23] we also discuss the cases  ,
,  and
and  .
.
We generalize and give additional results to the approach initiated by Black in [2] and the author in [21]. As a reference for harmonic maps theory we suggest the Eells-Lemaire [14] article.
In Section 3 we compute the second variation of energy for an arbitrary harmonic map on  . We state a basic perturbation lemma and a result for holomorphic-horizontal frames on
. We state a basic perturbation lemma and a result for holomorphic-horizontal frames on  .
.
According to the classification results in [25], among all Hermitian invariant structures there are two main classes. Thus, in the last section we state results concerning the stability of holomorphic-horizontal frames regarding metrics in such classes and in particular, the case of metrics that are Einstein and non Kähler on the geometrical flag manifold 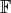 .
.
2. Generalities on invariant Hermitian geometry of flag manifolds
Let  be a root system and
be a root system and  a simple root system for a simple Lie algebra
a simple root system for a simple Lie algebra  . If
. If 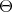 is a subset of
is a subset of  ,
,  denotes the roots generated by
denotes the roots generated by  . We have the root decomposition :
. We have the root decomposition :

where  is a Cartan subalgebra of
is a Cartan subalgebra of 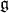 and
and 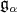 is the root space associated to the root
is the root space associated to the root  .
.
Let
|
| (6) |
The space  is called a flag manifold, where
is called a flag manifold, where  and
and  are the Lie algebras of
are the Lie algebras of  and
and  , respectively.
, respectively.
Each manifold  has families of complex geometries, i.e., families of invariant Hermitian structures denoted by
has families of complex geometries, i.e., families of invariant Hermitian structures denoted by  .
.
We denote by 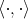 the Cartan-Killing form of
the Cartan-Killing form of  , and fix once and for all a Weyl basis of
, and fix once and for all a Weyl basis of  , which amounts to take
, which amounts to take 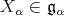 such that
such that  , and
, and ![[X α,X β] = m α,βX α+β](/img/revistas/ruma/v47n2/2a0863x.png) with
with  ,
,  , and
, and  if
if  is not a root.
is not a root.
We define the compact real form of 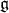 , as the real subalgebra
, as the real subalgebra
|
|
where  and
and  .
.
Let  be the origin of
be the origin of  .
.  is identified with
is identified with

where  . Complexifying
. Complexifying  we obtain
we obtain  , which can be identified with
, which can be identified with
|
|
We denote the irreducible components of 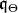 as
as  , where
, where  is the set of roots
is the set of roots  with
with  , thus
, thus  .
.
Let  be the collection of sets
be the collection of sets  originating the irreducible components. We write
originating the irreducible components. We write
|
|
Each  defines a field of complex subspaces
defines a field of complex subspaces  such that
such that  for each
for each  .
.
A  -invariant almost complex structure
-invariant almost complex structure  on
on 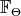 is completely determined by a linear map
is completely determined by a linear map  . The map
. The map 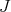 satisfies
satisfies 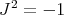 and commutes with the adjoint action of
and commutes with the adjoint action of  on
on 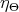 . We denote also by
. We denote also by 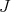 its complexification to
its complexification to  .
.
The invariance of  entails that
entails that  for all
for all  . The eigenvalues of
. The eigenvalues of 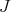 are
are  , and the eigenvectors in
, and the eigenvectors in  are
are 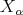 ,
,  . Hence, in each irreducible component
. Hence, in each irreducible component  ,
,  with
with  satisfying
satisfying  . A
. A  -invariant almost complex structure on
-invariant almost complex structure on  is completely determined by the numbers
is completely determined by the numbers  ,
,  .
.
A  -invariant Riemannian metric
-invariant Riemannian metric  on
on  is completely determined by the following inner product
is completely determined by the following inner product  on
on 
|
| (7) |
with  definite-positive with respect to the Cartan-Killing form. On each irreducible component of
definite-positive with respect to the Cartan-Killing form. On each irreducible component of  ,
, 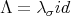 with
with 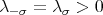 .
.
Consider  the conjugation of
the conjugation of  relatively to
relatively to  . Hence,
. Hence, 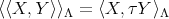 is a Hermitian form on
is a Hermitian form on  , that originates a
, that originates a  -invariant Hermitian form on
-invariant Hermitian form on  .
.
If 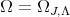 denotes the corresponding Kähler form then
denotes the corresponding Kähler form then
|
| (8) |
We recall that an almost-Hermitian manifold is said  -symplectic if
-symplectic if 
 when one of the vectors
when one of the vectors 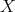 ,
, 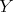 ,
,  is of type
is of type  , and the other two are of type
, and the other two are of type  . If
. If  is integrable and
is integrable and  , we say
, we say  is a Kähler manifold.
is a Kähler manifold.
From now on, for abuse of notation we will denote a map  by
by  where
where  , despite
, despite  and
and  being completely different objects.
being completely different objects.
Black for the cases  ,
,  and
and  (see [2]) and the author in the case
(see [2]) and the author in the case 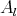 (see ([21]), obtained the Cauchy-Riemann equations in our situation:
(see ([21]), obtained the Cauchy-Riemann equations in our situation:
Proposition 3.1. A map  is
is  -holomorphic on
-holomorphic on  if and only if for every
if and only if for every  ,
, 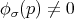 implies
implies  .
.
We define the energy of  as:
as:

To deduce the harmonic map equations, a basic remark is that


 , for any perturbations
, for any perturbations
 . In fact, every map
. In fact, every map  :
:  satisfies
satisfies



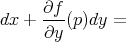
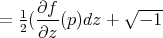

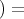


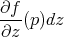 .
.
We now consider the map  :
:  .
. 
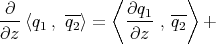




 . According to Stokes' Theorem we have
. According to Stokes' Theorem we have
 . Thus,
. Thus,


 .
.
We now perturb the map 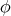 in the following natural way
in the following natural way

We are considering here the natural action of  on
on  and taking an arbitrary
and taking an arbitrary  map
map  .
.
In [23] we deduce the following Euler-Lagrange equations for our variational problem
Proposition 3.2. A map  is harmonic if and only if
is harmonic if and only if  if and only if
if and only if
|
| (9) |
We will use a generalization of  to an
to an  -structure following Yano ([29]). An
-structure following Yano ([29]). An  -structure
-structure 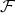 on
on  is a section of
is a section of  such that
such that  .
.
An invariant  -structure is given by the matrix
-structure is given by the matrix  with
with  ,
,  or
or  , according to the eigenvalues of
, according to the eigenvalues of 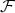 .
.
We now state the Cauchy-Riemann equations in the case of  -structures
-structures
Proposition 3.3. A map  is
is  -holomorphic if and only if it is subordinate to
-holomorphic if and only if it is subordinate to  .
.
Definition 3.1. Consider an invariant 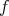 -structure
-structure on
on  . Let
. Let
|
|
and
|
|
 is said horizontal if
is said horizontal if ![[F ,F ] ⊂ 𝔭 + - Θ](/img/revistas/ruma/v47n2/2a08228x.png) .
.
The following theorem due to Black ([2]) is essential in our study
Theorem 3.4. Let 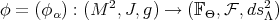 be subordinate to a horizontal
be subordinate to a horizontal  -structure
-structure  . Then
. Then  is equi-harmonic.
is equi-harmonic.
Consider now  . We can prove that
. We can prove that  is a horizontal
is a horizontal  -structure, and we will call it by
-structure, and we will call it by  -structure associated to
-structure associated to  .
.
We will now exhibit families of equi-harmonic and holomorphic maps 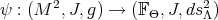 subordinate to an horizontal
subordinate to an horizontal  -structure, thus all of them are equi-harmonic according to Theorem 3.4. Any map in these families, is called a holomorphic and horizontal frame.
-structure, thus all of them are equi-harmonic according to Theorem 3.4. Any map in these families, is called a holomorphic and horizontal frame.
Let 
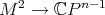 be a holomorphic and non-degenerate map. We consider its associate curve
be a holomorphic and non-degenerate map. We consider its associate curve  , where
, where  and
and  .
.
We define the map  . We can prove that
. We can prove that 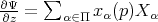 , with
, with  if
if  , where
, where 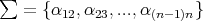 denotes a simple root system for
denotes a simple root system for  .
.
We can prove that any such map 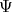 is holomorphic and subordinate to
is holomorphic and subordinate to 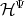 , thus, again according to Theorem 3.4, it is an equi-harmonic map.
, thus, again according to Theorem 3.4, it is an equi-harmonic map.
More generally, we will now construct families of holomorphic and equi-harmonic maps  .
.
Let 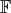 be the geometric flag manifold
be the geometric flag manifold 
 , where
, where  ,
,  and
and  .
.
A root system of height one with respect to  , is given by:
, is given by:

Let  any holomorphic and nondegenerate map, and
any holomorphic and nondegenerate map, and  as we have defined above.
as we have defined above.
We define the map  by:
by:  .
.
We prove in [23] that any such 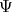 is a holomorphic-horizontal frame.
is a holomorphic-horizontal frame.
4. The second variation of energy and stability on 
We compute now the second variation of the energy in our situation.
Theorem 4.1. Consider a harmonic map  .
.
Thus,
![( ∫ ⟨[ ] ⟩ ) d2 || ( q(p), ∂q(p) , ∂φ(p) + --2|| E(φt) = IφΛ(q) = Re ( M ⟨[ ∂∂qz ] ∂∂φz ⟩ Λ ) (10 ) dt t=0 + q(p),∂z(p) ,∂z(p) Vg ( ∫ ⟨ ⟩ ) Λ + 1-Re ∂q-(p), ∂q-(p) νg (11 ) 2 M ∂z ∂z Λ 1 ( ∫ ⟨ ∂q ∂q ⟩ ) + 2-Re ∂z-(p),∂z-(p) νg (12 ) ( ∫ M⟨ [ ] Λ ⟩ ) M ( q(p ), ∂∂qz(p) , ∂∂φz(p) + = Re ( ⟨[ ∂q ] ∂φ ⟩ Λ ) , (13 ) + q(p),∂z(p) ,∂z(p) Λ )υg 1 ∑ ∫ + --Re( λα(⟨qα(p),qα (p)⟩ + ⟨q- α(p),q- α(p)⟩)υg) (14 ) 2 α∈Π M](/img/revistas/ruma/v47n2/2a08269x.png)
where the map  is defined by
is defined by 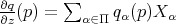 .
.
Definition 4.1. A harmonic map  is said stable if
is said stable if 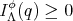 , for any variation
, for any variation  . Otherwise,
. Otherwise,  is said unstable.
is said unstable.
The following Theorem due to Lichnerowicz ([19]) is fundamental in our study of stability on flags.
Theorem 4.2. Let  be a
be a  -holomorphic map and
-holomorphic map and 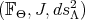 a Kähler structure. Then
a Kähler structure. Then  is stable.
is stable.
Definition 4.2. We say that  is a
is a  -perturbation of
-perturbation of  subordinate to
subordinate to 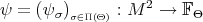 if
if
-
 ;
; -
 if
if 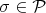 ;
; -
 ,
,  if
if 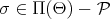 ;
; -
 if
if  .
.
Regarding the families of the holomorphic and horizontal frames we have just defined, we can simply consider  .
.
Using the above definition of perturbation we derive the following basic lemma.
Lemma 4.3. Let 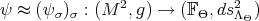 a holomorphic and horizontal frame. Then,
a holomorphic and horizontal frame. Then,

According to Gray-Hervella ([16]) the almost Hermitian structures can be decomposed into four irreducible components. For instance,  corresponds to Kähler metrics,
corresponds to Kähler metrics,  to the
to the  -symplectic ones and, so on. See [25] and [26].
-symplectic ones and, so on. See [25] and [26].
Lemma 4.4. A necessary and sufficient condition for 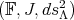 to be in
to be in  is:
is: 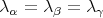 if
if  is a
is a  -triple.
-triple.
As an immediate consequence of this lemma we notice that the Cartan-Killing structure is in  . We will now consider perturbations of the Cartan-Killing structure.
. We will now consider perturbations of the Cartan-Killing structure.
We consider a  and denote by
and denote by  the subset of roots
the subset of roots  such that there exists a
such that there exists a 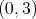 -triple
-triple  .
.
Let  given by
given by  for each
for each  , and
, and 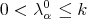 otherwise. According to Lemma 4.4,
otherwise. According to Lemma 4.4, 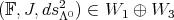 . We can prove the following theorem.
. We can prove the following theorem.
Theorem 4.5. Let 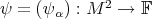 be an arbitrary holomorphic-horizontal frame. Then,
be an arbitrary holomorphic-horizontal frame. Then,  is unstable.
is unstable.
According to the results obtained in [25], among all the invariant Hermitian structures, the main cases are  and
and  . We will now discuss the stability phenomenon of holomorphic-horizontal frames in these two main classes.
. We will now discuss the stability phenomenon of holomorphic-horizontal frames in these two main classes.
Based on a crucial result derived in [25] we present the following definition.
Definition 5.1. Let  ,
,  and
and  . We fix a Kähler structure
. We fix a Kähler structure  . The metric
. The metric  is said a perturbation of type (1,2)-symplectic of
is said a perturbation of type (1,2)-symplectic of 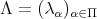 if
if
- for each
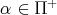 with
with 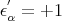 and,
and,  we have
we have  .
. - for each
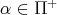 with
with  and if
and if  , where
, where  is the highest root, and each
is the highest root, and each 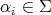 , then
, then  .
.
We now are ready to discuss the  case. We consider
case. We consider  equipped with an invariant Hermitian structure that comes from a perturbation of type (1,2)-symplectic of a Kähler structure
equipped with an invariant Hermitian structure that comes from a perturbation of type (1,2)-symplectic of a Kähler structure  . Thus, in [23] we prove
. Thus, in [23] we prove
Theorem 5.1. Let 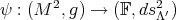 be a holomorphic-horizontal frame. Then
be a holomorphic-horizontal frame. Then  is stable.
is stable.
We will now concentrate our attention on the family of invariant Hermitian structures on  that are in
that are in  . We begin our discussion mentioning the classification of Einstein metrics on
. We begin our discussion mentioning the classification of Einstein metrics on  and
and  derived in [17] and [22], exploiting these results and obtaining (see [23])
derived in [17] and [22], exploiting these results and obtaining (see [23])
Theorem 5.2. Let  a holomorphic and horizontal frame with
a holomorphic and horizontal frame with  or
or  and
and  a Einstein and non-Kähler metric. Then, the map
a Einstein and non-Kähler metric. Then, the map 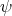 is unstable.
is unstable.
A basic result due to Arvanitoyeorgos [1] and Kimura [17] is the following one.
Theorem 5.3. The space  for
for  admits as Einstein metrics only the normal and the Kähler-Einstein metrics. If
admits as Einstein metrics only the normal and the Kähler-Einstein metrics. If  it admits at least
it admits at least  Einstein metrics. The
Einstein metrics. The  metrics are the already mentioned Kähler-Einstein metrics described by Borel, one is the usual normal metric and the remaining n are given explicitly as follows:
metrics are the already mentioned Kähler-Einstein metrics described by Borel, one is the usual normal metric and the remaining n are given explicitly as follows:

 .
.
More generally, in his Ph.D. thesis ([12]), dos Santos has found new families of Einstein non-Kähler metrics on arbitrary  . See also [9] and [13] for additional details.
. See also [9] and [13] for additional details.
We notice that any known invariant Einstein metric on  has a common feature: either it is Kähler or is in
has a common feature: either it is Kähler or is in  . In fact, we believe that this fact is true for any Einstein metric on
. In fact, we believe that this fact is true for any Einstein metric on  .
.
Using an appropriate Cartan-Killing perturbation (as in Theorem 4.5) we can prove.
Theorem 5.4. Let  equipped with any of the known Einstein non-Kähler metrics above described, and
equipped with any of the known Einstein non-Kähler metrics above described, and  be any arbitrary holomorphic-horizontal frame. Then,
be any arbitrary holomorphic-horizontal frame. Then,  is unstable.
is unstable.
[1] A. Arvanitoyeorgos, New invariant Einstein metrics on generalized flag manifolds, Trans. Amer. Math. Soc., 337 (1993), 981-995. [ Links ]
[2] M. Black, Harmonic Maps into Homogeneous Spaces, Pitman Res. Notes in Math. vol. 255, Longman, Harlow (1991). [ Links ]
[3] A. Borel, Kählerian coset spaces of semi-simple Lie groups, Proc. Nat. Acad. Sci. USA 40 (1954), 1147-1151. [ Links ]
[4] R. Bryant, Lie groups and twistor spaces, Duke Math. J. 52 (1985), 223-261. [ Links ]
[5] F.E. Burstall and S. Salamon, Tournaments, flags and harmonics maps, Math. Ann. 277 (1987), 249-265. [ Links ]
[6] E. Calabi, Minimal immersions of surfaces in Euclidean spheres, J. Diff. Geom. 1 (1967), 111-125. [ Links ]
[7] É. Cartan, Sur les domaines bornés homogènes de l'espace des n variables complexes, Abhandl. Math. Sem. Hamburg, 11 (1935), 116-162 [ Links ]
[8] S. S. Chern and J. G. Wolfson, Minimal surfaces by moving frames, Am. J. Math. 105 (1983), 59-83. [ Links ]
[9] Nir Cohen, E. C. F. dos Santos, Caio J.C. Negreiros, Properties of Einstein metrics on flag manifolds, IMECC-UNICAMP, preliminary version (2006). [ Links ]
[10] Nir Cohen, Caio J.C. Negreiros, Marlio Paredes, Sofia Pinzón and Luiz A. B. San Martin,  structures on the classical flag manifold wich admit (1,2)-simplectic metrics, Tohoku Math. J., 57 (2005), 261-271. [ Links ]
structures on the classical flag manifold wich admit (1,2)-simplectic metrics, Tohoku Math. J., 57 (2005), 261-271. [ Links ]
[11] N. Cohen, C. J. C. Negreiros and L. A. B. San Martin, A rank-three condition for invariant (1,2)-symplectic metrics on flag manifolds and tournaments, Bull. London Math. Soc. 34 (2002), 641-649. [ Links ]
[12] E. C. F. dos Santos, Métricas de Einstein em variedades bandeira, Ph.D. thesis, State University of Campinas, 2005. [ Links ]
[13] E. C. F. dos Santos and C. J. C. Negreiros , Einstein metrics on flag manifolds [ Links ]
[14] J. Eells and L. Lemaire, Another Report on Harmonic Maps, Bull. London Mat. Soc. 20 (1988), 385-524. [ Links ]
[15] J. Eells and J. C. Wood, Harmonic maps from surfaces to complex projective spaces, Adv. Math. 49 (1983), 217-263. [ Links ]
[16] A. Gray and L. M. Hervella, The sixteen classes of almost Hermitian manifolds and their linear invariants, Ann. Mat. Pura Appl. 123 (1980), 35-58. [ Links ]
[17] M. Kimura, Homogeneous Einstein Metrics on certain Kähler C-spaces, Advanced Studies in Pure Mathematics. 18-I, 1990. Recent topics in Differential and analytic Geometry (1986), 303-320. [ Links ]
[18] S. Kobayashi and K. Nomizu, Foundations of differential geometry, Interscience Publishers, vol II., (1969). [ Links ]
[19] A. Lichnerowicz, Applications harmoniques et variétés Kählériennes, Symposia Mathematica 3, Bologna (1970), 341-402. [ Links ]
[20] X. Mo and C. J. C. Negreiros, (1,2)-Symplectic structures on flag manifolds, Tohoku Math. J. 52 (2000), 271-282. [ Links ]
[21] C. J. C. Negreiros, Some remarks about harmonic maps into flag manifolds, Indiana Univ. Math. J. 37 (1988), 617-636. [ Links ]
[22] Y. Sakane, Homogeneous Einstein metrics on flag manifolds, Lobatchevskii J. of Math., vol. 4, (1999), 71-87. [ Links ]
[23] C. J. C. Negreiros and L. A. B. San Martin, Stability properties of holomorphic maps on flag manifolds, preprint, State University of Campinas (2005). [ Links ]
[24] J. Rawnsley, f-structures, f-twistor spaces and harmonic maps, in Geometry Seminar "Luigi Bianchi", II, 1984, Lecture Notes in Math., vol. 1164 (1985); Ed.: E. Vesentini. [ Links ]
[25] L. A. B. San Martin e C. J. C. Negreiros, Invariant almost Hermitian structures on flag manifolds, Advances in Math., 178 (2003), 277-310. [ Links ]
[26] L. A. B. San Martin and R. C. J. Silva, Invariant nearly-Kähler structures, preprint, State University of Campinas (2003). [ Links ]
[27] K. Uhlenbeck, Harmonic maps into Lie groups (classical solutions of the chiral model), J. Diff. Geom. 30 (1989), 1-50. [ Links ]
[28] K. Yang, Horizontal holomorphic curves in  -flag manifolds, Proc. A. M. S. 103, # 1 (1988), 265-273. [ Links ]
-flag manifolds, Proc. A. M. S. 103, # 1 (1988), 265-273. [ Links ]
[29] K. Yano, On a structure defined by a tensor field of type (1,1) satisfying  , Tensor 14 (1963), 99-109. [ Links ]
, Tensor 14 (1963), 99-109. [ Links ]
[30] M. Wang and W. Ziller, On normal homogeneous Einstein metrics, Ann. Sci. Ec. Norm. Sup.18 (1985), 563-633. [ Links ]
Caio J. C. Negreiros
Department of Mathematics.
Universidade Estadual de Campinas.
Cx. Postal 6065 13081-970, Campinas-SP, Brasil
Recibido: 5 de octubre de 2005
Aceptado: 19 de septiembre de 2006