Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.47 n.2 Bahía Blanca jul./dic. 2006
Small oscillations on 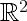 and Lie theory
and Lie theory
Gabriela Ovando
Abstract: Making use of Lie theory we propose a model for the simple harmonic oscillator and for the linear inverse pendulum of  . In both cases the phase space are orbits of the coadjoint representation of the Heisenberg Lie group. These orbits and the Heisenberg Lie algebra are included in a solvable Lie algebra admitting an ad-invariant metric. The corresponding quadratic form induces the Hamiltonian and the associated Hamiltonian system is a Lax equation.
. In both cases the phase space are orbits of the coadjoint representation of the Heisenberg Lie group. These orbits and the Heisenberg Lie algebra are included in a solvable Lie algebra admitting an ad-invariant metric. The corresponding quadratic form induces the Hamiltonian and the associated Hamiltonian system is a Lax equation.
In classical mechanics a simple harmonic oscillator with one degree of freedom has a Hamiltonian  of the form
of the form
|
| (1) |
where  is the position and
is the position and 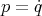 is the canonical momentum. This yields the following equation of motion
is the canonical momentum. This yields the following equation of motion
|
| (2) |
Another possible motion to consider in  is the linear inverse pendulum which has a Hamiltonian of the form
is the linear inverse pendulum which has a Hamiltonian of the form
|
| (3) |
which induces the equation of motion
|
| (4) |
These equations predict the position and the velocity at any time if initial conditions  ,
, 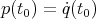 are known. Both systems correspond to quadratic Hamiltonians on
are known. Both systems correspond to quadratic Hamiltonians on  given by
given by

where 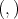 denotes the canonical inner product and
denotes the canonical inner product and 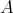 is a symmetric transformation for
is a symmetric transformation for  . For the harmonic oscillator we are taking
. For the harmonic oscillator we are taking  as the identity and for the linear inverse pendulum we have
as the identity and for the linear inverse pendulum we have

In quantum mechanics a good approach to the harmonic oscillator is through the Heisenberg Lie algebra. In dimension three this is the Lie algebra generated by the position operator  = multiplication by x, the momentum operator
= multiplication by x, the momentum operator 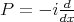 and
and  with the only non trivial commutation relation
with the only non trivial commutation relation
![[Q, P] = 1](/img/revistas/ruma/v47n2/2a1122x.png)
These operators evolve according to the Heisenberg equations

In this work we shall show that the Heisenberg Lie algebra also allows an approach to the classical harmonic oscillator and to the linear inverse pendulum. To this end we shall make use of Lie theory, which was proved to be successful when studying some mechanical systems [A] [Ko2] [Sy]. This gives a general setting so that the Hamiltonian system is a Lax equation and functions in involution arise from the ad-invariant ones or with other weaker conditions as in [R1]. This algebraic framework was used with semisimple Lie algebras and the power of representation theory to describe for instance generalised Toda lattices. What we need is a Lie algebra with an ad-invariant metric, a splitting of this Lie algebra into a direct sum as vector subspaces of two subalgebras and a given function. In the case of semisimple Lie algebra the Killing form is the natural candidate for the ad-invariant metric.
However there are more Lie algebras admitting an ad-invariant metric. We shall endow a four dimensional solvable Lie algebra with such metric and we use the algebraic tools to construct a Hamiltonian system whose phase space are orbits of the coadjoint action of the Heisenberg Lie group, which is a proper normal subgroup of the corresponding solvable Lie group. By considering the restriction to the orbits of the function induced by the quadratic form of the metric, one constructs a Hamiltonian system which in one of the orbits is equivalent to (2). Since the function is ad-invariant, the Hamiltonian system takes the form of a Lax equation and the solution can be computed with help of the Adjoint map. We show a matrix realization for this system.
A similar procedure can be done for the inverse pendulum. It can be constructed also from a four dimensional solvable Lie algebra admitting an ad-invariant neutral metric. A certain splitting of the Lie algebra gives rise to the phase space as orbits of the coadjoint representation of the Heisenberg Lie algebra. The Hamiltonian system takes also the form of a Lax equation. But in this case the trajectories are not bounded.
The solvable Lie algebras we are making use of are the two solvable non abelian low-dimensional Lie algebras having an ad-invariant metric, which is not definite (see for instance [B-K] [O1]). In particular the ad-invariant metric in the first case is of Lorentzian type.
Let  be a Lie group with Lie algebra
be a Lie group with Lie algebra 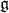 and exponential map
and exponential map  . Let
. Let 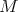 be a smooth manifold and
be a smooth manifold and  be a smooth action of
be a smooth action of 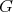 on
on  . The vector fields on
. The vector fields on 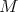

will denote the infinitesimal generators of this action. If 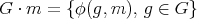 denotes the
denotes the 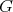 -orbit through
-orbit through  its tangent space is the set
its tangent space is the set

Here we also make use of the notation  . The following actions are important in our setting:
. The following actions are important in our setting:
- the adjoint action 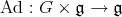 whose infinitesimal generators are
whose infinitesimal generators are 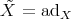 , where
, where ![adX Y = [X, Y ]](/img/revistas/ruma/v47n2/2a1140x.png) denotes the Lie bracket of
denotes the Lie bracket of  ;
;
- the coadjoint action of  on
on  is the dual of the adjoint action and it is given by
is the dual of the adjoint action and it is given by  , for
, for  , whose infinitesimal generator is
, whose infinitesimal generator is 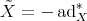 .
.
The coadjoint orbits are examples of symplectic manifolds. Recall that they are endowed with the Kirillov-Kostant-Souriau symplectic structure given by:
![ω β( ˜X, ˜Y) = - β([X, Y ]), β ∈ G ⋅ μ.](/img/revistas/ruma/v47n2/2a1147x.png)
Assume now that  has a bi-invariant non-degenerate symmetric bilinear form
has a bi-invariant non-degenerate symmetric bilinear form  ; bi-invariant means that the maps
; bi-invariant means that the maps 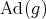 are isometries for all
are isometries for all  . Then
. Then  is skew symmetric with respect to
is skew symmetric with respect to 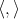 for any
for any 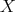 and
and 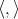 induces a diffeomorphism between the adjoint orbit
induces a diffeomorphism between the adjoint orbit  and the coadjoint orbit
and the coadjoint orbit 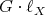 where
where  .
.
Suppose that the Lie algebra 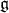 admits a splitting
admits a splitting

as a direct sum of linear subspaces, where 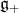 ,
, 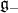 are subalgebras of
are subalgebras of  . Then the Lie algebra
. Then the Lie algebra  also splits as
also splits as 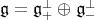 , where
, where 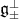 is isomorphic as vector spaces (via
is isomorphic as vector spaces (via  ) to
) to 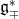 . Let
. Let  denotes a subgroup of
denotes a subgroup of 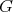 with Lie algebra
with Lie algebra  . Then the coadjoint action of
. Then the coadjoint action of  on
on  induces an action of
induces an action of  on
on  :
:

where  denotes the projection of
denotes the projection of  on
on 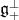 . Thus the infinitesimal generator corresponding to
. Thus the infinitesimal generator corresponding to 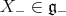 is
is
![⊥ ˜X (Y ) = π𝔤⊥+ ([X - ,Y ]) Y ∈ 𝔤+.](/img/revistas/ruma/v47n2/2a1181x.png)
The orbit  becomes a symplectic manifold with the symplectic structure given by
becomes a symplectic manifold with the symplectic structure given by
|
| (5) |
which is induced by the Kostant-Kirillov-Souriau symplectic form on the coadjoint orbits in 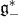 .
.
Recall that the gradient of a function 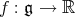 at the vector
at the vector  is defined by
is defined by

Consider the restriction of the function  to an orbit
to an orbit  . Then the Hamiltonian vector field of
. Then the Hamiltonian vector field of 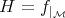 is given by
is given by
|
| (6) |
where 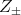 denotes the projection of
denotes the projection of  with respect to the decomposition
with respect to the decomposition  . In fact for
. In fact for 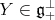 ,
, 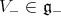 we have
we have
![ωY (V˜- ,XH ) = dHY (˜V) = ⟨∇f (Y ),π𝔤⊥([V- ,Y])⟩ = ⟨∇f - (Y ),[V- ,Y ]⟩ + ˜ ˜ = ⟨Y, [∇f - (Y),V- ]⟩ = ωY (∇f - (Y ),V ).](/img/revistas/ruma/v47n2/2a1197x.png)
Since  is non degenerate, one gets (6). Therefore the Hamiltonian equation for
is non degenerate, one gets (6). Therefore the Hamiltonian equation for  follows
follows
|
| (7) |
In particular if  is ad-invariant then
is ad-invariant then ![0 = [∇f (Y ),Y ] = [∇f (Y ),Y ] + [∇f (Y ),Y ] - +](/img/revistas/ruma/v47n2/2a11102x.png) . Since the metric is ad-invariant it holds
. Since the metric is ad-invariant it holds ![⊥ ⊥ [𝔤+,𝔤+ ] ⊂ 𝔤 +](/img/revistas/ruma/v47n2/2a11103x.png) and thus equation (7) takes the form
and thus equation (7) takes the form
|
| (8) |
that is, the equation (7) becomes a Lax equation.
If we assume now that the multiplication map 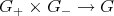 ,
,  , is a diffeomorphism, then the initial value problem
, is a diffeomorphism, then the initial value problem
|
| (9) |
can be solved by factorization. In fact if 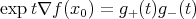 , then
, then  is the solution of (9).
is the solution of (9).
Remark. If the multiplication map  is a bijection onto an open subset of
is a bijection onto an open subset of 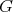 , then equation (7) has a local solution in an interval
, then equation (7) has a local solution in an interval 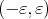 for some
for some  .
.
3. The motion of the Harmonic oscillator
Let us now go back to the harmonic oscillator. The phase space in this case is 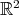 , which is a symplectic manifold with the canonical structure given by
, which is a symplectic manifold with the canonical structure given by
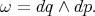
This has an associated Poisson structure, which for smooth functions 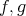 on
on 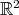 is defined by
is defined by
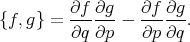
Consider the vector space over 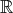 generated by the functions
generated by the functions  ,
,  ,
, 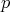 , and
, and  . Since it is a closed subspace for the bracket
. Since it is a closed subspace for the bracket  then it becomes a solvable Lie algebra of dimension four. In fact we have the following rules
then it becomes a solvable Lie algebra of dimension four. In fact we have the following rules

In order to simplify notations let us rename these elements identifying 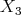 with
with  ,
,  with
with  ,
, 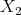 with
with  and
and 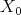 with the constant function 1 and set
with the constant function 1 and set 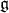 for the Lie algebra generated by these vectors with the Lie bracket
for the Lie algebra generated by these vectors with the Lie bracket ![[,]](/img/revistas/ruma/v47n2/2a11134x.png) derived from the Poisson structure.
derived from the Poisson structure.
The quadratic form on  which for
which for  is given by
is given by
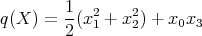
induces an ad-invariant metric on  denoted by
denoted by  .
.
The restriction of the quadratic form to  coincides with the canonical one on
coincides with the canonical one on  . In other words, the Lie algebra
. In other words, the Lie algebra  is the double extension of
is the double extension of  with the canonical metric by the skew symmetric linear map which acts on
with the canonical metric by the skew symmetric linear map which acts on  as the restriction of
as the restriction of 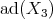 to this space (see for instance [M-R] for the double extension procedure).
to this space (see for instance [M-R] for the double extension procedure).
Consider the splitting of 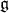 into a vector space direct sum
into a vector space direct sum 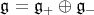 , where
, where  denote the Lie subalgebras
denote the Lie subalgebras
|
| (10) |
Notice that the ideal 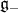 is isomorphic to the 3-dimensional Heisenberg Lie algebra we denote by
is isomorphic to the 3-dimensional Heisenberg Lie algebra we denote by  . The metric induces a decomposition of the Lie algebra
. The metric induces a decomposition of the Lie algebra 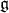 into a vector subspace direct sum of
into a vector subspace direct sum of  and
and  where
where

and it also induces linear isomorphisms  . Let
. Let  denote a Lie group with Lie algebra
denote a Lie group with Lie algebra  and let
and let 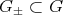 be a Lie subgroup whose Lie algebra is
be a Lie subgroup whose Lie algebra is 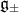 . The Lie subgroup
. The Lie subgroup 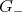 acts on
acts on 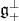 by the "coadjoint" representation; indeed in terms of
by the "coadjoint" representation; indeed in terms of 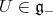 and
and  we have
we have
|
| (11) |
Therefore the infinitesimal action of  on
on 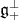 is
is
|
| (12) |
It is not difficult to see that the orbits are trivial or 2-dimensional if 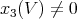 and furthermore
and furthermore 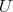 and
and 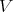 belong to the same orbit if and only if
belong to the same orbit if and only if 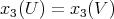 , hence the orbits are parametrized by the
, hence the orbits are parametrized by the 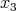 -coordinate; so we denote them by
-coordinate; so we denote them by  . They are topologically like
. They are topologically like  . In fact
. In fact  , where
, where  denotes the Heisenberg Lie group and
denotes the Heisenberg Lie group and  its center.
its center.
Let us endow the orbits with the symplectic structure defined as in (5). Computing this explicitly for the orbit  we have
we have

that is, the coordinates 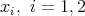 , are the canonical symplectic coordinates and one can identify this orbit with
, are the canonical symplectic coordinates and one can identify this orbit with  , fact which will be reforced in the following.
, fact which will be reforced in the following.
Let 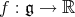 be the ad-invariant function given by
be the ad-invariant function given by 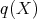 . The gradient of
. The gradient of  at a point
at a point  is
is
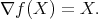
The Hamiltonian system of  , the restriction of the ad-invariant function to the orbit, reduces to
, the restriction of the ad-invariant function to the orbit, reduces to
|
| (13) |
where  .
.
For 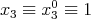 this system is equivalent to (2). Then the trajectories
this system is equivalent to (2). Then the trajectories  are parametrized circles of angular velocity
are parametrized circles of angular velocity  . More generally the trajectories on
. More generally the trajectories on 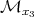 are curves
are curves 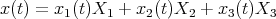 where
where
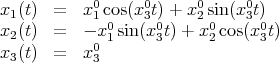
This solution coincides with that computed in the previous section, when we considered systems on coadjoint orbits. In fact it can be written as
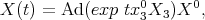
and one verifies that the flow at the point 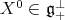 is then
is then
|
| (14) |
System (13) is a Lax pair equation ![′ L = [M, L ] = M L - LM](/img/revistas/ruma/v47n2/2a11200x.png) , taking as
, taking as  and
and  the following matrices:
the following matrices:

Consider a linear system of one degree of freedom with Hamiltonian given by:  , which yields the equation of motion
, which yields the equation of motion
|
| (15) |
The phase space for this system is  . Our aim now is to construct a model for this system in a similar setting as that of the previous section.
. Our aim now is to construct a model for this system in a similar setting as that of the previous section.
As in the case of the Harmonic oscillator let us consider the four dimensional real Lie algebra 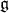 generated by
generated by 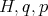 and
and  with the Lie bracket induced from the Poisson bracket on
with the Lie bracket induced from the Poisson bracket on 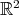 . Rename these elements as above identifying
. Rename these elements as above identifying 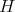 with
with 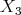 ,
,  with
with  ,
, 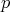 with
with  and
and  with
with  . Then we have the following non trivial Lie bracket relations:
. Then we have the following non trivial Lie bracket relations:
![[X3, X1] = X2, [X3,X2 ] = X1, [X1, X2 ] = X0.](/img/revistas/ruma/v47n2/2a11219x.png)
The quadratic form on 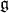 which for
which for  is given by
is given by

induces an ad-invariant neutral metric on  denoted by
denoted by 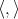 .
.
The Lie algebra 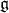 is the double extension of
is the double extension of  by the skew symmetric linear map with respect to the neutral metric on
by the skew symmetric linear map with respect to the neutral metric on  which acts on
which acts on 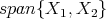 as the restriction of
as the restriction of  to this space. Notice that this map acts as the map
to this space. Notice that this map acts as the map  we mentioned in our introduction.
we mentioned in our introduction.
Consider the splitting of 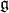 into a vector space direct sum
into a vector space direct sum 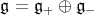 , where
, where  denote the Lie subalgebras
denote the Lie subalgebras  ,
,  . The Lie subalgebra
. The Lie subalgebra 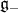 is isomorphic to the 3-dimensional Heisenberg Lie algebra
is isomorphic to the 3-dimensional Heisenberg Lie algebra  . The Lie algebra
. The Lie algebra  decomposes as a vector space direct sum of
decomposes as a vector space direct sum of 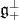 and
and 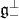 where
where

If 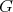 denotes a Lie group with Lie algebra
denotes a Lie group with Lie algebra  , set
, set  the Lie subgroup with Lie subalgebra
the Lie subgroup with Lie subalgebra 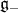 . Indeed
. Indeed 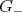 acts on
acts on 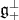 by the coadjoint action which in terms of
by the coadjoint action which in terms of  and
and  is given by
is given by
|
| (16) |
Hence the action of 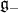 on
on 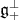 is
is
|
| (17) |
It is not difficult to verify that the orbits are 2-dimensional if  and in this case the orbits are topologically like
and in this case the orbits are topologically like  ; in fact they are diffeomorphic to
; in fact they are diffeomorphic to 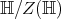 . The orbits can be parametrized by the
. The orbits can be parametrized by the 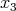 -coordinate since two vectors
-coordinate since two vectors  belong to the same orbit if
belong to the same orbit if 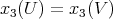 . So we denote them by
. So we denote them by 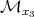 .
.
Endow the orbits with the symplectic structure induced from the coadjoint orbits (5).
Let 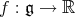 be the ad-invariant function given by
be the ad-invariant function given by 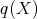 . The gradient of
. The gradient of  at a point
at a point 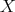 is
is  and therefore the Hamiltonian system of
and therefore the Hamiltonian system of  , the restriction of the ad-invariant quadratic function to the orbit, is given by
, the restriction of the ad-invariant quadratic function to the orbit, is given by
|
| (18) |
where  . Notice that the function
. Notice that the function 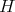 on
on 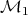 can be identified with the Hamiltonian for the linear inverse pendulum on
can be identified with the Hamiltonian for the linear inverse pendulum on  and the Hamiltonian system (18) for
and the Hamiltonian system (18) for  is equivalent to (15).
is equivalent to (15).
The trajectories  are
are

This solution coincides with that computed when we considered systems on coadjoint orbits. In fact it can be written as
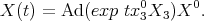
One can verify that the flow at the point  is then
is then
|
| (19) |
System (18) is a Lax pair equation ![L ′ = [M, L ] = M L - LM](/img/revistas/ruma/v47n2/2a11278x.png) , taking as
, taking as 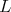 and
and 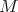 the following matrices:
the following matrices:

[AM] Abraham, R., Marsden, J, Foundations of Mechanics , 2nd edition. Benjamin Cummings, (1985). [ Links ]
[A] Adler, M., On a trace for formal pseudodifferential operators and the symplectic structure for the KdV type equations, Invent. Math., 50, 219-248, (1979). [ Links ]
[Ar] Arnold, V. I., Mathematical methods of classical mechanics, Springer Verlag, (1980). [ Links ]
[B-K] Baum, H., Kath, I., Doubly extended Lie groups-curvature, holonomy and parallel spinors, Diff. Geom. Appl., 19, 253-280, (1998). [ Links ]
[G] Guest, M, Harmonic Maps, Loop Groups and Integrable Systems. (London Math. Soc. Student Texts; 38). New York: Cambridge University Press (1997). [ Links ]
[G-S] Guillemin, V., Sternberg, S., Symplectic tecniques in physics. Cambridge: Cambridge University Press (1991). [ Links ]
[F-M] Fomenko, A., Mischenko, A., Generalized Liouville method of integration of Hamiltonian systems, Funct. Anal. and its Applic., 12, 113 -121, (1978). [ Links ]
[Ko1] Kostant, B., Quantization and Representation Theory, in: Representation Theory of Lie groups, Proc. SRC/LMS Res. Symp., Oxford 1977. London Math. Soc. Lecture Notes Series, 34, 287-316, (1979). [ Links ]
[Ko2] Kostant, B., The solution to a generalized Toda lattice and representation theory, Advances in Math., 39, 195-338, (1979). [ Links ]
[L-M] Libermann, P., Marle C.M., Symplectic Geometry and Analytical Mechanics, D. Reidel Publishing Company, 1987. [ Links ]
[M-R] Medina, A., Revoy, Ph., Algèbres de Lie et produit scalaire invariant, Ann. Sci. École Norm. Sup. (4), t. 18, 391-404, (1985). [ Links ]
[O1] Ovando, G., Estructuras complejas y sistemas hamiltonianos en grupos de Lie solubles, Tesis Doctoral, Fa.M.A.F. Univ. Nac. de Córdoba, (Marzo 2002). [ Links ]
[R1] Ratiu, T., Involution theorems, Geometric methods in Math. Phys., Lect. Notes in Math., 775, Proceedings, Lowell, Massachusetts 1979, Springer Verlag, (1980). [ Links ]
[R2] Ratiu, T., The motion of the free n-dimensional rigid body, Indiana Univ. Math. Journal, 29, 609-629, (1980). [ Links ]
[Sy] Symes, W., Systems of Toda type, inverse spectral problems and representation theory, Invent. Math., 59, 13-53, (1978). [ Links ]
[Va] Varadarajan, V., Lie groups, Lie algebras and their representations, Springer, (1984). [ Links ]
Gabriela Ovando
FaMAF-CIEM, Universidad Nacional de Córdoba,
Córdoba 5000, Argentina
ovando@mate.uncor.edu
Recibido: 25 de octubre de 2005
Aceptado: 22 de septiembre de 2006















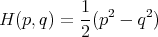
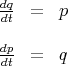
![ωX (U˜- ,V˜- ) = ⟨X, [U- ,V- ]⟩ for U- ,V - ∈ 𝔤- ,](/img/revistas/ruma/v47n2/2a1183x.png)
![XH (Y ) = - π 𝔤⊥+([∇f - (Y),Y ])](/img/revistas/ruma/v47n2/2a1191x.png)
![x ′(t) = - π 𝔤⊥ ([∇f - (x ),x]). +](/img/revistas/ruma/v47n2/2a11100x.png)
![x′(t) = [∇f (x),x] = [x,∇f (x)], + -](/img/revistas/ruma/v47n2/2a11104x.png)
![{ dx = - [x,∇f (x )] dt + x(0) = x0](/img/revistas/ruma/v47n2/2a11107x.png)

![exp U ⋅ V = [x3(V )x2(U ) + x1(V )]X1 + [- x3 (V)x1(U ) + x2(V)]X2 + x3(V)X3.](/img/revistas/ruma/v47n2/2a11165x.png)

![dx dt = [x3X3, x1X1 + x2X2 + x3X3 ] x(0) = x0](/img/revistas/ruma/v47n2/2a11189x.png)


![exp U ⋅ V = [x3(V )x2(U ) + x1 (V )]X1 + [x3(V )x1(U) + x2(V )]X2 + x3(V )X3.](/img/revistas/ruma/v47n2/2a11250x.png)
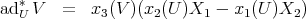
![dx = [x X ,x X + x X + x X ] dt 30 3 1 1 2 2 3 3 x(0) = x](/img/revistas/ruma/v47n2/2a11267x.png)


