Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.48 n.1 Bahía Blanca ene./jun. 2007
On the characterization of convex functions
Hugo Álvarez
Abstract: A simple characterization of convex functions as indefinite integrals of non-decreasing ones is obtained, using only Riemann integrals.
Key words and phrases. convex functions
2000 Mathematics Subject Classification. 52A41, 30C45
1.- INTRODUCTION
Characterization of convex functions ([3], App. III, theor. 2) is usually performed within Lebesgue's integration theory, despite the fact that the involved integrands are non-decreasing (therefore Riemann integrable) functions. We transcribe its statement as it appears in the cited book:
Theorem 1. The class of functions which are convex downward on the interval 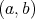 coincides with the class of indefinite integrals of functions which are increasing on
coincides with the class of indefinite integrals of functions which are increasing on 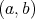 and bounded on every
and bounded on every ![[p,q] ⊂ (a,b).](/img/revistas/ruma/v48n1/1a013x.png)
The same result can be achieved with a much less expensive treatment, by using only Riemann integrals. In order to remember the usual proof and show the simpler one, we prefer to adopt the following point of view.
Theorem 1 is an immediate corollary of the next result:
Theorem 2. Let 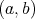 be an interval and
be an interval and 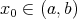 . Let
. Let 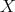 be the space of (a. e. classes of) non-decreasing functions on
be the space of (a. e. classes of) non-decreasing functions on 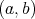 and let
and let 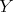 be the space of convex functions on the same interval vanishing at
be the space of convex functions on the same interval vanishing at 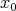 . Then the operators “indefinite integration from
. Then the operators “indefinite integration from 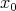 ” and “differentiation” are inverse to each other. So,
” and “differentiation” are inverse to each other. So,
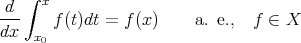 | (1) |
and
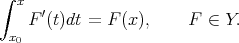 | (2) |
An elementary general result furnishes the suitable framework for this point of view.
Theorem 3. Let 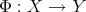 and
and 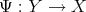 be two mappings such that
be two mappings such that
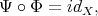 | (3) |
Then, they are inverse to each other, i. e.
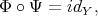 | (4) |
if and only if one of the following conditions is satisfied
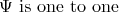 | (5) |
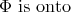 | (6) |
In our case, hypothesis (3) is identity (1), which is assured by Lebesgue's differentiation theorem (see ![[5]](/img/revistas/ruma/v48n1/1a0119x.png) (7.2)). Then identity (2), which implies the characterization of convex functions, is given by conclusion (4) of theorem 3 if condition (5) is fulfilled: differentiation is a one to one mapping from convex functions to non-decreasing ones. This is another well-known result. Since convex functions satisfy a Lipschitz condition (see
(7.2)). Then identity (2), which implies the characterization of convex functions, is given by conclusion (4) of theorem 3 if condition (5) is fulfilled: differentiation is a one to one mapping from convex functions to non-decreasing ones. This is another well-known result. Since convex functions satisfy a Lipschitz condition (see ![[5]](/img/revistas/ruma/v48n1/1a0120x.png) (7.4)), they are absolutely continuous. Hence the difference of two convex functions which have the same derivative a.e. is an absolutely continuous and singular function and it must reduce to a constant. This fact is proved by using sophisticated tools as Vitali's covering lemma (
(7.4)), they are absolutely continuous. Hence the difference of two convex functions which have the same derivative a.e. is an absolutely continuous and singular function and it must reduce to a constant. This fact is proved by using sophisticated tools as Vitali's covering lemma (![[5]](/img/revistas/ruma/v48n1/1a0121x.png) (7.28)) or F. Riesz's lemma (
(7.28)) or F. Riesz's lemma (![[2]](/img/revistas/ruma/v48n1/1a0122x.png) , Ch. 9). Of course, the conditions
, Ch. 9). Of course, the conditions  (the indefinite integral of a non-decreasing function is convex) and
(the indefinite integral of a non-decreasing function is convex) and 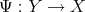 (the a. e. derivative of a convex function is non-decreasing) must be verified as well.
(the a. e. derivative of a convex function is non-decreasing) must be verified as well.
However, theorem 1 may be derived alternatively from the following (Riemannian) version of theorem 2.
Theorem 4. Let 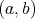 be an interval and
be an interval and 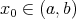 . Let
. Let 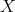 be the space of right continuous non-decreasing functions on
be the space of right continuous non-decreasing functions on 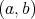 and let
and let 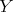 be the space of convex functions on the same interval vanishing at
be the space of convex functions on the same interval vanishing at 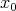 . Then the operators
. Then the operators
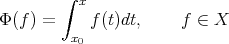 |
and
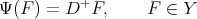 |
are inverse to each other.
The proof of theorem 4 is obtained by applying theorem 3. In order to verify that the hypotheses are fulfilled, we must prove the following propositions:
- If
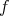 is (Riemann) integrable, the limit
is (Riemann) integrable, the limit 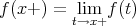
(7) exists and
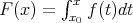 , then
, then 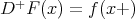 .
.
This proposition is hypothesis (3). - If
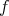 is a non-decreasing function then
is a non-decreasing function then 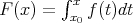 is convex on
is convex on 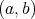 (i.e.
(i.e. 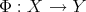 ).
). - The right derivative of a convex function is right continuous (i.e.
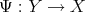 ).
). - Two convex functions with coincident right derivative at every point of an interval which have the same value at the point
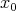 are equal. This proposition says that
are equal. This proposition says that 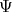 is one to one, which is hypothesis (5) of theorem 3.
is one to one, which is hypothesis (5) of theorem 3.
The proof of the first proposition is very simple in Riemann integration theory. The second one is a well-known fact from convex functions theory and will be discussed in section 2. The third statement will be proved in section 3. The fourth one will be proved in section 4. It constitutes a simplified version of a theorem of Scheeffer (see ![[4a]](/img/revistas/ruma/v48n1/1a0144x.png) or
or ![[1]](/img/revistas/ruma/v48n1/1a0145x.png) , Ch 5).
, Ch 5).
2.- WELL-KNOWN FACTS ABOUT CONVEX FUNCTIONS
Convexity of the function 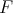 on the interval
on the interval 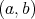 , characterized by
, characterized by
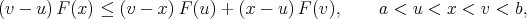 | (8) |
is equivalent to the increase of the following function
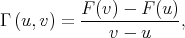 |
in one of its variables.
Since 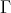 is symmetric, if it is non-decreasing with respect to one variable, then it is also non-decreasing with respect to the other. Hence, if
is symmetric, if it is non-decreasing with respect to one variable, then it is also non-decreasing with respect to the other. Hence, if 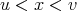 , then
, then 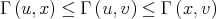 . As a consequence,
. As a consequence,
 | (9) |
This condition is also sufficient for convexity, since it implies (8)
From (9), the existence of lateral derivatives at every point of the interval (and hence continuity of 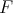 ) becomes clear:
) becomes clear:
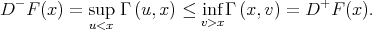 |
Moreover, if 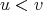 , then
, then
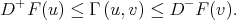 |
Hence we have the following series of inequalities:
 | (10) |
which implies that 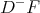 and
and  are non-decreasing functions. Hence, lateral derivatives are continuous functions with an exceptional denumerable set of jump discontinuities.
are non-decreasing functions. Hence, lateral derivatives are continuous functions with an exceptional denumerable set of jump discontinuities.
At any point where one of the lateral derivatives is continuous (i.e. at every point but in a denumerable set), the other one exists and takes the same value (i.e. there exists the derivative). If, for instance, 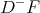 is continuous at
is continuous at 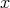 , it follows from (10) that
, it follows from (10) that
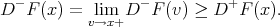 |
One can ask if continuity points of lateral derivatives are the only ones for which the derivative exists. The answer is yes and it follows from theorem 6 below.
Another immediate consequence of the sufficiency of (9) is that indefinite integrals of non-decreasing functions are convex. In fact, if 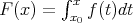 and
and 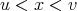 ,
,
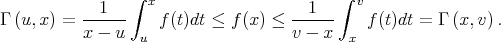 | (11) |
Then statement 2 is proved.
3.- LATERAL CONTINUITY OF LATERAL DERIVATIVES
Firstly we will demonstrate a convex version of the mean value theorem.
Lemma 5. Let 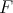 be a convex function on the open interval
be a convex function on the open interval 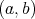 and let
and let 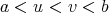 . Then there exists an intermediate value
. Then there exists an intermediate value 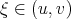 such that
such that
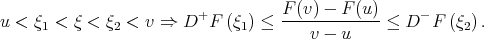 |
Proof. Let
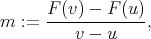 |
and consider the line 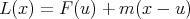 . The difference
. The difference  is a convex (and therefore continuous) function vanishing at the end points of the interval
is a convex (and therefore continuous) function vanishing at the end points of the interval ![[u,v].](/img/revistas/ruma/v48n1/1a0175x.png)
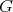 reaches its minimum in the closed interval
reaches its minimum in the closed interval ![[u,v]](/img/revistas/ruma/v48n1/1a0177x.png) , but since, because of its convexity,
, but since, because of its convexity,  in
in 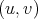 , the minimum is attained at some interior point
, the minimum is attained at some interior point 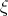 . Hence, for
. Hence, for 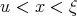 , we have
, we have  . i.e.
. i.e. 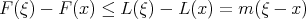 . Or, equivalently,
. Or, equivalently,
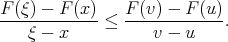 |
Hence,
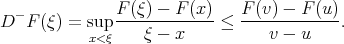 |
As a consequence, by virtue of (10),
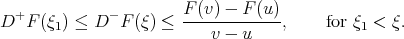 |
The other inequality is proved in the same way.
By the way, it is deduced from the lemma that a convex function with a lateral derivative vanishing in the whole interval must reduce to a constant.
Theorem 6. The right lateral derivative of a convex function is right continuous.
Proof. Since 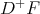 is non-decreasing, there exists
is non-decreasing, there exists
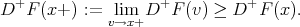 |
For the opposite inequality, given  , applying the lemma in the interval
, applying the lemma in the interval 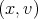 we obtain:
we obtain:
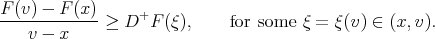 |
The right member has limit for 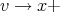 , since
, since 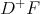 does and
does and 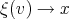 . Hence
. Hence
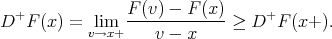 |
Obviously, the same result is valid in the left side.
4.- LATERAL DIFFERENTIATION IS A ONE TO ONE OPERATOR
Lemma 7. Let 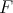 be a continuous function on the interval
be a continuous function on the interval 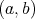 and suppose in addition that for every
and suppose in addition that for every 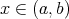 ,
, 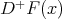 exists and is equal to
exists and is equal to 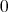 . Hence
. Hence 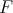 is constant in
is constant in 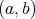 .
.
Proof. It will be proved that, for any 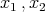 with
with 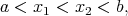
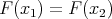 . It suffices to prove that, for any
. It suffices to prove that, for any 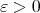 ,
, 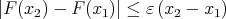 . Let us consider the set
. Let us consider the set
![A = {x ∈ [x1 ,x2] : |F (x) - F(x1)| ≤ ɛ(x - x1 )}](/img/revistas/ruma/v48n1/1a01108x.png) |
and let 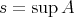 . Note that by virtue of the continuity of
. Note that by virtue of the continuity of 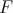 ,
, 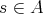 . Then we only need to prove that
. Then we only need to prove that 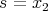 . Of course,
. Of course, 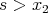 is not possible, since
is not possible, since 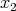 is an upper bound for
is an upper bound for 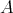 ; but neither is
; but neither is 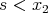 , because
, because 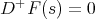 would imply the existence of a point
would imply the existence of a point 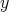 near
near  ,
, 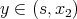 such that
such that 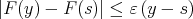 In such a case, using that
In such a case, using that 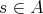 and then
and then 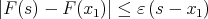 , it would yield
, it would yield
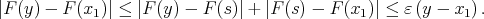 |
This inequality implies that  , which is in contradiction with
, which is in contradiction with 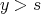 and therefore
and therefore 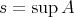 .
.
With the aid of lemma 7, the following theorem becomes immediate and constitutes a proof of proposition 4
Theorem 8. If 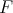 and
and 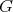 are convex functions on
are convex functions on 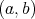 , with
, with 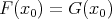 for certain
for certain 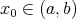 , and
, and 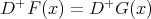 for every
for every 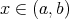 , then
, then 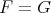 on
on 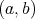 .
.
REFERENCES
[1] Hobson, E. W. The theory of functions of a real variable and the theory of Fourier's series. Vol. I. Dover Publications, Inc., New York, N.Y., 1958. xv+736 pp. [ Links ]
[2] Kolmogorov, A. N.; Fomin, S. V. Introductory real analysis. Revised English edition. Translated from the Russian and edited by Richard A. Silverman Prentice-Hall, Inc., Englewood Cliffs, N.Y. 1970 xii+403 pp. (loose errata). [ Links ]
[3] Natanson, I. P. Theory of functions of a real variable. Vol. II. Translated from the Russian by Leo F. Boron Frederick Ungar Publishing Co., New York 1961 265 pp. [ Links ]
[4a] Scheeffer, Ludwig. Zur Theorie der Stetigen Funktionen einer Reellen Vernderlichen. (German) Acta Math. 5 (1884), no. 1, 279s296. MR1554657 [ Links ]
[4b] Scheeffer, Ludwig. Zur Theorie der stetigen Funktionen einer reellen Vernderlichen. (German) Acta Math. 5 (1884), no. 1, 183-194. MR1554652 [ Links ]
[4c] Scheeffer, Ludwig. Allgemeine Untersuchungen ber Rectification der Curven. (German) Acta Math. 5 (1884), no. 1, 49-82. MR1554648 [ Links ]
[4d] Scheeffer, Ludwig. Beweis des Laurent'schen Satzes. (German) Acta Math. 4 (1884), no. 1, 375-380. MR1554641 [ Links ]
[5] Wheeden, Richard L.; Zygmund, Antoni. Measure and integral. An introduction to real analysis. Pure and Applied Mathematics, Vol. 43. Marcel Dekker, Inc., New York-Basel, 1977. x+274 pp. [ Links ]
Hugo Álvarez
Departamento de Matemáticas,
Universidad Nacional de San Luis,
San Luis 5700, Argentina
halvarez@unsl.edu.ar
Recibido: 30 de junio de 2005
Aceptado: 21 de febrero de 2006














