Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932versão On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.48 n.1 Bahía Blanca jan./jun. 2007
Characterisations of Nelson algebras
M. Spinks and R. Veroff
Abstract. Nelson algebras arise naturally in algebraic logic as the algebraic models of Nelson's constructive logic with strong negation. This note gives two characterisations of the variety of Nelson algebras up to term equivalence, together with a characterisation of the finite Nelson algebras up to polynomial equivalence. The results answer a question of Blok and Pigozzi and clarify some earlier work of Brignole and Monteiro.
Key words and phrases. Nelson algebra, residuated lattice, BCK-algebra, equationally definable principal congruences
The first author would like to thank Nick Galatos for several helpful conversations about residuated lattices.
The final version of this paper was prepared while the first author was a Visiting Professor in the Department of Education at the University of Cagliari. The facilities and assistance provided by the University and the Department are gratefully acknowledged.
Recall from the theory of distributive lattices [2, Chapter XI] that a De Morgan algebra is an algebra 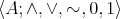 of type
of type 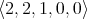 where
where 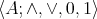 is a bounded distributive lattice and for all
is a bounded distributive lattice and for all 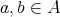 ,
, 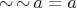 ,
, 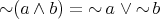 and
and 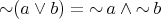 .
.
A Nelson algebra (also 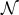 -lattice or quasi-pseudo-Boolean algebra in the literature) is an algebra
-lattice or quasi-pseudo-Boolean algebra in the literature) is an algebra  of type
of type 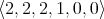 such that the following conditions are satisfied for all
such that the following conditions are satisfied for all 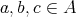 [26, Section 0]:
[26, Section 0]:
(N1) 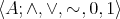 is a De Morgan algebra with lattice ordering
is a De Morgan algebra with lattice ordering  ;
;
(N2) The relation 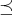 defined for all
defined for all  by
by  if and only if
if and only if 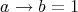 is a quasiordering (reflexive and transitive relation) on
is a quasiordering (reflexive and transitive relation) on 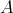 ;
;
(N3) 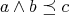 if and only if
if and only if 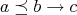 ;
;
(N4) 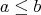 if and only if
if and only if 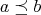 and
and  ;
;
(N5) 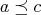 and
and 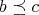 implies
implies 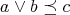 ;
;
(N6) 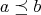 and
and 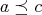 implies
implies 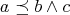 ;
;
(N7) 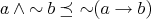 and
and 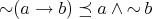 ;
;
(N8) 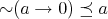 and
and 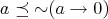 ;
;
(N9) 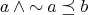 .
.
The class 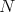 of all Nelson algebras is a variety [11], which arises naturally in algebraic logic as the equivalent quasivariety semantics (in the sense of [4]) of Nelson's constructive logic with strong negation [25, Chapter XII]. For studies of Nelson algebras see in particular Sendlewski [26], Vakarelov [31], and Rasiowa [25, Chapter V].
of all Nelson algebras is a variety [11], which arises naturally in algebraic logic as the equivalent quasivariety semantics (in the sense of [4]) of Nelson's constructive logic with strong negation [25, Chapter XII]. For studies of Nelson algebras see in particular Sendlewski [26], Vakarelov [31], and Rasiowa [25, Chapter V].
A commutative, integral residuated lattice is an algebra 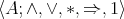 of type
of type 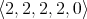 , where: (i)
, where: (i) 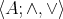 is a lattice with lattice ordering
is a lattice with lattice ordering  such that
such that  for all
for all 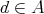 ; (ii)
; (ii) 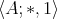 is a commutative monoid; and (iii) for all
is a commutative monoid; and (iii) for all 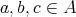 ,
, 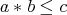 if and only if
if and only if 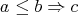 . By Blount and Tsinakis [9, Proposition 4.1] the class
. By Blount and Tsinakis [9, Proposition 4.1] the class 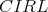 of all commutative, integral residuated lattices is a variety. An
of all commutative, integral residuated lattices is a variety. An 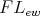 -algebra
-algebra  is a commutative, integral residuated lattice with distinguished least element
is a commutative, integral residuated lattice with distinguished least element 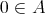 . The variety
. The variety 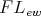 of all
of all 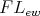 -algebras arises naturally in algebraic logic in connection with the study of substructural logics; see [19, 21, 22, 23] for details.
-algebras arises naturally in algebraic logic in connection with the study of substructural logics; see [19, 21, 22, 23] for details.
An 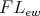 -algebra
-algebra 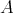 is said to be 3-potent when
is said to be 3-potent when 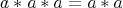 for all
for all 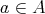 , distributive when its lattice reduct is distributive, and classical when
, distributive when its lattice reduct is distributive, and classical when 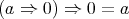 for all
for all 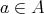 . Rewriting
. Rewriting 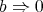 as
as 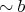 for all
for all 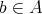 , classicality expresses the law of double negation in algebraic form. A Nelson
, classicality expresses the law of double negation in algebraic form. A Nelson 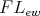 -algebra is a 3-potent, distributive classical
-algebra is a 3-potent, distributive classical 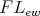 -algebra such that
-algebra such that 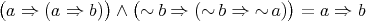 for all
for all  .
.
The following description (to within term equivalence) of the variety of Nelson algebras was obtained by the authors in [29, 30].
Theorem 1.1. [29, Theorem 1.1]
- Let
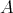 be a Nelson algebra. Define the derived binary terms
be a Nelson algebra. Define the derived binary terms  and
and 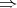 by:
by: 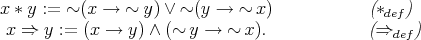
Then the term reduct
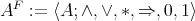 is a Nelson
is a Nelson 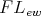 -algebra.
-algebra. - Let
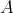 be a Nelson
be a Nelson 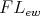 -algebra. Define the derived binary term
-algebra. Define the derived binary term  and the derived unary term
and the derived unary term  by:
by: 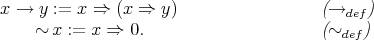
Then the term reduct
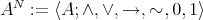 is a Nelson algebra.
is a Nelson algebra. - Let
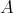 be a Nelson algebra. Then
be a Nelson algebra. Then 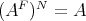 .
. - Let
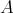 be a Nelson
be a Nelson 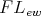 -algebra. Then
-algebra. Then 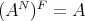 .
.
Hence the varieties of Nelson algebras and Nelson 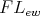 -algebras are term equivalent.
-algebras are term equivalent. 
In this note we give several further characterisations of Nelson algebras, all of which may be understood as corollaries of Theorem 1.1. We shall make implicit use of Theorem 1.1 without further reference throughout the paper.
A BCK-algebra is a 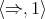 -subreduct of a commutative, integral residuated lattice [32, Theorem 5.6]; for an equivalent quasi-equational definition, see Section 2. We show in Section 2 that every finite Nelson algebra
-subreduct of a commutative, integral residuated lattice [32, Theorem 5.6]; for an equivalent quasi-equational definition, see Section 2. We show in Section 2 that every finite Nelson algebra 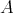 is polynomially equivalent to its own BCK-algebra term reduct
is polynomially equivalent to its own BCK-algebra term reduct 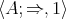 .
.
A pseudo-interior algebra is a hybrid of a (topological) interior algebra and a residuated partially ordered monoid; for a precise definition, see Section 3 below. We prove in Section 3 that the variety of Nelson algebras is term equivalent to a congruence permutable variety of pseudo-interior algebras with compatible operations. We obtain this result as a byproduct of the solution to a problem of Blok and Pigozzi [5].
A lower BCK-semilattice is the conjunction of a meet semilattice with a BCK-algebra such that the natural partial orderings on both algebras coincide; for a formal definition see Section 4 below. We verify in Section 4 that the variety of Nelson algebras is term equivalent to a variety of bounded BCK-semilattices. The result clarifies earlier work on the axiomatics of Nelson algebras due to Brignole [10].
2. Finite Nelson algebras as BCK-algebras
A BCK-algebra is an algebra 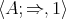 of type
of type 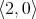 such that the following identities and quasi-identity are satisfied:
such that the following identities and quasi-identity are satisfied:
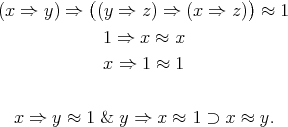 | (1) |
By Wroński [34] the quasivariety  of all BCK-algebras is not a variety. BCK-algebras have been considered extensively in the literature; for surveys, see Iséki and Tanaka [17] or Cornish [13]. Here we simply recall that for any BCK-algebra
of all BCK-algebras is not a variety. BCK-algebras have been considered extensively in the literature; for surveys, see Iséki and Tanaka [17] or Cornish [13]. Here we simply recall that for any BCK-algebra  , the relation
, the relation  on
on  defined for all
defined for all  by
by  if and only if
if and only if 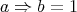 is a partial ordering, which has the property that for any
is a partial ordering, which has the property that for any 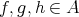 ,
,
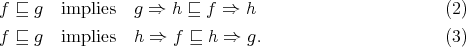
A non-empty subset 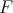 of a BCK-algebra
of a BCK-algebra 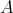 is said to be a BCK-filter if
is said to be a BCK-filter if 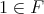 and
and 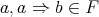 implies
implies 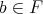 for all
for all 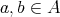 . Also, a non-empty subset of an
. Also, a non-empty subset of an 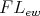 -algebra
-algebra 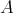 is said to be an
is said to be an 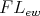 -filter if: (i)
-filter if: (i)  and
and 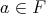 implies
implies 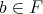 ; and (ii)
; and (ii) 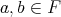 implies
implies 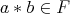 for all
for all 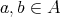 . It is easy to see that a non-empty subset of an
. It is easy to see that a non-empty subset of an 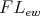 -algebra
-algebra 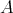 is an
is an 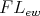 -filter if and only if it is a BCK-filter of the BCK-algebra reduct of
-filter if and only if it is a BCK-filter of the BCK-algebra reduct of 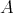 [19, p. 12].
[19, p. 12].
Let 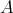 be an
be an 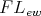 -algebra [resp. BCK-algebra]. It is well known and easy to see that every congruence
-algebra [resp. BCK-algebra]. It is well known and easy to see that every congruence 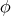 on
on 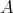 [resp. congruence
[resp. congruence 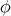 on
on 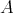 such that
such that 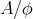 is a BCK-algebra] is of the form
is a BCK-algebra] is of the form 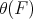 for some
for some 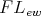 -filter [resp. BCK-filter]
-filter [resp. BCK-filter] 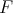 , where for all
, where for all 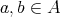 ,
, 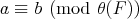 if and only if
if and only if 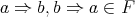 (put
(put 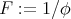 ). See [19, Proposition 1.3] for the case of
). See [19, Proposition 1.3] for the case of  -algebras and [7, Proposition 1] for the case of BCK-algebras.
-algebras and [7, Proposition 1] for the case of BCK-algebras.
For any 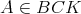 , let
, let 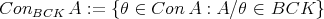 . In view of the preceding discussion, we have
. In view of the preceding discussion, we have
Lemma 2.1. For any 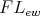 -algebra
-algebra 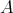 ,
, 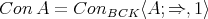 . In particular, if
. In particular, if 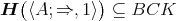 , then
, then 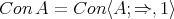 .
. 
Recall from [3] that a class 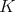 of similar algebras has definable principal congruences (DPC) if and only if there exists a formula
of similar algebras has definable principal congruences (DPC) if and only if there exists a formula 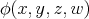 in the first-order language of
in the first-order language of 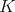 (whose only free variables are
(whose only free variables are 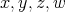 ) such that for any
) such that for any 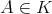 and
and 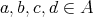 ,
, 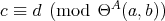 if and only if
if and only if ![A |= φ[a, b,c,d]](/img/revistas/ruma/v48n1/1a04147x.png) . When
. When 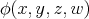 can be taken as a conjunction (viz., finite set) of equations, then
can be taken as a conjunction (viz., finite set) of equations, then 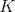 is said to have equationally definable principal congruences (EDPC) [15].
is said to have equationally definable principal congruences (EDPC) [15].
For any integer 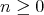 , consider the unary
, consider the unary 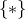 -terms
-terms 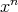 defined recursively by
defined recursively by 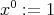 and
and  when
when 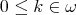 . Given
. Given  , an element
, an element  of an
of an 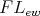 -algebra
-algebra 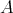 is said to be
is said to be  -potent if
-potent if  .
. 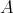 is said to be
is said to be  -potent if it satisfies an identity of the form
-potent if it satisfies an identity of the form
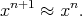 | (E ) ) |
Clearly the class 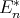 of all
of all 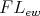 -algebras satisfying (E
-algebras satisfying (E ) is equationally definable.
) is equationally definable.
Theorem 2.2. [18, Theorem 2.1] For a variety 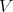 of
of 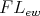 -algebras the following conditions are equivalent:
-algebras the following conditions are equivalent:
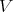 has DPC;
has DPC;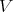 has EDPC; and
has EDPC; and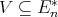 for some
for some  .
.
A ternary term 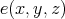 is a ternary deductive (TD) term for an algebra
is a ternary deductive (TD) term for an algebra 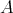 if
if 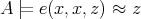 , and, for all
, and, for all 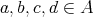 ,
,  if
if 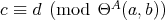 [5, Definition 2.1].
[5, Definition 2.1]. 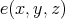 is said to be a ternary deductive (TD) term for a class
is said to be a ternary deductive (TD) term for a class 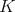 of similar algebras if it is a TD term for every member of
of similar algebras if it is a TD term for every member of 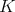 . By [5, Theorem 2.5],
. By [5, Theorem 2.5], 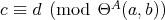 for any
for any 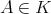 if and only if
if and only if  , whence
, whence 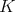 has EDPC. A TD term
has EDPC. A TD term 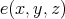 for an algebra
for an algebra 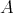 is said to be commutative if in addition
is said to be commutative if in addition 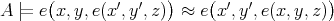 . A TD term
. A TD term 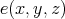 for a class
for a class 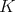 of similar algebras is said to be commutative if it is commutative for every member of
of similar algebras is said to be commutative if it is commutative for every member of 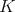 [5, Definition 3.1].
[5, Definition 3.1].
For any integer 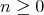 , consider the binary
, consider the binary 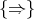 -terms
-terms 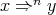 defined recursively by
defined recursively by 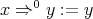 and
and 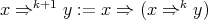 when
when 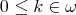 . Given
. Given  , a BCK-algebra is said to be
, a BCK-algebra is said to be  -potent if it satisfies an identity of the form
-potent if it satisfies an identity of the form

By Cornish [12, Theorem 1.4] the class  of all BCK-algebras satisfying (2) is a variety.
of all BCK-algebras satisfying (2) is a variety.
Theorem 2.3. [8, Theorem 4.2] For 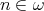 , the following conditions are equivalent for a variety
, the following conditions are equivalent for a variety 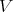 of BCK-algebras:
of BCK-algebras:
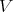 has DPC;
has DPC; has EDPC;
has EDPC;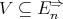 ; and
; and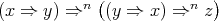 is a commutative TD term for
is a commutative TD term for 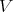 .
.
Let 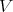 be a variety of
be a variety of 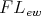 -algebras. Suppose
-algebras. Suppose 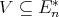 for some
for some 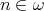 and let
and let 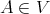 . By [7, Proposition 13, Lemma 14],
. By [7, Proposition 13, Lemma 14], 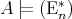 if and only if
if and only if 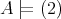 if and only if
if and only if 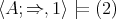 , whence
, whence 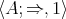 is
is  -potent. Since
-potent. Since 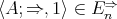 and
and 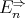 is a variety of BCK-algebras,
is a variety of BCK-algebras, 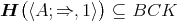 . By Lemma 2.1, therefore,
. By Lemma 2.1, therefore, 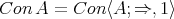 and hence
and hence
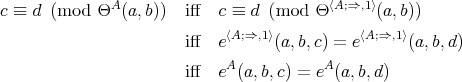
where 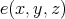 denotes the commutative TD term of Theorem 2.3. Of course,
denotes the commutative TD term of Theorem 2.3. Of course, 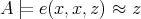 . Thus
. Thus 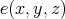 is a commutative TD term for
is a commutative TD term for  .
.
Conversely, suppose 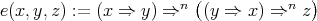 is a commutative TD term for
is a commutative TD term for 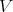 . Let
. Let 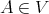 . By [5, Theorem 2.3, Corollary 2.4],
. By [5, Theorem 2.3, Corollary 2.4], 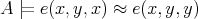 , which is to say
, which is to say 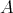 satisfies
satisfies
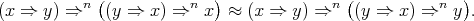 | (4) |
Therefore 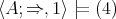 . But by [7, Proposition 13], a BCK-algebra satisfies (4) if and only if it satisfies (2). Hence
. But by [7, Proposition 13], a BCK-algebra satisfies (4) if and only if it satisfies (2). Hence 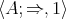 is
is  -potent. By the remarks following Theorem 2.3 we infer that
-potent. By the remarks following Theorem 2.3 we infer that 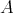 is
is  -potent, whence
-potent, whence 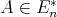 . We have established
. We have established
Proposition 2.4. For  ,
, 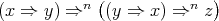 is a commutative TD term for a variety
is a commutative TD term for a variety 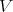 of
of 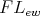 -algebras if and only if
-algebras if and only if 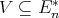 .
. 
In [29, Proposition 3.2] the authors showed that the variety of Nelson algebras satisfies the identity 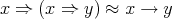 , where
, where  denotes the derived binary term defined as in (⇒def). See also Viglizzo [33, Chapter 1]. Since the variety of all Nelson
denotes the derived binary term defined as in (⇒def). See also Viglizzo [33, Chapter 1]. Since the variety of all Nelson 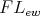 -algebras is 3-potent, we have
-algebras is 3-potent, we have
Corollary 2.5. [28, Theorem 3.3, Remark 3.5] 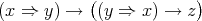 is a commutative TD term for the variety of Nelson algebras, where
is a commutative TD term for the variety of Nelson algebras, where  denotes the derived binary term defined as in (⇒def).
denotes the derived binary term defined as in (⇒def).
Proof. By Blok and Pigozzi [5, Theorem 2.3(iii)] the property of being a commutative TD term for a variety can be characterised solely by equations, so the result follows from the remarks preceding the corollary and Proposition 2.4. □
Next, recall the following classic result from the theory of 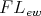 -algebras.
-algebras.
Proposition 2.6. [16, Theorem 2] The variety of 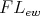 -algebras is arithmetical. A Mal'cev term for
-algebras is arithmetical. A Mal'cev term for 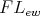 is
is 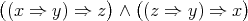 .
. 
From Proposition 2.6 we infer
Theorem 2.7. [28, Theorem 4.4] The variety of Nelson algebras is arithmetical. A Mal'cev term for 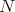 is
is 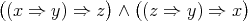 , where
, where 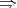 denotes the derived binary term defined as in (⇒def).
denotes the derived binary term defined as in (⇒def). 
Let 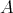 be a finite
be a finite 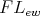 -algebra. Because the monoid reduct of
-algebra. Because the monoid reduct of 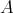 is finite,
is finite, 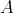 must be
must be  -potent for some
-potent for some  . See also Cornish [13, p. 419]. By the remarks following Theorem 2.3, we infer that
. See also Cornish [13, p. 419]. By the remarks following Theorem 2.3, we infer that 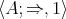 is
is  -potent and hence that
-potent and hence that 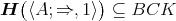 . We therefore have
. We therefore have
Theorem 2.8. Every finite 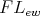 -algebra
-algebra 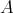 is polynomially equivalent to its BCK-algebra reduct
is polynomially equivalent to its BCK-algebra reduct 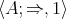 .
.
Proof. The result follows Lemma 2.1, Proposition 2.6 and a result due to Pixley [24, Theorem 1], which asserts that if 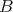 is a finite algebra in an arithmetical variety and
is a finite algebra in an arithmetical variety and 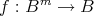 is a function preserving congruences on
is a function preserving congruences on 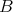 then
then 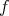 is a polynomial of
is a polynomial of 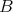 . □
. □
Corollary 2.9. Every finite Nelson algebra 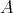 is polynomially equivalent to its BCK-algebra term reduct
is polynomially equivalent to its BCK-algebra term reduct 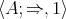 .
. 
The class 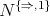 of all
of all 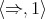 -term reducts of Nelson algebras is strictly contained within the variety of all 3-potent BCK-algebras. In particular, it can be shown that
-term reducts of Nelson algebras is strictly contained within the variety of all 3-potent BCK-algebras. In particular, it can be shown that 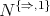 satisfies the identity
satisfies the identity
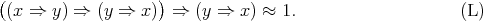 |
(Commutative) BCK-algebras satisfying the identity (L) have been studied extensively by Dvurečenskij and his collaborators in a series of papers beginning with [14].
It is easy to see that 3-potent BCK-algebras need not satisfy (L) in general. Hence, Corollary 2.9 prompts the following
Problem 2.10. Characterise the 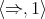 -reducts of Nelson algebras.
-reducts of Nelson algebras. 
3. Nelson algebras as pseudo-interior algebras
A BCI-monoid is an algebra 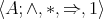 where: (i)
where: (i) 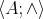 is a semilattice; (ii)
is a semilattice; (ii) 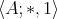 is a commutative monoid; and for all
is a commutative monoid; and for all 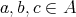 , both (iii)
, both (iii) 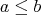 implies
implies  and
and 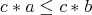 ; and (iv)
; and (iv) 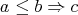 if and only if
if and only if 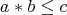 [1, Section 2]. An integral BCI-monoid is a BCI-monoid
[1, Section 2]. An integral BCI-monoid is a BCI-monoid 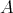 satisfying
satisfying  for all
for all 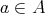 . By [1, Proposition 2.8] the class of all (integral) BCI-monoids is equationally definable. For a recent study of BCI-monoids, see Olson [20].
. By [1, Proposition 2.8] the class of all (integral) BCI-monoids is equationally definable. For a recent study of BCI-monoids, see Olson [20].
For any integer 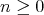 , consider again the unary
, consider again the unary 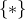 -terms
-terms 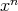 defined recursively by
defined recursively by 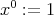 and
and  when
when 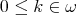 . A unary operation
. A unary operation 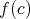 on an integral BCI-monoid
on an integral BCI-monoid 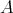 is said to be compatible if for any
is said to be compatible if for any 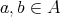 there is an
there is an  such that
such that 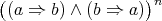
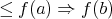 [1, Section 2]. An
[1, Section 2]. An 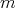 -ary operation
-ary operation  on
on 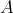 is said to be compatible if
is said to be compatible if 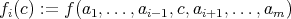 is compatible for any
is compatible for any 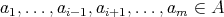 and
and 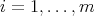 . An integral BCI-monoid with compatible operations is an algebra
. An integral BCI-monoid with compatible operations is an algebra 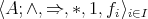 such that
such that 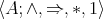 is an integral BCI-monoid and any
is an integral BCI-monoid and any  is compatible. By Aglianó [1, Remarks following Proposition 2.13]
is compatible. By Aglianó [1, Remarks following Proposition 2.13] 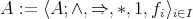 is an integral BCI-monoid with compatible operations if and only if
is an integral BCI-monoid with compatible operations if and only if 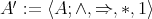 is an integral BCI-monoid and the congruences on
is an integral BCI-monoid and the congruences on 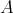 are determined by
are determined by 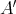 in the sense that
in the sense that 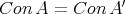 .
.
Lemma 3.1. The variety of commutative, integral residuated lattices satisfies the identity:
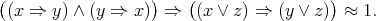 | (5) |
Proof. Let  and let
and let 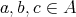 . To establish (5), note first that
. To establish (5), note first that 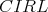 satisfies the identities
satisfies the identities
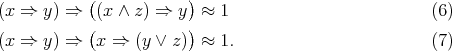
Indeed, from 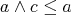 and (2) we have
and (2) we have 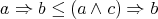 , which yields (6). Similarly, from
, which yields (6). Similarly, from 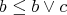 and (3) we have
and (3) we have 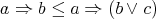 , which gives (7).
, which gives (7).
Next, note that  satisfies the identity
satisfies the identity
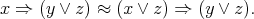 | (8) |
Indeed, from the theory of residuated lattices [9, Lemma 3.2] we have that  satisfies the identity
satisfies the identity
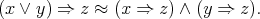 | (9) |
But then
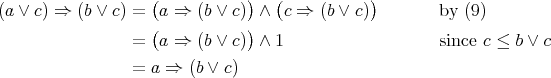
which yields (8) as claimed.
Now it is clear that
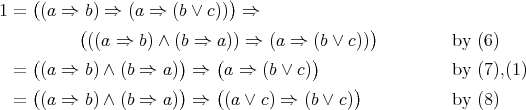
which gives (5) as desired. □
It is well known and easy to see that for any  ,
,  implies
implies  and
and 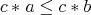 for all
for all 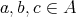 . The
. The 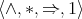 -reduct of any commutative, integral residuated lattice is thus an integral BCI-monoid. Moreover, commutativity of the monoid operation
-reduct of any commutative, integral residuated lattice is thus an integral BCI-monoid. Moreover, commutativity of the monoid operation  together with Lemma 3.1 guarantees that the lattice join
together with Lemma 3.1 guarantees that the lattice join 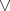 is compatible with
is compatible with 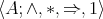 . Hence we have
. Hence we have
Lemma 3.2. The variety of commutative, integral residuated lattices, hence 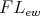 -algebras, is a variety of integral BCI monoids with compatible operations.
-algebras, is a variety of integral BCI monoids with compatible operations. 
A TD term 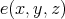 for an algebra
for an algebra 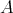 with a constant term
with a constant term  is said to be regular (for
is said to be regular (for 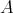 ) with respect to
) with respect to  if
if 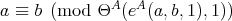 for all
for all 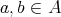 [5, Definition 4.1]. A TD term
[5, Definition 4.1]. A TD term 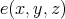 for a variety
for a variety 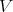 with a constant term
with a constant term  is said to be regular (for
is said to be regular (for 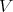 ) with respect to
) with respect to  if it is regular with respect to
if it is regular with respect to  for every member of
for every member of 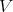 .
.
Theorem 3.3. [1, Theorem 3.1, Corollary 3.2] For 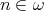 , the following conditions are equivalent for a variety
, the following conditions are equivalent for a variety 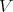 of integral BCI-monoids with compatible operations:
of integral BCI-monoids with compatible operations:
- The ternary term
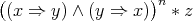 is a commutative, regular TD term for
is a commutative, regular TD term for  with respect to
with respect to  ;
;  has EDPC: for any
has EDPC: for any  and
and 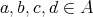 ,
, 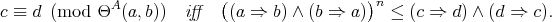

Let 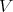 be a variety of
be a variety of 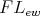 -algebras. Observe that for any
-algebras. Observe that for any 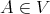 and
and 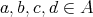 , the statement
, the statement
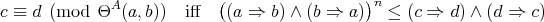 | (10) |
is equivalent to its corresponding statement about 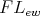 -filters, viz.:
-filters, viz.:
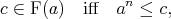 | (11) |
where 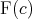 denotes the principal filter generated by
denotes the principal filter generated by 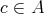 . We claim that (11) is equivalent to the assertion
. We claim that (11) is equivalent to the assertion 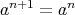 . So assume
. So assume  is
is  -potent. We have
-potent. We have 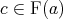 if and only if
if and only if 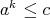 for some
for some 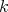 if and only if
if and only if 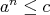 (because
(because 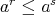 , for
, for  ). Conversely, suppose (11) holds. Clearly,
). Conversely, suppose (11) holds. Clearly,  -potency is equivalent to
-potency is equivalent to 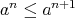 , which in view of (11) reduces to
, which in view of (11) reduces to 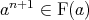 , which statement is true.
, which statement is true.
From the preceding discussion it follows that 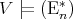 if and only if (10) holds for any
if and only if (10) holds for any 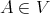 and
and 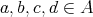 . Combining Lemma 3.2 with Theorem 3.3 therefore yields
. Combining Lemma 3.2 with Theorem 3.3 therefore yields
Proposition 3.4. For  ,
, 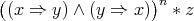 is a commutative, regular TD term with respect to
is a commutative, regular TD term with respect to  for a variety
for a variety 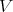 of
of 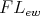 -algebras if and only if
-algebras if and only if 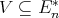 .
. 
In [5, Problem 7.4] Blok and Pigozzi asked whether the variety of Nelson algebras has a commutative, regular TD term, or even a TD term; for a discussion and references, see Spinks [28]. The following corollary, in conjunction with Corollary 2.5, completely resolves this question. But first, for a term 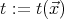 in the language of Nelson algebras, let
in the language of Nelson algebras, let 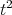 abbreviate
abbreviate  , where
, where  denotes the derived binary term defined as in (∗def).
denotes the derived binary term defined as in (∗def).
Corollary 3.5. 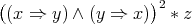 is a commutative, regular TD term with respect to
is a commutative, regular TD term with respect to  for the variety of Nelson algebras, where
for the variety of Nelson algebras, where 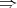 and
and  denote the derived binary terms defined as in (⇒def) and (∗def) respectively.
denote the derived binary terms defined as in (⇒def) and (∗def) respectively.
Proof. Since the property of being a commutative, regular TD term for a variety can be characterised solely by equations (by [5, Theorem 2.3(iii)] and [5, Corollary 4.2(i)]), the result follows from 3-potency and Proposition 3.4. □
Let 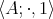 be a semigroup with a constant
be a semigroup with a constant  that acts as a left identity for
that acts as a left identity for  . A unary operation
. A unary operation  on
on 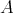 is said to be a pseudo-interior operation on
is said to be a pseudo-interior operation on 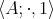 if the following identities are satisfied [6, Definition 2.1]:
if the following identities are satisfied [6, Definition 2.1]:

Given a semigroup 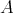 with left identity
with left identity  and pseudo-interior operation
and pseudo-interior operation  , the inverse right-divisibility ordering on
, the inverse right-divisibility ordering on 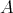 is the partial ordering
is the partial ordering  defined for all
defined for all 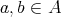 by
by  if and only if there exists
if and only if there exists 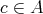 such that
such that 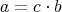 [6, Lemma 2.3].
[6, Lemma 2.3].
An algebra  of type
of type 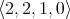 is said to be a pseudo-interior algebra if [6, Definition 2.6]: (i)
is said to be a pseudo-interior algebra if [6, Definition 2.6]: (i) 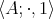 is a semigroup with left identity
is a semigroup with left identity  ; (ii)
; (ii)  is a pseudo-interior operation on
is a pseudo-interior operation on 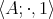 ; and (iii)
; and (iii)  is an open left residuation on
is an open left residuation on 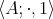 in the sense that
in the sense that 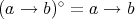 for all
for all 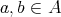 , and moreover
, and moreover 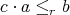 if and only if
if and only if 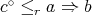 for all
for all 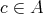 . An algebra
. An algebra 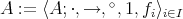 is said to be a pseudo-interior algebra with compatible operations if
is said to be a pseudo-interior algebra with compatible operations if 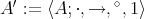 is a pseudo-interior algebra and the congruences on
is a pseudo-interior algebra and the congruences on 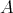 are determined by
are determined by 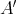 in the sense that
in the sense that 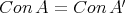 [6, Definition 2.7, Corollary 2.17]. By [6, Theorem 3.1] the class of all pseudo-interior algebras, with or without compatible operations, is equationally definable.
[6, Definition 2.7, Corollary 2.17]. By [6, Theorem 3.1] the class of all pseudo-interior algebras, with or without compatible operations, is equationally definable.
Theorem 3.6. [6, Theorem 4.1, Corollary 4.2] A variety 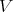 has a commutative, regular TD term if and only if it is term equivalent to a variety of pseudo-interior algebras with compatible operations. If
has a commutative, regular TD term if and only if it is term equivalent to a variety of pseudo-interior algebras with compatible operations. If 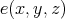 is a commutative, regular TD term for
is a commutative, regular TD term for 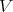 with respect to
with respect to  , then
, then
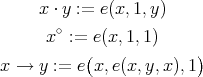
define terms realising the pseudo-interior operations  ,
,  , and
, and  on any
on any 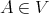 such that all the fundamental operations of
such that all the fundamental operations of 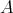 are compatible with
are compatible with 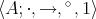 .
. 
Let 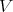 be a variety of
be a variety of 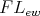 -algebras. If
-algebras. If 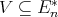 for some
for some 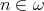 , then
, then 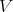 is term equivalent to a congruence permutable variety of pseudo-interior algebras with compatible operations by Proposition 2.6, Proposition 3.4, and Theorem 3.6. Conversely, if
is term equivalent to a congruence permutable variety of pseudo-interior algebras with compatible operations by Proposition 2.6, Proposition 3.4, and Theorem 3.6. Conversely, if 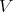 is term equivalent to a congruence permutable variety of pseudo-interior algebras with compatible operations, then
is term equivalent to a congruence permutable variety of pseudo-interior algebras with compatible operations, then 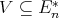 for some
for some 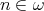 by Theorem 3.6, EDPC, and Theorem 2.2. Therefore we have
by Theorem 3.6, EDPC, and Theorem 2.2. Therefore we have
Theorem 3.7. A variety 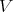 of
of 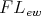 -algebras is term equivalent to a congruence permutable variety of pseudo-interior algebras with compatible operations if and only if
-algebras is term equivalent to a congruence permutable variety of pseudo-interior algebras with compatible operations if and only if 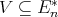 for some
for some 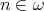 . If
. If 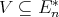 , then for any
, then for any 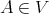 , terms realising the pseudo-interior operations
, terms realising the pseudo-interior operations  ,
,  , and
, and  on
on 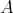 are defined by
are defined by
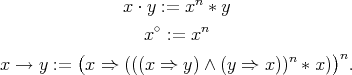
Proof. It remains only to establish the second assertion of the theorem. When 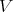 is
is  -potent, the terms realising the pseudo-interior operations on any member of
-potent, the terms realising the pseudo-interior operations on any member of 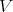 may be obtained by instantiating Theorem 3.6 with the TD term of Proposition 3.4 and simplifying the resulting expressions for
may be obtained by instantiating Theorem 3.6 with the TD term of Proposition 3.4 and simplifying the resulting expressions for  ,
, 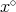 and
and  using the now well-developed arithmetic of commutative, integral residuated lattices [9, 19]. □
using the now well-developed arithmetic of commutative, integral residuated lattices [9, 19]. □
Since the variety of all Nelson 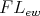 -algebras is 3-potent, from Theorem 3.7 we have
-algebras is 3-potent, from Theorem 3.7 we have
Corollary 3.8. The variety of Nelson algebras is term equivalent to a congruence permutable variety of pseudo-interior algebras with compatible operations. For any 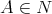 , terms realising the pseudo-interior operations
, terms realising the pseudo-interior operations  ,
,  , and
, and  on
on 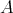 are defined by
are defined by
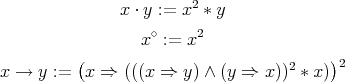
where the derived binary terms  and
and  are defined as in (⇒def) and (∗def) respectively.
are defined as in (⇒def) and (∗def) respectively. 
4. Nelson algebras as bounded BCK-semilattices
In 1963 D. Brignole resolved a problem, posed by A. Monteiro, that asked whether Nelson algebras could be defined in terms of the connectives  ,
, 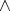 and the constant
and the constant 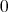 . See [10] or [33, Chapter 1, p. 21]. Let
. See [10] or [33, Chapter 1, p. 21]. Let 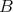 (for Brignole) denote the variety of all algebras
(for Brignole) denote the variety of all algebras 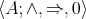 of type
of type 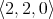 axiomatised by the following collection of identities
axiomatised by the following collection of identities
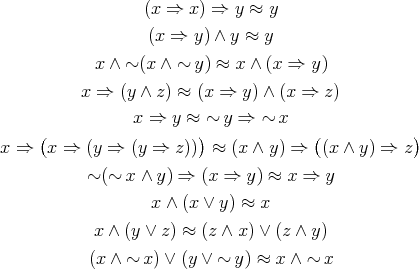
where the derived nullary term  is defined as
is defined as

the derived unary term  is defined as in (2), and the derived binary term
is defined as in (2), and the derived binary term 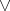 is defined by
is defined by

Brignole established the following result:
Theorem 4.1. [10]
- Let
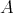 be a Nelson algebra and define the derived binary term
be a Nelson algebra and define the derived binary term  as in (⇒def). Then the term reduct
as in (⇒def). Then the term reduct 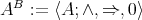 is a member of
is a member of 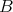 .
. - Let
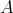 be a member of
be a member of 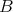 . Define the derived binary terms
. Define the derived binary terms 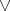 and
and  as in (4) and (2) respectively, the derived unary term
as in (4) and (2) respectively, the derived unary term  as in (2) and the derived nullary term
as in (2) and the derived nullary term  as in (4). Then the term reduct
as in (4). Then the term reduct 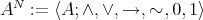 is a Nelson algebra.
is a Nelson algebra. - Let
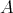 be a Nelson algebra. Then
be a Nelson algebra. Then 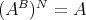 .
. - Let
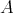 be a member of
be a member of 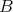 . Then
. Then 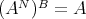 .
.
Hence the variety of Nelson algebras and the variety 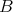 are term equivalent.
are term equivalent. 
A lower BCK-semilattice is an algebra 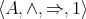 where [27, Lemma 1.6.24]: (i)
where [27, Lemma 1.6.24]: (i) 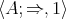 is a BCK-algebra; (ii)
is a BCK-algebra; (ii) 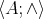 is a lower semilattice; and (iii) for all
is a lower semilattice; and (iii) for all 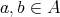 ,
, 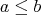 if and only if
if and only if  , where
, where  and
and  denote the semilattice and BCK-algebra partial orderings respectively. Lower BCK-semilattices have been studied in particular by Idziak [16]. A bounded lower BCK-semilattice
denote the semilattice and BCK-algebra partial orderings respectively. Lower BCK-semilattices have been studied in particular by Idziak [16]. A bounded lower BCK-semilattice 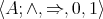 is a lower BCK-semilattice with distinguished least element
is a lower BCK-semilattice with distinguished least element 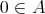 . A (bounded) lower BCK-semilattice is said to be
. A (bounded) lower BCK-semilattice is said to be  -potent if its BCK-algebra reduct is
-potent if its BCK-algebra reduct is  -potent.
-potent.
Let 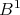 denote the variety of all algebras
denote the variety of all algebras 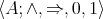 having type
having type 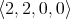 axiomatised by the identities defining
axiomatised by the identities defining 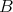 given above together with the identity
given above together with the identity 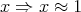 . It is clear that
. It is clear that 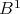 is term equivalent to
is term equivalent to 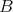 and therefore also to both
and therefore also to both 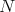 and
and 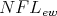 . The following result illuminates Brignole's description of Nelson algebras given in Theorem 4.1 above.
. The following result illuminates Brignole's description of Nelson algebras given in Theorem 4.1 above.
Theorem 4.2. The variety of Nelson algebras is term equivalent to a variety of bounded 3-potent BCK-semilattices.
Proof. It suffices to show any 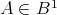 is a bounded 3-potent lower BCK-semilattice. By [29, Theorem 3.7] the
is a bounded 3-potent lower BCK-semilattice. By [29, Theorem 3.7] the 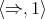 -term reducts of members of
-term reducts of members of 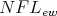 are 3-potent BCK-algebras. Hence
are 3-potent BCK-algebras. Hence 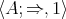 is a 3-potent BCK-algebra. Of course,
is a 3-potent BCK-algebra. Of course, 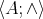 is a lower semilattice. By Rasiowa [25, Theorem V.1.1],
is a lower semilattice. By Rasiowa [25, Theorem V.1.1], 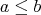 if and only if
if and only if 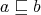 for all
for all 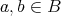 for any Nelson algebra
for any Nelson algebra 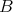 , where
, where  and
and  denote the lattice and BCK-algebra partial orders respectively. Hence the semilattice partial order and the BCK-algebra partial order coincide on
denote the lattice and BCK-algebra partial orders respectively. Hence the semilattice partial order and the BCK-algebra partial order coincide on 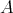 , and
, and 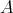 is a 3-potent lower BCK-semilattice. Finally,
is a 3-potent lower BCK-semilattice. Finally, 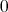 is clearly the least element of
is clearly the least element of 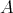 , whence
, whence 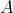 is a bounded 3-potent lower BCK-semilattice. □
is a bounded 3-potent lower BCK-semilattice. □
[1] P. Aglianó, Ternary deduction terms in residuated structures, Acta Sci. Math. (Szeged) 64 (1998), 397-429. [ Links ]
[2] R. Balbes and P. Dwinger, Distributive Lattices, University of Missouri Press, Columbia, 1974. [ Links ]
[3] J. T. Baldwin and J. Berman, The number of subdirectly irreducible algebras in a variety, Algebra Universalis 5 (1975), 379-389. [ Links ]
[4] W. J. Blok and D. Pigozzi, Algebraisable logics, Mem. Amer. Math. Soc. 77 (1989), no. 396.
[5] W. J. Blok and D. Pigozzi, On the structure of varieties with equationally definable principal congruences III, Algebra Universalis 32 (1994), 545-608. [ Links ]
[6] W. J. Blok and D. Pigozzi, On the structure of varieties with equationally definable principal congruences IV, Algebra Universalis 31 (1994), 1-35. [ Links ]
[7] W. J. Blok and J. G. Raftery, On the quasivariety of BCK-algebras and its subvarieties, Algebra Universalis 33 (1995), 68-90. [ Links ]
[8] W. J. Blok and J. G. Raftery, Varieties of commutative residuated integral pomonoids and their residuation subreducts, J. Algebra 190 (1997), 280-328. [ Links ]
[9] K. Blount and C. Tsinakis, The structure of residuated lattices, Internat. J. Algebra Comput. 13 (2003), 437-461. [ Links ]
[10] D. Brignole, Axiomatización de un N-reticulado, Rev. Un. Mat. Argentina XXI (1963), 147-148. [ Links ]
[11] D. Brignole, Equational characterisation of Nelson algebra, Notre Dame J. Formal Logic 10 (1969), 285-297. [ Links ]
[12] W. H. Cornish, Varieties generated by finite BCK-algebras, Bull. Austral. Math. Soc. 22 (1980), 411-430. [ Links ]
[13] W. H. Cornish, On Iséki's BCK-algebras, in Algebraic Structures and Applications: Proceedings of the First Western Australian Conference on Algebra (P. Schultz, C. E. Praeger, and R. P. Sullivan, Eds.), Lecture Notes in Pure and Applied Mathematics, no. 74, Marcel Dekker, New York, 1982, pp. 101-122. [ Links ]
[14] A. Dvurečenskij and M. G. Graziano, On representations of commutative BCK-algebras, Demonstratio Math. 32 (1999), 227-246. [ Links ]
[15] E. Fried, G. Grätzer and R. Quackenbush, Uniform congruence schemes, Algebra Universalis 10 (1980), 176-188. [ Links ]
[16] P. Idziak, Lattice operations in BCK-algebras, Mathematica Japonica 29 (1984), 839-846. [ Links ]
[17] K. Iséki and S. Tanaka, An introduction to the theory of BCK-algebras, Mathematica Japonica 23 (1978), 1-26. [ Links ]
[18] T. Kowalski, Semisimplicity, EDPC and discriminator varieties of residuated lattices, Studia Logica 77 (2004), 255-265. [ Links ]
[19] T. Kowalski and H. Ono, Residuated Lattices: An Algebraic Glimpse at Logics without Contraction, Manuscript, 2000, 67 pp. [ Links ]
[20] J. S. Olson, Finiteness conditions on varieties of residuated structures, Ph.D. thesis, University of Illinois at Chicago, 2006. [ Links ]
[21] H. Ono and Y. Komori, Logics without the contraction rule, J. Symbolic Logic 50 (1985), 169-201. [ Links ]
[22] H. Ono, Logics without contraction rule and residuated lattices I, Festschrift of Prof. R. K. Meyer, To appear. [ Links ]
[23] H. Ono, Substructural logics and residuated lattices — an introduction, in Trends in Logic: 50 Years of Studia Logica, Kluwer Academic Publishers, Dordrecht, 2003, pp. 193-228.
[24] A. F. Pixley, Characterisation of arithmetical varieties, Algebra Universalis 9 (1979), 87-98. [ Links ]
[25] H. Rasiowa, An Algebraic Approach to Non-Classical Logics, Studies in Logic and the Foundations of Mathematics, no. 78, North-Holland Publ. Co., Amsterdam, 1974. [ Links ]
[26] A. Sendlewski, Some investigations of varieties of 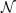 -lattices, Studia Logica 43 (1984), 257-280. [ Links ]
-lattices, Studia Logica 43 (1984), 257-280. [ Links ]
[27] M. Spinks, Contributions to the theory of pre-BCK-algebras, Ph.D. thesis, Monash University, 2003. [ Links ]
[28] M. Spinks, Ternary and quaternary deductive terms for Nelson algebras, Algebra Universalis 51 (2004), 125-136. [ Links ]
[29] M. Spinks and R. Veroff, Constructive logic with strong negation is a substructural logic over 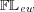 , I, Studia Logica, To appear. [ Links ]
, I, Studia Logica, To appear. [ Links ]
[30] M. Spinks and R. Veroff, Constructive logic with strong negation is a substructural logic over 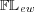 , II, Studia Logica, To appear. [ Links ]
, II, Studia Logica, To appear. [ Links ]
[31] D. Vakarelov, Notes on 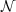 -lattices and constructive logic with strong negation, Studia Logica 36 (1977), 109-125. [ Links ]
-lattices and constructive logic with strong negation, Studia Logica 36 (1977), 109-125. [ Links ]
[32] C. J. van Alten and J. G. Raftery, Rule separation and embedding theorems for logics without weakening, Studia Logica 76 (2004), 241-274. [ Links ]
[33] I. D. Viglizzo, Algebras de Nelson, Tesis de Magister en Matemática, Universidad Nacional del Sur, Bahía Blanca, 1999. [ Links ]
[34] A. Wroński, BCK-algebras do not form a variety, Mathematica Japonica 28 (1983), 211-213. [ Links ]
Matthew Spinks
Department of Education,
University of Cagliari,
Cagliari 09123 Italy
mspinksau@yahoo.com.au
Robert Veroff
Department of Computer Science,
University of New Mexico,
Albuquerque, NM 87131 USA
veroff@cs.unm.edu
Recibido: 3 de mayo de 2005
Aceptado: 28 de marzo de 2007