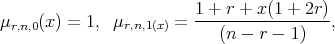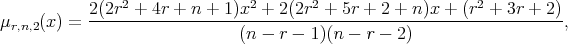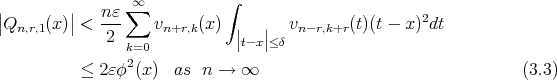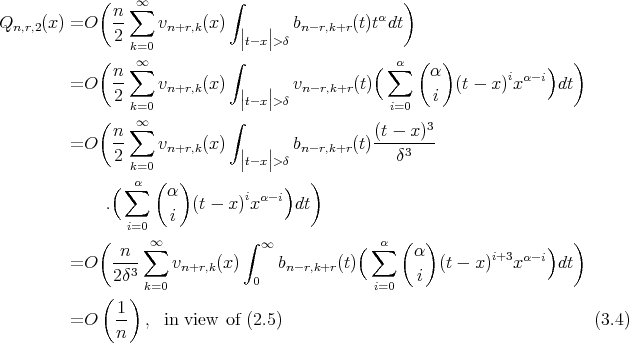Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.48 n.1 Bahía Blanca ene./jun. 2007
Voronovskaya Type Asymptotic Formula For Lupaş-Durrmeyer Operators
Naokant Deo
Abstract. In the present paper, we study some direct results in simultaneous approximation for linear combinations of Lupaş-Beta type operators.
2000 Mathematics Subject Classification. 41A35.
Key words and phrases. Lupaş operator, Linear combinations, Voronovskaya formula.
This research is supported by CAS-TWAS Postdoctoral Fellowship, (Chinese Academy of Sciences, Beijing, China and ICTP, Trieste, Italy).
Permanent address of author: Department of Applied Mathematics, Delhi College of Engineering, Bawana Road, Delhi-110042, India.
The Bernstein-Durrmeyer 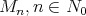 (the set of non-negative integers), were introduced by Durrmeyer [2] and independently by Lupaş [5]. For a function
(the set of non-negative integers), were introduced by Durrmeyer [2] and independently by Lupaş [5]. For a function ![f ∈ L1[0,1]](/img/revistas/ruma/v48n1/1a062x.png) they are defined by
they are defined by
![∫ ∑n 1 (Mnf )(x) = (n + 1) pn,k(x) pn,k(t)f(t)dt, x ∈ [0,1], k=0 0](/img/revistas/ruma/v48n1/1a063x.png)
where
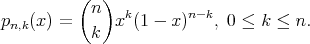
Later, starting with this integral modification of Bernstein polynomials, Heilmann [3] first defined modified Lupaş operators (see also Heilmann and Müller [4] as well as Sinha et al. [7]). More recently the present author [1] studied another modification of Lupaş operators. Now we consider Beta operator as a weight function on  namely,
namely,
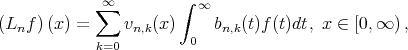 | (1.1) |
where 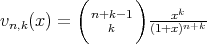 and
and
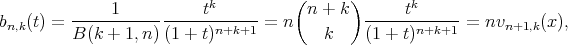
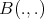 denoting the Beta function. Therefore
denoting the Beta function. Therefore
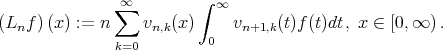 |
Let us remark that many years ago W. Meyer-König and K. Zeller [6] have introduced, in order to approximate functions 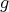 from
from ![C [0,1 ]](/img/revistas/ruma/v48n1/1a0612x.png) , the so-called Bernstein-power series
, the so-called Bernstein-power series 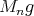 defined as
defined as
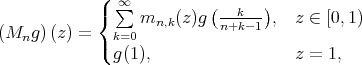 |
with 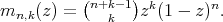 Because
Because 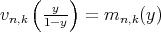 , we see that
, we see that
![( ) ∑∞ ∫ 1 ( ) (Lnf ) --y--- = n mn,k(y ) mn,k (T)f --T--- dT, y ∈ [0,1]. 1 - y k=0 0 1 - T](/img/revistas/ruma/v48n1/1a0617x.png)
The main object of this paper is to establish a Voronovskaya type asymptotic formula and an error estimate for the linear combination of the operators (1.1).
In this section, we shall give certain definition and lemmas which will be used in the sequel.
For every 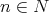 and
and 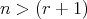 we have
we have
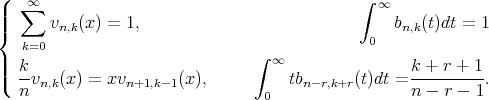 | (2.1) |
Lemma 2.1. Let 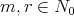 (the set of non-negative integers), we define
(the set of non-negative integers), we define
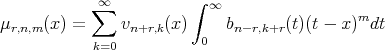
then
|
| (2.2) |
|
| (2.3) |
and there holds the recurrence relation:
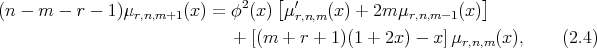
where 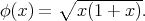 Consequently, for each
Consequently, for each 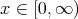
![( -[(m+1 )∕2]) μr,n,m(x) = O n .](/img/revistas/ruma/v48n1/1a0628x.png) | (2.5) |
Proof. We can easily obtain (2.2) and (2.3) by using the definition of 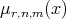 . For the proof of (2.4), we proceed as follows. First
. For the proof of (2.4), we proceed as follows. First
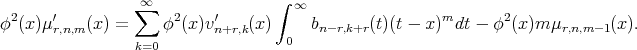
Now, using relations
![2 ′ 2 ′ φ (x)vn,k(x) = (k - nx )vn,k(x) and φ (t)bn,k(t) = [k - (n + 1)t]bn,k(t),](/img/revistas/ruma/v48n1/1a0631x.png)
we obtain
![[ ] φ2 (x) μ′r,n,m(x ) + m μr,n,m -1(x) ∞ ∫ ∞ = ∑ [k - (n + r)x ]v (x ) b (t)(t - x)mdt n+r,k 0 n- r,k+r k=0 ∫ ∑∞ ∞ m = vn+r,k(x ) [(k + r) - (n + 1 - r)t]bn- r,k+r(t)(t - x) dt k=0 0 + [x - r(1 + 2x)]μr,n,m(x ) + (n + 1 - r)μr,n,m+1 (x ) ∞ ∫ ∞ = ∑ v (x ) t(1 + t)b′ (t)(t - x)mdt + [x - r(1 + 2x)]μ (x ) n+r,k 0 n- r,k+r r,n,m k=0 + (n + 1 - r)μr,n,m+1(x) ∑∞ ∫ ∞ [ ] = vn+r,k(x ) (2x + 1)(t - x) + (t - x)2 + (x + 1)x b′n- r,k+r(t)(t - x)mdt k=0 0 + [x - r(1 + 2x)]μr,n,m(x ) + (n + 1 - r)μr,n,m+1 (x ) = - (2x + 1)(m + 1)μr,n,m(x) - (m + 2)μr,n,m+1(x) - m φ2(x)μr,n,m- 1(x ) + [x - r(1 + 2x)]μr,n,m(x ) + (n + 1 - r)μr,n,m+1 (x ).](/img/revistas/ruma/v48n1/1a0632x.png)
This leads to (2.4). The proof of (2.5) easily follow from (2.2) and (2.4). □
Lemma 2.2. If 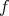 is differentiable
is differentiable  times
times 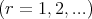 on
on 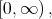 then we get
then we get
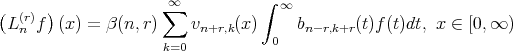 | (2.6) |
where
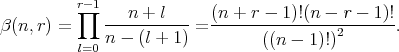
Proof. By using the Leibniz theorem, we obtain
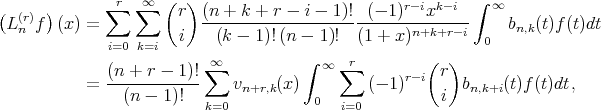
using again Leibniz theorem, we get
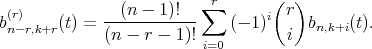
Thus
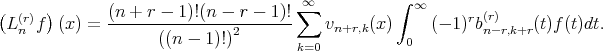
On integrating  times by parts, we get the required result. □
times by parts, we get the required result. □
3. Voronovskaya Asymptotic Formula
Theorem 3.1. Let  integrable in
integrable in 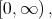 admits its
admits its 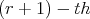 and
and 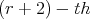 derivatives, which are bounded at a fixed point
derivatives, which are bounded at a fixed point 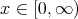 and
and  as
as 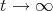 for some
for some  then
then
![[ 1 ( ) ] lim n ------- L (rn)f (x )- f (r)(x) = {1 + r + x(1+ 2r)}f(r+1 )(x) + 2φ2(x)f (r+2)(x), n→ ∞ β(n, r)](/img/revistas/ruma/v48n1/1a0651x.png)
where
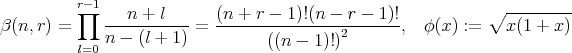
Proof. Using Taylor's formula, we have
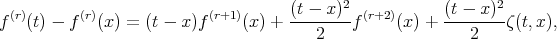 | (3.1) |
where
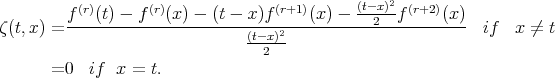
Now, for arbitrary 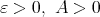 there exists a
there exists a 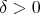 such that
such that
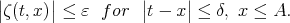 | (3.2) |
Using the value of (2.6) in (3.1), we get
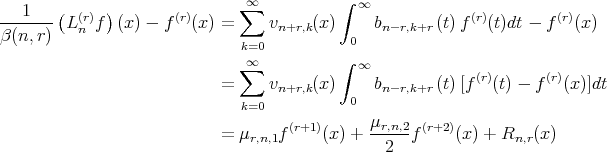
where
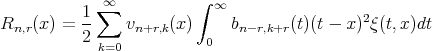
In order to completely prove the theorem, it is sufficient to show that

Now
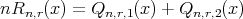
where
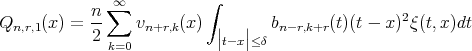
and
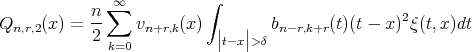
Finally we estimate 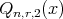 , using the assumption of theorem,
, using the assumption of theorem,
Thus, from (3.3) and (3.4), we have
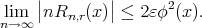
Since  is arbitrary, therefore
is arbitrary, therefore
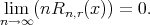
This completes the proof. □
Theorem 3.2. Let 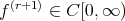 and
and ![[0,λ ] ⊆ [0,∞ )](/img/revistas/ruma/v48n1/1a0671x.png) and let
and let 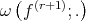 be the modulus of continuity of
be the modulus of continuity of 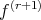 then for
then for 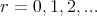
![∥ ∥ ∥∥ ---1---( (r) ) (r)∥∥ ∥ β(n,r ) L n f - f ∥ C[0,λ]](/img/revistas/ruma/v48n1/1a0675x.png)
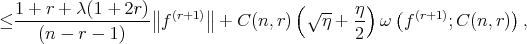
where the norm is sup-norm over ![[0,λ]](/img/revistas/ruma/v48n1/1a0677x.png) ,
,
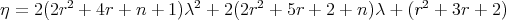
and
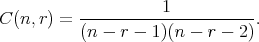
Proof. Applying the Taylor formula
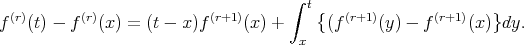
Thus
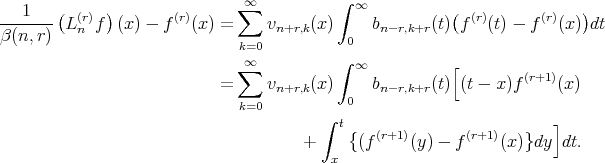
Since,
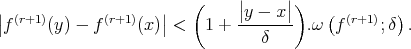
Hence, by Schwartz's inequality
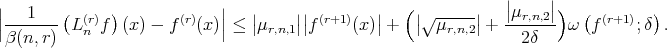
Further, choosing 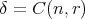 and using Lemma 2.1, we get the required result. □
and using Lemma 2.1, we get the required result. □
Acknowledgement. The author is extremely grateful to the referee for making valuable suggestions leading to the better presentation of the paper.
[1] Deo N., Direct result on the Durrmeyer variant of Beta operators, Southeast Asian Bull. Math.,32 (2008) (in press). [ Links ]
[2] Durrmeyer J. L., Une formule d'inversion de la transformée de Laplace-applications à la théorie des moments, Thése de 3e cycle, Faculté des Sciences de l' Université de Paris, (1967). [ Links ]
[3] Heilmann M., Approximation auf [0,∞) durch das Verfahren der Operatoren vom Baskakov-Durrmeyer Typ, Dissertation, Universität Dortmund, (1987).
[4] Heilmann M. and Müller M. W., On simultaneous approximation by the method of Baskakov-Durrmeyer operators, Numer. Funct. Anal. and Optimiz., 10(1989), 127-138. [ Links ]
[5] Lupaş A., Die Folge der Betaoperatoren, Dissertation, Universität Stuttgart, (1972). [ Links ]
[6] Meyer-Köning W. and Zeller K. “Bernsteinsche Poetnzreihen”, Studia Math., 19(1960), 89-94, (see also E. W. Cheney and A. Sharma)
[7] Sinha R. P., Agrawal P. N. and Gupta V., On simultaneous approximation by modified Baskakov operators, Bull. Soc. Math. Belg. Ser. B, 42(2)(1991), 217-231. [ Links ]
Naokant Deo
School of Information Science and Engineering, Graduate University of Chinese Academy of Sciences, Zhongguancun Nan Yi Tiao No. 3, Haidian District, Beijing-100080, P. R. China.
dr_naokant_deo@yahoo.com
Recibido: 29 de septiembre de 2006
Aceptado: 28 de marzo de 2007