The Boltzmann equation with Force Term near the Vacuum

Rafael Galeano Andrades

Abstract. We prove a theorem of existence, uniqueness and positivity of the solution for the Boltzmann equation with force term and initial data near the Vacuum.

Key words and phrases. Force Term, Boltzmann equation, Near the vacuum

This article is a result of the project of investigation ”Evolution of Equations of Kinetic Type”, financed by the University of Cartagena.

1. INTRODUCTION

The aim in this article it is prove global existence of the problem for small data (near to the vacuum) in the case of a solid sphere. For the density 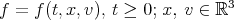,we write the equation of Boltzmann:

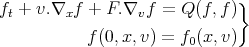(1)

Let us also consider the following problem:

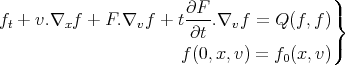(2)

where

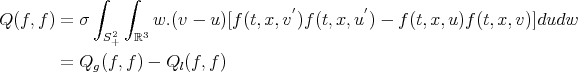
here 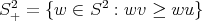, is a constant proportional to the area of the sphere and

.

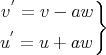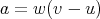The Conservation momentum is given by

and the Energy of conservation is

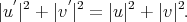
We write 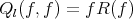, where

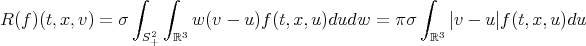
Let 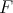be a vectorial field not depending on f such that:

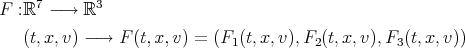
and for a given , let

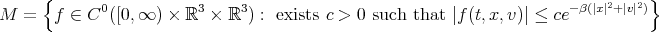
with norm

This makes 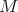into a Banach Space [8].

To solve problem (2) we introduce the following notation:

(3)

with F differentiable with regard to time. Therefore

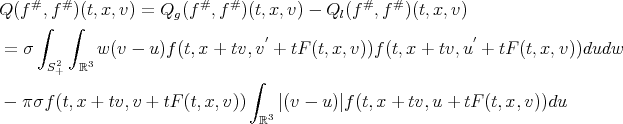
we write the equation (1) as

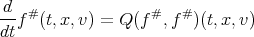(4)

Integrating (3) with respect to time, we obtain

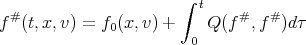(5)

We observe that if F is constant in time, (2) reduces to (1). We will prove the following theorems:

Theorem 1. There exists a constant 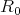, such that if 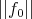and 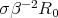are sufficiently small and 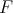is differentiable with regard to the time 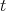, then the equation (4) has a unique solution .

Theorem 2. Let us consider

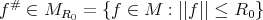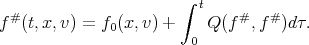(6)

There are constants and 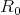such that if 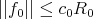and 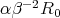are sufficiently small, then the equation (5) has a unique non-negative solution .

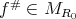To solve problem (1) we consider:

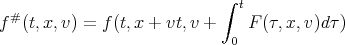(7)

Assuming F integrable with regard to the time and therefore

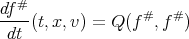(8)

and integrating we obtain again (5) and the theorems are completed, but with F integrable with regard to the time.
This topic is developed in [4], as well as in the articles [11], [9], [5] and [15].  

Article [11] refers to a gas with a strong sphere and to a initial condition which tends exponentially to zero at infinity in phase space. Article [9] generalizes results of [11] to the Boltzmann equation with interaction potential between two particles. In both articles, the mass of the gas is infinite. In another direction the result of [5] refers to a gas with infinite mass where the initial condition is assumed to decay in a physical space with behavior of power inverse. In this case for sufficiently small decay the mass of the gas can be infinite. Another generalization is given in the article [15] where global existence is proven for initial conditions decaying with behavior of power inverse in the whole phase space. The articles [5] and [13] refer both to Boltzmann equation with interaction of general potential for the couples of internal forces of particles. Besides these previously mentioned articles, we also have to mention two results given by Polewczak. In the first one [13], the author generalizes the theory of previously limited existence to the case of mild solution, also to the case of classic solution. In the second [14] the mathematical results are generalized to the case of initial conditions with more general decay at infinity in phase space.

On the Problem of Cauchy with field of External force

First, let us consider the spatially inhomogeneous equation for neuter particles in a force field 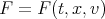. In relationship with this topic we should mention the article of Asano [1] in which local existence is proven for general initial conditions. The formulation of Asano is the starting point of all the studies developed in this article.  

Some studies of the problem can be seen in the articles [2], [7], [10] and [6]. In particular, the articles of Asano [2] and Grunfeld [7] provide a global existence proof for the solution with initial condition close to equilibrium and a conservative force field. Hamdache [10] gives us a result with initial conditions decaying exponentially to zero at infinity in phase space and trajectories prescribed by a oscillating field. In [6] it is given a result of global existence for decaying conditions and for a force field acting in an interval of time with 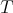big, but finite. Recently in [12] Lions developed the problem of Cauchy in 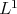in the presence of an external field. The important aspect of the result in [12] is that refers to force fields depending on the distribution function, this case is entirely different from the cases previously prescribed.  

This article divides into two parts, the first one has to do with a theorem which, as opposed to the articles previously mentioned, solves the problem for fields differentiable with regard to time, and subsequently we extend it to a theorem of positivity of the solutions.

Demonstration of the theorem 1. Indeed, let us consider :

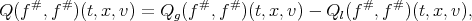
where

(a)

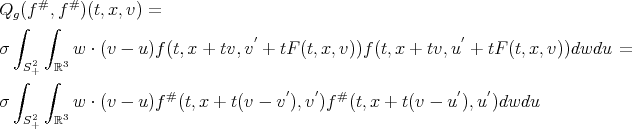
(b)

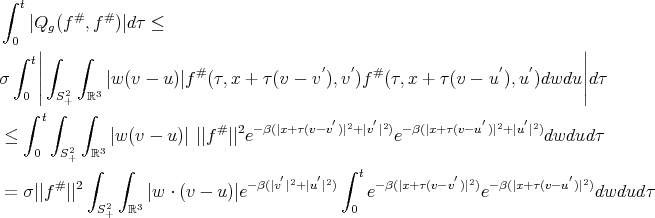
now

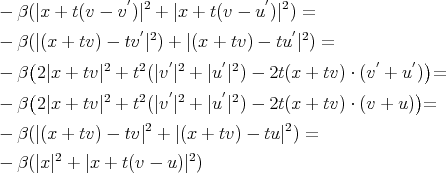
therefore

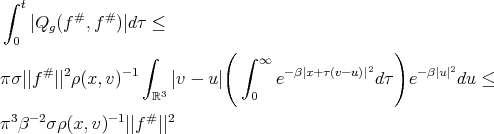
(c)

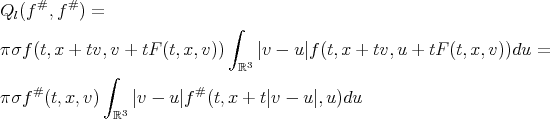
(d)

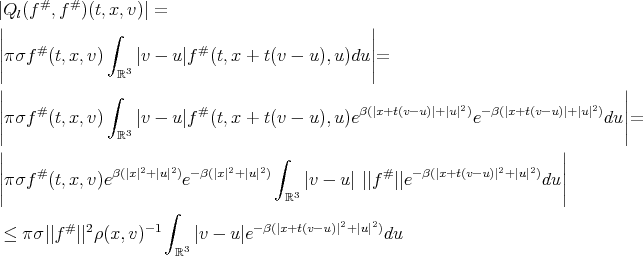
here 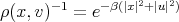, therefore

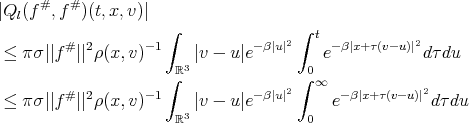
now 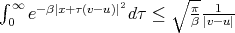; [8, pag. 28]

This is,

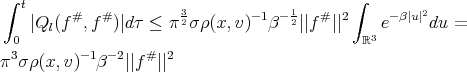
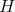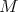(e) We define the operator on by

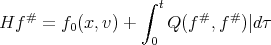
and let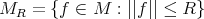

The previous estimates show that if 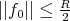and 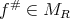, then

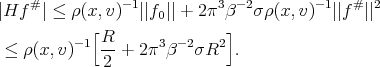
We choose 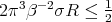. Therefore 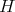applies 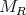into itself for 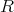sufficiently small. Now 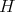is a contraction on 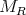. Since the elements of 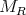are continuous, by the fixed point theorem the statement is proven. □

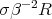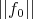Demonstration of the theorem 2. If and are sufficiently small, then

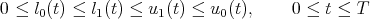(9)

and therefore the system

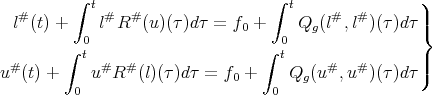(10)

has a unique global solution 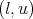with 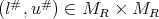. Indeed, if

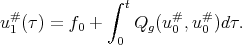
This is , with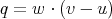

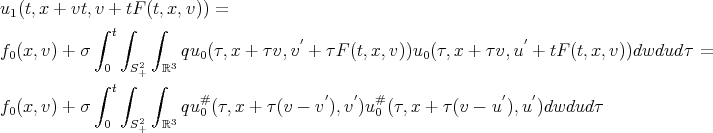
That is, condition (6) is true if

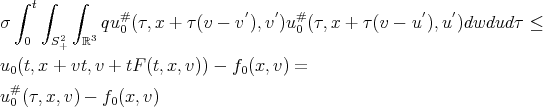
If we define 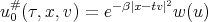, we have that

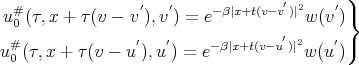and therefore

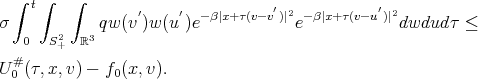
We write 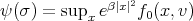. This is

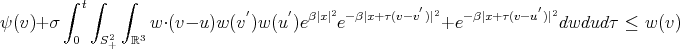(11)

We want a non negative solution 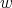for (8), and a sufficient condition is:

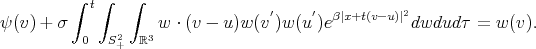
This is

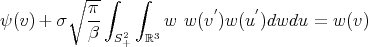(12)

To prove the existence of a solution 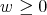of (9 ) let us consider the space

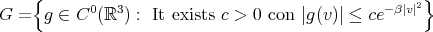
with norm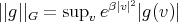

Let us consider the operator 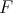defined on by:

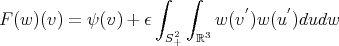
with .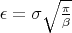
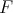applies a sufficiently small ball in 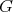into itself. Indeed, let 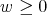, since 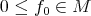, 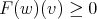and

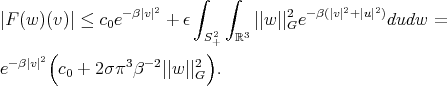
This is, for such 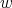, 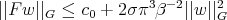. Therefore for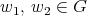

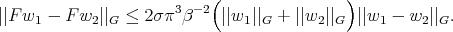
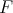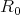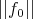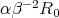Namely, applies non-negative functions in the ball of radius into itself, and it is a contraction there if and are sufficiently small.

As 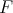is a contraction, 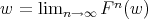, we can take 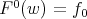, and the solution for (9) is non-negative.

It remains to show that . By definition

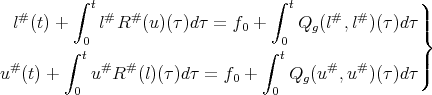then

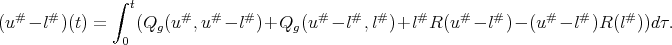
This is 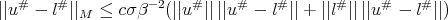. Now 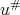, 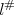both are in 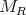and in this way 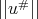and 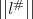are bounded by 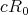; therefore the conclusion follows if 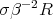is sufficiently small. □

Bibliography

[1]    ASANO K. Local solutions to the initial and initial Boundary value Problem for the Boltzmann equation with and external force. J. Math. Kyoto Univ., 24 (1984), 225-247.        [ Links ]

[2]    ASANO K. Global Solutions to the initial boundary value Problem for the Boltzmann equation with an external force. Transp. Theory Statist. Phys., 16 (1987), 735-761.        [ Links ]

[3]    ARLOTTI, BELLOMO N., LACHOWICZ M., POLEWCZAK J., WAHIS Lecture notes on the mathematical theory of the Boltzmann equation. Series on advances in mathematics for applied Sciences, 33 World Scientific (1998).        [ Links ]

[4]    BELLOMO N., PALCZEWSKI A., TOSCANI G. Mathematical Topics in nonlinear kinetic Theory. World Scientific, (1998).        [ Links ]

[5]    BELLOMO N. and TOSCANI G.On the Cauchy Problem for the nonlinear Boltzmann equation: Global existence, uniqueness and asymptotic behaviour. J. Math. Phys., 26 (1985) 334-33.        [ Links ]

[6]    BELLOMO N., LACHOWICZ M., PALCZEWSKI A., TOSCANI G. On the initial value problem for the Boltzmann equation with force term. Transp. Theory Statist. Phys., 18 (1989), 87 - 102.        [ Links ]

[7]    GRUNFELD C. P.On the Nonlinear Boltzmann equation with force term. Transp. Theory Statist Phys, 14 (1985), 291-322.        [ Links ]

[8]    GLASSEY ROBERT.The Cauchy Problem in kinetic theory. SIAM        [ Links ]

[9]    HAMDACHE R.Existence in the Large and Asymptotic behaviour for the Boltzmann equation. Japan J. Appl. Math., 2 (1985),1-15.        [ Links ]

[10]    HAMDACHE R. Thése, Univ.Pierre et Marie Curie. Paris 1988.        [ Links ]

[11]    ILLNER R., SHIMBROT M. The Boltzman equation: Global existence for a rare gas in an Infinite Vacuum. Commun. Math. Phys. 95 (1984), 117-126.        [ Links ]

[12]    LIONS P. L. Compactness in Boltzmann equation via Fourier integrals operator and applications III. J. Math. Kyoto Univ.,34(1994), 539-584.        [ Links ]

[13]    POLEWCZAK J. Classical solution of the nonolinear Boltzmann equation in all 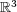: asymptotic behaviour of solution. J. Stat. Phys,50 (1988), 611-632.        [ Links ]

[14]    POLEWCZAK J. New estimates of the nonlinear Boltzmann operator and their application to existence theorem. Transp. Theory Statist. Phys., 18(1988), 235-247.        [ Links ]

[15]    TOSCANI G.On the Boltzmann equation in unbounded domains. Arch. Rat. Mech. Anal. 95(1996),37-49.        [ Links ]

Rafael Galeano Andrades Programa de Matemáticas, Universidad de Cartagena,
rgaleanoa@unicartagena.edu.co

Recibido: 9 de noviembre de 2006
Aceptado: 15 de agosto de 2007