Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.48 n.2 Bahía Blanca jul./dic. 2007
Group actions on algebras and module categories
J. A. de la Peña
Introduction and notations
Let 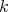 be a field and
be a field and 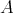 a finite dimensional (associative with
a finite dimensional (associative with  )
) 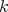 -algebra. By
-algebra. By 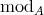 we denote the category of finite dimensional left
we denote the category of finite dimensional left  -modules. In many important situations we may suppose that
-modules. In many important situations we may suppose that  is presented as a quiver with relations
is presented as a quiver with relations 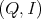 (e.g. if
(e.g. if 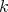 is algebraically closed, then
is algebraically closed, then 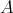 is Morita equivalent to
is Morita equivalent to 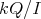 ). We recall that if
). We recall that if 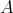 is presented by
is presented by 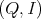 , then
, then  is a finite quiver and
is a finite quiver and 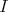 is an admissible ideal of the path algebra
is an admissible ideal of the path algebra 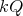 , that is,
, that is, 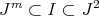 for some
for some 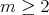 , where
, where 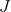 is the ideal of
is the ideal of 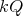 generated by the arrows of
generated by the arrows of  , see [6].
, see [6].
It is convenient to consider 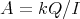 as a
as a 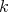 -linear category with objects
-linear category with objects 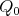 (= vertices of
(= vertices of  ) and morphisms given by linear maps
) and morphisms given by linear maps 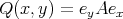 , where
, where 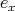 is the trivial path at
is the trivial path at 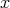 (for
(for 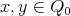 ). In this categorical approach we do not need to assume that
). In this categorical approach we do not need to assume that  is finite (therefore the
is finite (therefore the 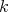 -algebra
-algebra 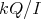 may not have unity). Ocasionally we write
may not have unity). Ocasionally we write  if we do not need to explicit the quiver
if we do not need to explicit the quiver  .
.
The purpose of these notes is to present an introduction to the study of actions of groups on algebras 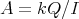 and their module categories
and their module categories 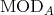 and to consider associated constructions that have proved useful in the Representation Theory of Algebras.
and to consider associated constructions that have proved useful in the Representation Theory of Algebras.
A symmetry of the quiver  is a permutation of the set of vertices
is a permutation of the set of vertices 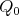 inducing an automorphism of
inducing an automorphism of  . We denote by
. We denote by 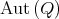 the group of all symmetries of
the group of all symmetries of  . Those symmetries
. Those symmetries 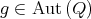 inducing a morphism
inducing a morphism 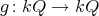 such that
such that 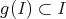 form the group
form the group 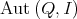 . In natural way, any
. In natural way, any 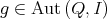 induces an automorphism of the module category
induces an automorphism of the module category 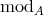 and on the Auslander-Reiten quiver
and on the Auslander-Reiten quiver 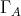 of
of 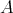 (since the action commutes with the Auslander-Reiten translation
(since the action commutes with the Auslander-Reiten translation 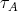 of
of 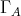 ).
).
In section 1, we present some basic facts about the actions of groups 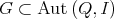 on
on 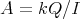 (orbits, stabilizers, Burnside's lemma) and show that for a representation-finite standard algebra
(orbits, stabilizers, Burnside's lemma) and show that for a representation-finite standard algebra 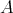 , we have
, we have 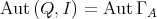 , where
, where 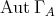 is formed by the symmetris of
is formed by the symmetris of 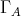 commuting with the translation
commuting with the translation 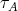 . We recall that
. We recall that 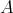 is standard if
is standard if 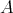 is representation-finite and for a choice of representatives of the isoclasses of indecomposables, the induced full subcategory of
is representation-finite and for a choice of representatives of the isoclasses of indecomposables, the induced full subcategory of 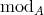 (denoted by
(denoted by 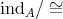 ) is equivalent to
) is equivalent to 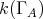 which is the quotient of the path algebra
which is the quotient of the path algebra 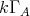 by the ideal generated by the meshes
by the ideal generated by the meshes 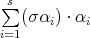 of the almost split sequences
of the almost split sequences 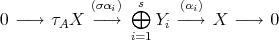 . We recall that for
. We recall that for 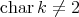 , any representation-finite algebra
, any representation-finite algebra 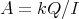 is standard.
is standard.
In section 2 we consider relations between the structure of 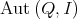 and the Coxeter polynomial of
and the Coxeter polynomial of 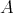 (recall that,
(recall that, 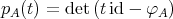 is the Coxeter polynomial associated to the Coxeter matrix
is the Coxeter polynomial associated to the Coxeter matrix 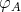 which is
which is  -invertible in case
-invertible in case 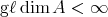 ).
).
In section 3 we present the main constructions associated to groups acting on algebras:
 if
if 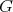 acts freely on
acts freely on 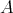 (that is,
(that is, 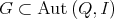 and
and 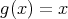 for a vertex
for a vertex 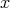 , implies
, implies  ), then the Galois covering
), then the Galois covering 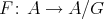 is a
is a 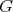 -invariant functor of
-invariant functor of 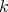 -categories.
-categories.
 if
if 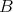 is a
is a 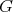 -graded
-graded 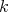 -category, the smash product
-category, the smash product  is a
is a 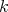 -category accepting the free action of
-category accepting the free action of 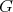 . Moreover,
. Moreover, 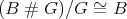 .
.
Galois coverings were introduced by Bongartz and Gabriel [6, 7, 2] for the study of representation type of algebras. Smash products is a well-known construction in ring theory (see [1]), but only recently was observed by Cibils and Marcos [4] that it yields the inverse operation to Galois coverings. Indeed, if 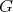 acts freely on
acts freely on 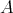 , then
, then 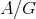 is a
is a 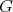 -graded category such that
-graded category such that 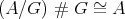 .
.
In section 4, following [2], we introduce functors relating the module categories of 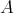 and
and 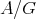 when
when 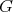 acts freely on
acts freely on 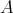 . The main results in these notes (section 5) relate the representation types of
. The main results in these notes (section 5) relate the representation types of 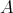 and
and 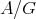 (which was the original purpose of the introduction of Galois coverings). Indeed, given a Galois covering
(which was the original purpose of the introduction of Galois coverings). Indeed, given a Galois covering 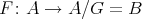 with
with 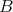 a finite dimensional
a finite dimensional 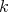 -algebra, then
-algebra, then 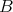 is representation-finite if and only if
is representation-finite if and only if 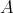 is locally representation-finite (that is, for each
is locally representation-finite (that is, for each 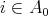 , there are only finitely many indecomposable
, there are only finitely many indecomposable 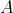 -modules
-modules 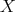 , up to isomorphism, with
, up to isomorphism, with 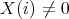 ). The proof of this result was partially given in [7] and completed in [10], and provides an efficient tool to deal with representation-finite algebras.
). The proof of this result was partially given in [7] and completed in [10], and provides an efficient tool to deal with representation-finite algebras.
The representation-infinite situation is more involved. We recall that 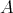 is said to be tame if for every
is said to be tame if for every 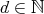 there are finitely many
there are finitely many ![A - k[t]](/img/revistas/ruma/v48n2/2a02114x.png) -bimodules
-bimodules 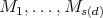 wich are free finitely generated as right
wich are free finitely generated as right ![k[t]](/img/revistas/ruma/v48n2/2a02116x.png) -modules and such that any indecomposable
-modules and such that any indecomposable 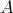 -module
-module 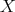 with dimension
with dimension 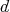 is of the form
is of the form ![Mi ⊗k [t] (k[t]∕(t - λ))](/img/revistas/ruma/v48n2/2a02120x.png) for some
for some 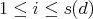 and some
and some 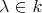 . We say that a tame algebra
. We say that a tame algebra 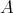 is domestic (resp. of polynomial growth) if
is domestic (resp. of polynomial growth) if 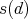 can be chosen
can be chosen 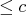 (resp.
(resp. 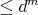 for some
for some 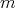 ) for all
) for all 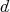 . It is not hard to show that
. It is not hard to show that 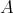 is tame if
is tame if 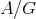 is tame for a group acting freely on
is tame for a group acting freely on 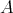 . The converse was shown to be false in [8]; nevertheless there are many interesting, general situations where it holds true.
. The converse was shown to be false in [8]; nevertheless there are many interesting, general situations where it holds true.
In section 5 we give examples of results [5, 12] showing that for a Galois covering  , the category
, the category 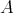 is tame if and only if
is tame if and only if 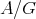 is tame, provided certain restrictions on the group
is tame, provided certain restrictions on the group 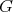 or on the category
or on the category 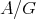 are satisfied.
are satisfied.
We denote by 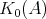 the Grothendieck group of
the Grothendieck group of 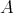 , freely generated by representatives
, freely generated by representatives  of the simple
of the simple 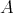 -modules, where
-modules, where 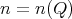 is the number of vertices of
is the number of vertices of  . We denote
. We denote 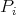 (resp.
(resp. 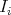 ) the projective cover (resp. injective envelope) of
) the projective cover (resp. injective envelope) of 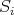 . With the categorical approach an
. With the categorical approach an 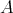 -module is a functor
-module is a functor 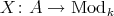 , and a morphism
, and a morphism 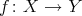 is a natural transformation. In case
is a natural transformation. In case 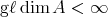 , the Coxeter matrix
, the Coxeter matrix 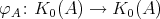 is defined by
is defined by ![φ ([P ]) = - [I] A i i](/img/revistas/ruma/v48n2/2a02151x.png) .
.
These notes follow closely the lectures given at the Workshop on Representation Theory in Mar del Plata, Argentina in March 2006. The intention of the lectures was to present an elementary introduction to the topic which would serve as a source of motivation and information on the techniques used. While we cannot provide complete proofs of every result, we tried to sketch some representative arguments. We thank the organizers of the Workshop for his hospitality.
1. The group of automorphisms of an algebra
1.1. Let 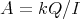 be a finite dimensional
be a finite dimensional 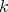 -algebra:
-algebra:
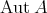 denotes the group of automorphisms of
denotes the group of automorphisms of 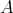 . By
. By 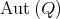 we denote the group of symmetries of
we denote the group of symmetries of  and by
and by 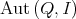 the group of symmetries of
the group of symmetries of  fixing
fixing 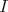 (that is,
(that is, 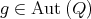 induces
induces 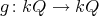 such that
such that 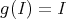 ).
).
- Lemma.
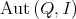 is a subgroup of
is a subgroup of 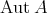 .
. 
Each symmetry 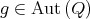 gives rise to a matrix
gives rise to a matrix 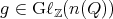 sending
sending 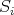 to
to 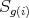 . This representation
. This representation  is called the canonical representation.
is called the canonical representation.
1.2. Let 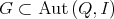 be a subgroup. For a given
be a subgroup. For a given 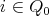 ,
, 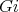 denotes the orbit of
denotes the orbit of 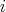 and subgroup of
and subgroup of 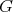 ,
, 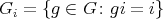 denotes the stabilizer of
denotes the stabilizer of 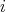 . Clearly
. Clearly 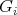 is a subgroup of
is a subgroup of 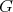 .
.
- Lemma.
- The mapping
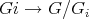 ,
, 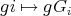 is a bijection from the orbit to the set of left cosets
is a bijection from the orbit to the set of left cosets 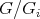 .
. 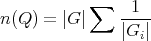

1.3. Let 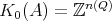 be the Grothendieck group of
be the Grothendieck group of 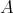 . Consider
. Consider

 -space of
-space of 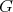 -invariant vectors. Then
-invariant vectors. Then 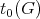 the number of orbits of
the number of orbits of 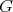 in
in 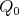 equals
equals  .
. Let  be a set of representatives of the irreducible
be a set of representatives of the irreducible  -representations of
-representations of 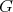 (here
(here 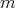 is the number of conjugacy classes of
is the number of conjugacy classes of 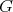 ). Let
). Let 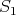 be the trivial representation.
be the trivial representation.
Consider 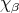 the character corresponding to
the character corresponding to 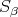 (that is,
(that is, 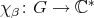 ,
, 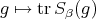 ). The characters
). The characters 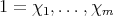 form an orthonormal basis of the class group
form an orthonormal basis of the class group 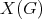 , with the scalar product
, with the scalar product 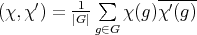 .
.
- Lemma.
- [Burnside's lemma].
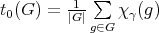 where
where 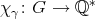 , is the character of the canonical representation
, is the character of the canonical representation 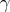 .
.
Proof. Observe that 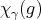 is the number of fixed points of
is the number of fixed points of  .
.
 . □
. □ 1.4. Let 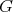 be a subgroup of
be a subgroup of 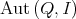 then
then 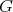 acts on
acts on 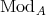 as follows:
as follows:
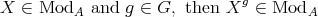
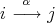 , we have
, we have 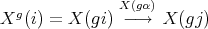 . Similarly, for
. Similarly, for 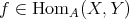 , we define
, we define 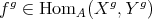 .
. Clearly, this action preserves indecomposable modules and induces an action of 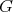 of the Auslander-Reiten quiver
of the Auslander-Reiten quiver 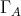 , satisfying:
, satisfying:
- the action preserves projective, injective and simple modules;
- the action preserves Auslander-Reiten sequences (in particular,
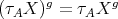 );
); 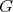 is a subgroup of
is a subgroup of 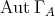 , the group of automorphisms of the quiver
, the group of automorphisms of the quiver 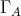 (commuting with the
(commuting with the 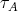 -structure).
-structure).
For (c), let 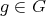 be an element inducing a trivial action on
be an element inducing a trivial action on 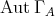 ; we shall prove
; we shall prove  . Indeed,
. Indeed, 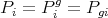 implies
implies 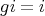 for every vertex
for every vertex 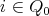 .
.
Let  ,
, 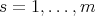 be all arrows between
be all arrows between 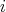 and
and 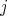 , then
, then 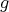 establishes a permutation of the
establishes a permutation of the 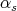 . Let
. Let 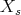 be the
be the 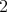 dimensional
dimensional 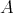 -module with
-module with 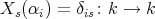 . Since
. Since 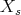 is indecomposable,
is indecomposable, 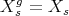 or
or 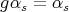 . Therefore
. Therefore 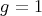 .
.
- Proposition.
- Let
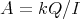 be an algebra satisfying:
be an algebra satisfying: (a)
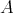 is representation finite, (b)
is representation finite, (b) 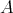 is standard
is standardthen
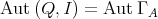 .
.
Proof. We already know that 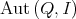 is a subgroup of
is a subgroup of 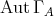 . Let
. Let 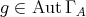 and consider the induced automorphism
and consider the induced automorphism 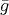 of the mesh category
of the mesh category 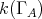 . Clearly,
. Clearly, 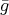 restricts to an automorphism of
restricts to an automorphism of 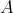 (considering the full embedding
(considering the full embedding  ,
, 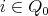 ). By definition there is an automorphism
). By definition there is an automorphism 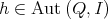 inducing
inducing 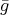 , and therefore inducing
, and therefore inducing 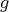 . □
. □
2. The canonical representation and the Coxeter matrix
2.1. Let 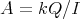 and assume that
and assume that 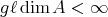 . For example, this happens if
. For example, this happens if 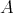 is triangular, that is,
is triangular, that is,  has no oriented cycles.
has no oriented cycles.
Recall that 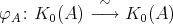 ,
, 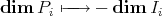 is the Coxeter matrix if
is the Coxeter matrix if 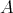 , which is
, which is  -invertible. In case
-invertible. In case 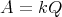 (i.e.
(i.e.  ), then
), then 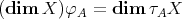 for any non-projective indecomposable
for any non-projective indecomposable 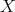 .
.
The characteristic polynomial 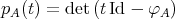 is called the Coxeter polynomial.
is called the Coxeter polynomial.
- Examples:
-
 Dynkin type, then
Dynkin type, then 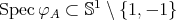 .
. extended Dynkin type, then
extended Dynkin type, then 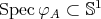 and
and  is a root of multiplicity
is a root of multiplicity 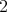 .
.
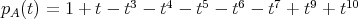 is irreducible (over
is irreducible (over ![ℤ [t]](/img/revistas/ruma/v48n2/2a02289x.png) ).
).
- Proposition [11].
-
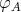 is an automorphism of the representation
is an automorphism of the representation 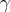 .
.- If
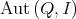 is not trivial, then
is not trivial, then 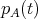 is not irreducible.
is not irreducible.
Proof. (a): It suffices to observe that  for any
for any 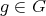 .
.
(b): Let  be a set of representatives of the irreducible
be a set of representatives of the irreducible  -representations of
-representations of 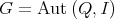 . Let
. Let 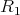 be the trivial representation. Up to conjugation (with
be the trivial representation. Up to conjugation (with 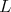 )
)
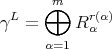
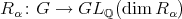 , then
, then 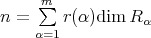 .
. By Schur's lemma  , where
, where 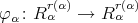 is an automorphism. Hence
is an automorphism. Hence 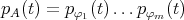 . Therefore if
. Therefore if 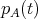 is irreducible then
is irreducible then 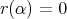 for
for 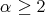 .
.
If 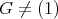 , then
, then 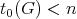 . Moreover, the characters
. Moreover, the characters
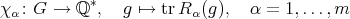
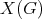 with scalar product
with scalar product 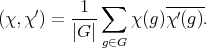
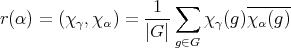
 ,
, 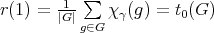 .
. Finally, 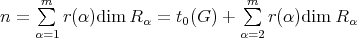 , with implies the existence of
, with implies the existence of 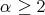 with
with 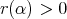 . Therefore
. Therefore 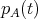 is not irreducible. □
is not irreducible. □
Consider 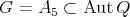 and
and  the canonical representation. It is not hard to calculate the character table of
the canonical representation. It is not hard to calculate the character table of 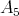 :
:

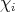 corresponds to
corresponds to 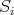 irreducible
irreducible 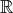 -representation of
-representation of 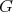 (with
(with 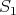 the trivial representation).
the trivial representation).
Then
![⊕ s γT = Snβ(β), n(1) = t0(G ) = 2 β=1 1 ∑ ------ 1 n(2) = (χ γ,χ2) = --- χγ(g)χ2(g) = --[24 + 60 - 24] = 1 60 g∈G 60](/img/revistas/ruma/v48n2/2a02332x.png)
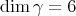 ,
, 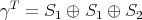 which is also a
which is also a  -decomposition. Moreover,
-decomposition. Moreover, 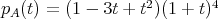 is an irreducible factorization.
is an irreducible factorization. 3. Constructions of algebras asociated to groups of automorphisms (coverings and smash products)
3.1. Let 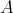 be a
be a 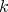 -category given as
-category given as 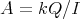 . Let
. Let 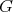 be a subgroup of
be a subgroup of 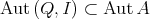 . We say that
. We say that 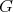 acts freely on
acts freely on 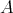 if
if 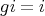 for some
for some 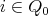 implies
implies  .
.
- Lemma.
- Let
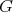 be a group acting freely on
be a group acting freely on 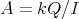 . Then there exists a
. Then there exists a 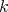 -category
-category 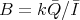 and a functor
and a functor 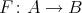 satisfying:
satisfying: - (
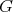 -invariant):
-invariant):  for every
for every 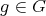
- (universal
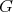 -invariant): for any functor
-invariant): for any functor 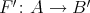 which is
which is 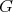 -invariant, there exists a unique functor
-invariant, there exists a unique functor 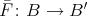 such that
such that 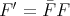
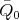 is formed by the
is formed by the 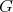 -orbits of vertices in
-orbits of vertices in 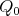 and for any
and for any 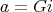 and
and 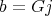
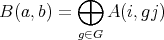
- (
Proof. Let 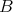 be defined as in (c) with composition maps
be defined as in (c) with composition maps
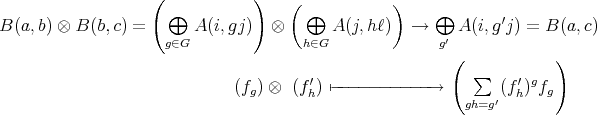
 ,
,  in the unique possible way (since
in the unique possible way (since  implies
implies 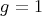 ). □
). □ 3.2. If 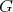 acts freely on
acts freely on 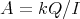 , the functor
, the functor 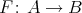 as in (2.1) is called a Galois covering defined by
as in (2.1) is called a Galois covering defined by 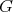 and
and 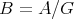 is a Galois quotient of
is a Galois quotient of 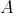 .
.
We say that a 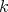 -category
-category 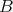 is
is 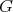 -graded if for each pair of objects
-graded if for each pair of objects 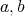 there is a vector space decomposition
there is a vector space decomposition 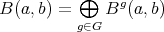 such that the composition induces linear maps
such that the composition induces linear maps
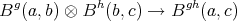
- Lemma.
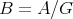 is a
is a 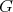 -graded
-graded 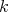 -category.
-category. 
3.3. For a 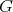 -graded
-graded 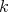 -category
-category 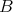 we define the smash product as the
we define the smash product as the 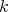 -category
-category  with objects
with objects 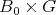 and for any pair
and for any pair 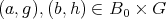 , the morphisms are
, the morphisms are
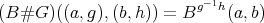
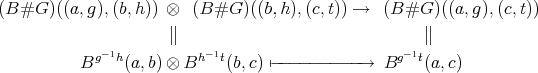
- Theorem
- [4]. The category
 accepts a free action of
accepts a free action of 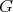 such that
such that 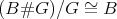 .
. Moreover, if
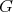 acts freely on
acts freely on 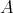 , then
, then 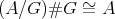 .
.
Proof. Clearly there is a 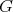 -invariant functor
-invariant functor 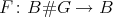 inducing a functor
inducing a functor 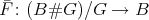 which is the identity on objects. Check that
which is the identity on objects. Check that 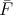 is an isomorphism.
is an isomorphism.
Assume 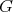 acts freely on
acts freely on 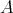 and let
and let 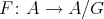 be the induced Galois covering.
be the induced Galois covering.
Since 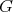 acts freely, there is a bijection
acts freely, there is a bijection 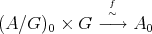 which commutes with the
which commutes with the 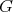 -action. Moreover, if
-action. Moreover, if 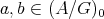 ,
, 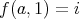 ,
, 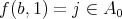 then
then
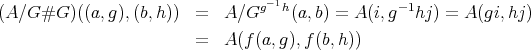
In other words, smash products and Galois quotients are inverse operations in the class of  -categories.
-categories.
3.4. Galois correspondence. Let 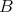 be a
be a 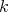 -category. There is a
-category. There is a  correspondence
correspondence
(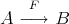 Galois covering defined by
Galois covering defined by 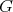 )
) 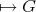 group grading
group grading 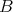 , such that for any
, such that for any
two Galois coverings 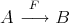 defined by
defined by 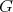 and
and 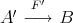 defined by
defined by 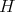 , there exist a commutative diagram
, there exist a commutative diagram
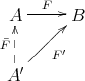
 , such that
, such that 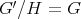 .
. A Galois triple 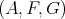 of
of 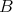 is a Galois covering
is a Galois covering 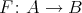 defined by the (free) action of a group
defined by the (free) action of a group 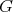 . There is a universal object in this set of Galois triples. Indeed, let
. There is a universal object in this set of Galois triples. Indeed, let 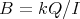 and consider
and consider 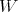 the set of all walks in
the set of all walks in  starting and ending at a fixed vertex
starting and ending at a fixed vertex 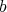 . Let
. Let  be the equivalence relation induced by the following elementary relations:
be the equivalence relation induced by the following elementary relations:
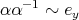 and
and 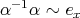 for any arrow
for any arrow 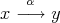 ;
;- if
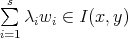 with
with 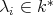 , such that for any
, such that for any 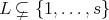 we have
we have 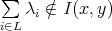 , then
, then 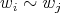 for
for 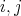 ;
; - if
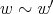 , then
, then 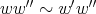 , whenever the products are defined.
, whenever the products are defined.
Then 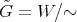 has a group structure such that
has a group structure such that 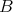 is
is 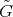 -graded. The group
-graded. The group 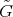 is called the fundamental group of
is called the fundamental group of 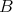 .
.
- Proposition
- [9]. Let
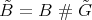 and
and 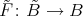 be defined by
be defined by 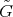 . The triple
. The triple 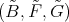 is a universal Galois covering, that is, for any Galois covering
is a universal Galois covering, that is, for any Galois covering 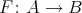 defined by the action of a group
defined by the action of a group 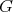 , there exists a covering
, there exists a covering 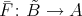 defined by
defined by  such that
such that 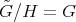 .
. 
4. Actions induced on module categories
4.1. Let 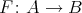 be a Galois covering of
be a Galois covering of 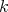 -categories defined by the action of
-categories defined by the action of 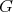 . We shall denote by
. We shall denote by
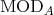 the category of left
the category of left 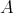 -modules;
-modules;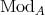 those
those 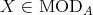 with
with 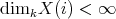 for every
for every 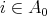 ;
;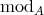 those
those 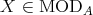 with
with 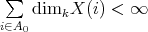 .
.
There are naturally defined functors:

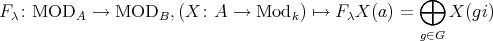
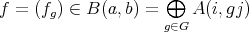 , then
, then 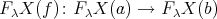 , sends
, sends 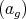 to
to 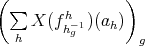 , called the push-down functor. We observe that
, called the push-down functor. We observe that 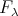 is a left adjoint to
is a left adjoint to 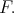 . Similarly, there is a right adjoint
. Similarly, there is a right adjoint 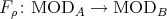 to
to 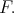 . For modules
. For modules 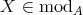 , the modules
, the modules  and
and 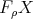 coincide.
coincide. Recall that 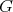 acts on
acts on 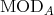 and
and 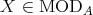 is
is 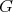 -stable if
-stable if 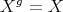 for every
for every 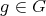 . The category of
. The category of 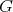 -stable
-stable 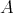 -modules is denoted by
-modules is denoted by 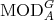 .
.
4.2. Proposition [7, 2]. Let 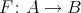 be a Galois covering defined by the action of
be a Galois covering defined by the action of 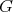 . Then the following happens:
. Then the following happens:
- The categories
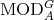 and
and 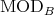 are equivalent.
are equivalent. - For any
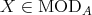 and
and 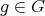 , we have
, we have  . Moreover,
. Moreover,
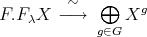 as
as 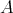 -modules.
-modules. - Let
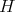 be a subgroup of
be a subgroup of 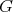 and
and 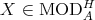 . Then
. Then  has a natural structure as
has a natural structure as 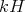 -module. If
-module. If 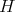 is a finite group and
is a finite group and 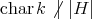 , then
, then  decomposes as a direct sum of at least
decomposes as a direct sum of at least  factors.
factors.
Proof. (a): clear.
(b): Observe that 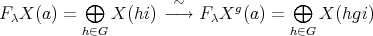 canonically.
canonically.
Hence 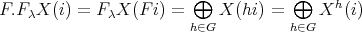 and correspondingly in morphisms.
and correspondingly in morphisms.
(c): Choose a set 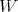 of representatives in
of representatives in 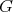 of the right cosets
of the right cosets 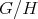 . Then
. Then 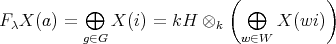 and correspondingly in morphisms.
and correspondingly in morphisms.
Hence we get 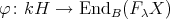 a group homomorphism such that for each idempotent
a group homomorphism such that for each idempotent  of
of 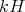 ,
, 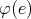 is idempotent and there is a factorization of
is idempotent and there is a factorization of  .
.
In case 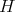 is a finite group with
is a finite group with 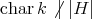 , by Mashké theorem, the group algebra
, by Mashké theorem, the group algebra 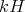 is semisimple (with
is semisimple (with 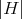 idempotents). The result follows. □
idempotents). The result follows. □
4.3. Assume 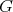 acts freely on
acts freely on 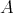 and
and 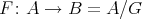 is the corresponding Galois covering.
is the corresponding Galois covering.
Let 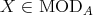 , the stabilizer
, the stabilizer 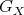 is the subgroup of
is the subgroup of 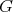 formed by those
formed by those 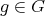 such that
such that  . That is,
. That is, 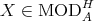 if
if 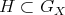 .
.
- Proposition [7].
-
- If
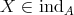 and
and 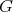 is torsion free, then
is torsion free, then 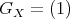 .
. - If
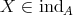 and
and 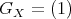 , then
, then  is indecomposable and for any module
is indecomposable and for any module 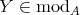 with
with  , then
, then 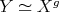 for some
for some 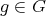 .
.
- If
Proof. (a): Let 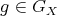 for some
for some 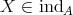 , then
, then 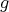 establishes a permutation of
establishes a permutation of 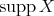 (a finite set). Then for some
(a finite set). Then for some 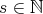 ,
,  on
on 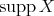 . Since
. Since 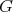 acts freely on
acts freely on 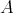 , then
, then 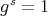 . Since
. Since 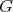 is torsion free, then
is torsion free, then  and
and 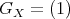 .
.
(b): Assume  , then
, then 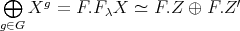 . Assume
. Assume 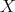 is a direct summand of
is a direct summand of  , then
, then 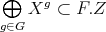 and
and 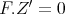 . Therefore
. Therefore  is indecomposable.
is indecomposable.
If  , then
, then 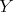 is indecomposable and
is indecomposable and 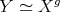 for some
for some 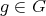 . □
. □
5. Coverings and the representation type of an algebra
(a) Let 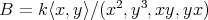
Let 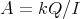 be the infinite
be the infinite 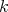 -category with quiver
-category with quiver
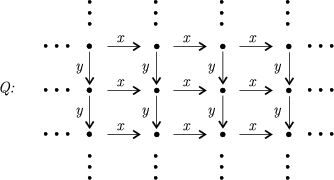
and 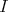 generated by all relations of the form
generated by all relations of the form 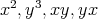 . Then we get a Galois covering
. Then we get a Galois covering 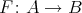 defined by the action of
defined by the action of 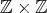 on
on 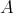 .
.
The module
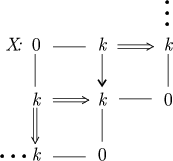
It is stable under the action of 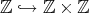 ,
, 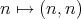 .
.
The universal Galois covering of  is given by
is given by 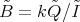
where the free group in two generators  acts on
acts on 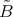 . The normal subgroup
. The normal subgroup  of
of  acts on
acts on  inducing the covering
inducing the covering 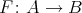 .
.
Observe that for 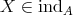 , we have
, we have 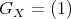 and therefore
and therefore 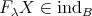 .
.
(b) [13] Let 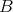 be a standard
be a standard 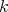 -algebra of finite representation type. Then the Auslander-Reiten quiver
-algebra of finite representation type. Then the Auslander-Reiten quiver 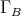 is finite and equipped with the mesh relations:
is finite and equipped with the mesh relations: 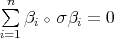 , for each almost split sequence
, for each almost split sequence 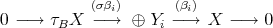 .
.
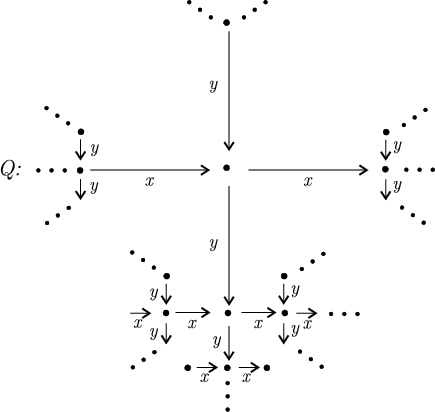
There is an universal Galois cover 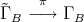 of translation quivers defined by the action of a free group
of translation quivers defined by the action of a free group  . Moreover,
. Moreover, 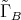 is the Auslander-Reiten quiver of a
is the Auslander-Reiten quiver of a 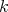 -category
-category 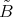 such that
such that 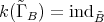 .
.
We illustrate the situation in the following example:
A full subcategory  of
of  is convex in
is convex in  if
if 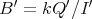 for a quiver
for a quiver 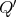 which is path closed in
which is path closed in  (i.e.
(i.e.  with
with 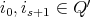 implies
implies 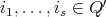 ).
).
- Theorem.
- Let
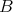 be a representation-finite
be a representation-finite 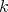 -algebra. Then
-algebra. Then - [13] There exists a universal Galois covering
 defined by the action of a free group
defined by the action of a free group 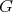 . Moreover
. Moreover 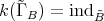 for a
for a 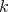 -category
-category 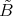 . If
. If 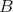 is standard, then
is standard, then 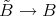 is a universal Galois covering.
is a universal Galois covering. - [3] For every finite convex subcategory
 of
of 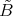 , we have
, we have  and
and  is representation-directed (i.e.
is representation-directed (i.e.  is representation-finite and
is representation-finite and 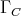 is a preprojective component).
is a preprojective component). 
- [13] There exists a universal Galois covering
5.2. We say that the group 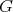 acts freely on indecomposable classes of
acts freely on indecomposable classes of 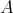 -modules if
-modules if  for
for 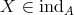 implies
implies  . Observe that for the algebra
. Observe that for the algebra  with quiver
with quiver
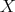 has non-trivial stabilizer.
has non-trivial stabilizer. - Theorem.
- Let
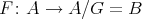 be a Galois covering defined by a group
be a Galois covering defined by a group 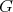
- [2] If
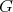 acts freely on indecomposable classes of
acts freely on indecomposable classes of 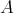 -modules, then
-modules, then 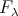 induces an injection (
induces an injection (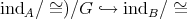 and preserves Auslander-Reiten sequences.
and preserves Auslander-Reiten sequences. - [2, 10] If
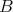 is finite (hence a
is finite (hence a 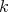 -algebra), then
-algebra), then 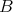 is representation-finite if and only if (i)
is representation-finite if and only if (i) 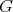 acts freely on
acts freely on 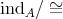 and (ii)
and (ii) 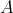 is locally representation-finite (i.e. for each
is locally representation-finite (i.e. for each 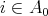 ,
, 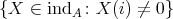 is finite). In that case,
is finite). In that case, 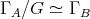 .
.
- [2] If
Proof. (a): Let 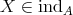 , then we know
, then we know 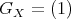 and
and 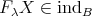 . Moreover
. Moreover  implies
implies 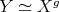 for some
for some 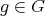 . For an almost split sequence
. For an almost split sequence 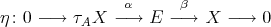 with
with 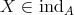 we get an exact sequence
we get an exact sequence

 ,
, 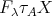 indecomposable. For
indecomposable. For  a non-invertible epi in
a non-invertible epi in 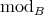 , we get a map
, we get a map 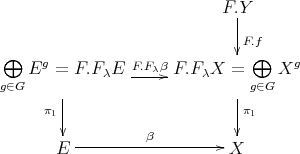
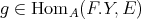 such that
such that 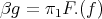 . From the adjunction
. From the adjunction 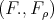 we get
we get 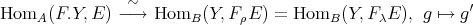
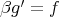 and
and 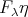 is almost split sequence in
is almost split sequence in 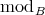 .
. (b): Assume 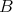 is representation-finite and
is representation-finite and  are representatives of
are representatives of 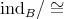 . Let
. Let 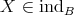 and suppose
and suppose 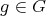 is such that
is such that  . We shall prove that
. We shall prove that  . Let
. Let 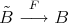 be a covering defined by a free group
be a covering defined by a free group 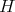 as in (5.1), that is, we get commutative diagrams:
as in (5.1), that is, we get commutative diagrams:
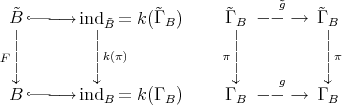
Then 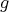 induces an automorphism
induces an automorphism 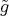 on
on 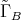 such that
such that  and
and 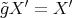 for some
for some 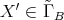 with
with 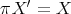 . We get an automorphism
. We get an automorphism 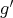 of
of 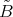 acting freely (since
acting freely (since 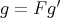 acts freely on
acts freely on 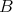 ).
).
Let  be the full subcategory of
be the full subcategory of 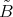 formed by
formed by 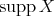 . It is easy to see that
. It is easy to see that  is convex in
is convex in 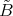 and therefore
and therefore 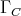 is a preprojective component. Since
is a preprojective component. Since 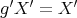 , then we get
, then we get 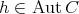 with
with 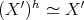 . Since
. Since 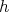 commutes with
commutes with 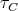 , there is a projective
, there is a projective  -module
-module 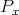 with
with 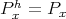 , which is a contradiction unless
, which is a contradiction unless  .
.
We check that 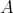 is locally representation-finite: let
is locally representation-finite: let 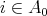 and let
and let 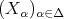 be all indecomposable
be all indecomposable 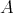 -modules which are direct summands of
-modules which are direct summands of 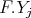 for some
for some 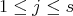 and
and 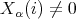 . This set is finite [indeed,
. This set is finite [indeed, 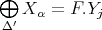 , then
, then 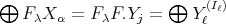 and
and 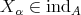 , for all
, for all 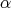 . Since
. Since 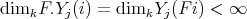 , the set is finite].
, the set is finite].
Finally, let 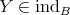 . Then
. Then 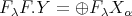 and
and
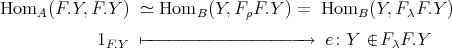
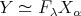 for some
for some 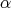 . Therefore
. Therefore 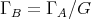 . □
. □ 5.3. Let 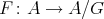 be a Galois covering with group
be a Galois covering with group 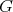 . In case
. In case 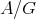 is a representation-finite
is a representation-finite 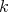 -algebra, we have seen that
-algebra, we have seen that 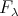 covers all indecomposable modules. The situation is different for representation-infinite algebras. We shall briefly discuss the new occuring phenomena. By
covers all indecomposable modules. The situation is different for representation-infinite algebras. We shall briefly discuss the new occuring phenomena. By 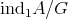 we denote the full subcategory of
we denote the full subcategory of 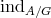 formed by all objects isomorphic to
formed by all objects isomorphic to  for some
for some 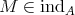 (these modules are called
(these modules are called 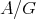 -modules of the first kind). The remaining indecomposable modules (called of the second kind) form the category
-modules of the first kind). The remaining indecomposable modules (called of the second kind) form the category 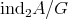 .
.
If 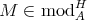 is such that
is such that 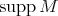 is not finite but
is not finite but 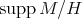 is finite, then
is finite, then 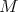 is called a weakly
is called a weakly 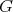 -periodic module.
-periodic module.
- Lemma [5].
- Let
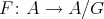 be a Galois covering such that
be a Galois covering such that 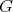 acts freely on
acts freely on 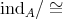 . For
. For 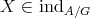 the following conditions hold:
the following conditions hold: 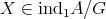 if and only if
if and only if 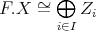 , where all
, where all 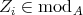 .
.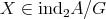 if and only if
if and only if 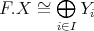 , where each
, where each 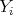 is weakly
is weakly 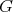 -periodic.
-periodic.
Proof. (1): If 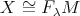 for some
for some 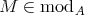 , then
, then 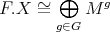 . Assume now that
. Assume now that 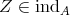 is a direct summand of
is a direct summand of 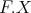 . Let
. Let 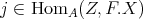 and
and 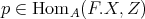 be such that
be such that 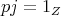 . We get morphisms
. We get morphisms 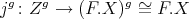 and
and 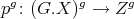 which yield a pair of maps
which yield a pair of maps 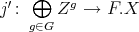 and
and 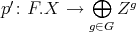 . Since
. Since 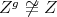 for
for 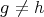 , then the endomorphism
, then the endomorphism 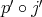 of
of 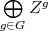 is invertible.
is invertible.
Since 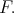 induces an equivalence of categories
induces an equivalence of categories 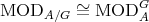 , then
, then 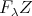 is a direct summand of
is a direct summand of 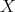 . Thus
. Thus 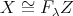 .
.
(2): Let 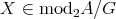 . By the proof of (1),
. By the proof of (1), 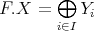 where
where 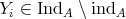 . Then we have to show that an indecomposable direct summand
. Then we have to show that an indecomposable direct summand 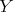 of
of 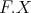 is weakly
is weakly 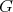 -periodic. Indeed, let
-periodic. Indeed, let  be a set of representatives of the cosets of
be a set of representatives of the cosets of 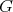 with respect to
with respect to 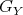 . Then
. Then 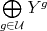 is a direct summand of
is a direct summand of 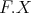 . Since
. Since 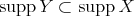 is contained in a finite number of
is contained in a finite number of 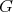 -orbits, then
-orbits, then 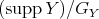 is finite. The converse follows from (1). □
is finite. The converse follows from (1). □
5.4. A category 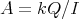 is called locally support finite if for each
is called locally support finite if for each 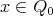 , the full subcategory
, the full subcategory 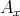 of
of 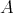 , consisting of the vertices of all
, consisting of the vertices of all 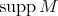 with
with 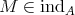 and
and 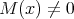 , is finite.
, is finite.
- Proposition.
- Let
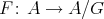 be a Galois covering. Then
be a Galois covering. Then - If
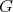 acts freely on
acts freely on 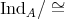 , then
, then 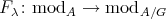 induces a bijection
induces a bijection 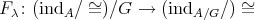 .
. - If
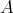 is locally support finite, then
is locally support finite, then  . In particular if
. In particular if 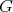 acts freely on
acts freely on 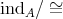 , then
, then 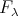 induces a bijection between
induces a bijection between 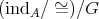 and
and 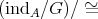 . Moreover, in this case
. Moreover, in this case 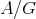 is tame (resp. domestic, poynomial growth) if and only if so is
is tame (resp. domestic, poynomial growth) if and only if so is 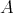 . For the Auslander-Reiten quivers we have
. For the Auslander-Reiten quivers we have  .
.
- If
Proof. (a): Follows from (4.2) since there are no weakly 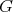 -periodic indecomposable
-periodic indecomposable 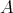 -modules.
-modules.
(b): Let 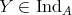 and consider
and consider 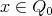 with
with 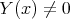 . Let
. Let 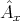 be the (finite) full subcategory of
be the (finite) full subcategory of 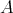 consisting in the objects
consisting in the objects 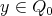 such that
such that 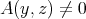 or
or 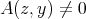 for some
for some 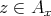 . Let
. Let 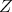 be an indecomposable direct summand of the restriction
be an indecomposable direct summand of the restriction 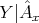 such that
such that 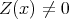 . Hence
. Hence 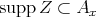 and it is easy to check that
and it is easy to check that 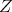 is a direct summand of
is a direct summand of 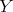 in
in 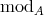 .
.
Thus 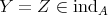 . The last claim is easy to prove. □
. The last claim is easy to prove. □
- Example:
- The category
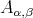 given by the quiver with relations
given by the quiver with relations 
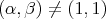 , is locally support finite (why?). Moreover the group
, is locally support finite (why?). Moreover the group  generated by the action
generated by the action 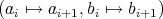 acts freely on
acts freely on 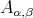 and on
and on 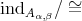 . Hence the Galois covering
. Hence the Galois covering 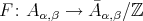 yields a bijection
yields a bijection 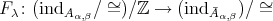 . The algebra
. The algebra 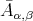 is given by the quiver with relations
is given by the quiver with relations 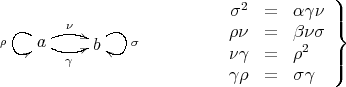
 is tame (resp. polynomial growth for
is tame (resp. polynomial growth for  ), so is
), so is 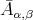 .
.
5.5. Given a natural number  , a group
, a group 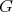 is said to be
is said to be 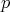 -residually finite if for each finite subset
-residually finite if for each finite subset 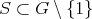 there is a normal subgroup of finite index
there is a normal subgroup of finite index 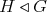 such that
such that 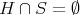 and
and 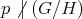 . For example, free groups are
. For example, free groups are 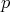 -residually finite.
-residually finite.
- Theorem [12].
- Let
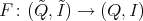 be a Galois covering given by the action of a
be a Galois covering given by the action of a 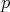 -residually finite group
-residually finite group 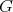 , where
, where 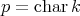 . Assume that
. Assume that 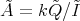 is locally support finite. Then
is locally support finite. Then 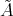 is tame if and only if
is tame if and only if 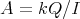 is tame.
is tame.
Proof. Without loss of generality, we assume that  is finite. We denote also by
is finite. We denote also by 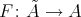 the induced covering functor. We divide the proof in several steps.
the induced covering functor. We divide the proof in several steps.
(1) Let 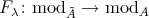 be the push-down functor. Consider a sequence
be the push-down functor. Consider a sequence 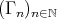 of finite full subcategories of
of finite full subcategories of 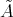 such that
such that 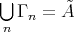 and if
and if 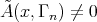 or
or 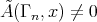 , then
, then 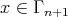 . The restriciton functor
. The restriciton functor 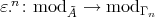 has a left adjoint
has a left adjoint 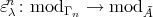 such that
such that 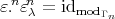 . Therefore, the functor
. Therefore, the functor
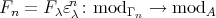
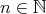 .
. (2) Let 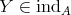 , we shall prove that
, we shall prove that 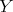 is a direct summand of
is a direct summand of 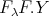 . Indeed, since
. Indeed, since 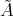 is locally support-finite, by (5.3), the pull-up
is locally support-finite, by (5.3), the pull-up 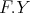 decomposes as
decomposes as 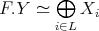 , where
, where 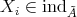 . Thus
. Thus 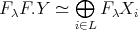 . We proceed in two steps.
. We proceed in two steps.
(2.1) There exists a normal subgroup 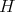 of
of 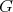 with finite index not divisible by
with finite index not divisible by 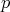 , such that the Galois covering
, such that the Galois covering 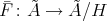 induces a bijection
induces a bijection 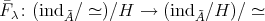 .
.
Since 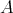 is finite, the set of vertices of
is finite, the set of vertices of  is a disjoint union of a finite number of
is a disjoint union of a finite number of 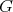 -orbits
-orbits 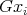 ,
, 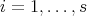 . With the notation introduced above, we consider the full subcategory
. With the notation introduced above, we consider the full subcategory 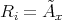 , of
, of 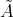 . Let
. Let 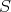 be the set of all elements
be the set of all elements 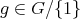 such that
such that 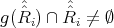 , for some
, for some 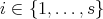 . Since
. Since 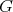 acts freely on
acts freely on  , then
, then 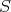 is finite and there is a normal subgroup
is finite and there is a normal subgroup 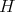 of
of 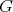 such that
such that 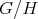 is finite of order not divisible by
is finite of order not divisible by 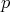 and
and 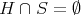 . Hence
. Hence  ,
, 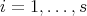 . By (5.1), the induced Galois covering
. By (5.1), the induced Galois covering  yields an injection
yields an injection 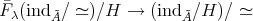 . We show that this map is also surjective. Let
. We show that this map is also surjective. Let 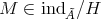 and
and 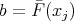 a vertex of
a vertex of 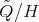 such that
such that 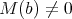 . The restriction
. The restriction 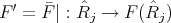 is a bijection and there is an indecomposable
is a bijection and there is an indecomposable 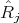 -module
-module  with
with 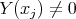 and such that
and such that 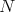 is an indecomposable direct summand of the restriction
is an indecomposable direct summand of the restriction 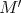 of
of 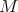 to
to 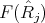 . We conclude that
. We conclude that 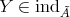 and
and 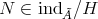 , showing that
, showing that 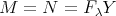 .
.
(2.2) For the proof of (2), consider a normal subgroup 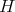 of
of 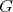 as in (2.1) and a factorization of Galois coverings
as in (2.1) and a factorization of Galois coverings
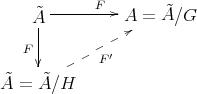
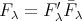 and
and 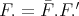 . For an indecomposable
. For an indecomposable 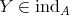 , we get
, we get 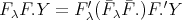
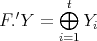 with
with 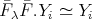 for
for 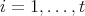 . Then
. Then 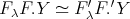 and the result follows from (4.2). In particular,
and the result follows from (4.2). In particular, 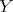 is a direct summand of
is a direct summand of 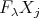 for some
for some 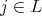 .
. (3) There is some 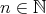 and a function
and a function 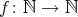 such that
such that
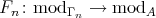
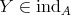 with
with 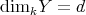 , there exists some
, there exists some 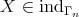 with
with 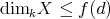 and such that
and such that 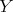 is a direct summand of
is a direct summand of 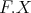 .
. Indeed, the set of vertices 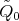 is the disjoint union
is the disjoint union 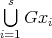 , then there is some
, then there is some  such that
such that 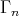 contains all the categories
contains all the categories 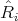 for
for  ,
, 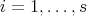 . By (2),
. By (2),  is a direct summand of
is a direct summand of 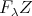 for some
for some 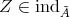 . For some
. For some 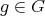 ,
, 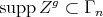 and
and  satisfies that
satisfies that 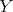 is a direct summand of
is a direct summand of 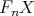 . Clearly,
. Clearly, 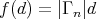 (where
(where 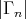 denotes the number of objects of
denotes the number of objects of 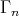 ) satisfies the desired property.
) satisfies the desired property.
(4) Assume that 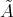 is tame, we show that
is tame, we show that 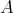 is tame. Indeed, let
is tame. Indeed, let 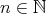 and
and 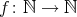 be as in (3). Since
be as in (3). Since 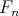 is right exact (1), there is a
is right exact (1), there is a 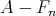 -bimodule
-bimodule 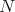 such that
such that 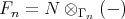 . Let
. Let 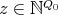 .
.
Since 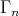 is tame, there is a family
is tame, there is a family  of
of ![Γ n - k[T ]](/img/revistas/ruma/v48n2/2a02987x.png) -bimodules which are finitely generated free as
-bimodules which are finitely generated free as ![k[T]](/img/revistas/ruma/v48n2/2a02988x.png) -right modules and such that any indecomposable
-right modules and such that any indecomposable 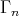 -module
-module 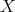 with
with 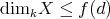 is isomorphic to
is isomorphic to ![Mi ⊗k[T] S](/img/revistas/ruma/v48n2/2a02992x.png) for some
for some 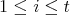 and
and 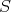 a simple
a simple ![k[T]](/img/revistas/ruma/v48n2/2a02995x.png) -module. By (3), for every
-module. By (3), for every 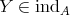 with
with 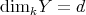 , there exists some
, there exists some 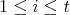 and
and 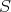 a simple
a simple ![k [T ]](/img/revistas/ruma/v48n2/2a021000x.png) -module such that
-module such that 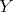 is a direct summand of
is a direct summand of ![(N ⊗ Γ n Mi ) ⊗k[T] S](/img/revistas/ruma/v48n2/2a021002x.png) . It is easy to see that this (aparently) weaker property is equivalent to the tameness of
. It is easy to see that this (aparently) weaker property is equivalent to the tameness of 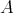 .
.
(5) Assume now that 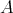 is tame. It is enough to show that each
is tame. It is enough to show that each 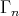 is tame. Consider the right exact functors
is tame. Consider the right exact functors
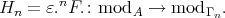
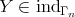 . Thus
. Thus 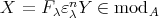 and
and 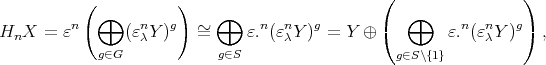
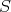 is the finite set of
is the finite set of 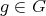 such that
such that 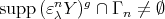 . As in (3), (4) we get that
. As in (3), (4) we get that 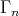 is tame. □
is tame. □ 5.6. We consider several examples:
(a) Let 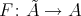 be a Galois covering induced from a Galois covering of quivers with relations and defined by the action of a group
be a Galois covering induced from a Galois covering of quivers with relations and defined by the action of a group 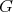 . Assume that
. Assume that 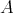 is locally support-finite.
is locally support-finite.
- If
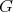 is a finite group such that
is a finite group such that 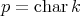 does not divide the order of
does not divide the order of 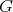 , then (5.5) applies and
, then (5.5) applies and 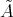 is tame if and only if so is
is tame if and only if so is 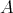 .
. - If
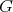 is a free group, then both (5.2) and (5.7) apply.
is a free group, then both (5.2) and (5.7) apply.
(b) Consider example (5.4). For 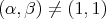 , the category
, the category 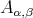 is tame and locally support finite. Hence the algebra
is tame and locally support finite. Hence the algebra 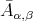 is tame.
is tame.
(c) [8] Consider the Galois covering
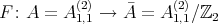
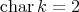 . We know that
. We know that 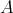 is tame. We show that
is tame. We show that 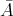 is a wild algebra.
is a wild algebra. Set 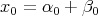 ,
,  ,
, 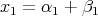 ,
,  . Then
. Then 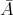 is isomorphic to the algebra
is isomorphic to the algebra 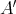 given by the quiver with relations.
given by the quiver with relations.
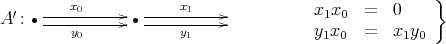
 constructed as in (2.3) admits a full convex subcategory
constructed as in (2.3) admits a full convex subcategory  as follows
as follows 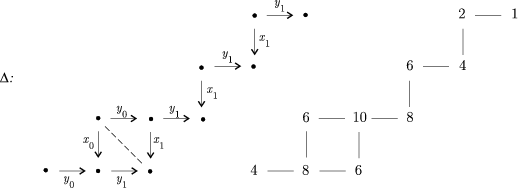
Since  is wild (observe that the Tits form
is wild (observe that the Tits form 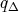 takes value
takes value  in the indicated vector), then
in the indicated vector), then 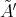 is wild. Then
is wild. Then 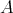 is also wild.
is also wild.
(d) The algebra 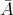 of example (c) provides another example of a wild algebra whose Tits form
of example (c) provides another example of a wild algebra whose Tits form 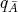 is weakly non-negative. Indeed,
is weakly non-negative. Indeed,
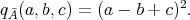
5.7. We consider briefly the situation of coverings 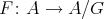 where
where 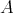 is not necessarily locally support-finite.
is not necessarily locally support-finite.
Let 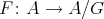 be a Galois covering. A line in
be a Galois covering. A line in 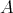 is a full convex subcategory isomorphic to the path category of a linear quiver (of type
is a full convex subcategory isomorphic to the path category of a linear quiver (of type 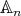 ,
, 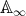 or
or 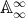 ). A line
). A line 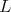 is
is 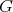 -periodic if its stabilizer
-periodic if its stabilizer 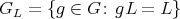 is non-trivial (then
is non-trivial (then 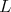 is of type
is of type  ).
).
Let 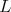 be a
be a 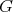 -periodic line in
-periodic line in 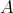 , we construct an indecomposable weakly
, we construct an indecomposable weakly 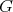 -periodic
-periodic 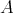 -module
-module 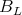 by setting
by setting 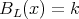 for
for 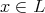 and
and 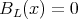 for
for 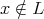 and
and 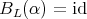 for any arrow
for any arrow 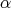 in
in 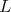 . Then
. Then  is isomorhic to
is isomorhic to  . Let
. Let 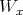 be a set of representatives of the
be a set of representatives of the 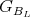 -orbits in
-orbits in 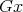 , for any object
, for any object 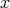 in
in 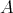 . Then
. Then 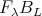 is a
is a ![A ∕G - k[T, T -1]](/img/revistas/ruma/v48n2/2a021083x.png) -bimodule such that for each
-bimodule such that for each 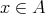 ,
, 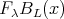 is a free
is a free ![k[T, T -1]](/img/revistas/ruma/v48n2/2a021086x.png) -module of rank
-module of rank 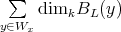 . We consider the functor
. We consider the functor
![φL = FλBL ⊗k[T,T- 1] (- ): modk [T,T-1] → modA ∕G.](/img/revistas/ruma/v48n2/2a021088x.png)
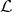 be the set of all lines in
be the set of all lines in 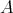 and
and 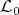 be the set of representatives of the
be the set of representatives of the 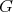 -orbits in
-orbits in 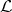 .
. - Theorem [5].
- Let
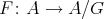 be a Galois covering such that
be a Galois covering such that 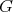 acts freely on
acts freely on  . Assume that for any weakly
. Assume that for any weakly 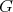 -periodic
-periodic 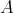 -module
-module 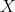 ,
, 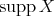 is a line. Then
is a line. Then - Every module in
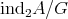 is of the form
is of the form 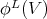 for some
for some 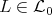 and some indecomposable
and some indecomposable ![k [T, T- 1]](/img/revistas/ruma/v48n2/2a021104x.png) -module
-module 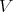 .
. ![Γ = Γ ∕G ∨ ∨ Γ -1 A∕G A L∈L0 k[T,T ]](/img/revistas/ruma/v48n2/2a021106x.png) , where
, where ![Γ k[T,T-1]](/img/revistas/ruma/v48n2/2a021107x.png) is the translation quiver of finite dimensional indecomposable
is the translation quiver of finite dimensional indecomposable ![k[T,T -1]](/img/revistas/ruma/v48n2/2a021108x.png) -modules, consisting of a
-modules, consisting of a 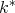 -family of stable tubes of rank one.
-family of stable tubes of rank one.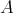 is tame if and only if so is
is tame if and only if so is 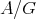 .
. 
- Every module in
[1] M. Beattie. A generalization of the smash product of a graded ring. J. Pure Appl. Algebra 52 (1988) 219-229. [ Links ]
[2] K. Bongartz and P. Gabriel. Covering spaces in Representation Theory. Invent. Math. 65 (3) (1982) 331-378. [ Links ]
[3] O. Butscher and P. Gabriel. The standard form of a representation-finite algebra. Bull. Soc. Math. France 111 (1983) 21-40. [ Links ]
[4] C. Cibils and E. Marcos. Skew categories. Galois coverings and smash product of a category over a ring. Preprint (2004). [ Links ]
[5] P. Dowbor and A. Skowronski. Galois coverings of representation infinite algebras. Comment. Math. Helv. 62 (1987) 311-337. [ Links ]
[6] P. Gabriel. Auslander-Reiten sequences and representation-finite algebras. In 'Representation of Algebras', Springer LNM 831 (1975) 1-71. [ Links ]
[7] P. Gabriel. The universal cover of a representation-finite algebra. In 'Representation of Algebras'. Springer LNM 903 (1981) 68-105. [ Links ]
[8] Ch. Geiss and J. A. de la Peña. An interesting family of algebras. Archiv. Math. 60 (1993) 25-35. [ Links ]
[9] R. Martínez-Villa and J. A. de la Peña. The universal cover of a quiver with relations. J. Pure and Appl. Algebra 30 (3) (1983) 277-292. [ Links ]
[10] R. Martínez-Villa and J. A. de la Peña. Automorphisms of representation-finite algebras. Invent. Math. 72 (1983) 359-362. [ Links ]
[11] J. A. de la Peña. Symmetries of quivers and the Coxeter transformation. J. Algebra 169 (1994) 200-215. [ Links ]
[12] J. A. de la Peña. Tame algebras: some fundamental notions. Ergänzungsreihe 95-010 (1995) Universität Bielefeld. [ Links ]
[13] Ch. Riedtmann. Darstellungsköcher, Überlagerungen und zurück. Comment. Math. Helv. 55 (1980) 199-224. [ Links ]
J. A. de la Peña
Instituto de Matemáticas, UNAM.
Circuito Exterior.
Ciudad Universitaria.
México 04510, D. F. México
jap@matem.unam.mx
Recibido: 6 de octubre de 2006
Aceptado: 3 de junio de 2007