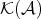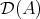Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932versão On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.48 n.3 Bahía Blanca 2007
Derived categories and their applications
María Julia Redondo and Andrea Solotar
Abstract. In this notes we start with the basic definitions of derived categories, derived functors, tilting complexes and stable equivalences of Morita type. Our aim is to show via several examples that this is the best framework to do homological algebra, We also exhibit their usefulness for getting new proofs of well known results. Finally we consider the Morita invariance of Hochschild cohomology and other derived functors.
Derived categories were invented by A. Grothendieck and his school in the early sixties. The volume [Ve77] reproduces some notes of his pupil J.L.Verdier, dating from 1963, which are the original source on derived categories (see also [Ve96]).
Let 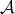 be an abelian category and
be an abelian category and 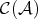 the category of complexes in
the category of complexes in  , that is, objects are sequences of maps
, that is, objects are sequences of maps
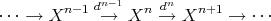
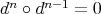 for all
for all 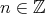 , and a morphism
, and a morphism 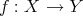 between complexes is a family of morphisms
between complexes is a family of morphisms 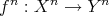 in
in 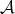 such that
such that 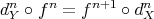 . The cohomology groups of the complex
. The cohomology groups of the complex 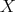 are by definition
are by definition 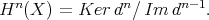
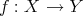 induces a group morphism
induces a group morphism 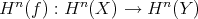 in each degree. We say that
in each degree. We say that 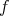 is a quasi-isomorphism if
is a quasi-isomorphism if 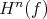 is an isomorphism for all
is an isomorphism for all 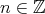 .
. The derived category 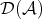 of
of 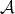 is obtained from
is obtained from 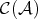 by formally inverting all quasi-isomorphisms.
by formally inverting all quasi-isomorphisms.
Recall that the definition of derived functors in homological algebra is as follows. Assume that 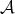 has enough projectives and let
has enough projectives and let  be a contravariant left exact functor. Then the right derived functor
be a contravariant left exact functor. Then the right derived functor 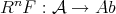 is defined in the following way. Let
is defined in the following way. Let 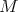 be an object in
be an object in 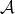 and let
and let
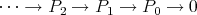
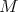 , that is,
, that is, 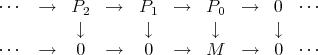
is a quasi-isomorphism. Then  is the group homology in degree
is the group homology in degree 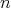 of the complex
of the complex
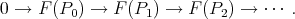
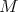 is unique up to quasi-isomorphisms. Moreover, for any short exact sequence
is unique up to quasi-isomorphisms. Moreover, for any short exact sequence 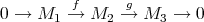 there is a long exact sequence
there is a long exact sequence 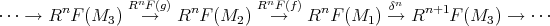
 is the so called connecting morphism.
is the so called connecting morphism. In fact, when we are doing homological algebra, we are not dealing with objects and cohomology groups but with complexes up to quasi-isomorphisms and their cohomology groups. Hence it is natural to work in 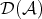 instead of
instead of 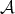 or
or 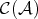 .
.
Any object 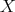 in
in 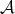 can be identified in
can be identified in 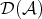 by the complex concentrated in degree zero, which will be denoted by
by the complex concentrated in degree zero, which will be denoted by ![X [0]](/img/revistas/ruma/v48n3/3a0141x.png) . Let
. Let 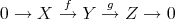 be a short exact sequence in
be a short exact sequence in 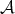 . Then
. Then ![0 → X [0]→f Y [0] g→ Z[0] → 0](/img/revistas/ruma/v48n3/3a0144x.png) is a short exact sequence in
is a short exact sequence in 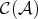 . Since
. Since
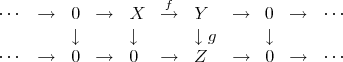
is a quasi-isomorphism, we can replace ![Z [0]](/img/revistas/ruma/v48n3/3a0147x.png) by the complex appearing in the first line of the previous picture, hence the short exact sequence
by the complex appearing in the first line of the previous picture, hence the short exact sequence ![0 → X [0]→f Y [0] g→ Z[0] → 0](/img/revistas/ruma/v48n3/3a0148x.png) can be identified in
can be identified in 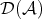 by the sequence of complexes
by the sequence of complexes
which is not an exact sequence.
In this new category, the concept of "short exact sequences" (which are determined by two morphisms 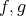 ) will be replaced by that of "distinguished triangles"(determined by three morphisms
) will be replaced by that of "distinguished triangles"(determined by three morphisms 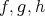 ). If
). If 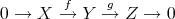 is a short exact sequence in
is a short exact sequence in 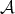 , then
, then
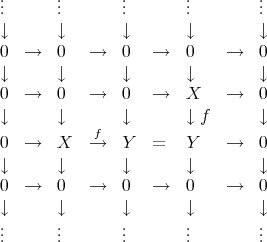
![... ... ... ... ↓ ↓ ↓ ↓ 0 → 0 → 0 → 0 ↓ ↓ ↓ ↓ 0 → 0 → X = X ↓ ↓ ↓ f ↓ f X → Y = Y → 0 ↓ ↓ ↓ ↓ 0 → 0 → 0 → 0 ↓ ↓ ↓ ↓ . . . . .. .. .. .. X [0] → Y [0] → Z [0] → X [1]](/img/revistas/ruma/v48n3/3a0155x.png)
is a triangle in 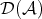 .
.
We will consider "cohomological functors" defined in 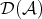 , that applied to distinguished triangles will give long exact sequences with morphisms induced by
, that applied to distinguished triangles will give long exact sequences with morphisms induced by 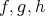 . That is, the extra morphism we are considering when defining triangles is a morphism of complexes that induces the corresponding connecting morphism.
. That is, the extra morphism we are considering when defining triangles is a morphism of complexes that induces the corresponding connecting morphism.
So, when considering the derived category 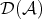 of
of 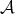 , we replace objects in
, we replace objects in 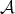 by complexes, and invert quasi-isomorphisms between complexes. As we shall see,
by complexes, and invert quasi-isomorphisms between complexes. As we shall see, 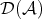 is not abelian if
is not abelian if 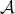 is not semisimple. The abelian structure of
is not semisimple. The abelian structure of 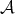 , and of
, and of 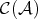 , has to be replaced by a triangulated structure.
, has to be replaced by a triangulated structure.
Given an algebra 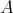 over a commutative ring
over a commutative ring 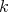 , for simplicity, we will write
, for simplicity, we will write 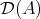 for the derived category
for the derived category 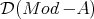 . Given two
. Given two 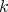 -algebras
-algebras 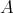 and
and 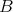 the natural question is: when are
the natural question is: when are 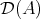 and
and 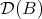 equivalent categories? (triangle equivalent?). Of course, if
equivalent categories? (triangle equivalent?). Of course, if 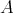 and
and 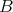 are Morita equivalent (that is,
are Morita equivalent (that is, 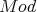 -
-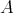 and
and 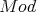 -
-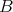 are
are 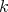 -linearly equivalent) then
-linearly equivalent) then 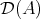 and
and 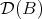 are equivalent. We will see that there other equivalences and we shall present some examples.
are equivalent. We will see that there other equivalences and we shall present some examples.
Let 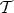 be an additive category with an additive automorphism
be an additive category with an additive automorphism 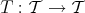 called the translation functor. We will write
called the translation functor. We will write ![X [n ]](/img/revistas/ruma/v48n3/3a0186x.png) and
and ![f[n]](/img/revistas/ruma/v48n3/3a0187x.png) for
for 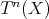 and
and 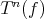 respectively. A triangle in
respectively. A triangle in 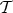 is a diagram of the form
is a diagram of the form
![f g h X → Y → Z → X [1]](/img/revistas/ruma/v48n3/3a0191x.png)
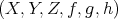 , and a morphism of triangles is a triple
, and a morphism of triangles is a triple 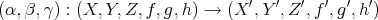
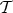
![f g h X → Y → Z → X [1] ↓ α ↓ β ↓ γ ↓ α[1] X ′ f→′ Y ′ g→′ Z ′ h→′ X ′[1 ]](/img/revistas/ruma/v48n3/3a0195x.png)
A morphism of triangles is said to be an isomorphism if 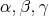 are isomorphisms in
are isomorphisms in 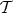 .
.
DEFINITION 2.1. A structure of triangulated category on 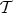 is given by a translation functor
is given by a translation functor 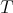 and a class of distinguished triangles verifying the following four axioms:
and a class of distinguished triangles verifying the following four axioms:
-
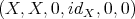 is a distinguished triangle, for any object
is a distinguished triangle, for any object 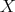 ;
;- Every triangle isomorphic to a distinguished one is distinguished;
- Every morphism
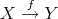 can be embedded in a distinguished triangle
can be embedded in a distinguished triangle 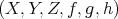 .
.
- (Rotation) A triangle
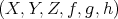 is distinguished if and only if
is distinguished if and only if ![(Y,Z, X [1],g,h,- f [1])](/img/revistas/ruma/v48n3/3a01105x.png) is distinguished.
is distinguished. - (Morphisms) Every commutative diagram
![f g X → Y → Z →h X [1] ↓ α ↓ β ′ f′ ′ g′ ′ h′ ′ X → Y → Z → X [1]](/img/revistas/ruma/v48n3/3a01106x.png)
whose rows are distinguished triangles can be completed to a morphism of triangles by a morphism
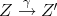 .
. - (The octahedral axiom) Given
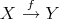 and
and 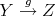 morphisms in
morphisms in  , and distinguished triangles
, and distinguished triangles 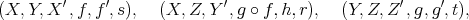
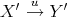 ,
, 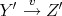 such that
such that ![′ ′ ′ ′ (X ,Y ,Z ,u,v,f [1] ∘ t)](/img/revistas/ruma/v48n3/3a01114x.png)
![f f′ ′ s X → Y → X → X [1] ∥ ↓ g ↓ u ∥ g∘f h ′ r X → Z → Y → X [1] ↓ f ∥ ′ ↓ v ↓ f [1] Y →g Z →g Z ′ →t Y[1] ↓ f′ ↓ h ∥ ↓ f ′[1] ′ u ′ v ′ w ′ X --→ Y --→ Z → X [1]](/img/revistas/ruma/v48n3/3a01115x.png)
is a commutative diagram.
Observe that all the rows in the previous diagram are distinguished triangles, and morphisms between rows determined the following morphisms of triangles
![′ ′ (idX,g,u) ′ (f,idZ,v) ′ ′ (X, Y,X ,f,f ,s) (f′-,h→,idZ′) (X, Z,Y ,g ∘f,h,r) (-s,t→v,w) (Y,Z,Z,g,g,t) (Y,Z,Z′,g,g′,t) -→ (X′,Y′,Z′,u,v,w) - → (X [1],Y[1],X′[1],f[1],f′[1],s[1])](/img/revistas/ruma/v48n3/3a01116x.png)
The name of last axiom comes from the fact that it can be viewed as a picture of a octahedron, where four faces are distinguished triangles, and all the other faces are commutative.
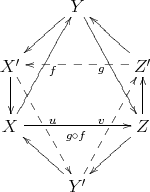
DEFINITION 2.2. Let 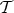 be a triangulated category and
be a triangulated category and 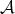 an abelian category. An additive functor
an abelian category. An additive functor 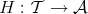 is said to be a cohomological functor if, for any distinguished triangle
is said to be a cohomological functor if, for any distinguished triangle 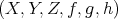 in
in 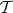 , we get an exact sequence in
, we get an exact sequence in 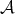
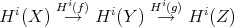
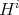 denotes
denotes ![i H ∘ T = H (- [i])](/img/revistas/ruma/v48n3/3a01126x.png) .
. REMARK 2.3. By TR2, if 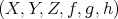 is a distinguished triangle then
is a distinguished triangle then 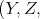
![X [1],g,h,- f[1])](/img/revistas/ruma/v48n3/3a01129x.png) is also distinguished. Then, if
is also distinguished. Then, if 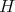 is a cohomological functor,
is a cohomological functor,
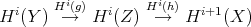
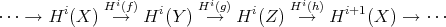
LEMMA 2.4. Let 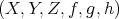 be a distinguished triangle in
be a distinguished triangle in 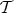 . Then
. Then
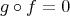 ;
;- If
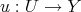 is such that
is such that 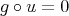 , then there exists
, then there exists 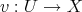 such that
such that 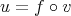 ;
; - If
 is such that
is such that 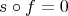 , then there exists
, then there exists  such that
such that 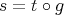 .
.
Proof.
- From TR1 we know that
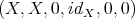 is a distinguished triangle, and from TR3 we know that there exists a morphism of triangles
is a distinguished triangle, and from TR3 we know that there exists a morphism of triangles ![idX X → X → 0 → X [1] ↓ idX ↓ f ↓ s ↓ idX [1 ] X f→ Y →g Z →h X [1]](/img/revistas/ruma/v48n3/3a01145x.png)
and hence
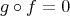 .
. - From TR2 and TR3 we know that the diagram
![id U →U U → 0 → U [1] ↓ u ↓ f g h X → Y → Z → X [1]](/img/revistas/ruma/v48n3/3a01147x.png)
can be completed to a morphism of triangles. Hence, there exists
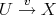 such that
such that 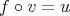 .
. - It follows as (ii).

REMARK 2.5. Using TR2 we also get that 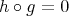 and
and ![f [1] ∘ h = 0](/img/revistas/ruma/v48n3/3a01152x.png) .
.
COROLLARY 2.6. If 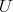 is an object in a triangulated category
is an object in a triangulated category 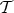 , then
, then 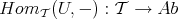 and
and 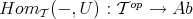 are cohomological functors.
are cohomological functors.
COROLLARY 2.7. Any distinguished triangle is determined, up to isomorphisms, by one of its morphisms.
Proof. From TR2, it suffices to prove that the distinguished triangles 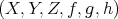 and
and 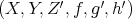 are isomorphic. By TR3, there exists a morphism of triangles
are isomorphic. By TR3, there exists a morphism of triangles
![f g h X → Y → Z → X [1] ↓ idX ↓ idY ↓ t ↓ idX[1] f g′ ′ h′ ′ X → Y → Z → X [1]](/img/revistas/ruma/v48n3/3a01159x.png)
If we apply the cohomological functors 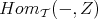 and
and 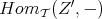 , by the 5-lemma we get that
, by the 5-lemma we get that

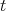 has left and right inverse, and therefore,
has left and right inverse, and therefore, 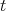 is an isomorphism.
is an isomorphism. 
PROPOSITION 2.8. For any distinguished triangle 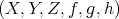 , the following conditions are equivalent:
, the following conditions are equivalent:
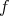 is a monomorphism;
is a monomorphism; ;
;- there exists
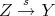 such that
such that 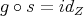 ;
; 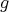 is an epimorphism;
is an epimorphism;- there exists
 such that
such that 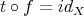 .
.
Proof.
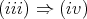 and
and 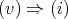 are immediate.
are immediate.
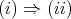 By
By 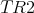 and Lemma 2.4(i) we have that
and Lemma 2.4(i) we have that ![f [1 ] ∘ h = 0](/img/revistas/ruma/v48n3/3a01178x.png) . Since
. Since 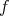 is a monomorphism,
is a monomorphism,  .
.
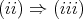 If
If  , by Corollary 2.6,
, by Corollary 2.6,
![g* 0 HomT (Z,Y ) → HomT (Z, Z) → HomT (Z, X [1])](/img/revistas/ruma/v48n3/3a01183x.png)
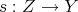 such that
such that 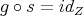 .
. 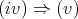 By Lemma 2.4(i) we know that
By Lemma 2.4(i) we know that 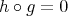 . Since
. Since 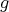 is an epimorphism we have that
is an epimorphism we have that  , and by Corollary 2.6,
, and by Corollary 2.6,
![g* 0 HomT (Y, X )→ HomT (X, X )→ HomT (Z [- 1 ],X )](/img/revistas/ruma/v48n3/3a01190x.png)
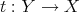 such that
such that 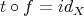 .
. 
COROLLARY 2.9. In any triangulated category any monomorphism splits and any epimorphism splits. Moreover, 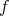 is an isomorphism if and only if
is an isomorphism if and only if 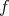 is a monomorphism and an epimorphism.
is a monomorphism and an epimorphism.
Let 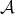 be an abelian category, and let
be an abelian category, and let 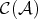 be the category of complexes in
be the category of complexes in 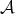 . The homotopy category
. The homotopy category 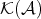 is defined as follows: the objects of
is defined as follows: the objects of 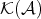 are the objects in
are the objects in  , and morphisms in
, and morphisms in 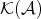 are the homotopy equivalence classes of morphisms in
are the homotopy equivalence classes of morphisms in 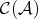 . That is,
. That is, 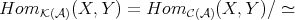 , where
, where  if there exists
if there exists 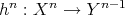 with
with 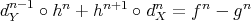 . So, the morphisms homotopic to zero in
. So, the morphisms homotopic to zero in 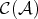 become the zero morphisms in
become the zero morphisms in 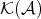 and the homotopic equivalences become isomorphisms.
and the homotopic equivalences become isomorphisms.
It can be checked that 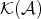 is well defined as a category, and moreover, it is an additive category, and the quotient
is well defined as a category, and moreover, it is an additive category, and the quotient  is an additive functor.
is an additive functor.
Observe that 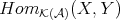 can also be defined as the quotient of
can also be defined as the quotient of 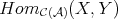 by the subgroup
by the subgroup
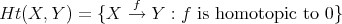
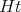 is an ideal in
is an ideal in 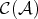 , that is,
, that is, 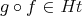 if
if 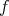 or
or 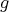 belongs to
belongs to 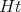 .
. Let 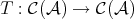 be the automorphism defined in the following way: for any complex
be the automorphism defined in the following way: for any complex 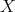 in
in 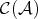 ,
, 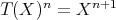 and
and  ; for any morphism
; for any morphism 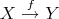 in
in 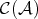 ,
, 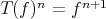 . The functor
. The functor 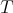 is additive and it is an automorphism. Since
is additive and it is an automorphism. Since 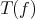 is a morphism homotopic to zero if and only if
is a morphism homotopic to zero if and only if 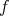 is a morphism homotopic to zero, it induces an additive automorphism
is a morphism homotopic to zero, it induces an additive automorphism 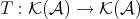 . We denote
. We denote ![X [n] = Tn (X )](/img/revistas/ruma/v48n3/3a01234x.png) and
and ![n d[n ] = T (d)](/img/revistas/ruma/v48n3/3a01235x.png) , for any
, for any 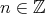 .
.
We will see that 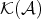 is a triangulated category with translation functor
is a triangulated category with translation functor 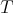 .
.
LEMMA 3.1. The cohomology functors 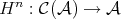 induce well defined functors
induce well defined functors 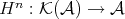 .
.
Proof. If 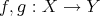 are homotopic, then
are homotopic, then 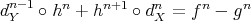 , so
, so 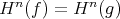 .
. 
DEFINITION 3.2. Let 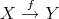 be a morphism in
be a morphism in 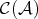 .
.
- The mapping cone of
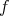 is the complex
is the complex 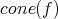 such that
such that 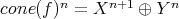 , and the differential
, and the differential 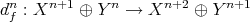 is given by
is given by 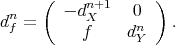
- The mapping cylinder of
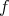 is the complex
is the complex 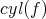 such that
such that 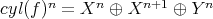 , and the differential
, and the differential 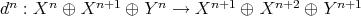 is given by
is given by 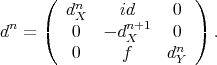
PROPOSITION 3.3. Any short exact sequence 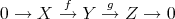 in
in  fits into a commutative diagram
fits into a commutative diagram
![h δ 0 → Y → cone(f ) → X [1] → 0 ↓ α ∥ 0 → X ν→ cyl(f) π→ cone(f ) → 0 ∥ f ↓ β g ↓ γ 0 → X → Y → Z → 0](/img/revistas/ruma/v48n3/3a01259x.png)
defined in degree  by the following diagram
by the following diagram
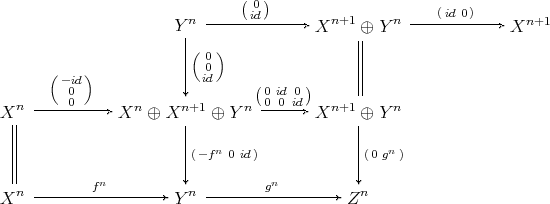
with exact rows,  ,
, 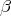 homotopy inverse equivalences and
homotopy inverse equivalences and 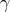 a quasi-isomorphism.
a quasi-isomorphism.
Proof. A direct computation shows that all the maps are morphisms of complexes. It is clear that 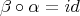 . On the other hand,
. On the other hand,
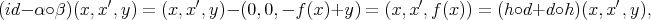
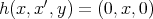 . Then
. Then 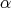 and
and 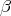 are homotopy equivalences, so they are quasi-isomorphisms. Now, since
are homotopy equivalences, so they are quasi-isomorphisms. Now, since 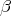 is a quasi-isomorphism, the 5-lemma applied to the long exact sequences obtained from the second and the third row, implies that
is a quasi-isomorphism, the 5-lemma applied to the long exact sequences obtained from the second and the third row, implies that 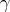 is a quasi-isomorphism.
is a quasi-isomorphism. 
- A short exact sequence
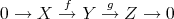 in
in 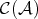 semi-splits if
semi-splits if 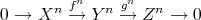 splits, for all
splits, for all 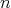 .
. - A triangle in
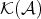 is a distinguished triangle if it is isomorphic, in
is a distinguished triangle if it is isomorphic, in 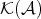 , to one of the form
, to one of the form ![X →f Y →h cone (f )→δ X [1]](/img/revistas/ruma/v48n3/3a01279x.png) .
.
THEOREM 3.5. [Ve96, II.1.3.2] The category 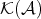 is a triangulated category with translation functor
is a triangulated category with translation functor 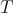 .
.
Let 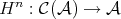 be the functor defined by
be the functor defined by 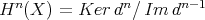 . For any morphism
. For any morphism 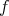 homotopic to zero,
homotopic to zero, 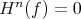 . Then
. Then 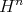 factors uniquely through
factors uniquely through 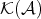 .
.
The following are immediate consequences of Proposition 3.3.
PROPOSITION 3.6. Any short exact sequence in 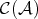 is quasi-isomorphic to a semi-split short exact sequence.
is quasi-isomorphic to a semi-split short exact sequence.
PROPOSITION 3.7. Any distinguished triangle in 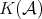 is quasi-isomorphic to one induced by a semi-split short exact sequence in
is quasi-isomorphic to one induced by a semi-split short exact sequence in 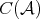 .
.
PROPOSITION 3.8. The functor 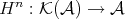 is a cohomological functor, for any
is a cohomological functor, for any 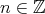 .
.
Proof. Let ![f X → Y → Z → X [1]](/img/revistas/ruma/v48n3/3a01293x.png) be a distinguished triangle in
be a distinguished triangle in 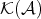 . By definition, it is isomorphic to
. By definition, it is isomorphic to
![X f→ Y →h cone(f )→δ X [1]](/img/revistas/ruma/v48n3/3a01295x.png)
![h δ 0 → Y → cone(f) → X [1] → 0](/img/revistas/ruma/v48n3/3a01296x.png) is a short exact sequence in
is a short exact sequence in 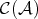 , it induces an exact sequence
, it induces an exact sequence 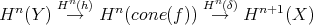

A simple computation shows that the connecting morphism  associated to the exact sequence appearing in the previous proof is
associated to the exact sequence appearing in the previous proof is 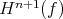 : recall that the connecting morphism is defined by chasing the following diagram
: recall that the connecting morphism is defined by chasing the following diagram
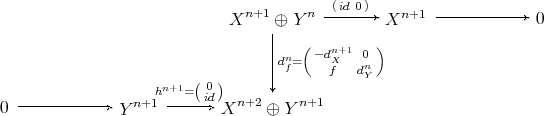
so, if 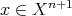 is such that
is such that 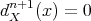 , then
, then 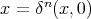 . Finally,
. Finally,
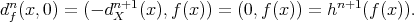
REMARK 3.9. Let 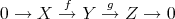 be a semi-split short exact sequence in
be a semi-split short exact sequence in 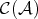 , that is,
, that is, 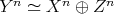 . Then
. Then 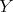 is isomorphic to the complex
is isomorphic to the complex
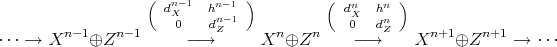
![h : Z → X [1 ]](/img/revistas/ruma/v48n3/3a01312x.png) is a morphism of complexes and
is a morphism of complexes and ![f g h X → Y → Z → X [1]](/img/revistas/ruma/v48n3/3a01313x.png)
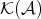 . Moreover, the connecting morphism
. Moreover, the connecting morphism  in the long exact sequence
in the long exact sequence 
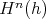 .
. As we said in the introduction, the derived category 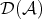 of
of 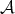 is obtained from
is obtained from 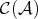 by formally inverting all quasi-isomorphisms. So
by formally inverting all quasi-isomorphisms. So 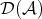 is the localization of
is the localization of 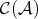 with respect to the class of quasi-isomorphisms in
with respect to the class of quasi-isomorphisms in 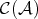 : there exists a functor
: there exists a functor 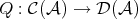 sending quasi-isomorphisms to isomorphisms which is universal for such property, that is, for any functor
sending quasi-isomorphisms to isomorphisms which is universal for such property, that is, for any functor  sending quasi-isomorphisms to isomorphisms, there exists a functor
sending quasi-isomorphisms to isomorphisms, there exists a functor 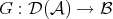 making the following diagram commutative
making the following diagram commutative
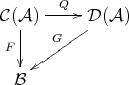
The category 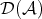 can be obtained just by adding formally inverses for all quasi-isomorphisms. But in this case, morphisms in
can be obtained just by adding formally inverses for all quasi-isomorphisms. But in this case, morphisms in 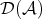 are just formal expressions of the form
are just formal expressions of the form
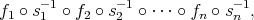
 are morphism in
are morphism in 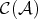 and
and 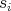 are quasi-isomorphisms en
are quasi-isomorphisms en 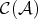 . To work with these kind of expressions, we would like to find a "common denominator". It was Verdier's observation that we can obtain a better description of the morphisms by a "calculus of fractions" if we construct
. To work with these kind of expressions, we would like to find a "common denominator". It was Verdier's observation that we can obtain a better description of the morphisms by a "calculus of fractions" if we construct 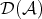 in several steps:
in several steps: 
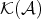 . Then
. Then ![- 1 D (A ) = K (A)[S ]](/img/revistas/ruma/v48n3/3a01338x.png) is the localization of
is the localization of 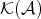 with respect to the class
with respect to the class  of all quasi-isomorphisms.
of all quasi-isomorphisms. DEFINITION 4.1. A class 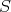 of maps in a category
of maps in a category  is said to be a multiplicative system if it satisfies the following conditions:
is said to be a multiplicative system if it satisfies the following conditions:
- For any object
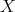 in
in  ,
, 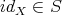 . If
. If 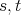 are composable maps in
are composable maps in 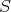 , then
, then 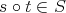 .
. - Given
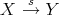 ,
, 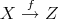 and
and 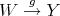 with
with 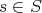 , there exist morphisms in
, there exist morphisms in  completing the following diagrams in a commutative way
completing the following diagrams in a commutative way 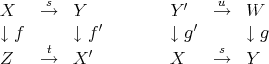
with
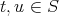 , that is,
, that is, 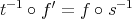 and
and 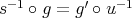 .
. - Given
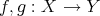 , there exists
, there exists 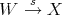 with
with  if and only if there exists
if and only if there exists 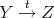 with
with  ,
, 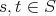 .
.
The multiplicative system 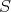 is said to be saturated if it satisfies:
is said to be saturated if it satisfies:
- A morphism
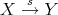 belongs to
belongs to 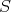 if and only if there exist morphisms
if and only if there exist morphisms 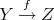 and
and 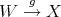 such that
such that 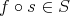 and
and 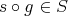 .
.
If  is a triangulated category with translation functor
is a triangulated category with translation functor 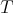 , the multiplicative system
, the multiplicative system 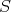 is said to be compatible with the triangulation if it satisfies:
is said to be compatible with the triangulation if it satisfies:
- A morphism
 belongs to
belongs to 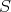 if and only if
if and only if 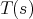 belongs to S.
belongs to S. - Given a morphism of triangles
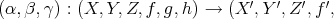
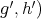 , if
, if 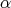 and
and 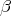 belong to
belong to 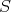 , then
, then 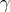 belongs to
belongs to 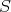 .
.
If 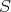 is a multiplicative system, the morphisms of the localization of
is a multiplicative system, the morphisms of the localization of  with respect to
with respect to 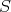 can be described by a "calculus of fractions".
can be described by a "calculus of fractions".
If 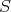 is saturated and
is saturated and ![Q : C → C[S -1]](/img/revistas/ruma/v48n3/3a01388x.png) is the localization functor, then
is the localization functor, then  belongs to
belongs to 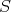 if and only if
if and only if 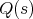 is an isomorphism.
is an isomorphism.
Finally, if 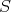 is compatible with the triangulation,
is compatible with the triangulation, ![C [S -1]](/img/revistas/ruma/v48n3/3a01393x.png) is a triangulated category, with distinguished triangles isomorphic to images of distinguished triangles in
is a triangulated category, with distinguished triangles isomorphic to images of distinguished triangles in  .
.
We refer to [Ve96, II.2] for more details.
PROPOSITION 4.2. Let 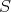 be the class of quasi-isomorphisms in
be the class of quasi-isomorphisms in 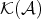 . Then
. Then 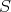 is a saturated multiplicative system in
is a saturated multiplicative system in 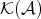 , compatible with the triangulation.
, compatible with the triangulation.
Proof. See for instance [Ha66, I.4]. 
- The class
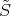 of quasi-isomorphism in
of quasi-isomorphism in 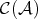 is not a multiplicative system.
is not a multiplicative system. - The localization of
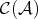 with respect to
with respect to 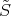 is isomorphic to the localization of
is isomorphic to the localization of 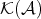 with respect to
with respect to 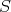 .
.
Now we can describe 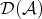 . The objects are those of
. The objects are those of 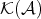 . The morphisms
. The morphisms 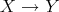 in
in 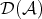 are equivalence classes of pairs
are equivalence classes of pairs
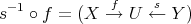
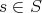 . The equivalence relation is defined as follows:
. The equivalence relation is defined as follows: 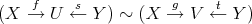

with 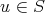 , that is,
, that is, 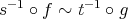 if and only if
if and only if 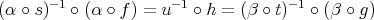 . The composition of morphisms in
. The composition of morphisms in 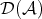 can be visualized by the diagram
can be visualized by the diagram
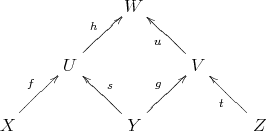
that is,
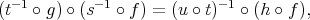
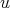 and
and 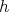 comes from S2.
comes from S2. Finally, the functor 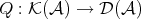 is defined as the identity in objects and sends a morphism
is defined as the identity in objects and sends a morphism 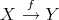 to the equivalence class of the pair
to the equivalence class of the pair 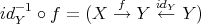 .
.
Since 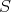 is saturated, a morphism
is saturated, a morphism 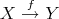 in
in 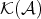 is a quasi-isomorphism if and only if
is a quasi-isomorphism if and only if 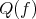 is an isomorphism.
is an isomorphism.
- A complex
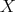 in
in 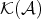 is quasi-isomorphic to zero if and only if
is quasi-isomorphic to zero if and only if 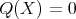 in
in 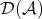 .
. - Let
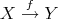 be a morphism in
be a morphism in 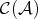 . Then
. Then 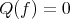 in
in 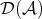 if and only if there exists a quasi-isomorphism
if and only if there exists a quasi-isomorphism 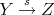 such that
such that  is homotopic to zero in
is homotopic to zero in 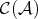 . Moreover, if
. Moreover, if 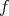 is a monomorphism (epimorphism) in
is a monomorphism (epimorphism) in 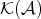 , then
, then 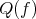 is so.
is so. - The cohomological functor
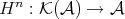 sends quasi-isomorphisms to isomorphisms, so it factors through
sends quasi-isomorphisms to isomorphisms, so it factors through 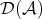 , inducing a cohomological functor
, inducing a cohomological functor  , for any
, for any 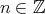 .
.
The automorphism 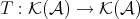 sends quasi-isomorphisms to quasi-isomorphisms, so it induces an automorphism
sends quasi-isomorphisms to quasi-isomorphisms, so it induces an automorphism 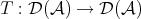 .
.
THEOREM 4.5. The category 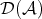 is a triangulated category with translation functor
is a triangulated category with translation functor 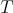 and
and 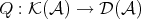 is an additive functor of triangulated categories.
is an additive functor of triangulated categories.
Proof. The class of quasi-isomorphisms in 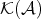 is a multiplicative system compatible with the triangulation, so the localization is triangulated and the distinguished triangles are those isomorphic to images by
is a multiplicative system compatible with the triangulation, so the localization is triangulated and the distinguished triangles are those isomorphic to images by  of distinguished triangles in
of distinguished triangles in 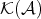 . Clearly
. Clearly  commutes with the translation functor
commutes with the translation functor 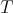 and sends distinguished triangles to distinguished triangles.
and sends distinguished triangles to distinguished triangles. 
Since 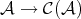 is fully faithful, we identify objects and morphisms in
is fully faithful, we identify objects and morphisms in 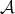 with objects and morphisms in
with objects and morphisms in 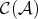 concentrated in degree zero.
concentrated in degree zero.
PROPOSITION 4.6. The composition 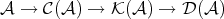 is a fully faithful functor.
is a fully faithful functor.
Proof. Denote 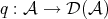 the composition functor. For any object
the composition functor. For any object 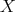 in
in 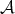 ,
, 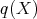 is the complex concentrated in degree zero, and for any morphism
is the complex concentrated in degree zero, and for any morphism 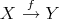 ,
, 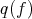 is the equivalence class of the pair
is the equivalence class of the pair 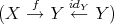 . Observe that the composition of
. Observe that the composition of 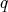 with the cohomological functor
with the cohomological functor 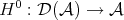 is the identity of
is the identity of 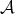 .
.
The functor 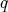 is faithful: if
is faithful: if 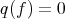 , there exists a quasi-isomorphism
, there exists a quasi-isomorphism  such that
such that  is homotopic to zero; then
is homotopic to zero; then 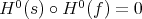 , but
, but 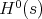 is an isomorphism, and hence
is an isomorphism, and hence 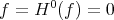 .
.
The functor 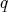 is full: let
is full: let 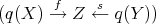 be a representative of the equivalence class of a morphism in
be a representative of the equivalence class of a morphism in 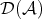 from
from 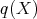 to
to 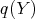 . Since
. Since  is a quasi-isomorphism, the complex
is a quasi-isomorphism, the complex  has cohomology
has cohomology  in degree zero, and zero otherwise. Then, the morphism of complexes
in degree zero, and zero otherwise. Then, the morphism of complexes
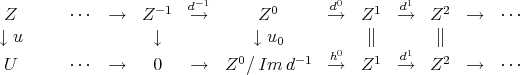
is a quasi-isomorphism and 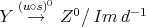 is the kernel of
is the kernel of 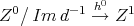 . Now,
. Now, 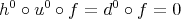 , so there exists a unique morphism
, so there exists a unique morphism 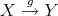 in
in 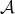 such that
such that 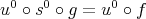 . Finally the commutative diagram
. Finally the commutative diagram

says that 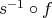 and
and 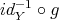 are equivalent, so
are equivalent, so 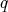 is full.
is full. 
From now on, we will identify 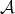 with the full subcategory
with the full subcategory 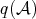 . We already know that
. We already know that 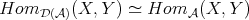 for any pair of objects
for any pair of objects 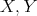 in
in 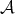 . Now we want to describe
. Now we want to describe ![Hom (X [m ],Y [n]) D(A)](/img/revistas/ruma/v48n3/3a01504x.png) for any
for any 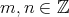 .
.
It is clear that ![HomD (A)(X [m ],Y [n ]) ≃ HomD (A)(X, Y [n - m ])](/img/revistas/ruma/v48n3/3a01506x.png) , so we only have to study
, so we only have to study ![HomD (A)(X, Y [n])](/img/revistas/ruma/v48n3/3a01507x.png) for
for 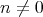 .
.
Following Yoneda, let 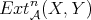 be the set of isomorphism classes of exact sequences
be the set of isomorphism classes of exact sequences
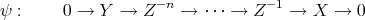
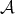 . It is clear that we can define a map
. It is clear that we can define a map ![Extn (X,Y ) → HomD (A)(X,Y [n]) A](/img/revistas/ruma/v48n3/3a01512x.png) by sending
by sending 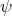 to the equivalence class of the morphism
to the equivalence class of the morphism ![f s (X → Z ← Y [n])](/img/revistas/ruma/v48n3/3a01514x.png) given by
given by ![X ⋅⋅⋅ → 0 → 0 → ⋅⋅⋅ → 0 → X → 0 → ⋅⋅⋅ ↓ f ↓ ↓ ↓ ∥ ↓ Z ⋅⋅⋅ → 0 → Z- n → ⋅⋅⋅ → Z -1 → X → 0 → ⋅⋅⋅ ↑ s ↑ ↑ ↑ ↑ ↑ Y [n ] ⋅⋅⋅ → 0 → Y → ⋅⋅⋅ → 0 → 0 → 0 → ⋅⋅⋅](/img/revistas/ruma/v48n3/3a01515x.png)
with  a quasi-isomorphism.
a quasi-isomorphism.
On the other hand, let ![f s (X → Z ← Y [n ])](/img/revistas/ruma/v48n3/3a01517x.png) be a representative of a map from
be a representative of a map from 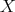 to
to ![Y [n]](/img/revistas/ruma/v48n3/3a01519x.png) . Since
. Since  is a quasi-isomorphism, the complex
is a quasi-isomorphism, the complex 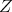 has cohomology zero except in degree
has cohomology zero except in degree  . Consider the following quasi-isomorphism
. Consider the following quasi-isomorphism
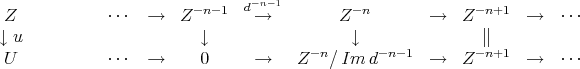
Observe that if  , then
, then 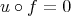 , so
, so 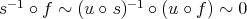 . Hence
. Hence ![HomD (A )(X, Y [n ]) = 0](/img/revistas/ruma/v48n3/3a01527x.png) for any
for any 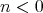 .
.
If  , consider the quasi-isomorphism
, consider the quasi-isomorphism 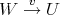 given by
given by
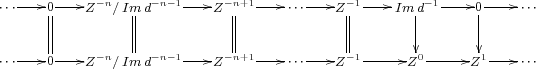
and observe that there exists a commutative diagram
![Z| f |u s u∘f | X -----U| -u∘s-Y [n] | g v | t W](/img/revistas/ruma/v48n3/3a01532x.png)
where 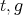 are given by
are given by
![X| ⋅⋅⋅----0-----------0----------- ⋅⋅⋅------0--------X|-------0-----⋅⋅⋅ | | | | | | |g | | W ⋅⋅⋅----0-----Z-n∕ Im d-n- 1-----⋅⋅⋅-----Z-1-----Im d -1----0-----⋅⋅⋅ | | | | | | |t | | | | | Y [n ] ⋅⋅⋅----0-----------Y -----------⋅⋅⋅------0---------0-------0-----⋅⋅⋅](/img/revistas/ruma/v48n3/3a01534x.png)
Finally the morphism 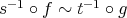 from
from 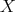 to
to ![Y [n]](/img/revistas/ruma/v48n3/3a01537x.png) can be associated with the exact sequence appearing in the first row of the diagram
can be associated with the exact sequence appearing in the first row of the diagram
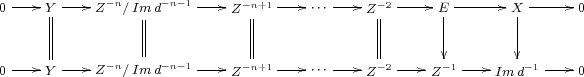
This shows that there is a close connection between ![HomD (A)(X, Y [n ])](/img/revistas/ruma/v48n3/3a01539x.png) and
and 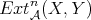 . In fact, the following theorem holds.
. In fact, the following theorem holds.
THEOREM 4.7. Let 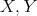 be objects in
be objects in 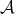 . Then
. Then
![Hom (X [m ],Y [n ]) = Hom (X, Y [n - m ]) D(A) D (A )](/img/revistas/ruma/v48n3/3a01543x.png) for all
for all 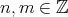 ;
;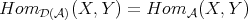 ;
;![HomD (A)(X, Y[n]) = ExtnA(X, Y )](/img/revistas/ruma/v48n3/3a01546x.png) for all
for all  ;
;![HomD (A)(X, Y[n]) = 0](/img/revistas/ruma/v48n3/3a01548x.png) for all
for all 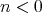 .
.
An abelian category 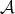 is said to be semisimple if any short exact sequence in
is said to be semisimple if any short exact sequence in 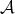 splits.
splits.
THEOREM 4.8. The derived category 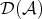 is abelian if and only if
is abelian if and only if 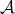 is semisimple.
is semisimple.
Proof. If 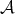 is semisimple then
is semisimple then 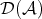 is equivalent to the abelian semisimple category
is equivalent to the abelian semisimple category 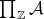 , as we shall see in the second example of the following section.
, as we shall see in the second example of the following section.
Assume that 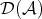 is abelian. We know from Proposition 2.8 that any monomorphism splits, and that any epimorphism splits. Let
is abelian. We know from Proposition 2.8 that any monomorphism splits, and that any epimorphism splits. Let 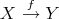 be a morphism in
be a morphism in 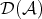 . Then
. Then 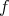 is equal to the composition
is equal to the composition 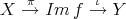 . Since
. Since 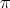 is an epimorphism and
is an epimorphism and  is a monomorphism, they split. Hence there exist
is a monomorphism, they split. Hence there exist 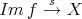 and
and 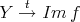 such that if
such that if 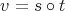 then
then 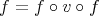 . Assume that
. Assume that 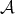 is not semisimple and let
is not semisimple and let 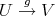 be a non-split monomorphism. Then there exists a morphism
be a non-split monomorphism. Then there exists a morphism  in
in 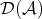 such that
such that 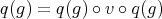 . Now,
. Now, 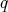 is fully faithfull, so there exists a morphism
is fully faithfull, so there exists a morphism 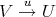 in
in 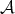 such that
such that  . But
. But 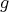 is a monomorphism, so
is a monomorphism, so 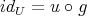 , a contradiction.
, a contradiction. 
5.1. Hereditary categories. Let 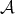 be an hereditary category, that is,
be an hereditary category, that is, 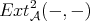
 . For instance, the category of abelian groups is hereditary. In this case we can easily describe objects, morphisms and triangles in
. For instance, the category of abelian groups is hereditary. In this case we can easily describe objects, morphisms and triangles in 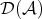 .
.
We start with the description of the objects of 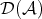 . Let
. Let 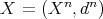 be a complex in
be a complex in 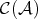 . The vanishing of
. The vanishing of 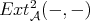 implies that
implies that 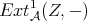 is right exact for any
is right exact for any  in
in 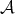 . Let
. Let  and consider the short exact sequences
and consider the short exact sequences
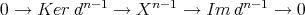
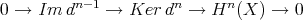
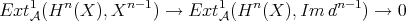
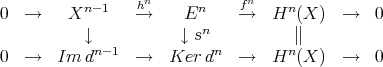
which induces the following quasi-isomorphisms
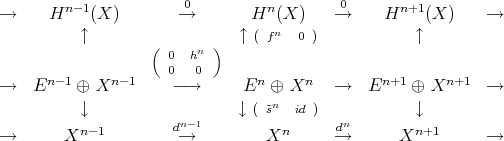
where 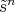 is the composition
is the composition 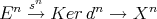 . So
. So 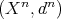 is quasi-isomorphic to
is quasi-isomorphic to ![(Hn (X ),0) = ∏ Hn (X )[- n] n](/img/revistas/ruma/v48n3/3a01600x.png) .
.
Let 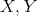 be objects in
be objects in 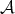 . Then
. Then
![Hom (X [n],Y [m ]) ≃ Hom (X, Y [m - n ]) ≃ Extm -n(X, Y) D(A) D (A ) A](/img/revistas/ruma/v48n3/3a01603x.png)
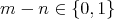 . Finally,
. Finally, ![HomD (A)(X [n ],Y [n]) ≃ HomA (X, Y )](/img/revistas/ruma/v48n3/3a01605x.png) and
and ![HomD (A)(X [n],Y [n + 1]) ≃ Ext1A(X, Y)](/img/revistas/ruma/v48n3/3a01606x.png) .
. Concerning triangles, let ![f X [n]→ Y [n]](/img/revistas/ruma/v48n3/3a01607x.png) be a morphism in
be a morphism in 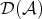 . The previous computation applied to the complex
. The previous computation applied to the complex
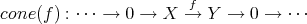

![f X [n] → Y [n] → Ker f[n + 1] ⊕ Coker f[n] → X [n + 1]](/img/revistas/ruma/v48n3/3a01611x.png)
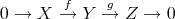 is a short exact sequence in
is a short exact sequence in 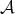 , then
, then ![f g δ X → Y → Z → X [1]](/img/revistas/ruma/v48n3/3a01614x.png)
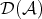 , and
, and ![δ ∈ HomD (A)(Z,X [1])](/img/revistas/ruma/v48n3/3a01616x.png) is the morphism associated to the given short exact sequence.
is the morphism associated to the given short exact sequence. 5.2. Semisimple categories. Let 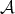 be a semisimple category. In this case,
be a semisimple category. In this case, 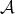 is hereditary, so the conclusions in the previous example hold. But now
is hereditary, so the conclusions in the previous example hold. But now 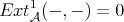 , so
, so ![HomD (A)(X [n ],Y [n]) ≃ HomA (X, Y)](/img/revistas/ruma/v48n3/3a01620x.png) and
and ![HomD (A )(X [n],Y [m ]) = 0](/img/revistas/ruma/v48n3/3a01621x.png) for all
for all 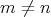 . Hence
. Hence 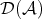 is equivalent to
is equivalent to 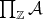 .
.
5.3. 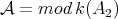 . Let
. Let 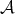 be the full subcategory of finitely generated left modules over the path algebra associated to the quiver
be the full subcategory of finitely generated left modules over the path algebra associated to the quiver 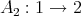 . In this case we only have three non-isomorphic indecomposable modules: the simple projective module
. In this case we only have three non-isomorphic indecomposable modules: the simple projective module 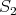 , the projective module of length two
, the projective module of length two 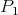 , and the simple module
, and the simple module 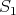 . Moreover, if
. Moreover, if  , then
, then 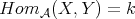 if
if 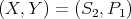 or
or 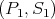 and it is zero otherwise, and
and it is zero otherwise, and 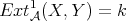 if
if 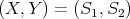 and it is zero otherwise. Then
and it is zero otherwise. Then 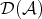 has the following picture
has the following picture
![S1[-1] P1[0] S2[1] S1[1] ... ... S2[0] S1[0] P1[1]](/img/revistas/ruma/v48n3/3a01638x.png)
where the composition of any two consecutive arrows is zero. Observe that this category has neither monomorphisms nor epimorphisms. All distinguished triangles can be visualized in the picture as the diagrams of three consecutive arrows.
Given an algebra 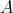 over a commutative ring
over a commutative ring 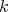 , we shall denote
, we shall denote 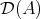 for the derived category
for the derived category 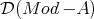 . Given two
. Given two 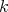 -algebras
-algebras 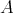 and
and 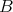 the natural question is: when are
the natural question is: when are 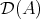 and
and 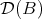 equivalent categories? (triangle equivalent?). Of course, if
equivalent categories? (triangle equivalent?). Of course, if 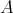 and
and 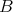 are Morita equivalent (that is,
are Morita equivalent (that is, 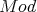 -
-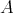 and
and 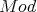 -
-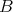 are
are 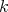 -linearly equivalent) then
-linearly equivalent) then 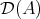 and
and 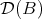 are equivalent. Are there other equivalences ? The answer is yes. In fact, we shall present some examples later.
are equivalent. Are there other equivalences ? The answer is yes. In fact, we shall present some examples later.
Rickard developed [Rick89], [Rick91] a Morita theory for derived categories based on the notion of tilting complex. As we shall see this is a generalization of the notion of tilting module. A summary of the history of the subject is developed for example in [KZ98]. Keller's approach [Ke94] is a little different and we will follow it. This is also the point of view of [DG02].
- A functor
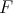 between triangulated categories
between triangulated categories 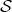 and
and 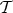 is said exact if it commutes whith shifts and preserves distinguished triangles, that is,
is said exact if it commutes whith shifts and preserves distinguished triangles, that is, 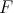 is equipped with a natural isomorphism
is equipped with a natural isomorphism ![iX : F (X [1]) → F (X )[1]](/img/revistas/ruma/v48n3/3a01662x.png) ,
, 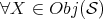 such that for every distinguished triangle
such that for every distinguished triangle ![f g h X → Y → Z → X [1]](/img/revistas/ruma/v48n3/3a01664x.png)
in
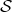 ,
,![F (X ) F→(f)F (Y ) F→(g)F (Z ) iX∘→F(h)F (X )[1]](/img/revistas/ruma/v48n3/3a01666x.png)
is a distinguished triangle in
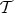 .
. - An equivalence between two triangulated categories is an equivalence of categories which is exact and whose inverse functor is also exact.
REMARK 6.2. If 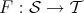 is exact then it is automatically additive.
is exact then it is automatically additive.
We know from classical Morita theory that two 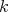 -algebras
-algebras 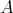 and
and 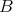 are Morita equivalent if and only if there exists a bimodule
are Morita equivalent if and only if there exists a bimodule 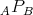 such that it is finitely generated projective, balanced and generator
such that it is finitely generated projective, balanced and generator 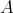 -module and
-module and 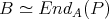 as a
as a 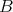 -bimodule. We have that
-bimodule. We have that 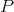 is a generator for
is a generator for 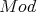 -
-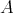 , that is for every
, that is for every 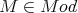 -
-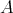 , there exists a set
, there exists a set 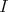 and an epimorphism
and an epimorphism  . For example,
. For example, 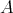 is a generator
is a generator 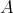 -module but this progenerator gives the trivial equivalence. The fact that
-module but this progenerator gives the trivial equivalence. The fact that 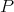 is f.g. projective implies that
is f.g. projective implies that 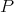 is a direct summand of
is a direct summand of 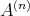 , for some
, for some 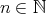 , in particular
, in particular 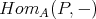 commutes with direct sums. The notion of tilting complex appears naturally if we look at the properties verified by
commutes with direct sums. The notion of tilting complex appears naturally if we look at the properties verified by ![A [0]](/img/revistas/ruma/v48n3/3a01690x.png) in
in 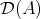 .
.
The free rank one 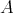 -module
-module 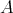 considered as a cochain complex concentrated in degree
considered as a cochain complex concentrated in degree 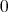 verifies that,
verifies that, 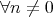 ,
,
![-n HomD (A)(A [n ],A ) = HomD (A)(A,A [- n ]) = Ext A (A, A ) = 0.](/img/revistas/ruma/v48n3/3a01696x.png)
DEFINITION 6.3. A complex 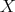 in
in 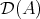 is a generator of this category if and only if the smallest full triangulated subcategory of
is a generator of this category if and only if the smallest full triangulated subcategory of 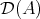 containing
containing 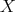 and closed by infinite direct sums is
and closed by infinite direct sums is 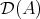 .
.
EXAMPLE 6.4. ![A [0]](/img/revistas/ruma/v48n3/3a01702x.png) is a generator of
is a generator of 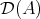 .
.
DEFINITION 6.5. A tilting complex 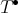 for a
for a 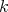 -algebra
-algebra 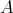 is a bounded cochain complex of f.g. projective
is a bounded cochain complex of f.g. projective 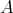 -modules which generates the derived category
-modules which generates the derived category 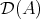 and such that the graded ring of endomorphisms
and such that the graded ring of endomorphisms 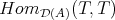 is concentrated in degree
is concentrated in degree 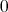 .
.
As a special case of tilting complexes we have the tilting modules over a finite dimensional 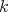 -algebra (
-algebra (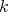 is a field) (when thinking them as their projective resolutions).
is a field) (when thinking them as their projective resolutions).
DEFINITION 6.6. Let 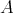 be a finite dimensional
be a finite dimensional 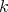 -algebra and
-algebra and 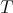 a finitely generated
a finitely generated 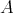 -module. We say that
-module. We say that 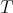 is a tilting module if
is a tilting module if
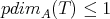 .
.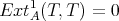 (that is, there are no self-extensions of
(that is, there are no self-extensions of 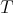 ).
).- There exists a short exact sequence of
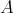 -modules
-modules 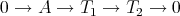
such that
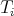 are direct summands of finite direct sums of
are direct summands of finite direct sums of 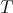 (that is,
(that is, 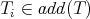 ) for
) for 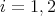 .
.
REMARK 6.7. If 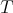 is a projective
is a projective 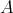 -module the first and second conditions are automatic. In that case the exact sequence in 3 splits, so
-module the first and second conditions are automatic. In that case the exact sequence in 3 splits, so 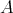 is a direct summand of
is a direct summand of 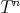 , for some
, for some 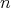 . The third condition is verified if and only if
. The third condition is verified if and only if 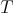 is a generator in
is a generator in 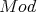 -
-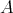 . As a consequence
. As a consequence 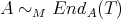 .
.
When 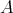 is self-injective, every
is self-injective, every 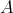 -module of finite projective dimension is projective. Then for these algebras, tilting complexes are the same as Morita equivalences. The following theorem is due to Rickard [Rick89]
-module of finite projective dimension is projective. Then for these algebras, tilting complexes are the same as Morita equivalences. The following theorem is due to Rickard [Rick89]
THEOREM 6.8. Given two 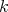 -algebras
-algebras 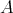 and
and 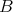 such that
such that 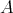 or
or 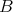 is
is 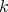 -flat, then the following are equivalent:
-flat, then the following are equivalent:
- The unbounded derived categories of
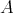 and
and 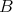 are equivalent as triangulated categories.
are equivalent as triangulated categories. - There is a tilting complex
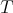 in
in 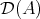 whose endomorphism ring
whose endomorphism ring 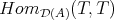 is isomorphic to
is isomorphic to 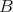 .
. - There exists a cochain complex of
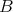 -
-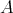 -bimodules
-bimodules 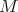 such that the derived tensor product
such that the derived tensor product 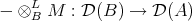
is an equivalence of categories.
We shall give a proof of this theorem following Keller. For this we must recall some preliminaries first.
7. Derived category of a differential graded algebra
7.1. DG algebras. Let 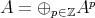 be a differential graded algebra (DG algebra for short), that is,
be a differential graded algebra (DG algebra for short), that is, 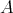 is
is  -graded algebra with a morphism
-graded algebra with a morphism 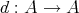 of degree one such that
of degree one such that 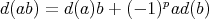 , if
, if 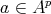 ,
, 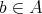 . The map
. The map 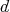 is called differential.
is called differential.
- Let
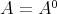 be a
be a 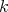 -algebra, and
-algebra, and  .
. - Given a
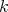 -algebra
-algebra 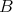 and a complex
and a complex 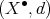 of
of 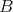 -modules, let us take
-modules, let us take 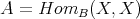 , that is,
, that is, 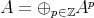 with
with 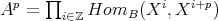 and differential defined by
and differential defined by 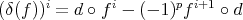 , for
, for 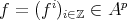 .
.
7.2. DG modules. Let 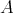 be a DG algebra.
be a DG algebra.
DEFINITION 7.2. A differential graded 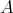 -module (DG
-module (DG 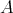 -module for short) is a
-module for short) is a  -graded right
-graded right 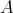 -module
-module 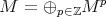 together with a
together with a 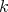 -linear differential
-linear differential 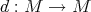 (of degree one) such that
(of degree one) such that
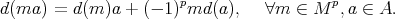
A morphism of DG modules 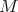 and
and 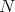 is an
is an 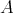 -linear map
-linear map 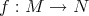 of degree zero wich commutes with the differentials.
of degree zero wich commutes with the differentials.
- The DG modules for the DG algebra
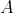 of the first example of the previous subsection are the same as the cochain complexes of
of the first example of the previous subsection are the same as the cochain complexes of 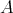 -modules.
-modules. - Let
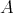 be the DG algebra of the second example of the previous subsection. Each complex
be the DG algebra of the second example of the previous subsection. Each complex 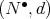 of
of 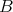 -modules gives rise to a DG
-modules gives rise to a DG 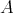 -module
-module 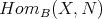 with
with  -action
-action 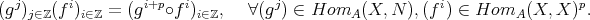
Also,
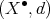 is a DG
is a DG 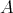 -module by means of the action:
-module by means of the action: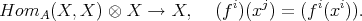
7.3. The homotopy category 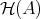 . We recall that the homotopy category
. We recall that the homotopy category 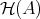 is defined as follows.
is defined as follows.
Its class of objects is given by 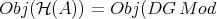 -
-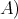 and the set of morphisms
and the set of morphisms 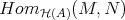 is defined as
is defined as 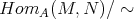 where
where  is the equivalence relation given by identifying homotopic maps.
is the equivalence relation given by identifying homotopic maps.
There is a shift operator
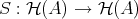
defined by
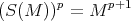
and 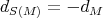 ,
,  .
.
We recall that endowed with 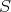 and all the triangles isomorphic to the standard triangles,
and all the triangles isomorphic to the standard triangles, 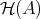 becomes a triangulated category.
becomes a triangulated category.
EXAMPLE 7.4. For the first example of the previous subsection we have that 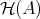 is the standard homotopy category of cochain complexes of
is the standard homotopy category of cochain complexes of 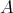 -modules.
-modules.
7.4. The derived category. We also recall that ![D(A ) = H (A)[Σ- 1]](/img/revistas/ruma/v48n3/3a01814x.png) , where
, where  denotes the class of all the homotopy classes of quasi-isomorphisms.
denotes the class of all the homotopy classes of quasi-isomorphisms.
EXAMPLE 7.5. For the first example of the previous subsection we have that 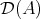 may be identified with the standard derived category of cochain complexes of
may be identified with the standard derived category of cochain complexes of 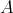 -modules.
-modules.
REMARK 7.6. We notice that 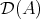 has infinite direct sums (ordinary sums of DG
has infinite direct sums (ordinary sums of DG 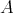 -modules).
-modules).
Consider now the free DG 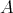 -module
-module 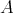 and let
and let 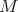 be a DG
be a DG 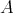 -module. Then
-module. Then
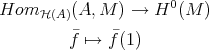 |
is bijective. In particular, each quasi-isomorphism 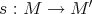 induces a bijection
induces a bijection
 | (1) |
Since 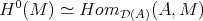 then
then 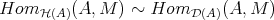 .
.
DEFINITION 7.7. A DG 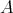 -module
-module 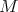 is said to be closed if
is said to be closed if
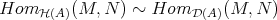
 . We shall denote by
. We shall denote by 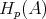 the full subcategory of
the full subcategory of 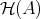 formed by closed objects.
formed by closed objects. - Free DG
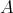 -modules of finte type are closed.
-modules of finte type are closed. - Complexes of f.g. projective
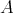 -modules are closed.
-modules are closed. - Suppose that
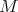 and
and 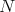 are closed and let
are closed and let 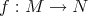 be a morphism of DG
be a morphism of DG 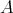 -modules. Consider the mapping cone
-modules. Consider the mapping cone 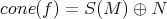 . Then
. Then 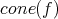 is also closed.
is also closed.
REMARK 7.9. As a consequence 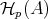 is a triangulated subcategory of
is a triangulated subcategory of 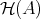 .
.
Why are we interested in considering the subcategory 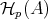 ?
?
- For all
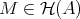 there is a quasi-isomorphism
there is a quasi-isomorphism  with
with 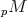 closed.
closed. - The map
 may be completed to a triangulated functor commuting with infinite direct sums and such that it gives a triangulated equivalence
may be completed to a triangulated functor commuting with infinite direct sums and such that it gives a triangulated equivalence 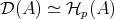 .
. 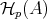 is the smallest full subcategory of
is the smallest full subcategory of 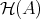 containing
containing 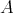 and closed under infinite direct sums.
and closed under infinite direct sums.
We will say that 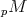 is the projective resolution of
is the projective resolution of 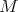 .
.
EXAMPLE 7.11. For 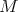 and
and 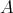 concentrated in degree zero, choose
concentrated in degree zero, choose 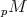 to be the homotopy class of any projective resolution of
to be the homotopy class of any projective resolution of 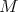 . Then
. Then 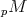 is closed since all epimorphisms split.
is closed since all epimorphisms split.
- If
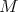 is a right bounded complex,
is a right bounded complex, 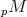 is a "projective resolution" of the complex
is a "projective resolution" of the complex 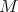 (see [Ha66]).
(see [Ha66]). - For
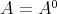 ,
,  and arbitrary
and arbitrary 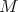 the description of
the description of 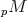 has been obtained by Spaltenstein ([Sp88]).
has been obtained by Spaltenstein ([Sp88]). - For
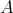 and
and 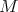 arbitrary, see [Ke94].
arbitrary, see [Ke94].
REMARK 7.13. The two last items of the previous proposition imply that 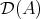 coincides with the smallest full subcategory containing
coincides with the smallest full subcategory containing 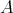 and closed by infinite direct sums.
and closed by infinite direct sums.
7.5. Left derived tensor functors. Let 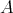 and
and 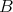 be two DG algebras and let
be two DG algebras and let 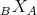 be a DG
be a DG 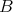 -
-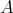 -bimodule, that is,
-bimodule, that is, 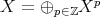 with a
with a 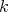 -linear map
-linear map 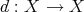 of degree one such that
of degree one such that

for 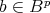 ,
, 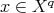 and
and 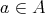 .
.
Define the DG algebra 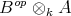 by
by 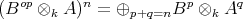 and the map
and the map 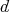 is given by
is given by
| dn : (Bop ⊗kA)n | → (Bop ⊗kA)n+1 |
| d(b ⊗ a) | = dB(b) ⊗ a + (-1)pb ⊗ dA(a), |
for 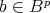 and
and 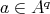 . The product is given by
. The product is given by
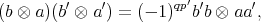
for 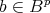 ,
, 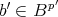 ,
, 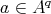 and
and 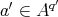 .
.
We notice then that 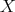 is a right DG
is a right DG  -module since
-module since
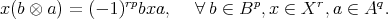
Let 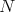 be a right DG
be a right DG 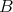 -module. We define
-module. We define  as the DG
as the DG 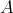 -module with action of
-module with action of 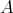 in
in 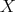 as before and with the DG structure given by
as before and with the DG structure given by
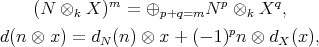 |
for 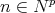 and
and 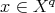 .
.
The 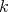 -submodule generated by all differences
-submodule generated by all differences  is stable under
is stable under 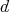 and under multiplication by elements of
and under multiplication by elements of 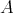 . So
. So 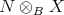 , the quotient module of
, the quotient module of  by this submodule, is a well defined DG
by this submodule, is a well defined DG 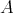 -module. Moreover, this construction is functorial in
-module. Moreover, this construction is functorial in 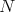 and
and 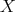 .
.
The functor 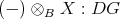 -
- -
-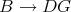 -
-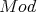 -
-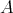 yields a triangulated functor from
yields a triangulated functor from 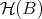 to
to 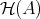 , denoted by the same symbol.
, denoted by the same symbol.
We define the left derived tensor product 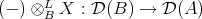 by
by
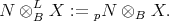
Notice that  commutes with direct sums since
commutes with direct sums since 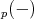 and
and  do.
do.
LEMMA 7.14. The functor 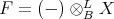 is an equivalence if and only if the following conditions hold:
is an equivalence if and only if the following conditions hold:
- The functor
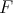 induces bijections
induces bijections ![HomD (B)(B,B [n]) ≃ HomD (A)(XA, XA [n]), ∀ n ∈ ℤ.](/img/revistas/ruma/v48n3/3a01929x.png)
- The functor
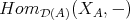 commutes with (infinite) direct sums.
commutes with (infinite) direct sums. - The smallest full triangulated subcategory of
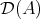 containing
containing 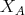 and closed under (infinite) direct sums coincides with
and closed under (infinite) direct sums coincides with 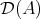 .
.
Proof. The conditions are necessary since they hold in 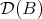 for
for 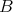 and they must be preserved by equivalences.
and they must be preserved by equivalences.
In order to prove that they are sufficient let us consider the full subcategory  of objects
of objects 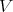 in
in 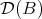 for which the maps
for which the maps
![HomD (B)(B [n ],V ) → HomD (A)(XA [n],F (V ))](/img/revistas/ruma/v48n3/3a01939x.png)
are bijective for all 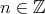 . This category is clearly closed under the shift and its inverse. Using the
. This category is clearly closed under the shift and its inverse. Using the  -lemma we check that it is a triangulated subcategory. Using
-lemma we check that it is a triangulated subcategory. Using  we get that it is closed under (infinite) direct sums. Also, using
we get that it is closed under (infinite) direct sums. Also, using  we see that
we see that  contains
contains 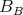 . Thus we must have that
. Thus we must have that 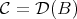 . So, the full subcategory
. So, the full subcategory 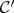 of objects
of objects 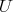 in
in 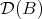 such that
such that
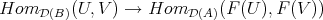
is bijective for all 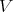 in
in 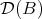 contains
contains 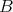 . Again it is closed under the shift and its inverse, and also closed under (infinite) direct sums. It is a triangulated category by the
. Again it is closed under the shift and its inverse, and also closed under (infinite) direct sums. It is a triangulated category by the  -lemma. Thus
-lemma. Thus 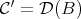 and as a consequence
and as a consequence 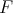 is fully faithful.
is fully faithful.
Condition (c) shows that 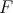 is surjective.
is surjective. 
EXAMPLE 7.15. Suppose that 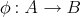 is a quasi-isomorphism, that is, a morphism of DG algebras inducing an isomorphism
is a quasi-isomorphism, that is, a morphism of DG algebras inducing an isomorphism  . Then
. Then 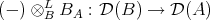 is an equivalence. In fact,
is an equivalence. In fact, 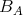 is isomorphic to
is isomorphic to 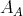 in
in 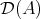 , so the conditions
, so the conditions  and
and  of the lemma before hold. In order to prove
of the lemma before hold. In order to prove  consider the commutative diagram
consider the commutative diagram
![HomD (B)(B, B [n ]) -----HomD (A)(BA, B [n ]A) | | ~ | ~ | | ~ Hn (B )-----------HomH (A )(A, B [n ]A ).](/img/revistas/ruma/v48n3/3a01968x.png)
Similarly, 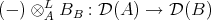 is an equivalence.
is an equivalence.
We may perform compositions of left derived functors of this kind.
LEMMA 7.16. If 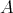 ,
, 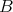 and
and  are DG
are DG 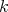 -algebras,
-algebras, 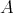 is a flat
is a flat 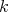 -module,
-module, 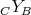 is a DG
is a DG  -
-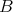 -bimodule, we have
-bimodule, we have
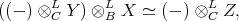
for some DG  -
-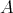 -bimodule
-bimodule 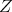 .
.
Proof. Take 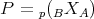 , considering
, considering 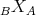 as a DG right
as a DG right  -module. The morphism of functors
-module. The morphism of functors

is clearly invertible since the composition
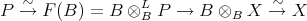
is an isomorphism and, using a result of [Ke94], a morphism of functor between triangulated categories is invertible if and only if it is an isomorphism when one applies the functors to a generator of the category.
Also the morphism
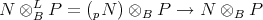
is invertible in 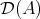 for each
for each 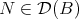 , using the same result and the facts that
, using the same result and the facts that 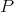 is closed over
is closed over  and that the functor
and that the functor 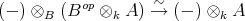 preserves quasi-isomorphisms by the
preserves quasi-isomorphisms by the 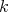 -flatness of
-flatness of 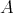 . Thus
. Thus
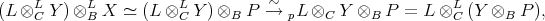
and we take 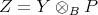 .
. 
8. Applications to tilting theory
Let 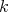 be a commutative ring,
be a commutative ring, 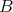 a
a 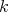 -algebra,
-algebra, 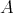 a flat
a flat 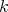 -algebra. Recall Rickard's theorem:
-algebra. Recall Rickard's theorem:
THEOREM 8.1. Given two 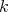 -algebras
-algebras 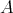 and
and 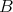 such that
such that 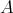 or
or 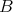 is
is 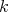 -flat, then the following are equivalent
-flat, then the following are equivalent
- The unbounded derived categories of
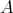 and
and 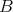 are equivalent as triangulated categories.
are equivalent as triangulated categories. - There exists a cochain complex of
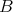 -
-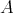 -bimodules
-bimodules 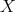 such that the derived tensor product
such that the derived tensor product 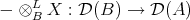
is an equivalence of categories.
Proof. 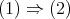
Let 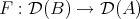 be the given triangulated equivalence. Take
be the given triangulated equivalence. Take 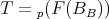 and
and 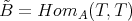 . There are canonical isomorphisms
. There are canonical isomorphisms
![n ~ H (B ˜) → HomH (A)(T,T [n ]), ∀ n ∈ ℤ.](/img/revistas/ruma/v48n3/3a011020x.png)
Since 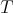 is closed in
is closed in 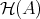 , we also have
, we also have
![~ ~ HomH (A)(T,T [n ]) → HomD (A)(T,T [n ]) → HomD (B)(B, B[n]), ∀n ∈ ℤ.](/img/revistas/ruma/v48n3/3a011023x.png)
Thus 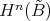 if
if 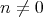 and
and 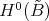 may be identified with
may be identified with 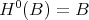 . If we view
. If we view 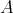 as a DG algebra concentrated in degree zero we may view
as a DG algebra concentrated in degree zero we may view 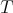 as a DG
as a DG 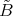 -A-bimodule. We claim that
-A-bimodule. We claim that 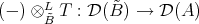 is an equivalence. Since
is an equivalence. Since 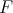 is an equivalence, conditions
is an equivalence, conditions  and
and  of lemma 7.14 clearly hold. For
of lemma 7.14 clearly hold. For  use the commutative diagram
use the commutative diagram
![Hom (B˜, ˜B [n ]) -----Hom (T, T[n]) D (B˜)| D (A ) ~ | ~ | | Hn ( ˜B )------~---HomH (A)(T,T [n]).](/img/revistas/ruma/v48n3/3a011036x.png)
To establish a connection between 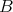 and
and 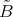 , let us introduce the DG subalgebra
, let us introduce the DG subalgebra 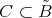 with
with  for
for 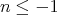 ,
, 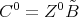 and
and  for
for 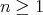 . Note that there are canonical morphisms
. Note that there are canonical morphisms
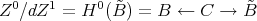
which are both quasi-isomorphisms. So, by example 7.15, we have a chain of equivalences
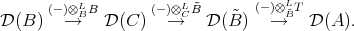
Applying the previous lemma twice we get the required complex 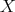 of
of 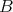 -
-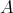 -bimodules.
-bimodules. 
In this section we show an example of tilting equivalence which is not a Morita equivalence. The example is due to Schwede ([Sch04]).
Consider a field 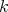 and take the
and take the 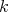 -algebra
-algebra 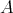 defined by:
defined by:
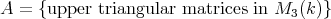
Up to isomorphism, there are three indecomposable 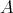 -projective modules:
-projective modules:
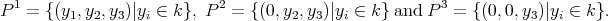
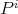 are the projective covers of the simple modules
are the projective covers of the simple modules 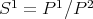 ,
, 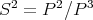 and
and  . In particular,
. In particular, 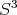 is projective and
is projective and 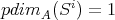 for
for 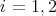 .
. Let us take  , which is clearly not projective. The following projective resolution of
, which is clearly not projective. The following projective resolution of 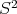 :
:
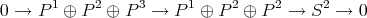
may be used to compute 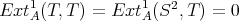 . The module
. The module 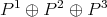 is
is 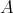 -free of rank one, then
-free of rank one, then 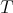 is a tilting
is a tilting 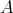 -module.
-module.
The 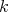 -algebra
-algebra 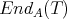 may be identified, by a direct computation, to the subalgebra of
may be identified, by a direct computation, to the subalgebra of 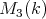 consisting of upper triangular matrices
consisting of upper triangular matrices 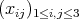 such that
such that 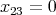 .
.
Now 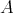 and
and 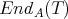 are NOT Morita equivalent since their lattices of projective modules differ.
are NOT Morita equivalent since their lattices of projective modules differ.
Acknowledgement: we want to thank Estanislao Herscovich for his help in the preparation of this notes.
[Ve77] Deligne, P. Cohomologie étale. Séminaire de Géométrie Algébrique du Bois-Marie SGA 4 . Avec la collaboration de J. F. Boutot, A. Grothendieck, L. Illusie et J. L. Verdier. Lecture Notes in Mathematics, Vol. 569. Springer-Verlag, Berlin-New York, 1977. [ Links ]
. Avec la collaboration de J. F. Boutot, A. Grothendieck, L. Illusie et J. L. Verdier. Lecture Notes in Mathematics, Vol. 569. Springer-Verlag, Berlin-New York, 1977. [ Links ]
[DG02] Dwyer, W.; Greenless, P. Complete modules and torsion modules. Amer. J. Math. 124, (2002), pp. 199-220. [ Links ]
[GM03] Gelfand, S. I.; Manin, Y. I. Methods of homological algebra. Second edition. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003. [ Links ]
[Ha66] Hartshorne, R. Residues and duality. Lecture notes of a seminar on the work of A. Grothendieck, given at Harvard 1963/64. With an appendix by P. Deligne. Lecture Notes in Mathematics, No. 20 Springer-Verlag, Berlin-New York, 1966, vii+423 pp. [ Links ]
[Ke94] Keller, B. Derived DG-categories. Ann. Sci. Éc. Norm. Sup. (4) 27, (1994), pp. 63-102. [ Links ]
[K96] Keller, B. Derived categories and their uses. Handbook of algebra, Vol. 1, 671-701, North-Holland, Amsterdam, 1996. [ Links ]
[KZ98] König, S.; Zimmermann, A. Derived equivalences for group rings. Lecture Notes in Math. 1685, Springer-Verlag, 1998. [ Links ]
[Kr05] Krause, H. Derived categories, resolutions, and Brown representability. arXiv math.KT/0511047. [ Links ]
[P62] Puppe, D. On the formal structure of stable homotopy theory. Colloq. algebr. Topology, Aarhus 1962, 65-71 (1962). [ Links ]
[Rick89] Rickard, J. Morita theory for derived categories. J. London Math. Soc. (2) 39, (1989), 436-456. [ Links ]
[Rick91] Rickard, J. Derived equivalences as derived functors. J. London Math. Soc. (2) 43, (1991), 37-48. [ Links ]
[Sp88] Spaltenstein, N. Resolutions of unbounded complexes. Compositio Math. 65 (1988), no. 2, 121-154. [ Links ]
[Sch04] Schwede, S. Morita theory in abelian, derived and stable model categories. Structured ring spectra, 33-86, London Math. Soc. Lecture Note Ser., 315, Cambridge Univ. Press, Cambridge, 2004. [ Links ]
[Ve96] Verdier, J.L. Des catégories dérivées des catégories abéliennes. Astérisque 239 (1996). [ Links ]
María Julia Redondo
Instituto de Matemática,
Universidad Nacional del Sur,
Av. Alem 1253,
(8000) Bahía Blanca, Argentina.
mredondo@criba.edu.ar
Andrea Solotar
Departamento de Matemática,
FCEyN, Universidad Nacional de Buenos Aires,
Ciudad Universitaria, Pabellón I,
(1428) Ciudad Autónoma de Buenos Aires, Argentina.
asolotar@dm.uba.ar
Recibido: 26 de octubre de 2006
Aceptado: 10 de abril de 2007