Non-homogeneous N-Koszul Algebras

Roland Berger

Abstract. This is a joint work with Victor Ginzburg [4] in which we study a class of associative algebras associated to finite groups acting on a vector space. These algebras are non-homogeneous N-Koszul algebra generalizations of symplectic reflection algebras. We realize the extension of the N-Koszul property to non-homogeneous algebras through a Poincaré-Birkhoff-Witt property.

 

PART I - HOMOGENEOUS N-KOSZUL ALGEBRAS

I introduced these algebras in [2]. These algebras extend classic Koszul algebras (Priddy, 1970) corresponding to . A natural question is: why higher 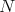's? I list below four answers.

1. There are some relevant examples coming from

- noncommutative projective algebraic geometry: cubic Artin-Schelter regular algebras [1] of global dimension 3, as

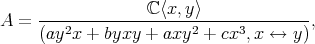
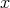where the second relation is obtained from the first one by exchanging and 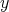. The two generators 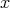and 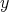have degree one, and the two relations are cubic. Artin-Schelter regular algebras are noncommutative analogues of polynomial rings which are used to make noncommutative projective algebraic geometry in sense of M. Artin and J. Zhang.

- representation theory: skew-symmetrizer killing algebras (introduced in [2]):

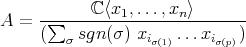
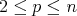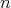for . The sum runs over all the permutations of . There are generators of degree one, and the relations have degree 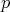. The number of relations is the binomial coefficient 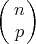. I will go back to this example in Part III.

- theoretical physics: Yang-Mills algebras (A. Connes and M. Dubois-Violette [7]):

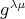where are entries of an invertible symmetric real 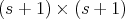matrix. There are generators of degree one, and cubic relations.

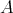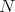2. Poincaré duality in Hochschild (co)homology (R.B. and N. Marconnet [5]): if is -Koszul and AS-Gorenstein, then

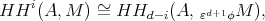
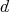where is the global dimension of 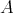, and 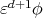is a certain automorphism of the algebra 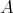twisting the left action on .

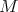3. Extension of 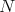-Koszulity to quiver algebras with relations by E. Green, E. Marcos, R. Martínez-Villa, P. Zhang [10].

4. Extension of Koszul duality in terms of 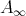-algebras by J.-W. He and D.-M. Lu [11].

PART II - SYMPLECTIC REFLECTION ALGEBRAS

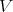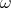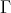These algebras were introduced by P. Etingof and V. Ginzburg [8], and play an important role in representation theory and algebraic geometry (desingularization). Let be a finite dimensional complex vector space which is endowed with a symplectic 2-form . Let be a finite subgroup of Sp 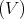and 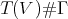be the smash product of the tensor algebra 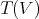of 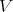with the group algebra 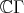of 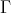. From these data, a 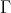-invariant linear map

is defined, and the symplectic reflection algebra is the -algebra

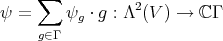
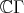The algebra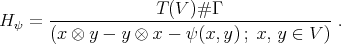 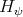is filtered and there is a natural graded algebra morphism .

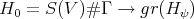Theorem (P.E.-V.G. [8]) This morphism is an isomorphism, i.e., the Poincaré-Birkhoff-Witt (PBW) property holds for .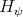

Ginzburg and I are able to provide an 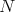-version of this theorem [4]. First we define an 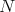-version of 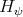with 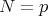(the notation 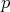is more convenient as far as symplectic reflection algebras are concerned). These generalized 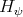's are called higher symplectic reflection algebras [4].

PART III - HIGHER SYMPLECTIC REFLECTION ALGEBRAS

Fix 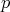, . We have generalizations

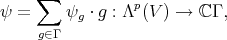
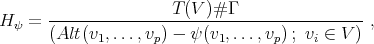
where .

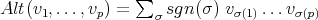Theorem (R.B.-V.G. [4]) The PBW property holds for generalized .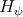

The undeformed algebra 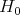is the skew-symmetrizer killing algebra of Part I (up to the change of rings 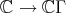) which is still 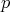-Koszul for the new ground ring. In order to prove the previous theorem, we state and prove the following.

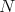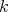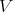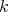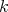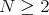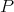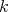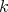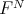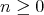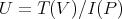-PBW Theorem (R.B.-V.G. [4]) Assume that is a von Neumann regular ring, is a --bimodule, , and is a sub---bimodule of , where for any . Set and 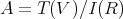, where 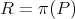and 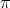is the projection of 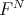onto 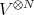modulo .

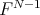Assume that 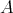is 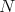-Koszul (this assumption can be weakened). Then the combination of the two conditions

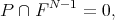(0.1)

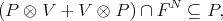(0.2)

is equivalent to the PBW property for .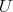

Next, we check conditions (0.1) and (0.2) for generalized 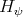. Condition (0.1) is easily drawn from the 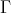-invariance of 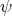, while condition (0.2) (which can be viewed as an 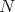-version of the Jacobi identity) is obtained by a close analysis of a standard Koszul complex.

Comments on the 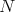-PBW Theorem

- For and 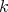field, this theorem is due to A. Braverman-D. Gaitsgory [6], and A. Polishchuk-L. Positselski [12] (during the 1990's).

- The 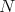-PBW theorem for 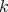field and 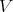finite-dimensional is independently stated and proved by G. Fløystad and J. Vatne [9].

Definitions Let us keep notations and assumptions of the 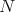-PBW theorem. If the PBW property holds for 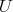, one says that 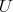is Koszul (R.B.-V.G.), or that 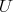is a PBW-deformation of 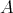(G.F.-J.V.).

The first definition extends nicely the definition of homogeneous 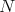-Koszul algebras. A historical argument in favour of this terminology is given by the first Lie theory use by J. L. Koszul of his complex (mentioned in Cartan-Eilenberg's book, p. 281): working in the filtered context of the enveloping algebra of a Lie algebra, J. L. Koszul used the classical PBW property as a tool to carry over the exactness of his complex to the standard complex. The second definition is useful when one wants to find all the 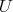's corresponding to a given .

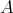There are already some various applications of the 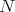-PBW theorem:

1. G. Fløystad and J. Vatne have found [9] all the PBW-deformations of
- any cubic Artin-Schelter regular algebra of global dimension 3,
- any skew-symmetrizer killing algebra for 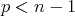between (note that, for this second point, the intersection of their result and our result is very small since it corresponds to a trivial group ).

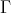2. The PBW-deformations of Yang-Mills algebras have been determined by M. Dubois-Violette and R.B. [3].

In these applications, the 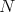-PBW theorem of G.F.-J.V. suffices. However, our general setting for the 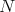-PBW theorem allows us to include significant examples (as higher symplectic reflection algebras) for which the ground field is enlarged to group algebras 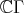with non trivial .

References

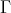[1]    M. Artin, W. F. Schelter, Graded algebras of global dimension 3, Adv. Math. 66 (1987), 171-216.        [ Links ]

[2]    R. Berger, Koszulity for nonquadratic algebras, J. Algebra 239 (2001), 705-734.        [ Links ]

[3]    R. Berger, M. Dubois-Violette, Inhomogeneous Yang-Mills Algebras, Lett. Math. Phys. 76 (2006), 65-75.        [ Links ]

[4]     R. Berger, V. Ginzburg, Symplectic reflection algebras and non-homogeneous N-Koszul property, J. Algebra 304 (2006), 577-601.        [ Links ]

[5]    R. Berger, N. Marconnet, Koszul and Gorenstein properties for homogeneous algebras, Alg. and Rep. Theory 9 (2006), 67-97.        [ Links ]

[6]    A. Braverman, D. Gaitsgory, Poincaré-Birkhoff-Witt theorem for quadratic algebras of Koszul type, J. Algebra 181 (1996), 315-328.        [ Links ]

[7]    A. Connes, M. Dubois-Violette, Yang-Mills algebra, Lett. Math. Phys. 61 (2002), 149-158.        [ Links ]

[8]    P. Etingof, V. Ginzburg, Symplectic reflection algebras, Calogero-Moser space, and deformed Harish-Chandra homomorphism, Invent. math. 147 (2002), 243-348.        [ Links ]

[9]    G. Fløystad, J.E. Vatne, PBW-deformations of N-Koszul algebras, J. Algebra 302 (2006), 116 -155.        [ Links ]

[10]    E.L. Green, E.N. Marcos, R. Martínez-Villa, P. Zhang, D-Koszul algebras, J. Pure and Applied Algebra 193 (2004), 141-162.        [ Links ]

[11]    J.-W. He, D.-M. Lu, Higher Koszul algebras and A-infinity algebras. J. Algebra 293 (2005), no. 2, 335-362.        [ Links ]

[12]    A. Polishchuk, L. Positselski, Quadratic algebras. University Lecture Series 37, American Mathematical Society, Providence, RI, 2005.        [ Links ]

Roland Berger
LaMUSE,
Faculté des Sciences et Techniques,
23, Rue P. Michelon,
42023 Saint-Etienne Cedex 2, France
Roland.Berger@univ-st-etienne.fr

Recibido: 6 de abril de 2006
Aceptado: 10 de octubre de 2006