Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.48 n.3 Bahía Blanca 2007
On pointed Hopf algebras associated with alternating and dihedral groups
Nicolás Andruskiewitsch and Fernando Fantino
Abstract. We classify finite-dimensional complex pointed Hopf algebras with group of group-like elements isomorphic to 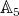 . We show that any pointed Hopf algebra with infinitesimal braiding associated with the conjugacy class of
. We show that any pointed Hopf algebra with infinitesimal braiding associated with the conjugacy class of 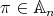 is infinite-dimensional if the order of
is infinite-dimensional if the order of 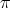 is odd except for
is odd except for 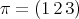 in
in 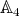 . We also study pointed Hopf algebras over the dihedral groups.
. We also study pointed Hopf algebras over the dihedral groups.
2000 Mathematics Subject Classification. 16W30; 17B37
This work was partially supported by Agencia Córdoba Ciencia, ANPCyT-Foncyt, CONICET and Secyt (UNC)
Dedicado a María Inés Platzeck en sus #  años
años
In this article, we continue the work of [AZ, AF] on the classification of finite-dimensional complex pointed Hopf algebras 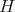 with
with 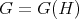 non-abelian. We follow the Lifting Method - see [AS2] for a general reference; in particular, we focus on the problem of determining when the dimension of the Nichols algebra associated with conjugacy classes of
non-abelian. We follow the Lifting Method - see [AS2] for a general reference; in particular, we focus on the problem of determining when the dimension of the Nichols algebra associated with conjugacy classes of 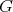 is infinite. The paper is organized as follows. In Section 1, we review some general facts on Nichols algebras corresponding to finite groups. We discuss the notion of absolutely real element of a finite group in subsection 1.2. We then provide generalizations of [AZ, Lemma 1.3], a basic tool in [AZ, AF], see Lemmata 1.8 and 1.9. Section 2 is devoted to pointed Hopf algebras with coradical
is infinite. The paper is organized as follows. In Section 1, we review some general facts on Nichols algebras corresponding to finite groups. We discuss the notion of absolutely real element of a finite group in subsection 1.2. We then provide generalizations of [AZ, Lemma 1.3], a basic tool in [AZ, AF], see Lemmata 1.8 and 1.9. Section 2 is devoted to pointed Hopf algebras with coradical 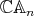 . We prove that any finite-dimensional complex pointed Hopf algebra
. We prove that any finite-dimensional complex pointed Hopf algebra 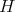 with
with 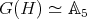 is isomorphic to the group algebra of
is isomorphic to the group algebra of 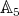 ; see Theorem 2.6. This is the first finite non-abelian group
; see Theorem 2.6. This is the first finite non-abelian group 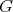 such that all pointed Hopf algebras
such that all pointed Hopf algebras 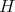 with
with 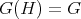 are known. We also prove that
are known. We also prove that 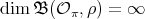 , for any
, for any 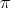 in
in 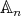 of odd order, except for
of odd order, except for 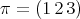 or
or 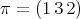 in
in 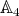 - see Theorem 2.3. This last case is particularly interesting. It corresponds to a "tetrahedron" rack with constant cocycle
- see Theorem 2.3. This last case is particularly interesting. It corresponds to a "tetrahedron" rack with constant cocycle 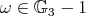 . The technique in the present paper does not provide information on the corresponding Nichols algebra. We also give partial results on pointed Hopf algebras with groups
. The technique in the present paper does not provide information on the corresponding Nichols algebra. We also give partial results on pointed Hopf algebras with groups 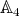 and
and 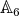 , and on Nichols algebras
, and on Nichols algebras 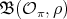 , with
, with 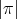 even. In Section 3, we apply the technique to conjugacy classes in dihedral groups. It turns out that it is possible to decide when the associated Nichols algebra is finite-dimensional in all cases except for
even. In Section 3, we apply the technique to conjugacy classes in dihedral groups. It turns out that it is possible to decide when the associated Nichols algebra is finite-dimensional in all cases except for 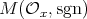 (if
(if 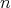 is odd), or
is odd), or 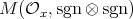 or
or 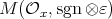 or
or 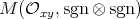 or
or 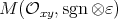 (if
(if 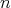 is even). See below for undefined notations. We finally observe in Section 4 that there is no finite-dimensional Hopf algebra with coradical isomorphic to the Hopf algebra
is even). See below for undefined notations. We finally observe in Section 4 that there is no finite-dimensional Hopf algebra with coradical isomorphic to the Hopf algebra 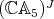 discovered in [Ni], except for
discovered in [Ni], except for 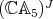 itself.
itself.
For 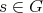 we denote by
we denote by 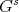 the centralizer of
the centralizer of  in
in 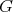 . If
. If 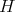 is a subgroup of
is a subgroup of 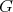 and
and 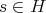 we will denote
we will denote 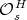 the conjugacy class of
the conjugacy class of  in
in 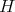 . Sometimes we will write in rack notations
. Sometimes we will write in rack notations 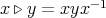 ,
, 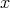 ,
, 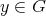 . Also, if
. Also, if 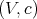 is a braided vector space, that is
is a braided vector space, that is 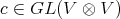 is a solution of the braid equation, then
is a solution of the braid equation, then 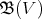 denotes its Nichols algebra.
denotes its Nichols algebra.
We denote by 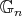 the group of
the group of 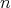 -th roots of 1 in
-th roots of 1 in  .
.
1.1. Preliminaries. Let 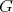 be a finite group,
be a finite group,  a conjugacy class of
a conjugacy class of 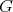 ,
, 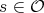 fixed,
fixed, 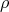 an irreducible representation of
an irreducible representation of 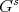 ,
,  the corresponding irreducible Yetter-Drinfeld module. Let
the corresponding irreducible Yetter-Drinfeld module. Let 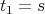 , …,
, …, 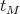 be a numeration of
be a numeration of  and let
and let 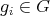 such that
such that 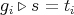 for all
for all 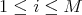 . Then
. Then 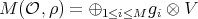 . Let
. Let 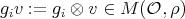 ,
, 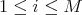 ,
, 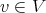 . If
. If 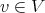 and
and 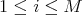 , then the coaction and the action of
, then the coaction and the action of 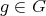 are given by
are given by

where 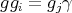 , for some
, for some 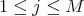 and
and 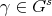 . The Yetter-Drinfeld module
. The Yetter-Drinfeld module  is a braided vector space with braiding given by
is a braided vector space with braiding given by
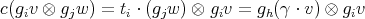 | (1) |
for any 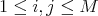 ,
, 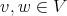 , where
, where 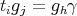 for unique
for unique 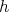 ,
, 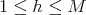 and
and 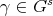 . Since
. Since 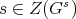 , the Schur Lemma says that
, the Schur Lemma says that
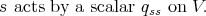 | (2) |
Let 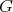 be a finite non-abelian group. Let
be a finite non-abelian group. Let  be a conjugacy class of
be a conjugacy class of 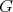 and let
and let 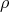 be an irreducible representation of the centralizer
be an irreducible representation of the centralizer 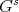 of a fixed
of a fixed 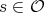 . Let
. Let  be the irreducible Yetter-Drinfeld module corresponding to
be the irreducible Yetter-Drinfeld module corresponding to 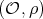 and let
and let 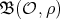 be its Nichols algebra. As explained in [AZ, AF, Gñ], we look for a braided subspace
be its Nichols algebra. As explained in [AZ, AF, Gñ], we look for a braided subspace 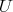 of
of  of diagonal type such that the dimension of the Nichols algebra
of diagonal type such that the dimension of the Nichols algebra 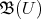 is infinite. This implies that the dimension of
is infinite. This implies that the dimension of 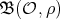 is infinite too.
is infinite too.
Lemma 1.1. If 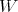 is a subspace of
is a subspace of 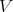 such that
such that 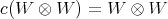 and
and 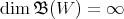 , then
, then 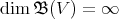 .□
.□
Recall that a braided vector space 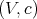 is of diagonal type if there exists a basis
is of diagonal type if there exists a basis  of
of 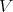 and non-zero scalars
and non-zero scalars 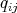 ,
, 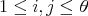 , such that
, such that 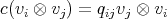 , for all
, for all 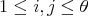 . A braided vector space
. A braided vector space 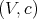 is of Cartan type if it is of diagonal type and there exists
is of Cartan type if it is of diagonal type and there exists 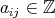 ,
, 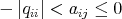 such that
such that 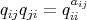 for all
for all 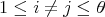 ; by
; by 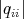 we mean
we mean 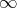 if
if 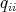 is not a root of 1, otherwise it means the order of
is not a root of 1, otherwise it means the order of 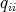 in the multiplicative group of the units in
in the multiplicative group of the units in  . Set
. Set 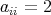 for all
for all 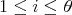 . Then
. Then 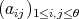 is a generalized Cartan matrix.
is a generalized Cartan matrix.
Theorem 1.2. ([H, Th. 4], see also [AS1, Th. 1.1]). Let 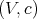 be a braided vector space of Cartan type. Then
be a braided vector space of Cartan type. Then 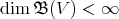 if and only if the Cartan matrix is of finite type. □
if and only if the Cartan matrix is of finite type. □
We say that 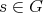 is real if it is conjugate to
is real if it is conjugate to 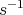 ; if
; if  is real, then the conjugacy class of
is real, then the conjugacy class of  is also said to be real. We say that
is also said to be real. We say that 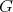 is real if any
is real if any 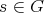 is real.
is real.
The next application of Theorem 1.2 was given in [AZ]. Let 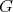 be a finite group,
be a finite group, 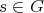 ,
,  the conjugacy class of
the conjugacy class of  ,
,  irreducible;
irreducible; 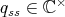 was defined in (2).
was defined in (2).
Lemma 1.3. Assume that  is real. If
is real. If 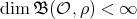 then
then 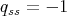 and
and  has even order.□
has even order.□
If 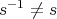 , this is [AZ, Lemma 2.2]; if
, this is [AZ, Lemma 2.2]; if  then
then 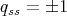 but
but 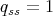 is excluded by Lemma 1.1.
is excluded by Lemma 1.1.
The class of real groups includes finite Coxeter groups. Indeed, all the characters of a finite Coxeter group are real valued, see subsection 1.2 below, and [BG] for 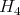 . Therefore, we have:
. Therefore, we have:
Theorem 1.4. Let 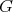 be a finite Coxeter group. If
be a finite Coxeter group. If 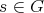 has odd order, then
has odd order, then 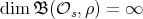 , for any
, for any 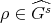 . □
. □
1.2. Absolutely real groups. Let 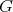 be a finite group. We say that
be a finite group. We say that 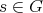 is absolutely real if there exists an involution
is absolutely real if there exists an involution  in
in 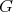 such that
such that 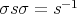 . If this happens, any element in the conjugacy class of
. If this happens, any element in the conjugacy class of  is absolutely real and we will say that the conjugacy class of
is absolutely real and we will say that the conjugacy class of  is absolutely real. We say that
is absolutely real. We say that 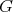 is absolutely real if any
is absolutely real if any 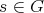 is so. The finite Coxeter groups are absolutely real. Indeed,
is so. The finite Coxeter groups are absolutely real. Indeed,
- the dihedral groups are absolutely real, by straightforward computations.
- the Weyl groups of semisimple finite dimensional Lie algebras are absolutely real, by [C, Th. C (iii), p. 45].
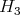 is absolutely real, by Proposition 1.7 below.
is absolutely real, by Proposition 1.7 below.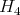 is absolutely real, we have checked it using GAP3, [S].
is absolutely real, we have checked it using GAP3, [S].
Remark 1.5. Let 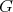 ,
, 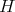 be finite groups. We note:
be finite groups. We note:
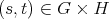 is absolutely real iff both
is absolutely real iff both 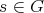 and
and 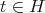 are absolutely real.
are absolutely real. is absolutely real iff both
is absolutely real iff both 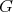 and
and 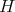 are absolutely real.
are absolutely real.- Assume
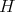 abelian. Then
abelian. Then 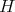 is absolutely real iff
is absolutely real iff 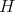 has exponent 2, i. e.
has exponent 2, i. e.  for some integer
for some integer 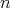 .
. - If
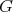 is absolutely real and
is absolutely real and 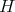 is abelian of exponent 2 then
is abelian of exponent 2 then  is absolutely real.
is absolutely real.
We first discuss when an element of 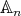 is absolutely real. Assume that
is absolutely real. Assume that 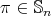 is of type
is of type 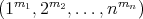 . Then
. Then 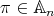 iff
iff 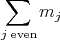 is even.
is even.
Lemma 1.6. (a). If 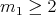 , then
, then 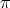 is absolutely real in
is absolutely real in 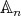 .
.
(b). If 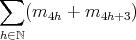 is even then
is even then 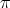 is absolutely real in
is absolutely real in 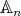 .
.
Proof. Let 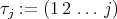 for some
for some 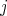 and take
and take
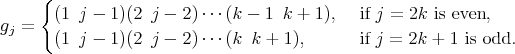
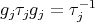 ,
, 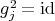 and
and 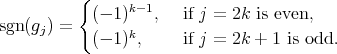
To prove (b), observe that there exists an involution 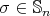 such that
such that  , which is a product of "translations" of the
, which is a product of "translations" of the 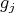 's. Since the sign of
's. Since the sign of  is
is 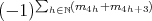 ,
, 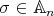 iff
iff 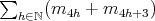 is even; (b) follows. We prove (a). By assumption there are at least two points fixed by
is even; (b) follows. We prove (a). By assumption there are at least two points fixed by 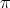 , say
, say  ,
, 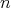 . By the preceding there exists an involution
. By the preceding there exists an involution 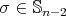 such that
such that  . If
. If 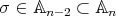 we are done, otherwise take
we are done, otherwise take  ;
; 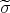 is an involution and
is an involution and  . □
. □
Proposition 1.7. The groups 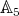 and
and 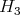 are absolutely real.
are absolutely real.
Proof. The type of 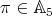 is either
is either 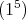 ,
, 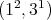 ,
, 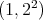 or
or 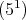 ; in the first two cases
; in the first two cases 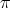 is absolutely real by Lemma 1.6 part (a), in the last two by part (b). Since
is absolutely real by Lemma 1.6 part (a), in the last two by part (b). Since 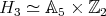 (see [Hu, Section 2.13]), then the Coxeter group is absolutely real by Remark 1.5. □
(see [Hu, Section 2.13]), then the Coxeter group is absolutely real by Remark 1.5. □
1.3. Generalizations of Lemma 1.3. The next two Lemmata are variations of [AZ, Lemma 2.2]. A result in the same spirit appears in [FGV]. We deal with elements  having a power in
having a power in  , the conjugacy class of
, the conjugacy class of  . Clearly, if
. Clearly, if 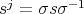 is in
is in  , then
, then 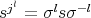 is in
is in  , for every
, for every 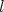 . So,
. So, 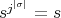 ; this implies that
; this implies that 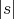 divides
divides 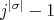 . Hence
. Hence
with 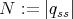 , recall (2).
, recall (2).
Lemma 1.8. Let 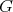 be a finite group,
be a finite group, 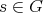 ,
,  the conjugacy class of
the conjugacy class of  and
and 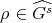 . Assume that there exists an integer
. Assume that there exists an integer 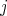 such that
such that  ,
, 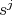 and
and 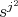 are distinct elements and
are distinct elements and 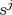 is in
is in  . If
. If 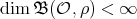 , then
, then  has even order and
has even order and 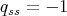 .
.
Proof. We assume that 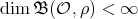 , thus
, thus 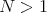 . It is easy to see that
. It is easy to see that
for every 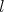 ,
, 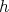 . We will call
. We will call 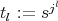 ,
, 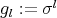 ,
,  ,
,  ,
, 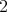 ; so
; so 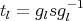 , for
, for  ,
,  ,
, 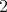 . The other relations between
. The other relations between 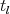 's and
's and 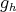 's are obtained from (4). For
's are obtained from (4). For 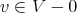 and
and  or
or 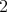 , we define
, we define 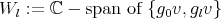 . Hence,
. Hence, 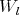 is a braided vector subspace of
is a braided vector subspace of  of Cartan type with
of Cartan type with
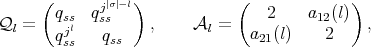
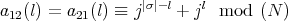 . Since
. Since 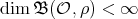 , we have that
, we have that 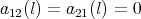 or
or  . We consider now two cases.
. We consider now two cases. (i) Let us suppose that
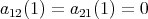 . This implies that
. This implies that 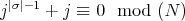 . Since
. Since 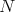 divides
divides 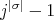 , we have that
, we have that 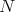 divides
divides  . We consider now two possibilities.
. We consider now two possibilities. - Assume that
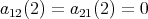 . Then
. Then 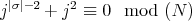 . Since
. Since 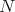 divides
divides 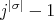 , we have that
, we have that 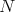 divides
divides  . So,
. So, 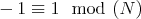 ; hence the result follows.
; hence the result follows. - Assume that
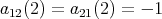 . Then
. Then 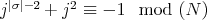 . We can see that
. We can see that 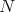 divides
divides 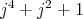 . This implies that
. This implies that 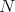 divides
divides  , a contradiction.
, a contradiction.
(ii) Let us suppose that 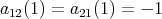 . This implies that
. This implies that 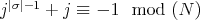 . Since
. Since 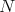 divides
divides 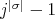 , we have that
, we have that 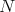 divides
divides 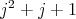 . We consider now two possibilities.
. We consider now two possibilities.
- Assume that
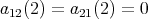 . Then
. Then 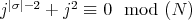 . So,
. So, 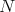 divides
divides  . It is easy to see that
. It is easy to see that 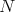 divides
divides 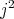 . Since
. Since 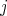 and
and 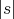 are relatively prime,
are relatively prime, 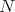 must be
must be  , a contradiction.
, a contradiction. - Assume that
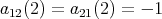 . This means that the subspace
. This means that the subspace 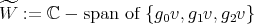 of
of  is of Cartan type with
is of Cartan type with 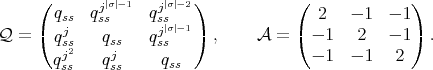
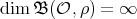 , a contradiction.
, a contradiction.
This concludes the proof. □
Lemma 1.9. Let 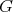 be a finite group,
be a finite group, 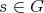 ,
,  the conjugacy class of
the conjugacy class of  and
and 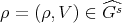 such that
such that 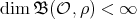 . Assume that there exists an integer
. Assume that there exists an integer 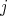 such that
such that 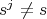 and
and 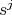 is in
is in  .
.
- If
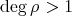 , then
, then  has even order and
has even order and 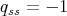 .
. - If
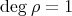 , then either
, then either  has even order and
has even order and 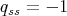 , or
, or 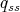
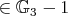 .
.
Proof. We will proceed and use the notation as in the proof of Lemma 1.8. If 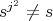 , then the result follows by Lemma 1.8. Assume that
, then the result follows by Lemma 1.8. Assume that  . This implies that
. This implies that 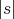 divides
divides 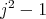 , so
, so 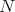 divides
divides 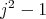 .
.
(a) Let 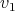 and
and 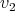 in
in 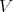 linearly independent and let
linearly independent and let  - span of
- span of 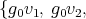
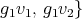 , with
, with 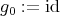 and
and 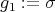 . Thus
. Thus 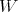 is a braided vector subspace of
is a braided vector subspace of  of Cartan type with
of Cartan type with
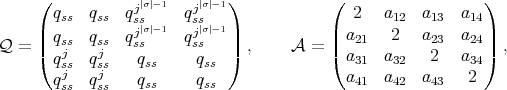
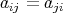 ,
, 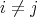 ,
, 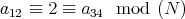 ,
,  and
and 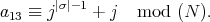
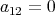 or
or 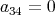 , then
, then 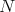 divides
divides 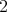 and the result follows. Besides, if
and the result follows. Besides, if 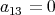 , then
, then 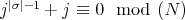 ; this implies that
; this implies that 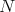 divides
divides  , so
, so 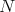 divides 2 and the result follows. On the other hand, if
divides 2 and the result follows. On the other hand, if 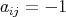 , for all
, for all 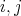 , we have that the matrix
, we have that the matrix 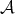 is not of finite type; hence
is not of finite type; hence 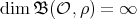 , from Theorem 1.2. This is a contradiction by hypothesis. Therefore, (a) is proved.
, from Theorem 1.2. This is a contradiction by hypothesis. Therefore, (a) is proved. (b) For 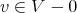 we define
we define 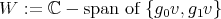 , with
, with 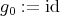 and
and 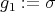 . Hence,
. Hence, 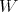 is a braided vector subspace of
is a braided vector subspace of  of Cartan type with
of Cartan type with
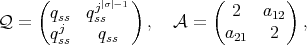
 . Since
. Since 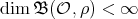 , we have that
, we have that 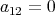 or
or  . We consider now two possibilities.
. We consider now two possibilities. (i) Assume that
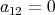 . This implies that
. This implies that 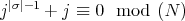 . Since
. Since 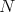 divides
divides 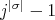 , we have that
, we have that 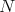 divides
divides 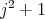 . Thus,
. Thus, 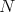 divides
divides 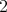 ; hence
; hence  , and the result follows.
, and the result follows. (ii) Assume that
 . This implies that
. This implies that 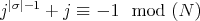 . Since
. Since 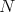 divides
divides 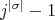 , we have that
, we have that 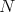 divides
divides 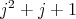 . Hence,
. Hence,  divides
divides  . If
. If  is a prime divisor of
is a prime divisor of  , then
, then 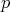 divides
divides  or
or  , because
, because 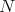 divides
divides 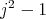 . If
. If 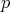 divides
divides  , then
, then 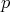 divides
divides  , a contradiction. So,
, a contradiction. So, 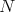 divides
divides  . Hence,
. Hence, 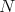 divides
divides 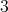 , i.e.
, i.e.  and the result follows. □
and the result follows. □ We recall that we will denote  or
or  the conjugacy class of an element
the conjugacy class of an element 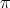 in
in 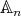 , and
, and 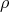 in
in 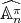 , a representative of an isomorphism class of irreducible representations of
, a representative of an isomorphism class of irreducible representations of 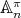 . We want to determine pairs
. We want to determine pairs 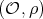 , for which
, for which 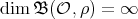 , following the strategy given in [AZ, AF]; see also [Gñ].
, following the strategy given in [AZ, AF]; see also [Gñ].
The following is a helpful criterion to decide when a conjugacy class of an even permutation 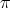 in
in 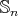 splits in
splits in 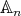 .
.
Proposition 2.1. [JL, Proposition 12.17] Let 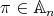 , with
, with  .
.
- If
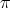 commutes with some odd permutation in
commutes with some odd permutation in 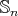 , then
, then 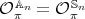 and
and ![π π [𝕊n : 𝔸 n] = 2](/img/revistas/ruma/v48n3/3a04440x.png) .
. - If
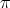 does not commute with any odd permutation in
does not commute with any odd permutation in 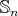 , then
, then 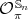 splits into two conjugacy classes in
splits into two conjugacy classes in 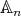 of equal size, with representatives
of equal size, with representatives 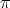 and
and 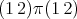 , and
, and 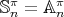 .□
.□
Remarks 2.2. (i) Notice that if 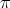 satisfies (1) of Proposition 2.1, then
satisfies (1) of Proposition 2.1, then 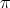 is real. The reciprocal is not true, e.g. consider
is real. The reciprocal is not true, e.g. consider 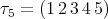 in
in 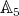 .
.
(ii) One can see that if 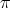 in
in 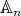 is of type
is of type 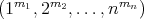 , then
, then 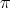 satisfies (2) of Proposition 2.1 if and only if
satisfies (2) of Proposition 2.1 if and only if 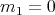 or
or  ,
, 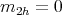 and
and 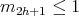 , for all
, for all 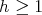 . Thus, if
. Thus, if 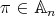 has even order, then
has even order, then 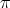 is real.
is real.
We state the main Theorem of the section.
Theorem 2.3. Let 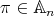 and
and 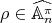 . Assume that
. Assume that 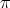 is neither
is neither 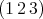 nor
nor 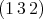 in
in 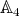 . If
. If 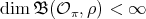 , then
, then 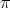 has even order and
has even order and 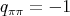 .
.
Proof. If 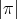 is even the result follows by Lemma 1.3 and Remark 2.2 (ii). Let us suppose that
is even the result follows by Lemma 1.3 and Remark 2.2 (ii). Let us suppose that  and odd . If
and odd . If  is in
is in  , then the result follows by Lemma 1.3. Assume that
, then the result follows by Lemma 1.3. Assume that 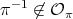 . We consider two cases.
. We consider two cases.
(i) If 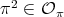 , then
, then 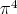 is in
is in  , and
, and 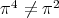 because
because  . Hence, the result follows from Lemma 1.8.
. Hence, the result follows from Lemma 1.8.
(ii) Assume that 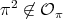 . We know that there exist
. We know that there exist  and
and 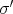 in
in 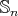 , necessarily odd permutations, such that
, necessarily odd permutations, such that 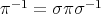 and
and 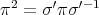 . Then
. Then 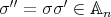 and
and 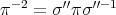 ; so
; so 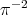 is in
is in  . This implies that
. This implies that 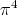 is in
is in  , and
, and 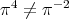 because
because 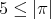 is odd. Now, the result follows from Lemma 1.8.
is odd. Now, the result follows from Lemma 1.8.
Finally, let us suppose that 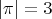 , with type
, with type 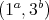 . If
. If 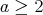 or
or  , then
, then 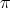 is real, by Lemma 1.6 (a) and Remark 2.2, respectively. Hence, the result follows by Lemma 1.3. This concludes the proof. □
is real, by Lemma 1.6 (a) and Remark 2.2, respectively. Hence, the result follows by Lemma 1.3. This concludes the proof. □
2.1. Case 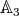 . Obviously,
. Obviously,  ; thus
; thus 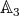 is not real. This case was considered in [AS1, Theorem 1.3].
is not real. This case was considered in [AS1, Theorem 1.3].
2.2. Case 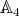 . It is straightforward to check that
. It is straightforward to check that 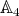 is not real, since
is not real, since 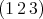 is not real in
is not real in 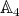 . Let
. Let 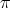 in
in 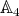 ; then the type of
; then the type of 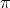 may be
may be 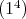 ,
, 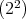 or
or 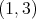 . If the type of
. If the type of 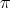 is
is 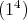 , then
, then 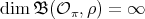 , for any
, for any 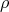 in
in 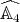 , by Lemma 1.1. If the type of
, by Lemma 1.1. If the type of 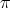 is
is 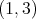 , then
, then 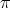 is not real; moreover we have
is not real; moreover we have
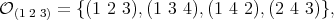
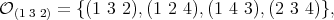
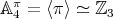 . If
. If 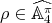 is trivial, then
is trivial, then 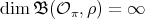 ; otherwise it is not known.
; otherwise it is not known. The following result is a variation of [AZ, Theorem 2.7].
Proposition 2.4. Let 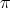 in
in 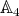 of type
of type 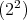 . Then
. Then 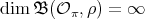 , for every
, for every 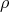 in
in 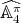 .
.
Proof. We can assume that 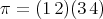 . If we call
. If we call 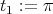 ,
, 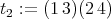 and
and 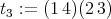 , then
, then 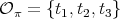 and
and 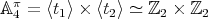 . If
. If  ,
, 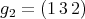 and
and 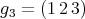 , then
, then 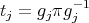 ,
, 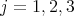 , and
, and 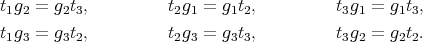
Let 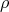 in
in 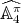 and
and 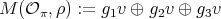 , where
, where  is the vector space affording
is the vector space affording 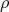 . Thus
. Thus  is a braided vector space with braiding given by - see (1)-
is a braided vector space with braiding given by - see (1)-  and
and 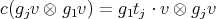 ,
, 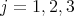 and
and 
Clearly,  , by Lemma 1.1. If we consider
, by Lemma 1.1. If we consider 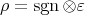 (resp.
(resp.  ), then
), then 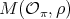 is of Cartan type with matrix of coefficients
is of Cartan type with matrix of coefficients 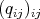 given by
given by
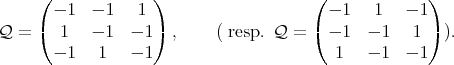
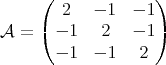 . Therefore,
. Therefore, 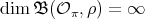 , by Theorem 1.2. □
, by Theorem 1.2. □ 2.3. Case 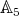 . Here is the key step in the consideration of this case.
. Here is the key step in the consideration of this case.
Lemma 2.5. Let 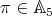 . Then
. Then 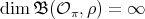 , for every
, for every 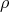 in
in 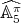 .
.
Proof. Let 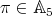 . If the type of
. If the type of 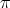 is either
is either 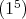 ,
, 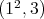 or
or 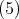 , we have that
, we have that 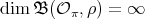 , by Lemma 1.3 and Proposition 1.7. Let us assume that the type of
, by Lemma 1.3 and Proposition 1.7. Let us assume that the type of 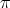 is
is 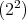 . For
. For 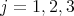 , let
, let 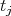 and
and 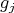 be as in the proof of Proposition 2.4. By Proposition 2.1 and straightforward computations, we have that
be as in the proof of Proposition 2.4. By Proposition 2.1 and straightforward computations, we have that 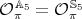 and
and 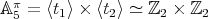 . Notice that
. Notice that 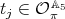 ,
, 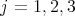 . Let
. Let 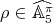 and
and  , where
, where  is the vector space affording
is the vector space affording 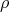 ; then
; then 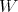 is a braided vector subspace of
is a braided vector subspace of 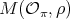 . Therefore,
. Therefore, 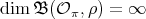 , by the same argument as in the proof of Proposition 2.4. □
, by the same argument as in the proof of Proposition 2.4. □
As an immediate consequence of Lemma 2.5 we have the following result.
Theorem 2.6. Any finite-dimensional complex pointed Hopf algebra 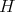 with
with 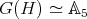 is necessarily isomorphic to the group algebra of
is necessarily isomorphic to the group algebra of 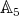 .
.
Proof. Let 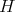 be a complex pointed Hopf algebra with
be a complex pointed Hopf algebra with 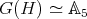 . Let
. Let 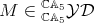 be the infinitesimal braiding of
be the infinitesimal braiding of 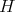 -see [AS2]. Assume that
-see [AS2]. Assume that 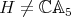 ; thus
; thus 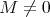 . Let
. Let 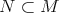 be an irreducible submodule. Then
be an irreducible submodule. Then 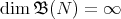 , by Lemma 2.5. Hence,
, by Lemma 2.5. Hence, 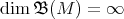 and
and 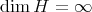 . □
. □
2.4. Case 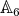 . Let
. Let 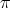 be in
be in 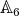 . If the type of
. If the type of 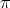 is
is 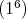 ,
, 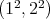 ,
, 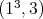 ,
,  or
or 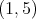 , then
, then 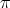 is absolutely real by Lemma 1.6, and if the type of
is absolutely real by Lemma 1.6, and if the type of 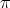 is
is 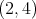 , then
, then 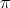 is real because it has even order - see Remark 2.2 (ii). Hence,
is real because it has even order - see Remark 2.2 (ii). Hence, 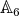 is a real group. We summarize our results in the following statement.
is a real group. We summarize our results in the following statement.
Theorem 2.7. Let  be an irreducible Yetter-Drinfeld module over
be an irreducible Yetter-Drinfeld module over 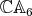 , corresponding to a pair
, corresponding to a pair 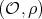 . If
. If 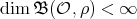 , then
, then 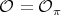 , with
, with 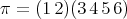 , and
, and 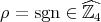 .
.
Remark 2.8. In this Theorem we do not claim that the condition is sufficient.
Proof. Let 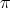 be in
be in 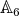 . If the type of
. If the type of 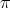 is
is
Let us suppose that the type of 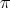 is
is 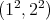 ; we can assume that
; we can assume that 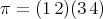 . It is easy to check that
. It is easy to check that
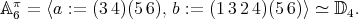
Notice that  . It is known that
. It is known that 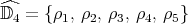 , where
, where 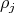 ,
,  ,
, 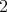 ,
, 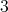 and
and 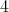 , are the following characters
, are the following characters
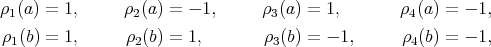
and 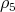 is the
is the 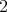 -dimensional representation given by
-dimensional representation given by
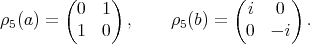
It is clear that 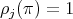 ,
,  ,
, 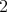 ,
, 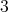 and
and 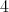 . Then
. Then 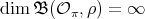 , by Lemma 1.1. Let us consider now that
, by Lemma 1.1. Let us consider now that 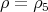 . We define
. We define 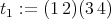 ,
, 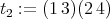 ,
, 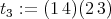 ,
, 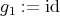 ,
, 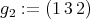 and
and 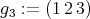 . It is clear that
. It is clear that
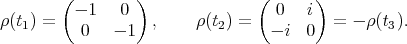
If 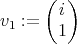 we have that
we have that 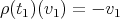 and
and 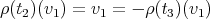 . We define
. We define 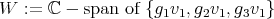 . Then
. Then 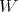 is a braiding subspace of
is a braiding subspace of 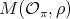 of Cartan type with
of Cartan type with
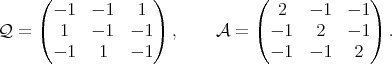
Since 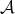 is not of finite type we have that
is not of finite type we have that 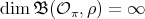 , by Theorem 1.2.
, by Theorem 1.2.
Finally, let us assume that the type of 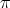 is
is 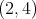 . Then
. Then  has
has 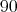 elements and
elements and 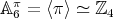 . We call
. We call 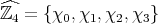 , where
, where 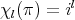 ,
,  ,
,  ,
, 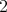 ,
, 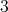 . It is clear that if
. It is clear that if 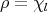 , with
, with  ,
,  or
or 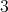 , then
, then 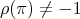 . This implies that
. This implies that 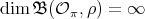 , by Lemma 1.3. □
, by Lemma 1.3. □
Remark 2.9. We can see that every maximal abelian subrack of 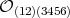 has two elements. Hence,
has two elements. Hence, 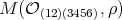 is a negative braided space in the sense of [AF].
is a negative braided space in the sense of [AF].
2.5. Case 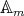 ,
, 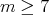 . Let
. Let 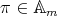 , with
, with 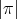 even. We now investigate the Nichols algebras associated with
even. We now investigate the Nichols algebras associated with 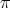 by reduction to the analogous study for the orbit of
by reduction to the analogous study for the orbit of 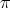 in
in 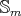 , [AF]. By Remark 2.2 (ii),
, [AF]. By Remark 2.2 (ii),  and
and ![[𝕊π : 𝔸 π] = 2 m m](/img/revistas/ruma/v48n3/3a04704x.png) . So, we can determinate the irreducible representations of
. So, we can determinate the irreducible representations of 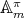 from those of
from those of 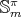 . We know that if the type of
. We know that if the type of 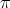 is
is 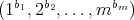 , then
, then 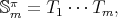 with
with  ,
, 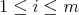 .
.
Some generalities and notation. Let 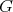 be a finite group,
be a finite group, 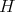 a subgroup of
a subgroup of 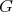 of index two, and
of index two, and 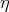 a representation of
a representation of 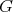 . It is easy to see that
. It is easy to see that
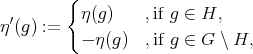
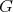 . Notice that
. Notice that  . On the other hand, any representation
. On the other hand, any representation 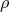 of
of 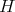 defines a representation
defines a representation 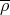 of
of 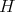 , call it the conjugate representation of
, call it the conjugate representation of 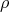 , given by
, given by 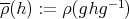 , for every
, for every 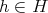 , where
, where 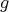 is an arbitrary fixed element in
is an arbitrary fixed element in 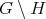 . Since
. Since 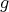 is unique up to multiplication by an element of
is unique up to multiplication by an element of 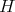 , the conjugate representation is unique up to isomorphism.
, the conjugate representation is unique up to isomorphism. Let 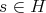 such that
such that  ; thus
; thus ![[Gs : Hs ] = 2](/img/revistas/ruma/v48n3/3a04733x.png) . Let
. Let 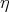 in
in 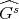 . Then we have two cases:
. Then we have two cases:
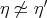 . If
. If  , then
, then 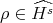 ,
, 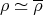 and
and 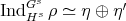 .
. . We have that
. We have that 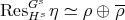 and
and 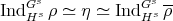 .
.
Moreover, if 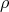 is an irreducible representation of
is an irreducible representation of 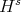 , then
, then 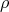 is a restriction of some
is a restriction of some 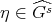 or is a direct summand of
or is a direct summand of 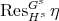 as in (ii), see [FH, Ch. 5].
as in (ii), see [FH, Ch. 5].
Remark 2.10. If 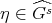 and
and 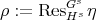 , it is easy to check that
, it is easy to check that
as braided vector spaces.
We apply these observations to the case 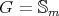 and
and 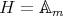 . We use some notations given in [AF, Section II.D].
. We use some notations given in [AF, Section II.D].
Lemma 2.11. Assume that the type of 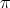 is
is 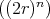 , with
, with 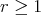 and
and 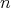 even. Let
even. Let 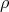 in
in 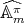 , with
, with 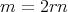 .
.
- If
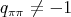 , then
, then 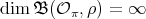 .
. - If
 and
and 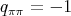 , then
, then - if
 , then
, then 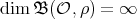 .
. - Assume that
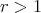 . If
. If 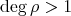 , then
, then 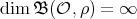 . Assume that
. Assume that 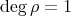 . If
. If 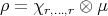 , with
, with  even or odd, or if
even or odd, or if 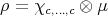 , with
, with  even and
even and 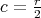 or
or 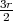 , where
, where 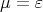 or
or 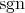 , then the braiding is negative; otherwise,
, then the braiding is negative; otherwise, 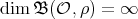 .
.
- if
Proof. (a) follows by Remark 2.2 (ii) and Lemma 1.3. (b). Since 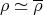 ,
, 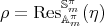 , with
, with 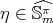 ,
, 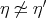 and
and 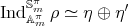 . Notice that
. Notice that 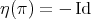 because
because  . Now, as the racks are the same, i.e.
. Now, as the racks are the same, i.e. 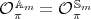 , we can apply [AF, Theorem 1]. □
, we can apply [AF, Theorem 1]. □
Remark 2.12. Keep the notation of the Lemma. If 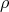 is not isomorphic to its conjugate representation
is not isomorphic to its conjugate representation 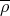 , then there exists
, then there exists 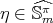 such that
such that 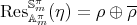 and
and 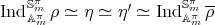 . Clearly,
. Clearly, 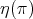 and
and 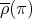 act by scalar
act by scalar  , and we have that
, and we have that 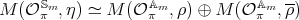 as braided vector spaces. We do not get new information with the techniques available today.
as braided vector spaces. We do not get new information with the techniques available today.
We fix the notation: the dihedral group 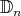 of order
of order 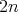 is generated by
is generated by 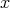 and
and 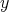 with defining relations
with defining relations 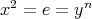 and
and 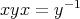 . Let
. Let 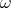 be a primitive
be a primitive 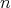 -th root of 1 and let
-th root of 1 and let 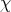 be the character of
be the character of  ,
, 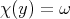 . If
. If 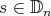 then we denote the conjugacy class by
then we denote the conjugacy class by 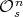 or simply
or simply 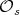 .
.
Theorem 3.1. Let  be the irreducible Yetter-Drinfeld module over
be the irreducible Yetter-Drinfeld module over  corresponding to a pair
corresponding to a pair 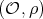 . Assume that its Nichols algebra
. Assume that its Nichols algebra 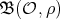 is finite-dimensional.
is finite-dimensional.
- If
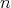 is odd, then
is odd, then 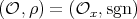 , where
, where  ,
, 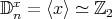 .
. - If
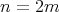 is even, then
is even, then 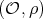 is one of the following:
is one of the following: 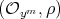 where
where 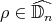 satisfies
satisfies 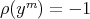 .
.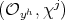 where
where 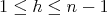 ,
, 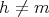 and
and 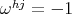 .
.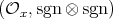 or
or 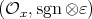 , where
, where  ,
, 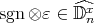 ,
, 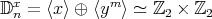 .
.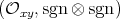 or
or 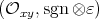 , where
, where  ,
, 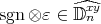 ,
, 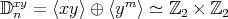 .
.
In the cases (i) and (ii) the dimension is finite. In the cases (iii) and (iv), the braiding is negative in the sense of [AF].
Remark 3.2. There are isomorphisms of braided vector spaces
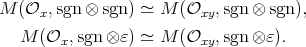
Remark 3.3. Assume for simplicity that 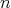 is odd and that
is odd and that 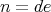 , where
, where 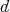 ,
,  are integers
are integers 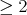 . Then the (indecomposable) rack
. Then the (indecomposable) rack 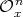 is a disjoint union of
is a disjoint union of  racks isomorphic to
racks isomorphic to 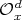 ; in other words,
; in other words, 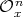 is an extension of
is an extension of 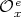 by
by 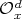 (and vice versa), see [AG, Section 2]. Thus, there is an epimorphism of braided vector spaces
(and vice versa), see [AG, Section 2]. Thus, there is an epimorphism of braided vector spaces 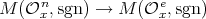 , as well as an inclusion
, as well as an inclusion  . The techniques available today do not allow to compute the Nichols algebra
. The techniques available today do not allow to compute the Nichols algebra 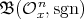 from the knowledge of the Nichols algebra
from the knowledge of the Nichols algebra 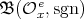 .
.
Remark 3.4. In Theorem 3.1 we do not claim that the conditions are sufficient. See Tables 1, 2. For instance, it is known that 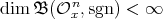 when
when  - see [MS]; for other odd
- see [MS]; for other odd 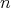 , this is open.
, this is open.
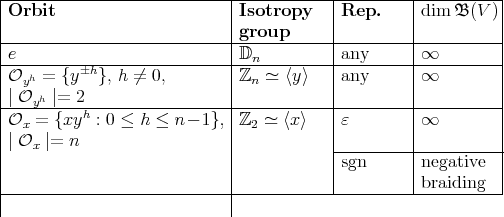
Table 1. Nichols algebras of irreducible Yetter-Drinfeld modules over 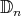 ,
, 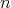 odd.
odd.
Let us now proceed with the proof of Theorem 3.1.
Proof. If  , then
, then 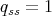 and
and 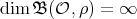 , from Lemma 1.1.
, from Lemma 1.1.
We consider now two cases.
CASE 1: 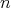 odd.
odd.
(I) If 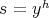 , with
, with 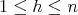 , it is easy to see that
, it is easy to see that 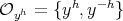 and
and 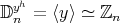 . Then
. Then 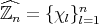 , where
, where 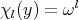 , with
, with 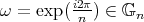 a primitive
a primitive  -th root of
-th root of  . Let us consider
. Let us consider  ; it is a braided vector space of diagonal type. If
; it is a braided vector space of diagonal type. If  , then
, then  , from Lemma 1.3. Assume
, from Lemma 1.3. Assume 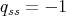 ; so we have
; so we have 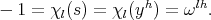 This is a contradiction because
This is a contradiction because 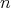 is odd.
is odd.
(II) If  , then
, then 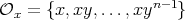 and
and 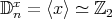 . Clearly,
. Clearly, 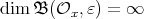 . On the other hand,
. On the other hand, 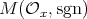 is a negative braided vector space, since every abelian subrack of
is a negative braided vector space, since every abelian subrack of 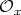 has one element; indeed
has one element; indeed 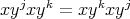 ,
, 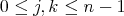 , if and only if
, if and only if 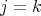 .
.
Therefore, the part (a) of the Theorem is proved.

Table 2. Nichols algebras of irreducible Yetter-Drinfeld modules over 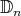 ,
,  even.
even.
CASE 2: 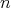 even. Let us say
even. Let us say 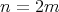 .
.
(I) If 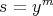 , then
, then 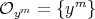 and
and  . Clearly,
. Clearly, 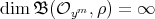 , for every
, for every 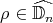 with
with 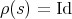 . On the other hand, if
. On the other hand, if 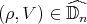 is such that
is such that 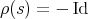 , then it is straightforward to prove that
, then it is straightforward to prove that 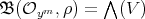 , the exterior algebra of
, the exterior algebra of 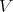 ; hence
; hence 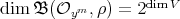 .
.
(II) If 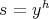 ,
, 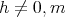 ; then
; then 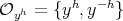 and
and 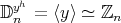 . From Lemma 1.3, it is clear that
. From Lemma 1.3, it is clear that 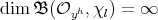 , for every
, for every 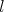 such that
such that 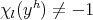 , i.e.
, i.e. 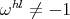 . On the other hand, it is easy to see that
. On the other hand, it is easy to see that 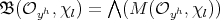 , hence
, hence 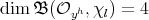 , for every
, for every 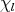 with
with 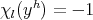 .
.
(III) If  , then
, then 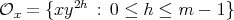 and
and 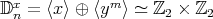 . From Lemma 1.1,
. From Lemma 1.1,  .
.
For the cases 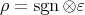 or
or  , we note the following fact.
, we note the following fact.
- If
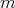 is odd and
is odd and  , we have that
, we have that 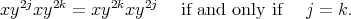
- If
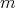 is even and
is even and 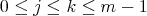 , we have that
, we have that 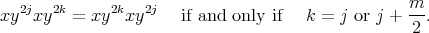
The cases (i) and (ii) say that every maximal abelian subrack of 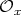 has one and two elements, respectively. Hence, in both cases the braiding is negative. Indeed, the result is obvious for the case (i), while in the case (ii) we have that if
has one and two elements, respectively. Hence, in both cases the braiding is negative. Indeed, the result is obvious for the case (i), while in the case (ii) we have that if 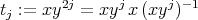 and
and 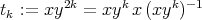 commute in
commute in 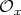 , then
, then 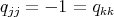 and
and 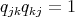 ; thus the braiding is negative.
; thus the braiding is negative.
(IV) If 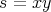 , then
, then 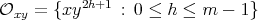 and
and 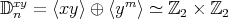 . The result follows as in (III) using the isomorphism
. The result follows as in (III) using the isomorphism  ,
,  ,
,  . □
. □
4. On Nichols algebras over semisimple Hopf algebras
Let 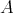 be a Hopf algebra. Let
be a Hopf algebra. Let 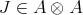 be a twist and let
be a twist and let 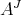 be the corresponding twisted Hopf algebra. If
be the corresponding twisted Hopf algebra. If 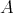 is a Hopf subalgebra of a Hopf algebra
is a Hopf subalgebra of a Hopf algebra 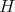 , then
, then 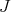 is a twist for
is a twist for 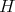 and
and 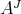 is a Hopf subalgebra of
is a Hopf subalgebra of 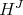 . Now, if
. Now, if 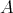 is semisimple, then this induces a bijection
is semisimple, then this induces a bijection
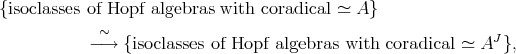 | (7) |
that preserves standard invariants like dimension, Gelfand-Kirillov dimension, etc. Let now 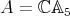 and let
and let 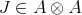 be the non-trivial twist defined in [Ni]. By (7), we conclude immediately from Theorem 2.6.
be the non-trivial twist defined in [Ni]. By (7), we conclude immediately from Theorem 2.6.
Theorem 4.1. Let 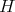 be a finite-dimensional Hopf algebra with coradical isomorphic to
be a finite-dimensional Hopf algebra with coradical isomorphic to 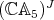 . Then
. Then 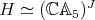 . □
. □
Again, this is the first classification result we are aware of, for finite-dimensional Hopf algebras with coradical isomorphic to a fixed non-trivial semisimple Hopf algebra. Recently, a semisimple Hopf algebra 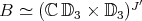 was discovered in [GN]. This Hopf algebra
was discovered in [GN]. This Hopf algebra 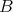 is simple, that is it has no non-trivial normal Hopf subalgebra. Since there are finite-dimensional non-semisimple pointed Hopf algebras with group
is simple, that is it has no non-trivial normal Hopf subalgebra. Since there are finite-dimensional non-semisimple pointed Hopf algebras with group  , there is a finite-dimensional non-semisimple Hopf algebra with coradical isomorphic to
, there is a finite-dimensional non-semisimple Hopf algebra with coradical isomorphic to 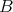 .
.
Acknowledgement. We are grateful to Professor John Stembridge for information on Coxeter groups, in particular reference [BG]. We thank Matías Graña, Sebastián Freyre and Leandro Vendramín for interesting discussions.
[AF] N. Andruskiewitsch and F. Fantino, On pointed Hopf algebras associated with unmixed conjugacy classes in 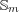 , J. Math. Phys. 48 (2007), 033502-1 - 033502-26. [ Links ]
, J. Math. Phys. 48 (2007), 033502-1 - 033502-26. [ Links ]
[AG] N. Andruskiewitsch and M. Graña, From racks to pointed Hopf algebras, Adv. Math. 178 (2003), 177 - 243. [ Links ]
[AS1] N. Andruskiewitsch and H.-J. Schneider, Finite quantum groups and Cartan matrices, Adv. Math. 154 (2000), 1-45. [ Links ]
[AS2] N. Andruskiewitsch, Pointed Hopf Algebras, in "New directions in Hopf algebras", 1-68, Math. Sci. Res. Inst. Publ. 43, Cambridge Univ. Press, Cambridge, 2002. [ Links ]
[AZ] N. Andruskiewitsch and S. Zhang, On pointed Hopf algebras associated to some conjugacy classes in 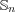 , Proc. Amer. Math. Soc. 135 (2007), 2723-2731. [ Links ]
, Proc. Amer. Math. Soc. 135 (2007), 2723-2731. [ Links ]
[BG] C. T. Benson and L. C. Grove, The Schur indices of the reflection group 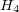 , J. Algebra, 27 (1973), 574-578. [ Links ]
, J. Algebra, 27 (1973), 574-578. [ Links ]
[C] R. W. Carter, Conjugacy classes in the Weyl group, Compos. Math. 25 (1972), 1-59. [ Links ]
[FGV] S. Freyre, M. Graña and L. Vendramin, On Nichols algebras over 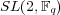 and
and 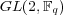 , preprint math.QA/0703498. [ Links ]
, preprint math.QA/0703498. [ Links ]
[FH] W. Fulton and J. Harris, Representation theory, Springer-Verlag, New York 1991. [ Links ]
[GN] C. Galindo and S. Natale, Simple Hopf algebras and deformations of finite groups, Math. Res. Lett., to appear. [ Links ]
[Gñ] M. Graña, On Nichols algebras of low dimension, Contemp. Math. 267 (2000), 111-134. [ Links ]
[H] I. Heckenberger, The Weyl groupoid of a Nichols algebra of diagonal type, Invent. Math. 164 (2006), 175-188. [ Links ]
[Hu] J. E. Humphreys, Reflection groups and Coxeter groups, Cambridge University Press, Cambridge 1990. [ Links ]
[JL] A. James and M. Liebeck, Representations and characters of groups, Cambridge University Press, Cambridge 2001. [ Links ]
[MS] A. Milinski and H-J. Schneider, Pointed Indecomposable Hopf Algebras over Coxeter Groups, Contemp. Math. 267 (2000), 215-236. [ Links ]
[Ni] D. Nikshych, 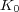 -rings and twisting of finite dimensional semisimple Hopf algebras, Commun. Algebra 26 (1998), 321-342. (Corrigendum: Commun. Algebra 26 (1998), 2019.) [ Links ]
-rings and twisting of finite dimensional semisimple Hopf algebras, Commun. Algebra 26 (1998), 321-342. (Corrigendum: Commun. Algebra 26 (1998), 2019.) [ Links ]
[S] Martin Schönert et al. "GAP - Groups, Algorithms, and Programming - version 3 release 4 patchlevel 4". Lehrstuhl D für Mathematik, Rheinisch Westfälische Technische Hochschule, Aachen, Germany, 1997. [ Links ]
Nicolás Andruskiewitsch
Facultad de Matemática, Astronomía y Física,
Universidad Nacional de Córdoba. CIEM - CONICET.
Medina Allende s/n
(5000) Ciudad Universitaria, Córdoba, Argentina
andrus@mate.uncor.edu
Fernando Fantino
Facultad de Matemática, Astronomía y Física,
Universidad Nacional de Córdoba. CIEM - CONICET.
Medina Allende s/n
(5000) Ciudad Universitaria, Córdoba, Argentina
fantino@mate.uncor.edu
Recibido: 16 de febrero de 2007
Aceptado: 2 de agosto de 2007














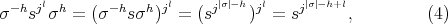
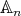
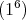 , then
, then 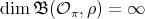 , for any
, for any 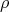 in
in  , by Lemma
, by Lemma 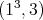 ,
,  or
or 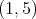 , then
, then 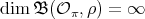 , for any
, for any 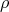 in
in  , by Lemma
, by Lemma