Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.48 n.3 Bahía Blanca 2007
Classification of split TTF-triples in module categories
Pedro Nicolás and Manuel Saorín
Abstract. In our work [9], we complete Jans' classification of TTF-triples [8] by giving a precise description of those two-sided ideals of a ring associated to one-sided split TTF-triples in the corresponding module category.
2000 Mathematics Subject Classification. 16D, 16E
Key words and phrases. Idempotent ideal; Torsion pair; Torsion theory; TTF-triple
Since the 1960s torsion theories have played an important role in algebra. They translate to general abelian categories (and so, significantly, to arbitrary module categories) many features of modules over a PID [3], they have been a fundamental tool for developing a general theory of noncommutative localization [10], they have had a great impact in the representation theory of Artin algebras [6, 5, 1], …
In the context of module categories over arbitrary rings, one of the important concepts related to torsion theory is that of TTF-triple. This notion was introduced by J. P. Jans [8], who proved that TTF-triples in the category  of modules over an arbitrary ring
of modules over an arbitrary ring 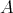 are in bijection with idempotent two-sided ideals of the ring
are in bijection with idempotent two-sided ideals of the ring 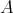 . He also proved that this bijection restricts to a bijection between the socalled centrally split TTF-triples and the two-sided ideals generated by a single central idempotent. Then, a natural question arises: which are the idempotent ideals corresponding to the TTF-triples which are not centrally split but only one-sided split?
. He also proved that this bijection restricts to a bijection between the socalled centrally split TTF-triples and the two-sided ideals generated by a single central idempotent. Then, a natural question arises: which are the idempotent ideals corresponding to the TTF-triples which are not centrally split but only one-sided split?
In section 2, we recall the notion of torsion pair and its basic properties. In section 3, we recall the notion of TTF-triple, its basic properties and Jans' parametrization by means of idempotent two-sided ideals. We also recall some deep results of G. Azumaya relating properties of a TTF-triple and properties of the associated idempotent ideal. These results have been crucial for our classification of one-sided split TTF-triples. In section 4, we give a precise description of those two-sided ideals corresponding to the socalled left split TTF-triples according to Jans' parametrization. The analogous description for right split TTF-triples is more complicated and it is explained in section 5: firstly for 'good' rings, and finally for arbitrary rings.
2. Torsion theory: the axiomatic of Dickson
S. E. Dickson introduced torsion theories (also called torsion pairs) in arbitrary abelian categories [3]. If 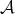 is an abelian category, a pair
is an abelian category, a pair 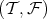 of classes of objects of
of classes of objects of 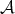 is a torsion pair if it satisfies
is a torsion pair if it satisfies
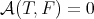 for all
for all 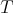 in
in 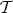 and
and 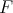 in
in 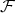 .
.- If
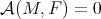 for all
for all 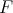 in
in 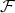 then
then 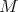 is in
is in 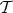 .
. - If
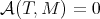 for all
for all 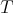 in
in 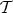 then
then 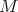 is in
is in 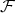 .
.
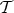 is said to be the torsion class, and its objects are the torsion objects. Similarly,
is said to be the torsion class, and its objects are the torsion objects. Similarly, 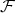 is the torsionfree class and its objects are the torsionfree objects. A torsion pair
is the torsionfree class and its objects are the torsionfree objects. A torsion pair 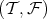 can be uniquely determined in different ways. For instance, it is uniquely determined by its torsion class, since
can be uniquely determined in different ways. For instance, it is uniquely determined by its torsion class, since 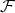 agrees with the class of objects
agrees with the class of objects 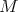 such that
such that 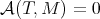 for all torsion objects
for all torsion objects  . Also, torsion pairs in
. Also, torsion pairs in  are in bijection with the (isomorphism classes of) idempotent radicals, i.e. subfunctors
are in bijection with the (isomorphism classes of) idempotent radicals, i.e. subfunctors  of the identity functor such that
of the identity functor such that 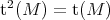 and
and 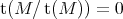 for each object
for each object 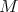 of
of 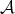 . Given a torsion pair
. Given a torsion pair 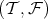 in
in 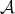 , its associated idempotent radical
, its associated idempotent radical 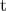 is uniquely determined by the fact that for each object
is uniquely determined by the fact that for each object 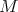 of
of 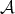 the object
the object 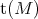 is the largest torsion subobject of
is the largest torsion subobject of 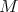 . We say that a torsion pair with idempotent radical
. We say that a torsion pair with idempotent radical 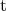 is split if
is split if 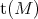 is a direct summand of
is a direct summand of 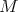 for each object
for each object 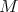 of
of 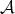 .
.
3.1. Jans' classification. Shortly after the axiomatic of S. E. Dickson appeared, J. P. Jans introduced and studied in [8] what he called torsion torsionfree(=TTF) theories (also called TTF-triples) in module categories. The definition still make sense for arbitrary abelian categories, and it is as follows. A triple 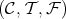 of classes of objects of an abelian category
of classes of objects of an abelian category 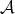 is a TTF-triple if both
is a TTF-triple if both 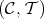 and
and 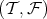 are torsion pairs. A TTF-triple is uniquely determined by its central class, which is said to be a TTF-class since it is both a torsion class of
are torsion pairs. A TTF-triple is uniquely determined by its central class, which is said to be a TTF-class since it is both a torsion class of 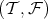 and a torsionfree class of
and a torsionfree class of 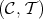 . A TTF-triple
. A TTF-triple 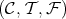 is left split (resp. right split) if
is left split (resp. right split) if 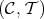 (resp.
(resp. 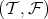 ) splits, and it is centrally split if it is both left and right split.
) splits, and it is centrally split if it is both left and right split.
J. P. Jans proved [8, Corollary 2.2], by using a result of P. Gabriel [4], that TTF-triples in the category  of right modules over an arbitrary ring
of right modules over an arbitrary ring 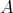 are in bijection with the idempotent ideals of that ring
are in bijection with the idempotent ideals of that ring 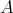 . This is the most remarkable result result concerning TTF-triples, and this is why they are interesting mainly in the framework of module categories.
. This is the most remarkable result result concerning TTF-triples, and this is why they are interesting mainly in the framework of module categories.
Theorem. Let 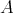 be a ring. There exists a one-to-one correspondence between:
be a ring. There exists a one-to-one correspondence between:
- Idempotent two-sided ideals
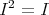 of
of 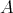 .
. - TTF-triples in
 .
.
The bijection is as follows. Given an idempotent ideal 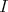 of
of 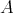 , the corresponding TTF-triple is the one whose TTF-class
, the corresponding TTF-triple is the one whose TTF-class 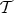 is formed by the modules
is formed by the modules 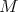 such that
such that 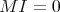 . Reciprocally, if
. Reciprocally, if 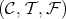 is a TTF-triple and
is a TTF-triple and 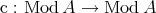 is the idempotent radical associated to the torsion class
is the idempotent radical associated to the torsion class  , the corresponding ideal is
, the corresponding ideal is 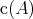 (where
(where 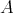 is regarded as a right
is regarded as a right 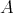 -module with its regular structure).
-module with its regular structure).
J. P. Jans also studied some elementary properties of centrally split TTF-triples and he essentially proved in [8, Theorem 2.4] the following:
Corollary. Let 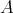 be a ring. The one-to-one correspondence of Theorem 3.1 restricts to a one-to-one correspondence between:
be a ring. The one-to-one correspondence of Theorem 3.1 restricts to a one-to-one correspondence between:
- (Ideals of
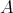 generated by single) central idempotents of
generated by single) central idempotents of 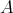 .
. - Centrally split TTF-triples in
 .
.
3.2. The main question. Let 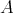 be an arbitrary ring, and put
be an arbitrary ring, and put 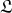 ,
, 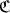 and
and 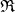 for the sets of left, centrally and right split TTF-triples in
for the sets of left, centrally and right split TTF-triples in  , respectively. The existence of TTF-triples for which only one of the constituent torsion pairs split, which we shall call one-sided split, has been known for a long time [11] (see also the remark 5.2), and so we should have a diagram of the form:
, respectively. The existence of TTF-triples for which only one of the constituent torsion pairs split, which we shall call one-sided split, has been known for a long time [11] (see also the remark 5.2), and so we should have a diagram of the form:

The main question tackled in our work is: What should replace the question marks in the diagram above?
3.3. The work of Azumaya. Some efforts have been made to answer this question (cf. [2], [7], …). Specially useful for us has been the paper of G. Azumaya [2] in which he expresses some deep properties of TTF-triples in module categories in terms of the associated idempotent ideal. We present in the following theorem the results of G. Azumaya we have used [2, Theorem 3, Theorem 6 and Theorem 8].
Theorem. Let 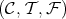 be a TTF-triple in a module category
be a TTF-triple in a module category  and let
and let 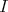 be the corresponding idempotent ideal of
be the corresponding idempotent ideal of 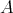 . The following properties hold:
. The following properties hold:
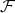 is a TTF-class if and only if
is a TTF-class if and only if  for some idempotent
for some idempotent  of
of 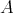 .
. is a TTF-class if and only if
is a TTF-class if and only if 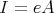 for some idempotent
for some idempotent  of
of 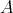 .
. is closed under submodules if and only if
is closed under submodules if and only if 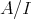 is a flat right
is a flat right 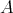 -module.
-module. is a TTF-class if and only if
is a TTF-class if and only if  is closed under submodules and the left
is closed under submodules and the left 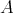 -module
-module 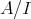 has a projective cover.
has a projective cover.
4. Classification of left split TTF-triples over arbitrary rings
Let 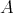 be an arbitrary ring. Recall that an
be an arbitrary ring. Recall that an 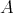 -module
-module 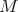 is hereditary
is hereditary  -injective if every quotient of a direct sum of copies of
-injective if every quotient of a direct sum of copies of 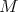 is an injective
is an injective 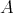 -module. Now we present Theorem 3.1 and Corollary 3.2 of [9].
-module. Now we present Theorem 3.1 and Corollary 3.2 of [9].
Theorem. Let 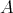 be a ring. The one-to-one correspondence of Theorem 3.1 restricts to a one-to-one correspondence between
be a ring. The one-to-one correspondence of Theorem 3.1 restricts to a one-to-one correspondence between
- Left split TTF-triples in
 .
. - Two-sided ideals of
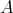 of the form
of the form  where
where  is an idempotent of
is an idempotent of 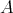 such that
such that 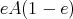 is hereditary
is hereditary  -injective as a right
-injective as a right 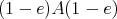 -module.
-module.
Proof. If the TTF-triple 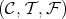 is left split, then
is left split, then 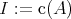 is of the form
is of the form 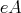 for some idempotent
for some idempotent  of
of 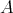 . The difficult part is to prove that
. The difficult part is to prove that 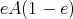 is hereditary
is hereditary  -injective as a right
-injective as a right 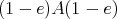 -module.
-module.
On the other hand, if  is an idempotent of
is an idempotent of 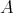 such that
such that  is a two-sided ideal, then
is a two-sided ideal, then 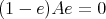 . Then
. Then 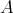 is isomorphic to the triangular matrix ring
is isomorphic to the triangular matrix ring
![[ C 0 ] [ (1 - e)A(1 - e) 0 ] := M B eA(1 - e) eAe](/img/revistas/ruma/v48n3/3a05130x.png)
where the  -bimodule
-bimodule 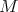 is hereditary
is hereditary  -injective in
-injective in  . This property of
. This property of 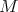 allows us to prove that
allows us to prove that 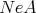 is a direct summand of
is a direct summand of 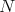 for every
for every 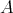 -module
-module 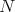 .
. 
5. Classification of right split TTF-triples
The 'dual' of the Theorem 4 is not true in general but only for some classes of rings.
5.1. Over 'good' rings. Recall that if 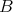 is a ring, then a
is a ring, then a 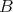 -module
-module 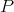 is hereditary projective (resp. hereditary
is hereditary projective (resp. hereditary  -projective) in case every submodule of
-projective) in case every submodule of 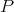 (resp. every submodule of a direct product of copies of
(resp. every submodule of a direct product of copies of 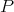 ) is projective. Recall also that a
) is projective. Recall also that a 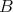 -module
-module 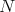 is called FP-injective if it is injective relative to the class of finitely presented modules, i.e. if
is called FP-injective if it is injective relative to the class of finitely presented modules, i.e. if 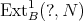 vanishes on all the finitely presented
vanishes on all the finitely presented 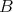 -modules. Now we present Proposition 4.5 of [9].
-modules. Now we present Proposition 4.5 of [9].
Proposition. Let 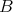 be a ring and
be a ring and 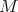 be a left
be a left 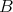 -module. The following conditions are equivalent:
-module. The following conditions are equivalent:
- For every bimodule structure
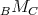 and every right
and every right  -module
-module 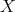 , the right
, the right 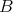 -module
-module 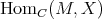 is hereditary projective.
is hereditary projective. - There exists a bimodule structure
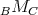 such that for every right
such that for every right  -module
-module 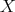 the right
the right 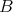 -module
-module 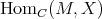 is hereditary projective.
is hereditary projective. - Put
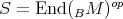 . If
. If  is the minimal injective cogenerator of
is the minimal injective cogenerator of 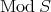 , then the right
, then the right 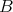 -module
-module 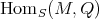 is hereditary
is hereditary  -projective.
-projective. - The character module
 is a hereditary
is a hereditary  -projective right
-projective right 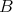 -module.
-module. 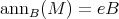 for some idempotent
for some idempotent 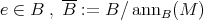 is a hereditary perfect ring and
is a hereditary perfect ring and 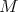 is FP-injective as a left
is FP-injective as a left 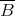 -module.
-module.
When 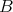 is an algebra over a commutative ring
is an algebra over a commutative ring 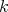 , the above assertions are equivalent to:
, the above assertions are equivalent to:
- If
 is a minimal injective cogenerator of
is a minimal injective cogenerator of  , then
, then 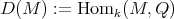 is a hereditary
is a hereditary  -projective right
-projective right 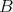 -module.
-module.
A left 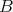 -module
-module 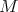 satisfying the equivalent conditions of the proposition above is said to have a hereditary
satisfying the equivalent conditions of the proposition above is said to have a hereditary  -projective dual. Now we can formulate the classification of right split TTF-triples under particularly good circumstances (cf. section 4 of [9]):
-projective dual. Now we can formulate the classification of right split TTF-triples under particularly good circumstances (cf. section 4 of [9]):
Theorem. Let 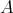 be a ring. The one-to-one correspondence of Theorem 3.1 restricts to a one-to-one correspondence between:
be a ring. The one-to-one correspondence of Theorem 3.1 restricts to a one-to-one correspondence between:
- Right split TTF-triples in
 whose associated idempotent ideal
whose associated idempotent ideal 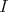 is finitely generated on the left.
is finitely generated on the left. - Two-sided ideals of
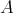 of the form
of the form  where
where  is an idempotent of
is an idempotent of 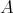 such that the left
such that the left 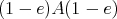 -module
-module 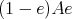 has hereditary
has hereditary  -projective dual.
-projective dual.
In particular, when 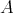 satisfies one of the following two conditions, all the TTF-triples in
satisfies one of the following two conditions, all the TTF-triples in  have the associated idempotent ideal finitely generated on the left:
have the associated idempotent ideal finitely generated on the left:
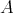 is semiperfect.
is semiperfect.- Every idempotent ideal of
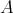 which is pure on the left is also finitely generated on the left (e.g. if
which is pure on the left is also finitely generated on the left (e.g. if 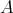 is left Nœtherian).
is left Nœtherian).
Proof. If 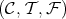 is right split, then
is right split, then 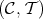 is hereditary. By Theorem 3.3,
is hereditary. By Theorem 3.3,  is pure as a left ideal. Since
is pure as a left ideal. Since 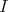 is finitely generated on the left, then
is finitely generated on the left, then  for some idempotent
for some idempotent  of
of 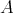 . The difficult part is to prove that the left
. The difficult part is to prove that the left 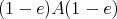 -module
-module 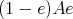 has hereditary
has hereditary  -projective dual.
-projective dual.
On the other hand, let  be an ideal like in (2). Since
be an ideal like in (2). Since 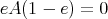 , then
, then 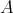 is isomorphic to the triangular matrix ring
is isomorphic to the triangular matrix ring
![[ ] [ ] C (1 - e)A(1 - e) 0 M B = (1 - e)Ae eAe .](/img/revistas/ruma/v48n3/3a05215x.png)
The fact that the left 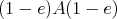 -module
-module 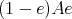 has hereditary
has hereditary  -projective dual allows us to prove that the TTF-triple associated to
-projective dual allows us to prove that the TTF-triple associated to  is right split.
is right split.
We use Theorem 3.3 to prove that if 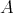 satisfies either condition
satisfies either condition 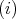 or
or 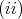 then all the TTF-triples in
then all the TTF-triples in  have the associated idempotent ideal finitely generated on the left.
have the associated idempotent ideal finitely generated on the left. 
5.2. Over arbitrary rings. The parametrization of the right split TTF-triples over arbitrary rings is more involved. The first observation is the following (cf. Proposition 5.1. of [9]):
Proposition. The one-to-one correspondence of Theorem 3.1 restricts to a one-to-one correspondence between:
- Right split TTF-triples in
 .
. - Idempotent ideals
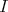 of
of 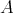 such that, for some idempotent
such that, for some idempotent  of
of 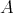 , one has that
, one has that 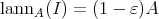 and the TTF-triple in
and the TTF-triple in 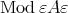 associated to
associated to 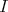 is right split.
is right split.
In the situation of the proposition above one has that 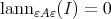 , that is, the TTF-triple
, that is, the TTF-triple 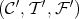 in
in 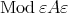 associated to
associated to 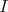 has the property that
has the property that 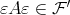 . Therefore the problem of classifying right split TTF-triples reduces to answering the following:
. Therefore the problem of classifying right split TTF-triples reduces to answering the following:
Question. Let 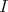 be an idempotent ideal of a ring
be an idempotent ideal of a ring 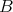 such that
such that 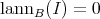 , i.e. the
, i.e. the 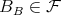 where
where  is the associated TTF-triple in
is the associated TTF-triple in  . Which conditions on
. Which conditions on 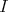 are equivalent to saying that
are equivalent to saying that 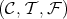 is right split?
is right split?
The elucidation of these conditions leads us to the following 'arithmetic' definition: Given a right 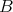 -module
-module 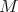 and a submodule
and a submodule 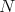 , we shall say that
, we shall say that 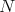 is I-saturated in
is I-saturated in 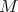 when
when  , with
, with 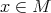 , implies that
, implies that 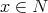 . Equivalently, this occurs when
. Equivalently, this occurs when 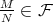 .
.
When 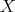 is a subset of
is a subset of 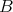 , we shall denote by
, we shall denote by 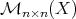 the subset of matrices of
the subset of matrices of 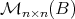 with entries in
with entries in 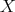 .
.
Definition. An idempotent ideal 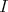 of a ring
of a ring 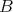 is called right splitting if:
is called right splitting if:
- it is pure as a left ideal,
 ,
,- it satisfies one of the following two equivalent conditions:
- for every integer
 and every
and every 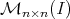 -saturated right ideal
-saturated right ideal  of
of 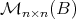 , there exists
, there exists 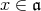 such that
such that 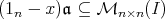 ,
, - for every integer
 and every
and every  -saturated submodule
-saturated submodule  of
of 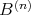 , the quotient
, the quotient 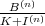 is projective as a right
is projective as a right 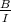 -module.
-module.
- for every integer
The fact that conditions (i) and (ii) are equivalent is proved in [9, Lemma 5.2].
Finally, we can formulate the general classification of right split TTF-triples (cf. Theorem 5.4 of [9]):
Theorem. Let 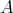 be an arbitrary ring. The one-to-one correspondence of Theorem 3.1 restricts to a one-to-one correspondence between:
be an arbitrary ring. The one-to-one correspondence of Theorem 3.1 restricts to a one-to-one correspondence between:
- Right split TTF-triples in
 .
. - Idempotent ideals
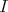 such that
such that 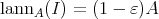 for some idempotent
for some idempotent  of
of 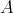 and
and 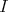 is a right splitting ideal of
is a right splitting ideal of 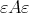 with
with 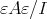 a hereditary perfect ring.
a hereditary perfect ring.
Example. Let 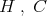 be rings, the first one being hereditary perfect, and let
be rings, the first one being hereditary perfect, and let 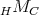 be a bimodule such that
be a bimodule such that 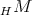 is faithful. The idempotent ideal
is faithful. The idempotent ideal
![~ [ C 0 ] I → M 0](/img/revistas/ruma/v48n3/3a05287x.png)
of
![~ [ C 0 ] A → M H](/img/revistas/ruma/v48n3/3a05288x.png)
is clearly pure on the left and 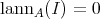 . One can see that
. One can see that 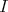 is right splitting if, and only if,
is right splitting if, and only if, 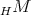 is FP-injective (equivalently,
is FP-injective (equivalently, 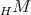 has a hereditary
has a hereditary  -projective dual).
-projective dual).
Remark. Let 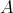 be a commutative ring. Denote by
be a commutative ring. Denote by 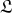 ,
, 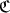 and
and 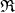 the sets of left, centrally and right split TTF-triples in
the sets of left, centrally and right split TTF-triples in  , respectively. Then
, respectively. Then 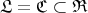 and the last inclusion may be strict. Indeed, since all idempotents in
and the last inclusion may be strict. Indeed, since all idempotents in 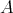 are central, the equality
are central, the equality  follows from Theorem 4. On the other hand, if
follows from Theorem 4. On the other hand, if 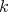 is a field and
is a field and 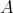 is the ring of all the eventually constant sequences of elements of
is the ring of all the eventually constant sequences of elements of 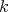 , then the set of all the sequences of elements of
, then the set of all the sequences of elements of 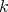 with finite support,
with finite support, 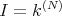 , is an idempotent ideal of
, is an idempotent ideal of 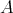 which is pure and satisfies that
which is pure and satisfies that 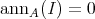 . Moreover, one has
. Moreover, one has 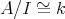 and then
and then 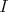 is right splitting. Then, by the Theorem 5.2 the TTF-triple in
is right splitting. Then, by the Theorem 5.2 the TTF-triple in  associated to
associated to 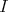 is right splitting, but it is not centrally split.
is right splitting, but it is not centrally split.
[1] I. Assem, M. Saorín, Abelian exact subcategories closed under predecessors, Comm. Algebra 33 (2005), 1205-1216. [ Links ]
[2] G. Azumaya Some properties of TTF-classes, Proc. Confer. 'Orders, group rings and related topics' (Columbus, Ohio 1972). Springer Lecture Notes in Mathematics, 353 (1973), 72-83. [ Links ]
[3] S. E. Dickson, A torsion theory for abelian categories, Trans. Amer. Math. Soc. 121 (1966), 223-235. [ Links ]
[4] P. Gabriel, Des catégories abéliennes, Bull. Soc. Math. France, 90 (1962), 323-448. [ Links ]
[5] D. Happel, I. Reiten, S. Smalø, Tilting in Abelian Categories and Quasitilted Algebras, Memoirs Amer. Math. Soc. 575 (1996). [ Links ]
[6] D. Happel, C. M. Ringel, Tilted algebras, Trans. Amer. Math. Soc. 274 (2) (1982), 399-443. [ Links ]
[7] T. Ikeyama, Splitting torsion theories, Comm. Algebra 8 (13)(1980), 1267-1282. [ Links ]
[8] J. P. Jans, Some aspects of torsion, Pacific J. Math. 15 (1965), 1249-1259. [ Links ]
[9] P. Nicolás, M. Saorín, Classification of split torsion torsionfree triples in module categories, Journal of Pure and Applied Algebra 208 (2007), 979-988. [ Links ]
[10] B. Stenström, Rings of quotients, Grundlehren der math. Wissensch., 217, Springer-Verlag, 1975. [ Links ]
[11] M.L. Teply, Homological dimension and splitting torsion theories, Pacif. J. Math. 34 (1970), 193-205. [ Links ]
Pedro Nicolás
Departamento de Matemáticas,
Universidad de Murcia,
Aptdo. 4021,
30100 Espinardo, Murcia, España
pedronz@um.es
Manuel Saorín
Departamento de Matemáticas,
Universidad de Murcia,
Aptdo. 4021,
30100 Espinardo, Murcia, España
msaorinc@um.es
Recibido: 31 de enero de 2007
Aceptado: 1 de abril de 2007














