Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932On-line version ISSN 1669-9637
Rev. Unión Mat. Argent. vol.48 no.3 Bahía Blanca 2007
Gröbner Basis in Algebras Extended by Loops
G. Chalom, E. Marcos, P. Oliveira
We dedicate this work to the 60th birthday of Maria Ines Platzeck and the 70th birthday of Hector Merklen.
Abstract. In this work we extend, to the path algebras context, some results obtained in the commutative context, [2]. The main result is that one can extend the Gröbner bases of an ungraded ideal to one possible definition of homogenization for the non commutative case.
The second author thanks CNPq for support in the form of a research grant, and the third one for partially financing his master degree. The three authors take the opportunity to thank Prof. Ed. Green for suggesting the subject.
We will introduce very briefly the homogenization process in the commutative case, just to explain the main motivation of our work. In the commutative context, the Buchberger Algorithm give us a very direct strategy for computing Gröbner Basis for a given ideal ![I ∈ k[x1,x2,...,xn ]](/img/revistas/ruma/v48n3/3a062x.png) : we consider a finite set
: we consider a finite set 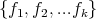 of generators of I, compute the S polynomials, for any pair i,j, reduce them, and if the remainder is non zero, add this remainder to the list of the given polynomials, to make all the S polynomials reduce to zero.
of generators of I, compute the S polynomials, for any pair i,j, reduce them, and if the remainder is non zero, add this remainder to the list of the given polynomials, to make all the S polynomials reduce to zero.
Although this process always finish, in the commutative case, it can be very inefficient and time consuming, by instance getting S polynomials of much higher degree that the ones we begin with. It is easy to see ( see [1]) that if we begin with a set of homogeneos polynomials this problem does not occur and the S polynomials we obtain are again homogeneous.
So, lets define this process for ![Λ = k[x1,x2,...,xn]](/img/revistas/ruma/v48n3/3a064x.png) : Let
: Let 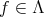 and
and 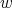 a new variable. If
a new variable. If 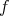 has total degree
has total degree 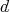 then the polynomial given by
then the polynomial given by 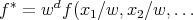
![,xn∕w ) ∈ k [x1, x2,...,xn,w ]](/img/revistas/ruma/v48n3/3a0610x.png) is a homogeneous polynomial in the extended polynomial algebra, called the homogenization of
is a homogeneous polynomial in the extended polynomial algebra, called the homogenization of 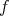 . For an ideal
. For an ideal ![I ∈ k [x ,x ,...,x ] 1 2 n](/img/revistas/ruma/v48n3/3a0612x.png) define
define 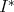 to be the ideal of
to be the ideal of ![k[x1,x2,...,xn, w]](/img/revistas/ruma/v48n3/3a0614x.png) given by
given by 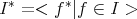 . For any
. For any ![h ∈ k [x1,x2, ...,xn,w ]](/img/revistas/ruma/v48n3/3a0616x.png) , define
, define ![h * = h(x1,x2,...,xn, 1) ∈ k [x1,x2, ...,xn]](/img/revistas/ruma/v48n3/3a0617x.png) .
.
As we will prove, in the last section, if G is a Gröbner basis for I with respect to a certain order, then the set 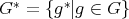 is a Gröbner Basis for the ideal
is a Gröbner Basis for the ideal 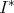 with respect to the extended order.
with respect to the extended order.
For the non commutative case, this process has been extended in many contexts, and most computer programs devoted to non commutative Grobner Basis work only with homogeneous ideals [4].
In this section, we define some concepts that will be used in the following sections. All these concepts can be found in [3], with a detailed description of the theory of Gröbner basis.
In order to have a Gröebner basis theory in an algebra we need a multiplicative basis with an admissible order. We define, in the sequence, these concepts.
A 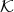 -basis is called a multiplicative basis of
-basis is called a multiplicative basis of 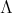 . if for every
. if for every 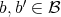 we have
we have 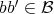 or
or  .
.
We also will need the multiplicative basis to be completely ordered. We stress that we are not interested in an arbitrary order in  , but we want an order that preserves the multiplicative structure of
, but we want an order that preserves the multiplicative structure of  .
.
DEFINITION. 2.1. [3] We will say that a well order in  , is admissible, if it satisfies the following conditions, for every
, is admissible, if it satisfies the following conditions, for every 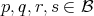 :
:
- If
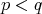 then
then 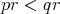 , if both are non zero;
, if both are non zero; - If
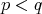 then
then 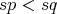 , if both are non zero;
, if both are non zero; - If
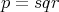 then
then  .
.
Let 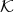 be a field and
be a field and 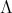 a
a 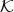 -algebra with a fixed
-algebra with a fixed 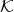 -basis
-basis 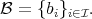
Since  is a
is a 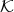 -basis of
-basis of 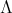 , for each
, for each 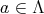 , there is a unique family
, there is a unique family 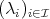 such that
such that 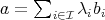 , where
, where  , except for a finite number of indices.
, except for a finite number of indices.
If 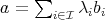 , we will say that
, we will say that 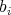 occurs in
occurs in  if
if 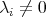 . We define now the notion of tip, which is also called in the literature by leading term.
. We define now the notion of tip, which is also called in the literature by leading term.
DEFINITION. 2.2. [3] If 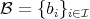 is a
is a 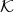 -basis of
-basis of 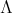 , as a vector space, well ordered by
, as a vector space, well ordered by  in
in  , and if
, and if 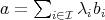 is non zero, we will call tip of a and denote by
is non zero, we will call tip of a and denote by 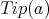 the largest basis element in the support of
the largest basis element in the support of  and its coefficient
and its coefficient 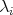 is denoted by
is denoted by 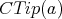 .
.
If 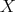 is a subset of
is a subset of 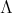 , we define
, we define
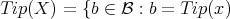 for some
for some 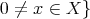
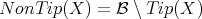
So, both 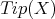 and
and 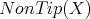 are subsets of
are subsets of  depending on the choice of the well order of
depending on the choice of the well order of  .
.
DEFINITION. 2.3. [3] Let 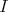 be a two sided ideal of
be a two sided ideal of 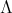 , we will say that a set
, we will say that a set 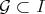 is a Gröbner basis for
is a Gröbner basis for 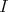 with respect to the order
with respect to the order  , if
, if
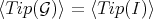
DEFINITION. 2.4. [3] Let 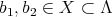 , we will say that
, we will say that 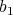 divides
divides 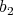 (in
(in 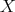 ) if there exist
) if there exist 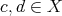 such that
such that 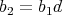 ,
, 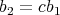 or
or 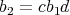 .
.
We will say that a 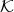 -algebra
-algebra 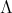 has Gröbner basis theory if
has Gröbner basis theory if 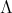 has a multiplicative basis
has a multiplicative basis  with an admissible order
with an admissible order  in this basis.
in this basis.
From this point on, we assume that the 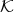 -algebra
-algebra 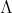 has a Gröbner basis theory. Moreover
has a Gröbner basis theory. Moreover 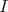 will always denote a two-sided ideal in
will always denote a two-sided ideal in 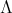 .
.
Given a multiplicative basis 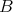 of an arbitrary algebra and
of an arbitrary algebra and 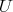 and a fixed minimal set of generators of
and a fixed minimal set of generators of 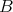 , as a semigroup, we define
, as a semigroup, we define 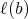 the length of
the length of 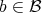 as the smaller
as the smaller 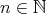 such that
such that 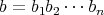 with
with 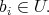 If
If 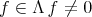 define the length of f by
define the length of f by 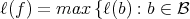 occurs in
occurs in 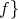 .
.
We say that an element 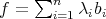 , with
, with 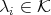 and
and 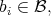 is homogeneous if
is homogeneous if 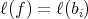 for every
for every 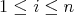 . An ideal
. An ideal 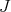 is homogeneous if can be generated by homogeneous elements.
is homogeneous if can be generated by homogeneous elements.
In this section, we present our main results, which extend the algorithms used in commutative algebra, and also some results obtained in [2].
Since the polynomial ring on 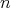 commutative variables is a special case of a quotient of a path algebra and, as it was proved in [2], any algebra with 1 that admits Gröbner basis theory is isomorphic to a quotient of a path algebra, we asked ourselves if the same process ( that is, the homogenization process) can be extended, and which results remain true in the general case of quotient path algebras. In this work, we consider the non commutative version of the homogenization process, for path algebras
commutative variables is a special case of a quotient of a path algebra and, as it was proved in [2], any algebra with 1 that admits Gröbner basis theory is isomorphic to a quotient of a path algebra, we asked ourselves if the same process ( that is, the homogenization process) can be extended, and which results remain true in the general case of quotient path algebras. In this work, we consider the non commutative version of the homogenization process, for path algebras 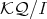 , where
, where 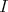 is a two-sided ideal in
is a two-sided ideal in 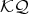 .
.
In [2], Green used a similar technic of the extension by loops, to construct Gröbner basis to some indecomposable projectives in Mod-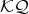 , based on a special admissible order, where the loops where always maximal elements.
, based on a special admissible order, where the loops where always maximal elements.
In our work, we start with a quotient of a path algebra with an admissible order, and we define another quotient of path algebra, also with an admissible order, which we will call the extended by loops algebra.
Let 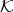 be a field and
be a field and  a finite quiver. Let
a finite quiver. Let 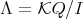 be the path algebra associated to
be the path algebra associated to  and
and 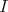 a two-sided ideal of
a two-sided ideal of 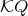 . Consider in
. Consider in 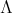 the multiplicative basis
the multiplicative basis  and
and  an admissible order in
an admissible order in  .
.
DEFINITION. 3.1. Let 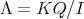 , as above, we define
, as above, we define  , where
, where  has the same vertices of
has the same vertices of  and for each vertex
and for each vertex 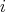 of
of  , we add a loop
, we add a loop 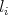 in
in 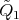 , and we consider the
, and we consider the 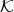 -algebra
-algebra 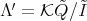 , where
, where 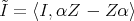 as a two-sided ideal of
as a two-sided ideal of 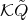 , with
, with 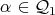 and
and 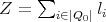 . We call
. We call 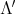 the extended by loops algebra of
the extended by loops algebra of 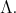
Observe that 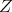 is the sum of all the new loops that were added to the quiver. For
is the sum of all the new loops that were added to the quiver. For 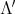 we consider the following basis
we consider the following basis 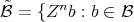 and
and 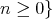 . Both
. Both 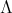 and
and 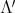 are finitely generated as
are finitely generated as 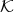 -algebras, moreover
-algebras, moreover  and
and 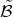 are finitely generated as semigroups.
are finitely generated as semigroups.
For each generator set 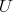 of
of 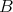 , as a semigroup, we associate the following generator for
, as a semigroup, we associate the following generator for  ,
, 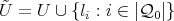 . It is not hard to see that
. It is not hard to see that 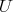 is minimal if and only if
is minimal if and only if 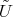 is minimal.
is minimal.
Define in 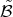 the order
the order
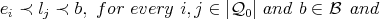
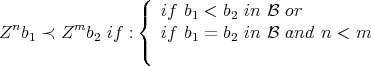
We show now that this is, in fact, an admissible order.
Let 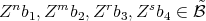 , then:
, then:
- if
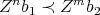 and
and 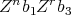 and
and 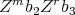 are non zero, we have that, if
are non zero, we have that, if  then
then  . Now, if
. Now, if  ,
,  and so
and so  and
and 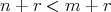 . Then,
. Then, 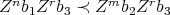 .
. - in the same way, if
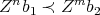 , then
, then 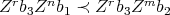 , if the products are non zero.
, if the products are non zero. - if
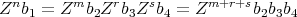 , we have that
, we have that  and
and 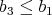 so
so 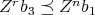 .
.
Therefore, the order 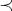 given above is an admissible order.
given above is an admissible order.
DEFINITION. 3.2. For 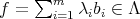 , we define the homogenization of f in
, we define the homogenization of f in 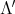 by
by
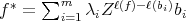 .
.
Observe that, for every 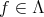 , the homogenization of
, the homogenization of 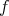 is an homogeneous element.
is an homogeneous element.
LEMMA 3.3. For every 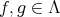 , we have
, we have 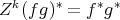 , with
, with 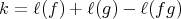 .
.
PROOF. Let 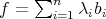 and
and 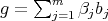 , with
, with 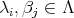 and
and 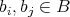 . Since
. Since 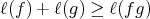 , consider the natural number
, consider the natural number 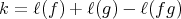 . Then,
. Then,

∎
Now, we define the following application, between the algebras 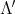 and
and 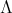 :
:
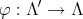
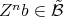 the element
the element 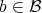 , for every
, for every 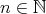 . Observe that, for every
. Observe that, for every 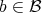 , there exists
, there exists 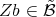 such that
such that 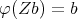 . In this way, we have that
. In this way, we have that 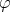 extended by linearity to every element in
extended by linearity to every element in 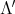 is, in fact, an epimorphism of algebras. Also, observe that
is, in fact, an epimorphism of algebras. Also, observe that 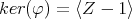 .
. To simplify the notation, we call 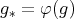 for every
for every  .
.
LEMMA 3.4. For every 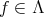 we have
we have 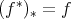 .
.
PROOF. Let 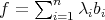 , with
, with 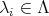 and
and 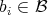 . Observe that
. Observe that
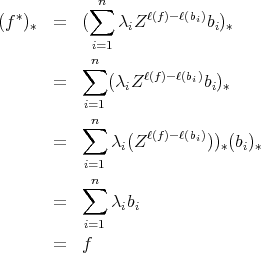
∎
LEMMA 3.5. Let 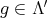 homogeneous of length
homogeneous of length 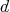 and let
and let 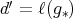 . Then
. Then  and
and 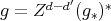 .
.
PROOF. The inequality  follows from the definition of
follows from the definition of 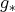 . Let
. Let 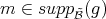 ,
, 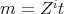 , with
, with 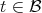 . Then the monomial
. Then the monomial 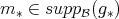 correspondent to
correspondent to 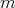 is
is 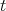 . As
. As 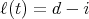 the monomial in
the monomial in 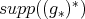 correspondent to
correspondent to 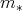 is
is 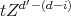 . Then
. Then 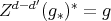 . ∎
. ∎
DEFINITION. 3.6. Let 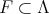 and
and  , we define by
, we define by
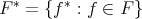
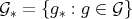
PROOF. Consider 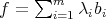 with
with 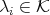 and
and 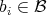 , where
, where  is a basis of
is a basis of 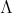 ,
, 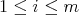 .
.
By definition we have that 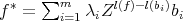 . For every summand of
. For every summand of 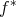 we have:
we have:
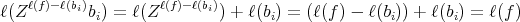
Then, 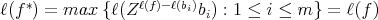 ∎
∎
LEMMA 3.8. Let 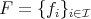 be a subset of
be a subset of 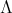 , not necessarily finite, and
, not necessarily finite, and 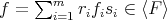 . If
. If 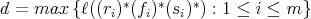 and
and 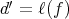 . Then
. Then 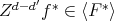 .
.
PROOF. Consider 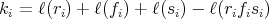 ,
, 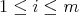 , by 3.3 we have
, by 3.3 we have 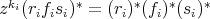
Let 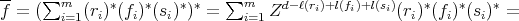
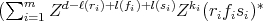 , by lemma 3.3. So,
, by lemma 3.3. So, 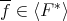 and is homogeneous (by construction ) with
and is homogeneous (by construction ) with 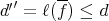 . Moreover, using lemma 3.3 and lemma 3.4, we have
. Moreover, using lemma 3.3 and lemma 3.4, we have
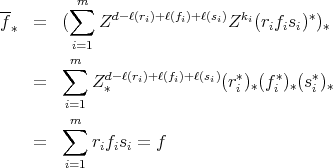
Using Lemma 3.5, we can conclude that
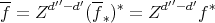
As  , finally we have:
, finally we have:
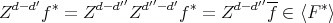
∎
LEMMA 3.9. Let 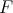 be a subset of
be a subset of 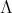 . Then
. Then 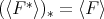 .
.
PROOF. Let 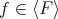 . By Lemma 3.8,
. By Lemma 3.8, 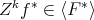 , for some
, for some 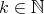 , and then
, and then
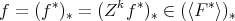
By the other hand, if 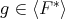 , say
, say 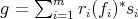 with
with 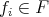 and
and 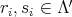 for
for 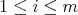 , we have
, we have
![m∑ * g* = ( ri(fi)si)* i=1 ∑m = (ri)*[(fi)*]*(si)* i=1 ∑m = (r )f (s ) i* i i* i=1](/img/revistas/ruma/v48n3/3a06275x.png)
So, 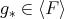 . ∎
. ∎
We reproduce here the Elimination Theorem, found in [2], to discuss and compare the two results. For that, we define some new concepts.
Let  be a quiver and
be a quiver and 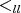 a length-lexicographic order defined in the basis of paths
a length-lexicographic order defined in the basis of paths  of
of  . Let
. Let 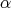 be a maximal arrow with respect to
be a maximal arrow with respect to 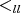 in
in  .
.
We define the quiver 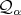 in the following way:
in the following way: 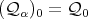 and
and 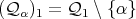 .
.
For 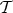 a set of indices, we define the following application
a set of indices, we define the following application 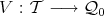 . Let
. Let 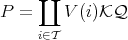 a ( right) projective in
a ( right) projective in 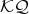 -Mod.
-Mod.
We define 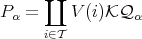 a right projective module in
a right projective module in
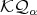 -Mod.
-Mod.
Let 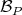 be a
be a 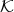 -basis of
-basis of 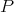 with order
with order 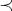 such that:
such that:
- For every
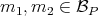 and every
and every 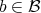 , if
, if 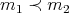 , then
, then 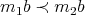 , if
, if 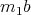 and
and 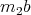 are non zero.
are non zero. - For every
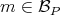 and every
and every 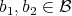 , if
, if 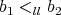 , then
, then 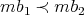 , if both are non zero.
, if both are non zero. - For every
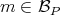 and every
and every 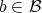 ,
, 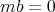 or
or 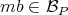 .
.
Let 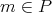 ,
, 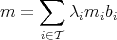 , with
, with 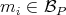 ,
, 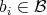 e
e 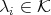 . We call
. We call 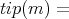 the
the 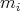 such that
such that 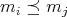 for every
for every 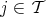 . For
. For 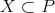 , we will call by
, we will call by 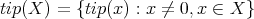 .
.
Following Green, we say that 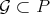 is right a Gröbner basis for
is right a Gröbner basis for 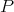 , with respect to the order
, with respect to the order 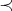 , if
, if 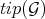 generates
generates 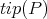 as a right module.
as a right module.
Here is Green's Elimination Theorem, found in [2].
THEOREM 3.10. [2] Let  be a quiver and let
be a quiver and let 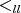 be a length-lexicographic order in
be a length-lexicographic order in  , where
, where  is the set of paths in
is the set of paths in  . Let
. Let 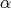 be a maximal arrow with respect to
be a maximal arrow with respect to 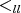 in
in  and
and 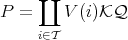 a projective in
a projective in 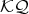 -Mod. Let
-Mod. Let 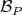 be an ordered basis ( as defined above ) for
be an ordered basis ( as defined above ) for 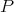 . If
. If 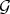 is a right uniform (reduced ) Gröbner basis for P, then
is a right uniform (reduced ) Gröbner basis for P, then 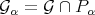 is a right uniform (reduced ) Gröbner basis for
is a right uniform (reduced ) Gröbner basis for 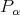 .
.
As a consequence of the Elimination Theory, Green find a new algebra ![KQ [T]](/img/revistas/ruma/v48n3/3a06342x.png) , that we will call added by loops.
, that we will call added by loops.
This algebra ![KQ [T]](/img/revistas/ruma/v48n3/3a06343x.png) is an hereditary algebra, obtained adding loops to
is an hereditary algebra, obtained adding loops to  , as above, but without adding any relation. Observe that both are hereditary algebras and the basis of
, as above, but without adding any relation. Observe that both are hereditary algebras and the basis of ![KQ [T ]](/img/revistas/ruma/v48n3/3a06345x.png) is ordered in such a way that the new loops are maximal elements. In this situation, given two ideals and generators sets (Gröbner basis), we can find, as described in [2], a generators set (Gröbner basis), of the intersection of these ideals, constructed by the Elimination Theorem (that can be found, with more details, in [2], section 8).
is ordered in such a way that the new loops are maximal elements. In this situation, given two ideals and generators sets (Gröbner basis), we can find, as described in [2], a generators set (Gröbner basis), of the intersection of these ideals, constructed by the Elimination Theorem (that can be found, with more details, in [2], section 8).
In our work, there are no additional hypothesis over the given order, the only additional assumption is that the extra loops must be between the vertices and the arrows.
Moreover, we consider the more general case, where 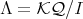 , is not necessarily hereditary.
, is not necessarily hereditary.
THEOREM 3.11. Let 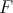 be a subset of
be a subset of 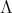 and let
and let  be homogeneous. If
be homogeneous. If 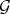 is a Gröbner basis for
is a Gröbner basis for 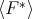 , then
, then 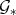 is a Gröbner basis for
is a Gröbner basis for 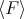 .
.
PROOF. Suppose that 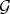 is a Gröbner basis for
is a Gröbner basis for 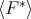 . We will prove the theorem, using the definition of Gröbner basis.
. We will prove the theorem, using the definition of Gröbner basis.
As 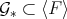 , then
, then 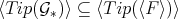 , and we only need to verify that
, and we only need to verify that 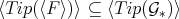 , that is, if given
, that is, if given 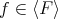 there exists
there exists 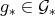 such that
such that 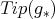 divides
divides 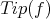 .
.
Let 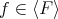 , we can write
, we can write 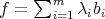 , where
, where 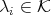 and
and 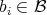 for
for 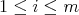 .
.
Without lost of generality, assume that 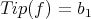 , then
, then
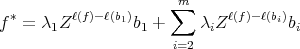
it follows by the given order that 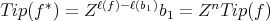 .
.
By lemma 3.8, there exists 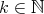 such that
such that 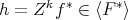 . By the above observation,
. By the above observation, 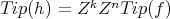 .
.
As 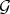 is a Gröbner basis for
is a Gröbner basis for 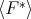 , there exists
, there exists 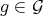 such that
such that 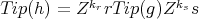 , for some
, for some 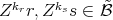 .
. 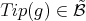 , so
, so 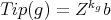 for some
for some 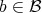 and
and 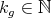 . By the definition of order in
. By the definition of order in 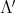 , for every
, for every 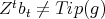 that occurs in
that occurs in 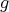 ,
,  , then
, then  , or
, or 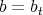 and
and 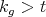 , but this cannot occur, because
, but this cannot occur, because 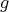 is homogeneous, so
is homogeneous, so 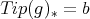 .
.
Then, 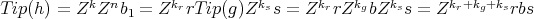 . So, we have
. So, we have
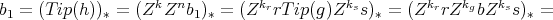
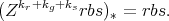
Then 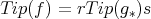 , and s
, and s 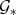 is a Gröbner basis for
is a Gröbner basis for 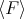 . ∎
. ∎
[1] Becker, T., Weispfenning, V., Gröbner Bases, A Computational Approach to Commutative Algebra, Graduate Texts in Mathematics, Springer-Verlag. 1993. [ Links ]
[2] Green, E. L., Multiplicative Bases,Gröbner Bases, and Right Grbner Bases, J. Symbolic Computation, 29, 2000, n.4-5, 601-623. [ Links ]
[3] Green, E. L., Non commutative Gröbner Bases and Projectives Resolutions, In Michler and Schneider, eds, Proceedings of the Euroconference Computational Methods for Representations of Groups and Algebras, Essen, 1997, vol. 173 of Progress in Mathematics, 29-60. Basel, Bikhaser Verlag. [ Links ]
[4] Nordbeck,P. On some Basic Applications of Gröbner Bases in Non-commutative Polynomial Rings Gröbner Basis and Applications, London Mathematical Society Lecture Note Series, Vol. 251, Edited by B. Buchberger and Franz Winkler. [ Links ]
Gladys Chalom
Departamento de Matemática - IME,
Universidade de São Paulo,
CP 66281, 05315-970, São Paulo, Brasil
agchalom@ime.usp.br
Eduardo do Nascimento Marcos
Departamento de Matemática - IME,
Universidade de São Paulo,
CP 66281, 05315-970, São Paulo, Brasil
enmarcos@ime.usp.br
P. Oliveira
Departamento de Matemática - IME,
Universidade de São Paulo,
CP 66281, 05315-970, São Paulo, Brasil
Recibido: 31 de enero de 2007
Aceptado: 20 de diciembre de 2007













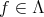 . Then
. Then 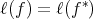 .
.
