Mischa Cotlar, in memoriam
(1913 - 2007)

Este volumen especial de la revista de la Unión Matemática Argentina está dedicado a la memoria de Mischa Cotlar.

Adiós a Mischa

por Lolina Alvarez Alonso

"Siempre admiré a Mischa como matemático y como persona", "Mischa fue muy bueno conmigo", "Me da mucha pena el saber de la muerte de Mischa", "... Mischa, como él prefería ser llamado, fue un matemático de renombre internacional y de gran modestia. Sus contribuciones distinguidas y originales enriquecieron el análisis armónico, la teoría de operadores y la teoría ergódica... Mischa nos deja, junto con sus enseñanzas matemáticas, su ejemplo personal y sus ideas acerca de la importancia de la calidad humana...", "Aún uso sus libros maravillosos en mis clases".

En estas y otras palabras similares, matemáticos de muchas partes del mundo me han dado su reacción al saber de la muerte de Mischa Cotlar. A estas palabras quiero unir mi pena y repetir algo de lo que dije hace menos de un año, cuando el Noticiero de la Unión Matemática Argentina No. 39 rindió su homenaje a Mischa en ocasión de haber recibido el Premio Sarmiento: "... Es en su manera de vivir que se siente una determinación inmensa de no traicionar a sus principios. ..."

N. de R.: esta nota fue publicada por el Noticiero de la UMA en marzo de 2007, pág. 9, Vol. 41.

A Mischa, con admiración y cariño

Mi primer encuentro personal con Mischa Cotlar ocurrió en Buenos Aires en 1973. Ambos asistíamos a un curso que Alberto Calderón estaba dando en Núñez explicando los resultados de Hörmander sobre los operadores integrales de Fourier.

Por supuesto que antes había oído el nombre de Mischa y sabía de sus resultados, entre ellos el hermoso lema llamado Lema de Cotlar. Lo que primero me llamó la atención en Mischa fue su humildad. Lo vi actuar como otro estudiante más entre nosotros, tomando notas y mostrando la misma admiración por Calderón. Una vez Mischa tuvo que faltar a un par de clases por razones de salud y me preguntó si le podía dejar mis notas. Cuando le ofrecí llevarle una copia a su casa, me emocionó el enorme agradecimiento que mostró por un gesto tan pequeño. Recuerdo su afición a la música para piano y su admiración por las concertistas Martha Argerich y Alicia de Larrocha. A mitad del curso, Mischa debió ser operado por un problema cardíaco y en las siguientes semanas vi a Yanni bastante a menudo. No puedo hablar de Mischa sin mencionar a Yanni y la relación en cuerpo y alma que los ha unido a través de muchos años y muchos avatares.

Perdí contacto personal con Mischa por bastantes años, hasta que en 1984 lo vi en Princeton, EEUU, donde Mischa estaba visitando el Instituto de Estudios Avanzados. Lo encontré i gual en apariencia física que el Mischa que recordaba de once años atrás. Los visité a él y a Yanni a menudo, disfrutando de las suculentas comidas vegetarianas que preparaban. En estas visitas observé otra cualidad de Mischa, su agudeza para percibir el estado anímico de su interlocutor. Me habló de su filosofía de vida, que creo estaba basada en el principio budista que dice que uno no puede cambiar su contorno hasta que no ha logrado cambiarse a sí mismo. Nunca oí a Mischa criticar a otros ni lo oí hablar de política a menudo. Es en su manera de vivir que se siente una determinación inmensa de no traicionar a sus principios.

En enero de 1994, sus estudiantes y colegas venezolanos organizaron una conferencia en Caracas para celebrar los 82 años de Mischa. Una buena parte de los nombres más i lustres en el análisis armónico participaron, dando testimonio a la profundidad de la obra matemática de Mischa. Un momento i nolvidable para mí fue ver a Mischa, Jean Pierre Kahane y Laurent Schwartz como panelistas en una discusión sobre la responsabilidad social de los matemáticos. Allí Mischa i nvitó a los participantes a elegir la ruta pacifista, a no buscar el dinero que el aparato militar controla con creciente intensidad.

En la recepción en honor de Mischa que cerró la conferencia, varios le pidieron que tocara el piano, cosa que raramente hacía en público. Mischa aceptó esa vez y por un rato nos regaló el oído y el espíritu con varias piezas muy hermosas.

Hace ya varios años que no me he encontrado con Mischa personalmente. Un amigo común me enseñó hace menos de dos meses varias fotografías de Mischa tomadas en Buenos Aires. En estas fotos veo al mismo Mischa de veinte años atrás, con su apariencia de tener no más de setenta años.

Mischa respondió con la misma serena humildad de siempre a los mensajes de felicitación que muchos le enviamos con motivo de habérsele otorgado en Argentina el Premio Sarmiento. En su contestación, Mischa se disculpa porque su salud no le ha permitido contestar individualmente a cada felicitación.

Lolina Alvarez Alonso, Las Cruces, junio de 2006.

N. de R.: esta nota fue publicada por el Noticiero de la UMA en junio de 2006, pág. 8, Vol. 39.

El aspecto pitagórico-platónico de la matemática

Reproducimos el discurso pronunciado por el Dr. Cotlar agradeciendo el Premio "Senador Domingo Faustino Sarmiento" que le fuera otorgado por el Senado de la Nación Argentina en abril de 2006.

Estoy conmovido por tan alto honor que se me confiere a través de este galardón cuyo nombre está asociado nada menos que a Sarmiento. A quién se debe el sistema educativo y la enseñanza laica.

Expreso mi muy sentido agradecimiento al Presidente del Honorable Senado Nación Lic. Daniel Scioli y al Senador Dr. Rodolfo Terragno. Así como a todos Uds. que han venido gentilmente a acompañarme. Dadas las características de este premio, Uds. esperarían que hable de cultura general, y particularmente de lo que la Universidad fue durante el período 1955-1966, ya que yo fui testigo de los i nicios de un proyecto de Universidad Nacional en una época dorada y también fui el testigo de su lamentable destrucción, comenzada en la noche de los bastones largos.

En esta época donde el mercado parece ser el objetivo de la vida, conviene no olvidar que cada golpe de agresión que intente destruir a la Universidad producirá daños de los que se tardará decenios en volver a retomar aquel camino trazado por aquellos que eran la verdadera universidad, enamorados de la ciencia y la cultura, con diferentes i deologías y a pesar de ello con lazos de amistad perdurables. Donde las agrupaciones estudiantiles no estaban teñidas por intereses de partidos políticos. No hay que olvidar que la formación de científicos e intelectuales en aquel proyecto universitario requirió no sólo de personas notables sino también de un momento excepcional del que deberíamos reflexionar.

Sin embargo, para hablar sobre aquellos tiempos hay pocas personas preparadas tanto en lo científico como en lo social que pueden hacerlo con la debida altura. Mientras que mis conocimientos están limitados a algunas áreas particulares de la ciencia. Pero hay otro problema de gran i mportancia que responde al área de la cultura y podría desarrollar un poco más detalladamente y lo quiero compartir con Uds.

Voy a referirme a un aspecto de la matemática que desde mi juventud más me atrajo hacia ella que suele llamarse el aspecto pitagórico-platónico de la matemática. Y que más tarde fui sorprendido por la similaridad de estas i deas con los principios de los Upanishads y el Budismo.

Los pitagóricos del siglo VI a. de C. observaron que la armonía musical, los entes geométricos y los fenómenos astronómicos obedecían a leyes que se expresaban mediante los números; que los números y sus proporciones gobernaban en áreas tan distintas y alejadas como la geometría, la música y la astronomía.

Y más aún, que enunciados abstractos de naturaleza muy distinta y alejada pueden resultar lógicamente equivalentes y esta equivalencia se establece a través de un razonamiento lógico también abstracto.

Ellos intuyeron así, y lo afirmaron, que todos los campos del universo estaban conectados entre sí por una Unidad universal que se manifestaba y se realizaba a través de los números y la abstracción, y que la abstracción era la manifestación de la Unidad en el mundo mental.

Al avanzar en mi aprendizaje matemático fue una alegría comprobar que el desarrollo de la matemática confirmó plenamente aquellas ideas pitagóricas-platónicas. Y que también los grandes fundadores de la ciencia actual, como Heisenberg, Pauli, Schroedinger, Andre Weil, Alexander Grothendieck, tenían un profundo conocimiento de los Upanishads y del budismo.

Que Whitehead, el colaborador de Bertrand Russell y máximo experto del pitagorismo platónico reunió sus mejores i deas en una teoría conocida como "Proces Philosophy" y más tarde quedó claro que esta teoría coincide esencialmente con principios básicos del budismo.

El conocimiento de Einstein del Budismo, impulsado por las filosofías de Spinoza y Schopenhauer era tal vez deficiente y a veces equivocado, pero él señaló un hecho de importancia fundamental: "el objetivo de la matemática o de la física matemática es el mismo que el de la Ética pero con aplicaciones a campos diferentes. Que la Ética sin Ciencia es ciega y la Ciencia sin Etica es coja".

El objetivo de ambas es realizar la Unidad, pero esta realización será completa sólo si no se contradicen al ser aplicadas en un área común a ambos campos. O sea, Einstein busca unificar el pitagorismo platónico que realiza la unidad por la abstracción en el mundo de objetos mentales, con el Budismo y la tradición Judeo- Cristiana que buscan la unidad en el mundo de los seres vivos, problema básico de la Etica.

El mundo en que vivimos contiene aquellos otros dos mundos y aquí es esencial que las aplicaciones de la Ética y de la ciencia no se contradigan.

Si bien Einstein no escribió un tratado sobre esto, dejó muy claras sus i deas en breves observaciones informales, a veces de tipo metafórico o místico.

Es interesante que sus i deas se acercan mucho a las del budismo en la i nterpretación que le dieron Krishnamurti y el físico David Bohm.

Einstein no dejó ningún trabajo formal en el cual se formule algún sistema de axiomas que permita deducir teoremas acerca la Unidad de la Ciencia y la Ética. Y es que todavía Platón creía que era posible desarrollar una ética una ciencia que no se base en ningún axioma.

Estos problemas son de máxima importancia en el momento actual. Pensar que aún hoy, a principios del siglo veinte, muchas personas de gran inteligencia y bien intencionadas creen que la ética exige que todo ciudadano debe obedecer ciegamente a su gobierno y que puede glorificar a su país matando a seres vivientes del país enemigo, y hoy día no son muchos los que se preocupan por el hecho que la ciencia se use en proyectos que ponen en peligro la vida de la Tierra.

En cambio Einstein y Russell advertían que la alianza de la ciencia con el militarismo destruía la esencia de la misma, y que el problema prioritario de la humanidad es buscar un acuerdo entre los científicos sobre el uso correcto de la ciencia, prohibiendo su aplicación a fines destructivos o de explotación. Sin cultura ética basada en el amor y la cooperación, y no en la rivalidad, la competencia y el deseo de poder, difícilmente habrá solución a los grandes problemas de la humanidad.

Sin cultura ética basada en el amor y la cooperación, el desarrollo de la tecnología será como un arma peligrosa en manos de un niño. Las grandes riquezas están en el interior de los hombres.

Si uno necesita lujos y placeres excesivos es porque su interior esta vacío aún. Es necesaria una i ntensa y urgente difusión de las nociones básicas de la Etica y una clara comprensión de que los problemas humanos no se resuelven por la violencia sino por el uso de las facultades superiores latentes en todos los seres humanos. Antes de terminar quiero expresar mi gratitud a la Universidad de Buenos Aires y en particular al Instituto de Matemática (IAM), así como La Universidad Central de Venezuela, y también del Dr. Saúl Drajer y mi amigo César Orda por su constante ayuda en los momentos difíciles de los últimos años. Y a mi compañera de toda la vida Yanny, que es la riqueza más grande que tengo.

Y finalmente debo resaltar el hecho, particularmente importante en mi formación general, que tanto mis maestros, grandes matemáticos, como mis amigos y colaboradores argentinos y uruguayos, eran personas de excepcional cualidad humana con profundas y nobles i nquietudes que trascienden el frío profesionalismo. Mi gratitud hacia aquellos por todo lo que me enseñaron en el campo matemático y en la comprensión que la cualidad humana está antes que el científico.

Muchas Gracias.

TRABAJOS DE MISCHA COTLAR

[1]    M. Cotlar and C. Sadosky, Revisiting almost orthogonality and eigenexpansions, in Function spaces, interpolation theory and related topics (Lund, 2000), 249-271, de Gruyter, Berlin.

[2]    G. Cedeño and M. Cotlar, Uniqueness condition for the Pick problem, Divulg. Mat. 8 (2000), no. 2, 99-112.

[3]    M. Cotlar and C. Sadosky, Hankel forms and operators in Hardy spaces with two Szegő weights, in Operator theory and interpolation (Bloomington, IN, 1996), 145-162, Birkhäuser, Basel.

[4]    P. Alegría and M. Cotlar, Generalized Toeplitz forms and interpolation colligations, Math. Nachr. 190 (1998), 5-29.

[5]    M. Cotlar and C. Sadosky, A polydisk version of Beurling's characterization for invariant subspaces of finite multi-codimension, in Operator theory for complex and hypercomplex analysis (Mexico City, 1994), 51-56, Contemp. Math., 212, Amer. Math. Soc., Providence, RI.

[6]    M. Cotlar and C. Sadosky, Two distinguished subspaces of product BMO and Nehari-AAK theory for Hankel operators on the torus, Integral Equations Operator Theory 26 (1996), no. 3, 273-304.

[7]    M. Cotlar and L. Recht, Rodolfo A. Ricabarra (August 1925-November 1984), in Volume in homage to Dr. Rodolfo A. Ricabarra (Spanish), i-v, Univ. Nac. del Sur, Bahía Blanca, 1995.

[8]    M. Cotlar and C. Sadosky, The Adamjan-Arov-Kreĭn theorem in general and regular representations of R² and the symplectic plane, in Toeplitz operators and related topics (Santa Cruz, CA, 1992), 54-78, Birkhäuser, Basel, 1994.

[9]    M. Cotlar and C. Sadosky, Nehari and Nevanlinna-Pick problems and holomorphic extensions in the polydisk in terms of restricted BMO, J. Funct. Anal. 124 (1994), no. 1, 205-210.

[10]    M. Cotlar and C. Sadosky, Abstract, weighted, and multidimensional Adamjan-Arov-Kreĭn theorems, and the singular numbers of Sarason commutants, Integral Equations Operator Theory 17 (1993), no. 2, 169-201.

[11]    M. Cotlar and C. Sadosky, Transference of metrics induced by unitary couplings, a Sarason theorem for the bidimensional torus, and a Sz.-Nagy-Foias theorem for two pairs of dilations, J. Funct. Anal. 111 (1993), no. 2, 473-488.

[12]    M. Cotlar and C. Sadosky, Weakly positive matrix measures, generalized Toeplitz forms, and their applications to Hankel and Hilbert transform operators, in Continuous and discrete Fourier transforms, extension problems and Wiener-Hopf equations, 93-120, Birkhäuser, Basel, 1992.

[13]    M. Cotlar, Quadratic inequalities for Hilbert transforms and Hankel forms in the spaces 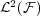and 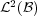, in Geometry and complex variables (Bologna, 1988/1990), 147-153, Dekker, New York, 1991.

[14]    M. Cotlar and C. Sadosky, Toeplitz liftings of Hankel forms bounded by non-Toeplitz norms, Integral Equations Operator Theory 14 (1991), no. 4, 501-532.

[15]    M. Cotlar and C. Sadosky, Toeplitz and Hankel forms related to unitary representations of the symplectic plane, Colloq. Math. 60/61 (1990), no. 2, 693-708.

[16]    M. Cotlar and C. Sadosky, Two-parameter lifting theorems and double Hilbert transforms in commutative and noncommutative settings, J. Math. Anal. Appl. 150 (1990), no. 2, 439-480.

[17]    M. Cotlar and C. Sadosky, The Helson-Szegő theorem in L^p of the bidimensional torus, in Harmonic analysis and partial differential equations (Boca Raton, FL, 1988), 19-37, Contemp. Math., 107, Amer. Math. Soc., Providence, RI, 1990.

[18]    M. Cotlar and C. Sadosky, Nonlinear lifting theorems, integral representations and stationary processes in algebraic scattering systems, in The Gohberg anniversary collection, Vol. II (Calgary, AB, 1988), 97-123, Birkhäuser, Basel, 1989.

[19]    M. Cotlar and C. Sadosky, Generalized Bochner theorem in algebraic scattering systems, in Analysis at Urbana, Vol. II (Urbana, IL, 1986-1987), 144-169, Cambridge Univ. Press, Cambridge, 1989.

[20]    M. Cotlar and C. Sadosky, Integral representations of bounded Hankel forms defined in scattering systems with a multiparametric evolution group, in Contributions to operator theory and its applications (Mesa, AZ, 1987), 357-375, Birkhäuser, Basel, 1988.

[21]    M. Cotlar and C. Sadosky, Toeplitz liftings of Hankel forms, in Function spaces and applications (Lund, 1986), 22-43, Lecture Notes in Math., 1302, Springer, Berlin, 1988.

[22]    M. Cotlar, J. León and M. C. Pereyra, Eigenfunction expansions of covariance kernels of Hilbert space processes, Acta Cient. Venezolana 38 (1987), no. 5-6, 563-569.

[23]    M. Cotlar and C. Sadosky, Prolongements des formes de Hankel généralisées en formes de Toeplitz, C. R. Acad. Sci. Paris Sér. I Math. 305 (1987), no. 5, 167-170.

[24]    M. Cotlar, Some aspects of the trigonometric moment problem, in First conference on analysis (Spanish) (Mérida, 1986), 65-82, Univ. de los Andes, Mérida, 1986.

[25]    M. Cotlar and C. Sadosky, Lifting properties, Nehari theorem and Paley lacunary inequality, Rev. Mat. Iberoamericana 2 (1986), no. 1-2, 55-71.

[26]    R. Arocena, M. Cotlar and J. León, Toeplitz kernels, scattering structures and covariant systems, in Aspects of mathematics and its applications, 77-95, North-Holland, Amsterdam, 1986.

[27]    M. Cotlar and C. Sadosky, A lifting theorem for subordinated invariant kernels, J. Funct. Anal. 67 (1986), no. 3, 345-359.

[28]    M. Cotlar and L. Recht, Rodolfo A. Ricabarra (August 1925-November 1984), Rev. Un. Mat. Argentina 32 (1985), no. 2, 159-161 (1986).

[29]    M. Cotlar and C. Sadosky, Generalized Toeplitz kernels, stationarity and harmonizability, J. Analyse Math. 44 (1984/85), 117-133.

[30]    M. Cotlar and C. Sadosky, Inégalités à poids pour les coefficients lacunaires de certaines fonctions analytiques. (French) [Weighted inequalities for lacunary coefficients of analytic functions] C. R. Acad. Sci. Paris Sér. I Math. 299 (1984), no. 13, 591594

[31]    M. Cotlar and C. Sadosky, On some L^p versions of the Helson-Szegő theorem, in Conference on harmonic analysis in honor of Antoni Zygmund, Vol. I, II (Chicago, Ill., 1981), 306-317, Wadsworth, Belmont, CA, 1983.

[32]    R. Arocena and M. Cotlar, A generalized Herglotz-Bochner theorem and L²-weighted inequalities with finite measures, in Conference on harmonic analysis in honor of Antoni Zygmund, Vol. I, II (Chicago, Ill., 1981), 258-269, Wadsworth, Belmont, CA, 1983.

[33]    M. Cotlar and C. Sadosky, Vector-valued inequalities of Marcinkiewicz-Zygmund and Grothendieck type for Toeplitz forms, in Harmonic analysis (Cortona, 1982), 278-308, Lecture Notes in Math., 992, Springer, Berlin, 1983.

[34]    M. Cotlar, Moment theory and continuity of the Hilbert and Poisson transforms in L² spaces, in Functional analysis, holomorphy, and approximation theory (Rio de Janeiro, 1979), 33-57, Dekker, New York, 1983.

[35]    R. Arocena and M. Cotlar, Dilation of generalized Toeplitz kernels and some vectorial moment and weighted problems, in Harmonic analysis (Minneapolis, Minn., 1981), 169-188, Lecture Notes in Math., 908, Springer, Berlin, 1982.

[36]    M. Cotlar and C. Sadosky, Majorized Toeplitz forms and weighted inequalities with general norms, in Harmonic analysis (Minneapolis, Minn., 1981), 139-168, Lecture Notes in Math., 908, Springer, Berlin, 1982

[37]    R. Arocena and M. Cotlar, Generalized Toeplitz kernels, Hankel forms and Sarason's conmutation theorem, Acta Cient. Venezolana 33 (1982), no. 2, 89-98.

[38]    R. Arocena and M. Cotlar, Generalized Toeplitz kernels and Adamjan-Arov-Kreĭn moment problems, in Toeplitz centennial (Tel Aviv, 1981), 37-55, Birkhäuser, Basel, 1982.

[39]    R. Arocena and M. Cotlar, On a lifting theorem and its relation to some approximation problems, in Functional analysis, holomorphy and approximation theory (Rio de Janeiro, 1980), 1-25, North-Holland, Amsterdam, 1982.

[40]    R. Arocena, M. Cotlar and C. Sadosky, Weighted inequalities in L² and lifting properties, in Mathematical analysis and applications, Part A, 95-128, Academic Press, New York, 1981.

[41]    R. Arocena and M. Cotlar, Continuous generalized Toeplitz kernels in R, Portugal. Math. 39 (1980), no. 1-4, 419-434 (1985).

[42]    M. Cotlar and C. Sadosky, On the Helson-Szegő theorem and a related class of modified Toeplitz kernels, in Harmonic analysis in Euclidean spaces (Proc. Sympos. Pure Math., Williams Coll., Williamstown, Mass., 1978), Part 1, 383-407, Amer. Math. Soc., Providence, R.I., 1979

[43]    M. Cotlar and C. Sadosky, Characterization of two measures satisfying the Riesz inequality for the Hilbert transform in L², Acta Cient. Venezolana 30 (1979), no. 4, 346-348.

[44]    M. Cotlar and C. Sadosky, Transformée de Hilbert, théorème de Bochner et le problème des moments, C. R. Acad. Sci. Paris Sér. A-B 285 (1977), no. 6, A433-A436.

[45]    M. Cotlar and C. Sadosky, Transformée de Hilbert, théorème de Bochner et le problème des moments, C. R. Acad. Sci. Paris Sér. A-B 285 (1977), no. 10, A661-A664.

[46]    M. Cotlar and C. Sadosky, A moment theory approach to the Riesz theorem on the conjugate function with general measures, Studia Math. 53 (1975), no. 1, 75-101.

[47]    M. Cotlar and R. Cignoli, An introduction to functional analysis, Translated from the Spanish by A. Torchinsky and A. Gonzalez Villalobos, North-Holland, Amsterdam, 1974. xiv+585 pp.

[48]    M. Cotlar, Equipación con espacios de Hilbert. (Spanish) [Equipping with Hilbert spaces] Cursos y Seminarios de Matemática, Fasc. 15 Universidad de Buenos Aires, Buenos Aires, 1968 xix+366 pp.

[49]    C. Sadosky and M. Cotlar, On quasi-homogeneous Bessel potential operators, in Singular integrals (Proc. Sympos. Pure Math., Chicago, Ill., 1966), 275-287, Amer. Math. Soc., Providence, R.I., 1967.

[50]    M. Cotlar and R. Cignoli, Nociones de espacios normados. (Spanish) [Concepts in the theory of normed spaces] Preliminary edition Editorial Universitaria de Buenos Aires, Buenos Aires, 1967 xxiii+361 pp.

[51]    C. A. Berenstein; M. Cotlar; N. Kerzman and P. Kre, Some remarks on the Marcinkiewicz convexity theorem in the upper triangle. Studia Math. 29 1967 79-95.

[52]    M. Cotlar and C. R. de Sadosky, Introducción al álgebra. Nociones de álgebra lineal. (Spanish) [Introduction to algebra. Concepts of linear algebra] Fourth edition Editorial Universitaria de Buenos Aires, Buenos Aires, 1966 278 pp.

[53]    M. Cotlar, Introducción a la teoría de la representación de grupos. (Spanish) [Introduction to the theory of group representations] Cursos y Seminarios de Matemática, Fasc. 11 Universidad de Buenos Aires 1963 xv+5-239 pp.

[54]    M. Cotlar, Archimedean semigroups and operator algebras, in Proc. Third Brazilian Math. Colloq. (1961) (Portuguese) Summa Brasil. Math. 5 (1962), 5-46, Conselho Nac. Pesquisas, São Paulo.

[55]    M. Cotlar and E. L. Ortiz, On some inequalities of potential operators, Univ. Nac. La Plata Publ. Fac. Ci. Físicomat. Serie Segunda Rev. 8 (1962), no. 1, 16-34 (1962).

[56]    M. Cotlar, Generalized potential operators and orthogonal sums, Rev. Un. Mat. Argentina 19 (1960), 112-134 (1960).

[57]    M. Cotlar and R. Panzone, Generalized potential operators, Rev. Un. Mat. Argentina 19 (1960), 3-41 (1960).

[58]    M. Cotlar, Condiciones de continuidad de operadores potenciales y de Hilbert. (Spanish) [Continuity conditions for potential and Hilbert operators] Cursos y Seminarios de Matemática, Fasc. 2 Departamento de Matemática, Facultad de Ciencias Exactas y Naturales, Universidad Nacional de Buenos Aires 1959 iii+354 pp. (mimeographed).

[59]    M. Cotlar and R. Panzone, On almost orthogonal operators in L^p-spaces, Acta Sci. Math. Szeged 19 (1958), 165-171.

[60]    M. Cotlar and M. Bruschi, On the convexity theorems of Riesz-Thorin and Marcinkiewicz, Univ. Nac. La Plata. Publ. Fac. Ci. Fisicomat. Serie Segunda. Rev. 5 (1956), 162-172 (1957).

[61]    M. Cotlar and R. Ricabarra, On the integral of Caratheodory, Univ. Nac. La Plata. Publ. Fac. Ci. Fisicomat. Serie Segunda. Rev. 5 (1956), 153-161 (1957).

[62]    M. Cotlar, On ergodic theorems, Math. Notae 14 (1955), 85-119 (1956).

[63]    M. Cotlar, Some generalizations of the Hardy-Littlewood maximal theorem, Rev. Mat. Cuyana 1 (1955), 85-104 (1956).

[64]    M. Cotlar, A general interpolation theorem for linear operations, Rev. Mat. Cuyana 1 (1955), 57-84 (1956).

[65]    M. Cotlar, A unified theory of Hilbert transforms and ergodic theorems, Rev. Mat. Cuyana 1 (1955), 105-167 (1956).

[66]    M. Cotlar, On the algebraic theory of the mean and the Hahn-Banach theorem, Rev. Un. Mat. Argentina 17 (1955), 9-24 (1956).

[67]    M. Cotlar, A combinatorial inequality and its applications to L²-spaces, Rev. Mat. Cuyana 1 (1955), 41-55 (1956).

[68]    M. Cotlar, The problem of moments and the theory of Hermitian operators, in Segundo symposium sobre algunos problemas matemáticos que se están estudiando en Latino América, Julio, 1954, 71-85, Centro de Cooperación Científica de la UNESCO para América Latina, Montevideo, Uruguay, 1954.

[69]    M. Cotlar, On a theorem of Beurling and Kaplansky, Pacific J. Math. 4 (1954), 459-465.

[70]    M. Cotlar and R. Ricabarra, On the existence of characters in topological groups, Amer. J. Math. 76 (1954), 375-388.

[71]    M. Cotlar, On the foundations of ergodic theory, in Symposium sobre algunos problemas matemáticos que se están estudiando en Latino América, Diciembre, 1951, 71-84, Centro de Cooperación Científica de la Unesco para América Latina, Montevideo, Uruguay, 1952.

[72]    M. Cotlar and R. Ricabarra, The Caratheodory integral, Mem. Real Acad. Ci. Exact. Fís. Nat. Madrid. 4 (1950), 1-47.

[73]    M. Cotlar and Y. Frenkel, On Kolmogoroff's integral, Univ. Buenos Aires. Contrib. Ci. Ser. A. 1 (1950), 46-63.

[74]    Y. Frenkel and M. Cotlar, Non-additive majorants and minorants in the theory of the Perron-Denjoy integral, Revista Acad. Ci. Madrid 44 (1950), 411-426.

[75]    M. Cotlar and R. A. Ricabarra, On transformations of sets and Koopman's operators, Revista Unión Mat. Argentina 14 (1950), 232-254.

[76]    M. Cotlar and R. A. Ricabarra, Invariant measures in compact topological spaces, Math. Notae 9 (1949), 52-77.

[77]    M. Cotlar and R. A. Ricabarra, On a theorem of E. Hopf, Revista Unión Mat. Argentina 14 (1949), 49-63.

[78]    M. Cotlar and E. Roxin, On the variation of discontinuous and multivalued functions of a real variable. (Spanish) Revista Unión Mat. Argentina 14, (1949). 38-46.

[79]    M. Cotlar, An extension of Rolle's theorem for continuous transformations of the plane, Math. Notae 8 (1948), 79-84.

[80]    M. Cotlar and E. Zarantonello, Semiordered groups and Riesz-Birkhoff L-ideals, Fac. Ci. Mat. Univ. Nac. Litoral. Publ. Inst. Mat. 8 (1948), 105-192.

[81]    M. Cotlar and Y. Frenkel, A general theory of integral based on an extension of the concept of limit, Univ. Nac. Tucumán. Revista A. 6 (1947), 113-159.

[82]    M. Cotlar, A method for obtaining congruences of Bernoulli numbers, Math. Notae 7 (1947), 1-29.

[83]    M. Cotlar, Study of a class of Bernoulli polynomials, Math. Notae 6 (1946), 69-95.

[84]    M. Cotlar and Y. Frenkel, On nonadditive set functions and generalization of the decomposition of Vallée Poussin, Univ. Nac. Tucumán. Revista A. 5 (1946), 227-253.

[85]    P. Capelli and M. Cotlar, Some questions related to a possible extension of the principle of conservation of domains, Publ. Inst. Mat. Univ. Nac. Litoral 6 (1946), 63-96.

[86]    M. Cotlar and B. Levi, Exercises on the cosine function, Math. Notae 5 (1945), 193-214.

[87]    M. Cotlar, A generalization of the factorials, Math. Notae 5 (1945), 89-107.

[88]    M. Cotlar, A method of construction of structures and its application to topological spaces and abstract arithmetic, Univ. Nac. Tucumán. Revista A. 4 (1944), 105-157.

[89]    J. C. Vignaux and M. Cotlar, Asymptotic Laplace-Stieltjes integrals, Univ. Nac. La Plata. Publ. Fac. Ci. Fisicomat. (2) 3(14) (1944), no. 180(4), 345-400.

[90]    J. C. Vignaux and M. Cotlar, Totally normal families of holomorphic functions, Publ. Inst. Mat. Univ. Nac. Litoral 7 (1944), 152 pp.

[91]    M. Cotlar and B. Levi, Considerations concerning a proposition of W. H. Young, Math. Notae 4 (1944), 145-155.

[92]    B. Levi, P. Capelli and M. Cotlar, The origins of the theory of the Wronskian algorithm within the Pythagorean doctrine, Math. Notae 3 (1943), 74-100.

[93]    M. Cotlar, Functions which are univalent on a subset of the boundary of a domain of regularity, Publ. Inst. Mat. Univ. Nac. Litoral 4 (1942), 47-96.

[94]    M. Cotlar, On non-measurable sets and a generalization of the Lebesgue integral, Publ. Inst. Mat. Univ. Nac. Litoral 2 (1940), 149-176.

[95]    M. Cotlar, Normal families of non-analytic functions, An. Soc. Ci. Argentina 129 (1940), 3-25.