Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.49 n.1 Bahía Blanca ene./jun. 2008
Iterated Aluthge transforms: a brief survey
Jorge Antezana*, Enrique R. Pujals† and Demetrio Stojanoff*
* Partially supported by CONICET (PIP 4463/96), Universidad de La Plata (UNLP 11 X472) and ANPCYT (PICT03-09521).
† Partially supported by CNPq
Dedicated to the memory of Mischa Cotlar
Abstract. Given an r × r complex matrix T, if 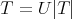 is the polar decomposition of T, then the Aluthge transform is defined by
is the polar decomposition of T, then the Aluthge transform is defined by
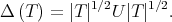
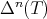 denote the n-times iterated Aluthge transform of T, i.e.
denote the n-times iterated Aluthge transform of T, i.e. 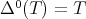 and
and 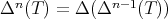 ,
, 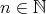 . In this paper we make a brief survey on the known properties and applications of the Aluthge trasnsorm, particularly the recent proof of the fact that the sequence
. In this paper we make a brief survey on the known properties and applications of the Aluthge trasnsorm, particularly the recent proof of the fact that the sequence 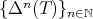 converges for every r × r matrix T. This result was conjectured by Jung, Ko and Pearcy in 2003.
converges for every r × r matrix T. This result was conjectured by Jung, Ko and Pearcy in 2003. 2000 Mathematics Subject Classification. Primary 37D10. Secondary 15A60.
Key words and phrases. Aluthge transform, stable manifold theorem, similarity orbit, polar decomposition.
Let  be a Hilbert space and
be a Hilbert space and 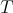 a bounded operator defined on
a bounded operator defined on 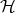 whose (left) polar decomposition is
whose (left) polar decomposition is 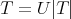 . The Aluthge transform of
. The Aluthge transform of 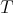 is the operator defined by
is the operator defined by
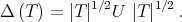 | (1) |
This transform was introduced in [1] by Aluthge, in order to study p-hyponormal and log-hyponormal operators. Roughly speaking, the idea behind the Aluthge transform is to convert an operator into another operator which shares with the first one some spectral properties but it is closer to being a normal operator.
The Aluthge transform has received much attention in recent years. One reason is its connection with the invariant subspace problem. Jung, Ko and Pearcy proved in [15] that 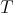 has a nontrivial invariant subspace if an only if
has a nontrivial invariant subspace if an only if 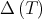 does. On the other hand, Dykema and Schultz proved in [10] that the Brown measure is preserved by the Aluthge transform. Another reason is related with the iterated Aluthge transform. Let
does. On the other hand, Dykema and Schultz proved in [10] that the Brown measure is preserved by the Aluthge transform. Another reason is related with the iterated Aluthge transform. Let 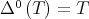 and
and 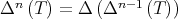 for every
for every 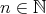 . In [16] Jung, Ko and Peacy raised the following conjecture:
. In [16] Jung, Ko and Peacy raised the following conjecture:
Conjecture 1. The sequence of iterates 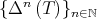 converges, for every matrix
converges, for every matrix 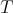 .
. 
This paper intends to give a brief survey on different properties of the Aluthge transform, making special emphasis on those results related with Conjecture 1, which was originally stated for operators on Hilbert spaces, and remains open for finite factors.
We begin the article with a historical summary that helps to explain the connection of the Aluthge transform with the invariant subspace problem and to describe some results that motivated and suggested that the conjecture might be true for operators on Hilbert spaces. Nevertheless, some couterexamples were found in this setting. We will expose one of them with some detail, which is particularly interesting because it shows an operator 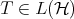 such that the sequence
such that the sequence 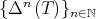 does not converge even in the weak operator topology.
does not converge even in the weak operator topology.
In the second part of the article, we summarize two works ([6] and [8]) which contain a proof of a positive answer to Conjecture 1 and some results on the regularity of the limit function. In these papers a new approach, based on techniques from dynamical systems, is introduced. The most important result used is the so-called stable manifold theorem for pseudo-hyperbolic systems (briefly described in Appendix A). Using this dynamical approach Conjecture 1 is firstly proved in [6], for every diagonalizable matrix. In the second article [8], using again a dynamical approach, combined this time with geometrical arguments in order to manage some technical difficulties, Conjecture 1 is completely solved. Although we shall not describe it, we also refer to the reader to the work by Huajun Huang and Tin-Yau Tam [13], where some related results are shown using different techniques
We also include a section with some open problems regarding the continuity of the limit function and the convergence for some particular operators acting on infinite dimensional space. Finally, we add two appendices where we give the precise statements of the stable manifold theorem, and describe the geometrical properties of similarity and unitary orbits of matrices.
Notation. Throughout this paper 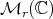 denotes the algebra of complex
denotes the algebra of complex  matrices,
matrices, 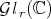 the group of all invertible elements of
the group of all invertible elements of 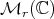 , and
, and 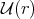 the group of unitary operators. We denote
the group of unitary operators. We denote 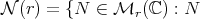 is normal
is normal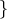 . If
. If 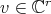 , we denote by
, we denote by 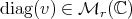 the diagonal matrix with
the diagonal matrix with  in its diagonal.
in its diagonal.
Given 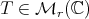 ,
, 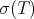 denotes the spectrum of
denotes the spectrum of 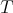 ,
, 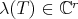 the vector of eigenvalues of
the vector of eigenvalues of 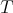 (counted with multiplicity), and
(counted with multiplicity), and 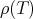 the spectral radius of
the spectral radius of 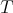 . We shall consider the space of matrices
. We shall consider the space of matrices 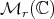 as a real Hilbert space with the inner product defined by
as a real Hilbert space with the inner product defined by 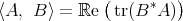 . The norm induced by this inner product is the Frobenius norm, that is denoted by
. The norm induced by this inner product is the Frobenius norm, that is denoted by  . For
. For 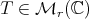 and
and 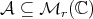 , by means of
, by means of 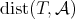 we denote the distance between them, with respect to the Frobenius norm. If
we denote the distance between them, with respect to the Frobenius norm. If 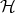 is a Hilbert space,
is a Hilbert space, 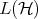 denotes the algebra of bounded operators on
denotes the algebra of bounded operators on 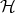 .
.
One of the most challenging problems in operator theory is the invariant subspace problem (ISP from now on). This problem states that every operator in 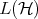 has a non trivial invariant subspace. It is a property that has every operator in a (complex) finite dimensional space because of the existence of eigenvectors. It is not difficult to see that the ISP also has a positive answer if the underlying Hilbert space is not separable. However, for separable Hilbert spaces, the problem is still open.
has a non trivial invariant subspace. It is a property that has every operator in a (complex) finite dimensional space because of the existence of eigenvectors. It is not difficult to see that the ISP also has a positive answer if the underlying Hilbert space is not separable. However, for separable Hilbert spaces, the problem is still open.
Although the ISP is very difficult to deal with, it was proved that some particular classes of operators have many non-trivial invariant subspaces. One of the most important is the class of normal operators. Indeed, using the functional calculus developed by von Neumann, it can be proved that a normal operator has as many invariant subspaces. This suggested the idea of isolating some properties of normal operators that could be related with the fact of having invariant subspaces. This motivated the definition of hyponormal and p-hyponormal operators. Recall that, given a Hilbert space 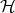 and
and ![p ∈ (0,1]](/img/revistas/ruma/v49n1/1a0462x.png) , and operator
, and operator 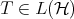 is called
is called 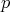 -hyponormal (
-hyponormal (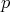 -hn) if
-hn) if
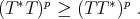
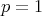 , i.e., if
, i.e., if 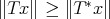 for every
for every 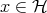 , then
, then 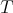 is simply called hyponormal (
is simply called hyponormal (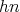 ).
). In 1987, Brown was able to prove that every hyponormal operator whose spectrum has non-empty interior has a non trivial invariant subspace. In 1990, Aluthge considered the possibility of extending this result to p-hyponormal operator and defined what is now called Aluthge transform. The first result that caught the attention on this transformation is summarized in the following statement:
Theorem 2.1 (Aluthge [1]). Let 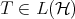 be p-hyponormal. Then
be p-hyponormal. Then
- If
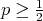 , then
, then 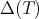 is hn,
is hn, - If
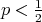 , then
, then 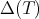 is
is  -hn,
-hn, - It holds that
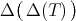 is hn.
is hn. 
Later on, Jung, Ko and Pearcy proved the next result that allowed to extend Brown's result to p-hyponormal operators:
Theorem 2.2 (Jung-Ko-Pearcy [15]). If 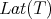 denotes the lattice of invariant subspaces of a given operator
denotes the lattice of invariant subspaces of a given operator 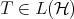 , then
, then 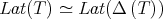 .
. 
This result led to the first version of Jung-Ko-Pearcy conjecture on the iterated Aluthge transform sequence: The sequence of iterates 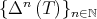 converges to a normal operator for every
converges to a normal operator for every 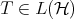 . As soon as they raised this conjecture, many results supporting this conjecture appeared. The following formula for the spectral radius due to Yamazaki (see also Wang [19]) was one of the most important:
. As soon as they raised this conjecture, many results supporting this conjecture appeared. The following formula for the spectral radius due to Yamazaki (see also Wang [19]) was one of the most important:
Theorem 2.3 (Yamazaki [21]). Given 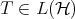 , then
, then 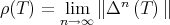 .
. 
However, after several positive partial results, some counterexamples appeared. One of the most interesting was found by Yanahida's [20]. Using a smart selection of weights, Yanahida defines a weighted shift operator whose sequence of iterated Aluthge transforms does not converge, even with respect to the weak operator topology! Let us briefly describe it: let 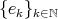 be the canonical basis of
be the canonical basis of 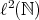 , and
, and 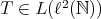 the weighted shift operator defined by
the weighted shift operator defined by 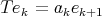 where
where
![{ 2n-1 2n a = a = 1 if k ∈ [4 + 1,4 ] . 0,k k e if k ∈ [0,4] or k ∈ [42n + 1,42n+1]](/img/revistas/ruma/v49n1/1a0496x.png)
Straightforward computations show that 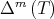 is also a weighted shift with weights:
is also a weighted shift with weights: 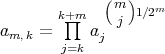 ,
, 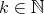 . Then, using some tricky estimates, it can be proved that the sequence
. Then, using some tricky estimates, it can be proved that the sequence 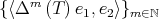 does not converge, which implies that the sequence of iterates does not converge in the weak operator topology. After these counterexamples, the conjecture was restricted to matrices and takes the form stated in the introduction. Although the ISP has no sense for matrices, several authors have kept working on the conjecture in this setting because of the following reasons:
does not converge, which implies that the sequence of iterates does not converge in the weak operator topology. After these counterexamples, the conjecture was restricted to matrices and takes the form stated in the introduction. Although the ISP has no sense for matrices, several authors have kept working on the conjecture in this setting because of the following reasons:
- Despite the positive computational evidence, it was surprisingly difficult. For example, very complicated computations were needed to prove the
 case (see [3]).
case (see [3]). - It would be considered as a first step in order to get a characterization of the operators
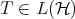 for which the sequence
for which the sequence 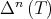 converges (see [14] and the references therein).
converges (see [14] and the references therein). - The conjecture remains open in the context of finite von Neumann factors (i.e. II
 factors), where the ISP has growing interest (see [10]).
factors), where the ISP has growing interest (see [10]).
We conclude this section with some results that have been very useful in order to study Conjecture 1. The first result is on the limit points of the iterated sequence. Note that, by Theorem 2.3, the sequence 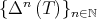 is bounded. Hence, if we restrict our attention to matrices, it has limit points. The following result, independently proved by Ando [2] and Jung, Ko and Pearcy [16], gives more details on them:
is bounded. Hence, if we restrict our attention to matrices, it has limit points. The following result, independently proved by Ando [2] and Jung, Ko and Pearcy [16], gives more details on them:
Proposition 2.4 (Ando, Jung-Ko-Pearcy). If 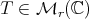 , the limit points of the sequence
, the limit points of the sequence 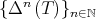 are normal. Moreover, if
are normal. Moreover, if  is a limit point, then
is a limit point, then 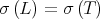 with the same algebraic multiplicity.
with the same algebraic multiplicity. 
Then, studying the Jordan structure of 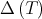 with respect with the Jordan structure of
with respect with the Jordan structure of 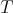 , the next reduction of the conjecture was proved in [5]:
, the next reduction of the conjecture was proved in [5]:
Proposition 2.5. If the Aluthge transform sequence converges for every invertible matrix (resp. invertible diagonalizable matrix), then it does for every matrix (resp. diagonalizable matrix). 
These two results motivate us to consider the dynamical approach that will be described in the next section. In the next proposition we summarize some easy properties of the Aluthge transform which are necessary to understand this approach.
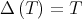 if and only if
if and only if 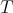 is normal.
is normal.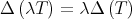 for every
for every 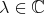 .
.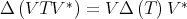 for every
for every 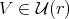 .
.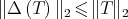 . In [5] it is proved that equality holds only if
. In [5] it is proved that equality holds only if 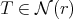 .
.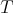 and
and 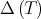 have the same spectrum and characteristic polynomial.
have the same spectrum and characteristic polynomial.- If
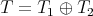 then
then 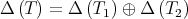 (orthogonal decompositions).
(orthogonal decompositions). 
We will also use systematically the following result on the regularity properties of 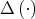 on
on 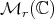 (see [10] or [6]):
(see [10] or [6]):
Theorem 2.7. The map  is continuous in
is continuous in 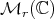 and it is of class
and it is of class 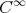 in
in 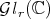 .
. 
Remark 2.8. The map  fails to be differentiable at several non invertible matrices.
fails to be differentiable at several non invertible matrices. 
Throughout this section, we fixe a matrix 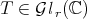 . We denote by
. We denote by 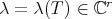 , the vector of eigenvalues of
, the vector of eigenvalues of 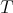 (counted with multiplicity). In the following subsections (3.1 and 3.2) we shall describe briefly the proof of Conjecture 1, following the articles [6], for the diagonalizable case, and [8], for the general case. Let
(counted with multiplicity). In the following subsections (3.1 and 3.2) we shall describe briefly the proof of Conjecture 1, following the articles [6], for the diagonalizable case, and [8], for the general case. Let 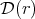 denote the set of diagonalizable matrices of
denote the set of diagonalizable matrices of 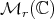 .
.
3.1. The diagonalizable case. As we mentioned in the previous section, Conjecture 1 can be reduced to the invertible case. Since 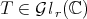 , it holds that
, it holds that 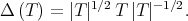 So,
So,
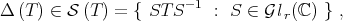
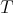 . This suggests that we can study the Aluthge transform restricted to
. This suggests that we can study the Aluthge transform restricted to 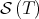 , which has a rich geometric structure. In particular, it is a riemannian submanifold of
, which has a rich geometric structure. In particular, it is a riemannian submanifold of 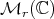 (see Appendix B for more details).
(see Appendix B for more details). If the Aluthge transform is studied restricted to the similarity orbit, the diagonalizable case has some advantages. Note that, if 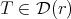 , then
, then 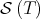 contains a compact submanifold of fixed points, and the sequence
contains a compact submanifold of fixed points, and the sequence 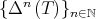 goes to this submanifold as
goes to this submanifold as 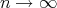 . In fact, since
. In fact, since 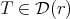 , then
, then 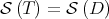 for some diagonal matrix
for some diagonal matrix 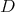 which has the same characteristic polynomial as
which has the same characteristic polynomial as 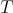 . The unitary orbit
. The unitary orbit 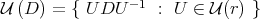 of
of 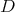 , is a compact submanifold of
, is a compact submanifold of 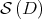 that consists of all normal matrices in
that consists of all normal matrices in 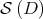 . By Proposition 2.4,
. By Proposition 2.4, 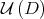 is fixed by the Aluthge transform and every limit points of the sequence
is fixed by the Aluthge transform and every limit points of the sequence 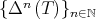 belongs to
belongs to 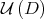 . In contrast, if
. In contrast, if 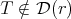 , then
, then 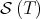 does not have fixed points, and the sequence of iterated Aluthge transforms still goes to
does not have fixed points, and the sequence of iterated Aluthge transforms still goes to 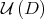 , which is not contained in
, which is not contained in 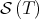 , but in its boundary. The key result in order to perform the dynamical approach to this problem is the following:
, but in its boundary. The key result in order to perform the dynamical approach to this problem is the following:
Theorem 3.1. Let  be an invertible diagonal matrix. For every
be an invertible diagonal matrix. For every 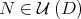 , there exists a subspace
, there exists a subspace 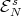 of the tangent space
of the tangent space 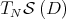 such that
such that
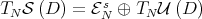 ;
;- Both,
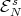 and
and 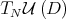 , are
, are 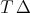 -invariant;
-invariant; 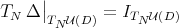 and
and 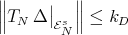 , where
, where 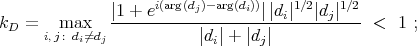
- If
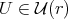 satisfies
satisfies 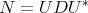 , then
, then 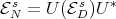 .
.
In particular, the map 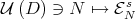 is smooth. This fact can be formulated in terms of the projections
is smooth. This fact can be formulated in terms of the projections 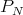 onto
onto 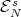 parallel to
parallel to 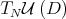 ,
, 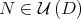 .
. 
The basic idea of the proof is that 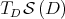 has an easy description in terms of coordinates (see Eq (4) in Appendix B). By a sequence of steps, one can describe
has an easy description in terms of coordinates (see Eq (4) in Appendix B). By a sequence of steps, one can describe 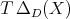 , for
, for 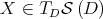 , as a Hadamard multiplication
, as a Hadamard multiplication  , for a matrix
, for a matrix 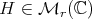 . These facts allow to find the subspace
. These facts allow to find the subspace 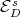 as well as bounds for
as well as bounds for 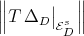 . The general case (
. The general case (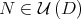 ) follows by unitary conjugations.
) follows by unitary conjugations.
The idea behind Theorem 3.1 is the following: when we iterate the derivative of the Aluthge transform on an element of the tangent space of 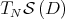 , for some
, for some 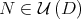 , the sequence of iterates converge exponentially to
, the sequence of iterates converge exponentially to 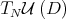 . This is the behavior that one expects the Aluthge transform (instead of its derivative) to have. In order to extrapolate this result to the non-linear setting, we used the stable manifold theorem, which is a well known result of dynamical systems introduced independently by Hadamard and Perron (see Appendix). Under the conditions which Theorem 3.1 assures for the Aluthge transform, this theorem states that there exists a local submanifold
. This is the behavior that one expects the Aluthge transform (instead of its derivative) to have. In order to extrapolate this result to the non-linear setting, we used the stable manifold theorem, which is a well known result of dynamical systems introduced independently by Hadamard and Perron (see Appendix). Under the conditions which Theorem 3.1 assures for the Aluthge transform, this theorem states that there exists a local submanifold 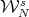 through each
through each 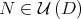 such that:
such that:
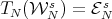 , in particular
, in particular 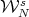 is transversal to
is transversal to 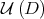 .
.- The submanifold
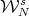 is characterized as the set of matrices near
is characterized as the set of matrices near 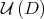 that converge exponentially to
that converge exponentially to 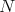 by the iteration of the Aluthge transform.
by the iteration of the Aluthge transform.
Since the problem of the convergence of the iterates of the Aluthge transform has a symmetry due to the invariance by unitary conjugation, the size of the submanifolds 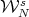 as well as the exponential rate of convergence is uniform along the unitary orbit
as well as the exponential rate of convergence is uniform along the unitary orbit 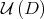 . These fact allow to prove, using arguments that involve the inverse mapping theorem, that the union of the submanifolds
. These fact allow to prove, using arguments that involve the inverse mapping theorem, that the union of the submanifolds 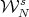 form an open neighborhood of
form an open neighborhood of 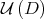 (see Fig. 1). Thus, as the sequence
(see Fig. 1). Thus, as the sequence 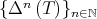 goes toward
goes toward 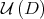 , for some
, for some 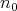 large enough the sequence of iterated Aluthge transforms enters into this open neighborhood, and, from that
large enough the sequence of iterated Aluthge transforms enters into this open neighborhood, and, from that 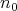 on, the sequence converges exponentially. Moreover, standard computations also show that the functional sequence
on, the sequence converges exponentially. Moreover, standard computations also show that the functional sequence 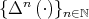 converges uniformly on
converges uniformly on 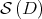 to a limit function, denoted by
to a limit function, denoted by  , which is a strong (continuous) retraction from
, which is a strong (continuous) retraction from 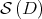 onto
onto 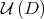 .
.

Figure 1: Union of stable manifolds
From the above mentioned facts, we can only deduce that  is continuous. However, better regularity properties can be proved. Let
is continuous. However, better regularity properties can be proved. Let 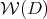 be an open neighborhood of
be an open neighborhood of 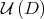 contained in the union of the submanifolds
contained in the union of the submanifolds 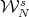 . As
. As 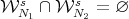 by the uniqueness of the limit, we can define a projection
by the uniqueness of the limit, we can define a projection 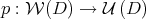 by:
by:
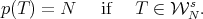
It is not difficult to prove that this map is of class 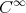 . Moreover, the limit function
. Moreover, the limit function 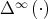 can be locally written as the composition of
can be locally written as the composition of 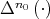 with
with 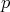 . Since both functions are
. Since both functions are 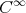 on
on 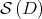 ,
,  is also of class
is also of class 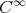 on
on 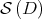 .
.
Similar arguments, which involve a more specific version of the stable manifold theorem, allow to prove that the limit function  is also
is also 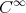 when it is restricted to the open dense set consisting of those matrices have all their eigenvalues different.
when it is restricted to the open dense set consisting of those matrices have all their eigenvalues different.
3.2. The nondiagonalizable case. The non-diagonalizable case is different, since the geometry context of the problem is more complicated. Let 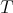 be non diagonalizable and
be non diagonalizable and 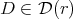 such that
such that 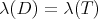 . Then
. Then 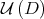 is contained in the boundary of
is contained in the boundary of 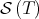 , which also contains the orbits of matrices with smaller Jordan forms than the Jordan form of
, which also contains the orbits of matrices with smaller Jordan forms than the Jordan form of 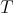 . The boundary of
. The boundary of 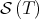 can be thought as a sort of lattice of boundaries. Therefore, in order to prove Conjecture 1, the problem is set in a more appropriate context so that both cases, diagonalizable and non-diagonalizable can be analyzed together. In this new approach, the Aluthge transform is thought as an endomorphism of the open set
can be thought as a sort of lattice of boundaries. Therefore, in order to prove Conjecture 1, the problem is set in a more appropriate context so that both cases, diagonalizable and non-diagonalizable can be analyzed together. In this new approach, the Aluthge transform is thought as an endomorphism of the open set 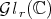 , and all the orbits mentioned before are considered, not as a manifold, but as the basin of attraction
, and all the orbits mentioned before are considered, not as a manifold, but as the basin of attraction 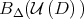 of
of 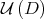 . By definition, in this case, the basin of attraction consists of those matrices
. By definition, in this case, the basin of attraction consists of those matrices 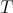 such that the sequence
such that the sequence 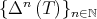 goes to
goes to 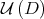 as
as  . Note that, by Proposition 2.4, the basin
. Note that, by Proposition 2.4, the basin 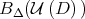 can also be characterized as the set of those matrices that have the same characteristic polynomial as
can also be characterized as the set of those matrices that have the same characteristic polynomial as 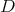 .
.
Since the Aluthge transform is thought as an endomorphism on the open set 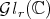 , the descomposition of Theorem 3.1 has to be extended to a decomposition of
, the descomposition of Theorem 3.1 has to be extended to a decomposition of 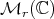 in
in 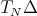 -invariant subspaces, for each
-invariant subspaces, for each 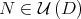 . This extension follows using that,
. This extension follows using that,
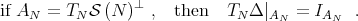 | (2) |
This fact can be proved by the standard properties of  , since
, since 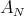 can be characterized as the commutant of
can be characterized as the commutant of 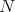 . Hence, just take the decomposition
. Hence, just take the decomposition 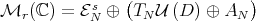 . The stable manifold theorem used in this context is a standard extension to
. The stable manifold theorem used in this context is a standard extension to 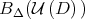 (see Remark A.4), and no differential structure is required in the basin. This theorem implies the existence of
(see Remark A.4), and no differential structure is required in the basin. This theorem implies the existence of  -invariant manifolds
-invariant manifolds 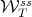 through each
through each 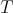 in the basin close enough to
in the basin close enough to 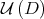 . One of the most important properties of these manifolds is that
. One of the most important properties of these manifolds is that
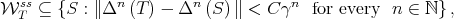 | (3) |
where  and
and  are constants that only depend on the distance among different eigenvalues of
are constants that only depend on the distance among different eigenvalues of 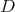 . Hence, if the sequence
. Hence, if the sequence 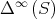 converges for some
converges for some 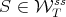 , then the same must happen for
, then the same must happen for 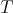 (with the same limit).
(with the same limit).
In the diagonalizable case, we have considered only the stable manifolds 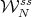 for points
for points 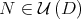 and it was proved that the union of these manifolds contains an open neighborhood of
and it was proved that the union of these manifolds contains an open neighborhood of 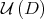 in
in 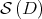 .
.
That approach fails in the general case, because the basin in not a manifold. So, a different idea is used. Inside the basin, there is a distinguished subset of matrices which satisfy Conjecture 1. This set, denoted by 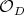 consists of those matrices, in the basin, with orthogonal spectral projections. Indeed, given
consists of those matrices, in the basin, with orthogonal spectral projections. Indeed, given 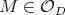 , let
, let 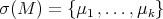 be the spectrum of
be the spectrum of 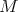 ,
, 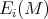 the spectral projection of
the spectral projection of 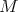 associated to each
associated to each 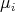 , and
, and 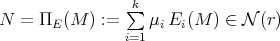 . Observe that
. Observe that 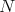 is uniquely determined (as a normal matrix) by its vector
is uniquely determined (as a normal matrix) by its vector 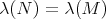 and the spectral projections
and the spectral projections 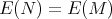 . But Proposition 2.4 assures that all the limit points of the sequence
. But Proposition 2.4 assures that all the limit points of the sequence 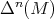 must be normal matrices with this vector, and item 6 of Proposition 2.6 assures that they must have the same spectral projections as
must be normal matrices with this vector, and item 6 of Proposition 2.6 assures that they must have the same spectral projections as 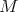 (because they are orthogonal). Hence
(because they are orthogonal). Hence 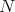 is the unique possible limit point, so that
is the unique possible limit point, so that 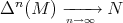 .
.
Having identified this set in the basin, the strategy is to prove that, for every 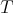 in the basin near
in the basin near 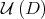 , the stable manifolds
, the stable manifolds 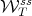 intersect the set
intersect the set 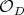 . This fact would be enough by the remark which follows Eq. (3), and the previous study about
. This fact would be enough by the remark which follows Eq. (3), and the previous study about 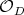 .
.
However, 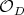 does not have a differential structure, which is an important technical obstacle. To avoid this problem, the stable manifolds
does not have a differential structure, which is an important technical obstacle. To avoid this problem, the stable manifolds 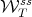 as well as
as well as 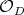 are projected onto the orbit
are projected onto the orbit 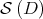 , using the above mentioned function
, using the above mentioned function 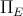 , which is smooth (see Kato's book [17]). Observe that
, which is smooth (see Kato's book [17]). Observe that 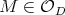 if and only if
if and only if 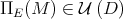 . On the other hand, the derivative of
. On the other hand, the derivative of 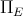 at
at 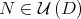 is an orthogonal projection with range equal to
is an orthogonal projection with range equal to 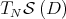 . By a continuity argument, this implies that, for every
. By a continuity argument, this implies that, for every 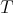 close enough to
close enough to 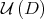 , the nullspace of the derivative of
, the nullspace of the derivative of 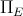 at the different points of
at the different points of 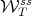 is transversal to the corresponding tangent spaces of
is transversal to the corresponding tangent spaces of 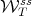 . This implies that the projection onto
. This implies that the projection onto 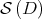 of the manifolds
of the manifolds 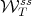 are submanifolds of
are submanifolds of 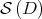 . Moreover, it can be proved that
. Moreover, it can be proved that 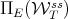 is "close" in some sense to
is "close" in some sense to 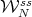 , where
, where 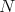 is certain normal operator close to
is certain normal operator close to 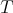 . Observe that
. Observe that 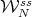 is one of the stable manifolds studied in the diagonalizable case. Therefore
is one of the stable manifolds studied in the diagonalizable case. Therefore 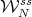 intersects transversally
intersects transversally 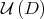 . These facts imply, by some well known results about transversal intersections (see [11]), that
. These facts imply, by some well known results about transversal intersections (see [11]), that 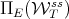 also intersects
also intersects 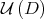 . Finnaly, if
. Finnaly, if 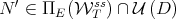 , then
, then 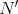 is the projection of a matrix
is the projection of a matrix 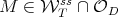 (see Fig. 2).
(see Fig. 2).
Figure 2: The projection argument
Similar (but slightly more complicated) arguments show that the limit map 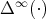 is continuous on
is continuous on 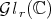 . Nevertheless, the previous techniques are not useful to study continuity outside of
. Nevertheless, the previous techniques are not useful to study continuity outside of 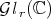 because the map
because the map  fails to be differentiable there.
fails to be differentiable there.
Rate of convergence. In [6] it was proved that, if 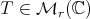 is diagonalizable, then after some iterations the rate of convergence of the sequence
is diagonalizable, then after some iterations the rate of convergence of the sequence 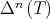 becomes exponential. More precisely, for some
becomes exponential. More precisely, for some 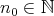 and every
and every  , there exist
, there exist 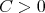 and
and 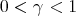 such that
such that 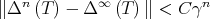 . This exponential rate depends on the spectrum of
. This exponential rate depends on the spectrum of 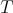 . Actually, if
. Actually, if 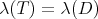 for some diagonal matrix
for some diagonal matrix 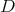 , then
, then 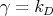 , the constant which appears in Theorem 3.1. Using the formula for
, the constant which appears in Theorem 3.1. Using the formula for 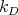 , one can see that it is closer to
, one can see that it is closer to  (so that the rate of convergence becomes slower) if the different eigenvalues are closer one to each other.
(so that the rate of convergence becomes slower) if the different eigenvalues are closer one to each other.
These facts are no longer true if 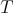 is not diagonalizable, since the rate of convergence for such a
is not diagonalizable, since the rate of convergence for such a 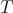 depends on the rate of convergence for some
depends on the rate of convergence for some 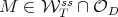 , which can be much slower (and not exponential). Observe that the proof of the convergence of the sequence
, which can be much slower (and not exponential). Observe that the proof of the convergence of the sequence 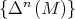 , does not study the rate of convergence. It only shows that there exists an unique possible limit point for the sequence.
, does not study the rate of convergence. It only shows that there exists an unique possible limit point for the sequence.
Nevertheless, if one denotes by 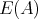 the system of spectral projections of a matrix
the system of spectral projections of a matrix 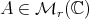 associated to its different eigenvalues, the previous approach shows that
associated to its different eigenvalues, the previous approach shows that 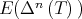 converges to
converges to 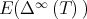 exponentially, because
exponentially, because 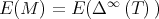 . As in the case of diagonalizable matrices the rate of convergence of the spectral projections depends on the spectrum of
. As in the case of diagonalizable matrices the rate of convergence of the spectral projections depends on the spectrum of 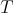 , which agree with the spectrum of
, which agree with the spectrum of 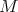 . Note that the spectrum of
. Note that the spectrum of 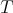 and the spectral projections of
and the spectral projections of 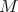 completely characterize the limit
completely characterize the limit 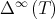 . Indeed, if
. Indeed, if 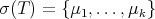 , then
, then
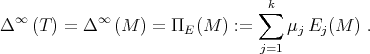
 -Aluthge transform. Given
-Aluthge transform. Given 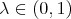 and a matrix
and a matrix 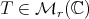 whose polar decomposition is
whose polar decomposition is 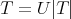 , the
, the 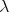 -Aluthge transform of
-Aluthge transform of 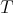 is defined by
is defined by
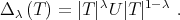
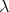 -Aluthge transform for every
-Aluthge transform for every 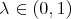 , with almost the same proofs. Indeed, note that the basic results about Aluthge transform used throughout sections 3 and 4 are Theorem 3.1 and those stated in subsection 2.1. All these results were extended to every
, with almost the same proofs. Indeed, note that the basic results about Aluthge transform used throughout sections 3 and 4 are Theorem 3.1 and those stated in subsection 2.1. All these results were extended to every 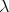 -Aluthge transform (see [5] and [7]). The unique difference is that the constant
-Aluthge transform (see [5] and [7]). The unique difference is that the constant 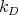 of Theorem 3.1 now depends on
of Theorem 3.1 now depends on 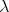 (see Theorem 3.2.1 of [7]). Anyway, the new constants are still lower than one for every
(see Theorem 3.2.1 of [7]). Anyway, the new constants are still lower than one for every 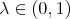 . Moreover, they are uniformly lower than one on compact subsets of
. Moreover, they are uniformly lower than one on compact subsets of 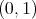 .
. Another result which depends particularly on the Aluthge transform is Eq. (2), and the extended decomposition 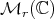 . Nevertheless, it is easy to see that both results are still true for every
. Nevertheless, it is easy to see that both results are still true for every 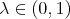 . On the other hand, the proof of the continuity of the map
. On the other hand, the proof of the continuity of the map 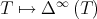 on
on 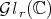 uses the same facts about the Aluthge transform. So that, it also remains true for
uses the same facts about the Aluthge transform. So that, it also remains true for 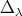 , for every
, for every 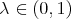 . We resume all these remarks in the following statement:
. We resume all these remarks in the following statement:
Theorem 3.2. For every 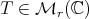 and
and 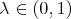 , the sequence
, the sequence 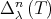 converges to a normal matrix
converges to a normal matrix 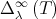 . The map
. The map 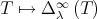 is continuous on
is continuous on 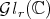 .
. 
3.3. Some open problems. Concerning the convergence of iterated Aluthge sequences, the following problems are of great interest, and they still remain unsolved:
- The continuity of the map
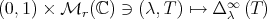 . Using the techniques mentioned in this survey, it can be proved that this map is continuous in
. Using the techniques mentioned in this survey, it can be proved that this map is continuous in 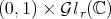 . But, as
. But, as 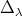 is not globally
is not globally 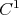 outside
outside 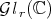 , new methods should be developed in order to prove the continuity of
, new methods should be developed in order to prove the continuity of 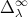 in
in 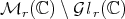 . We remark that this fact is supported by computational evidence.
. We remark that this fact is supported by computational evidence. - If
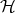 is a separable Hilbert space, to get a characterization of those
is a separable Hilbert space, to get a characterization of those 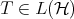 such that the sequence
such that the sequence 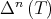 converges. The first step might be to study compact operators, using the convergence for matrices.
converges. The first step might be to study compact operators, using the convergence for matrices. - To prove that, if
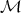 is a II
is a II factor (i.e. an infinite dimensional finite von Neumann algebra with trivial center), then the sequence
factor (i.e. an infinite dimensional finite von Neumann algebra with trivial center), then the sequence  converges to a normal element of
converges to a normal element of  , for every
, for every 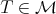 . This fact might be very important in order to get an affirmative answer of the ISP for these algebras, a problem which has great interest in operator theory and remains open. As in the case of compact operators, the finite dimensional case could be useful to prove Conjecture 1 in this setting, because there exist good finite dimensional methods of approximation for these particular class of von Neumann algebras.
. This fact might be very important in order to get an affirmative answer of the ISP for these algebras, a problem which has great interest in operator theory and remains open. As in the case of compact operators, the finite dimensional case could be useful to prove Conjecture 1 in this setting, because there exist good finite dimensional methods of approximation for these particular class of von Neumann algebras.
Appendix A. The stable manifold theorem
As a general reference of this theory, we refer to the books [12] and [18]. Let 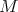 be a smooth Riemann manifold and
be a smooth Riemann manifold and 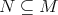 a submanifold (not necessarily compact). Throughout this subsection
a submanifold (not necessarily compact). Throughout this subsection 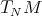 denotes the tangent bundle of
denotes the tangent bundle of 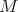 restricted to
restricted to 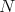 .
.
Definition A.1. A 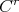 pre-lamination indexed by
pre-lamination indexed by 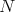 is a continuous choice of a
is a continuous choice of a 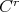 embedded disc
embedded disc 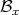 through each
through each 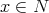 . Continuity means that
. Continuity means that 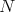 is covered by open sets
is covered by open sets  in which
in which  is given by
is given by 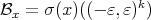 where
where 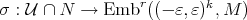 is a continuous section. Note that
is a continuous section. Note that 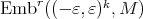 is a
is a 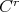 fiber bundle over
fiber bundle over 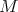 whose projection is
whose projection is 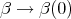 . Thus
. Thus 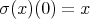 . If the sections mentioned above are
. If the sections mentioned above are 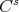 ,
, 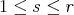 , we say that the
, we say that the 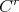 pre-lamination is of class
pre-lamination is of class 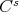 . A pre-lamination is called self coherent if the interiors of each pair of its discs meet in a relatively open subset of each one.
. A pre-lamination is called self coherent if the interiors of each pair of its discs meet in a relatively open subset of each one. 
Theorem A.2 (Stable manifold theorem). Let 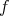 be a
be a 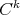 endomorphism of
endomorphism of 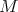 and let
and let 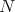 be a compact subset of
be a compact subset of 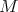 consisting of fixed points of
consisting of fixed points of 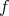 . Assume that there exist two continuous subbundles of
. Assume that there exist two continuous subbundles of 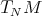 , denoted by
, denoted by 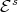 and
and 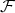 , such that, for every
, such that, for every 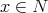 ,
,
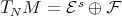 .
.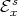 is
is 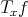 -invariant.
-invariant.- There exists
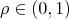 such that
such that 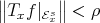 .
.
Then, there is a continuous, 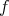 -invariant and self coherent
-invariant and self coherent 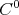 -pre-lamination
-pre-lamination 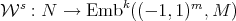 (endowed with the
(endowed with the 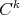 -topology) such that, for every
-topology) such that, for every 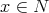 ,
,
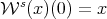 ,
, is tangent to
is tangent to 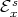 ,
,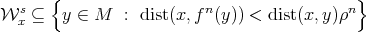 .
. 
Remark A.3. As 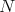 is compact and
is compact and 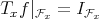 , using the so-called
, using the so-called 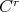 -prelamination theorem, it can be proved that the prelamination
-prelamination theorem, it can be proved that the prelamination 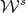 is of class
is of class 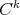 .
. 
Remark A.4. Under the hypothesis of Theorem A.2, recall that the basin of attraction of 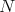 is the set
is the set  . Also recall that, for every
. Also recall that, for every 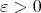 , a local basin of
, a local basin of 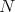 is the set
is the set
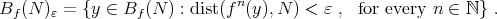
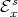 and
and 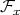 of Theorem A.2 can be extended to a local basin
of Theorem A.2 can be extended to a local basin 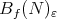 , for some
, for some 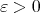 small enough, so that the extended distribution of subspaces
small enough, so that the extended distribution of subspaces 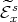 and
and 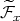 satisfy:
satisfy: 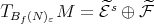 .
.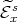 is
is 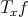 -invariant in the sense that
-invariant in the sense that 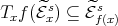 .
.- There exists
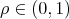 such that
such that 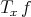 restricted to
restricted to 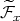 expand it by a factor greater than
expand it by a factor greater than 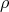 , and
, and 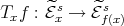 has norm lower than
has norm lower than 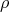 .
.
In this case, an extended version of the stable manifold theorem assures that there is a 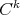 -pre-lamination
-pre-lamination  which is continuous,
which is continuous, 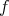 -invariant, self coherent and satisfies for every
-invariant, self coherent and satisfies for every 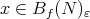 (1) and (2) of Theorem A.2 and the following modified version of (3):
(1) and (2) of Theorem A.2 and the following modified version of (3): 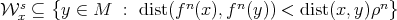 .
. 
Appendix B. Similarity orbit of a diagonal matrix
Let 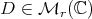 be diagonal, with
be diagonal, with  ,
, 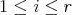 . By means of
. By means of 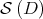 we denote the similarity orbit of
we denote the similarity orbit of 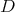 , i.e.,
, i.e., 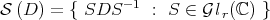 . On the other hand,
. On the other hand, 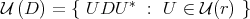 denotes the unitary orbit of
denotes the unitary orbit of 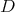 . We denote by
. We denote by 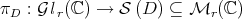 the
the  map defined by
map defined by 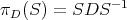 . With the same name we note its restriction to the unitary group:
. With the same name we note its restriction to the unitary group: 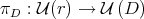 .
.
Proposition B.1 (See [9] or [4]). The similarity orbit 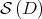 is a
is a 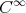 submanifold of
submanifold of 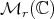 , and the projection
, and the projection 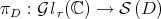 becomes a submersion. Moreover,
becomes a submersion. Moreover, 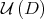 is a compact submanifold of
is a compact submanifold of 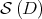 , which consists of the normal elements of
, which consists of the normal elements of 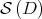 , and
, and 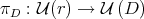 is a submersion.
is a submersion. 
As a consequence of this result, it is not difficult to see that:
TD 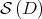 = {X ∈ = {X ∈  : Xij = 0 for every (i,j) such that di = dj.} : Xij = 0 for every (i,j) such that di = dj.} | (4) |
Straightforward computations also show that, 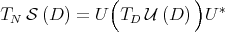 provided that
provided that 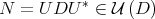 . We consider on
. We consider on 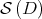 (and on
(and on 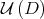 ) the Riemannian structure inherited from
) the Riemannian structure inherited from 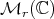 (using the usual inner product on their tangent spaces). For
(using the usual inner product on their tangent spaces). For 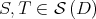 , we denote by
, we denote by 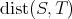 the Riemannian distance between
the Riemannian distance between 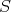 and
and 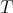 (in
(in 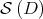 ). Observe that, for every
). Observe that, for every 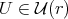 , one has that
, one has that 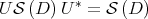 and the map
and the map 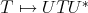 is isometric, on
is isometric, on 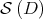 , with respect to the Riemannian metric as well as with respect to the
, with respect to the Riemannian metric as well as with respect to the  metric of
metric of 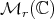 .
.
[1] A. Aluthge, On p-hyponormal operators for 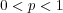 , Integral Equations Operator Theory 13 (1990), 307-315. [ Links ]
, Integral Equations Operator Theory 13 (1990), 307-315. [ Links ]
[2] T. Ando, Aluthge Transforms and the Convex Hull of the Eigenvalues of a Matrix, Linear Multilinear Algebra 52 (2004), 281-292. [ Links ]
[3] T. Ando and T. Yamazaki, The iterated Aluthge transforms of a 2-by-2 matrix converge, Linear Algebra Appl. 375 (2003), 299-309. [ Links ]
[4] E. Andruchow and D. Stojanoff, Differentiable structure of similarity orbits, J. Operator Theory 21 (1989), 349-366. [ Links ]
[5] J. Antezana, P. Massey and D. Stojanoff, 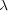 -Aluthge transforms and Schatten ideals, Linear Algebra Appl. 405 (2005), 177-199. [ Links ]
-Aluthge transforms and Schatten ideals, Linear Algebra Appl. 405 (2005), 177-199. [ Links ]
[6] J. Antezana, E. Pujals and D. Stojanoff, Convergence of iterated Aluthge transform sequence for diagonalizable matrices, Advances in Mathematics 216 (2007) 255-278. [ Links ]
[7] J. Antezana, E. Pujals and D. Stojanoff, Convergence of iterated Aluthge transform sequence for diagonalizable matrices II - 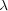 -Aluthge transform, preprint available in arXiv. [ Links ]
-Aluthge transform, preprint available in arXiv. [ Links ]
[8] J. Antezana, E. Pujals and D. Stojanoff, The iterated Aluthge transforms of a matrix converge, preprint available in arXiv. [ Links ]
[9] G. Corach, H. Porta and L. Recht, The geometry of spaces of projections in C*-algebras, Adv. Math. 101 (1993), 59-77. [ Links ]
[10] K. Dykema and H. Schultz, On Aluthge Transforms: continuity properties and Brown measure, preprint available in arXiv. [ Links ]
[11] M. W. Hirsch, Differential topology, Graduate Texts in Mathematics 33, Springer-Verlag, New York 1994. [ Links ]
[12] M. W. Hirsch, C. C. Pugh, and M. Shub, Invariant manifolds, Lecture Notes in Mathematics, Vol. 583. Springer-Verlag, Berlin-New York, 1977. [ Links ]
[13] Huajun Huang and Tin-Yau Tam, On the Convergence of the Aluthge sequence, Oper. Matrices 1 (2007), no. 1, 121-141. [ Links ]
[14] M. Ito, T. Yamazaki and M. Yanagida, On the polar decomposition of the Aluthge transformation and related results, J. Operator Theory 51 (2004), no. 2, 303-319. [ Links ]
[15] I. Jung, E. Ko, and C. Pearcy, Aluthge transform of operators, Integral Equations Operator Theory 37 (2000), 437-448. [ Links ]
[16] I. Jung, E. Ko, and C. Pearcy, The Iterated Aluthge Transform of an operator, Integral Equations Operator Theory 45 (2003), 375-387. [ Links ]
[17] T. Kato, Perturbation theory for linear operators. Reprint of the 1980 edition. Classics in Mathematics. Springer-Verlag, Berlin, 1995. [ Links ]
[18] M. Shub, Global Stability of Dynamical Systems, Springer, 1986. [ Links ]
[19] D. Wang, Heinz and McIntosh inequalities, Aluthge Transformation and the spectral radius, Mathematical Inequalities and Applications Vol.6 No.1 (2003), 121-124. [ Links ]
[20] M. Yanagida , On convergence to n-th Aluthge transformation, unpublished, 2001. [ Links ]
[21] T. Yamazaki, An expression of the spectral radius via Aluthge tranformation, Proc. Amer. Math. Soc. 130 (2002), 1131-1137. [ Links ]
Jorge Antezana
Departamento de Matemática,
Facultad de Ciencias Exactas,
Universidad Nacional de La Plata,
Calle 50 y 115, La Plata, Argentina
and IAM-CONICET
antezana@mate.unlp.edu.ar
Enrique R. Pujals
Instituto Nacional de Matemática Pura y Aplicada (IMPA),
Rio de Janeiro, Brasil
enrique@impa.br
Demetrio Stojanoff
Departamento de Matemática,
Facultad de Ciencias Exactas,
Universidad Nacional de La Plata,
Calle 50 y 115, La Plata, Argentina
and IAM-CONICET
demetrio@mate.unlp.edu.ar
Recibido: 10 de abril de 2008
Aceptado: 22 de abril de 2008













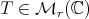 . Then:
. Then:
