Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.49 n.1 Bahía Blanca ene./jun. 2008
The 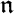 -homology of representations
-homology of representations
Tim Bratten
Abstract. The 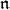 -homology groups of a
-homology groups of a 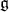 -module provide a natural and fruitful extension of the concept of highest weight to the representation theory of a noncompact reductive Lie group. In this article we give an introduction to the
-module provide a natural and fruitful extension of the concept of highest weight to the representation theory of a noncompact reductive Lie group. In this article we give an introduction to the 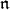 -homology groups and a survey of some developments, with a particular emphasis on results pertaining to the problem of caculating
-homology groups and a survey of some developments, with a particular emphasis on results pertaining to the problem of caculating 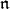 -homology groups.
-homology groups.
The concept of a highest weight and its use to classify irreducible representations of compact Lie groups can traced back nearly a century, to seminal work by E. Cartan and H. Weyl. For a compact, connected Lie group, the highest weight theory gives a tight parametrization of irreducible representations in terms of specific invariants associated to the group. If one tries to extend this concept to the representation theory of a noncompact, real reductive group one immediately encounters two problems. On the one hand, in the noncompact case, it turns out there are several conjugacy classes of complex Borel subalgebras, and what might be called a highest weight depends on the choice of a conjugacy class. On the other hand, it is quite common that what should be called a highest weight turns out to be zero for every choice of Borel subalgebra. This means, in the traditional sense, the highest weight does not exist for a great majority of irreducible representations.
Although there is no way to avoid the first problem, representation theorists have confronted the second problem by considering the highest weight to be a functorial construction and studying the related derived functors. This has proved to be especially fruitful, producing a strong and useful family of invariants associated to a representation. In this article we give a brief introduction to the 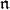 -homology (and
-homology (and 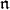 -cohomology) groups, followed by a survey of some results, focusing on developments related to the problem of calculating the
-cohomology) groups, followed by a survey of some results, focusing on developments related to the problem of calculating the 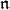 -homology of representations.
-homology of representations.
The author would like to take this opportunity to thank the organizers of the 2007 meeting of the UMA for giving him an opportunity to present some results in the form of a conference and for asking him to submit this article. He would also like to acknowledge the help and encouragement he has received from Jorge Vargas. This article is dedicated to the memory of Mischa Cotlar, with a special recognition to Dr. Cotlar's role as advisor and mentor to the late José Pererya.
In this section we introduce the 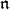 -homology and
-homology and 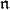 -cohomology of
-cohomology of 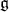 -modules (for more details see [10]).
-modules (for more details see [10]).
Let 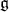 be a complex reductive Lie algebra. By definition, a Borel subalgebra of
be a complex reductive Lie algebra. By definition, a Borel subalgebra of 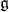 is a maximal solvable subalgebra and a parabolic subalgebra of
is a maximal solvable subalgebra and a parabolic subalgebra of 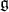 is a subalgebra that contains a Borel subalgebra. If
is a subalgebra that contains a Borel subalgebra. If 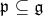 is a parabolic subalgebra then the nilradical
is a parabolic subalgebra then the nilradical 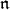 of
of 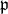 is the largest solvable ideal in
is the largest solvable ideal in ![[𝔭,𝔭]](/img/revistas/ruma/v49n1/1a1119x.png) . A Levi factor is a complementary subalgebra to
. A Levi factor is a complementary subalgebra to 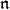 in
in 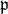 . One knows that Levi factors exist and that they are exactly the subalgebras which are maximal with respect to being reductive in
. One knows that Levi factors exist and that they are exactly the subalgebras which are maximal with respect to being reductive in 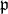 . When
. When  is a Levi factor than
is a Levi factor than
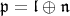 |
is called a Levi decomposition.
Fix a parabolic subalgebra 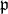 with nilradical
with nilradical 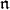 and Levi factor
and Levi factor  . Let
. Let 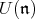 denote the enveloping algebra of
denote the enveloping algebra of 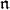 and let
and let  be the 1-dimensional trivial module. If
be the 1-dimensional trivial module. If 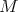 is a
is a 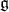 -module then the zero
-module then the zero 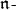 homology of
homology of 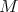 is the
is the  -module
-module
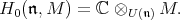 |
This  -module is sometimes referred to as the space of coinvariants, although it clearly depends on the choice of parabolic subalgebra. The definition of the zero homology determines a right exact functor from the category of
-module is sometimes referred to as the space of coinvariants, although it clearly depends on the choice of parabolic subalgebra. The definition of the zero homology determines a right exact functor from the category of 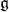 -modules to the category of
-modules to the category of  -modules. The
-modules. The 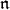 -homology groups of
-homology groups of 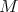 are the
are the  -modules obtained as the corresponding derived functors. There is a standard complex for calculating these homology groups, defined as follows. The right standard resolution of
-modules obtained as the corresponding derived functors. There is a standard complex for calculating these homology groups, defined as follows. The right standard resolution of  is the complex of free right
is the complex of free right 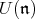 -modules given by
-modules given by
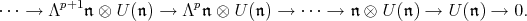 |
Applying the functor
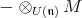 |
to the standard resolution we obtain a complex
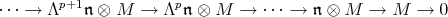 |
of left  -modules called the standard
-modules called the standard 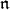 -homology complex. Here
-homology complex. Here  acts via the tensor product of the adjoint action on
acts via the tensor product of the adjoint action on 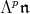 with the given action on
with the given action on 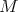 . Since
. Since 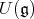 is a free
is a free 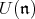 -module, a routine homological argument identifies the pth homology of the standard complex with the pth
-module, a routine homological argument identifies the pth homology of the standard complex with the pth 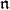 -homology group
-homology group
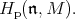 |
One can prove that the induced  -action on the homology groups of the standard complex is the correct one.
-action on the homology groups of the standard complex is the correct one.
The zero 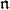 -cohomology of a
-cohomology of a 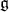 -module
-module 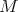 is the
is the  -module
-module
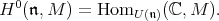 |
This  -module is sometimes referred to as the space of invariants, and also clearly depends on the choice of parabolic subalgebra The definition of the zero cohomology determines a left exact functor from the category of
-module is sometimes referred to as the space of invariants, and also clearly depends on the choice of parabolic subalgebra The definition of the zero cohomology determines a left exact functor from the category of 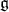 -modules to the category of
-modules to the category of  -modules. By definition, the
-modules. By definition, the 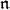 -cohomology groups of
-cohomology groups of 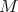 are the
are the  -modules obtained as the corresponding derived functors. These
-modules obtained as the corresponding derived functors. These  -modules can be calculated by applying the functor
-modules can be calculated by applying the functor
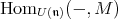 |
to the standard resolution of  , this time by free left
, this time by free left 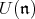 -modules. In a natural way, one obtains a complex of
-modules. In a natural way, one obtains a complex of  -modules and the pth cohomology of this complex realizes the pth
-modules and the pth cohomology of this complex realizes the pth 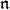 -cohomology group
-cohomology group
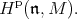 |
It turns out that the structure of the 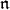 -cohomology is determined by the structure of the
-cohomology is determined by the structure of the 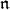 -homology, in a simple way . Thus, it is often a matter of convenience whether one works with homology groups or cohomology groups. In this article, we will focus on results framed in terms of homology. The following proposition, whose proof is established by an analysis of standard complexes, can be used to translate results about
-homology, in a simple way . Thus, it is often a matter of convenience whether one works with homology groups or cohomology groups. In this article, we will focus on results framed in terms of homology. The following proposition, whose proof is established by an analysis of standard complexes, can be used to translate results about 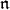 -homology into results about
-homology into results about 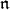 -cohomology [9, Section 2].
-cohomology [9, Section 2].
Proposition 2.1. Suppose 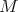 is a
is a 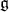 -module. Let
-module. Let 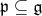 be a parabolic subalgebra with nilradical
be a parabolic subalgebra with nilradical 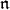 and Levi factor
and Levi factor  . Let d denote the dimension of
. Let d denote the dimension of 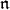 . Then there are natural isomorphisms
. Then there are natural isomorphisms
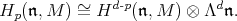 |
3. Representations of linear reductive Lie groups
In this section we review some classical results about the representation theory of reductive Lie groups (for details see [16]) and introduce the canonical globalizations.
For simplicity we work with a class of reductive Lie groups we call linear, although there is no problem working in the more general context of a reductive group of Harish-Chandra class. In particular, we assume the following setup. 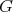 will denote a connected, complex reductive group. This means
will denote a connected, complex reductive group. This means 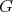 is a connected, complex Lie group with the property that the maximal compact subgroups are real forms of
is a connected, complex Lie group with the property that the maximal compact subgroups are real forms of 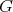 . The group
. The group  will denote a real form of
will denote a real form of 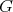 and is assumed to have finitely many connected components. We call
and is assumed to have finitely many connected components. We call  a linear reductive Lie group. The Lie algebras of
a linear reductive Lie group. The Lie algebras of 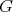 and
and  will be denoted
will be denoted 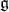 and
and 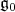 , respectively. For the remainder of this article we fix a maximal compact subgroup
, respectively. For the remainder of this article we fix a maximal compact subgroup 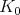 of
of  and let
and let  be the complexification of
be the complexification of 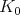 . In general, we write
. In general, we write 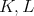 etc. to indicate complex subgroups of
etc. to indicate complex subgroups of 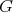 and denote the corresponding Lie algebras by
and denote the corresponding Lie algebras by 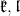 etc. Subgroups of
etc. Subgroups of  will be denoted by
will be denoted by 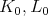 etc. with the corresponding real Lie algebras written as
etc. with the corresponding real Lie algebras written as 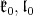 etc.
etc.
A representation of  will mean a continuous linear action of
will mean a continuous linear action of  in a complete, locally convex topological vector space. When we speak of irreducible or finite length representations, the corresponding definitions should be framed in terms of invariant closed subspaces. A vector
in a complete, locally convex topological vector space. When we speak of irreducible or finite length representations, the corresponding definitions should be framed in terms of invariant closed subspaces. A vector  in a representation
in a representation 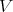 is called smooth when
is called smooth when
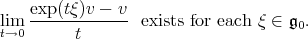 |
In order to define 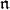 -homology groups, we will be primarily interested in smooth representations. These are representations where every vector is smooth. In a natural way a smooth representation carries a compatible
-homology groups, we will be primarily interested in smooth representations. These are representations where every vector is smooth. In a natural way a smooth representation carries a compatible 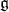 -action. For a compact Lie group one can show that a finite length representation is finite-dimensional and therefore smooth.
-action. For a compact Lie group one can show that a finite length representation is finite-dimensional and therefore smooth.
We recall some basic results about the infinite-dimensional representations of reductive groups. In the 1950s, Harish-Chandra proved that an irreducible unitary representation 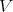 has the property that each irreducible
has the property that each irreducible 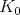 -submodule has finite multiplicity in
-submodule has finite multiplicity in 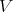 . This led him to define and study admissible representations. By definition, this means each irreducible
. This led him to define and study admissible representations. By definition, this means each irreducible 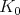 -submodule has finite multiplicity. Harish-Chandra then considered the subspace of
-submodule has finite multiplicity. Harish-Chandra then considered the subspace of 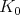 -finite vectors. By definition, a vector
-finite vectors. By definition, a vector  in a representation is called
in a representation is called 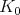 -finite if the span of the
-finite if the span of the 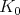 -orbit of
-orbit of  is finite-dimensional. Although the subspace of
is finite-dimensional. Although the subspace of 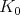 -finite vectors is not
-finite vectors is not  -invariant, Harish-Chandra proved that
-invariant, Harish-Chandra proved that 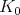 -finite vectors are smooth, and thus form a
-finite vectors are smooth, and thus form a 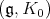 -module called the underlying Harish-Chandra module.
-module called the underlying Harish-Chandra module.
On the other hand, it is possible to define abstractly the concept of a Harish-Chandra module. This is a 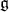 -module equipped with a compatible, locally finite
-module equipped with a compatible, locally finite 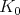 -action. Harish-Chandra proved that an irreducible Harish-Chandra module appears as the underlying
-action. Harish-Chandra proved that an irreducible Harish-Chandra module appears as the underlying 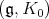 -module of
-module of 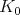 -finite vectors in an irreducible admissible Banach space representation for
-finite vectors in an irreducible admissible Banach space representation for  and W. Casselman proved that the same holds for any finite-length Harish-Chandra module. By now we know more. In particular, given a Harish-Chandra module
and W. Casselman proved that the same holds for any finite-length Harish-Chandra module. By now we know more. In particular, given a Harish-Chandra module 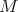 we define a globalization
we define a globalization 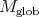 of
of 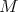 to be an admissible representation for
to be an admissible representation for  whose underlying Harish-Chandra is
whose underlying Harish-Chandra is 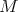 . We assume our Harish-Chandra modules have finite-length. Then we can assert that several canonical and functorial globalizations exist on the category of Harish-Chandra modules. These are: the smooth globalization of Casselman and Wallach [5], its dual (called: the distribution globalization), Schmid's minimal globalization [14] and its dual (the maximal globalization). All four globalizations are smooth. We will let
. We assume our Harish-Chandra modules have finite-length. Then we can assert that several canonical and functorial globalizations exist on the category of Harish-Chandra modules. These are: the smooth globalization of Casselman and Wallach [5], its dual (called: the distribution globalization), Schmid's minimal globalization [14] and its dual (the maximal globalization). All four globalizations are smooth. We will let 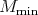 ,
, 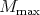 ,
, 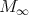 and
and 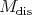 denote respectively, the minimal, the maximal, the smooth and the distribution globalizations of a Harish-Chandra module
denote respectively, the minimal, the maximal, the smooth and the distribution globalizations of a Harish-Chandra module 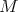 . If
. If 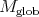 denotes a Banach globalization of
denotes a Banach globalization of 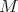 , then there is a natural chain of inclusions
, then there is a natural chain of inclusions
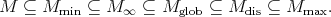 |
In this chain the minimal globalization is known to coincide with the analytic vectors in 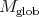 while
while 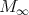 coincides with the smooth vectors in
coincides with the smooth vectors in 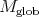 . In particular, one knows that a finite-length admissible Banach space representation for
. In particular, one knows that a finite-length admissible Banach space representation for  is smooth if and only if it is finite dimensional. Later in this article we will review various results, often called comparison theorems, relating the
is smooth if and only if it is finite dimensional. Later in this article we will review various results, often called comparison theorems, relating the 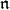 -homologies of a Harish-Chandra module to the
-homologies of a Harish-Chandra module to the 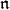 -homologies of a canonical globalization.
-homologies of a canonical globalization.
In this section we recall some structure theory and an important technical result about the decomposition of 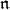 -homology groups for certain
-homology groups for certain 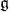 -modules, giving special emphasis on the case of a Borel subalgebra. Recall that a Cartan subalgebra
-modules, giving special emphasis on the case of a Borel subalgebra. Recall that a Cartan subalgebra 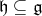 is a maximal abelian subalgebra whose elements are semisimple under the adjoint representation of
is a maximal abelian subalgebra whose elements are semisimple under the adjoint representation of 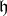 in
in 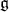 . A nonzero eigenvalue
. A nonzero eigenvalue 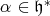 for the adjoint representation is called a root.
for the adjoint representation is called a root.  will denote the set of roots. Thus
will denote the set of roots. Thus
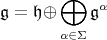 |
where 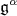 is the eigenspace corresponding to root
is the eigenspace corresponding to root 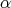 . One knows that
. One knows that 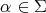 if and only if
if and only if 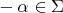 . If
. If 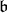 is a Borel subalgebra of
is a Borel subalgebra of 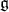 containing
containing 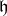 then the roots of
then the roots of 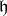 in
in 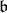 define a subset
define a subset 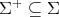 called the corresponding set of positive roots. When the sum of two positive roots is a root, then that sum is positive. One also knows that
called the corresponding set of positive roots. When the sum of two positive roots is a root, then that sum is positive. One also knows that  is a disjoint union:
is a disjoint union:
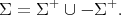 |
One can show there is a unique ![α - α Hα ∈ [𝔤 ,𝔤 ]](/img/revistas/ruma/v49n1/1a11171x.png) such that
such that 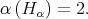 We use this element to define the value of the dual root. In particular, the dual root is given by
We use this element to define the value of the dual root. In particular, the dual root is given by
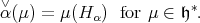 |
The linear reflection 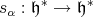 corresponding to
corresponding to 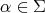 is defined as
is defined as
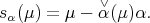 |
These reflections generate a finite subgroup of the general linear group of 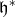 , denoted
, denoted 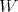 and called the Weyl group of
and called the Weyl group of 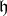 in
in 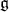 .
.
Let 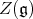 denote the center of the enveloping algebra
denote the center of the enveloping algebra 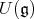 of
of 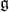 . A
. A 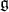 -infinitesimal character
-infinitesimal character 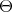 is a homomorphism of algebras
is a homomorphism of algebras
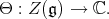 |
Since 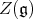 acts on an irreducible Harish-Chandra module (and also any corresponding smooth globalization) by a scalar, the infinitesimal character is an important invariant associated to an irreducible, admissible representation. We now recall Harish-Chandra's parametrization of infinitesimal characters. We choose a Borel subalgebra
acts on an irreducible Harish-Chandra module (and also any corresponding smooth globalization) by a scalar, the infinitesimal character is an important invariant associated to an irreducible, admissible representation. We now recall Harish-Chandra's parametrization of infinitesimal characters. We choose a Borel subalgebra 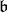 containing
containing 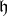 . Thus
. Thus
![𝔟 = 𝔥 ⊕ 𝔫 where 𝔫 = [𝔟,𝔟] is the nilradical of 𝔟.](/img/revistas/ruma/v49n1/1a11190x.png) |
Then one knows that 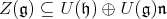 and that the corresponding projection of
and that the corresponding projection of 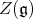 in
in 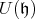 defines an injective morphism of algebras called the unnormalized Harish-Chandra map. We can use this morphism to identify infinitesimal characters with Weyl group orbits in
defines an injective morphism of algebras called the unnormalized Harish-Chandra map. We can use this morphism to identify infinitesimal characters with Weyl group orbits in 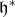 in the following way. Let
in the following way. Let 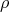 denote one-half the sum of the positive roots and suppose
denote one-half the sum of the positive roots and suppose 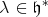 . Then, via the unnormalized Harish-Chandra map, the composition
. Then, via the unnormalized Harish-Chandra map, the composition
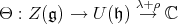 |
defines an infinitesimal character 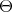 . One knows that for
. One knows that for 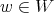 , the element
, the element 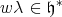 defines the same infinitesimal character
defines the same infinitesimal character 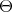 . Abusing notation somewhat, we write
. Abusing notation somewhat, we write 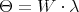 . The infinitesimal character is called regular when the only element of
. The infinitesimal character is called regular when the only element of 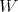 fixing an element in the orbit
fixing an element in the orbit 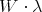 , is the identity. This is equivalent to the condition that
, is the identity. This is equivalent to the condition that
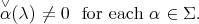 |
For a 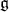 -module
-module 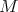 with regular infinitesimal character one has the following result. The notes by D. Milicic [13] contain a proof.
with regular infinitesimal character one has the following result. The notes by D. Milicic [13] contain a proof.
Theorem 4.1. Let 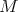 be a
be a 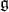 -module with regular infinitesimal character
-module with regular infinitesimal character 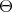 . Suppose
. Suppose 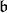 is a Borel subalgebra of
is a Borel subalgebra of 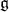 with Levi decomposition
with Levi decomposition
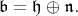 |
Let 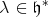 such that
such that 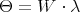 and let
and let 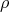 be one half the sum of the positive roots. Then the Cartan subalgebra
be one half the sum of the positive roots. Then the Cartan subalgebra 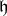 acts semisimply on the
acts semisimply on the 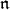 -homology groups
-homology groups 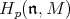 with eigenvalues of the form
with eigenvalues of the form 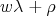 for
for 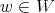 . In particular
. In particular
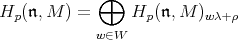 |
where
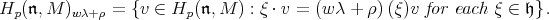 |
A generalization of this result works for any parabolic subalgebra 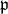 with Levi decomposition
with Levi decomposition
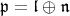 |
although the parametrization is not quite as tight. In particular, if 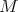 is a
is a 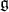 -module
-module 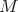 with regular infinitesimal character
with regular infinitesimal character 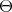 and if
and if 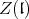 denotes the center of the enveloping algebra of
denotes the center of the enveloping algebra of  then
then 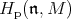 is a semisimple
is a semisimple 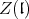 -module and decomposes into a direct sum of
-module and decomposes into a direct sum of 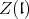 -eigenspaces, where the associated
-eigenspaces, where the associated  -infinitesimal characters that appear are related to
-infinitesimal characters that appear are related to 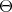 by an appropriately defined Harish-Chandra map.
by an appropriately defined Harish-Chandra map.
When  is a connected, compact Lie group, there is a result, called Kostant's theorem, that calculates the
is a connected, compact Lie group, there is a result, called Kostant's theorem, that calculates the 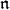 -homolgy groups of an irreducible representation. In this section we review that result, with special emphasis on the case of a Borel subalgebra.
-homolgy groups of an irreducible representation. In this section we review that result, with special emphasis on the case of a Borel subalgebra.
Assume  is a compact real form of
is a compact real form of 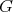 . Fix a Borel subalgebra
. Fix a Borel subalgebra 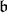 . Then the normalizer of
. Then the normalizer of 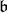 in
in  is a maximal torus
is a maximal torus 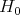 and a real form for a Cartan subgroup
and a real form for a Cartan subgroup 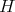 of
of 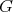 . We let
. We let 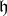 be the Lie algebra of
be the Lie algebra of 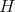 and
and 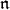 the nilradical of
the nilradical of 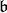 .
.  is the set of roots. The roots of
is the set of roots. The roots of 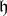 in
in 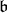 determine a set of positive roots
determine a set of positive roots 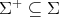 . Let
. Let 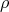 be one-half the sum of the positive roots. Suppose
be one-half the sum of the positive roots. Suppose
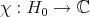 |
is a continuous character and let 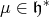 denote the complexification of the derivative of
denote the complexification of the derivative of 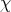 . To be consistent with the notation in Section 7 we use the shifted parameter
. To be consistent with the notation in Section 7 we use the shifted parameter
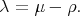 |
One knows that
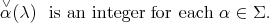 |
The character 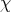 is called antidominant and regular if
is called antidominant and regular if
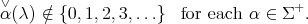 |
The Cartan-Weyl parametrization of irreducible representations is as follows.
Theorem 5.1. Maintain the established notations.
(a) Suppose 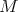 is an irreducible
is an irreducible  -module. Then the space of coinvariants
-module. Then the space of coinvariants 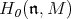 is an irreducible
is an irreducible 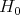 -module and the associated character
-module and the associated character 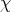 is antidominant and regular. This character is called the lowest weight.
is antidominant and regular. This character is called the lowest weight.
(b) If two irreducible representations have the same lowest weight then they are isomorphic.
(c) To each antidominant and regular character there is an irreducible  -module with the given character as its lowest weight.
-module with the given character as its lowest weight.
We need to define the length function on the Weyl group. One knows that the Weyl group permutes the roots of 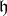 in
in 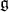 . We can define the length of
. We can define the length of 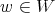 to be the number of roots in
to be the number of roots in
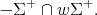 |
Kostant's theorem is the following:
Theorem 5.2. Suppose 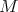 is the irreducible representation for
is the irreducible representation for  with lowest weight
with lowest weight 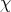 and let
and let 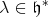 be the shifted parameter. Then
be the shifted parameter. Then 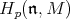 is a sum of irreducible
is a sum of irreducible 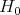 -modules each having multiplicity one. The characters of
-modules each having multiplicity one. The characters of 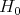 that show up as eigenvalues in
that show up as eigenvalues in 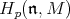 are exactly those whose derivative have the form
are exactly those whose derivative have the form 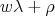 where the length of
where the length of 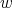 is p
is p
In the more general case of a parabolic subalgebra 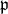 , let
, let 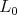 be the normalizer of
be the normalizer of 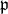 in
in  and let
and let  be the complexified Lie algebra of
be the complexified Lie algebra of 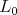 . One knows that
. One knows that 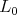 is connected and that
is connected and that  is a Levi factor of
is a Levi factor of 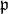 . Indeed, if
. Indeed, if 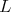 is the connected subgroup of
is the connected subgroup of 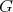 with Lie algebra
with Lie algebra 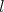 then
then 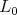 is the compact real form of
is the compact real form of 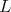 . Suppose
. Suppose 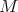 is an irreducible representation for
is an irreducible representation for  and let
and let 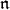 be the nilradical of
be the nilradical of 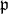 . Then Kostant's Theorem describes the structure of the pth homology group
. Then Kostant's Theorem describes the structure of the pth homology group 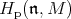 as an
as an 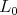 -module. In particular, the theorem states that an irreducible representation
-module. In particular, the theorem states that an irreducible representation 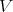 of
of 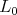 has, at most, multiplicity one in
has, at most, multiplicity one in 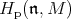 and gives a precise condition when
and gives a precise condition when 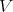 appears, in terms of the degree p, the lowest weight of
appears, in terms of the degree p, the lowest weight of 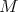 and the lowest weight of
and the lowest weight of 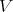 . We refer the reader to [10, Chapter IV, Section 9] for more details.
. We refer the reader to [10, Chapter IV, Section 9] for more details.
6. Flag manifolds and comparison theorems
As we mentioned before, when  is noncompact, there are several conjugacy classes of Borel subalgebras and the structure of the
is noncompact, there are several conjugacy classes of Borel subalgebras and the structure of the 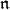 -homology groups of a representation can depend on the choice of
-homology groups of a representation can depend on the choice of  -conjugacy class. On the other hand, when
-conjugacy class. On the other hand, when 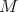 is a Harish-Chandra module, then the locally finite
is a Harish-Chandra module, then the locally finite 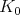 -action on
-action on 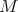 extends naturally to a locally holomorphic
extends naturally to a locally holomorphic 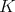 -action, and it turns out that the
-action, and it turns out that the 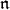 -homology groups of
-homology groups of 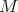 depend on the
depend on the 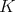 -conjugacy classes of Borel subalgebras. In order to compare the
-conjugacy classes of Borel subalgebras. In order to compare the 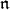 -homology groups of
-homology groups of 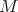 with the
with the 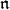 -homology groups of a smooth globalization, we therefore need to know something about the relationship between
-homology groups of a smooth globalization, we therefore need to know something about the relationship between  -conjugacy classes and
-conjugacy classes and 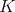 -conjugacy classes. There is an elegant geometric result, referred to as Matsuki duality, that gives us the needed information. We now review that result.
-conjugacy classes. There is an elegant geometric result, referred to as Matsuki duality, that gives us the needed information. We now review that result.
One knows that the group 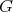 acts transitively on the set of Borel subalgebras of
acts transitively on the set of Borel subalgebras of 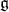 . The corresponding
. The corresponding 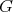 -homogeneous complex manifold
-homogeneous complex manifold 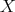 is called the full flag space. In general, if
is called the full flag space. In general, if 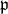 is a parabolic subalgebra of
is a parabolic subalgebra of 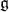 then the normalizer of
then the normalizer of 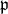 in
in 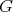 is the connected subgroup
is the connected subgroup 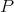 with Lie algebra
with Lie algebra 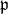 and the corresponding quotient
and the corresponding quotient
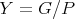 |
is called a flag manifold. The points in  are naturally identified with the
are naturally identified with the  -conjugates to
-conjugates to 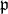 .
.
Let 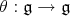 be the complexification of a Cartan involution of
be the complexification of a Cartan involution of 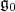 corresponding to the maximal compact subgroup
corresponding to the maximal compact subgroup 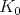 . A Cartan subalgebra
. A Cartan subalgebra 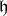 of
of 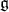 is called stable if
is called stable if 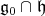 is a real form and if
is a real form and if 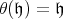 . A Borel subalgebra is called very special if it contains a stable Cartan subalgebra. A stable Cartan subalgebra of a Borel subalgebra is unique. A point in the full flag space is called very special if the corresponding Borel subalgebra is.
. A Borel subalgebra is called very special if it contains a stable Cartan subalgebra. A stable Cartan subalgebra of a Borel subalgebra is unique. A point in the full flag space is called very special if the corresponding Borel subalgebra is.
Matsuki has established the following [11].
Theorem 6.1. Let 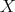 be the full flag space. Then
be the full flag space. Then
(a) The subset of very special points in a  -orbit is a nonempty
-orbit is a nonempty 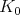 -orbit.
-orbit.
(b) The subset of very special points in a 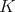 -orbit is a nonempty
-orbit is a nonempty 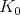 -orbit.
-orbit.
It follows that the very special points give a one-to-one correspondence between the  -orbits and the
-orbits and the 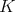 -orbits on
-orbits on 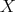 , defined by the following duality. A
, defined by the following duality. A  -orbit
-orbit 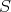 is said to be dual to a
is said to be dual to a 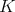 -orbit
-orbit  when
when  contains a special point. In this duality, open
contains a special point. In this duality, open  -orbits correspond to closed
-orbits correspond to closed 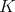 -orbits and the (unique) closed
-orbits and the (unique) closed  -orbit corresponds to the (unique) open
-orbit corresponds to the (unique) open 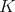 -orbit. We note that Matsuki has established a similar result for any flag manifold [12].
-orbit. We note that Matsuki has established a similar result for any flag manifold [12].
Example 6.2. Suppose 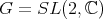 , the group of
, the group of  complex matrices with determinant 1 and let
complex matrices with determinant 1 and let 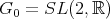 . Then the full flag space
. Then the full flag space 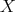 is isomorphic to the Riemann sphere.
is isomorphic to the Riemann sphere.  has three orbits on
has three orbits on 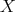 . The closed
. The closed  -orbit can be identified with an equatorial circle and the other two orbits are the corresponding open hemispheres. It turns out every point in the closed orbit is very special, independent of the choice of
-orbit can be identified with an equatorial circle and the other two orbits are the corresponding open hemispheres. It turns out every point in the closed orbit is very special, independent of the choice of 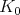 (this is true in general). Put
(this is true in general). Put 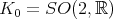 . Thus
. Thus 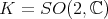 . Then the three
. Then the three 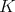 -orbits on
-orbits on 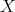 are a punctured plane, containing the closed
are a punctured plane, containing the closed  -orbit, and two fixed points, which can be identified with the respective poles in each of the open hemispheres. These two poles are the other very special points.
-orbit, and two fixed points, which can be identified with the respective poles in each of the open hemispheres. These two poles are the other very special points.
When 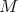 is a Harish-Chandra module and
is a Harish-Chandra module and 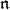 is the nilradical of a Borel subalgebra then one knows that the homology groups
is the nilradical of a Borel subalgebra then one knows that the homology groups 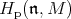 are finite-dimensional, so it may seem reasonable to ask when
are finite-dimensional, so it may seem reasonable to ask when 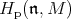 coincides with the
coincides with the 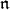 -homolgy groups of a smooth globalization. It turns out this not only depends on the choice of Borel subalgebra, but also in the the choice of smooth globalization. When
-homolgy groups of a smooth globalization. It turns out this not only depends on the choice of Borel subalgebra, but also in the the choice of smooth globalization. When 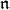 is the nilradical of a very special Borel subalgebra,
is the nilradical of a very special Borel subalgebra, 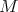 is a Harish-Chandra module, and
is a Harish-Chandra module, and 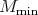 is the minimal globalization, then H. Hecht and J. Taylor have shown [8] that the natural map
is the minimal globalization, then H. Hecht and J. Taylor have shown [8] that the natural map
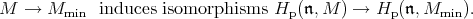 |
On the other hand, for the maximal globalization, there are counterexamples to this result.
The result of Hecht and Taylor has been generalized in the following form. A Levi factor  of a parabolic subalgebra
of a parabolic subalgebra 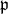 is called stable if
is called stable if 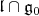 is a real form
is a real form  of
of  and if
and if 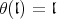 . The parabolic subalgebra
. The parabolic subalgebra 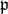 is called very special if it contains a stable Levi factor. Such a Levi factor is unique. Unlike the case of the full flag space, there may be parabolic subalgebras which are not
is called very special if it contains a stable Levi factor. Such a Levi factor is unique. Unlike the case of the full flag space, there may be parabolic subalgebras which are not  -conjugate to a very special parabolic subalgebra, so we are not considering all orbits on every flag manifold. However, suppose
-conjugate to a very special parabolic subalgebra, so we are not considering all orbits on every flag manifold. However, suppose  is very special and
is very special and  is the stable Levi factor. Define
is the stable Levi factor. Define 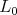 to be the subgroup of
to be the subgroup of  that normalizes
that normalizes 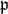 and normalizes
and normalizes  . Then
. Then 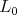 is a linear reductive Lie group with complexified Lie algebra
is a linear reductive Lie group with complexified Lie algebra  and maximal compact subgroup
and maximal compact subgroup  , called the associated real Levi subgroup. We have have the following result [9, Proposition 2.24].
, called the associated real Levi subgroup. We have have the following result [9, Proposition 2.24].
Proposition 6.3. Suppose 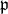 is a very special parabolic subalgebra with
is a very special parabolic subalgebra with 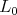 and
and  defined as above. Let
defined as above. Let 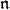 be the nilradical of
be the nilradical of 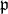 and suppose
and suppose 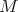 is a Harish-Chandra module for
is a Harish-Chandra module for 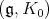 . Then the
. Then the 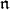 -homology groups are Harish-Chandra modules for
-homology groups are Harish-Chandra modules for 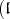 ,
,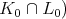 .
.
For the minimal globalization, we have the following [2].
Theorem 6.4. Maintain the hypothesis of the previous proposition. Then the standard complex induces a Hausdorff topology on 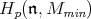 and the natural map
and the natural map 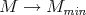 induces isomorphisms
induces isomorphisms
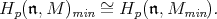 |
One might conjecture that above theorem works for the smooth globalization, and W. Casselman has informed the author that he has proven something along these lines, although details are unclear. Two partial comparison theorems about smooth globalizations have been published by other mathematicians. H. Hecht and J. Taylor have shown the result for minimal parabolic subgroups of  [6], while U. Bunke and M. Olbrich have shown the result for any real parabolic subgroup [4].
[6], while U. Bunke and M. Olbrich have shown the result for any real parabolic subgroup [4].
D. Vogan has conjectured that all four canonical globalizations commute with the 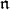 -homology groups of a very special parabolic subalgebra when the corresponding
-homology groups of a very special parabolic subalgebra when the corresponding  -orbit on the flag manifold is open [15]. We remark that it has recently been shown that Vogan's conjecture is true for one globalization if and only it's true for the dual [3]. Thus the conjecture is proven for both the minimal and maximal globalization.
-orbit on the flag manifold is open [15]. We remark that it has recently been shown that Vogan's conjecture is true for one globalization if and only it's true for the dual [3]. Thus the conjecture is proven for both the minimal and maximal globalization.
7. The 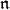 -homology of standard modules
-homology of standard modules
In the noncompact case, the problem of calculating 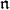 -homology groups can be quite complicated and there seems to be little hope of just writing down a formula that generalizes Kostant's theorem for all irreducible representations. However, there are certain representations, called standard modules, whose
-homology groups can be quite complicated and there seems to be little hope of just writing down a formula that generalizes Kostant's theorem for all irreducible representations. However, there are certain representations, called standard modules, whose 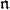 -homology groups are a bit more predictable. These standard modules are generically irreducible, coincide with irreducibles when
-homology groups are a bit more predictable. These standard modules are generically irreducible, coincide with irreducibles when  is compact, and can be used to classify the irreducible representations. In this section we define the standard representations and consider their
is compact, and can be used to classify the irreducible representations. In this section we define the standard representations and consider their 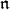 -homology groups, focusing on the case of the full flag space.
-homology groups, focusing on the case of the full flag space.
In particular, we use the construction of minimal globalizations given in [7]. Let 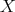 be the full flag space and, since we need to keep track of points, introduce the following notation. For
be the full flag space and, since we need to keep track of points, introduce the following notation. For 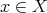 we let
we let 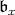 be the corresponding Borel subalgebra and let
be the corresponding Borel subalgebra and let 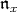 denote the nilradical of
denote the nilradical of 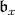 . When we are interested in calculating the
. When we are interested in calculating the 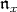 -homology of Harish-Chandra modules, we can assume
-homology of Harish-Chandra modules, we can assume 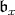 is a very special Borel subalgebra. In that case,
is a very special Borel subalgebra. In that case, 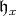 denotes the stable Cartan subalgebra of
denotes the stable Cartan subalgebra of 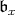 and
and 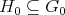 is the corresponding real Cartan subgroup (thus
is the corresponding real Cartan subgroup (thus 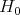 is the associated Levi subgroup). By our linear assumptions on
is the associated Levi subgroup). By our linear assumptions on  , it follows that
, it follows that 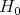 is abelian, so that an irreducible, admissible representation of
is abelian, so that an irreducible, admissible representation of 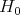 is a continuous character
is a continuous character
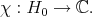 |
Let  be the
be the  -orbit of
-orbit of 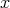 . In a natural way,
. In a natural way, 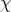 extends to a character of the normalizer of
extends to a character of the normalizer of 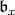 in
in  (we note that
(we note that 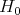 and the normalizer of
and the normalizer of 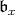 coincide exactly when
coincide exactly when 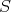 is open). Thus
is open). Thus 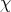 determines a
determines a  -homogeneous analytic line bundle over
-homogeneous analytic line bundle over 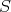 . One can then define the concept of a polarized section [7, Section 8]. When
. One can then define the concept of a polarized section [7, Section 8]. When 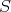 is open, the polarized sections are holomorphic sections, and in general the polarized sections are locally isomorphic with the restricted holomorphic functions. Let
is open, the polarized sections are holomorphic sections, and in general the polarized sections are locally isomorphic with the restricted holomorphic functions. Let 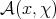 denote the sheaf of polarized sections on
denote the sheaf of polarized sections on 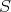 and, for p
and, for p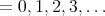 let
let
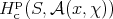 |
denote the corresponding compactly supported sheaf cohomology group. Suppose 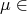
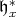 is the complexified differential of
is the complexified differential of 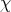 , let
, let 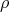 be one-half the sum of the positive roots for
be one-half the sum of the positive roots for 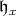 in
in 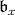 and let
and let 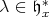 denote the corresponding shifted parameter. Thus
denote the corresponding shifted parameter. Thus
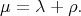 |
We have the following theorem [7].
Theorem 7.1. Maintain the previously defined notations. Let q be the codimension of the 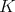 -orbit of
-orbit of 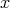 in
in 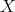 .
.
(a) 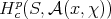 carries a natural topology and a continuous
carries a natural topology and a continuous  -action, so that the resulting representation is a minimal globalization.
-action, so that the resulting representation is a minimal globalization.
(b) 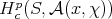 has infinitesimal character
has infinitesimal character 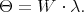 .
.
(c) When 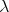 is antidominant then
is antidominant then 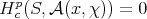 when p
when p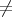 q.
q.
(d) When 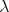 is antidominant and
is antidominant and 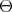 is regular then
is regular then 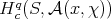 contains a unique irreducible submodule. In particular,
contains a unique irreducible submodule. In particular, 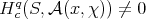 .
.
When 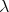 is antidominant and
is antidominant and 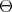 is regular, we call
is regular, we call 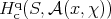 a regular standard module. These modules can be used to parametrize irreducible representations with regular infinitesimal character. For the remainder of this article we will make some remarks about how to calculate the
a regular standard module. These modules can be used to parametrize irreducible representations with regular infinitesimal character. For the remainder of this article we will make some remarks about how to calculate the 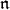 -homology of regular standard modules. But we first note that, in the case of a singular infinitesimal character, the definition of standard module is more subtle, and the calculation of
-homology of regular standard modules. But we first note that, in the case of a singular infinitesimal character, the definition of standard module is more subtle, and the calculation of 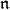 -homology is more elusive.
-homology is more elusive.
To state results we will need to differentiate points where we calculate 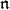 -homology and the corresponding parameters for eigenvalues of a Cartan subalgebra (see Theorem 4.1). In particular, we fix a very special point
-homology and the corresponding parameters for eigenvalues of a Cartan subalgebra (see Theorem 4.1). In particular, we fix a very special point 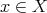 as a base point. For
as a base point. For 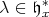 we put
we put 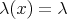 . When
. When 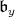 is a very special Borel subalgebra and
is a very special Borel subalgebra and 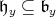 is the stable Cartan subalgebra, then there exists
is the stable Cartan subalgebra, then there exists 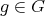 such that
such that
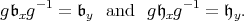 |
Thus
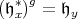 |
This isomorphism is independent of the choice of 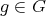 . For
. For 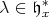 put
put
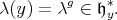 |
We note that 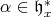 is a root of
is a root of 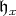 in
in 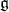

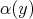 is a root of
is a root of 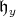 and that
and that 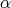 is positive at
is positive at 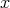

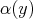 is positive at
is positive at 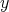 . In particular,
. In particular, 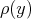 is one-half the sum of the positive roots for
is one-half the sum of the positive roots for 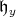 in
in 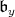 .
.
The circle of ideas utilized in [7] depend on an identification of the derived functor of 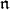 -homolgy, in a certain weight (Theorem 4.1), with the geometric fiber applied to a certain, corresponding localization functor. These ideas originate in the an elegant generalization of Casselman's submodule theorem, given by A. Beilinson and J. Bernstein in [1]. This identification, together with some functorial rigmarole, immediately leads to the following result.
-homolgy, in a certain weight (Theorem 4.1), with the geometric fiber applied to a certain, corresponding localization functor. These ideas originate in the an elegant generalization of Casselman's submodule theorem, given by A. Beilinson and J. Bernstein in [1]. This identification, together with some functorial rigmarole, immediately leads to the following result.
Proposition 7.2. Suppose 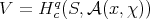 is a regular standard module. Maintain the previously introduced notations. Let
is a regular standard module. Maintain the previously introduced notations. Let 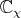 denote the 1-dimensional representation of
denote the 1-dimensional representation of 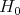 corresponding to
corresponding to 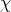 and let
and let 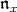 be the nilradical of
be the nilradical of 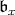 . Then we have the following.
. Then we have the following.
(a)
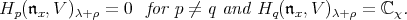 |
(b) If 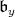 is a very special Borel subalgebra with nilradical
is a very special Borel subalgebra with nilradical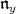 and
and 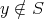 then
then
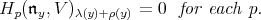 |
According to Theorem 4.1, the problem of calculating of the  -homology groups of
-homology groups of  , at a special point
, at a special point  , reduces to the problem of calculating the values in the weights
, reduces to the problem of calculating the values in the weights 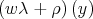 for
for 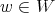 . In geometric terms, this means calculating the geometric fibers of certain localizations of
. In geometric terms, this means calculating the geometric fibers of certain localizations of 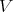 or, equivalently, calculating the result of the so called intertwining functor. We briefly consider this problem.
or, equivalently, calculating the result of the so called intertwining functor. We briefly consider this problem.
In general, a positive root is called simple if it cannot be decomposed into a nontrivial sum of positive roots. Let 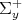 be the positive roots associated to
be the positive roots associated to 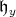 in
in 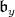 . For a simple root
. For a simple root 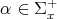 , the problem of calculating the values of the
, the problem of calculating the values of the 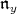 -homology groups in the weight
-homology groups in the weight 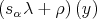 can be geometrically reduced to specific calculations for certain real subgroups of
can be geometrically reduced to specific calculations for certain real subgroups of  . To a large extent, this idea is already exploited and explained in [7] and some of the necessary calculations are dealt with there.
. To a large extent, this idea is already exploited and explained in [7] and some of the necessary calculations are dealt with there.
We finish with an example where, using these ideas, a general formula, like Kostant's, can be actually written down. Assume  is a connected, complex reductive Lie group. Fix a very special Borel subalgebra
is a connected, complex reductive Lie group. Fix a very special Borel subalgebra 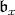 with stable Cartan subalgebra
with stable Cartan subalgebra 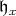 and let
and let 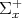 denote the corresponding positive roots. For each
denote the corresponding positive roots. For each 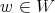 , the set
, the set
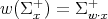 |
defines a new set of positive roots and thus a corresponding Borel subalgebra 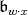 of
of 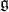 containing the stable Cartan subalgebra
containing the stable Cartan subalgebra 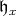 . Thus the point
. Thus the point 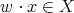 is very special. Because
is very special. Because  is a complex reductive group, one knows that each Borel subalgebra of
is a complex reductive group, one knows that each Borel subalgebra of 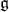 is
is  -conjugate to a Borel subalgebra of the form
-conjugate to a Borel subalgebra of the form 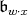 . Suppose
. Suppose 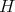 is the Cartan subgroup of
is the Cartan subgroup of 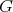 with Lie algebra
with Lie algebra 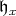 . Then each
. Then each 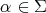 defines a holomorphic character of
defines a holomorphic character of 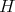 and by restriction, a corresponding character of
and by restriction, a corresponding character of 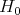 . We write
. We write 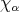 for this character of
for this character of 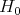 . If we let
. If we let 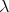 be the shifted parameter and put
be the shifted parameter and put 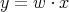 then
then 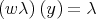 .
.
Using the above ideas, one can deduce the following.
Theorem 7.3. Let  be a connected, complex reductive group. Suppose
be a connected, complex reductive group. Suppose 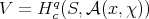 is the previously defined regular standard module and assume the
is the previously defined regular standard module and assume the  -orbit of
-orbit of 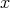 is open in
is open in 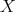 . We define a chain
. We define a chain  of simple roots to be a finite sequence of roots of
of simple roots to be a finite sequence of roots of 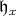 such that for each
such that for each 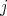 ,
, 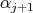 is simple for the set of positive roots defined by
is simple for the set of positive roots defined by
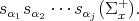 |
Suppose  is a chain of simple roots and let
is a chain of simple roots and let 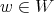 be the ordered product of reflections given by this chain. Let
be the ordered product of reflections given by this chain. Let 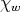 be the character of
be the character of 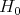 defined by
defined by
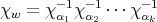 |
and let 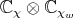 be the 1-dimensional representation of
be the 1-dimensional representation of 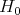 corresponding to the character
corresponding to the character 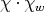 . Let q
. Let q denote the codimension of the
denote the codimension of the 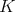 -orbit of
-orbit of 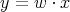 in
in 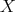 . Then
. Then
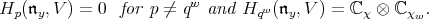 |
We note that the hypothesis of the theorem implies that the representation 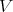 is irreducible, and also remark that any attempt to write down a similar result for other orbits (even in the case of a connected, complex reductive group), when the standard module is reducible, is considerably more complicated.
is irreducible, and also remark that any attempt to write down a similar result for other orbits (even in the case of a connected, complex reductive group), when the standard module is reducible, is considerably more complicated.
[1] Beilinson, A. and Bernstein, J.: A generalization of Casselman's submodule theorem. Birkhäuser, Progress in Math. 40, Boston, 1983, pp. 35-52. [ Links ]
[2] Bratten, T.: A comparison theorem for Lie algebra homology groups. Pacific J. Math. 182 (1998) 23-36. [ Links ]
[3] Bratten, T and Corti, S.:A simple proof of the algebraic version of a conjecture by Vogan. J. of Lie Theory 18 (2008) 83-91. [ Links ]
[4] Bunke, U. and Olbrich, M.: Cohomological properties of the canonical globalizations of Harish-Chandra modules. Ann. of Global Analysis and Geometry. 15 (1997) 401-418. [ Links ]
[5] Casselman, W.; Canonical extensions of Harish-Chandra modules to representations of G. Can. J. Math. 41 (1989) 385-438. [ Links ]
[6] Hecht, H and Taylor, J.: A remark on Caselman's comparison theorem. In the book "Geometry and Representation Theory of p-Adic Groups", editors: J. Tirao, D. Vogan and J. Wolf. Birhäuser, 1998. [ Links ]
[7] Hecht, H and Taylor, J.: Analytic localization of group representations. Advances in Math. 79 (1990) 139-212. [ Links ]
[8] Hecht, H. and Taylor, J.: A comparison theorem for  -homology. Compositio Math. 86 (1993) 187-207. [ Links ]
-homology. Compositio Math. 86 (1993) 187-207. [ Links ]
[9] Hecht, H. and Schmid, W.: Characters, asymptotics and  -homology of Harish-Chandra modules. Acta Math. 151 (1983) 49-151. [ Links ]
-homology of Harish-Chandra modules. Acta Math. 151 (1983) 49-151. [ Links ]
[10] Knapp, A and Vogan, D.: Cohomological Induction and Unitary Representations. Princeton University Press. Princeton, 1995. [ Links ]
[11] Matsuki, T.: The orbits of affine symetric spaces under the action of minimal parabolic subgroups. J. Math. Soc. Japan. 31 (1979) 331-357. [ Links ]
[12] Matsuki, T.: Orbits on affine symetric spaces under the action of parabolic subgroups. Hiroshima Math. J. 12 (1982) 307-320. [ Links ]
[13] Milicic, D.: Localization and Representation Theory of Reductive Lie Groups. Notes dated 1994 and available on Milicic's web page. [ Links ]
[14] Schmid, W.: Boundary value problems for group invariant differential equations. The mathematical heritage of Elie Cartan, Astérisque (1985) 311-321. [ Links ]
[15] Vogan, D.: Unitary representations and complex analysis. Notes from the Cime summer school, Venice, Italy 2004. Available on Vogan's web page http://www-math.mit.edu/~dav/paper.html. [ Links ]
[16] Warner, G.: Harmonic Analysis on Semi-Simple Lie Groups I. Springer-Verlag, 1972. [ Links ]
Tim Bratten
Facultad de Ciencias Exactas,
UNICEN. Tandil, Argentina
bratten@exa.unicen.edu.ar
Recibido: 10 de abril de 2008
Aceptado: 6 de mayo de 2008













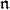 -homology and
-homology and 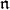 -cohomology
-cohomology
