Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.49 n.2 Bahía Blanca jul./dic. 2008
Matrix spherical functions and orthogonal polynomials: An instructive example
I. Pacharoni
This paper is partially supported by CONICET, FONCyT, Secyt-UNC and the ICTP.
Abstract. In the scalar case, it is well known that the zonal spherical functions of any compact Riemannian symmetric space of rank one can be expressed in terms of the Jacobi polynomials. The main purpose of this paper is to revisit the matrix valued spherical functions associated to the complex projective plane to exhibit the interplay among these functions, the matrix hypergeometric functions and the matrix orthogonal polynomials. We also obtain very explicit expressions for the entries of the spherical functions in the case of 2 × 2 matrices and exhibit a natural sequence of matrix orthogonal polynomials, beyond the group parameters.
The well known Legendre polynomials are a special case of spherical harmonics: the homogeneous harmonic polynomials of 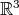 , considered as functions on the unit sphere
, considered as functions on the unit sphere 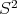 . Let
. Let 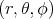 be ordinary polar coordinates in
be ordinary polar coordinates in 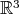 :
: 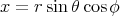 ,
, 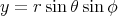 and
and 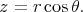 In terms of these coordinates the Riemannian structure of
In terms of these coordinates the Riemannian structure of  is given by the symmetric differential form
is given by the symmetric differential form 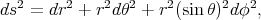 and the Laplace operator is
and the Laplace operator is
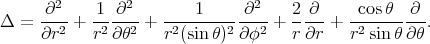
 is a homogeneous harmonic polynomial of degree
is a homogeneous harmonic polynomial of degree  which does not depend on the variable
which does not depend on the variable 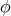 , then
, then 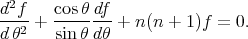
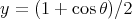 we get
we get 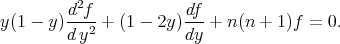
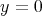 , up to a constant, is
, up to a constant, is 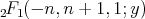 . Since the Legendre polynomial of degree
. Since the Legendre polynomial of degree 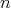 is given by
is given by 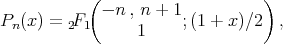
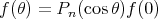 .
. Let
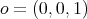 be the north pole of
be the north pole of  , and let
, and let 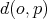 be the geodesic distance from a point
be the geodesic distance from a point 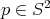 to
to  . Let
. Let 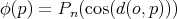 . Then we have proved that
. Then we have proved that 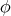 is the unique spherical harmonic of degree
is the unique spherical harmonic of degree 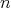 , constant along parallels and such that
, constant along parallels and such that 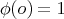 . Moreover the set of all complex linear combinations of translates
. Moreover the set of all complex linear combinations of translates 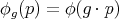 ,
, 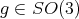 , is the linear space of all spherical harmonics of degree
, is the linear space of all spherical harmonics of degree  .
. Legendre and Laplace found that the Legendre polynomials satisfy the following addition formula
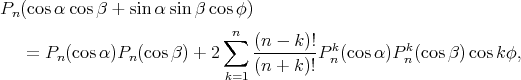 (1) (1) |
where the 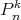 's are the associated Legendre polynomials.
's are the associated Legendre polynomials.
By integrating (1) we get
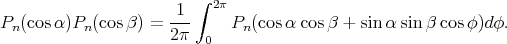 (2) (2) |
Moreover the Legendre polynomials can be determined as solutions to (2). This integral equation can now be expressed in terms of the function  on
on  defined by
defined by 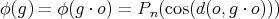 . In fact (2) is equivalent to
. In fact (2) is equivalent to
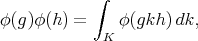 (3) (3) |
where 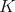 denotes the compact subgroup of
denotes the compact subgroup of 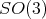 of all elements which fix the north pole
of all elements which fix the north pole  , and
, and 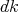 denotes the normalized Haar measure of
denotes the normalized Haar measure of 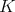 .
.
In fact, let 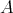 denote the subgroup of all elements of
denote the subgroup of all elements of 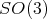 which fix the point
which fix the point 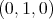 . Then
. Then 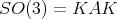 . Thus to prove (3) it is enough to consider rotations
. Thus to prove (3) it is enough to consider rotations 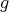 and
and 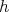 around the
around the 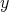 -axis through the angles
-axis through the angles 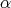 and
and 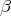 , respectively. Then if
, respectively. Then if 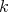 denotes the rotation of angle
denotes the rotation of angle 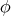 around the
around the  -axis we have
-axis we have

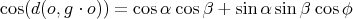 and
and 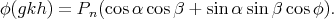
The functional equation (3) has been generalized to many different settings. One is the following. Let 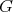 be a locally compact unimodular group and let
be a locally compact unimodular group and let 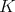 be a compact subgroup. A nontrivial complex valued continuous function
be a compact subgroup. A nontrivial complex valued continuous function 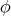 on
on 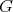 is a zonal spherical function if (3) holds for all
is a zonal spherical function if (3) holds for all 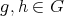 . Note that then
. Note that then 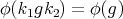 for all
for all 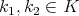 and all
and all 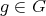 , and that
, and that 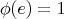 where
where  is the identity element of
is the identity element of 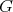 .
.
The example above arises when 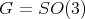
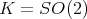 and
and 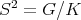 . The other compact connected rank one symmetric spaces have zonal spherical functions which are orthogonal polynomials in an appropriate variable. These polynomials are special cases of Jacobi polynomials and they can be given explicitly as hypergeometric functions.
. The other compact connected rank one symmetric spaces have zonal spherical functions which are orthogonal polynomials in an appropriate variable. These polynomials are special cases of Jacobi polynomials and they can be given explicitly as hypergeometric functions.
The complex projective plane 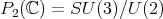 is another rank one symmetric space. In this case the zonal spherical functions are
is another rank one symmetric space. In this case the zonal spherical functions are 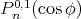 .
.
A very fruitful generalization of the functional equation (3) is the following (see [T1] and [GV]. Let 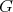 be a locally compact unimodular group and let
be a locally compact unimodular group and let 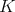 be a compact subgroup of
be a compact subgroup of 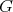 . Let
. Let 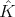 denote the set of all equivalence classes of complex finite dimensional irreducible representations of
denote the set of all equivalence classes of complex finite dimensional irreducible representations of 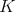 ; for each
; for each 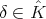 , let
, let 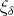 and
and 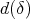 denote, respectively, the character and the dimension of any representation in the class
denote, respectively, the character and the dimension of any representation in the class  , and set
, and set 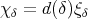 . We shall denote by
. We shall denote by 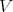 a finite dimensional complex vector space and by
a finite dimensional complex vector space and by 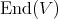 the space of all linear transformations of
the space of all linear transformations of 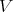 into
into 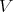 .
.
A spherical function 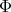 on
on 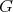 of type
of type 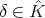 is a continuous function
is a continuous function  such that
such that 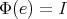 , (
, (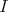 = identity transformation) and
= identity transformation) and
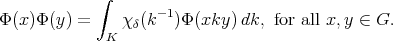
When  is the class of the trivial representation of
is the class of the trivial representation of 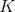 and
and  , the corresponding spherical functions are precisely the zonal spherical functions. From the definition it follows that
, the corresponding spherical functions are precisely the zonal spherical functions. From the definition it follows that 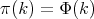 is a representation of
is a representation of 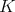 , equivalent to the direct sum of
, equivalent to the direct sum of 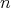 representations in the class
representations in the class  , and that
, and that 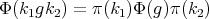 for all
for all 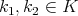 and all
and all 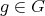 . The number
. The number 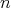 is the height of
is the height of 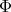 . The height and the type are uniquely determined by the spherical function.
. The height and the type are uniquely determined by the spherical function.
2. Matrix valued spherical functions associated to 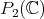
In [GPT1] the authors consider the problem of determining all irreducible spherical functions associated to the complex projective plane 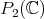 . This space can be realized as the homogeneous space
. This space can be realized as the homogeneous space 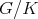 ,
, 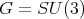 and
and 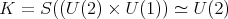 . In this case all irreducible spherical functions are of height one. Let
. In this case all irreducible spherical functions are of height one. Let 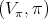 be any irreducible representation of
be any irreducible representation of 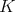 in the class
in the class  . Then an irreducible spherical function can be characterized as a function
. Then an irreducible spherical function can be characterized as a function 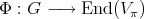 such that
such that
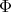 is analytic,
is analytic,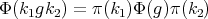 , for all
, for all 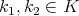 ,
, 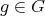 , and
, and 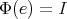 ,
, = λ(Δ )Φ (g )](/img/revistas/ruma/v49n2/2a02124x.png) , for all
, for all 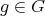 and
and 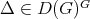 .
.
Here 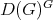 denotes the algebra of all left and right invariant differential operators on
denotes the algebra of all left and right invariant differential operators on 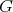 . In our case it is known that the algebra
. In our case it is known that the algebra 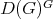 is a polynomial algebra in two algebraically independent generators
is a polynomial algebra in two algebraically independent generators 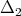 and
and 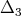 , explicitly given in [GPT1].
, explicitly given in [GPT1].
The set 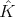 can be identified with
can be identified with 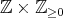 in the following way: If
in the following way: If 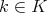 then
then
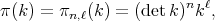
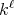 denotes the
denotes the 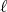 -symmetric power of the matrix
-symmetric power of the matrix 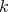 .
. For any 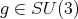 we denote by
we denote by 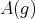 the left upper
the left upper  block of
block of 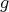 , and we consider the open dense subset
, and we consider the open dense subset 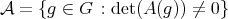 . Then
. Then 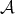 is left and right invariant under
is left and right invariant under 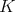 . For any
. For any 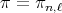 we introduce the following function defined on
we introduce the following function defined on 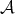 :
:
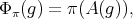
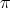 above denotes the unique holomorphic representation of
above denotes the unique holomorphic representation of 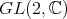 which extends the given representation of
which extends the given representation of 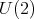 .
. To determine all irreducible spherical functions 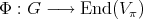 of type
of type 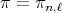 , we use the function
, we use the function 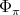 in the following way: in the open set
in the following way: in the open set 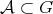 we define the function
we define the function 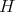 by
by
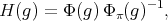 (4) (4) |
where 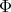 is supposed to be a spherical function of type
is supposed to be a spherical function of type  . Then
. Then 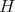 satisfies
satisfies
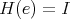 ,
,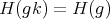 , for all
, for all 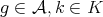 ,
,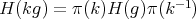 , for all
, for all 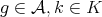 .
.
The canonical projection 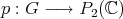 defined by
defined by 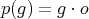 where
where 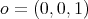 maps the open dense subset
maps the open dense subset 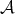 onto the affine space
onto the affine space  of those points in
of those points in 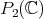 whose last homogeneous coordinate is not zero. Then property ii) says that
whose last homogeneous coordinate is not zero. Then property ii) says that 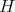 may be considered as a function on
may be considered as a function on 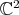 , and moreover from iii) it follows that
, and moreover from iii) it follows that 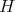 is determined by its restriction
is determined by its restriction 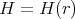 to the cross section
to the cross section 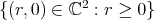 of the
of the 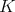 -orbits in
-orbits in 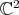 , which are the spheres of radius
, which are the spheres of radius  centered at the origin. That is
centered at the origin. That is 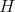 is determined by the function
is determined by the function 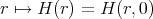 on the interval
on the interval  . Let
. Let 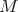 be the closed subgroup of
be the closed subgroup of 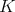 of all diagonal matrices of the form
of all diagonal matrices of the form 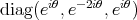 ,
, 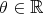 . Then
. Then 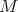 fixes all points
fixes all points 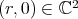 . Therefore iii) also implies that
. Therefore iii) also implies that 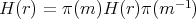 for all
for all 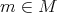 . Since any
. Since any 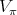 as an
as an 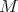 -module is multiplicity free, it follows that there exists a basis of
-module is multiplicity free, it follows that there exists a basis of 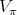 such that
such that 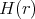 is simultaneously represented by a diagonal matrix for all
is simultaneously represented by a diagonal matrix for all  . Thus, if
. Thus, if 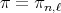 , we can identify
, we can identify 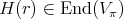 with a vector
with a vector

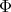 is an eigenfunction of
is an eigenfunction of 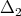 and
and 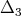 makes
makes 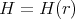 into an eigenfunction of certain differential operators
into an eigenfunction of certain differential operators 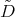 and
and 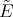 on
on 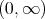 .
. Making the change of variables 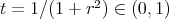 these operators become
these operators become 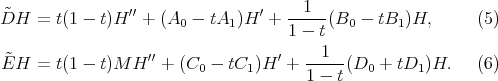
If we denote by 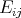 the
the 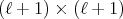 matrix with entry
matrix with entry 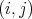 equal to 1 and 0 elsewhere, then the coefficient matrices are
equal to 1 and 0 elsewhere, then the coefficient matrices are 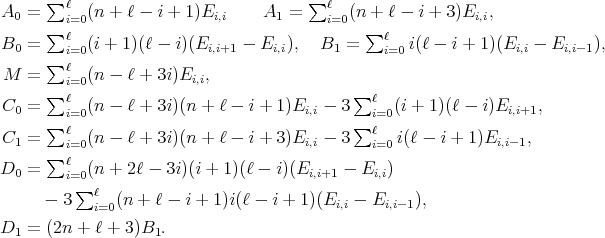
The following result, which characterizes the spherical functions associated to the complex projective plane is taken from Theorem 3.8 of [RT], see also [GPT1].
Theorem 2.1. The irreducible spherical functions 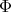 of
of 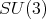 of type
of type 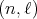 , correspond precisely to the simultaneous
, correspond precisely to the simultaneous 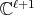 -valued polynomial eigenfunctions
-valued polynomial eigenfunctions 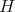 of the differential operators
of the differential operators 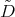 and
and 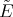 , introduced in (5) and (6), such that
, introduced in (5) and (6), such that 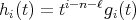 for all
for all 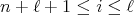 with
with 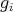 polynomial and
polynomial and 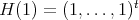 .
.
We also obtain, from [GPT1] or [PT1], that there is a bijective correspondence between the equivalence classes of all irreducible spherical functions 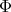 of type
of type 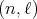 and the set of pairs of integers
and the set of pairs of integers
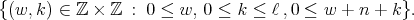 (7) (7) |
Under this correspondence the function 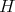 associated to the spherical function
associated to the spherical function 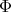 satisfies
satisfies  and
and  where
where
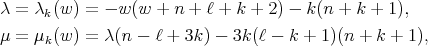 (8) (8) |
2.1. Hypergeometric operators. A key result to characterize the spherical functions of 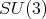 of any type
of any type 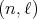 is the fact that the differential operator
is the fact that the differential operator 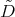 is conjugated, by a matrix polynomial function
is conjugated, by a matrix polynomial function 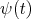 , to a hypergeometric operator
, to a hypergeometric operator 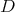 . From [RT], (or [PT2], for a more general situation) we obtain that the function
. From [RT], (or [PT2], for a more general situation) we obtain that the function 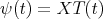 , where
, where
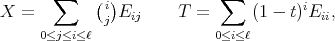
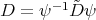 takes the hypergeometric form
takes the hypergeometric form 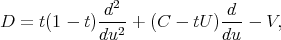 (9) (9) |
where the coefficient matrices are 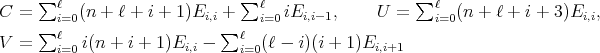
This fact allows us to describe the eigenfunctions of the differential operator 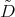 in term of the matrix valued hypergeometric functions, introduced in [T2]: Let
in term of the matrix valued hypergeometric functions, introduced in [T2]: Let 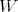 be a
be a 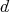 -dimensional complex vector space, and let
-dimensional complex vector space, and let 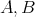 and
and 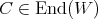 . The hypergeometric equation is
. The hypergeometric equation is 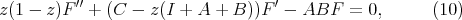
where 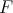 stands for a function of
stands for a function of  with values in
with values in 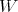 .
.
More generally we can consider the equation
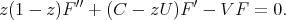 (11) (11) |
In the scalar case the differential operator (11) is always of the form (10). Nevertheless in a noncommutative setting the equations  and
and  may have no solutions
may have no solutions 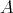 ,
, 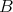 .
.
If the eigenvalues of  are not in
are not in 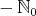 we define the function
we define the function
![( ) ∞∑ m 2H1 U ;V;z = z--[C; U ;V]m, C m=0 m!](/img/revistas/ruma/v49n2/2a02257x.png) (12) (12) |
where the symbol ![[C,U, V ]m](/img/revistas/ruma/v49n2/2a02258x.png) is defined inductively by
is defined inductively by ![[C; U ;V ]0 = I](/img/revistas/ruma/v49n2/2a02259x.png) and
and
![[C; U ;V] = (C + m )-1(m2 + m (U - 1) + V)[C; U;V ] , m+1 m](/img/revistas/ruma/v49n2/2a02260x.png) |
for all 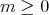 . The function
. The function 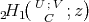 is analytic on
is analytic on  , with values in
, with values in 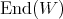 . Moreover if
. Moreover if 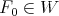 then
then 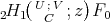 is a solution of the hypergeometric equation (11) such that
is a solution of the hypergeometric equation (11) such that 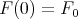 . Conversely any solution
. Conversely any solution 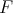 of (11), analytic at
of (11), analytic at  is of this form.
is of this form.
2.2. Spherical functions as matrix hypergeometric functions. The irreducible spherical functions of 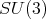 of type
of type 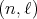 are in a one to one correspondence with certain simultaneous
are in a one to one correspondence with certain simultaneous 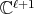 -polynomial eigenfunctions
-polynomial eigenfunctions 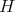 of the differential operators
of the differential operators 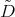 and
and 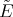 (see Theorem 2.1).
(see Theorem 2.1).
A delicate fact establish in [RT] is that the functions 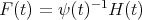 are also polynomials functions which are eigenfunctions of the differential operators
are also polynomials functions which are eigenfunctions of the differential operators 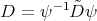 and
and 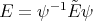 .
.
In the variable 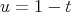 , these operators have the form
, these operators have the form
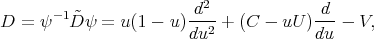 (13) (13) |
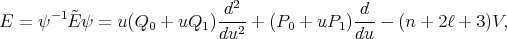 (14) (14) |
where the coefficient matrices are
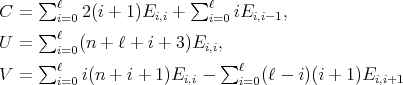 | (15) |
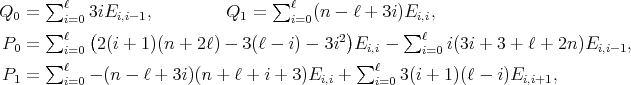
To describe all simultaneous 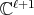 -polynomial eigenfunctions of the differential operators
-polynomial eigenfunctions of the differential operators 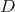 and
and 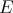 we start by considering the eigenfunctions of
we start by considering the eigenfunctions of 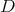 of eigenvalues
of eigenvalues 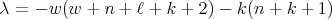 , with
, with 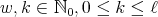 (see (8)). We let
(see (8)). We let
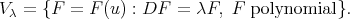
Remark. It is not difficult to prove that that 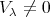 if and only if
if and only if 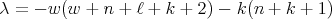 , for some
, for some 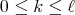 .
.
Therefore if 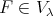 then it is of the form
then it is of the form
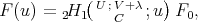
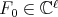 . The simultaneous eigenfunctions of
. The simultaneous eigenfunctions of 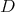 and
and 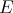 will correspond to particular choices of
will correspond to particular choices of  .
. Since the initial value 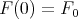 determines
determines 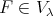 , we have that the linear map
, we have that the linear map  defined by
defined by 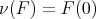 is a surjective isomorphism. Since
is a surjective isomorphism. Since 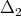 and
and 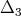 commute, the differential operators
commute, the differential operators 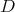 and
and 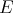 also commute. Moreover, since
also commute. Moreover, since 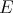 has polynomial coefficients whose degrees are less or equal to the corresponding orders of differentiation,
has polynomial coefficients whose degrees are less or equal to the corresponding orders of differentiation, 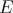 restricts to a linear operator of
restricts to a linear operator of 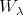 . Thus we have the following commutative diagram
. Thus we have the following commutative diagram
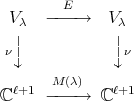 (16) (16) |
where 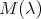 is the
is the 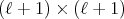 matrix given by
matrix given by
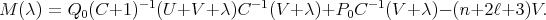 (17) (17) |
The eigenvalues of 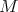 are given by (see Theorem 10.3 in [GPT1])
are given by (see Theorem 10.3 in [GPT1])

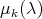 of
of 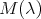 have geometric multiplicity one. In other words all eigenspaces are one dimensional. Moreover if
have geometric multiplicity one. In other words all eigenspaces are one dimensional. Moreover if 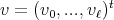 is a nonzero
is a nonzero 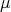 -eigenvector of
-eigenvector of 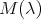 , then
, then 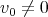 .
. The irreducible spherical functions of 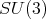 of type
of type 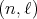 are parameterized by two nonnegative integers
are parameterized by two nonnegative integers 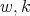 with
with 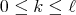 and
and  (see (7)). Under this correspondence the function
(see (7)). Under this correspondence the function 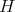 associated to the spherical function satisfies
associated to the spherical function satisfies  and
and  where
where
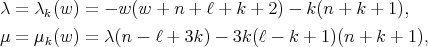 (18) (18) |
Then the characterization of the irreducible spherical functions is summarize in the following theorem, taking from [RT].
Theorem 2.2. The function 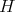 associated to a spherical function of type
associated to a spherical function of type 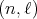 and parameters
and parameters 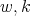 is of the form
is of the form 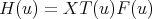 , where
, where 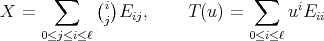
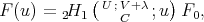 (19) (19) |
and  is the unique
is the unique 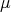 -eigenvector of
-eigenvector of 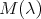 normalized by
normalized by 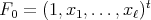 . The expressions of the matrices
. The expressions of the matrices 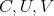 are given in (15) and the eigenvalues
are given in (15) and the eigenvalues 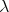 and
and 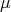 are given in (18).
are given in (18).
2.3. Orthogonality. Let 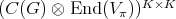 be the space of all continuous functions
be the space of all continuous functions 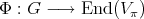 such that
such that 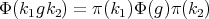 for all
for all 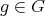 ,
, 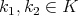 . Let us equip
. Let us equip 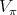 with an inner product such that
with an inner product such that 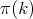 becomes unitary for all
becomes unitary for all 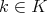 . We have the following inner product in
. We have the following inner product in 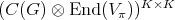 :
:
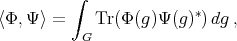 (20) (20) |
where 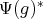 denotes the adjoint of
denotes the adjoint of 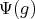 with respect to the inner product in
with respect to the inner product in 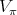 . Then we have the following inner product on the corresponding functions
. Then we have the following inner product on the corresponding functions 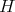 's associated to the spherical functions
's associated to the spherical functions
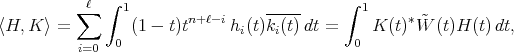 (21) (21) |
where
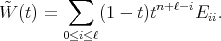
Since the Casimir operator is symmetric with respect to the 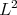 -inner product for matrix valued functions on
-inner product for matrix valued functions on 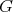 given in (20), it follows that the differential operators
given in (20), it follows that the differential operators 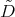 and
and 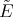 are symmetric with respect to the weight function
are symmetric with respect to the weight function 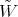 , that is they satisfy
, that is they satisfy
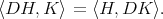
Now it is easy to verify that the differential operators 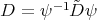 and
and 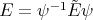 are symmetric with respect to the weight function
are symmetric with respect to the weight function 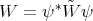
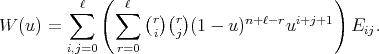 (22) (22) |
To illustrate the above result we will display the cases  (the scalar case) and
(the scalar case) and  , where the size of our matrices will be
, where the size of our matrices will be  .
.
3.1. The case  .. In this case the functions
.. In this case the functions 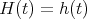 are scalar functions. If the parameter
are scalar functions. If the parameter 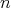 is 0 then we have the zonal spherical functions.
is 0 then we have the zonal spherical functions.
The operator 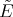 is proportional to
is proportional to 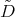 , (
, (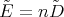 ) and
) and
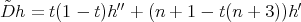
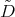 we put
we put 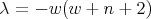 . Then
. Then 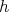 should be a solution of the hypergeometric equation with
should be a solution of the hypergeometric equation with 
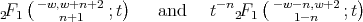 |
are linearly independent solutions. By Theorem 2.1 we have that 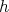 should be a polynomial function such that
should be a polynomial function such that 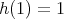 . Moreover if
. Moreover if 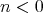 the function
the function 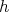 have to satisfies
have to satisfies 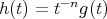 with
with 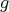 a polynomial function. Therefore we get: For
a polynomial function. Therefore we get: For 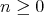 and
and 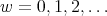
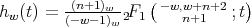
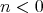 and
and 
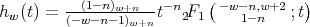
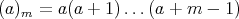 , for
, for 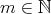 and
and 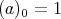 .
. By using the Pfaff's identity we get
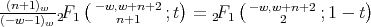
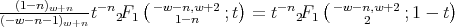
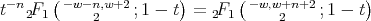
Therefore we obtain that
Proposition 3.1. The spherical functions associated to the complex projective plane of type 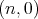 are
are
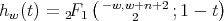
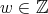 ,
, 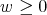 and
and 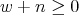 . Moreover these functions satisfy
. Moreover these functions satisfy 
3.2. The case  . In this case the operators
. In this case the operators 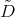 and
and 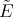 are
are 
In [GPT1], Section 11.1 we exhibit the complete list of spherical function of type 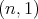 . We have two families of such functions, corresponding with the choice of the parameter
. We have two families of such functions, corresponding with the choice of the parameter  or
or  . For
. For 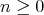 the parameter
the parameter 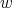 is in the range
is in the range 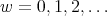 , and if
, and if 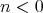
 .
.
First family. For  we have
we have 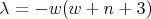 ,
, 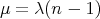 . The (vector valued) function
. The (vector valued) function 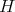 is given by, up to the normalizing constant such that
is given by, up to the normalizing constant such that 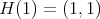 .
.
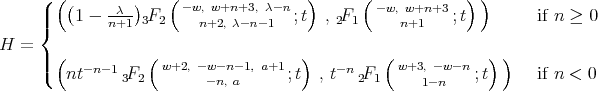
with 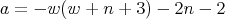 .
.
Second family. For  we have
we have 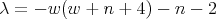 and
and 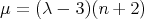 . The functions
. The functions 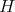 is
is
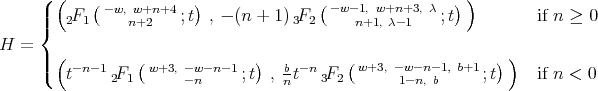
with 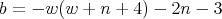 .
.
By taking the Taylor expansion at  these functions takes the following unified expression. We recall that
these functions takes the following unified expression. We recall that  corresponds to the identity of the group
corresponds to the identity of the group 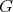 .
.
Theorem 3.2. The complete list of spherical functions associated to 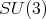 of type
of type 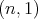 are given by
are given by
- For
 we have
we have 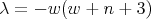 ,
, 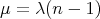 and
and 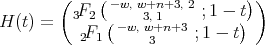
The parameter
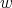 is an integer that satisfies
is an integer that satisfies  and
and 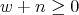 .
. - For
 , we have
, we have 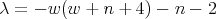 ,
, 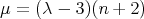 and
and 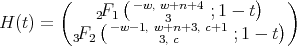
where
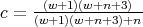 .
.
The parameter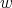 is an integer that satisfies
is an integer that satisfies  and
and  .
.
In this case the function 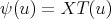 , where
, where 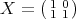 and
and 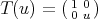 is
is
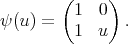 (24) (24) |
In the variable 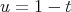 , the conjugated operators
, the conjugated operators 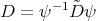 and
and 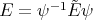 are
are
 (25) (25) |
The matrix 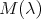 (see (17)), is
(see (17)), is
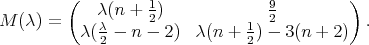
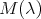 are
are 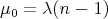 and
and 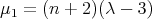 and the respective normalized eigenvectors are
and the respective normalized eigenvectors are 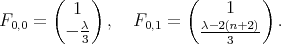
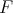 associated to the spherical functions are, for
associated to the spherical functions are, for 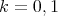 ,
, 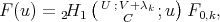
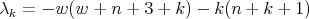 ,
, 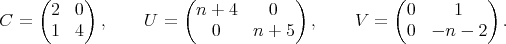
The explicit expression of the entries of these functions 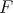 's are given in the following theorem.
's are given in the following theorem.
Theorem 3.3. The functions 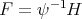 associated to the spherical functions of the pair
associated to the spherical functions of the pair 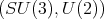 of type
of type 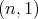 are given by
are given by
- For
 we have
we have 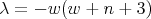 ,
, 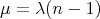 and
and 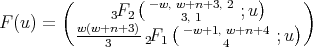
The parameter
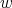 is an integer that satisfies
is an integer that satisfies  and
and 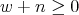 .
. - For
 , we have
, we have 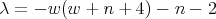 ,
, 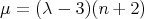 and
and where
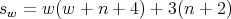 .
.
The parameter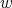 is an integer that satisfies
is an integer that satisfies  and
and  .
.
Proof. If 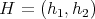 is an eigenfunction of
is an eigenfunction of 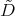 then
then 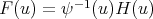 is an eigenfunction of
is an eigenfunction of 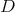 with the same eigenvalue. Explicitly the function
with the same eigenvalue. Explicitly the function 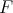 is
is
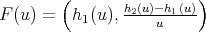 (26) (26) |
From
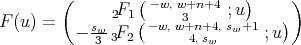 |
(26) we only have to prove the expression for the second entry of the function 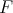 . For the first family, from Theorem 3.2 we get
. For the first family, from Theorem 3.2 we get 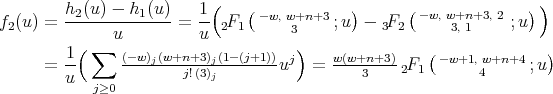
For the second family we obtain, with 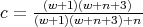
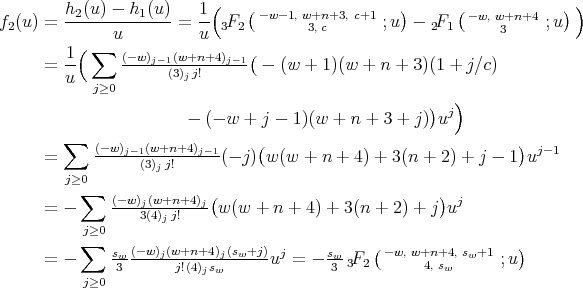
This concludes the proof of the theorem. □
3.3. Matrix valued orthogonal polynomials coming from spherical functions. In the scalar case, it is well known that the zonal spherical functions of the sphere 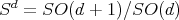 are given, in spherical coordinates, in terms of Gegenbauer polynomials. Therefore, it is not surprising that in the matrix valued setting the same phenomenon occurs: the matrix spherical functions are closely related to matrix orthogonal polynomials.
are given, in spherical coordinates, in terms of Gegenbauer polynomials. Therefore, it is not surprising that in the matrix valued setting the same phenomenon occurs: the matrix spherical functions are closely related to matrix orthogonal polynomials.
For a given nonnegative integers 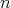 and
and 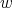 we define the matrix polynomial
we define the matrix polynomial 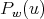 as the
as the  matrix function whose
matrix function whose 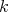 -row is the polynomial
-row is the polynomial 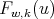 , associated to the spherical functions of type
, associated to the spherical functions of type 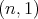 , given in the previous section. In other words
, given in the previous section. In other words
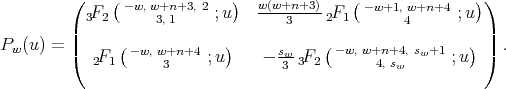
 .
. Since different spherical functions are orthogonal with respect to the natural inner product among these functions, we obtain that the matrices 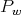 are orthogonal with respect to the weight function
are orthogonal with respect to the weight function 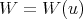 :
:
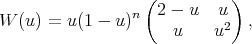
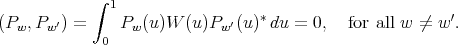
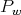 is a triangular nonsingular matrix. Therefore
is a triangular nonsingular matrix. Therefore 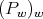 is a sequence of matrix valued orthogonal polynomials with respect to the weight matrix
is a sequence of matrix valued orthogonal polynomials with respect to the weight matrix 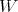 .
. The columns of 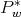 are eigenfunctions of the differential operators
are eigenfunctions of the differential operators 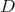 and
and 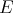 given in (25), thus we have that
given in (25), thus we have that 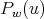 satisfies
satisfies

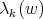 and
and 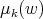 are
are 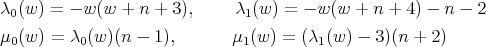
3.4. Extension of the group parameters. These results have a direct and fruitful generalization by replacing the complex projective plane by the 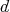 -dimensional complex projective space
-dimensional complex projective space 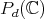 , which can be realized as the homogeneous space
, which can be realized as the homogeneous space 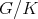 , where
, where 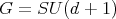 and
and 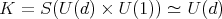 .
.
In this case, the finite dimensional irreducible representations of 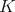 , are parameterized by the
, are parameterized by the 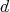 -tuples of integers
-tuples of integers 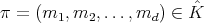 such that
such that 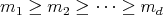 . By considering the irreducible spherical functions of type
. By considering the irreducible spherical functions of type 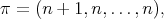 and proceeding as we explained for the complex projective plane, one obtains a situation that generalizes the one of
and proceeding as we explained for the complex projective plane, one obtains a situation that generalizes the one of  . Then by extending the parameters
. Then by extending the parameters 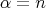 ,
, 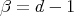 we have the following results.
we have the following results.
Theorem 3.4. Let 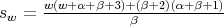 and let us define
and let us define
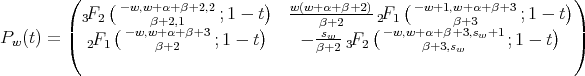
Then
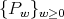 is a sequence of orthogonal polynomials with respect the weight matrix
is a sequence of orthogonal polynomials with respect the weight matrix 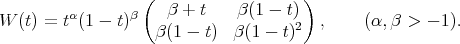
Let 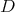 be the following second order differential operator
be the following second order differential operator
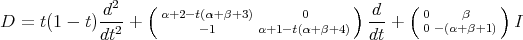
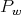 satisfies
satisfies 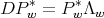
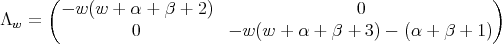
In [PT1] for  or in general in [P08], we obtain a multiplication formula for spherical functions by tensoring certain irreducible representations of
or in general in [P08], we obtain a multiplication formula for spherical functions by tensoring certain irreducible representations of 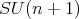 and decomposing them into irreducible representations. From this formula we derive a three term recursion relation for the "packages" of spherical functions. Restricting this to the variable
and decomposing them into irreducible representations. From this formula we derive a three term recursion relation for the "packages" of spherical functions. Restricting this to the variable 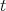 (the variable that parameterizes a section of the
(the variable that parameterizes a section of the 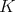 -orbits in
-orbits in 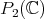 ), we obtain a three term recursion relation for the packages of functions
), we obtain a three term recursion relation for the packages of functions 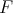 associated to the spherical functions. In this case we obtain the following
associated to the spherical functions. In this case we obtain the following
Theorem 3.5. The sequence 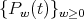 satisfies the following three term recursion relation
satisfies the following three term recursion relation
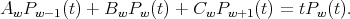 |
with
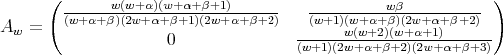
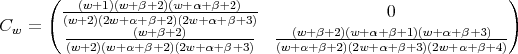
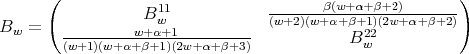
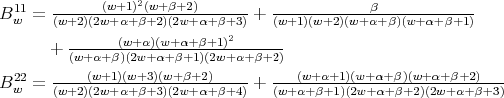
Remark 3.6. The three term recursion relation can be seen as a difference operator in the variable 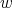 , given by a semiinfinite matrix
, given by a semiinfinite matrix 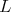 . The vector matrix
. The vector matrix 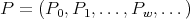 is an eigenfunction of
is an eigenfunction of 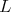 because it satisfies
because it satisfies 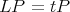 .
.
We observe that the semiinfinte matrix 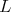 have the interesting property that the sum of all the matrix elements in any row is equal to one. Moreover all the entries of
have the interesting property that the sum of all the matrix elements in any row is equal to one. Moreover all the entries of 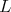 are nonnegative real numbers. This have important applications in the modeling of some stochastic phenomena.
are nonnegative real numbers. This have important applications in the modeling of some stochastic phenomena.
[GV] Gangolli R. and Varadarajan V. S. Harmonic analysis of spherical functions on real reductive groups, Springer-Verlag, Berlin, New York, 1988. Series title: Ergebnisse der Mathematik und ihrer Grenzgebiete, 101. [ Links ]
[GPT1] F. A. Grünbaum, I. Pacharoni and J. Tirao, Matrix valued spherical functions associated to the complex projective plane, J. Funct. Anal. 188 (2002), 350-441. [ Links ]
[P08] Pacharoni I.Three term recursion relation for spherical functions. Preprint, 2008. [ Links ]
[PT1] Pacharoni I. and Tirao J. A. Three term recursion relation for spherical functions associated to the complex projective plane. Math Phys. Anal. Geom. 7 (2004), 193-221. [ Links ]
[PT2] Pacharoni I. and Tirao J. A. Matrix valued orthogonal polynomials arising from the complex projective space. Constr. Approxim. 25, No. 2 (2007) 177-192. [ Links ]
[PR] Pacharoni, I. Román, P. A sequence of matrix valued orthogonal polynomials associated to spherical functions Constr. Approxim. 28, No. 2 (2008) 127-147. [ Links ]
[RT] P. Román and J. A. Tirao. Spherical functions, the complex hyperbolic plane and the hypergeometric operator. Intern. J. Math. 17, No. 10, (2006), 1151-1173. [ Links ]
[T1] J. Tirao. Spherical Functions. Rev. de la Unión Matem. Argentina, 28 (1977), 75-98. [ Links ]
[T2] J. Tirao, The matrix-valued hypergeometric equation. Proc. Natl. Acad. Sci. U.S.A., 100 No. 14 (2003), 8138-8141. [ Links ]
I. Pacharoni
CIEM-FaMAF,
Universidad Nacional de Córdoba,
Córdoba 5000, Argentina
pacharon@mate.uncor.edu
Recibido: 18 de mayo de 2008
Aceptado: 11 de agosto de 2008














