Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932versão On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.49 n.2 Bahía Blanca jul./dez. 2008
Weighted inequalities for generalized fractional operators
María Silvina Riveros
Abstract. In this note we present weighted Coifman type estimates, and two-weight estimates of strong and weak type for general fractional operators. We give applications to fractional operators given by an homogeneous function, and by a Fourier multiplier. The complete proofs of these results appear in the work [5] done jointly with Ana L. Bernardis and María Lorente.
2000 Mathematics Subject Classification. 42B20, 42B25.
Key words and phrases. Fractional integrals, Hörmander's condition of Young type, Muckenhoupt weights, two-weight estimates.
The author is partially supported by CONICET, Agencia Nación, and SECYT-UNC
1. Introduction and preliminaries
I would like to dedicate this note in memory of Dr Carlos Segovia. First we will give some basic definitions and preliminaries needed to state the results. Let us recall some of the background on Orlicz spaces. (See [24] and [21] to complete this topic.)
A function 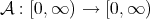 is a Young function if it is continuous, convex, increasing and satisfies
is a Young function if it is continuous, convex, increasing and satisfies  and
and 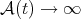 as
as 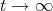 .
.
Given a Young function 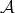 , we define the
, we define the 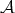 -mean Luxemburg norm of a function
-mean Luxemburg norm of a function 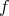 on a cube (or a ball)
on a cube (or a ball)  in
in 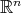 by
by
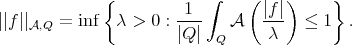 (1.1) (1.1) |
It is well known that if 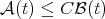 for all
for all 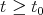 then
then 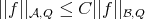 , for all cubes
, for all cubes  and functions
and functions 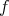 . Thus, the behavior of
. Thus, the behavior of 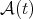 for
for  is not important. If
is not important. If 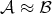 , that is there are constants
, that is there are constants 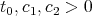 such that
such that 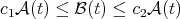 for
for  , the latter estimate implies that
, the latter estimate implies that 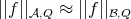 .
.
Each Young function 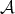 has an associated complementary Young function
has an associated complementary Young function 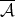 satisfying
satisfying
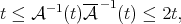 |
for all  . There is a generalization of Hölder's inequality
. There is a generalization of Hölder's inequality
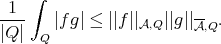 (1.2) (1.2) |
A further generalization of Hölder's inequality (see [21]) that will be useful later is the following: If 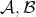 and
and  are Young functions and
are Young functions and
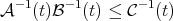
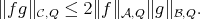 (1.3) (1.3) |
When 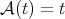 we understand that
we understand that 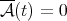 if
if 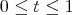 and
and 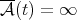 otherwise. Then
otherwise. Then 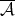 is not a Young function, but
is not a Young function, but  and the latter inequalities make sense if one of the functions is
and the latter inequalities make sense if one of the functions is 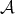 or
or 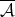 .
.
For each locally integrable function 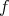 and
and 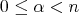 , the fractional maximal operator associated to the Young function
, the fractional maximal operator associated to the Young function 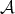 is defined by
is defined by
 we write
we write  instead of
instead of  . When
. When 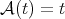 then
then 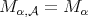 is the classical fractional maximal operator. For
is the classical fractional maximal operator. For  and
and 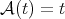 we obtain
we obtain 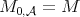 , the Hardy-Littlewood maximal operator. Consider the case
, the Hardy-Littlewood maximal operator. Consider the case  , for
, for 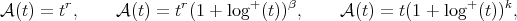
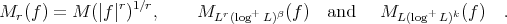
 ,
, 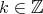 , then
, then 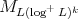 is pointwise equivalent to
is pointwise equivalent to 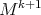 , where
, where 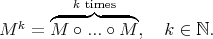 It is also easy to check that if
It is also easy to check that if 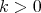 and
and 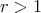 , then
, then 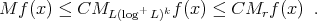
The good weights for 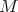 are those in the
are those in the 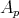 classes of Muckenhoupt (see [19] and also [26] and [18] for the one-sided case).
classes of Muckenhoupt (see [19] and also [26] and [18] for the one-sided case).
The good weights for the 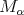 maximal operator are the
maximal operator are the 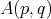 classes. It is proved in [20] ( see [1] for the one sided version) that
classes. It is proved in [20] ( see [1] for the one sided version) that 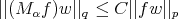 if and only if
if and only if 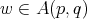 , for
, for 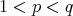 ,
, 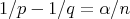 , where
, where
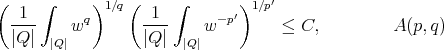
 .
. Also observe that for the case  ,
, 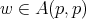 is equivalent to say that
is equivalent to say that 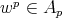 .
.
Let us define a generalization of the Hörmander condition, for a given kernel 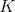 . We used the notation:
. We used the notation: 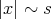 for
for 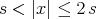 and
and 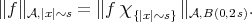
Definition 1.1. Let 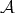 be a Young function and let
be a Young function and let 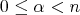 . The kernel
. The kernel 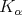 is said to satisfy the
is said to satisfy the 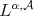 -Hörmander type condition, we write
-Hörmander type condition, we write 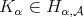 , if there exist
, if there exist  ,
, 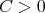 such that for any
such that for any 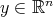 and
and 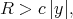
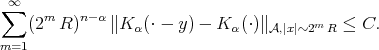
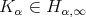 if
if 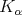 satisfies the previous condition with
satisfies the previous condition with 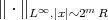 in place of
in place of  .
. Definition 1.2. The kernel 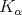 is said to satisfy the
is said to satisfy the 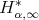 condition, if there exist
condition, if there exist  ,
, 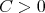 such that
such that
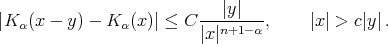
Observe that when  we obtain that
we obtain that 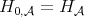 defined in [16].
defined in [16].
If 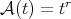 , for
, for  , then we write
, then we write 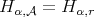 . This
. This 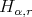 condition appears implicitly in [12]. On the other hand, since
condition appears implicitly in [12]. On the other hand, since 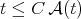 for
for  we have that
we have that 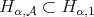 . Also, it is easy to see that
. Also, it is easy to see that 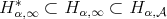 .
.
Suppose that 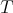 is an operator given by convolution with a kernel
is an operator given by convolution with a kernel 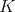 which satisfies some regularity condition and suppose that we know some behavior of
which satisfies some regularity condition and suppose that we know some behavior of 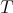 with respect to the Lebesgue's measure (weak or strong type inequalities for
with respect to the Lebesgue's measure (weak or strong type inequalities for 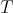 ). Sometimes, in order to know how is the behavior of
). Sometimes, in order to know how is the behavior of 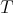 when we change the measure, (i.e., when we consider the measure
when we change the measure, (i.e., when we consider the measure 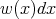 where
where 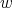 is a weight, (
is a weight, (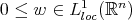 )) the following inequality is useful (we call it a Coifman type inequality)
)) the following inequality is useful (we call it a Coifman type inequality)
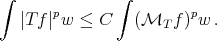 (1.4) (1.4) |
Here 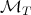 is a maximal operator related to the operator
is a maximal operator related to the operator 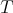 which is normally easier to deal with. In general,
which is normally easier to deal with. In general, 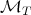 is strongly related with the kernel
is strongly related with the kernel 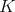 and its size is inverse to the smoothness of
and its size is inverse to the smoothness of 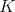 : the rougher the kernel, the bigger the maximal.
: the rougher the kernel, the bigger the maximal.
For 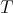 a Calderón-Zygmund singular integral operator (i.e.,
a Calderón-Zygmund singular integral operator (i.e., 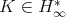 , see Definition 1.2, for
, see Definition 1.2, for  ) inequality (1.4) holds with
) inequality (1.4) holds with 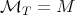 , the Hardy-Littlewood maximal function,
, the Hardy-Littlewood maximal function, 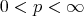 , and
, and 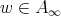 (see [8]).
(see [8]).
If 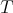 is a singular integral operator with less regular kernel, (see [13]) for example if the kernel
is a singular integral operator with less regular kernel, (see [13]) for example if the kernel 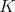 satisfies an
satisfies an 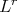 -Hörmander condition (Definition 1.1, for
-Hörmander condition (Definition 1.1, for 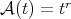 and
and  ), then inequality (1.4) holds with
), then inequality (1.4) holds with  , with
, with 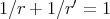 , for all
, for all 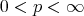 , and
, and 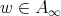 (see [25]).
(see [25]).
For a Young function 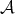 , the
, the 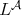 -Hörmander condition is introduced in [16], which generalized in the scale of the Orlicz spaces the
-Hörmander condition is introduced in [16], which generalized in the scale of the Orlicz spaces the 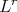 -Hörmander condition. In [16] the authors showed that, if the kernel
-Hörmander condition. In [16] the authors showed that, if the kernel 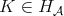 (Definition 1.1, for
(Definition 1.1, for  ), then inequality (1.4) holds with
), then inequality (1.4) holds with 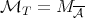 , where
, where 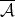 is the complementary function of
is the complementary function of 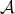 , for all
, for all 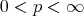 , and
, and 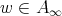 .
.
The differential transform operator was studied in [11] and [3]. In [14] it is proved an inequality of the type (1.4), by showing that the kernel satisfies the 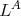 -Hörmander condition for
-Hörmander condition for 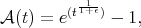 (
(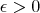 ). Therefore, this operator satisfies inequality (1.4) with the maximal operator
). Therefore, this operator satisfies inequality (1.4) with the maximal operator 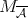 , where
, where 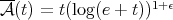 (actually they obtain a smaller operator since
(actually they obtain a smaller operator since 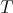 is a one-sided operator, because
is a one-sided operator, because 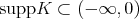 ).
).
The Coifman type inequality allows us to obtain, for general linear operators, two-weight inequalities of the type
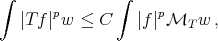 (1.5) (1.5) |
for 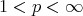 and in the endpoint case
and in the endpoint case 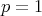 ,
,
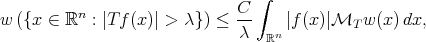 (1.6) (1.6) |
for every weight 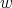 , with no assumptions on
, with no assumptions on 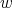 . The operators
. The operators 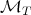 are again suitable maximal operators related with
are again suitable maximal operators related with 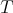 and not necessarily the same for inequalities (1.4), (1.5) and (1.6).
and not necessarily the same for inequalities (1.4), (1.5) and (1.6).
There is a great amount of works that deal with inequalities of the type (1.5) and (1.6). When 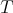 is a Calderón-Zygmund operator (with kernel
is a Calderón-Zygmund operator (with kernel 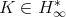 ), inequality (1.5) holds with
), inequality (1.5) holds with ![[p]+1 MT = M](/img/revistas/ruma/v49n2/2a04165x.png) , where
, where ![[p]](/img/revistas/ruma/v49n2/2a04166x.png) is the integer part of
is the integer part of 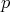 (see [22]). In the endpoint case
(see [22]). In the endpoint case 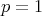 , inequality (1.6) for Calderón-Zygmund operators hold with
, inequality (1.6) for Calderón-Zygmund operators hold with 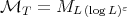 , for any
, for any 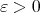 , where
, where 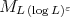 is the maximal function associated to the Young function
is the maximal function associated to the Young function 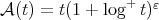 . This result was proved by Carlos Pérez in [22]. For
. This result was proved by Carlos Pérez in [22]. For 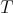 a singular integral associated to a kernel K satisfying a general Hörmander's condition given by a Young function
a singular integral associated to a kernel K satisfying a general Hörmander's condition given by a Young function 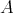 , the corresponding results, that include as particular cases those of C. Pérez, has been proved in [14] and [15].
, the corresponding results, that include as particular cases those of C. Pérez, has been proved in [14] and [15].
In 1974, Muckenhoupt and Wheeden [20] proved inequality (1.4) for 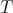 the classical Riesz potential
the classical Riesz potential 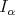 and
and 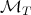 the fractional maximal function
the fractional maximal function 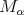 , defined for
, defined for 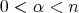 and locally integrable function
and locally integrable function 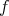 by
by
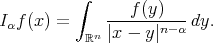
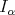 ,
, 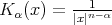 , belongs to
, belongs to 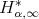 . For
. For 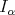 , inequality (1.5) holds with
, inequality (1.5) holds with ![MT = M αp(M [p])](/img/revistas/ruma/v49n2/2a04186x.png) (this result is also due to Carlos Pérez, see [23]). On the other hand, inequality (1.6) for
(this result is also due to Carlos Pérez, see [23]). On the other hand, inequality (1.6) for 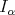 holds with
holds with 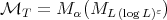 in [6] (see also [2]).
in [6] (see also [2]). There are fractional integrals with less regular kernel than the Riesz transform (see for example [7], [12], [27], [20], [9], [10]). Suppose that 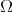 is homogeneous of degree zero and
is homogeneous of degree zero and 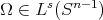 , where
, where 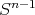 denotes the sphere of
denotes the sphere of 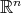 and
and  . Define the fractional integral associated to
. Define the fractional integral associated to 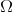 by
by
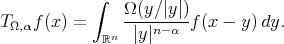
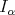 given by Muckenhoupt and Wheeden in [20]. In a more general context and with an aditional condition in
given by Muckenhoupt and Wheeden in [20]. In a more general context and with an aditional condition in 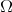 , that is,
, that is, 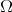 satisfying the
satisfying the 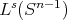 -Dini smoothness condition, Segovia and Torrea [27], studied the good weights for this operator and its commutators, using extrapolation theorems.
-Dini smoothness condition, Segovia and Torrea [27], studied the good weights for this operator and its commutators, using extrapolation theorems. In this note we state and briefly sketch the proofs of the corresponding results for general fractional integrals 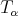 ,
, 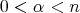 , given by convolution with a kernel
, given by convolution with a kernel 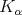 which satisfy a
which satisfy a 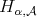 condition, for appropriate Young functions
condition, for appropriate Young functions 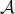 (see Theorems 2.1, 2.3 and 2.5).
(see Theorems 2.1, 2.3 and 2.5).
From now on, for 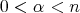 ,
, 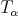 will be a fractional operator bounded from
will be a fractional operator bounded from 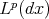 to
to  , for all
, for all 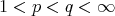 satisfying
satisfying 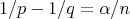 .
.
Theorem 2.1. Let 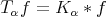 be a fractional operator given by a kernel
be a fractional operator given by a kernel 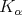 . Suppose
. Suppose 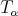 is of weak-type
is of weak-type 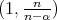 .
.

-
If
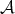 be a Young function and
be a Young function and 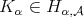 , then for any
, then for any 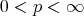 and
and 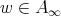 ,
,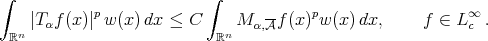 (2.1)
(2.1) 
-
Moreover, if the kernel
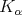 is supported in
is supported in  , then for any
, then for any 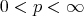 ,
, 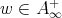 , it follows that (2.1) holds with
, it follows that (2.1) holds with 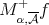 in place of
in place of 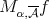 where
where 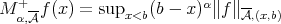 .
.
Remark 2.2. Observe that we can apply the theorem to 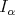 and
and 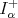 (respectively) obtaining the result in [20] and [17], for
(respectively) obtaining the result in [20] and [17], for 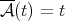 .
.
Proof. To prove this Theorem we use the sharp operator of 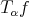 . Given
. Given 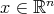 and a cube
and a cube 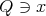 , decompose
, decompose 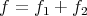 , where
, where 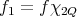 and
and 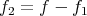 . For
. For  we use Kolmogorov and that
we use Kolmogorov and that 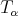 is of weak-type
is of weak-type 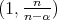 . For the global part we use that
. For the global part we use that 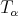 is the convolution with the kernel
is the convolution with the kernel 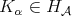 and the generalized Hölders inequality. □
and the generalized Hölders inequality. □
Theorem 2.3. Let 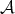 be a Young function and
be a Young function and 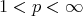 . Suppose that there exist Young functions
. Suppose that there exist Young functions 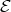 ,
, 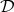 such that
such that 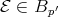 and
and 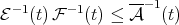 with
with 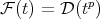 . Let
. Let 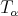 be a linear operator such that its adjoint
be a linear operator such that its adjoint 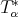 satisfies
satisfies
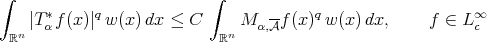 (2.2) (2.2) |
for all 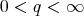 and
and 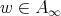 . Then, for
. Then, for  and for any weight
and for any weight 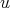 ,
,
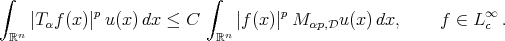 (2.3) (2.3) |
Remark 2.4. For the applications below, and since all our operators are of convolution type, proving (2.2) for 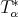 or
or 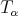 turns out to be equivalent.
turns out to be equivalent.
Proof. To prove this Theorem we use duality and apply Theorem 2.1. To do this we need the fact that the weight 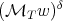 belongs to
belongs to 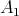 , for all
, for all 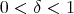 and any
and any 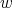 . For the maximal operators
. For the maximal operators 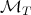 that appears in this proof, has been proved in [4]. □
that appears in this proof, has been proved in [4]. □
Theorem 2.5. Let 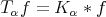 be a fractional operator. Suppose that there exists
be a fractional operator. Suppose that there exists 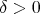 such that for any
such that for any 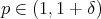 , there exists a Young function
, there exists a Young function 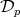 satisfying
satisfying
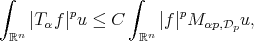 (2.4) (2.4) |
for all weight 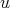 . If
. If 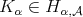 , then for any weight
, then for any weight 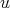 ,
,
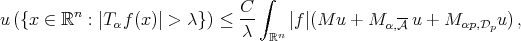 (2.5) (2.5) |
for all 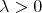 .
.
3.1. Fractional integrals associated to a homogeneous function. Denote by 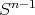 the unit sphere on
the unit sphere on 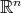 . For
. For 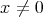 , we write
, we write 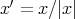 . Let us consider
. Let us consider 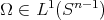 . This function can be extended to
. This function can be extended to 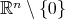 as
as 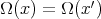 (abusing on the notation we call both functions
(abusing on the notation we call both functions 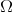 ). Thus
). Thus 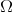 is a function homogeneous of degree
is a function homogeneous of degree 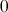 . Let
. Let 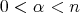 , and let
, and let 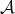 be a Young function such that
be a Young function such that 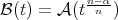 is also a Young function. Let
is also a Young function. Let 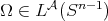 and satisfying the
and satisfying the 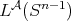 -Dini smoothness condition, i.e.,
-Dini smoothness condition, i.e.,
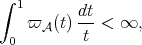 (3.1) (3.1) |
where
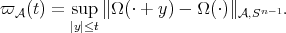
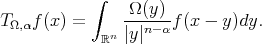
 and
and  it is easy to see that
it is easy to see that 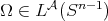 implies
implies 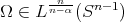 . Then, by the result in [7],
. Then, by the result in [7], 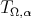 is of weak type
is of weak type 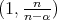 , with respect to the Lebesgue's measure and is bounded from
, with respect to the Lebesgue's measure and is bounded from 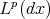 to
to  , whenever
, whenever 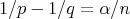 ,
, 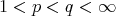 . We can prove (as in [14]) that the kernel
. We can prove (as in [14]) that the kernel 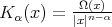 satisfies the
satisfies the 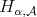 condition. Therefore Theorems 2.1, 2.3 and 2.5 can be applied to the operator
condition. Therefore Theorems 2.1, 2.3 and 2.5 can be applied to the operator 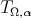 .
. In the particular case that 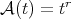 with
with 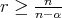 we get the following:
we get the following:
Theorem 3.1. Let 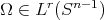 be as above and satisfying the
be as above and satisfying the 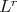 -Dini condition.
-Dini condition.
In both cases  and
and 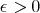 is small enough.
is small enough.
Proof. We only have to apply the theorems with the following Young functions: 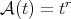 ,
, 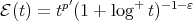 , and
, and 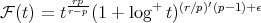 , where
, where 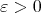 is some small enough number that is related with
is some small enough number that is related with 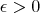 . Observe that in part (c) we obtain
. Observe that in part (c) we obtain 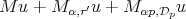 on the right hand side, but it is easy to see that
on the right hand side, but it is easy to see that 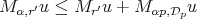 and
and  . □
. □
For 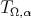 as above, we obtain the following weighted inequality as in [10] (see also [27]).
as above, we obtain the following weighted inequality as in [10] (see also [27]).
Corollary 3.2. Suppose that we are under the same hypothesis as in Theorem 3.1. Let 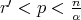 ,
, 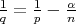 and
and 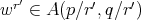 . Then
. Then
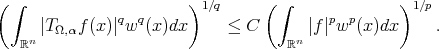
Proof. First of all observe that 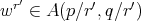 implies
implies 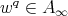 . Then by part (a) of Theorem 3.1
. Then by part (a) of Theorem 3.1
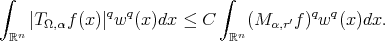
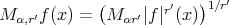 and
and 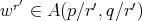 (see [20]) we have that
(see [20]) we have that 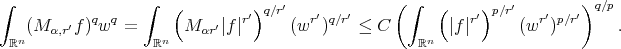
3.2. Fractional integrals associated to a multiplier. Let 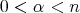 . Given a function
. Given a function 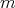 defined in
defined in 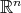 we consider the multiplier operator
we consider the multiplier operator 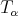 defined a priori for functions
defined a priori for functions 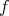 in the Schwartz class by
in the Schwartz class by 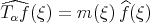 . Given
. Given 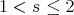 and
and 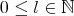 we say that
we say that 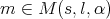 if there exists a constant
if there exists a constant 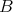 such that
such that  and
and
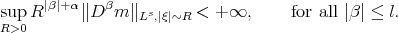
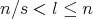 and
and 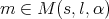 then
then 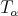 is bounded from
is bounded from 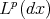 to
to  , for
, for 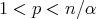 and
and 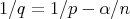 . If
. If 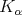 is the kernel of
is the kernel of 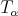 , he proved that
, he proved that 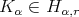 for all
for all 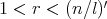 and, as a consequence, he obtained the following Coifman type inequality: for all
and, as a consequence, he obtained the following Coifman type inequality: for all 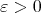 ,
, 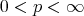 and
and 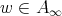 ,
, 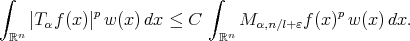 (3.5) (3.5) |
Now we can apply Theorems 2.3 and 2.5 to this operator.
Theorem 3.3. If 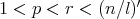 and
and 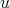 a weight, then
a weight, then
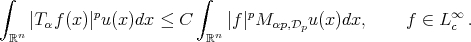 (3.6) (3.6) |
and
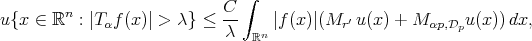 (3.7) (3.7) |
where 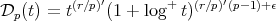 and
and 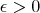 is small enough.
is small enough.
Observe that as  is at our choice, we can write
is at our choice, we can write 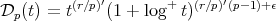
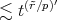 , for all
, for all 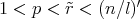 . Therefore, we can write
. Therefore, we can write  in (3.6) and (3.7).
in (3.6) and (3.7).
[1] K. F. Andersen and E. T. Sawyer, Weighted norm inequalities for the Riemann-Liouville and Weyl fractional integral operators, Trans. Amer. Math. Soc. 308 (1988), 547-558. [ Links ]
[2] A.L. Bernardis, M. Lorente, Sharp two weight inequalities for commutators of Riemann-Liouville and Weyl fractional integral operator, Preprint. [ Links ]
[3] A.L. Bernardis, M. Lorente, F.J. Martín-Reyes, M.T. Martínez, A. de la Torre and J.L. Torrea, Differential transforms in weighted spaces, J. Fourier Anal. Appl. 12 (2006), no. 1, 83-103. [ Links ]
[4] A.L. Bernardis, M. Lorente, G. Pradolini, M.S. Riveros,Composition of fractional Orlicz maximal operators and 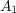 -weights on spaces of homogeneous type, Preprint. [ Links ]
-weights on spaces of homogeneous type, Preprint. [ Links ]
[5] A.L. Bernardis, M. Lorente, M.S. Riveros.On Weighted inequalities for generalized fractional integrals operators Preprint. [ Links ]
[6] M.J. Carro, C. Pérez, F. Soria and J. Soria, Maximal functions and the control of weighted inequalities for the fractional integral operator, Indiana Univ. Math. J. 54 (3) (2005), 627-644. [ Links ]
[7] S. Chanillo, D.K. Watson and R.L. Wheeden, Some integral and maximal operators related to starlike sets, Studia Math. 107(3) (1993), 223-255. [ Links ]
[8] R. Coifman, Distribution function inequalities for singular integrals, Proc. Acad. Sci. U.S.A. 69 (1972), 2838-2839. [ Links ]
[9] Y. Ding, Weak type bounds for a class of rough operators with power weights, Proc. Amer. Math. Soc. 125 (1997), no. 10, 2939-2942. [ Links ]
[10] Y. Ding and S. Lu, Weighted norm inequalities for fractional integral operators with rough kernel, Can. J. Math. 50 (1998), no. 1, 29-39. [ Links ]
[11] R.L. Jones and J. Rosenblatt, Differential and ergodic transform, Math. Ann. 323 (2002), 525-546. [ Links ]
[12] D.S. Kurtz, Sharp function estimates for fractional integrals and related operators, Trans. Amer. Math. Soc. 255 (1979), 343-362. [ Links ]
[13] D.S. Kurtz and R.L. Wheeden, Results on weighted norm inequalities for multipliers, J. Austral. Math. Soc. A 49 (1990), 129-137. [ Links ]
[14] M. Lorente, J.M. Martell, M.S. Riveros and A. de la Torre Generalized Hörmander's condition, commutators and weights, J. Math. Anal. Appl. (2008), doi:10.1016/j.jmaa.2008.01.003. [ Links ]
[15] M. Lorente, J.M. Martell, C. Pérez and M.S. Riveros Generalized Hörmander's conditions and weighted endpoint estimates, Preprint 2007. [ Links ]
[16] M. Lorente, M.S. Riveros and A. de la Torre, Weighted estimates for singular integral operators satisfying Hörmander's conditions of Young type, J. Fourier Anal. Apl. 11 (2005), no. 5, 497-509. [ Links ]
[17] F.J. Martín-Reyes and A. de la Torre, One Sided BMO Spaces, J. London Math. Soc. 2 (49) (1994), no. 3, 529-542. [ Links ]
[18] F.J. Martín-Reyes, P. Ortega and A. de la Torre, Weighted inequalities for one-sided maximal functions, Trans. Amer. Math. Soc. 319 (1990), no. 2, 517-534. [ Links ]
[19] B. Muckenhoupt, Weighted norm inequalities for the Hardy maximal function, Trans. Amer. Math. Soc. 165, (1972) 207-226. [ Links ]
[20] B. Muckenhoupt and R. L. Wheeden, Weighted norm inequalities for fractional integrals, Trans. Amer. Math. Soc. 192, (1974) 261-274. [ Links ]
[21] R. O'Neil, Fractional integration in Orlicz spaces, Trans. Amer. Math. Soc. 115, (1963) 300-328. [ Links ]
[22] C. Pérez, Weighted norm inequalities for singular integral operators,J. London Math. Soc.49 (1994) 296-308. [ Links ]
[23] C. Pérez, Sharp 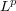 -weighted Sobolev inequalities, Ann. Inst. Fourier (Grenoble) 45 (3), (1995) 809-824. [ Links ]
-weighted Sobolev inequalities, Ann. Inst. Fourier (Grenoble) 45 (3), (1995) 809-824. [ Links ]
[24] M. Rao and Z.D. Ren, Theory of Orlicz spaces, Monographs and Textbooks in Pure and Applied Mathematics 146, Marcel Dekker, Inc., New York, 1991. [ Links ]
[25] J.L. Rubio de Francia, F.J. Ruiz and J. L. Torrea, Calderón-Zygmund theory for vector-valued functions, Adv. in Math. 62 (1986), 7-48. [ Links ]
[26] E. Sawyer, Weighted inequalities for the one-sided Hardy-Littlewood maximal functions. Trans. Amer. Math. Soc. 297 (1986), 53-61. [ Links ]
[27] C. Segovia and J.L. Torrea, Higher order commutators for vector-valued Calderón-Zygnund operators, Trans. Amer. Math. Soc. 336 (1993), 537-556. [ Links ]
M. S. Riveros
FaMAF,
Universidad Nacional de Córdoba,
CIEM (CONICET),
5000 Córdoba, Argentina
sriveros@mate.uncor.edu
Recibido: 10 de abril de 2008
Aceptado: 5 de junio de 2008














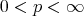 and
and 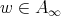 , then
, then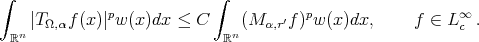 (3.2)
(3.2)
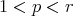 and
and 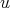 a weight, then
a weight, then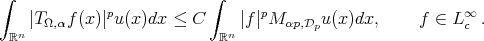 (3.3)
(3.3)
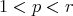 and
and 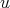 is a weight, then
is a weight, then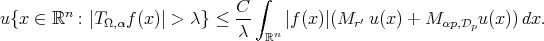 (3.4)
(3.4)