Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932On-line version ISSN 1669-9637
Rev. Unión Mat. Argent. vol.49 no.2 Bahía Blanca July/Dec. 2008
Quaternions and octonions in Mechanics
Aroldo Kaplan
This is a survey of some of the ways in which Quaternions, Octonions and the exceptional group 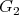 appear in today's Mechanics, addressed to a general audience.
appear in today's Mechanics, addressed to a general audience.
The ultimate reason of this appearance is that quaternionic multiplication turns the 3-sphere of unit quaternions into a group, acting by rotations of the 3-space of purely imaginary quaternions, by
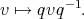
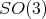 , the group of rotations of
, the group of rotations of 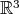 .
. This has been known for quite some time and is perhaps the simplest realization of Hamilton's expectations about the potential of quaternions for physics. One reason for the renewed interest is the fact that the resulting substitution of matrices by quaternions speeds up considerably the numerical calculation of the composition of rotations, their square roots, and other standard operations that must be performed when controlling anything from aircrafts to robots: four cartesian coordinates beat three Euler angles in such tasks.
A more interesting application of the quaternionic formalism is to the motion of two spheres rolling on each other without slipping, i.e., with infinite friction, which we will discuss here. The possible trajectories describe a vector 2-distribution on the 5-fold 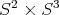 , which depends on the ratio of the radii and is completely non-integrable unless this ratio is 1. As pointed out by R. Bryant, they are the same as those studied in Cartan's famous 5-variables paper, and contain the following surprise: for all ratios different from 1:3 (and 1:1), the symmetry group is
, which depends on the ratio of the radii and is completely non-integrable unless this ratio is 1. As pointed out by R. Bryant, they are the same as those studied in Cartan's famous 5-variables paper, and contain the following surprise: for all ratios different from 1:3 (and 1:1), the symmetry group is 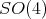 , of dimension 6; when the ratio is 1:3 however, the group is a 14-dimensional exceptional simple Lie group of type
, of dimension 6; when the ratio is 1:3 however, the group is a 14-dimensional exceptional simple Lie group of type 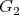 .
.
The quaternions  and (split) octonions
and (split) octonions 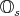 help to make this evident, through the inclusion
help to make this evident, through the inclusion

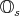 " in the 1:3 case. As a consequence,
" in the 1:3 case. As a consequence, 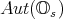 , which is preciely that exceptional group, acts by symmetries of the system.
, which is preciely that exceptional group, acts by symmetries of the system. This phenomenon has been variously described as "the 1:3 rolling mystery", "a mere curiosity", "uncanny" and "the first appearance of an exceptional group in real life". Be as it may, it is the subject of current research and speculation. For the history and recent mathematical developments of rolling systems, see [Agrachev][Bor-Montgomery][Bryant-Hsu][Zelenko].
The technological applications deserve a paragraph, given that this Volume is dedicated to the memory of somebody especially preoccupied with the misuse of beautiful scientific discoveries. Quaternions are used to control the flight of aircrafts due to the advantages already cited, and "aircrafts" include guided missiles. A look at the most recent literature reveals that research in the area is being driven largely with the latter in mind. Octonions and 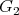 , on the other hand, although present in Physics via Joyce manifolds, seem to have had no technological applications so far - neither good nor bad. Still, the main application of Rolling Systems is to Robotics, a field with plenty to offer, of both kinds. The late Misha was rather pesimistic about the chances of the good eventually outweighting the bad. "Given the current state of the world", he said about a year before his death, "the advance of technology appears to be more dangerous than ever".
, on the other hand, although present in Physics via Joyce manifolds, seem to have had no technological applications so far - neither good nor bad. Still, the main application of Rolling Systems is to Robotics, a field with plenty to offer, of both kinds. The late Misha was rather pesimistic about the chances of the good eventually outweighting the bad. "Given the current state of the world", he said about a year before his death, "the advance of technology appears to be more dangerous than ever".
I would like to thank Andrei Agrachev for introducing me to the subject; John Baez, Gil Bor, Robert Bryant, Robert Montgomery and Igor Zelenko for enlightening exchanges; and the ICTP, for the fruitful and pleasant stay during which I became aquainted with Rolling Systems.
Recall the quaternions,
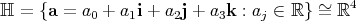
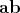 defined by the relations
defined by the relations 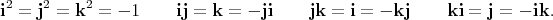
 is an associative algebra, like
is an associative algebra, like 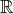 or
or  , where every non-zero element has an inverse, satisfying
, where every non-zero element has an inverse, satisfying 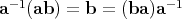 , i.e., it is a division algebra. But unlike
, i.e., it is a division algebra. But unlike 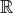 or
or  , it is clearly not commutative.
, it is clearly not commutative.  can also be defined as pairs of complex numbers - much as
can also be defined as pairs of complex numbers - much as  consists of pairs of real numbers. One sets
consists of pairs of real numbers. One sets

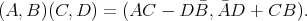
 ,
,  ,
, 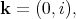 and the conjugation
and the conjugation 
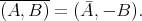
 shows that, just as in the case of
shows that, just as in the case of 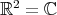 , the euclidean inner product in
, the euclidean inner product in 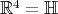 and the corresponding norm are
and the corresponding norm are 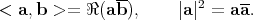
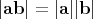 ,
, 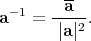
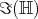 (= span of
(= span of 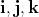 ) and the following fact: under quaternionic multiplication, the unit 3-sphere
) and the following fact: under quaternionic multiplication, the unit 3-sphere 
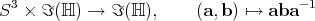
Inded, multiplying by a unit quaternion  on the left or on the right, is a linear isometry of
on the left or on the right, is a linear isometry of 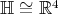 , as well as conjugating by it
, as well as conjugating by it
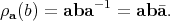
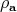 preserves
preserves 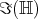 , since for an imaginary
, since for an imaginary 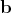 ,
, 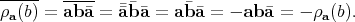 In fact,
In fact, 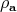 is isometry of
is isometry of 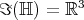 , i.e., an element of the orthogonal group
, i.e., an element of the orthogonal group 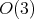 . Indeed,
. Indeed, 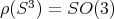 , because
, because 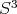 is compact and connected, and
is compact and connected, and 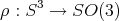
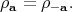
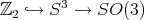
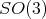 . In particular, the fundamental group of the rotation group is
. In particular, the fundamental group of the rotation group is 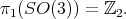
Quaternions themselves come in when fast computation of composition of rotations, or square roots thereof, are needed, as in the control of an aircraft. For this, one needs coordinates for the rotations - three of them, since SO(3) is the group de matrices
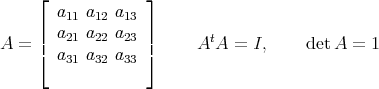
To coordinatize  one uses the Euler angles, or variations thereof, of a rotation, obtained by writing it as a product
one uses the Euler angles, or variations thereof, of a rotation, obtained by writing it as a product 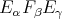 where
where
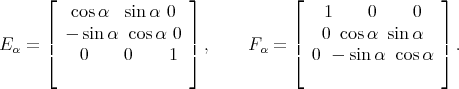
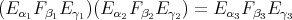
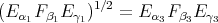
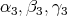 are complicated expressions in
are complicated expressions in 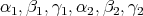 . Furthermore, when large rotations are involved, the multivaluedness and singularities of the Euler angles also lead to what numerical programmers know as "computational glitch". Instead,
. Furthermore, when large rotations are involved, the multivaluedness and singularities of the Euler angles also lead to what numerical programmers know as "computational glitch". Instead, 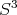 is easier to coordinatize, the formula for the quaternionic product is quadratic, and for
is easier to coordinatize, the formula for the quaternionic product is quadratic, and for 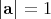 ,
, 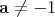 ,
, 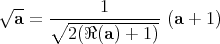
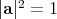 . There is an extensive recent literature assesing the relative computational advantages of each representation, easily found in the web.
. There is an extensive recent literature assesing the relative computational advantages of each representation, easily found in the web. The configuration space of a pair of adjacent spheres is 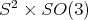 . Indeed, we can assume one of the spheres
. Indeed, we can assume one of the spheres 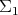 to be the unit sphere
to be the unit sphere 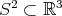 . Then, the position of the other sphere
. Then, the position of the other sphere 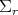 is given by the point of contact
is given by the point of contact 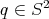 , together with an oriented orthonormal frame
, together with an oriented orthonormal frame 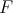 attached to
attached to 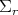 . This may be better visualized by substituting momentarely
. This may be better visualized by substituting momentarely 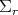 by an aircraft moving over the Earth
by an aircraft moving over the Earth 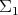 at a constant height, a system whose configuration space is the same (airplane pilots call the frame
at a constant height, a system whose configuration space is the same (airplane pilots call the frame 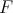 the "attitude" of the plane). Identifying
the "attitude" of the plane). Identifying 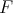 with the rotation
with the rotation 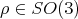 such that
such that 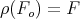 , where
, where 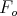 is the standard frame in
is the standard frame in 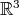 , the configuration is then given by the pair
, the configuration is then given by the pair
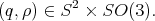
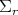 roll on
roll on 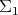 describing the curve
describing the curve 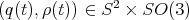 . The non-slipping condition is encoded into two equations, expressing the vanishing of the linear and of the angular components of the slipping ("no slipping or twisting"), namely
. The non-slipping condition is encoded into two equations, expressing the vanishing of the linear and of the angular components of the slipping ("no slipping or twisting"), namely 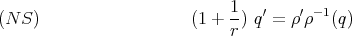

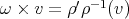 is the angular velocity of
is the angular velocity of 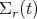 relative to the fixed frame
relative to the fixed frame 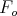 . (NS) says that the linear velocity of the point of contact on the fixed
. (NS) says that the linear velocity of the point of contact on the fixed 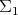 is the same as the velocity of the point of contact on
is the same as the velocity of the point of contact on 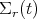 :
: 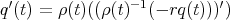
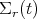 relative to the fixed frame
relative to the fixed frame 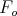 is
is 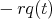 plus a translation. Explicitely, relative to the frame
plus a translation. Explicitely, relative to the frame 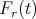 this point is (dropping the
this point is (dropping the 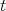 's)
's) 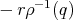 and moves with velocity
and moves with velocity 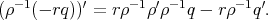
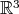 , i.e., relative to the frame
, i.e., relative to the frame 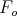 , it becomes
, it becomes 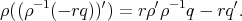
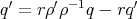 , or
, or 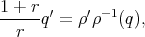
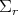 can rotate only about the axis perpendicular to the direction of motion and, because of (NS), tangent to
can rotate only about the axis perpendicular to the direction of motion and, because of (NS), tangent to 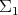 .
. From now on, we will abandon the use of boldface letters for quaternions.
Replace the configuration space 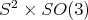 by its 2-fold cover
by its 2-fold cover  , viewed quaternionically as
, viewed quaternionically as
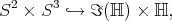
 from
from 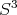 to
to 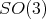 ,
, 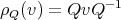 . Clearly,
. Clearly, 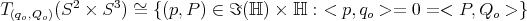
Theorem. A rolling trajectory 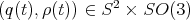 satisfies (NS) and (NT) if and only if
satisfies (NS) and (NT) if and only if 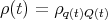 , where
, where 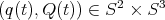 is tangent to the distribution
is tangent to the distribution
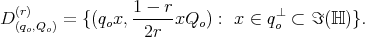
Proof: 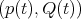 is tangent to
is tangent to 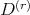 if and only if for some smooth
if and only if for some smooth 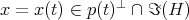 ,
, 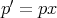 and
and 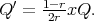 Eliminating
Eliminating 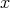 ,
,

 ,
, 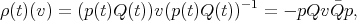
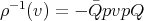 ,
, 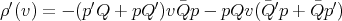 , and therefore
, and therefore 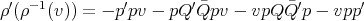 . In particular,
. In particular, 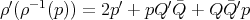
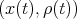 is then
is then 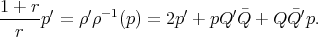
 , so is
, so is 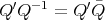 and, because
and, because 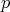 is purely imaginary,
is purely imaginary,  . We conclude that the last equation is the same as
. We conclude that the last equation is the same as 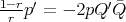 , as claimed. The rest of the proof proceeds along the same lines.
, as claimed. The rest of the proof proceeds along the same lines. The distribution 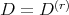 is integrable if and only if
is integrable if and only if  , that is, the spheres have the same radius. Otherwise, it is completely non integrable, of type (2,3,5), meaning that vector fields lying in it satisfy
, that is, the spheres have the same radius. Otherwise, it is completely non integrable, of type (2,3,5), meaning that vector fields lying in it satisfy ![dim {X + [Y,Z ]} = 3](/img/revistas/ruma/v49n2/2a06146x.png) ,
, ![dim {X + [Y, Z ] + [U,[V,W ]]} = 5](/img/revistas/ruma/v49n2/2a06147x.png) . These are the subject of E. Cartan's famous "Five Variables paper" and were recognized as rolling systems by R. Bryant. Cartan and Engel provided the first realization of the exceptional group
. These are the subject of E. Cartan's famous "Five Variables paper" and were recognized as rolling systems by R. Bryant. Cartan and Engel provided the first realization of the exceptional group 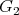 as the group of automorphisms of this differential system for
as the group of automorphisms of this differential system for 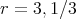 , the connection with "Cayley octaves" being made only later.
, the connection with "Cayley octaves" being made only later.
Given a vector distribution 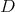 on a manifold
on a manifold 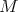 , a global symmetry of it is a diffeomorphism of
, a global symmetry of it is a diffeomorphism of 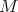 that carries
that carries 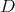 to itself. They form a group,
to itself. They form a group, 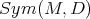 . But most often one needs local difeomorphisms too, hence the object of interest is really the Lie algebra
. But most often one needs local difeomorphisms too, hence the object of interest is really the Lie algebra 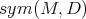 , but we shall not emphasize the distinction until it becomes significant.
, but we shall not emphasize the distinction until it becomes significant.
If 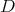 is integrable,
is integrable, 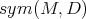 is infinite-dimensional, as can easily be seen by foliating the manifold. At the other end, if
is infinite-dimensional, as can easily be seen by foliating the manifold. At the other end, if 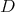 is completely non-integrable ("bracket generating"),
is completely non-integrable ("bracket generating"), 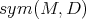 is generically trivial.
is generically trivial.
The rolling systems just described all have a 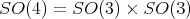 symmetry, as can be deduced from the physical set up. More formally, a pair of rotations
symmetry, as can be deduced from the physical set up. More formally, a pair of rotations 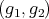 acts on
acts on 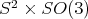 by
by
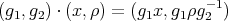
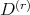 's and are clearly global. Indeed, these are the only global symmetries that these distributions have for any
's and are clearly global. Indeed, these are the only global symmetries that these distributions have for any 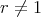 .
. In the covering space 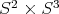 , however, the action of
, however, the action of 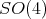 extends to an action of a group of type
extends to an action of a group of type 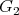 , yielding local diffeomorphisms of the configuration space, as we see next. More precisely,
, yielding local diffeomorphisms of the configuration space, as we see next. More precisely,
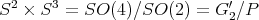
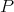 is maximal parabolic. However, the lifted distributions
is maximal parabolic. However, the lifted distributions 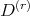 themselves are not left invariant under the
themselves are not left invariant under the 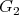 -action - except in the case
-action - except in the case 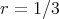 .
. The realization  can be continued recursively to define the sequence of Cayley-Dickson algebras:
can be continued recursively to define the sequence of Cayley-Dickson algebras:

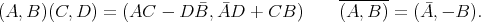
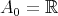 ,
, 
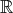 ; from
; from 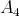 - the sedenions - on, they have zero divisors, i.e., nonzero elements
- the sedenions - on, they have zero divisors, i.e., nonzero elements 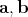 such that
such that 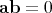 .
. There is a split version of these algebras, where the product is obtained by changing the first minus in the formula by a +:
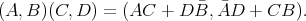
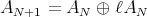
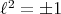 according if it is the split one or not. Note that in a split algebra,
according if it is the split one or not. Note that in a split algebra, 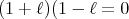 , hence they have zero divisors from the start.
, hence they have zero divisors from the start. The main contribution of the Cayley-Dickson algebras to mathematics so far has been the fact that the automorphisms of the octonions provide the simplest realization of Lie groups of type 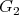 . More precisely, the complex Lie group of this type is the group of automorphisms of the complex octonions (i.e., with complex coefficients), its compact real form arises similarly from the ordinary real octonions and a non-compact real form
. More precisely, the complex Lie group of this type is the group of automorphisms of the complex octonions (i.e., with complex coefficients), its compact real form arises similarly from the ordinary real octonions and a non-compact real form 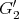 arises from the split one. In physics, the Joyce manifolds of CFT carry, by definition, riemannian metrics with the compact
arises from the split one. In physics, the Joyce manifolds of CFT carry, by definition, riemannian metrics with the compact 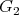 as holonomy, while in rolling it is
as holonomy, while in rolling it is 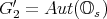 that matters.
that matters.
Since
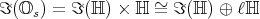
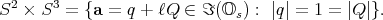
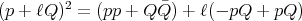 . Indeed, every imaginary split octonion
. Indeed, every imaginary split octonion 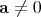 satisfying
satisfying 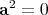 , is a positive multiple of one in
, is a positive multiple of one in 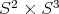 .
. The formula for the product in 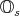 yields
yields 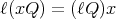 so that for all
so that for all  the distributions can be written as
the distributions can be written as
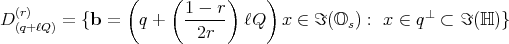
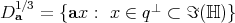 . This expression is still not all octonionic, but its canonical extension to a 3-distribution
. This expression is still not all octonionic, but its canonical extension to a 3-distribution 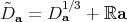 on the cone
on the cone 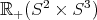 is:
is: Lemma: For every octonion 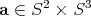 ,
,
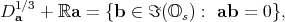
a subspace we will denote by 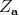 .
.
To prove the Lemma, note that every subalgebra of a 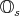 generated by two elements is associative (i.e.,
generated by two elements is associative (i.e., 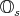 is "alternative"). Therefore
is "alternative"). Therefore 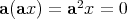 , proving one inclusion. The other uses the quadratic form associated to the split octonions, which also clarifies de action of
, proving one inclusion. The other uses the quadratic form associated to the split octonions, which also clarifies de action of 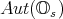 . It is
. It is 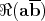 which on
which on 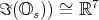 can be replaced by its negative
can be replaced by its negative

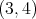 - in contrast to the one for ordinary Octonions, which is positive definite. Moreover,
- in contrast to the one for ordinary Octonions, which is positive definite. Moreover, 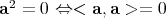 for imaginary
for imaginary  . It follows that
. It follows that 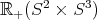 is the null cone of the quadratic form, and the same as the set of elements of square zero in
is the null cone of the quadratic form, and the same as the set of elements of square zero in  . It is now easy to see that if
. It is now easy to see that if 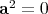 and
and 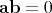 , then
, then 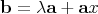 with
with 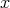 as required.
as required. Now, consider the group 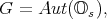 a non-compact simple Lie group of type
a non-compact simple Lie group of type 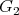 and dimension 14. It fixes
and dimension 14. It fixes  . On
. On  , which is the orthogonal complement of 1 under
, which is the orthogonal complement of 1 under 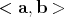 , this form is just
, this form is just 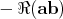 , which is also preserved by
, which is also preserved by 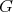 . Hence the quadratic form on all of
. Hence the quadratic form on all of 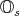 is
is 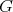 -invariant, hence so is
-invariant, hence so is  . This determines an inclusion
. This determines an inclusion
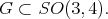
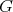 acts linearly on the null cone of the form there. This action descends to a non-linear, transitive action on
acts linearly on the null cone of the form there. This action descends to a non-linear, transitive action on 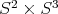 - much like the action of
- much like the action of 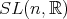 on
on 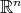 descends to one on
descends to one on 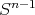 . Since
. Since 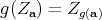 , the action preserves the descended
, the action preserves the descended 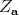 's, which are just the fibers of the distribution
's, which are just the fibers of the distribution 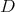 . Hence
. Hence 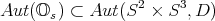
On the configuration space of the rolling system, the elements of 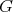 act only locally, via the local liftings of the covering map
act only locally, via the local liftings of the covering map 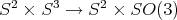 . The local action, of course, still preserves the distribution
. The local action, of course, still preserves the distribution 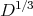 .
.
[Agrachev] Agrachev, A. A. Rolling balls and octonions. Proc. Steklov Inst. Math. 258 (2007), no. 1, 13-22 [ Links ]
[Bor-Montgomery] Bor, Gil; Montgomery, Richard. 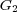 and the "Rolling Distribution". arXiv:math/0612469v1 [math.DG], 2006. [ Links ]
and the "Rolling Distribution". arXiv:math/0612469v1 [math.DG], 2006. [ Links ]
[Bryant-Hsu] Bryant, Robert L.; Hsu, Lucas. Rigidity of integral curves of rank 2 distributions. Invent. Math. 114 (1993), no. 2, 435-461. [ Links ]
[Zelenko] Zelenko, Igor. On variational approach to differential invariants of rank two distributions. Differential Geom. Appl. 24 (2006), no. 3, 235-259. [ Links ]
[Jacobson] Jacobson, Nathan. Basic algebra. I. W. H. Freeman, San Francisco, Calif., 1974. [ Links ]
Aroldo Kaplan
CIEM-FaMAF,
Universidad Nacional de Córdoba,
Córdoba 5000, Argentina
aroldokaplan@gmail.com
Recibido: 3 de julio de 2008
Aceptado: 26 de noviembre de 2008














