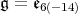Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932On-line version ISSN 1669-9637
Rev. Unión Mat. Argent. vol.49 no.2 Bahía Blanca July/Dec. 2008
Admissible restriction of holomorphic discrete series for exceptional groups
Jorge Vargas
To Mischa Cotlar with respect
Abstract. In this note, we give results about the restriction of a holomorphic discrete series of an exceptional simple Lie real group to a subgroup.
2000 Mathematics Subject Classification. Primary 22E46.
Key words and phrases. Holomorphic Discrete Series representations, branching laws.
Partially supported by FONCYT, CONICET, AgenciaCbaCiencia, SECYTUNC (Argentina), ICTP, TWAS (Italy)
A basic problem in representation theory of Lie groups is to derive "branching laws". By this we mean, for a given unitary irreducible representation of an ambient group  , consider its restriction to a fixed subgroup
, consider its restriction to a fixed subgroup  and find the decomposition as a direct integral, and in particular compute the multiplicity of each irreducible factor of the restriction. There is a vast literature on this subject, and here we just direct the reader's attention to the extensive reviews of [13], [14] and references therein. In this note, we consider a holomorphic discrete series of a connected simple exceptional Lie group, and determine whether or not it has an admissible restriction to a given closed connected reductive subgroup
and find the decomposition as a direct integral, and in particular compute the multiplicity of each irreducible factor of the restriction. There is a vast literature on this subject, and here we just direct the reader's attention to the extensive reviews of [13], [14] and references therein. In this note, we consider a holomorphic discrete series of a connected simple exceptional Lie group, and determine whether or not it has an admissible restriction to a given closed connected reductive subgroup  . Let us recall that a unitary representation of a topological group
. Let us recall that a unitary representation of a topological group 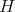 is admissible if it is a discrete Hilbert sum of irreducible unitary sub-representations and each irreducible summand occurs with finite multiplicity.
is admissible if it is a discrete Hilbert sum of irreducible unitary sub-representations and each irreducible summand occurs with finite multiplicity.
Holomorphic discrete series are associated to Hermitian symmetric spaces. We consider a Hermitian symmetric space 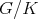 , where
, where 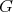 is a simple connected real Lie group
is a simple connected real Lie group 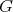 (which we shall assume for convenience, to minimize notations, with finite center), and
(which we shall assume for convenience, to minimize notations, with finite center), and 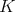 a maximal compact subgroup. For a Lie group we denote its Lie algebra by the corresponding German lower case letter. We write the Cartan decomposition of
a maximal compact subgroup. For a Lie group we denote its Lie algebra by the corresponding German lower case letter. We write the Cartan decomposition of 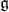 as
as 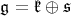 . Thus
. Thus 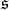 , the tangent space of
, the tangent space of 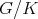 at the origin, is provided with a complex structure
at the origin, is provided with a complex structure 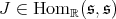 corresponding to a choice of square root
corresponding to a choice of square root 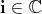 . To denote the complexification of a vector space, we add the subscript
. To denote the complexification of a vector space, we add the subscript  . We denote by
. We denote by 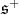 and
and 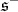 the eigenspaces of
the eigenspaces of  in
in 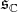 with respective eigenvalues
with respective eigenvalues 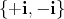 : a linear form
: a linear form  is
is  -linear if and only if its linear extension to
-linear if and only if its linear extension to 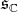 is zero on the subspace
is zero on the subspace 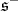 . Moreover,
. Moreover, 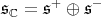 , is the decomposition of
, is the decomposition of 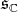 as a direct sum of two irreducible
as a direct sum of two irreducible 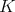 -modules, dual to each other.
-modules, dual to each other.
Recall (see [7]) that the center 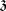 of
of 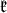 is one dimensional, and that we can choose uniquely a basis (denoted by the same letter
is one dimensional, and that we can choose uniquely a basis (denoted by the same letter 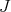 ) of
) of 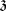 whose adjoint action in
whose adjoint action in 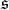 is the complex structure
is the complex structure 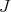 of the tangent space at the origin of
of the tangent space at the origin of 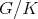 . We write
. We write ![𝔨ss = [𝔨,𝔨]](/img/revistas/ruma/v49n2/2a0834x.png) . We have
. We have  , and
, and 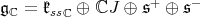 . Correspondingly, we have
. Correspondingly, we have 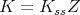 , where
, where 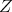 is isomorphic to
is isomorphic to 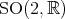 , and
, and 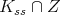 is finite.
is finite.
An irreducible unitary representation of 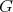 is called holomorphic if its underlying Harish-Chandra module has a non zero vector
is called holomorphic if its underlying Harish-Chandra module has a non zero vector  which is annihilated by
which is annihilated by 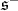 . An irreducible irreducible unitary representation of
. An irreducible irreducible unitary representation of 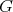 is called a discrete series representation if its coefficients are square integrable on
is called a discrete series representation if its coefficients are square integrable on 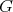 with respect to a given Haar measure.
with respect to a given Haar measure.
The exceptional connected simple Lie groups whose quotient by a maximal compact subgroup carries an invariant complex structure has been classified by E. Cartan. They are the connected groups with Lie algebras  and
and  . The respective complexified Cartan decompositions are :
. The respective complexified Cartan decompositions are :
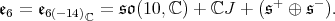
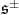 are the half spin
are the half spin 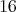 -dimensional representations.
-dimensional representations. 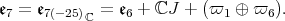
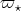 are the two fundamental representations of dimension twenty seven of the complex simple algebra
are the two fundamental representations of dimension twenty seven of the complex simple algebra 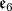 .
. In this paper, for 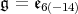 and
and 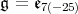 we give list closed connected reductive subgroups
we give list closed connected reductive subgroups 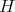 of
of 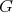 such that an holomorphic discrete series of
such that an holomorphic discrete series of 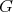 has an admissible restriction to
has an admissible restriction to 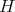 . In [6], we gave several results concerning restrictions of more general discrete series for more general reductive groups, in particular, we introduced a sufficient condition —we call it condition (C)— which implies admissibility of restriction, and allows to compute multiplicities of restrictions by mean of a Blattner-Kostant type formula involving a partition function. However, there exist many cases of admissibility where condition (C) is not satisfied —many examples are given in [6], all of them for compact groups
. In [6], we gave several results concerning restrictions of more general discrete series for more general reductive groups, in particular, we introduced a sufficient condition —we call it condition (C)— which implies admissibility of restriction, and allows to compute multiplicities of restrictions by mean of a Blattner-Kostant type formula involving a partition function. However, there exist many cases of admissibility where condition (C) is not satisfied —many examples are given in [6], all of them for compact groups 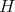 . One of our interests in studying precisely what happens for holomorphic discrete series of exceptional groups, besides our wish to understand the full picture, is to find other interesting examples. In particular, we give several non compact examples.
. One of our interests in studying precisely what happens for holomorphic discrete series of exceptional groups, besides our wish to understand the full picture, is to find other interesting examples. In particular, we give several non compact examples.
We would like to point out that in his Ph.D. thesis [21], S. Simondi has obtained the results on admissibility when rank of 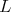 is equal to rank of
is equal to rank of 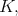 they follow from Theorem 1. His technique is different from the one is used in this note.
they follow from Theorem 1. His technique is different from the one is used in this note.
The author would like to express his gratitude to Michel Duflo for the enlighten comments on the topics of this note.
2.1. A criterium for admissibility of restriction.
We recall some results which we will use in our proofs. Let 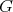 be a connected simple Lie group with finite center, choose a maximal compact group
be a connected simple Lie group with finite center, choose a maximal compact group 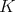 , and Cartan decomposition
, and Cartan decomposition 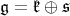 . We denote by
. We denote by 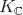 the corresponding complex group. Let
the corresponding complex group. Let 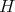 be a closed connected reductive subgroup. We assume that
be a closed connected reductive subgroup. We assume that 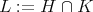 is a maximal compact subgroup of
is a maximal compact subgroup of 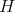 .
.
In [6], we prove a result which reduces the problem of admissibility of restriction of discrete series to the case of compact subgroups :
Proposition 1. Let 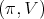 be a discrete series for
be a discrete series for 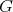 . Then its restriction to
. Then its restriction to 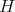 is admissible if and only if its restriction to
is admissible if and only if its restriction to 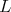 is admissible.
is admissible.
There are many criteria for admissibility of the restriction to a subgroup of an irreducible unitary representation 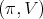 of
of 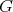 (see e. g. [13], [14]). When the subgroup is compact, we will use a criterium in term of the associated variety which we explain. We denote by
(see e. g. [13], [14]). When the subgroup is compact, we will use a criterium in term of the associated variety which we explain. We denote by 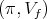 the representation of
the representation of 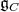 in the space of
in the space of 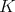 -finite vectors of
-finite vectors of 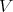 . Vogan [26] defined the associated variety
. Vogan [26] defined the associated variety 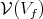 , which is a Zariski-closed
, which is a Zariski-closed 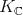 -invariant cone of dual
-invariant cone of dual 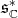 of
of 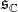 . Let us denote by
. Let us denote by ![ℂ [V (V )] f](/img/revistas/ruma/v49n2/2a0884x.png) the ring of regular functions on
the ring of regular functions on 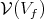 . The following criterium is known (see in particular Huang and Vogan [9], Kobayashi [12], Vergne [25]).
. The following criterium is known (see in particular Huang and Vogan [9], Kobayashi [12], Vergne [25]).
Proposition 2. Let 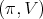 be an irreducible unitary representation of
be an irreducible unitary representation of 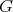 . Then its restriction to
. Then its restriction to 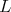 is admissible if and only if
is admissible if and only if ![Lℂ ℂ [V(Vf)] = ℂ](/img/revistas/ruma/v49n2/2a0889x.png) , that is the only
, that is the only 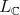 invariant regular functions on
invariant regular functions on 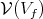 are the constant.
are the constant.
Assume now that 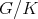 is hermitian symmetric. The criterium is particularly pleasant for holomorphic discrete series (see [12], [6], [25]) :
is hermitian symmetric. The criterium is particularly pleasant for holomorphic discrete series (see [12], [6], [25]) :
Proposition 3. Let 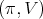 be a holomorphic discrete series of
be a holomorphic discrete series of 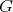 . Then
. Then 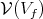 is the orthogonal of
is the orthogonal of 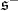 in
in 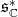 . Thus its restriction to
. Thus its restriction to 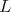 is admissible if and only if
is admissible if and only if ![+ Lℂ S[𝔰 ] = ℂ](/img/revistas/ruma/v49n2/2a0899x.png) .
.
The most obvious example of proposition 3 is the group 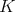 . The restriction to
. The restriction to 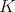 of an holomorphic discrete series is admissible (in fact it is true for any unitary irreducible representation of
of an holomorphic discrete series is admissible (in fact it is true for any unitary irreducible representation of 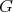 ), and we have also
), and we have also ![S [𝔰+ ]K ℂ = ℂ](/img/revistas/ruma/v49n2/2a08103x.png) . Thus our problem of restriction is a particular case of a well known problem in invariant theory (see [22],[23]): Find pairs of connected reductive groups complex linear groups
. Thus our problem of restriction is a particular case of a well known problem in invariant theory (see [22],[23]): Find pairs of connected reductive groups complex linear groups 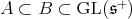 such that
such that ![S [𝔰+ ]A = S[𝔰+]B](/img/revistas/ruma/v49n2/2a08105x.png) .
.
Remark 1. If 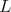 is semi-simple, the condition
is semi-simple, the condition ![+ L S[𝔰 ] ℂ = ℂ](/img/revistas/ruma/v49n2/2a08107x.png) holds if and only if
holds if and only if 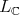 has an open orbit in
has an open orbit in 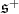 .
.
The subgroups 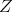 and
and 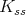 of
of 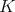 deserve a special attention. For completeness, we recall the following well known result (which can serve as an illustration of proposition 3)
deserve a special attention. For completeness, we recall the following well known result (which can serve as an illustration of proposition 3)
Proposition 4. Let 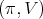 be a holomorphic discrete series of
be a holomorphic discrete series of 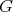 . Its restriction to
. Its restriction to 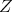 (and also to any closed subgroup
(and also to any closed subgroup 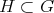 which contains
which contains 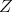 ) is admissible.
) is admissible.
To study the restriction to 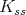 , recall that Hermitian symmetric spaces
, recall that Hermitian symmetric spaces 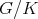 are divided in two categories: the tube type, and the non tube type. One of the many equivalent definitions of tube type is (see [7]):
are divided in two categories: the tube type, and the non tube type. One of the many equivalent definitions of tube type is (see [7]):
The Hermitian symmetric spaces 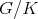 is of non tube type if and only if
is of non tube type if and only if ![S [𝔰+ ]Kssℂ = ℂ](/img/revistas/ruma/v49n2/2a08121x.png) .
.
We will also say that 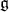 is of tube type. Hermitian symmetric spaces of tube type are related to simple Jordan algebras [7]; They are interesting because they have associated Zeta functions. However, from our point of view, non tube type is more interesting:
is of tube type. Hermitian symmetric spaces of tube type are related to simple Jordan algebras [7]; They are interesting because they have associated Zeta functions. However, from our point of view, non tube type is more interesting:
Proposition 5. Let 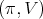 be a holomorphic discrete series of
be a holomorphic discrete series of 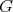 . Its restriction to
. Its restriction to 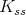 is admissible if and only if
is admissible if and only if 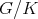 is not of tube type.
is not of tube type.
The list of Hermitian symmetric spaces 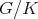 of tube type is well known (see [7]). Among the two exceptional ones,
of tube type is well known (see [7]). Among the two exceptional ones,  is not of tube type, and
is not of tube type, and  is of tube type. Thus we have the following preliminary results, which explains why the case
is of tube type. Thus we have the following preliminary results, which explains why the case  is richer.
is richer.
Theorem 1. Let 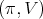 be a holomorphic discrete series of
be a holomorphic discrete series of 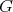 with Lie algebra
with Lie algebra  . Its restriction to
. Its restriction to 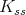 is admissible.
is admissible.
Theorem 2. Let 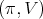 be a holomorphic discrete series of
be a holomorphic discrete series of 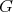 with Lie algebra
with Lie algebra  . Its restriction to
. Its restriction to 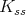 (and to any of its closed subgroups
(and to any of its closed subgroups 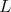 ) is not admissible.
) is not admissible.
We recall what is condition (C) of [6] in the particular case of a holomorphic discrete series. We choose a Cartan subgroup 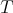 of
of 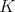 , and denote by
, and denote by 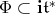 be set the roots of
be set the roots of 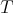 in
in 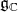 . We choose a positive system
. We choose a positive system  such that the set of non compact roots
such that the set of non compact roots 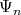 is exactly the set of roots of
is exactly the set of roots of 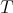 in
in 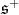 . We denote by
. We denote by 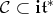 the closed convex pointed cone generated by
the closed convex pointed cone generated by 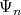 .
.
We assume that 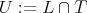 is a Cartan subgroup of
is a Cartan subgroup of 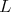 . Let
. Let 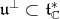 be the orthogonal of
be the orthogonal of 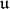 . Here is condition (C):
. Here is condition (C):
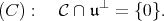 |
We rephrase condition (C). Let 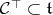 the cone dual to
the cone dual to 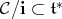 ; It is a closed convex cone whose interior
; It is a closed convex cone whose interior 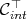 contains
contains 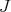 . Then condition (C) is equivalent to condition (C'):
. Then condition (C) is equivalent to condition (C'):
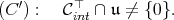 |
Condition (C) depends only on the maximal torus
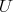 of
of 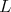 . We have:
. We have:
Theorem 3. Let 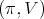 be a holomorphic discrete series of
be a holomorphic discrete series of 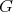 . Let
. Let 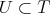 be a compact connected torus. Then the restriction of
be a compact connected torus. Then the restriction of 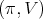 to
to 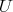 is admissible if and only if condition (C) holds.
is admissible if and only if condition (C) holds.
Proof. As a 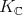 -module,
-module, 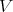 is isomorphic to
is isomorphic to ![+ F ⊗ S [𝔰 ]](/img/revistas/ruma/v49n2/2a08172x.png) , where
, where 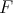 is an irreducible representation of
is an irreducible representation of 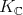 . Thus, as a
. Thus, as a 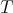 module, it is a finite direct sum of
module, it is a finite direct sum of ![ℂμ ⊗ S [𝔰+ ]](/img/revistas/ruma/v49n2/2a08176x.png) , where
, where 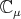 is a one dimensional representation of
is a one dimensional representation of 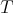 with weight
with weight 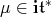 . The weights of
. The weights of 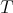 in
in ![S [𝔰+ ]](/img/revistas/ruma/v49n2/2a08181x.png) are exactly the weights of
are exactly the weights of 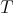 contained in
contained in  , occurring with finite multiplicity. The theorem follows. □
, occurring with finite multiplicity. The theorem follows. □
If condition (C) is satisfied for a torus 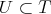 , it is also satisfied for some one dimensional torus
, it is also satisfied for some one dimensional torus 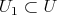 . Then
. Then 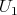 satisfies condition (C) if and only if
satisfies condition (C) if and only if 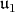 has a basis
has a basis 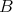 which belongs to
which belongs to 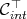 . In particular,
. In particular, 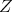 satisfies condition (C) (which is a way of proving proposition 4), and also all one dimensional torus
satisfies condition (C) (which is a way of proving proposition 4), and also all one dimensional torus 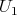 not to far away from
not to far away from 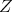 .
.
On the other hand, it is easy to see that condition (C) is never satisfied for 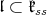 . Thus, for
. Thus, for 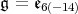 , the group
, the group 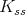 is an easy example where there is admissibility and condition (C) does not hold.
is an easy example where there is admissibility and condition (C) does not hold.
2.3. Formulation of the problem.
Let us explain more precisely what has to be done in general. We fix a compact connected semisimple group 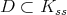 with a Cartan subgroup
with a Cartan subgroup 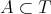 . Let
. Let 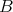 be the connected component group of the centralizer of
be the connected component group of the centralizer of 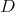 in
in 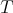 . Then
. Then 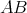 is a Cartan subgroup of
is a Cartan subgroup of 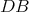 .
.
Consider a connected closed groups 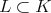 such that
such that 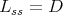 . Up to conjugation, it will be of the form
. Up to conjugation, it will be of the form 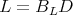 , where
, where 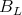 , the connected center of
, the connected center of 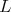 , is a closed connected subgroup of
, is a closed connected subgroup of 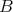 . Note that
. Note that 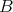 contains the center
contains the center 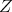 of
of 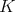 . For clarity, we distinguish two cases.
. For clarity, we distinguish two cases.
First, assume there is admissible restriction of holomorphic discrete series of 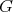 to
to 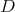 — or equivalently, that
— or equivalently, that 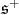 is a
is a 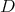 -prehomogeneous space. Then there will be admissible restriction to any subgroup
-prehomogeneous space. Then there will be admissible restriction to any subgroup 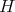 containing
containing 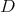 .
.
We assume now that the restriction of holomorphic discrete series of 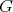 to
to 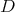 is not admissible. Since
is not admissible. Since 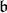 contains
contains 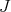 , the restriction of a holomorphic discrete series
, the restriction of a holomorphic discrete series 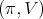 of
of 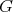 to the group
to the group 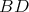 is admissible. Let us choose a positive Weyl chamber
is admissible. Let us choose a positive Weyl chamber 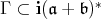 for the group
for the group 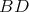 . Let
. Let 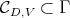 the set of highest weights of the irreducible representations of
the set of highest weights of the irreducible representations of 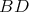 which occur in
which occur in 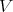 , and
, and 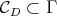 the asymptotic cone of
the asymptotic cone of 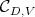 . It is known that
. It is known that 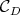 is a closed convex polyhedral cone, independent of
is a closed convex polyhedral cone, independent of 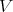 , contained in the projection on
, contained in the projection on  of the cone
of the cone 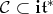 . We identify the orthogonal
. We identify the orthogonal 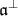 of
of 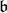 in
in  to
to 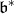 . We consider the cone
. We consider the cone  . The fact that the restriction of holomorphic discrete series of
. The fact that the restriction of holomorphic discrete series of 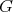 to
to 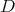 is not admissible is equivalent to the fact that the cone
is not admissible is equivalent to the fact that the cone 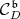 is not reduced to
is not reduced to 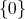 . We consider its dual cone
. We consider its dual cone 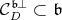 , and its interior
, and its interior 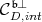 . Note that
. Note that 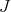 belongs to
belongs to 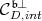 .
.
Theorem 4. Let 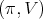 be a holomorphic discrete series of
be a holomorphic discrete series of 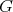 . Suppose that its restriction to
. Suppose that its restriction to 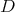 is not admissible. Then the restriction of
is not admissible. Then the restriction of 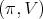 to
to 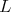 is admissible if and only if one of the two following equivalent conditions hold:
is admissible if and only if one of the two following equivalent conditions hold:
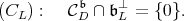 |
or
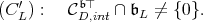 |
Thus, discrete series of 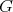 have admissible restriction to
have admissible restriction to 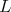 if and only if
if and only if 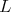 contains a closed subgroup
contains a closed subgroup 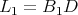 , where
, where 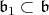 is a one-dimensional subspace which intersects
is a one-dimensional subspace which intersects 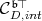 .
.
Theorem 4 suggests a method to find all closed connected reductive groups 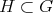 for which there is admissible restriction of holomorphic discrete series.
for which there is admissible restriction of holomorphic discrete series.
1. For each closed connected semisimple subgroup 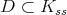 , determine whether there is admissibility of restriction of holomorphic discrete series. This step is not too difficult, for instance this is never the case when
, determine whether there is admissibility of restriction of holomorphic discrete series. This step is not too difficult, for instance this is never the case when 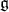 is of tube type, and we will give below the complete answer for
is of tube type, and we will give below the complete answer for 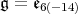 .
.
2. When it is not the case, compute (with the notation as above) the algebra 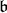 and the cone
and the cone 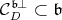 . This will give the list of closed connected subgroup
. This will give the list of closed connected subgroup 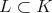 such that
such that 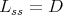 for which there is admissibility of restriction of holomorphic discrete series.
for which there is admissibility of restriction of holomorphic discrete series.
For each particular 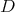 , this is probably a feasible task, and we give several examples. However, we do not know an useful statement for all
, this is probably a feasible task, and we give several examples. However, we do not know an useful statement for all 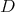 .
.
3. Given 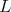 as in 2, list the closed connected reductive subgroups
as in 2, list the closed connected reductive subgroups 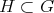 such that
such that 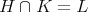 .
.
We use the notations of the previous subsection. We assume moreover that 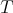 normalizes
normalizes 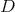 , or, equivalently, that
, or, equivalently, that  . This means that
. This means that 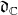 is the sum of the root spaces for a certain subset
is the sum of the root spaces for a certain subset 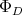 of roots, and of the space
of roots, and of the space 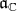 generated by the corresponding coroots. We give some bounds on the cone
generated by the corresponding coroots. We give some bounds on the cone 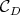 .
.
For this we need to recall some important facts proven in [20]. Let  be the real rank of
be the real rank of 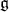 . There exists a set
. There exists a set 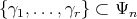 of pairwise strongly orthogonal roots such that the highest weights of the representations of
of pairwise strongly orthogonal roots such that the highest weights of the representations of 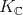 occurring in
occurring in ![+ S[𝔰 ]](/img/revistas/ruma/v49n2/2a08286x.png) are exactly those which belong to the cone generated by
are exactly those which belong to the cone generated by 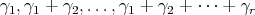 . We recall that
. We recall that 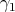 is the highest weight of the
is the highest weight of the 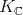 -module
-module 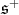 , that
, that 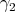 is the maximal element (for a suitable order) among the roots orthogonal to
is the maximal element (for a suitable order) among the roots orthogonal to 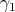 , etc...
, etc...
This means that 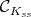 is the cone generated by
is the cone generated by 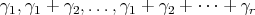 . Moreover,
. Moreover, 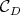 is a polyhedral cone such that
is a polyhedral cone such that 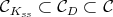 .
.
For later use, we introduce some related notations. We will label the simple compact roots as 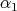 ,…,
,…, 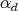 , and the unique simple non compact root will be denoted by
, and the unique simple non compact root will be denoted by 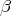 . Note that
. Note that 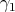 is the corresponding fundamental weight, and that
is the corresponding fundamental weight, and that 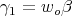 , where
, where 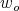 is the longest element of the Weyl group of
is the longest element of the Weyl group of 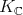 .
.
For this subsection 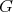 denotes one of the groups
denotes one of the groups 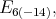
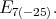 We fix a holomorphic discrete series representation
We fix a holomorphic discrete series representation 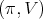 for
for 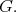 Then,
Then,
Theorem 5. For a maximal connected reductive subgroup 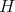 of
of 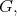
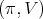 restricted to
restricted to 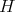 is admissible if and only if the center of
is admissible if and only if the center of 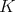 is a subgroup of
is a subgroup of 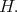
When 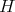 is so that
is so that 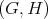 a symmetric space, the theorem is a result of Kobayashi, [12], [15].
a symmetric space, the theorem is a result of Kobayashi, [12], [15].
In [3] is shown that a maximal connected subgroup of 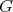 is either parabolic or reductive. For sake of completeness we list the maximal reductive subalgebras of
is either parabolic or reductive. For sake of completeness we list the maximal reductive subalgebras of 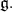 The classification of maximal connected subgroups of
The classification of maximal connected subgroups of 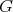 was completed by [16]. Some of the subalgebras has a compact abelian one dimensional factor which may not be the center of
was completed by [16]. Some of the subalgebras has a compact abelian one dimensional factor which may not be the center of 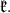
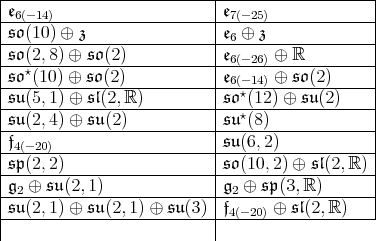
Proof. The subgroups 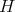 listed on the first seven lines corresponds to symmetric pairs
listed on the first seven lines corresponds to symmetric pairs 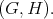 The result follows from Kobayashi [12]. Under his hypothesis, Kobayashi has shown that the multiplicity function is bounded. We do not know if this fact holds for other pairs
The result follows from Kobayashi [12]. Under his hypothesis, Kobayashi has shown that the multiplicity function is bounded. We do not know if this fact holds for other pairs 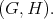
For 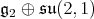 we have that the center of the maximal compact subgroup of
we have that the center of the maximal compact subgroup of  is contained in
is contained in 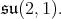 Hence, owing to Proposition 4 there is admissible restriction to the subgroup. In fact, center of K is contained in SU(2,1). For this, we consider the usual imbedding
Hence, owing to Proposition 4 there is admissible restriction to the subgroup. In fact, center of K is contained in SU(2,1). For this, we consider the usual imbedding 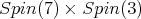 as a subgroup of
as a subgroup of 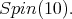 Then,
Then, 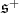 restricted to
restricted to 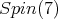 is equivalent to twice the spin representation of
is equivalent to twice the spin representation of 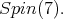
Counting dimensions, we get 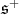 restricted to
restricted to 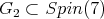 is equivalent to twice
is equivalent to twice  Here,
Here, 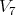 (resp.
(resp. 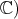 is the seven dimensional (resp. one dimensional) irreducible representation for
is the seven dimensional (resp. one dimensional) irreducible representation for 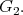 It follows from a computation that the Cartan decomposition of
It follows from a computation that the Cartan decomposition of 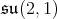 is
is 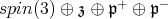 where
where 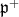 is a subspace of the two copies of the trivial representation. From this we get that the center of
is a subspace of the two copies of the trivial representation. From this we get that the center of 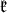 is contained in
is contained in 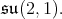
The maximal compact subgroup of 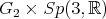 is
is 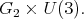 We show the center of
We show the center of 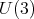 is the center of
is the center of 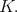 In fact, in [16] is stated
In fact, in [16] is stated 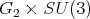 is a maximal subgroup of
is a maximal subgroup of 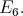 Hence, the projection of the center of
Hence, the projection of the center of 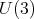 on the direction of
on the direction of 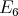 is trivial. Proposition 4 yields
is trivial. Proposition 4 yields 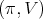 has admissible restriction to
has admissible restriction to 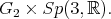
Next, we dealt with 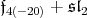 in
in 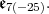 Let
Let 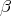 denote the noncompact simple root for the holomorphic system in
denote the noncompact simple root for the holomorphic system in  and let
and let 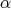 be the compact simple root adjacent to
be the compact simple root adjacent to 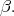 We claim that of
We claim that of 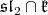 is spanned by
is spanned by  The root system for the immersion of
The root system for the immersion of  in
in  is spanned by
is spanned by  and the five compact simple roots different from
and the five compact simple roots different from 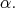 Hence,
Hence, 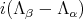 belongs to the centralizer of
belongs to the centralizer of  Since, [16],
Since, [16], 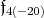 is a subalgebra of
is a subalgebra of  and the centralizer of
and the centralizer of 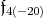 in
in 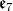 is
is 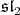 [1], the claim follows. Thus, a maximal compact subgroup of
[1], the claim follows. Thus, a maximal compact subgroup of 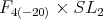 is
is 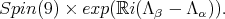 Moreover, the
Moreover, the 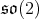 factor of the immersion
factor of the immersion 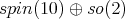 in
in 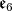 is spanned by
is spanned by 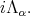
Now, 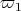 restricted to
restricted to 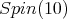 is equivalent to
is equivalent to 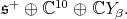 Also,
Also, 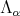 takes on the values
takes on the values 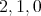 on each irreducible factor. Hence
on each irreducible factor. Hence  takes on the values
takes on the values 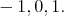 Therefore,
Therefore, 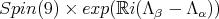 fix nonzero vectors in
fix nonzero vectors in 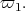 □
□
It may happen there is admissible restriction to a non compact subgroup which is not a maximal subgroup. In fact, we have,
Theorem 6. A holomorphic discrete series for 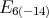 has admissible restriction to any of the subgroups
has admissible restriction to any of the subgroups
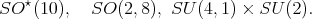
We notice that none of the subgroups listed above contain the center of 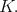 A consequence of Theorem 2 and Theorem 8 is
A consequence of Theorem 2 and Theorem 8 is
Theorem 7. If a holomorphic Discrete Series of an exceptional group has an admissible restriction to 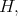 then center of
then center of 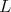 is a torus.
is a torus.
Theorem 7 does not hold for classical groups because Proposition 3 yields that holomorphic Discrete series for 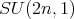 has an admissible restriction to
has an admissible restriction to 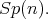
In this section, 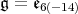 . Following [8], we label the Dynkin diagram as follows.
. Following [8], we label the Dynkin diagram as follows.

The real rank is 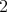 . We have
. We have 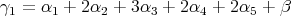 , and
, and  .
.
We provide 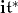 with the invariant scalar product for which
with the invariant scalar product for which 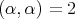 for each root.This scalar product produces an isomorphism
for each root.This scalar product produces an isomorphism  from
from 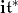 to
to 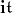 , and
, and 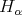 is the coroot corresponding to
is the coroot corresponding to 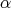 .
.
Let 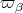 be the fundamental weight corresponding to
be the fundamental weight corresponding to 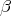 . We have
. We have 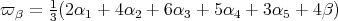 . We note that
. We note that 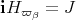 .
.
Since, by theorem 1, there is admissible restriction to 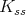 , we consider proper maximal subgroups of
, we consider proper maximal subgroups of 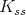 . We show
. We show
Theorem 8. Let 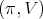 be a holomorphic discrete series representation for
be a holomorphic discrete series representation for 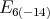 Then,
Then,
i) 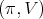 restricted to
restricted to 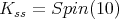 is admissible.
is admissible.
ii) Let 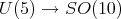 denote the usual imbedding and let
denote the usual imbedding and let 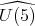 denote the analytic subgroup of
denote the analytic subgroup of 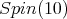 associated to
associated to 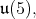 then the restriction of
then the restriction of 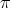 to
to  is admissible.
is admissible.
iii) For any other maximal subgroup 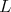 of
of 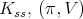 restricted to
restricted to 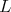 is not admissible.
is not admissible.
iv) Let 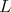 be a closed proper subgroup of
be a closed proper subgroup of 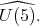 Then
Then  restricted to
restricted to 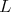 is not an admissible representation.
is not an admissible representation.
Proof. To begin with, we recall the Cartan decomposition of 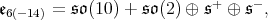 where
where 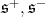 are the two spin representations of
are the two spin representations of 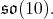 Let
Let 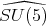 (resp.
(resp. 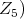 denote the simple factor of
denote the simple factor of 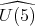 (resp. the center of
(resp. the center of 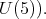
Owing to Proposition 3, Theorem 8 follows from:
a) ![+ Spin(10) S[𝔰 ] = ℂ,](/img/revistas/ruma/v49n2/2a08439x.png) b)
b)![+U (5) S [𝔰 ] = ℂ,](/img/revistas/ruma/v49n2/2a08440x.png)
c) ![+ L S[𝔰 ] ⁄= ℂ](/img/revistas/ruma/v49n2/2a08441x.png) for a maximal subgroup
for a maximal subgroup 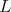 of
of 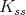 not locally isomorphic to
not locally isomorphic to 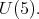
d) For subgroup 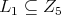 and maximal subgroup
and maximal subgroup 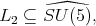 or
or
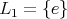 and
and 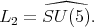 Then
Then ![+ L L S[𝔰 ] 1 2 ⁄= ℂ.](/img/revistas/ruma/v49n2/2a08449x.png)
In [2], we find a proof of ![S[𝔰+]Spin(10) = ℂ.](/img/revistas/ruma/v49n2/2a08450x.png) Thus a) follows.
Thus a) follows.
To continue, we fix an orthogonal basis  of
of 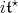 so that a system of positive compact roots is
so that a system of positive compact roots is 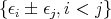 and the weights of the representation
and the weights of the representation 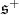 are
are 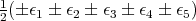 with and odd number of
with and odd number of 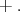 The positive roots of
The positive roots of 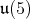 are
are 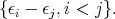 Let
Let 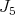 denotes an infinitesimal generator of
denotes an infinitesimal generator of 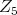 chosen so that
chosen so that  The
The  module
module 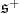 decomposes as
decomposes as
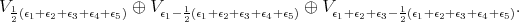
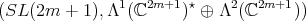
 has an open orbit in
has an open orbit in 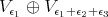
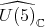 has an open orbit in
has an open orbit in 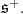 Hence,
Hence, ![S [𝔰+ ]U (5) = ℂ](/img/revistas/ruma/v49n2/2a08470x.png) and
and  follows. Since,
follows. Since, 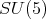 acts trivially on the factor
acts trivially on the factor 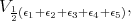 it follows
it follows  for
for 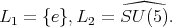 Since, an element of
Since, an element of 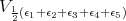 times un element of any of the other irreducible factors is invariant under
times un element of any of the other irreducible factors is invariant under 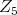 we obtain d) for the other extreme case.
we obtain d) for the other extreme case. In order to show 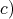 we list, up to conjugation, the maximal connected closed subgroups of
we list, up to conjugation, the maximal connected closed subgroups of 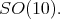 These subgroups have been classified by Dynkin in [5]. They are:
These subgroups have been classified by Dynkin in [5]. They are:
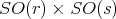 for
for 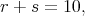
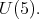
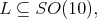 for
for 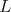 a connected, simple subgroup so that
a connected, simple subgroup so that 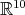 is an absolutely irreducible representation.
is an absolutely irreducible representation.
To continue, we assume ![S [𝔰+ ]L = ℂ](/img/revistas/ruma/v49n2/2a08488x.png) for each maximal subgroup
for each maximal subgroup 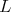 of
of 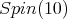 not locally isomorphic to
not locally isomorphic to 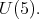 From this we derive a contradiction.
From this we derive a contradiction.
As before, 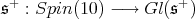 denote the half spin representation. To begin with, we consider
denote the half spin representation. To begin with, we consider 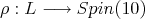 an irreducible, simple, maximal subgroup.
an irreducible, simple, maximal subgroup. 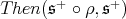 decomposes as the sum irreducible
decomposes as the sum irreducible 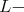 modules
modules

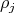 equal to the projection onto
equal to the projection onto 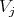 followed by
followed by  Owing to our hypothesis, it follows
Owing to our hypothesis, it follows ![S [V ]ρj(L ) = ℂ j](/img/revistas/ruma/v49n2/2a08500x.png) for
for 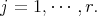 In [2], [10], [11] [17] we find the list of triples
In [2], [10], [11] [17] we find the list of triples 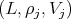 where:
where: 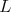 is a simple algebraic group,
is a simple algebraic group, 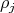 is an irreducible representation and
is an irreducible representation and ![ρ (L) S [Vj] j = ℂ.](/img/revistas/ruma/v49n2/2a08505x.png) The list is:
The list is: 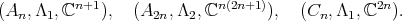
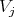 is equivalent to
is equivalent to 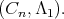 Since the ten dimensional irreducible representation of
Since the ten dimensional irreducible representation of 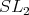 is symplectic, we have
is symplectic, we have  For
For 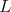 of type
of type 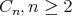 and
and  we obtain
we obtain 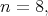 a contradiction. For
a contradiction. For 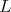 of type
of type 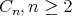 and
and  the symplectic form lead us to
the symplectic form lead us to ![+ L S[𝔰 ] ⁄= ℂ,](/img/revistas/ruma/v49n2/2a08518x.png) another contradiction.
another contradiction. For 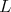 of type
of type 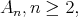 if at least one
if at least one 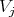 is equivalent to
is equivalent to 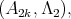 then
then 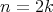 and
and 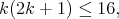 hence,
hence, 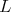 is one of
is one of 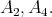
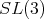 has two irreducible representations of dimension ten whose highest weight are
has two irreducible representations of dimension ten whose highest weight are 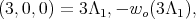 neither of these two representations are orthogonal [3].
neither of these two representations are orthogonal [3]. 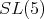 also has two ten dimensional representations of highest weight
also has two ten dimensional representations of highest weight 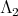 or
or 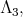 [3] neither of them is orthogonal.
[3] neither of them is orthogonal.
We are left to analyze the situation all 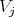 are equivalent to
are equivalent to 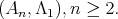 Since
Since 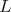 is a subgroup of
is a subgroup of 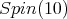 we have
we have 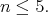 The case
The case 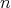 even was analyzed in the previous paragraph. The ten dimensional irreducible representations of
even was analyzed in the previous paragraph. The ten dimensional irreducible representations of 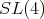 have highest weight
have highest weight 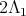 or
or 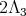 they are not orthogonal.
they are not orthogonal. 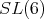 has no irreducible representation of dimension ten.
has no irreducible representation of dimension ten.
To conclude the proof of 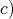 we show
we show
![+ 𝔰𝔬(p)⊕ 𝔰𝔬(q) S[𝔰 ] ⁄= ℂ for p ≥ 1, q ≥ 1,p + q = 10.](/img/revistas/ruma/v49n2/2a08543x.png)
We recall the following facts, for a proof, see [1], [3] Table 1.
- A half spin representations
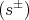 for
for 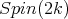 restricted to
restricted to
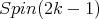 is equivalent to the spin representation
is equivalent to the spin representation 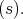
- The spin representation for
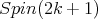 restricted to
restricted to 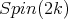 is equivalent to the sum of the two half spin representations.
is equivalent to the sum of the two half spin representations. - An irreducible spin representation for
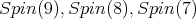 is orthogonal.
is orthogonal. - An irreducible spin representation for
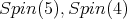 is symplectic.
is symplectic.
For 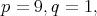
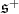 restricted to
restricted to 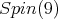 is equivalent to the spin representation of
is equivalent to the spin representation of 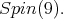 Since the spin representation of
Since the spin representation of 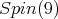 is orthogonal, we obtain
is orthogonal, we obtain ![S [𝔰+ ]𝔰𝔬(9)⊕𝔰𝔬(1) ⁄= ℂ.](/img/revistas/ruma/v49n2/2a08561x.png)
For 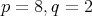
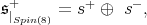 besides
besides 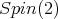 acts on
acts on 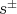 by
by 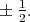 Let
Let 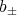 denote a
denote a 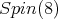 invariant quadratic form in
invariant quadratic form in 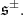 Then
Then 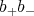 is invariant under
is invariant under 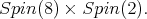
For 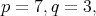
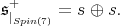 Hence,
Hence, 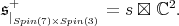 In [11] it is shown it is not an irreducible prehomogeneous vector space.
In [11] it is shown it is not an irreducible prehomogeneous vector space.
For 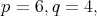
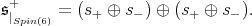
Here, 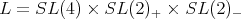 and the restriction of
and the restriction of 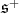 to
to 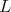 is equivalent to
is equivalent to
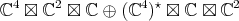
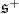 to
to 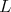 is equivalent to
is equivalent to 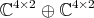
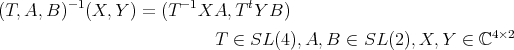 |
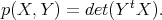 By duality
By duality ![S [𝔰+ ]SO (4)×SO(6)](/img/revistas/ruma/v49n2/2a08586x.png)
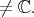 Actually, the invariant polynomial functions are the polynomial ring in
Actually, the invariant polynomial functions are the polynomial ring in 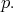
Finally we examine 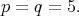 Here, the restriction of
Here, the restriction of 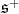 to
to 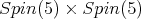 is equivalent to
is equivalent to  In [11] Apendix, it is shown that this representation is not a prehomogeneous vector space. Hence,
In [11] Apendix, it is shown that this representation is not a prehomogeneous vector space. Hence,
![S [𝔰+ ]Spin(5)×Spin(5) ⁄= ℂ](/img/revistas/ruma/v49n2/2a08593x.png) and we have verified c).
and we have verified c).
We now show d). For this we recall the work of [5] on the maximal subgroups of 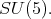 Up to conjugation, the maximal connect subgroups of
Up to conjugation, the maximal connect subgroups of 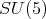 are among the subgroups
are among the subgroups
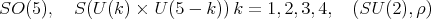
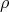 is the five dimensional irreducible representation of
is the five dimensional irreducible representation of 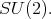
Either the representation of 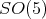 or
or 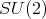 is orthogonal, [3], hence, an invariant for
is orthogonal, [3], hence, an invariant for 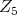 times one of these two groups, is given by an element of
times one of these two groups, is given by an element of 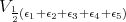 times the invariant quadratic form.
times the invariant quadratic form.
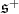 restricted to
restricted to 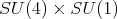 is equivalent to
is equivalent to
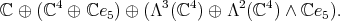
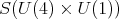 in
in 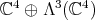 is orthogonal, the action of
is orthogonal, the action of 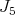 in
in 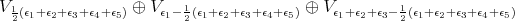
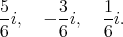
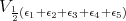 we obtain an invariant for the group
we obtain an invariant for the group 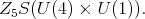
The decomposition of 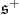 under
under 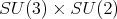 is
is
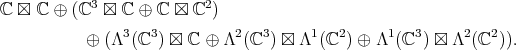 |
![2 1 2 S [ℂ ⊕ Λ (ℂ )]](/img/revistas/ruma/v49n2/2a08616x.png) an element of degree two
an element of degree two 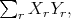 which is
which is 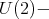 invariant. Also, in
invariant. Also, in ![S [ℂ3 ⊕ Λ2(ℂ3 )]](/img/revistas/ruma/v49n2/2a08619x.png) there is an invariant, under
there is an invariant, under 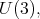 of degree two
of degree two 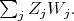 It readily follows that
It readily follows that 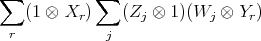
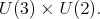 As for the previous case it follows there is an invariant under
As for the previous case it follows there is an invariant under 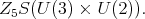 Thus, we have verified d) and we conclude the proof of Theorem 8. □
Thus, we have verified d) and we conclude the proof of Theorem 8. □ Finally, we analyze the admissibility of 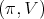 restricted to specific reductive subgroups of
restricted to specific reductive subgroups of 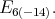 Let
Let 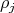 denote the fundamental weight of
denote the fundamental weight of 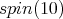 associated to
associated to 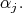 The centralizer of
The centralizer of 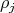 in
in 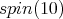 is equal to a semisimple Lie algebra
is equal to a semisimple Lie algebra 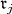 plus the line spanned by
plus the line spanned by 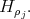
We fix 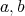 real numbers,
real numbers, 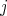 runs from
runs from 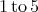
We define 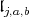 to be the subalgebra spanned by
to be the subalgebra spanned by 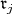 together with the vector
together with the vector 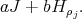 We only consider
We only consider 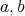 such that the analytic subgroup associated to
such that the analytic subgroup associated to 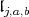 is compact. Either
is compact. Either 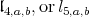 is isomorphic to
is isomorphic to 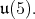
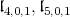 are the usual two immersions of
are the usual two immersions of 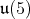 in
in 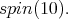 From now on, we write
From now on, we write 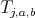 for the analytic subgroup of
for the analytic subgroup of 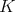 associated to
associated to 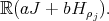
Proposition 6. A holomorphic discrete series for 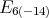 has an admissible restriction to the subgroups:
has an admissible restriction to the subgroups:
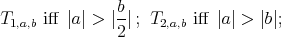
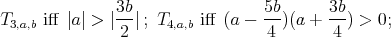
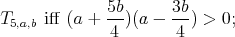
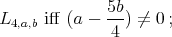
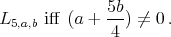
[1] Adams, J.F., Lectures on exceptional Lie groups, Chicago Lectures in Mathematics, (1996). University of Chicago Press. [ Links ]
[2] Benson, C., Ratcliff, G., A classification of multiplicity free actions, J. Algebra, (181), 152-186, (1996). [ Links ]
[3] Bourbaki, N., Groupes et Algèbres de Lie, Chap 8, Masson et Cie, (1982). [ Links ]
[4] Brion, M., Sur l'image de l'application moment. Springer Lecture Notes in Math., 1296, 177-192 (1987) [ Links ]
[5] Dynkin, E.B., Maximal subgroups of classical groups, Transl. AMS (2)6, 245-378, (1957). [ Links ]
[6] Duflo, M., Vargas, J., Proper maps and multiplicities, preprint. An announcement is in [24]. [ Links ]
[7] Faraut, J., Koranyi, A., Analysis on symmetric connes, Oxford University Press (1995). [ Links ]
[8] Freundenthal, H., de Vries, H., Linear Lie Groups, Academic Press,(1969). [ Links ]
[9] Huang, J., Vogan, D., The moment map and the geometry of admissible representations, preprint. [ Links ]
[10] Kimura, T., A classification of prehomogeneous vector spaces of simple algebraic groups with scalar multiplication, J. Algebra, 83, 72-100, (1983). [ Links ]
[11] Kimura, T., Introduction to prehomogeneous vector spaces, Translation of Mathematical Monographs, Vol. 215, AMS, (2002). [ Links ]
[12] Kobayashi, T., Discrete decomposability of the restriction of 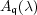 with respect to reductive subgroups, Invent. Math. 131, 229-256 (1998). [ Links ]
with respect to reductive subgroups, Invent. Math. 131, 229-256 (1998). [ Links ]
[13] Kobayashi, T., Branching Problems of Unitary representations, Proceedings of the International Congress of Mathematicians, Vol II, 615-627, (2002). [ Links ]
[14] Kobayashi, T. Restrictions of unitary representations of real reductive groups. In: Lie theory: Unitary representations and compactifications of symmetric spaces, 139-207, Progr. Math., 229, Birkhäuser Boston, Boston, MA, 2005. [ Links ]
[15] Kobayashi, T., Multiplicity free Representations and Visible actions on complex manifolds, preprint. [ Links ]
[16] Komrakov, B., Maximal subalgebras of real Lie algebras and a problem of Sophus Lie, Soviet Math. Dokl. Vol. 41, 269-273, (1990). [ Links ]
[17] Littelmann, P. Koreguläre und äquidimensionale Darstellungen. J. Algebra 123 (1989), no. 1, 193-222. [ Links ]
[18] Ness, L., with an appendix by Mumford, D., A stratification of the nullcone via moment map, Amer. J. Math. 106, 1281-1330 (1984) [ Links ]
[19] Paradan, E., Multiplicities of holomorphic representations relatively to compact subgroups, Harmonische Analysis und Darstellungstheorie Topologischer Gruppen, Oberwolfach Report, 49/2007. [ Links ]
[20] Schmid, W., Die Randerwerte holomorpher Funktionen auf hermitesch symmetrischen Räumen, Inventiones Math.. vol 9, 61-80, (1969). [ Links ]
[21] Simondi, S., Restricción de representaciones de cuadrado integrable, Ph. D. Thesis, FAMAF, Universidad Nacional de Córdoba, Argentina, (2006). [ Links ]
[22] Solomon, S., Irreducible linear group-subgroup pairs with the same invariants, J. Lie Theory 15, 105-123, (2005). [ Links ]
[23] Solomon, S., Orthogonal linear group-subgroup pairs with the same invariants, J. Algebra 299 623-647, (2006). [ Links ]
[24] Vargas, J., Restriction of square integrable representations, a review, Symposium in representation theory, edited by Yamashita, J., Hokadate, Japon, 62-79, (2003). [ Links ]
[25] Vergne, M., Quantization of algebraic cones and Vogan's conjecture, Pacific Journal of Math. Vol. 182, 114-135, (1998). [ Links ]
[26] Vogan, D., Associated varieties and unipotent representations, Harmonic Analysis on Reductive Lie groups, Progress in Math. Vol. 101, Birkhäuser, 315-388, (1991). [ Links ]
Jorge Vargas
CIEM-FaMAF,
Universidad Nacional de Córdoba,
Córdoba 5000, Argentina
vargas@famaf.unc.edu.ar
Recibido: 17 de julio de 2008
Aceptado: 4 de septiembre de 2008













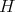 .
.