Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Unión Matemática Argentina
versión impresa ISSN 0041-6932versión On-line ISSN 1669-9637
Rev. Unión Mat. Argent. v.49 n.2 Bahía Blanca jul./dic. 2008
Best Local Approximations by Abstract Norms with Non-homogeneous Dilations
Norma Yanzón and Felipe Zó
In memorian of Mischa Cotlar.
Abstract. We introduce a concept of best local approximation using abstract norms and non-homogeneous dilations. The asymptotic behavior of the normalized error function as well as the limit of some net of best approximation polynomials 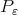 as
as 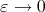 are studied.
are studied.
2000 Mathematics Subject Classification. 41A65.
Key words and phrases. Best local approximations, function norms, non-homogeneous dilations.
The authors where supported by UNSL, CONICET and FONCYT grants.
The notion of a best local approximation of a function has been introduced by Chui, Shisha and Smith [6] in the seventies although its origin goes as far as the paper of J. Walsh [23]. A rather general view of the problem is as follows. Let  be a function in a normed space
be a function in a normed space  with norm
with norm  . Let
. Let  denote a subset of
denote a subset of  , consider
, consider 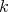 points
points  in
in  and small neighborhoods
and small neighborhoods  around each point
around each point  such that
such that 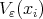 shrinks down to the point
shrinks down to the point  as
as  , for
, for  . We wish to approximate
. We wish to approximate 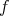 near the points
near the points  using an element of
using an element of 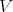 . For each
. For each 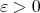 we select a
we select a 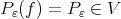 which minimizes
which minimizes
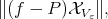 (1) (1) |
where 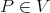 and
and 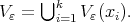 If
If  converges as
converges as  to an element
to an element  then
then 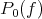 is said to be a best local approximant of
is said to be a best local approximant of 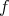 at the points
at the points  .
.
Thus we have 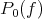 to be the set of cluster points of the net
to be the set of cluster points of the net 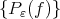 as
as  , which may be the empty set, a singleton or a set with more than one element, see [7] for one dimensional examples with non smooth functions and [14] for
, which may be the empty set, a singleton or a set with more than one element, see [7] for one dimensional examples with non smooth functions and [14] for 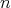 -dimensional examples where
-dimensional examples where  or card
or card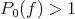 even for functions
even for functions  , the algebraic polynomials of degree at most
, the algebraic polynomials of degree at most 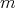 as the approximant class and
as the approximant class and  to be the
to be the 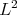 norm. In many situations
norm. In many situations 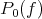 has one element and it is called the best local approximation of
has one element and it is called the best local approximation of 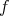 [23], [6], [7],[5], [25], [24] and more recently [9], [10] for one point. The case of more than one point, sometimes called the best multipoint local approximation is fully treated in [4] where the
[23], [6], [7],[5], [25], [24] and more recently [9], [10] for one point. The case of more than one point, sometimes called the best multipoint local approximation is fully treated in [4] where the 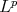 norm is used, see [20] and [1] for other approaches to best multipoint local approximations with
norm is used, see [20] and [1] for other approaches to best multipoint local approximations with 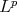 norms, for Orlicz norms see [13],[9],[15] and for a general family of norms [10] and [11].
norms, for Orlicz norms see [13],[9],[15] and for a general family of norms [10] and [11].
The minimizing problem in (1) for the particular case 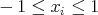 ,
, 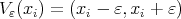 and
and 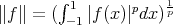 ,
, 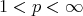 and
and 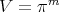 the algebraic polynomials of degree at most
the algebraic polynomials of degree at most 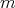 , is related to the following problem. For simplicity let us take
, is related to the following problem. For simplicity let us take  and let
and let 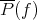 be the unique polynomial in
be the unique polynomial in 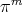 , which minimizes
, which minimizes
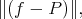 (2) (2) |
where 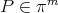 . It is readily seen that
. It is readily seen that  where
where 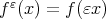 , and
, and 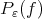 is the minimum problem described in (1) for this particular choice of norm. Not always the relationship between the best approximations
is the minimum problem described in (1) for this particular choice of norm. Not always the relationship between the best approximations 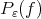 and
and  is so easily described as above, and some normalization in the norm used in problem (1) it is necessary to obtain a relationship between them see [18], [26] and [9]. Of course the problem (1) and the normalized one may have different solutions, see the last section of this paper. In this paper as it was done in [11] we study best approximation problems related to (2) and in term of these best approximations we define best approximations
is so easily described as above, and some normalization in the norm used in problem (1) it is necessary to obtain a relationship between them see [18], [26] and [9]. Of course the problem (1) and the normalized one may have different solutions, see the last section of this paper. In this paper as it was done in [11] we study best approximation problems related to (2) and in term of these best approximations we define best approximations  which play the role as the solutions of the problem (1) although in general they will give origin to different notions of best local approximations.
which play the role as the solutions of the problem (1) although in general they will give origin to different notions of best local approximations.
In [11] we studied the best local approximation problem, where the notion of closeness was given by a very general family of function seminorms acting on vector valued Lebesgue measurable functions. These seminorms embraced by far the norms used in these sort of problems, for example 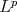 , Orlicz or Lorentz norms. The fact to consider best local approximation problems on vector valued functions of several variables it was due to understand better the solution to the so called multipoint best local approximation problems given in [4], [13] and [20], also this general set up gives origin to best local approximation problems not considered before, even using the standard
, Orlicz or Lorentz norms. The fact to consider best local approximation problems on vector valued functions of several variables it was due to understand better the solution to the so called multipoint best local approximation problems given in [4], [13] and [20], also this general set up gives origin to best local approximation problems not considered before, even using the standard  norms.
norms.
The main goal of this paper is to consider, within the general frame given by [11], best local approximation on regions induced by dilations of the form 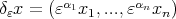 as treated in [26], [14].
as treated in [26], [14].
However, we should point out that our presentation doves not cover all the problems of the paper [4], for example the case when we approach a function on small neighborhood  with polynomials of degree at most
with polynomials of degree at most  , the number
, the number 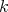 does not divide
does not divide  , and the neighborhood
, and the neighborhood 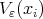 shrink dawn to the point
shrink dawn to the point  with different velocity at each
with different velocity at each 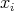 , for
, for  . This last problem it was solved rather exhaustively for
. This last problem it was solved rather exhaustively for 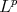 norms in [4] but it remains open in other general norms, for example in Orlicz norms, for a recent contribution in this direction see [15].
norms in [4] but it remains open in other general norms, for example in Orlicz norms, for a recent contribution in this direction see [15].
It is known, [14], that when non-homogeneous dilations  are used in best local approximation problems, the class
are used in best local approximation problems, the class 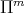 of algebraic polynomials of degree at most
of algebraic polynomials of degree at most 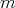 is not suitable as an approximation class and should be replaced by a class
is not suitable as an approximation class and should be replaced by a class 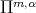 which depends
which depends  de
de  -tuple
-tuple 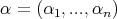 , see Definition 3.1. This paper extends results of [9] and [26] among others.
, see Definition 3.1. This paper extends results of [9] and [26] among others.
We will work with a family of function seminorms 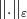 ,
,  , acting on Lebesgue measurable functions
, acting on Lebesgue measurable functions  where
where 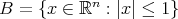 , and
, and  denotes the euclidean norm on
denotes the euclidean norm on 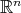 .
.
We assume the following properties for the family of function seminorms  ,
, 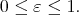
(1). For 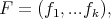 and
and 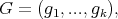 we have
we have  for every
for every  provided
provided  and
and 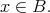
(2). If  is the function
is the function 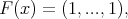 we have
we have  for all
for all 
(3). For every 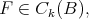 we have
we have  as
as  where
where 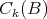 is the set of continuous functions
is the set of continuous functions  Moreover
Moreover 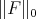 is a norm on
is a norm on 
From now on, if we do not specify the contrary, the statements will be valid for an abstract family of seminorms  ,
,  fulfilling conditions (1)-(3).
fulfilling conditions (1)-(3).
In order to give examples of norms 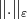 ,
,  with the properties (1)-(3) we recall a definition of convergence of measures early given in [16]. See also [2] for the notion of weak convergence of measures in general.
with the properties (1)-(3) we recall a definition of convergence of measures early given in [16]. See also [2] for the notion of weak convergence of measures in general.
Definition 2.1. Let 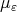 ,
,  be a family of probability measures on
be a family of probability measures on 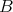 . We say that the measures
. We say that the measures 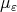 converge weakly in the proper sense to the measure
converge weakly in the proper sense to the measure 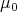 if we have
if we have
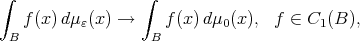
and 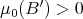 for any ball
for any ball 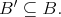
The assumption on the measure 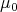 implies that
implies that
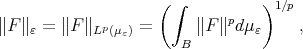
is actually a norm on  for
for  and
and 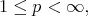 where
where  stands for any monotone norm on
stands for any monotone norm on 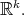 A seminorm fulfilling a property like (1) is called a monotone norm. We use a monotone norm on
A seminorm fulfilling a property like (1) is called a monotone norm. We use a monotone norm on  to assure property (1) for the family of seminorms
to assure property (1) for the family of seminorms  ,
, 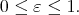 It is worthy to note we will not need this property on
It is worthy to note we will not need this property on  in proving some convergence results, see [10]
in proving some convergence results, see [10]
Let 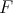 be in
be in 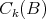 ; it is readily seen, by using the definition of weak convergence of measures, that there exists
; it is readily seen, by using the definition of weak convergence of measures, that there exists 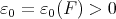 such that if
such that if 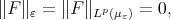 for some
for some 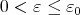 then
then  . Moreover we have that
. Moreover we have that 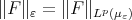 converges as
converges as 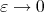 to the norm
to the norm 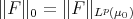 if
if 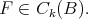
In the next example, and for the most of the paper, we will consider a fixed notion of dilation on 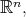 namely
namely
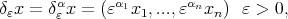
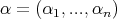 are given positive numbers. Associated with the above (nonisotropic) dilation is the metric
are given positive numbers. Associated with the above (nonisotropic) dilation is the metric  on
on 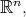 where
where 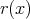 is defined for any
is defined for any 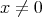 as the unique positive number
as the unique positive number  which is the solution of
which is the solution of 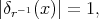 that is,
that is, 
 has the homogeneity property
has the homogeneity property  and there is polar like decomposition of
and there is polar like decomposition of 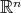 relative to
relative to 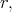 i.e. to each vector
i.e. to each vector  we assign
we assign  where
where 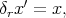 or
or 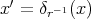 is in the unit sphere
is in the unit sphere  Finally we can integrate in polar like coordinates, according to the next formula
Finally we can integrate in polar like coordinates, according to the next formula 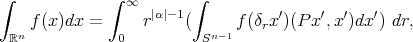 (3) (3) |
where  denotes the Lebesgues measure over the unit sphere
denotes the Lebesgues measure over the unit sphere 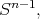
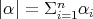 and
and 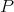 is the diagonal matrix which generates the semigroup of dilations
is the diagonal matrix which generates the semigroup of dilations 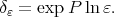 We refer to the article [8] for an early use of this dilations in harmonic analysis or for more general dilations see [21]. In the following example we introduce measure
We refer to the article [8] for an early use of this dilations in harmonic analysis or for more general dilations see [21]. In the following example we introduce measure  adapted to the dilations
adapted to the dilations 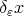 which plays an analogous role to those introduced in [18].
which plays an analogous role to those introduced in [18].
Example 2.2. Let 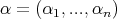 be a fix n-tuple of real numbers such that
be a fix n-tuple of real numbers such that  , the measures
, the measures 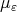 are given by
are given by
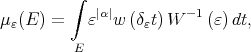 (4) (4) |
where , 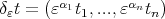 ,
,  and
and 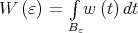 . The following condition on the weight function
. The following condition on the weight function 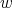 will be assumed
will be assumed
 (5) (5) |
We say that the weight function  is a radial function with respect to
is a radial function with respect to  if
if 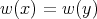 when
when 
Remark 2.3. If the weight function 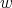 is a radial function, then the measures
is a radial function, then the measures  introduced in Example 2.2 converges weakly to the measure
introduced in Example 2.2 converges weakly to the measure
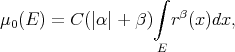 (6) (6) |
where  is a constant depending upon the weight function
is a constant depending upon the weight function 
The proof of this last remark follows the same pattern of Lemma 1 in [18] and now we will point out the necessary modifications of the proof.
Let us consider the function  and set
and set 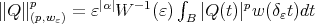 for
for 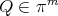 .
.
To deal with the weights 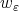 we consider a change of variables of polar type induced by the function
we consider a change of variables of polar type induced by the function  given by (3) .
given by (3) .
Using the above formula and following the steps of the proof of Lemma 1 in [18], we can see that
 (7) (7) |
where 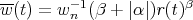 and
and 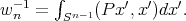 Now it is easy to obtain the weak convergence of the measures
Now it is easy to obtain the weak convergence of the measures  to
to 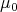 and that the constant
and that the constant  in equation (6) it turns to be
in equation (6) it turns to be 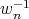 .
.
3. The Taylor polynomial and the limit of best approximation polynomials.
Throughout this paper 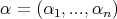 will denote a fix n-tuple of real numbers such that
will denote a fix n-tuple of real numbers such that  and
and 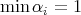 .
.
Definition 3.1. The class  Given a positive number
Given a positive number 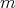 we say that a real polynomial
we say that a real polynomial 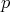 is in the class
is in the class 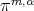 if it is of the form
if it is of the form
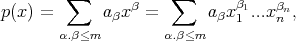
 and at least one of them satisfies
and at least one of them satisfies  . A polynomial
. A polynomial  is of
is of 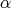 -degree
-degree 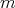 if
if 
Note that in the case  we obtain the classical definition of polynomial of degree
we obtain the classical definition of polynomial of degree 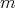 . We denote by
. We denote by 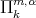 the set
the set 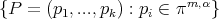 .
.
It is worthy to note that when we make reference to a polynomial of 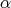 -degree
-degree  we do not mean the classic degree of polynomial. For example, for
we do not mean the classic degree of polynomial. For example, for  there exist polynomials of
there exist polynomials of 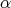 -degree
-degree 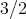 and they are of the form
and they are of the form  , for
, for 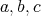 in
in 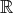 .
.
Given a function 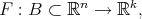 and a family of seminorms
and a family of seminorms 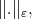
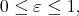 as in section 2, we introduce a general version of the "Peano's definition" of the Taylor polynomial, see [3], [8], [17], [18], [22], [26], [27]. We will use the notation
as in section 2, we introduce a general version of the "Peano's definition" of the Taylor polynomial, see [3], [8], [17], [18], [22], [26], [27]. We will use the notation  .
.
Definition 3.2. A function 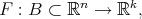 has a Taylor Polynomial of
has a Taylor Polynomial of 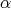 -degree
-degree 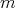 , if there exists
, if there exists  such that
such that
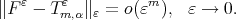
We write  if the function
if the function  has a Taylor Polynomial of
has a Taylor Polynomial of  -degree
-degree 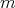 .
.
To prove the uniqueness of the Taylor polynomial we need the next result which is a consequence of an usual compactness argument. The proof is essentially given in [11], and it depends basically of the properties of the family of seminorms. See also [18].
Proposition 3.3. There exist 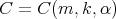 and
and  such that for every
such that for every 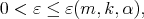
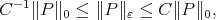
for every 
We make use of the standard notation,  for
for 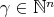 .
.
Proposition 3.4. There exists a constant  depending only on
depending only on 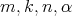 and the family of seminorms
and the family of seminorms  such that for any
such that for any  there holds
there holds

for any 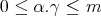 and
and 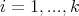 .
.
Proof. We consider the seminorm  . Using the above proposition we have
. Using the above proposition we have

 . Since
. Since 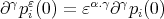 , the proposition follows. □
, the proposition follows. □ The next proposition is a consequence of Proposition 3.4.
Proposition 3.5. The polynomial 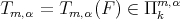 in Definition 3.2 is unique.
in Definition 3.2 is unique.
Proposition 3.6. If the function 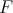 has the Taylor polynomial of
has the Taylor polynomial of 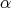 -degree
-degree  ,
,  then the Taylor polynomial of
then the Taylor polynomial of  -degree
-degree  is given by
is given by 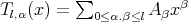 (if there exists
(if there exists  such that
such that 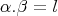 ) .We set
) .We set 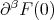 for the vector
for the vector 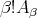 .
.
Proof. We have

 and
and  . □
. □ Let  ,
, 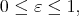 be a family of seminorms and
be a family of seminorms and  be a fixed measurable function such that
be a fixed measurable function such that  and
and  are finite for all
are finite for all 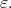 For any such
For any such 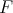 has a meaning the following definition.
has a meaning the following definition.
Definition 3.7. Set  and
and  for any polynomial in
for any polynomial in 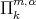 which minimizes
which minimizes 
Although the best approximation polynomial  is not unique in general, through this paper the notation
is not unique in general, through this paper the notation  does not mean a set of best approximation polynomials but any arbitrarily chosen polynomial in this set. We have the existence of
does not mean a set of best approximation polynomials but any arbitrarily chosen polynomial in this set. We have the existence of 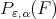 , at least for all small
, at least for all small 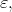 by Proposition 3.3.
by Proposition 3.3.
The next statement has its origin in [23] using the 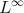 norm, and since then similar versions in
norm, and since then similar versions in 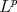 in one and several real variables appeared. Results dealing with weighted Luxemburg norms appeared recently in [9] and [10].
in one and several real variables appeared. Results dealing with weighted Luxemburg norms appeared recently in [9] and [10].
Proof. In fact  and by Proposition 3.4 it follows
and by Proposition 3.4 it follows ![|[P (ɛ,βα)]i(0 ) - [Tm(β,)α(F )]i(0)| ≤ ɛ-α.βC ∥P ɛɛ,α - Tmɛ,α(F )∥ɛ,](/img/revistas/ruma/v49n2/2a09288x.png) and
and  □
□
As in [6] we call the limit of  as
as  the best local approximation to
the best local approximation to 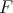 .
.
4. The asymptotic behavior of the error.
Let  be a subspace of polynomials
be a subspace of polynomials 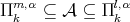 and let
and let 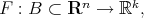 be a Lebesgue measurable function. Set
be a Lebesgue measurable function. Set 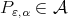 for a polynomial which is a best approximation of the function
for a polynomial which is a best approximation of the function 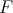 with the seminorm
with the seminorm  Observe that
Observe that  is a polynomial in
is a polynomial in  which is a best approximation of the function
which is a best approximation of the function 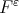 with the seminorm
with the seminorm 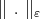 from the class
from the class  and we will also denote it by
and we will also denote it by 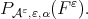 We insist that
We insist that 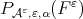 means, in our notation, a fixed best approximation polynomial and not a set of them.
means, in our notation, a fixed best approximation polynomial and not a set of them.
Let 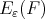 be the error function
be the error function 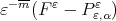 where
where 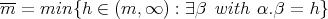 . Next, we will obtain an expression for the function
. Next, we will obtain an expression for the function  which has its origin in [19] see also [17, 18].
which has its origin in [19] see also [17, 18].
Let 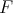 be in
be in 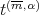 and set
and set 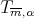 for the Taylor polynomial of
for the Taylor polynomial of  of
of 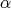 -degree
-degree 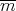 ; then by definition we have
; then by definition we have 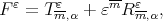 with
with 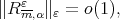 and
and 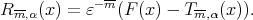 Moreover, observe that
Moreover, observe that 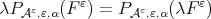 and
and 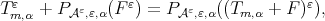 where we have used that
where we have used that 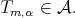 Using the equality
Using the equality 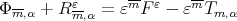 we obtain the following result
we obtain the following result
Proposition 4.1. Let  be a function in
be a function in  , and
, and 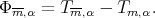 Then
Then


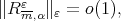 as
as 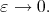
Proposition 4.1 is useful when  for every
for every 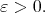 The case
The case  with
with  was considered in [18] and [17] for weighted
was considered in [18] and [17] for weighted 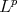 norms and in [9] for the Luxemburg norm. It is easy to find
norms and in [9] for the Luxemburg norm. It is easy to find  and
and  for every
for every  The following result is relevant to this matter.
The following result is relevant to this matter.
Theorem 4.2. Let  be a subspace of polynomials such that
be a subspace of polynomials such that  Then
Then  for all
for all 
Proof. Let 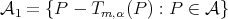 . We shall see if
. We shall see if 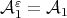 for all
for all  , then
, then  for all
for all  . Let
. Let 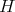 be in
be in  i.e.,
i.e., 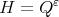 with
with  As
As 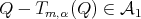 we have
we have

Thus  and there exists
and there exists 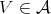 such that
such that 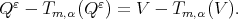 Therefore
Therefore 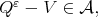 so
so 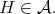 We have proved that
We have proved that  for all
for all 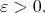 Since
Since 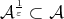 we get
we get  Therefore,
Therefore,  for all
for all 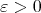 .
.
Clearly, there is a linear space 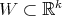 such that
such that 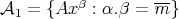 and
and 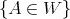 , then
, then 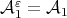 . □
. □
Theorem 4.3. Let 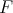 be in
be in 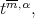 and
and  for every
for every  Then
Then 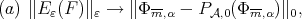 as
as 
 as
as 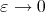 if
if 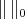 is a strictly convex norm. We have denoted by
is a strictly convex norm. We have denoted by 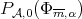 a polynomial in
a polynomial in 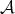 which is a best approximation of
which is a best approximation of 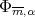 with respect to the norm
with respect to the norm 
Proof. Let us begin with  . By Proposition 4.1 we have, for any
. By Proposition 4.1 we have, for any 
 as
as  Therefore
Therefore
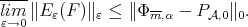 |
Let 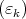 be a sequence tending to zero such that
be a sequence tending to zero such that
 |
Set 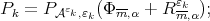 then
then 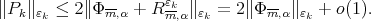 By Proposition 3.3 we can select a convergent subsequence of
By Proposition 3.3 we can select a convergent subsequence of 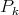 which is again denoted by
which is again denoted by 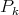 and then we have
and then we have 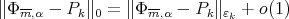 , as
, as  . Then
. Then 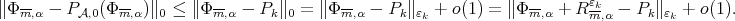 Thus we have
Thus we have
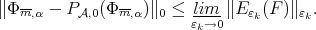 |
To prove  , consider any sequence
, consider any sequence  and select
and select 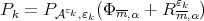 , then
, then  We will prove
We will prove  which implies (b). In fact we may assume, by taking subsequences if it is necessary, that
which implies (b). In fact we may assume, by taking subsequences if it is necessary, that 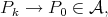 as
as  Thus by
Thus by 
 Since
Since 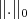 is a strictly convex norm we have
is a strictly convex norm we have  □
□
Consider the set  where
where  , for
, for 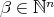 . Then
. Then  and
and  for every
for every 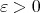 .
.
We now introduce an useful example of a subspace 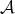 such that
such that 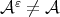 . Consider the set
. Consider the set
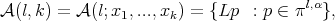 (8) (8) |
where, 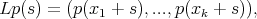 and
and  Now
Now 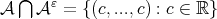 , see [11] in Proposition 4.2. Thus it is not possible to use Theorem 4.3 to study the function error with
, see [11] in Proposition 4.2. Thus it is not possible to use Theorem 4.3 to study the function error with 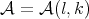 . The next condition on
. The next condition on 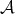 will be significant in the future and it was used in [11] to consider cases such as
will be significant in the future and it was used in [11] to consider cases such as 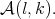
A subspace of polynomials which does not satisfies  is given in the following example.
is given in the following example.
Example 4.4. We denote by  the set of all algebraic polynomials of the form
the set of all algebraic polynomials of the form

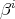 ,
, 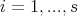 are fixed vectors in
are fixed vectors in  ,
,  ,
, 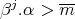 for
for 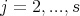 and
and 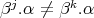 for
for 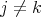 . Moreover
. Moreover 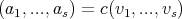 whit
whit  ,
, 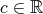 and
and  is a fixed vector in
is a fixed vector in 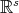 .
. Let  , where
, where 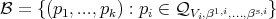 . It is clear that
. It is clear that  .
.
Condition 4.5. For 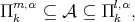 we assume that if
we assume that if  and
and  then
then  . Where
. Where  and
and 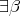 with
with 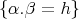 .
.
Let  be as in Example 4.4 , then the Condition 4.5 holds. We consider again the error function
be as in Example 4.4 , then the Condition 4.5 holds. We consider again the error function  where
where 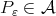 and
and 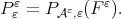 Set
Set 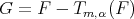 and recall that
and recall that 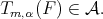 Then
Then 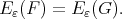 If
If 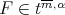 we have
we have
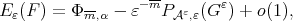 (9) (9) |
as  and
and  The next theorem give us a useful expression for the error function
The next theorem give us a useful expression for the error function  as well as we know the polynomials
as well as we know the polynomials 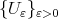 and
and 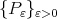 used to describe it. With the notation
used to describe it. With the notation 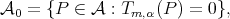 observe that
observe that  is the direct sum
is the direct sum 
Theorem 4.6. Let 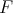 be a function in
be a function in 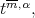 and assume Condition 4.5 for
and assume Condition 4.5 for  . Set
. Set 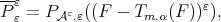 with
with 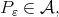
 and
and 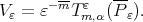 Then
Then 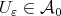 and
and  and
and
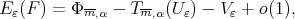 (10) (10) |
as  Moreover the two families of polynomials
Moreover the two families of polynomials  and
and  are uniformly bounded in
are uniformly bounded in  for a fixed norm
for a fixed norm  .
.
Proof. By (9) we have
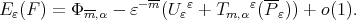 |
Or else, since 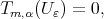
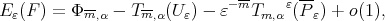 |
as  which is (10).
which is (10).
Now we will prove 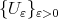 and
and  are uniformly bounded in
are uniformly bounded in  . For a norm
. For a norm  in
in  the expression
the expression
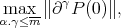 |
is a norm on  Here we are using that the subspace
Here we are using that the subspace 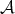 fulfills Condition 4.5.
fulfills Condition 4.5.
Since 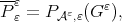 with
with 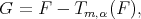 we have
we have  .
.
By Proposition 3.4 we have 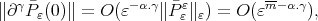 for
for  Thus
Thus  and hence
and hence  are uniformly bounded in
are uniformly bounded in  To estimate the polynomials
To estimate the polynomials 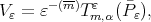 we note that
we note that  for
for  Then
Then 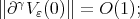 recall that
recall that  , and
, and 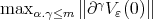 is a norm there. □
is a norm there. □
Theorem 4.7. Let 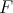 be in
be in 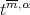 and assume Condition 4.5 for
and assume Condition 4.5 for  Then
Then 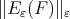 tends to
tends to
 |
as  and
and 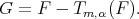
Proof. We will prove the following inequality
 (11) (11) |
Let  and
and  be two arbitrary polynomials and set
be two arbitrary polynomials and set  with
with 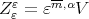 and
and 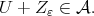 Then
Then


As 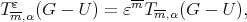 using the definition of the polynomial
using the definition of the polynomial 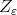 we have
we have
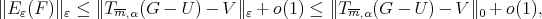 |
as  and the right inequality of (11) holds.
and the right inequality of (11) holds.
To prove left inequality in (11) let 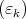 be sequence tending to zero such that
be sequence tending to zero such that
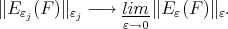 |
By Theorem 4.6 we select a subsequence  in such a way that the following limits exist:
in such a way that the following limits exist:
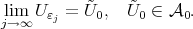 |
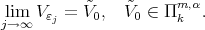 |
Thus by (10) we have
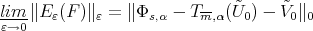 |
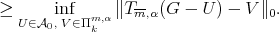 |
□
Proposition 4.8. Let  be a strictly convex norm and assume that the subspace
be a strictly convex norm and assume that the subspace 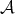 fulfills Condition 4.5. Then there exists a unique solution
fulfills Condition 4.5. Then there exists a unique solution  to the minimum problem in Theorem 4.7 .
to the minimum problem in Theorem 4.7 .
Proof.
If 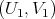 and
and 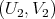 are solutions to the minimum problem in Theorem 4.7, we have
are solutions to the minimum problem in Theorem 4.7, we have 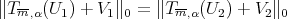 with
with 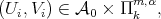
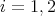 . Since
. Since  is a strictly convex norm
is a strictly convex norm  then by Condition 4.5,
then by Condition 4.5,  but
but 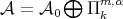 . □
. □
Theorem 4.9. Let 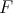 be in
be in  assume Condition 4.5 for
assume Condition 4.5 for  and that the minimum problem in 4.5 has a unique solution
and that the minimum problem in 4.5 has a unique solution 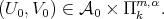 Then
Then  and
and  as
as  Moreover we have
Moreover we have

Proof. By Theorem 4.6, Theorem 4.7 and (10) any convergent subsequence of the net 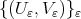 will converge to a solution of the minimum problem in Theorem 4.7. Thus if this solution is unique, the whole net converges to the solution. □
will converge to a solution of the minimum problem in Theorem 4.7. Thus if this solution is unique, the whole net converges to the solution. □
5. The limit of best approximation polynomials.
The main goal of this section will be to study the limit of 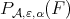 as
as  If
If 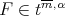 and
and 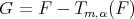 it will be enough to consider
it will be enough to consider  as
as  since
since 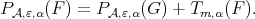
We set as before  Let
Let 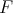 be in
be in  then
then  for
for  ; see the proof of Theorem 4.6. Then
; see the proof of Theorem 4.6. Then  Thus
Thus 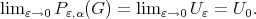 From Theorem 4.7 and Theorem 4.8 , this polynomial exists whenever
From Theorem 4.7 and Theorem 4.8 , this polynomial exists whenever 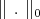 is a strictly convex norm. Then
is a strictly convex norm. Then 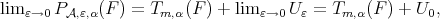 where
where  together with
together with  are the unique solution to the minimizing problem
are the unique solution to the minimizing problem
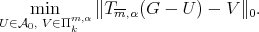
Thus if we set  for
for  then
then  in
in  will be the unique solution to the problem
will be the unique solution to the problem
 (12) (12) |
Thus, we have proved the following theorem.
Theorem 5.1. Let 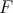 be in
be in  and assume Condition 4.5 for
and assume Condition 4.5 for  and that the minimum problem in (12) has a unique solution
and that the minimum problem in (12) has a unique solution  and denote by
and denote by 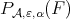 a polynomial in
a polynomial in 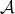 which minimizes
which minimizes 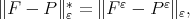 with
with  Then
Then  as
as 
6. On the best local approximation using Luxemburg norm.
We denote by  the measures given by (4), and let
the measures given by (4), and let 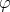 be a convex function such that
be a convex function such that 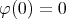 ,
, 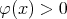 if
if  . For any measurable
. For any measurable  set
set
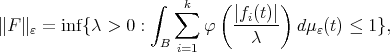 (13) (13) |
where 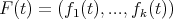 .
.
By Proposition (2.3) in [11] we have  converges to
converges to 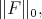 for any
for any  . Moreover the family
. Moreover the family  has the properties (1),(2) y (3) of the section 2.
has the properties (1),(2) y (3) of the section 2.
Recall that 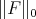 is the Luxemburg norm defined by (13) with the particular measure
is the Luxemburg norm defined by (13) with the particular measure  defined by (6) and denote by
defined by (6) and denote by 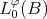 the Orlicz Space equipped with the norm
the Orlicz Space equipped with the norm 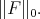 The following result is known .
The following result is known .
Remark 6.1. Let  be a strictly convex function, then
be a strictly convex function, then 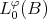 is a strictly convex Banach space with the Luxemburg norm
is a strictly convex Banach space with the Luxemburg norm 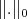 .
.
By Remak 6.1 we can use Proposition 4.8 and Theorem 5.1 for the Luxemburg norm 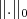 when
when 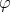 is a strictly convex function. Also we are free to apply Theorem 5.1 in [11]. We apply these results in the particular situation described below.
is a strictly convex function. Also we are free to apply Theorem 5.1 in [11]. We apply these results in the particular situation described below.
Given ![f : [- 1,1] → ℝ](/img/revistas/ruma/v49n2/2a09608x.png) and
and  set
set 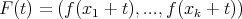 and the norm
and the norm 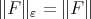 as in (13) and the measure
as in (13) and the measure  is the Lebesgue measure
is the Lebesgue measure 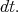
Theorem 6.2. Let  be a strictly convex function and let
be a strictly convex function and let 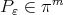 be the unique solution of the minimum problem
be the unique solution of the minimum problem
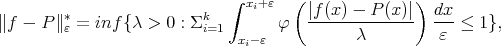 |
where 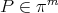 . Then for a smooth function
. Then for a smooth function  ,
, 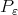 converges to a polynomial
converges to a polynomial 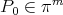 , which is uniquely determined by the solution of the minimum problem in (4) of [11].
, which is uniquely determined by the solution of the minimum problem in (4) of [11].
Now we will assume more restrictive conditions on the strictly convex function  , namely
, namely 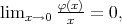
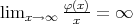 and
and  exists and it is a finite number for every
exists and it is a finite number for every  . Clearly
. Clearly 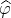 is convex function,
is convex function, 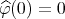 and it is easy to see that
and it is easy to see that 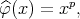 for
for  and if
and if  we have
we have 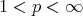 see [13]. From now on assume all the above conditions on the function
see [13]. From now on assume all the above conditions on the function 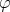 .
.
Theorem 6.3. For any  let
let 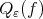 be the unique polynomial in
be the unique polynomial in 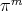 which minimizes
which minimizes
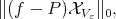 |
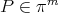 and
and 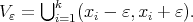 Then the limit
Then the limit  exist for smooth functions
exist for smooth functions  .
.
Theorem 6.3 may be obtained using results of [13] and [20]. For the case 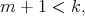 the polynomial
the polynomial 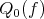 it is very easy to characterize as the unique element
it is very easy to characterize as the unique element 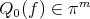 which minimizes the problem
which minimizes the problem
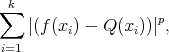 |
 see [13]. For the case
see [13]. For the case 
 also
also 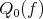 can be obtained as a discrete minimum
can be obtained as a discrete minimum 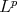 problem as in [20].
problem as in [20].
The best local approximation polynomials 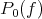 described in Theorem 6.2 and
described in Theorem 6.2 and 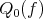 in Theorem 6.3 are different polynomials. Indeed, it is rather straightforward to obtain the next result when
in Theorem 6.3 are different polynomials. Indeed, it is rather straightforward to obtain the next result when 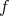 is a continuous function at each point
is a continuous function at each point  and
and 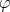 just a strictly convex function
just a strictly convex function 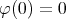 .
.
Theorem 6.4. For  and
and  let
let  the unique polynomial which minimizes
the unique polynomial which minimizes
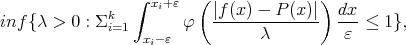 |
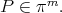 Then the limit
Then the limit 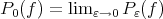 exist and it is characterized as the unique
exist and it is characterized as the unique  which minimizes
which minimizes
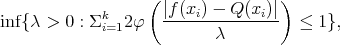 |
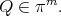
We point out that to prove the existence of the polynomial 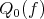 in Theorem 6.3 still remains an open problem when
in Theorem 6.3 still remains an open problem when  is just a strictly convex function and the existence of the function
is just a strictly convex function and the existence of the function 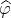 is not required.
is not required.
[1] A. Alzamel, J.M. Wolfe. Interpolation and Best Lp Local Approximation. Journal of Approximation Theory 32(1981), 96-102 . [ Links ]
[2] P. Billingsley. Convergence of Probability Measures. John Wiley & and Sons, Inc., 1968. [ Links ]
[3] A.P. Calderón, A. Zygmund. Local Properties of Solutions of Elliptic Partial Differential Equations. Studia Math. 20 (1961), 171-225. [ Links ]
[4] C.K. Chui, H. Diamond, L. Raphael. On Best Data Approximation. Approximation Theory and its Applications. 1 (1984), 37-56. [ Links ]
[5] C.K. Chui, H. Diamond, L. Raphael. Best Local Approximation in Several Variables. Journal of Approximation Theory 40 (1984), 343-350. [ Links ]
[6] C. K. Chui, O. Shisha, P. W. Smith. Best Local Approximation. Journal of Approximation Theory 15 (1975), 371-381. [ Links ]
[7] C. K. Chui, P. W. Smith, J.D. Ward. Best 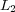 Approximation. Journal of Approximation Theory 22 (1978), 254-261. [ Links ]
Approximation. Journal of Approximation Theory 22 (1978), 254-261. [ Links ]
[8] M. Cotlar, C. Sadosky. On Quasi-homogeneous Bessel Potential Operators. Proceedings of Symposia in Pure Mathematics of the AMS vol.X (1967), 275-287. [ Links ]
[9] H. Cuenya, M. Lorenzo, C. Rodriguez. Weighted Inequalities and Applications to Best Local Approximation in Luxemburg norm. Analysis in Theory and Applications 20 (3)(2004), 265-280. [ Links ]
[10] H.H.Cuenya, M.D. Lorenzo, C.N. Rodriguez. A unified approach to certain problems of best local approximation. Analysis in Theory and Applications 23 (2) (2007), 162-170. [ Links ]
[11] H. H. Cuenya, F. Zó. Best Approximations on Small Regions. A general approach, in Procedings of the Second International School. Advanced Courses of Mathematical Analysis II. Edited by M. V. Velasco and A. Rodríguez- Palacios. World Scientific (2007), 193- 213. [ Links ]
[12] E. B. Fabes, N. M. Rivière. Singular Integrals with Mixed Homogeneity. Studia Math. 27 (1966), 19-38. [ Links ]
[13] S.Favier. Convergence of Functions Averages in Orlicz Spaces. Numer. Funct. Anal. and Optimiz. 15 (3&4) (1994), 263-278. [ Links ]
[14] S. Favier, C. Fernandez and F. Zó. The Taylor Polinomial on Best Local Approximation in Rectangles. Revista de la Unión Matemática Argentina 32 (1986), 254-262. [ Links ]
[15] S. Favier, C. Ridolfi. Weighted Best Local Approximation in Orlicz Spaces. To appear in Analysis in Theory and Applications. [ Links ]
[16] W. Feller . An Introduction to Probability and Its Applications. Wiley , Vol.II (1966), New York. [ Links ]
[17] V. B. Headly and R.A. Kerman. Best Local Approximation in 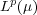 . Journal of Approximation Theory 62 (1990). [ Links ]
. Journal of Approximation Theory 62 (1990). [ Links ]
[18] R. Macías, F. Zó. Weighted Best Local  Approximation. Journal of Approximation Theory 42 (1984), 181-192. [ Links ]
Approximation. Journal of Approximation Theory 42 (1984), 181-192. [ Links ]
[19] H. Maehly, Ch. Witzgall. Tschebyscheff - Approximationen in kleinen Intervallen I. Approximation durch Polynome. Numerische Mathematik 2 (1960), 142-150. [ Links ]
[20] M. Marano. Mejor Aproximación Local. Phd Thesis, Universidad Nacional de San Luis (1986). [ Links ]
[21] N. M. Rivière. Singular Integrals and Multiplier Operators . Ark. Mat. 9 (1971), 243-278. [ Links ]
[22] C. Sadosky. On Some Properties of a Class of Singular Integrals. Studia Math. 27 (1966), 105-118. [ Links ]
[23] J. L. Walsh. On Approximation to an Analytic Function by Rational Functions of Best Approximation. Mathematische Zeitschrift (1934), 163-176. [ Links ]
[24] J. M. Wolfe. Interpolation and Best  Local Approximation. Journal of Approximation Theory 32 (1981), 96-102. [ Links ]
Local Approximation. Journal of Approximation Theory 32 (1981), 96-102. [ Links ]
[25] J.M. Wolfe. Best Multipoint Local Lp Approximation. Journal of Approximation Theory 62 (2)(1990), 96-102 . [ Links ]
[26] F. Zó . On Inequalities Arising From Best Local Approximations In Rectangles. Topics in Multivariate Approximation. Academic Press, Inc., 265-263. [ Links ]
[27] A. Zygmund. Trigonometric Series. Vols. I,II third edition Cambridge Mathematical Library, Cambridge University Press, 2002. [ Links ]
Norma Yanzón
Instituto de Matemática Aplicada San Luis. CONICET and
Departamento de Matemática,
Universidad Nacional de San Luis,
(5700) San Luis, Argentina
nbyanzon@unsl.edu.ar
Felipe Zó
Instituto de Matemática Aplicada San Luis. CONICET and
Departamento de Matemática,
Universidad Nacional de San Luis,
(5700) San Luis, Argentina
fzo@unsl.edu.ar
Recibido: 1 de septiembrede 2008
Aceptado: 25 de noviembre de 2008













 then
then  as
as 

