Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932On-line version ISSN 1669-9637
Rev. Unión Mat. Argent. vol.49 no.2 Bahía Blanca July/Dec. 2008
The problem of entanglement of quantum states
G. A. Raggio
Abstract. We give a brief and incomplete survey of the problem of entanglement of states of composite quantum systems.
A quantum system is kinematically specified by a complex Hilbert space 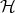 (there are hardly cases where a separable space will not do). The physical "observables" are identified with linear operators on
(there are hardly cases where a separable space will not do). The physical "observables" are identified with linear operators on 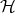 . Usually the most interesting physical observables for continuous systems are given by unbounded operators; but one avoids this problem by exponentiation and works in
. Usually the most interesting physical observables for continuous systems are given by unbounded operators; but one avoids this problem by exponentiation and works in 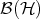 the bounded linear operators on
the bounded linear operators on 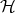 . Now
. Now 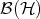 is a
is a  -algebra and a von Neumann algebra. In the 1960's - 1980's there were serious attempts (all of them anticipated by J. von Neumann) to do away with the underlying Hilbert space and work directly with the abstract algebraic structure modeled by
-algebra and a von Neumann algebra. In the 1960's - 1980's there were serious attempts (all of them anticipated by J. von Neumann) to do away with the underlying Hilbert space and work directly with the abstract algebraic structure modeled by 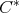 -algebras or
-algebras or 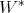 -algebras (abstract von Neumann algebras)[1, 2, 3]. This was particularly fruitful when dealing with systems of infinitely many degrees of freedom (quantum fields, thermodynamic limits, etc.). The problem of entanglement which we want to address here can be formulated quite straightforwardly in this algebraic framework of quantum theory. But we will stick to the quantum mechanics of the 1930's and keep the Hilbert space. Mainly because the results which are available concern the finite dimensional case.
-algebras (abstract von Neumann algebras)[1, 2, 3]. This was particularly fruitful when dealing with systems of infinitely many degrees of freedom (quantum fields, thermodynamic limits, etc.). The problem of entanglement which we want to address here can be formulated quite straightforwardly in this algebraic framework of quantum theory. But we will stick to the quantum mechanics of the 1930's and keep the Hilbert space. Mainly because the results which are available concern the finite dimensional case.
The "states" of the quantum system specified by 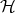 are associated with the linear functionals
are associated with the linear functionals 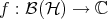 which are positive (i.e.,
which are positive (i.e., 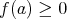 for all positive
for all positive 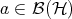 ), normalized (i.e.,
), normalized (i.e., 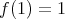 ) and normal (i.e.,
) and normal (i.e., 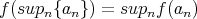 for any increasing family of selfadjoint operators
for any increasing family of selfadjoint operators 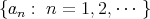 which is uniformly bounded). It is this normality condition which guarantees that the states are in one-to-one correspondence with positive trace class operators
which is uniformly bounded). It is this normality condition which guarantees that the states are in one-to-one correspondence with positive trace class operators 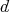 of unit trace (density operators) via the formula
of unit trace (density operators) via the formula 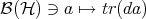 . This gives an extremely convenient representation of states and one often confuses the state
. This gives an extremely convenient representation of states and one often confuses the state 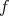 as a linear functional with the associated density operator
as a linear functional with the associated density operator 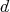 for which
for which 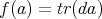 . States are automatically continuous, and satisfy
. States are automatically continuous, and satisfy  . The complex number
. The complex number 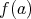 is interpreted probabilistically as the expected value of the "observable" associated with the operator
is interpreted probabilistically as the expected value of the "observable" associated with the operator  when the system is in the state
when the system is in the state 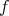 . The normalization condition is thus necessary for the consistency of this interpretation and the normality condition is seen as a non-commutative version of the
. The normalization condition is thus necessary for the consistency of this interpretation and the normality condition is seen as a non-commutative version of the  -additivity of probability measures.
-additivity of probability measures.
Clearly states, which we will denote by 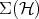 , form a convex set which is closed with respect to the metric induced by the usual norm of linear functionals. Moreover, given any countable set
, form a convex set which is closed with respect to the metric induced by the usual norm of linear functionals. Moreover, given any countable set 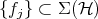 and any countable set
and any countable set ![{λj} ⊂ [0,1]](/img/revistas/ruma/v49n2/2a1127x.png) such that
such that 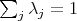 , the series
, the series 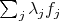 converges in the norm of functionals to a state of
converges in the norm of functionals to a state of 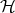 .
.
In physical jargon (due to H. Weyl!) the extremal points 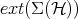 of
of 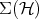 are called pure states. They are given by
are called pure states. They are given by
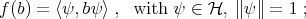
here 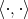 is the scalar product of
is the scalar product of 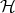 . That is: the associated density operator is an orthogonal projection of rank one projecting onto some one-dimensional subspace of
. That is: the associated density operator is an orthogonal projection of rank one projecting onto some one-dimensional subspace of 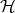 . This orthoprojection is written
. This orthoprojection is written 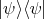 ; and
; and 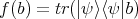 .
.
The representation theorem mentioned, and the spectral theorem for compact operators shows that the states are the closed convex hull of the pure states; in fact each state can be written as an infinite convex sum of extreme states:
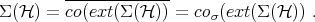
But the convex decomposition into extremal elements is never unique. 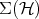 is never a (Choquet-) simplex; quite the opposite is true: there are uncountably many convex decompositions and you can choose almost freely the "ingredients" which enter a decomposition. This is a key feature of quantum theory in contradistinction with classical theories whose state spaces are simplices.
is never a (Choquet-) simplex; quite the opposite is true: there are uncountably many convex decompositions and you can choose almost freely the "ingredients" which enter a decomposition. This is a key feature of quantum theory in contradistinction with classical theories whose state spaces are simplices.
Composition, separability and entanglement
If system  is described by the Hilbert space
is described by the Hilbert space 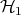 and system
and system 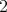 by
by 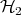 then the composite system "
then the composite system " " is described by
" is described by 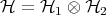 , the tensor product of the subsystem Hilbert spaces. This is the composition rule of quantum theory, and it is responsible for the most counterintuitive features of the theory. There are no indications from the real world that this rule is in need of change. I will consider mostly composition of two systems, but the definitions can be readily extended to more than two susbsytems. It is important to stress that we are always thinking of distinguishable (sub-) systems
, the tensor product of the subsystem Hilbert spaces. This is the composition rule of quantum theory, and it is responsible for the most counterintuitive features of the theory. There are no indications from the real world that this rule is in need of change. I will consider mostly composition of two systems, but the definitions can be readily extended to more than two susbsytems. It is important to stress that we are always thinking of distinguishable (sub-) systems  and
and 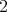 . The case of identical systems (bosons or fermions) is more involved and the entanglement issues are only partially understood.
. The case of identical systems (bosons or fermions) is more involved and the entanglement issues are only partially understood.
One has 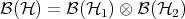 although I will not explain what the
although I will not explain what the  on the right means, [8]. Given
on the right means, [8]. Given 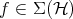 , define partial states
, define partial states 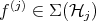 ,
, 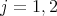 , by
, by
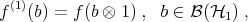
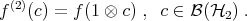
Given 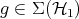 and
and 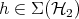 there is a unique element of
there is a unique element of 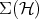 written
written  , such that
, such that
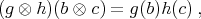
for all 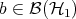 and all
and all 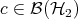 . A state
. A state 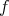 of the composite system is product if
of the composite system is product if 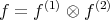 ; that is, if
; that is, if 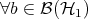 and
and 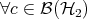 :
:
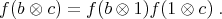
The product states, denoted by 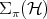 , not only do not show any correlation whatsoever between product-observables but also (for precisely that reason) the knowledge of the expected values of the observables of subsystem
, not only do not show any correlation whatsoever between product-observables but also (for precisely that reason) the knowledge of the expected values of the observables of subsystem  and of the expected values of the observables of subsystem
and of the expected values of the observables of subsystem 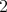 allows one to construct the state of the composite system. Since convex sums of states can be interpreted classically as classical mixtures, the separable states or EPR-correlation free states are defined as those in the closed convex hull of the product-states:
allows one to construct the state of the composite system. Since convex sums of states can be interpreted classically as classical mixtures, the separable states or EPR-correlation free states are defined as those in the closed convex hull of the product-states:
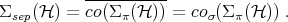
The states which are not separable are called entangled (verschränkt was the German word chosen by Schrödinger after his reaction [4, 5, 6] to the Einstein, Podolsky and Rosen paper [7]). In [4, 5], written in english, the words of Schrödinger are the following: ... I would not call that one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought. By interaction the two representatives [the quantum states] have become entangled.
A typical entangled state is a pure state 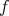 associated to a one-dimensional subspace such that the representative vector
associated to a one-dimensional subspace such that the representative vector 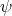 in this subspace is not a product vector:
in this subspace is not a product vector: 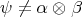 with
with 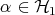 and
and 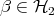 . Entangled states abound (mathematically) and naturally realized physical states are usually entangled (eigenstates of hamiltonians, thermal equilibrium states at low temperatures, etc.).
. Entangled states abound (mathematically) and naturally realized physical states are usually entangled (eigenstates of hamiltonians, thermal equilibrium states at low temperatures, etc.).
The problem is then: given a state 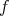 of the composite system decide whether
of the composite system decide whether 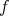 is separable or entangled. That is: are there states
is separable or entangled. That is: are there states 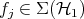 , states
, states 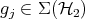 and weights
and weights ![λj ∈ [0,1]](/img/revistas/ruma/v49n2/2a1181x.png) such that
such that 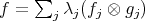 ? The sum may be an infinite series, in which case it is automatically convergent with respect to the distance associated to the norm of continuous functionals. There is no loss of generality if one restricts to pure states
? The sum may be an infinite series, in which case it is automatically convergent with respect to the distance associated to the norm of continuous functionals. There is no loss of generality if one restricts to pure states 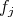 and
and 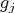 .
.
Via the representation theorem for states, one may rephrase the problem purely in terms of positive trace-class operators of unit trace on a Hilbert space tensor product; but the origin and flavor of the problem are then lost.
In the particular case where the given state 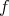 is pure, the problem was solved many years ago by, essentially, Schrödinger [4, 5]. For a modern, direct and beautiful presentation of the problem in this particular case the reader is directed to section 11-8 of Jauch's book [9] (a book which can be recommended warmly to any mathematician interested in learning quantum mechanics). The solution is:
is pure, the problem was solved many years ago by, essentially, Schrödinger [4, 5]. For a modern, direct and beautiful presentation of the problem in this particular case the reader is directed to section 11-8 of Jauch's book [9] (a book which can be recommended warmly to any mathematician interested in learning quantum mechanics). The solution is: 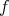 pure is separable if and only if
pure is separable if and only if 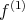 (or alternatively,
(or alternatively, 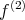 ) is pure. Thus, one has to determine one of the partial states and then check for purity which is easily done in various alternative ways. The simplest is perhaps: take the trace of the square of the associated density operator; if this number is below
) is pure. Thus, one has to determine one of the partial states and then check for purity which is easily done in various alternative ways. The simplest is perhaps: take the trace of the square of the associated density operator; if this number is below  the state is not pure, otherwise it is pure. This extends readily to the tensor product of any number of Hilbert spaces.
the state is not pure, otherwise it is pure. This extends readily to the tensor product of any number of Hilbert spaces.
However, when the given state is not pure our knowledge is rather limited. For 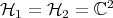 there is a criterion due to Wootters [10]; for
there is a criterion due to Wootters [10]; for  and
and  or
or  , the positive partial transpose criterion of Peres and M. Horodecki, P. Horodecki and R. Horodecki, solves the problem. A recent review is [11]. Gurvits [12], has proved that when the Hilbert spaces involved are finite dimensional, the problem is NP-hard in the hierarchy of computational complexity.
, the positive partial transpose criterion of Peres and M. Horodecki, P. Horodecki and R. Horodecki, solves the problem. A recent review is [11]. Gurvits [12], has proved that when the Hilbert spaces involved are finite dimensional, the problem is NP-hard in the hierarchy of computational complexity.
I describe the criteria just mentioned.
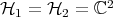 . Given
. Given 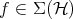 let
let 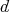 be the associated density operator, and put
be the associated density operator, and put
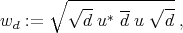
where 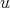 is the operator which for any orthonormal basis
is the operator which for any orthonormal basis 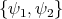 of
of 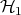 has associated to it the matrix
has associated to it the matrix
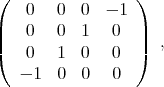
with respect to the orthonormal basis 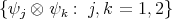 of
of 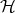 .
. 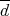 denotes the complex conjugate of
denotes the complex conjugate of 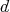 taking the product basis as real. Let
taking the product basis as real. Let 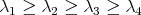 be the eigenvalues of
be the eigenvalues of 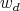 enumerated non-decreasingly according to their multiplicities.
enumerated non-decreasingly according to their multiplicities.
Theorem 1. 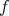 is separable if and only if
is separable if and only if  (equivalently:
(equivalently: 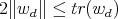 ).
).
2.2. Positive Partial Transpose Criterion.
 ,
, 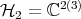 . Choose orthonormal bases for
. Choose orthonormal bases for 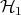 and for
and for 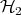 . Identify the tensor product such that the matrix associated to
. Identify the tensor product such that the matrix associated to 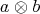 in the product orthonormal basis of
in the product orthonormal basis of 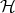 is
is
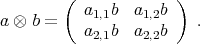
The general operator in 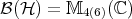 has the form
has the form
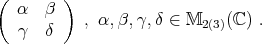
Let
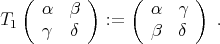
This is the partial transpose with respect to the first factor (one could proceed just as well with transposition with respect to the second factor).
Given 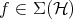 , let
, let 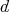 be the associated density operator; then
be the associated density operator; then
Theorem 2. 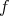 is separable if and only if
is separable if and only if 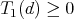 .
.
For the tensor product of two Hilbert spaces the positivity condition on the partial transpose is always necessary for separability irrespective of dimensions, as observed by A. Peres. The proof of sufficiency given by M. Horodecki, P. Horodecki and R. Horodecki [13], makes heavy use of the classification of positive linear maps of the  complex matrices
complex matrices 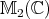 due to E. Størmer and S.L. Woronowicz. For
due to E. Størmer and S.L. Woronowicz. For  and
and  there are counterexamples (P. Horodecki):
there are counterexamples (P. Horodecki): 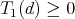 but
but 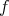 is entangled. This happens whenever the dimension of the tensor product Hilbert space
is entangled. This happens whenever the dimension of the tensor product Hilbert space 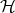 exceeds
exceeds 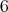 .
.
- In 1964, some thirty years after the EPR paper, J.S. Bell [14] succeeded in capturing and quantifying the separability/entanglement issue in an inequality involving expectation values (correlation inequality).
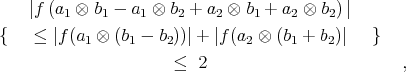
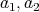 in the unit ball of
in the unit ball of 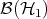 and every pair of selfadjoint
and every pair of selfadjoint 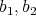 in the unit ball of
in the unit ball of 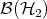 The inequality in brackets is just the triangle inequality and valid for any state. Assume
The inequality in brackets is just the triangle inequality and valid for any state. Assume 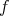 is a product state, i.e.,
is a product state, i.e., 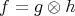 ; then
; then 
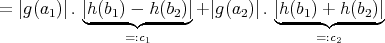
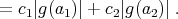
Since
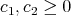 , and
, and 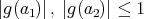 , we obtain
, we obtain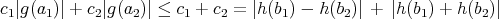

If now
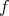 is a convex sum of product states, i.e.,
is a convex sum of product states, i.e., 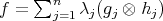 , then - using the triangle inequality, the positivity of
, then - using the triangle inequality, the positivity of 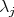 and the relation
and the relation 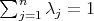 ,
,
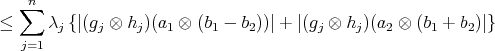
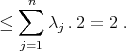
Finally, if
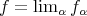 is a limit of states
is a limit of states 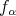 which are convex sums of product states, in a topology which makes expectation values continuous, then the inequality persists.
which are convex sums of product states, in a topology which makes expectation values continuous, then the inequality persists. For many years after 1964, "entanglement" was informally identified with "violation of Bell's inequality".
- The next huge leap forward was taken by R.F. Werner in 1989, [15]. For
 ,
, 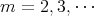 , he succeeded in constructing a family of entangled states which satisfy the inequality of Theorem 3 (or any other such correlation inequality which is necessary for separability). He thus showed that Bell-type correlation inequalities could not decide the issue. Werner does this by constructing a so-called "local hidden-variable model" for his states. In the present case of operators with discrete spectrum (denoted by
, he succeeded in constructing a family of entangled states which satisfy the inequality of Theorem 3 (or any other such correlation inequality which is necessary for separability). He thus showed that Bell-type correlation inequalities could not decide the issue. Werner does this by constructing a so-called "local hidden-variable model" for his states. In the present case of operators with discrete spectrum (denoted by  ), this means: Given a state
), this means: Given a state 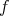 de
de  ,
, - Find a measurable space
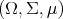
- For each
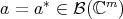 find a function
find a function 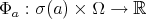 such that
such that 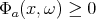 ,
, 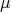 a.e. for every
a.e. for every 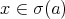 and
and 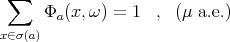
- For each
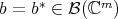 find a function
find a function 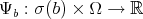 such that
such that 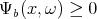 ,
, 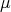 a.e. for every
a.e. for every 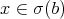 and
and 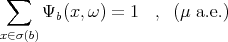
-
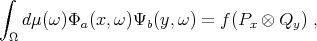
where
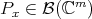 is the spectral orthoprojector of
is the spectral orthoprojector of  associated to the eigenvalue
associated to the eigenvalue 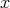 and
and 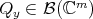 that of
that of 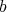 associated to the eigenvalue
associated to the eigenvalue 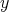 .
.
The qualifier "local" of the hidden-variable model is expressed by the fact that
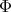 and
and 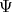 are independent. The correlation inequalities à la Bell are consequences of the integral formula: on the left-hand side we have the expectation of a product with respect to a probability measure.
are independent. The correlation inequalities à la Bell are consequences of the integral formula: on the left-hand side we have the expectation of a product with respect to a probability measure. - Find a measurable space
- Consider the following simple separability/entanglement criterion used by R.F. Werner in his seminal paper just described. If
 , let
, let 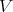 be the continuous linear extension of (the flip):
be the continuous linear extension of (the flip): 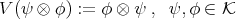
Consider the pure product state associated to
 ,
, 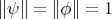 , that is
, that is 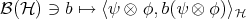 . Then,
. Then,  . Then, if
. Then, if 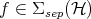 ,
, 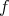 is a limit of convex sums of pure product states, and thus:
is a limit of convex sums of pure product states, and thus: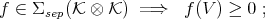
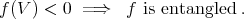
However, there are abundant entangled states
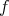 with
with 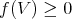 .
. 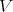 gives a simple example of a so-called entanglement witness. It is an instance of the Hahn-Banach separation theorem for convex sets: given a closed convex set (e.g., the separable states) a point not in the set can be separated by a hyperplane.
gives a simple example of a so-called entanglement witness. It is an instance of the Hahn-Banach separation theorem for convex sets: given a closed convex set (e.g., the separable states) a point not in the set can be separated by a hyperplane.
Other, different, criteria have been established (more along the non-geomet-ric lines of the positive partial transpose criterion; see 2.2.) which constitute necessary conditions for separability.
Among these, the range criterion [16] asserts that if the state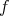 is separable, then there are product vectors
is separable, then there are product vectors  spanning the range of the density operator
spanning the range of the density operator 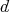 associated to
associated to 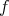 and such that
and such that  spans that of the partial transpose
spans that of the partial transpose 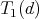 . This criterion is able to detect entanglement of states with positive partial transpose.
. This criterion is able to detect entanglement of states with positive partial transpose. Another class of necessary conditions for separability arises from certain maps which are contractive with respect to the trace-norm
 . Suppose the linear map
. Suppose the linear map 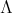 mapping
mapping 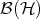 into itself, satisfies
into itself, satisfies 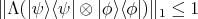 for all unit vectors
for all unit vectors 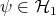 and
and 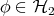 . Then if
. Then if 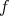 is separable and
is separable and 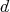 is the associated density operator, one has that
is the associated density operator, one has that 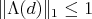 . An example of such a map is the realignment or reshuffling map
. An example of such a map is the realignment or reshuffling map 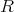 for the case
for the case  , [17], defined by matrix elements with respect to a product basis
, [17], defined by matrix elements with respect to a product basis  by:
by:
For twenty years now research on the problem has been going strong fueled mainly by the idea that entangled quantum states can be used as carriers of information, and that these
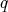 -bits combined to "quantum computers" can overcome some of the limitations of "classical computers". A very good review of the subject of "quantum vs. classical computation" is [18].
-bits combined to "quantum computers" can overcome some of the limitations of "classical computers". A very good review of the subject of "quantum vs. classical computation" is [18].
Although enormous progress has been made in understanding the subtleties of entanglement the basic problem of deciding whether or not a given state is or isn't entangled remains open. - When considering entanglement with respect to more than two subsystems, all the possible bipartite entanglement information for a given state is generically useless. A concrete example for
 with
with 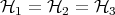
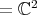 is given in [19]. For unitary vectors
is given in [19]. For unitary vectors 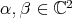 , with
, with 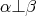 , let
, let 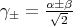 . Let
. Let 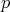 be the orthoprojector onto the subspace spanned by the four pairwise orthogonal vectors:
be the orthoprojector onto the subspace spanned by the four pairwise orthogonal vectors: 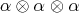 ,
,  ,
, 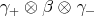 ,
, 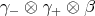 . Now
. Now  is a density operator acting on
is a density operator acting on  ; the associated state is not separable but it is, nevertheless, separable for each of the three possible bipartitions of the system:
; the associated state is not separable but it is, nevertheless, separable for each of the three possible bipartitions of the system: 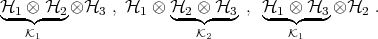
[1] G.G. Emch: Algebraic methods in statistical mechanics and quantum field theory. Wiley-Interscience, New York 1972 [ Links ]
[2] O. Bratteli, and D.W. Robinson: Operator algebras and quantum statistical mechanics I. Springer, New York 1979. [ Links ]
[3] O. Bratteli, and D.W. Robinson: Operator algebras and quantum statistical mechanics 2. Second edition. Springer, New York 1997. [ Links ]
[4] E. Schrödinger: Discussion of probability relations between separated systems. Proc. Cambridge Phil. Soc. 31, 555-563 (1935). [ Links ]
[5] E. Schrödinger: Probability relations between separated systems. Proc. Cambridge Phil. Soc. 32, 446-452 (1936). [ Links ]
[6] E. Schrödinger: Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschaften 23, 807-812, 823-828, 844-849 (1935). [ Links ]
[7] A. Einstein, B. Podolsky, and N. Rosen: Can quantum mechanical description of physical reality be considered complete? Phys. Rev. 47, 777-780 (1935). [ Links ]
[8] M. Takesaki: Theory of Operator Algebras I. Springer, New York 1979. [ Links ]
[9] J.M. Jauch: Foundations of quantum mechanics. Addison-Wesley, Reading (Mass.) 1968. [ Links ]
[10] W.K. Wootters: Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 80, 2245-2248 (1998). [ Links ]
[11] R. Horodecki, P. Horodecki, M. Horodecki, and K. Horodecki: Quantum entanglement. http://arxiv.org/abs/quant-ph/0702225. To appear in Reviews of Modern Physics. [ Links ]
[12] L. Gurvits: Classical deterministic complexity of Edmonds' problem and quantum entanglement. Proc. of the thirty-fifth ACM Symposium on Theory of Computing. ACM Press, New York 2003; p 10. [ Links ]
[13] M. Horodecki, P. Horodecki, and R. Horodecki: Separability of mixed states: necessary and sufficient conditions., Phys. Lett. A 223, 1-8 (1996). [ Links ]
[14] J.S. Bell: On the Einstein Podolsky Rosen Paradox. Physics 1, 195-200 (1964). [ Links ]
[15] R.F. Werner: Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 40, 4277-4281 (1989). [ Links ]
[16] P. Horodecki: Separability criterion and inseparable mixed states with positive partial transposition. Phys. Lett. A 232, 333-339 (1997). [ Links ]
[17] O. Rudolph: Some properties of the computable cross norm criterion for separability. Phys. Rev. A 67, 032312 (2003). [ Links ]
[18] A. Galindo, and M.A. Martin-Delgado: Information and computation: Classical and quantum aspects. Rev. Mod. Phys. 74, 347-423 (2002). [ Links ]
[19] D.P. Di Vincenzo, T. Mor, P.W. Shor, J.A. Smolin, and B.M. Terhal: Unextendible Product Bases, Uncompletable Product Bases and Bound Entanglement. Commun. Math. Phys. 238, 379-410 (2003). [ Links ]
G. A. Raggio
FaMAF,
Universidad Nacional de Córdoba,
Córdoba 5000, Argentina
Recibido: 10 de noviembre de 2008
Aceptado: 26 de noviembre de 2008













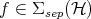 , then
, then
