Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932On-line version ISSN 1669-9637
Rev. Unión Mat. Argent. vol.49 no.2 Bahía Blanca July/Dec. 2008
A survey on hyper-Kähler with torsion geometry
M. L. Barberis
Abstract. Manifolds with special geometric structures play a prominent role in some branches of theoretical physics, such as string theory and supergravity. For instance, it is well known that supersymmetry requires target spaces to have certain special geometric properties. In many cases these requirements can be interpreted as restrictions on the holonomy group of the target space Riemannian metric. However, in some cases, they cannot be expressed in terms of the Riemannian holonomy group alone and give rise to new geometries previously unknown to mathematicians. An example of this situation is provided by hyper-Kähler with torsion (or HKT) metrics, a particular class of metrics which possess a compatible connection with torsion whose holonomy lies in Sp(n).
A survey on recent results on HKT geometry is presented.
A hyper-Hermitian structure on a 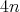 -dimensional manifold
-dimensional manifold 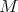 is given by a hypercomplex structure
is given by a hypercomplex structure  ,
,  (a triple of complex structures satisfying the imaginary quaternion relations) and a Riemannian metric
(a triple of complex structures satisfying the imaginary quaternion relations) and a Riemannian metric  with respect to which
with respect to which  is skew-symmetric, for any
is skew-symmetric, for any 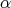 . The hyper-Hermitian manifold
. The hyper-Hermitian manifold 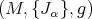 is said to be hyperkähler with torsion (HKT for short) [19] if there exists a hyper-Hermitian connection
is said to be hyperkähler with torsion (HKT for short) [19] if there exists a hyper-Hermitian connection  whose torsion tensor is a
whose torsion tensor is a 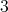 -form, that is,
-form, that is,
 (1) (1) |
where 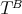 is the torsion of
is the torsion of  . It follows from the definition that the holonomy of
. It follows from the definition that the holonomy of 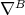 lies in
lies in 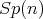 . HKT geometry is a generalization of hyper-Kähler geometry. In fact, when the
. HKT geometry is a generalization of hyper-Kähler geometry. In fact, when the 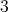 -form
-form  associated to an HKT structure vanishes, then the connection
associated to an HKT structure vanishes, then the connection 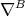 coincides with the Levi-Civita connection
coincides with the Levi-Civita connection 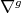 and the metric
and the metric  is hyper-Kähler.
is hyper-Kähler.
An HKT structure is called strong or weak depending on whether the  -form
-form  is closed or not.
is closed or not.
In [16] it was proved that the HKT condition is equivalent to
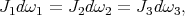 (2) (2) |
where 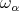 are the associated Kähler forms
are the associated Kähler forms
 (3) (3) |
Also, a holomorphic characterization has been given in [16], where the authors proved that (2) is equivalent to
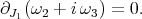 (4) (4) |
More recently, in [24], it has been shown that if  is almost hyper-Hermitian, then condition (2) implies the integrability of
is almost hyper-Hermitian, then condition (2) implies the integrability of 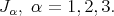
Given a Hermitian manifold  , there exists a unique Hermitian connection
, there exists a unique Hermitian connection  such that
such that
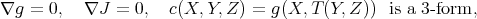
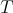 is the torsion of
is the torsion of  . Such a connection is called in Hermitian geometry the Bismut connection [7] (KT connection in the physics literature). In the case of an HKT manifold, the three Bismut connections associated to the Hermitian structures
. Such a connection is called in Hermitian geometry the Bismut connection [7] (KT connection in the physics literature). In the case of an HKT manifold, the three Bismut connections associated to the Hermitian structures 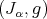 coincide and this connection is said to be an HKT connection. In contrast to the case of complex structures, not every hypercomplex structure on a manifold admits a compatible HKT metric. In fact, there exist hypercomplex manifolds of dimension
coincide and this connection is said to be an HKT connection. In contrast to the case of complex structures, not every hypercomplex structure on a manifold admits a compatible HKT metric. In fact, there exist hypercomplex manifolds of dimension  which do not admit any HKT metric compatible with the hypercomplex structure [10, 4]. These manifolds are nilmanifolds, that is, they are compact quotients of nilpotent Lie groups by co-compact discrete subgroups. We point out that in
which do not admit any HKT metric compatible with the hypercomplex structure [10, 4]. These manifolds are nilmanifolds, that is, they are compact quotients of nilpotent Lie groups by co-compact discrete subgroups. We point out that in  dimensions every hyper-Hermitian metric is HKT. This fact, which has been first proved in [12], also follows from (4).
dimensions every hyper-Hermitian metric is HKT. This fact, which has been first proved in [12], also follows from (4). The study of hyper-Hermitian connections satisfying (1) is motivated by the fact that these structures appear in some branches of theoretical physics, such as string theory, in the context of certain supersymmetric sigma models [11, 19, 20, 28]. These connections are also present in supergravity theories. For instance, it has been shown in [13] that the geometry of the moduli space of a class of black holes in five dimensions is hyper-Kähler with torsion (see also [27]).
Many examples of HKT manifolds have been obtained. A twistor construction of HKT manifolds was proposed in [19] and HKT reduction has been studied in [15] in order to construct new examples. A large family of strong HKT manifolds is given by compact Lie groups with the hypercomplex structure constructed in [31] and independently by Joyce in [22], which was generalized in [26] to the case of homogeneous spaces. On the other hand, there are partial results concerning HKT structures on solvable Lie groups, where weak examples abound [4, 9]. Strong HKT structures on Lie groups with compact Levi factor have been obtained in [5]. Using results of [29], it was shown in [16] that 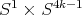 carries inhomogeneous weak HKT structures. Also, inhomogeneous examples of compact HKT manifolds which are not locally conformal hyper-Kähler can be obtained by considering the total space of a hyperholomorphic bundle over a compact HKT manifold [34].
carries inhomogeneous weak HKT structures. Also, inhomogeneous examples of compact HKT manifolds which are not locally conformal hyper-Kähler can be obtained by considering the total space of a hyperholomorphic bundle over a compact HKT manifold [34].
Some geometrical and topological properties have been investigated. Differential geometric properties of HKT manifolds and their twistor spaces have been studied in [21] and it was proved in [1] that, in analogy to the hyper-Kähler case, locally any HKT metric admits an HKT potential. A simple characterization of HKT geometry in terms of the intrinsic torsion of the 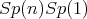 -structure was obtained in [24]. A version of Hodge theory for HKT manifolds has been given in [33] by exploiting a remarkable analogy between the de Rham complex of a Kähler manifold and the Dolbeault complex of an HKT manifold. More recently, in [35] balanced HKT metrics were studied, showing that the HKT metrics are precisely the quaternionic Calabi-Yau metrics defined in terms of the quaternionic Monge-Ampère equation. Moreover, by [35] a balanced HKT manifold has Obata connection with holonomy in
-structure was obtained in [24]. A version of Hodge theory for HKT manifolds has been given in [33] by exploiting a remarkable analogy between the de Rham complex of a Kähler manifold and the Dolbeault complex of an HKT manifold. More recently, in [35] balanced HKT metrics were studied, showing that the HKT metrics are precisely the quaternionic Calabi-Yau metrics defined in terms of the quaternionic Monge-Ampère equation. Moreover, by [35] a balanced HKT manifold has Obata connection with holonomy in 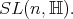
2. Hodge theory on HKT manifolds
We review in this section some fundamental facts from the theory developed by Verbitsky in [33] that will be relevant to explain the main result obtained in [4] (see §4).
We recall first the properties of the de Rham algebra of a Kähler manifold (see, for instance, [17]). Let 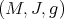 be a Hermitian manifold, that is,
be a Hermitian manifold, that is, 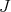 is a complex structure on
is a complex structure on 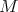 and
and 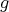 is a Riemannian metric such that
is a Riemannian metric such that 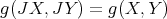 for all vector fields
for all vector fields  on
on 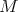 .
.
The Kähler form  is defined as in (3) and
is defined as in (3) and  is Kähler if and only if
is Kähler if and only if 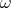 is closed.
is closed. 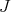 acts on differential forms as
acts on differential forms as
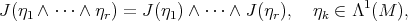
with  . Let
. Let 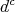 be the following differential operator acting on forms:
be the following differential operator acting on forms:
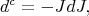
so that

Using the Kähler form  , it is possible to define the following linear operators:
, it is possible to define the following linear operators:
![Lω η = ω ∧ η, Λω = *L ω*, H ω = [Lω,Λ ω],](/img/revistas/ruma/v49n2/2a1257x.png) (5) (5) |
where  is the Hodge-star operator. When
is the Hodge-star operator. When 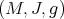 is Kähler, the operators
is Kähler, the operators
 (6) (6) |
satisfy the Kodaira relations (see [17]). For instance, one has
![[Λ ω,d] = *dc *, [Λω, dc] = - * d*,](/img/revistas/ruma/v49n2/2a1261x.png)
and, moreover,
![[H ,L ] = - 2L , [H ,Λ ] = 2 Λ , ω ω ω ω ω ω](/img/revistas/ruma/v49n2/2a1262x.png)
that is, when  is Kähler,
is Kähler, 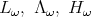 induce an action of
induce an action of  on the complex cohomology of
on the complex cohomology of 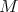 .
.
There are some cohomological restrictions imposed by the existence of a Kähler metric on a compact manifold. One necessary condition is that the odd Betti numbers must be even. The following classical result gives another cohomological condition satisfied by compact Kähler manifolds.
Hard Lefschetz Theorem. (See [17]) Let 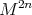 be a compact Kähler manifold with Kähler form
be a compact Kähler manifold with Kähler form 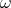 . Then, for any
. Then, for any 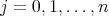 , the map
, the map

![Lω ([γ]) = [ω ∧ γ]](/img/revistas/ruma/v49n2/2a1271x.png) .
. Given an HKT manifold 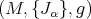 , it is shown in [33] that the Dolbeault differential graded algebra
, it is shown in [33] that the Dolbeault differential graded algebra  is an analogue of the de Rham algebra of a Kähler manifold. The roles of the de Rham differential
is an analogue of the de Rham algebra of a Kähler manifold. The roles of the de Rham differential  and of the Kähler form
and of the Kähler form 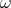 are played by
are played by  and by the
and by the  -form
-form  defined in (7) below, respectively. One can associate with
defined in (7) below, respectively. One can associate with 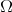 three operators
three operators  as in (5), thereby obtaining an action of
as in (5), thereby obtaining an action of  on
on  .
.
Let 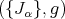 be a hyper-Hermitian structure on a
be a hyper-Hermitian structure on a 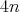 -dimensional manifold
-dimensional manifold  and consider the following
and consider the following 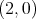 -form with respect to
-form with respect to 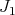 :
:
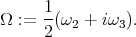 (7) (7) |
Using 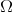 it is possible to construct three linear operators
it is possible to construct three linear operators 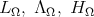 as in (5). We denote by
as in (5). We denote by 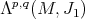 the forms of type
the forms of type 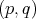 with respect to
with respect to 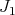 . Let
. Let
 (8) (8) |
be the Dolbeault operator with respect to the complex structure 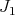 and
and
 (9) (9) |
It was shown in [33] that on an HKT manifold, 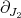 plays the role of
plays the role of 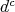 on a Kähler manifold. In fact, it follows from [33, Corollary 7.2] that on an HKT manifold, the operatots
on a Kähler manifold. In fact, it follows from [33, Corollary 7.2] that on an HKT manifold, the operatots
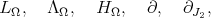 (10) (10) |
satisfy the same identities which hold for the operators (6).
The next result, which is a particular case of [33, Theorem 10.2] and is one of the main steps in the proof of Theorem 4.2, is an analogue of the Hard Lefschetz Theorem for the Dolbeault cohomology of HKT manifolds.
Theorem 2.1 ([33]). Let  be a compact
be a compact 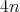 -dimensional HKT manifold with
-dimensional HKT manifold with 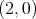 -form
-form  as in (7) and assume that the canonical bundle
as in (7) and assume that the canonical bundle  is holomorphically trivial. Then, for any
is holomorphically trivial. Then, for any 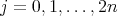 :
:
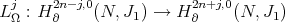
![LΩ ([γ ]) = [Ω ∧ γ]](/img/revistas/ruma/v49n2/2a12107x.png)
3. HKT structures on Lie groups
An HKT structure 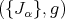 on a Lie group
on a Lie group  is called left-invariant when left translations
is called left-invariant when left translations  ,
, 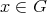 , are isometries and holomorphic maps with respect to
, are isometries and holomorphic maps with respect to 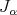 for any
for any 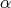 . In this case, it has been shown in [9] that the HKT condition is equivalent to:
. In this case, it has been shown in [9] that the HKT condition is equivalent to: ![g([J1X, J1Y ],Z ) + g([J1Y, J1Z ],X ) + g([J1Z,J1X ],Y ) = g([J2X, J2Y ],Z ) + g([J2Y,J2Z ],X ) + g ([J2Z, J2X ],Y) (11 ) = g([J3X, J3Y ],Z ) + g([J3Y,J3Z ],X ) + g ([J3Z, J3X ],Y).](/img/revistas/ruma/v49n2/2a12114x.png) for any
for any  , the Lie algebra of
, the Lie algebra of 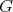 .
.
A large family of HKT manifolds is provided by 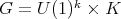 with the hypercomplex structure obtained in [31] (see also [22]), where
with the hypercomplex structure obtained in [31] (see also [22]), where  is a compact semisimple Lie group. In this case, the restriction of the HKT metric to
is a compact semisimple Lie group. In this case, the restriction of the HKT metric to 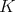 is the opposite of the Killing-Cartan form and the Bismut connection is the canonical affine connection
is the opposite of the Killing-Cartan form and the Bismut connection is the canonical affine connection  on
on  defined by
defined by
 (12) (12) |
Conversely, if (12) is the Bismut connection of some left invariant KT metric, then 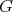 is isomorphic to a direct product of an abelian Lie group by a compact semisimple Lie group (Corollary 3.1). This fact is a consequence of a classical result due to Milnor [25].
is isomorphic to a direct product of an abelian Lie group by a compact semisimple Lie group (Corollary 3.1). This fact is a consequence of a classical result due to Milnor [25].
Lemma 3.1. Let 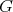 be a connected Lie group with a left invariant metric
be a connected Lie group with a left invariant metric  . Then
. Then
![τ (X, Y, Z) = g (X, [Y,Z ]), X, Y,Z ∈ 𝔤,](/img/revistas/ruma/v49n2/2a12126x.png) (13) (13) |
is a 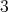 -form if and only if
-form if and only if 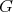 is isomorphic to
is isomorphic to  , where
, where 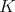 is a compact connected Lie group.
is a compact connected Lie group.
Proof. We observe that  is a
is a  -form if and only if
-form if and only if 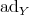 is skew-symmetric for any
is skew-symmetric for any 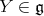 . It follows from [25, Lemmas 7.2 and 7.5] that this occurs if and only if
. It follows from [25, Lemmas 7.2 and 7.5] that this occurs if and only if 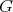 is as in the statement. □
is as in the statement. □
Corollary 3.1. Let  be a connected Lie group and
be a connected Lie group and  the canonical connection (12) on
the canonical connection (12) on 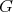 . If
. If  is the KT connection associated to some left invariant Hermitian metric
is the KT connection associated to some left invariant Hermitian metric  on
on 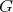 , then
, then 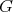 is isomorphic to
is isomorphic to 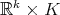 , where
, where 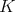 is a compact connected Lie group.
is a compact connected Lie group.
Proof. We observe that the torsion of  is
is ![T(U, V ) = - [U,V ], U, V ∈ 𝔤](/img/revistas/ruma/v49n2/2a12146x.png) . Therefore, if
. Therefore, if  is the Bismut connection of
is the Bismut connection of 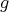 , we must have that
, we must have that  is a
is a  -form and the corollary follows from Lemma 3.1. □
-form and the corollary follows from Lemma 3.1. □
As a consequence of the above corollary, one has that if the canonical connection  defined in (12) is the Bismut connection of an HKT structure on
defined in (12) is the Bismut connection of an HKT structure on 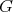 , then
, then 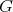 is as in Corollary 3.1.
is as in Corollary 3.1.
In [5] strong HKT structures have been constructed on non-semisimple Lie groups starting with a compact Lie group  acting on
acting on  by quaternionic linear maps which are isometries of the Euclidean metric.
by quaternionic linear maps which are isometries of the Euclidean metric.
A left invariant complex (resp. hypercomplex) structure on 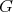 is called abelian (see [2]) when
is called abelian (see [2]) when ![[JX, J Y] = [X, Y]](/img/revistas/ruma/v49n2/2a12157x.png) for all
for all 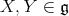 (resp.
(resp. ![[JαX, JαY ] = [X,Y ], α = 1,2,3](/img/revistas/ruma/v49n2/2a12159x.png) ). Observe that in this case (11) is automatically satisfied for any hyper-Hermitian metric
). Observe that in this case (11) is automatically satisfied for any hyper-Hermitian metric  , that is, given an abelian hypercomplex structure, any hyper-Hermitian metric is HKT. Moreover, it was shown in [9, Proposition 2.1] that left-invariant HKT structures arising from abelian hypercomplex structures are always weak.
, that is, given an abelian hypercomplex structure, any hyper-Hermitian metric is HKT. Moreover, it was shown in [9, Proposition 2.1] that left-invariant HKT structures arising from abelian hypercomplex structures are always weak.
It was shown in [9, Theorem 3.1] that for  -step nilpotent Lie groups every left-invariant HKT structure arises from an abelian hypercomplex structure. We proved in [4] that this theorem still holds for
-step nilpotent Lie groups every left-invariant HKT structure arises from an abelian hypercomplex structure. We proved in [4] that this theorem still holds for 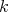 -step nilpotent Lie groups admitting lattices, for arbitrary
-step nilpotent Lie groups admitting lattices, for arbitrary  (see Theorem 4.2).
(see Theorem 4.2).
We point out that the left-invariant complex structure 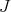 on
on  gives rise to a decomposition
gives rise to a decomposition

where  are the eigenspaces of the induced complex structure on
are the eigenspaces of the induced complex structure on  . It turns out that
. It turns out that 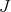 is abelian if and only if
is abelian if and only if 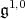 is an abelian subalgebra of
is an abelian subalgebra of 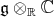 .
.
4. HKT structures on nilmanifolds
4.1. Generalities on nilmanifolds.
A nilmanifold (see[23]) is a quotient 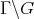 of a simply connected nilpotent Lie group by a lattice
of a simply connected nilpotent Lie group by a lattice 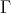 (a discrete co-compact subgroup). It is well known that
(a discrete co-compact subgroup). It is well known that
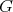 admits lattices if and only if
admits lattices if and only if  has a rational form.
has a rational form.
Moreover, there is a one-to-one correspondence:

Let 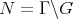 be a nilmanifold and assume that
be a nilmanifold and assume that 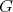 is equipped with a left-invariant complex structure
is equipped with a left-invariant complex structure 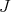 . Then
. Then 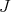 induces a complex structure on
induces a complex structure on 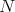 . A complex structure
. A complex structure 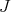 on
on 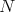 is called abelian if it is induced from a left-invariant abelian complex structure on
is called abelian if it is induced from a left-invariant abelian complex structure on 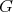 .
.
The first example of symplectic non-Kähler manifold was described by Thurston [32]: it is the nilmanifold  , where
, where

is the 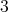 -dimensional Heisenberg group and
-dimensional Heisenberg group and 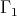 is the subgroup of matrices in
is the subgroup of matrices in 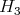 with integer entries.
with integer entries.
For each  one can define a lattice
one can define a lattice 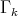 in
in 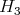 as follows (compare with [14]):
as follows (compare with [14]):

It follows that:

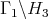 covers
covers 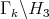 for any
for any  .
.![~ 2 Γ k∕[Γ k,Γ k] = ℤ ⊕ ℤk](/img/revistas/ruma/v49n2/2a12202x.png) .
.
The nilmanifolds 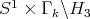 have fundamental group isomorphic to
have fundamental group isomorphic to 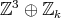 , in particular, they are not homeomorphic. These are examples of symplectic non-Kähler manifolds. In the 80's, many authors (Abbena, Cordero, Fernández, Gray, de León, among others) obtained families of symplectic non-Kähler manifolds as generalizations of the previous example. Later, in 1988, the following remarkable theorem was proved by Benson-Gordon (see also [18], where the author showed that a minimal model of a nilmanifold is formal if and only if it is a torus):
, in particular, they are not homeomorphic. These are examples of symplectic non-Kähler manifolds. In the 80's, many authors (Abbena, Cordero, Fernández, Gray, de León, among others) obtained families of symplectic non-Kähler manifolds as generalizations of the previous example. Later, in 1988, the following remarkable theorem was proved by Benson-Gordon (see also [18], where the author showed that a minimal model of a nilmanifold is formal if and only if it is a torus):
Theorem 4.1 ([6, Theorem A]). If 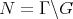 is a Kähler nilmanifold, then
is a Kähler nilmanifold, then 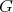 is abelian and
is abelian and 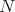 is diffeomorphic to a torus.
is diffeomorphic to a torus.
The main ingredients in the proof of the above theorem are:
- The de Rham cohomology of
 can be identified with the Lie algebra cohomology of
can be identified with the Lie algebra cohomology of 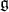 due to a result of Nomizu.
due to a result of Nomizu. - It is proved that if
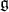 is nilpotent, the Hard Lefschetz Theorem implies that
is nilpotent, the Hard Lefschetz Theorem implies that 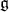 is abelian.
is abelian.
More precisely, Benson-Gordon show that if 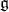 is non-abelian nilpotent, then the map
is non-abelian nilpotent, then the map
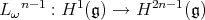
For the case of HKT nilmanifolds, we proved in [4] the following analogue of Theorem 4.1:
Theorem 4.2 ([4]). Let  be a
be a  -dimensional nilmanifold endowed with an HKT structure
-dimensional nilmanifold endowed with an HKT structure 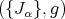 induced by a left-invariant HKT structure on
induced by a left-invariant HKT structure on  . Then
. Then  is abelian.
is abelian.
Sketch of proof. The aim is to show that  is abelian (equivalently,
is abelian (equivalently, 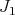 is abelian). We observe that the canonical bundle of
is abelian). We observe that the canonical bundle of 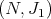 is trivial [8], therefore Theorem 2.1 applies.
is trivial [8], therefore Theorem 2.1 applies.
Consider the following commutative diagram:

where the vertical arrows are the natural identifications. The Lie algebra 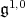 is nilpotent. If we assume that
is nilpotent. If we assume that 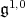 is not abelian, one can apply the same argument in [6, Lemma 2.11] to the bottom row of the previous diagram to obtain that
is not abelian, one can apply the same argument in [6, Lemma 2.11] to the bottom row of the previous diagram to obtain that



The following question was posed in [16]:
- Given a compact manifold
 with a hypercomplex structure, is it always possible to find a compatible HKT metric?
with a hypercomplex structure, is it always possible to find a compatible HKT metric?
A negative answer was given in [10] by exhibiting  -step nilmanifolds with non-abelian hypercomplex structures. In view of Theorem 4.2, any non-abelian hypercomplex structure on a
-step nilmanifolds with non-abelian hypercomplex structures. In view of Theorem 4.2, any non-abelian hypercomplex structure on a  -step nilmanifold admits no compatible HKT metric. Therefore, Theorem 4.2 provides a useful tool for obtaining many examples where the answer to the above question is negative. To illustrate this situation, we exhibit next a family of hypercomplex
-step nilmanifold admits no compatible HKT metric. Therefore, Theorem 4.2 provides a useful tool for obtaining many examples where the answer to the above question is negative. To illustrate this situation, we exhibit next a family of hypercomplex  -step nilmanifolds, for arbitrary
-step nilmanifolds, for arbitrary 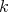 , admitting no compatible HKT metric (see [4]).
, admitting no compatible HKT metric (see [4]).
4.2. A family of examples. Let  be a finite dimensional associative algebra and let
be a finite dimensional associative algebra and let 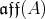 be the Lie algebra
be the Lie algebra  with Lie bracket:
with Lie bracket:
![′ ′ ′ ′ ′ ′ ′ ′ [(a,b),(a ,b)] = (aa - a a,ab - a b), a, b,a,b ∈ A.](/img/revistas/ruma/v49n2/2a12239x.png)
This class of Lie algebras has first been considered in [3].
We observe that:
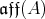 is a nilpotent Lie algebra if and only if
is a nilpotent Lie algebra if and only if 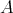 is nilpotent as an associative algebra.
is nilpotent as an associative algebra.
Let  be the endomorphism of
be the endomorphism of  defined by:
defined by:
 |
It has been shown in [3] that  is a complex structure on
is a complex structure on 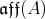 . If, moreover,
. If, moreover, 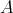 is a complex associative algebra, we can define another complex structure
is a complex associative algebra, we can define another complex structure  on
on  by:
by:

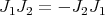 , setting
, setting  we obtain a hypercomplex structure on
we obtain a hypercomplex structure on 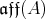 .
. Remark 4.1.  is abelian if and only if
is abelian if and only if  is conmutative.
is conmutative.
Let  be the algebra of
be the algebra of  strictly upper triangular matrices with complex entries and consider the simply connected Lie group Aff
strictly upper triangular matrices with complex entries and consider the simply connected Lie group Aff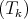 with Lie algebra
with Lie algebra 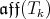 , which is
, which is 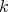 -step nilpotent. The structure constants of
-step nilpotent. The structure constants of 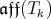 with respect to the standard basis are integers, hence Aff
with respect to the standard basis are integers, hence Aff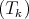 admits a lattice
admits a lattice 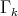 and we obtain:
and we obtain:
- The hypercomplex
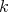 -step nilmanifold
-step nilmanifold 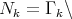 Aff
Aff does not admit a compatible HKT metric.
does not admit a compatible HKT metric.
Remark 4.2. We point out that for  the Lie algebra
the Lie algebra 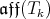 is not two-step solvable, hence it does not admit abelian hypercomplex structures (see [30]). Therefore, Theorem implies that any left-invariant hypercomplex structure on Aff
is not two-step solvable, hence it does not admit abelian hypercomplex structures (see [30]). Therefore, Theorem implies that any left-invariant hypercomplex structure on Aff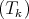 ,
,  , induces on the nilmanifold
, induces on the nilmanifold 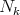 a hypercomplex structure admitting no compatible HKT metric.
a hypercomplex structure admitting no compatible HKT metric.
[1] B. Banos, A. Swann, Potentials for hyper-Kähler metrics with torsion, Class. Quant.Grav. 21 (2004) 3127-3136. [ Links ]
[2] M.L. Barberis, I. Dotti, R. Miatello, On certain locally homogeneous Clifford manifolds, Ann. Glob. Anal. Geom. 13 (1995), 289-301. [ Links ]
[3] M.L. Barberis, I. Dotti, Abelian complex structures on solvable Lie algebras, J. Lie Theory 14 (1) (2004), 25-34. [ Links ]
[4] M.L. Barberis, I. Dotti, M. Verbitsky, Canonical bundles of complex nilmanifolds, with applications to hypercomplex geometry, arXiv:math.DG/0712.3863, to appear in Math. Res. Lett. [ Links ]
[5] M.L. Barberis, A. Fino, New strong HKT manifolds arising from quaternionic representations, arXiv:0805.2335. [ Links ]
[6] C. Benson, C.S. Gordon, Kähler and symplectic structures on nilmanifolds, Topology 27(4) (1988) 513-518. [ Links ]
[7] J. M. Bismut, Local index theorem for non-Kähler manifolds, Math. Ann. 284 (1989), 681-699. [ Links ]
[8] G.R. Cavalcanti, M. Gualtieri, Generalized complex structures on nilmanifolds, arXiv:math/0404451, J. Symplectic Geom. 2 (3) (2004), 393-410. [ Links ]
[9] I. Dotti, A. Fino, Hyper-Kähler with torsion structures invariant by nilpotent Lie groups, Class. Quantum Grav. 19 (2002), 1-12. [ Links ]
[10] A. Fino, G. Grantcharov, Properties of manifolds with skew-symmetric torsion and special holonomy, Adv. Math. 189 (2004), 439-450. [ Links ]
[11] S. J. Gates, C.M. Hull, M. Roček, Twisted multiplets and new supersymmetric non-linear  -models, Nucl. Phys. B 248 (1984), 157-186. [ Links ]
-models, Nucl. Phys. B 248 (1984), 157-186. [ Links ]
[12] P. Gauduchon, K.P. Tod, Hyper-Hermitian metrics with symmetry, J. Geom. Phys. 25 (1998), 291-304. [ Links ]
[13] G. W. Gibbons, G. Papadopoulos, K. Stelle, HKT and OKT geometries on soliton blach hole moduli space, Nucl. Phys. B 508 (1997), 623. [ Links ]
[14] C. S. Gordon and E. N. Wilson, The spectrum of the Laplacian on Riemannian Heisenberg manifolds, Michigan Math. J. 33 (2) (1986), 253-271. [ Links ]
[15] G. Grantcharov, G. Papadopoulos,, Y. S. Poon, Reduction of HKT-Structures, J. Math. Phys. 43 (2002), 3766-3782. [ Links ]
[16] G. Grantcharov, Y. S. Poon, Geometry of hyper-Kähler connection with torsion, Comm. Math. Phys. 213 (2000), 19-37. [ Links ]
[17] P. Griffiths, J. Harris, Principles of algebraic geometry, Wiley-Interscience, New York, 1978. [ Links ]
[18] K. Hasegawa, Minimal models of nilmanifolds, Proc. Am. Math. Soc. 106 (1989), 65-71. [ Links ]
[19] P.S. Howe, G. Papadopoulos, Twistor spaces for HKT manifolds, Phys. Lett. B 379 (1996), 81-86. [ Links ]
[20] P.S. Howe, G. Papadopoulos, Finiteness and anomalies in 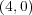 suspersymmetric sigma models for HKT manifolds, Nucl. Phys. B 381 (1992), 360-372.
suspersymmetric sigma models for HKT manifolds, Nucl. Phys. B 381 (1992), 360-372.
[21] S. Ivanov, I. Minchev, Quaternionic Kähler and hyper-Kähler manifolds with torsion and twistor spaces, J. Reine Angew. Math. 567 (2004), 215-233. [ Links ]
[22] D. Joyce, Compact hypercomplex and quaternionic manifolds, J. Diff. Geom. 35 (1992), 743-761. [ Links ]
[23] A. I. Mal'čev, On a class of homogeneous spaces, AMS Translation No. 39 (1951). [ Links ]
[24] F. Martín Cabrera, A. Swann, The intrinsic torsion of almost quaternion-Hermitian manifolds, arXiv:math.DG/0707.0939, to appear in Annales de l'Institute Fourier. [ Links ]
[25] J. Milnor, Curvatures of left invariant metrics on Lie groups, Adv. Math. 21 (3) (1976), 293-329. [ Links ]
[26] A. Opfermann, G. Papadopoulos, Homogeneous HKT and QKT manifolds, arXiv:math-ph9807026. [ Links ]
[27] G. Papadopoulos, A. Teschendorff, Multi angle five brane intersections, Phys. Lett. B 443 (1998), 159. [ Links ]
[28] G. Papadopoulos, KT and HKT geometries in strings and in black hole moduli spaces, Proceedings of the Bonn workshop on "Special Geometric Structures in String Theory", 8-11 September 2001, Eds.: D.V. Alekseevsky, V. Cortés, C. Devchand, A. Van Proeyen, arXiv:hep-th/0201111. [ Links ]
[29] H. Pedersen, Y.S. Poon, Inhomogeneous hypercomplex structures on homogeneous manifolds, J. Reine Angew. Math. 516 (1999), 159-181. [ Links ]
[30] P. Petravchuk, Lie algebras decomposable as a sum of an abelian and a nilpotent subalgebra, Ukr. Math. J. 40(3) (1988), 385-388. [ Links ]
[31] Ph. Spindel, A. Sevrin, W. Troost, A. Van Proeyen, Extended supersymmetric  -models on group manifolds, Nucl. Phys. B 308 (1988), 662-698. [ Links ]
-models on group manifolds, Nucl. Phys. B 308 (1988), 662-698. [ Links ]
[32] W.P. Thurston, Some simple examples of symplectic manifolds, Proc. Am. Math. Soc. 55 (1976), 476-478. [ Links ]
[33] M. Verbitsky, Hyperkähler manifolds with torsion, supersymmetry and Hodge theory, Asian J. Math. 6 (2002), 679-712 . [ Links ]
[34] M. Verbitsky, Hyperkähler manifolds with torsion obtained from hyperholomorphic bundles, Math. Res. Lett. 10 (2003), 501-513. [ Links ]
[35] M. Verbitsky, Balanced HKT metrics and strong HKT metrics on hypercomplex manifolds preprint math.DG/0808.3218. [ Links ]
Laura Barberis
FaMAF-CIEM,
Universidad Nacional de Córdoba,
Córdoba 5000, Argentina
barberis@mate.uncor.edu
Recibido: 26 de noviembre de 2008
Aceptado: 26 de noviembre de 2008














