Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932
Rev. Unión Mat. Argent. vol.50 no.1 Bahía Blanca June 2009
A description of hereditary skew group algebras of Dynkin and Euclidean type
Olga Funes
Abstract. In this work we study the skew group algebra Λ[G] when G is a finite group acting on Λ whose order is invertible in Λ. Here, we assume that Λ is a finite-dimensional algebra over an algebraically closed field k. The aim is to describe all possible actions of a finite abelian group on an hereditary algebra of finite or tame representation type, to give a description of the resulting skew group algebra for each action and finally to determinate their representation type.
In this work we assume that  is a finite-dimensional algebra over an algebraically closed field
is a finite-dimensional algebra over an algebraically closed field 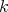 . Let
. Let  a finite group acting on
a finite group acting on 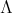 . The skew group algebra
. The skew group algebra ![Λ [G ]](/img/revistas/ruma/v50n1/1a0210x.png) is the free left
is the free left 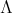 -module with basis all the elements in
-module with basis all the elements in 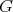 and multiplication given by
and multiplication given by 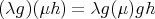 for all
for all 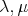 in
in  ,
,  in
in  . We study the skew group algebra
. We study the skew group algebra ![Λ[G ]](/img/revistas/ruma/v50n1/1a0218x.png) when
when  is a finite group acting on
is a finite group acting on 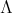 whose order is invertible in
whose order is invertible in  .
.
There is an extensive literature about skew group algebras ![Λ[G]](/img/revistas/ruma/v50n1/1a0222x.png) and crossed product algebras
and crossed product algebras 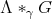 , and their relationship with the ring
, and their relationship with the ring 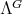 , given by elements in
, given by elements in  that are fixed by
that are fixed by  . It is of interest to study which properties of
. It is of interest to study which properties of  are inherited by
are inherited by ![Λ[G ]](/img/revistas/ruma/v50n1/1a0228x.png) ,
, 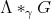 or
or  . Some of these ideas are rooted in trying to develop a Galois Theory for non-commutative rings. See [1, 3, 7, 9, 10, 11, 14, 13] for more details.
. Some of these ideas are rooted in trying to develop a Galois Theory for non-commutative rings. See [1, 3, 7, 9, 10, 11, 14, 13] for more details.
It is of interest to find ways to describe ![Λ [G]](/img/revistas/ruma/v50n1/1a0231x.png) in terms of
in terms of  because the algebras
because the algebras  and
and ![Λ [G ]](/img/revistas/ruma/v50n1/1a0234x.png) have many properties in common which are of interest in the representation theory of finite-dimensional algebras, like finite representation type, being hereditary, being an Auslander algebra, being Nakayama, see [2, 16] for more details. However, we must observe that there are properties which are not preserved by this construction, like being a connected algebra, so we are dealing with essentially different algebras.
have many properties in common which are of interest in the representation theory of finite-dimensional algebras, like finite representation type, being hereditary, being an Auslander algebra, being Nakayama, see [2, 16] for more details. However, we must observe that there are properties which are not preserved by this construction, like being a connected algebra, so we are dealing with essentially different algebras.
It is well known [6] that a connected hereditary algebra is of finite representation type if and only if the underlying graph of its quiver is one of the Dynkin diagrams  (
( ),
), 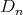 (
( ),
), 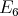 ,
, 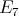 or
or 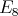 ; some years later it was shown that a a connected hereditary algebra is of tame representation type if and only if the underlying graph of its quiver is one of the euclidean diagrams
; some years later it was shown that a a connected hereditary algebra is of tame representation type if and only if the underlying graph of its quiver is one of the euclidean diagrams 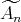 (
(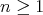 ),
), 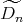 (
( ),
), 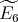 ,
,  or
or  , see [4, 12, 17].
, see [4, 12, 17].
The aim of this paper is to describe all possible actions of a finite abelian group on an hereditary algebra of finite or tame representation type, to give a description of the resulting skew group algebra for each action and finally to determinate their representation type.
Then, in order to classify the finite and tame representation type hereditary skew group algebras, it suffices to study the group actions on the Dynkin and the euclidean quivers. In order to do this description, we start by considering a short exact sequence of groups 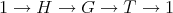 . We can express
. We can express ![Λ[G ]](/img/revistas/ruma/v50n1/1a0250x.png) in terms of the skew group algebra
in terms of the skew group algebra ![Λ [H ][T]](/img/revistas/ruma/v50n1/1a0251x.png) or the crossed product algebra
or the crossed product algebra ![Λ [H ] *γ T](/img/revistas/ruma/v50n1/1a0252x.png) . In this context, we describe when
. In this context, we describe when ![Λ [G ]](/img/revistas/ruma/v50n1/1a0253x.png) is isomorphic to
is isomorphic to ![Λ [H ][T]](/img/revistas/ruma/v50n1/1a0254x.png) , for
, for 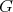 a finite group whose order is invertible in
a finite group whose order is invertible in  . In section
. In section  we provide an introduction to the subject, that is, the definition of skew group algebra and crossed product algebra. Finally, in section
we provide an introduction to the subject, that is, the definition of skew group algebra and crossed product algebra. Finally, in section 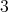 we consider hereditary algebras of finite representation type and in section
we consider hereditary algebras of finite representation type and in section  we consider hereditary algebras of tame type. In each one of these cases, that is, when the associated quiver is
we consider hereditary algebras of tame type. In each one of these cases, that is, when the associated quiver is 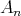 (
( ),
),  (
(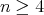 ),
),  ,
,  ,
,  ,
, 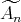 (
( ),
), 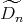 (
( ),
), 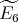 ,
,  or
or 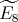 , we get a connection between
, we get a connection between ![Λ[G ]](/img/revistas/ruma/v50n1/1a0274x.png) and the crossed product algebra
and the crossed product algebra ![Λ [H ] * G ∕H](/img/revistas/ruma/v50n1/1a0275x.png) with a complete description of all the possible groups
with a complete description of all the possible groups 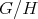 appearing in each case, where
appearing in each case, where 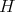 is the subgroup of
is the subgroup of  consisting on all the elements acting trivially on a complete set of primitive orthogonal idempotents of the algebra
consisting on all the elements acting trivially on a complete set of primitive orthogonal idempotents of the algebra  . As a consequence of all these results, we get that if
. As a consequence of all these results, we get that if 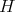 acts trivially on
acts trivially on 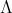 then the crossed product algebras obtained in each description are skew group algebras. Finally, the case
then the crossed product algebras obtained in each description are skew group algebras. Finally, the case 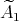 is considered at the end of section 4.
is considered at the end of section 4.
This section consists of the preliminaries necessary for the proof of the main results.
Let 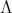 be a finite-dimensional
be a finite-dimensional  -algebra and
-algebra and 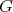 a finite group acting on
a finite group acting on 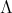 . The skew group algebra
. The skew group algebra ![Λ[G ]](/img/revistas/ruma/v50n1/1a0287x.png) is the free left
is the free left 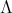 -module with basis all the elements in
-module with basis all the elements in 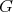 and multiplication given by
and multiplication given by  for all
for all 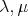 in
in 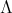 ,
,  in
in 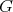 . Clearly
. Clearly ![Λ [G ]](/img/revistas/ruma/v50n1/1a0295x.png) is a finite-dimensional
is a finite-dimensional 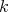 -algebra. If we identify each
-algebra. If we identify each  in
in  with
with 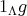 in
in ![Λ [G ]](/img/revistas/ruma/v50n1/1a02100x.png) and each
and each 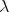 in
in 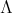 with
with 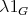 in
in ![Λ [G ]](/img/revistas/ruma/v50n1/1a02104x.png) , we have that
, we have that  is the group of units of
is the group of units of ![Λ[G ]](/img/revistas/ruma/v50n1/1a02106x.png) and
and 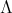 is a
is a 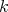 -subalgebra of
-subalgebra of ![Λ[G ]](/img/revistas/ruma/v50n1/1a02109x.png) .
.
Let  be a basic finite-dimensional algebra (associative with unity) over an algebraically closed field. A quiver
be a basic finite-dimensional algebra (associative with unity) over an algebraically closed field. A quiver 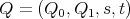 is a quadruple consisting of two sets
is a quadruple consisting of two sets 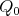 (whose elements are called points, or vertices ) and
(whose elements are called points, or vertices ) and 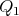 (whose elements are called arrows), and two maps
(whose elements are called arrows), and two maps 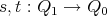 which associate to each arrow
which associate to each arrow  its source
its source 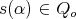 and its target
and its target 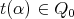 . An arrow
. An arrow 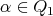 of source
of source 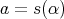 and target
and target 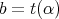 is usually denoted by
is usually denoted by  . A quiver
. A quiver 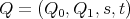 is usually denoted briefly by
is usually denoted briefly by 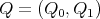 or even simply by
or even simply by  . Thus, a quiver is nothing but an oriented graph without any restriction as to the number of arrows between two points, to the existence of loops or oriented cycles.
. Thus, a quiver is nothing but an oriented graph without any restriction as to the number of arrows between two points, to the existence of loops or oriented cycles.
We write a path  in
in 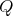 as a composition of consecutive arrows
as a composition of consecutive arrows 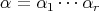 where
where 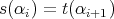 for all
for all  , and we set
, and we set 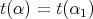 ,
, 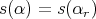 . The path algebra
. The path algebra 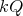 is the
is the 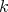 -vector space with basis all the paths in
-vector space with basis all the paths in 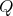 , including trivial paths
, including trivial paths 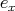 of length zero, one for each vertex
of length zero, one for each vertex 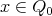 . The multiplication of two basis elements is the composition of paths if they are composable, and zero otherwise. A relation from
. The multiplication of two basis elements is the composition of paths if they are composable, and zero otherwise. A relation from 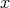 to
to  is a linear combination
is a linear combination 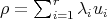 such that, for each
such that, for each 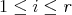 ,
, 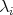 is a non-zero scalar and
is a non-zero scalar and 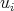 a path of length at least two from
a path of length at least two from 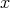 to
to  . A set of relations on
. A set of relations on 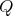 generates an ideal
generates an ideal 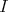 , said to be admissible, in the path algebra
, said to be admissible, in the path algebra 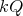 of
of 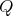 .
.
It is well-known that if 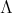 is basic there exists a quiver
is basic there exists a quiver  and a surjective algebra morphism
and a surjective algebra morphism  whose kernel
whose kernel 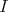 is admissible, where
is admissible, where  , the ordinary quiver of
, the ordinary quiver of 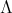 , is defined as follows:
, is defined as follows:
-
If
 is a complete set of primitive orthogonal idempotents of
is a complete set of primitive orthogonal idempotents of 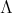 , the vertices of
, the vertices of 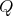 are the numbers
are the numbers  which are taken to be in bijective correspondence with the idempotents
which are taken to be in bijective correspondence with the idempotents  ;
; -
Given two points
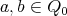 the arrows
the arrows 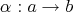 are in bijective correspondence with the vectors in a basis of the
are in bijective correspondence with the vectors in a basis of the 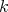 -vector space
-vector space 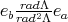 .
.
Thus we have  . We refer to [2] for more details.
. We refer to [2] for more details.
If 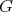 is acting on a basic algebra
is acting on a basic algebra  , we can view
, we can view  as
as 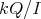 in such a way that the action of
in such a way that the action of 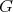 on
on  is induced by an action of
is induced by an action of  on
on  which leaves
which leaves 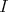 stable and preserves the natural grading on
stable and preserves the natural grading on 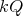 by the length of paths. Then
by the length of paths. Then ![Λ [G ]](/img/revistas/ruma/v50n1/1a02175x.png) is isomorphic to
is isomorphic to ![(kQ )[G ]∕I((kQ )[G ])](/img/revistas/ruma/v50n1/1a02176x.png) , see [16, Proposition 2.1]. Moreover, if
, see [16, Proposition 2.1]. Moreover, if 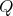 contains no multiple arrows, the action of
contains no multiple arrows, the action of  on
on  is simple: each
is simple: each 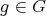 permutes the vertices in
permutes the vertices in 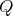 and maps each arrow
and maps each arrow 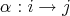 onto a multiple scalar of the unique arrow from
onto a multiple scalar of the unique arrow from  to
to 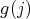 . From now on we assume
. From now on we assume 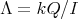 with the action of
with the action of 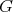 as described above,
as described above,  without double arrows.
without double arrows.
Proposition 2.1. Let 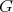 be a finite group acting on
be a finite group acting on  , let
, let 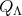 be the associated quiver of
be the associated quiver of  ,
,  without double arrows, and
without double arrows, and 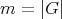 . We consider the action of
. We consider the action of 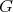 on
on 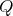 induced by an automorphism of algebras which preserves the length of paths of
induced by an automorphism of algebras which preserves the length of paths of  . Then
. Then
-
If
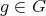 ,
,  , then
, then  for some
for some  ;
; -
If
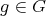 and
and 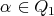 , then
, then 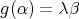 for some arrow
for some arrow 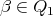 ,
, 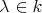 . In particular, if
. In particular, if 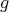 fixes the starting and ending point of
fixes the starting and ending point of  then
then 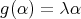 , with
, with 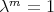 ;
; -
If
 is a source (sink) then
is a source (sink) then 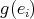 is a source (sink);
is a source (sink); -
The cardinal of the set of arrows that start (end) in
 is equal to the cardinal of the set of arrows that start (end) in
is equal to the cardinal of the set of arrows that start (end) in 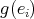 .
.
Proof.
-
Let
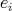 be a primitive idempotent in
be a primitive idempotent in  . Since the action of
. Since the action of 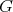 preserves the vector space generated by arrows,
preserves the vector space generated by arrows,  . Moreover,
. Moreover, 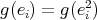 , then we have that
, then we have that  , and hence
, and hence 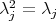 , that is,
, that is, 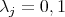 . On the other hand, suppose
. On the other hand, suppose 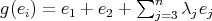 . Then
. Then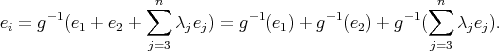
But this is a contradiction because
 es primitive. Then
es primitive. Then 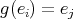 for some
for some  .
. -
If
 ,
,  with
with 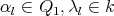 . Moreover if
. Moreover if 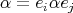 then
then 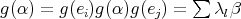 , for some arrow
, for some arrow 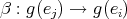 , because
, because 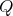 has no double arrows. Then
has no double arrows. Then  .
. -
Let
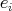 be an idempotent of
be an idempotent of 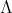 . Suppose that
. Suppose that 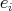 is a source and
is a source and 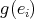 is not. Then, there exists an arrow
is not. Then, there exists an arrow 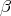 such that
such that 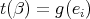 , that is, there exists an index
, that is, there exists an index  such that
such that 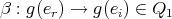 . Since the action of
. Since the action of  on
on 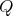 is induced by an automorphism of algebras which preserves the length of paths, there exists an arrow
is induced by an automorphism of algebras which preserves the length of paths, there exists an arrow  such that
such that 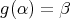 . Then we have
. Then we have 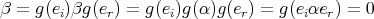 because
because  is a source. This contradiction arises from the assumption that
is a source. This contradiction arises from the assumption that 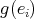 is not a source. Similarly we prove that if
is not a source. Similarly we prove that if  is a sink then
is a sink then 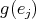 is a sink.
is a sink. -
Let
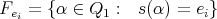 and
and 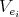 be the
be the 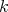 -vector space with basis
-vector space with basis  . If
. If  , by ii) we know that the automorphism
, by ii) we know that the automorphism 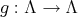 induces an isomorphism
induces an isomorphism 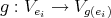 . Then the cardinal of
. Then the cardinal of  and
and 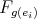 are equal.
are equal. 
2.1. Crossed product algebra ![Λ[H ] * T γ](/img/revistas/ruma/v50n1/1a02262x.png) . The purpose of this section is to present the crossed product algebras in order to study when
. The purpose of this section is to present the crossed product algebras in order to study when ![Λ [G ]](/img/revistas/ruma/v50n1/1a02263x.png) is isomorphic to
is isomorphic to ![Λ[H ][T ]](/img/revistas/ruma/v50n1/1a02264x.png) where
where 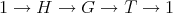 is a short exact sequence of groups. We start with the definition of crossed product algebras and prove, for completeness, Theorem 2.2 that connects the skew group algebras with the crossed product algebras. See [16] for more details.
is a short exact sequence of groups. We start with the definition of crossed product algebras and prove, for completeness, Theorem 2.2 that connects the skew group algebras with the crossed product algebras. See [16] for more details.
Let 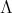 be a ring,
be a ring, 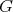 a finite group acting on
a finite group acting on  ,
,  the units of
the units of  and
and  , a map satisfying
, a map satisfying
-
 for
for  ,
,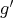 ,
, ;
; -
 for
for  ,
,  the identity element of
the identity element of 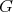 ;
; -
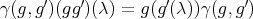 for
for  ,
,  .
.
Then the corresponding crossed product algebra  has elements
has elements  ;
; 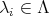 . Addition is componentwise, and multiplication is given by
. Addition is componentwise, and multiplication is given by 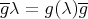 and
and 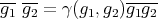 .
.
Let  be a group and
be a group and 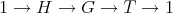 be a short exact sequence of groups. Let
be a short exact sequence of groups. Let  be a disjoint union of lateral classes. Then
be a disjoint union of lateral classes. Then  where
where  ,
, 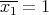 .
.
Theorem 2.2. If  is a short exact sequence of groups, then
is a short exact sequence of groups, then
![Λ[G ] ≃ Λ [H ] *γ T](/img/revistas/ruma/v50n1/1a02295x.png)
where the action of 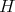 on
on 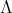 is induced by the action of
is induced by the action of  , the action of
, the action of  on
on ![Λ[H ]](/img/revistas/ruma/v50n1/1a02300x.png) is defined by
is defined by

and ![γ : T × T → U(Λ [H ])](/img/revistas/ruma/v50n1/1a02302x.png) is defined by
is defined by 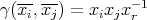 , with
, with 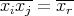 .
.
Proof. We consider the action of 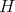 on
on 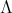 induced by the action of
induced by the action of  and the action of
and the action of 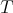 on
on ![Λ[H ]](/img/revistas/ruma/v50n1/1a02309x.png) given by
given by 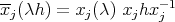 . We claim that the action is well defined since
. We claim that the action is well defined since 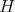 is a normal subgroup of
is a normal subgroup of  . If
. If 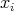 ,
,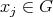 then
then  for some
for some  , that is
, that is  . Let
. Let ![γ : T × T → U (Λ[H ])](/img/revistas/ruma/v50n1/1a02318x.png) be defined by
be defined by

A direct computation shows that  is a crossed product. Now let us see that the map
is a crossed product. Now let us see that the map ![Φ : Λ [G ] - → Λ[H ] * T γ](/img/revistas/ruma/v50n1/1a02321x.png) given by
given by

is an isomorphism of 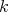 -algebras, where
-algebras, where 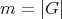 . Clearly
. Clearly 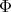 is a morphism of
is a morphism of 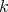 -vector spaces. If
-vector spaces. If  , then
, then
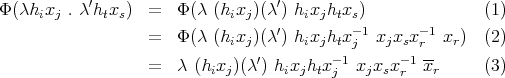
because  is a normal subgroup of
is a normal subgroup of  . On the other hand we have
. On the other hand we have
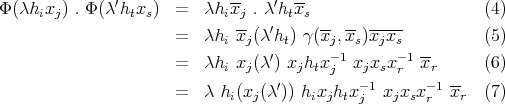
and  agrees with
agrees with  . Furthermore it is clear that
. Furthermore it is clear that 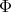 is bijective, hence we get
is bijective, hence we get ![Λ [G ] ≃ Λ[H ] *γ T](/img/revistas/ruma/v50n1/1a02335x.png) .
. 
Corollary 2.3. If  is a short exact sequence of groups that splits on the right, then
is a short exact sequence of groups that splits on the right, then ![Λ [G ] = Λ[H ][T ].](/img/revistas/ruma/v50n1/1a02338x.png)
Proof. We only have to prove that the map  defined in the theorem above is such that
defined in the theorem above is such that 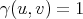 for any
for any 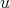 ,
, 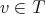 where
where 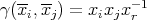 , with
, with  for some
for some  . If the sequence
. If the sequence  splits on the right, there exists a map
splits on the right, there exists a map 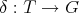 such that
such that 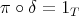 . Let
. Let 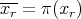 . Since
. Since 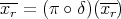 , then
, then  and hence we assume that
and hence we assume that 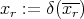 . Since
. Since  is a morphism of groups,
is a morphism of groups, 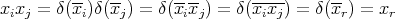 and therefore
and therefore 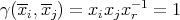 . Now it is clear that
. Now it is clear that ![Λ[G] = Λ [H ][T]](/img/revistas/ruma/v50n1/1a02356x.png) .
. 
It is clear that the map 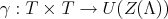 which defines a crossed product is by definition a cocycle with respect to group cohomology, see [8] for more details. We shall prove that if the cocycle
which defines a crossed product is by definition a cocycle with respect to group cohomology, see [8] for more details. We shall prove that if the cocycle  is a coboundary, then we have
is a coboundary, then we have ![Λ *γ T ≃ Λ [T ]](/img/revistas/ruma/v50n1/1a02363x.png) .
.
Proposition 2.5. [16, Lemma 5.6] Let 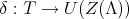 be a map,
be a map, 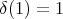 , and let
, and let 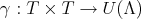 be given by
be given by
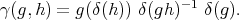
Then ![Λ *γ T ≃ Λ [T ]](/img/revistas/ruma/v50n1/1a02368x.png) .
.
Proof. A direct computation shows that  defines a crossed product. Let
defines a crossed product. Let ![Ψ : Λ *γ T -→ Λ [T ]](/img/revistas/ruma/v50n1/1a02370x.png) be defined by
be defined by 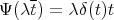 . Then
. Then 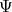 is a morphism of algebras because
is a morphism of algebras because
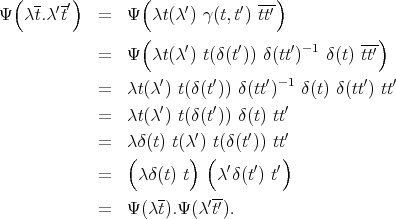
Therefore  is an isomorphism and hence
is an isomorphism and hence ![Λ * T ≃ Λ[T ] γ](/img/revistas/ruma/v50n1/1a02375x.png) .
.
We say that 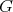 acts trivially on an element
acts trivially on an element 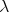 if
if  for all
for all  . If
. If 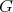 is a finite abelian group of order
is a finite abelian group of order  acting trivially on
acting trivially on 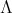 with
with  invertible in
invertible in 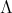 , then
, then ![∏m Λ[G ] ≃ i=1 Λ](/img/revistas/ruma/v50n1/1a02386x.png) . In fact, by Maschke's theorem we have that
. In fact, by Maschke's theorem we have that 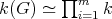 , see [14]. Now the map
, see [14]. Now the map ![ψ : Λ ⊗k k(G ) → Λ [G ]](/img/revistas/ruma/v50n1/1a02388x.png) given by
given by 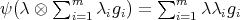 is an isomorphism of
is an isomorphism of 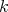 -algebras.
-algebras.
Proposition 2.6. [16, Proposition 5.8] Let  be a finite cyclic group acting on a commutative local algebra
be a finite cyclic group acting on a commutative local algebra 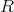 with the order of
with the order of  invertible in
invertible in 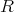 . Then
. Then  .
.
We may infer from the previous proposition that if 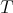 is a finite cyclic group with the order of
is a finite cyclic group with the order of 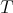 is invertible in
is invertible in 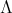 , and
, and 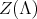 (the center of
(the center of  ) is a local algebra,
) is a local algebra, ![Λ *γ T ≃ Λ [T ]](/img/revistas/ruma/v50n1/1a02401x.png) because any cocycle is a coboundary. In particular, if
because any cocycle is a coboundary. In particular, if 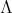 is a basic connected algebra without oriented cycles,
is a basic connected algebra without oriented cycles, 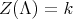 .
.
Corollary 2.7. Let 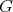 be a finite abelian group acting on a basic connected algebra
be a finite abelian group acting on a basic connected algebra  where the associated quiver has no oriented cycles, with the order of
where the associated quiver has no oriented cycles, with the order of 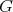 invertible in
invertible in 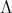 . Let
. Let 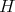 be a subgroup of
be a subgroup of  which acts trivially on
which acts trivially on 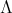 , with
, with 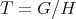 cyclic. Then
cyclic. Then ![Λ [G ] ≃ Λ[H ][T ]](/img/revistas/ruma/v50n1/1a02412x.png) .
.
Proof. It follows from Theorem 2.2 that ![Λ [G] ≃ Λ [H ] *γ T](/img/revistas/ruma/v50n1/1a02413x.png) , and
, and ![Λ [H ] ≃ Λ × ⋅⋅ ⋅ × Λ](/img/revistas/ruma/v50n1/1a02414x.png) by Maschke's theorem. Since
by Maschke's theorem. Since 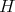 is abelian and acts trivially on
is abelian and acts trivially on  ,
, 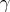 takes values in the set of invertible elements of the center of
takes values in the set of invertible elements of the center of ![Λ[H ]](/img/revistas/ruma/v50n1/1a02418x.png) . But
. But ![Z (Λ[H ]) ≃ k × ⋅⋅⋅ × k](/img/revistas/ruma/v50n1/1a02419x.png) and
and  is cyclic, so Proposition 2.6 implies that
is cyclic, so Proposition 2.6 implies that  is a coboundary. From Proposition 2.5 we may deduce that
is a coboundary. From Proposition 2.5 we may deduce that ![Λ [G ] ≃ Λ[H ][T ]](/img/revistas/ruma/v50n1/1a02422x.png) .
.
It is known that if 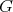 is a finite group of order
is a finite group of order 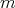 acting trivially on the idempotents of
acting trivially on the idempotents of  and
and  is invertible in
is invertible in 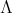 , then
, then 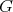 is an abelian group, see [15, Proposition 2.7]. In fact, given
is an abelian group, see [15, Proposition 2.7]. In fact, given 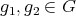 ,
, 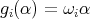 with
with  a
a 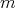 -root of unity. Hence
-root of unity. Hence  , and this equality holds for any arrow
, and this equality holds for any arrow  . Moreover, for every
. Moreover, for every 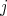
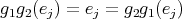 . So
. So 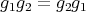 .
.
Finally, we state a result that will be used in the proof of the main theorem in this work.
Theorem 2.8. [5, Theorem 8]. Let 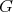 be a finite abelian group of order
be a finite abelian group of order 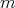 acting trivially on a complete set of primitive orthogonal idempotents of a simply connected algebra
acting trivially on a complete set of primitive orthogonal idempotents of a simply connected algebra  ,
, 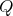 without double arrows and
without double arrows and 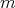 invertible in
invertible in  . Then
. Then ![Λ [G ] ≃ ∏m Λ i=1](/img/revistas/ruma/v50n1/1a02445x.png) .
.
3. ![Λ[G ]](/img/revistas/ruma/v50n1/1a02446x.png) with
with 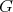 an abelian group and
an abelian group and 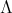 an hereditary algebra of finite representation type
an hereditary algebra of finite representation type
The aim of this section is to describe all possible actions of a finite abelian group on an hereditary algebra of finite representation type and to give a description of the skew group algebra for each action.
Gabriel has shown in [6] that a connected hereditary algebra is representation-finite if and only if the underlying graph of its quiver is one of the Dynkin diagrams 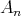 ,
,  (
(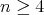 ),
), 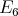 ,
, 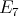 or
or 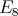 , that appear also in Lie theory, where the index in the Dynkin graph always refers to the number of points in the graph. Then, in order to classify the representation-finite hereditary skew group algebras, it suffices to study the group actions on the Dynkin quivers.
, that appear also in Lie theory, where the index in the Dynkin graph always refers to the number of points in the graph. Then, in order to classify the representation-finite hereditary skew group algebras, it suffices to study the group actions on the Dynkin quivers.


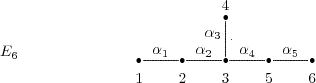
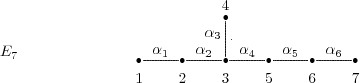
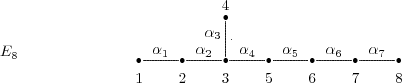
Before we present the results, we need some definitions.
Definition 3.1. We say that an quiver of type  has symmetric orientation if it is symmetric with respect to the middle point
has symmetric orientation if it is symmetric with respect to the middle point  .
.
Definition 3.2. We say that an quiver of type 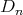 ,
, 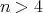 , has symmetric orientation if
, has symmetric orientation if 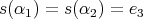 or
or 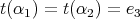 .
.
Definition 3.3. We say that an quiver of type  has
has
-
symmetric orientation of kind
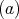 if
if 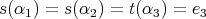 or
or 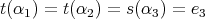 ; and,
; and, -
symmetric orientation of kind
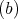 if
if 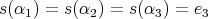 or
or  .
.
Definition 3.4. We say that the quiver 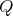 of type
of type 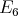 has symmetric orientation if it is symmetric with respect to the side
has symmetric orientation if it is symmetric with respect to the side 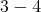 , that is,
, that is,
-
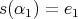 and
and 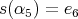 , or
, or  and
and 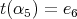 ;
;and,
-
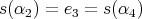 , or
, or  .
.
-
The quiver
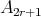 is symmetric with respect to the middle point
is symmetric with respect to the middle point  if that point is center of symmetry of the quiver.
if that point is center of symmetry of the quiver. -
The quiver
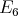 is symmetric with respect to the side
is symmetric with respect to the side  if the line obtained with the points
if the line obtained with the points  is a symmetry axis of the quiver.
is a symmetry axis of the quiver.
As we have already mentioned, if  is acting trivially on
is acting trivially on  , we have
, we have ![∏m Λ [G ] = t=1Λ](/img/revistas/ruma/v50n1/1a02489x.png) . Hence, from now on, we will assume that
. Hence, from now on, we will assume that  is acting non trivially on
is acting non trivially on  . Let
. Let  . Clearly
. Clearly  is a normal subgroup of
is a normal subgroup of 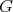 . Let
. Let  , then
, then 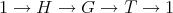 is a short exact sequence of groups.
is a short exact sequence of groups.
Theorem 3.6. Let  be an hereditary algebra, with
be an hereditary algebra, with  of type
of type 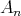 (
(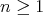 ),
), 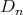 (
(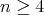 ),
),  ,
,  or
or 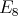 , and
, and 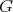 a finite abelian group of order
a finite abelian group of order 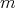 acting non trivially on
acting non trivially on 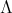 , with
, with  invertible in
invertible in  . Let
. Let 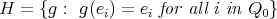 .
.
-
If
 then
then ![Λ [G ] = ∏m Λ t=1](/img/revistas/ruma/v50n1/1a02513x.png) ;
; -
If
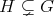 and
and 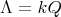 with
with  of type
of type 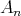 then
then 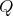 is of type
is of type 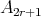 , with symmetric orientation, the order of
, with symmetric orientation, the order of 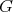 is even and
is even and ![∏ Λ [G ] ≃ ( mt=∕12Λ ) *γ ℤ∕2ℤ](/img/revistas/ruma/v50n1/1a02521x.png) ;
; -
If
 and
and 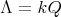 with
with  of type
of type 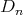 ,
, 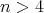 , then
, then 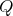 has symmetric orientation, the order of
has symmetric orientation, the order of 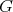 is even and
is even and ![∏m ∕2 Λ [G] ≃ ( t=1 Λ) *γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a02529x.png) ;
; -
If
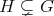 and
and 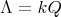 with
with 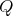 of type
of type 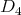 then
then-
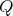 has symmetric orientation of kind
has symmetric orientation of kind 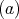 , the order of
, the order of 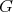 is even and
is even and ![∏m ∕2 Λ [G ] ≃ ( t=1 Λ ) *γ ℤ∕2 ℤ](/img/revistas/ruma/v50n1/1a02537x.png) ,
,or
-
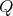 has symmetric orientation of kind
has symmetric orientation of kind  , the order of
, the order of  is divisible by
is divisible by  or
or 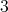 , and
, and ![∏m ∕2 Λ [G ] ≃ ( t=1 Λ ) *γ ℤ∕2 ℤ](/img/revistas/ruma/v50n1/1a02543x.png) or
or ![∏ Λ [G ] ≃ ( m∕3Λ ) *γ ℤ∕3ℤ. t=1](/img/revistas/ruma/v50n1/1a02544x.png)
-
-
If
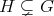 and
and  with
with  of type
of type 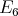 then
then  has symmetric orientation,
has symmetric orientation, 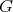 is a group of even order and
is a group of even order and ![∏ Λ [G] ≃ ( mt=∕21 Λ) *γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a02551x.png) ;
; -
If
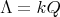 with
with  of type
of type 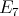 or
or 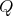 of type
of type  then
then 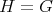 and
and ![∏m Λ[G ] = t=1 Λ](/img/revistas/ruma/v50n1/1a02558x.png) .
.
Proof. In order to prove the theorem, we need a precise description of all the possible actions of 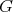 on
on  , for each type and orientation of
, for each type and orientation of  . We use Proposition 2.1 to describe all possible actions of
. We use Proposition 2.1 to describe all possible actions of 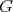 on
on 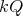 with
with 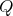 of type
of type  ,
,  ,
, 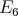 ,
,  or
or  .
.
-
See Theorem 2.8.
-
Let
 with
with  of type
of type 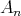 and let
and let 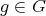 ,
, 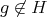 . If
. If 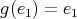 then
then  . This implies
. This implies 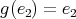 and
and  with
with 
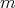 -roots of unity. Repeating this procedure we have that
-roots of unity. Repeating this procedure we have that  implies
implies 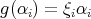 with
with 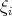 an
an  -root of unity, and this for all
-root of unity, and this for all  . Hence the action of
. Hence the action of 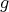 is trivial on the idempotents
is trivial on the idempotents 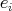 of
of  . So
. So  , a contradiction. So
, a contradiction. So 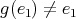 . In this case
. In this case  and
and 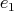 ,
, 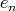 will have to be sinks or sources, see Proposition 2.1. This determines the orientation of
will have to be sinks or sources, see Proposition 2.1. This determines the orientation of  and
and  . Moreover
. Moreover  . So
. So  and
and 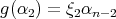 . Inductively,
. Inductively,  and
and 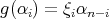 , and this for all
, and this for all  , with
, with 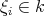 ,
, 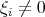 . If
. If 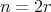 is an even number we have that
is an even number we have that 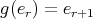 ,
, 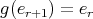 and if
and if  is the arrow
is the arrow 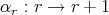 , then
, then 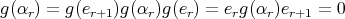 , contradiction. We also get a contradiction if
, contradiction. We also get a contradiction if 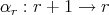 . Then if the number of vertices is an even number, the unique possible action on the set of idempotents is the trivial one.
. Then if the number of vertices is an even number, the unique possible action on the set of idempotents is the trivial one.Let
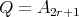 with
with 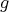 acting non trivially on the set
acting non trivially on the set  of idempotents of
of idempotents of  . Then
. Then 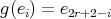 and
and 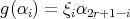 , hence the quiver
, hence the quiver  has symmetric orientation. Moreover,
has symmetric orientation. Moreover, 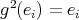 for all
for all  , so
, so 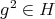 . Then
. Then  has even order
has even order 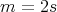 and
and  , for all
, for all 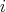 . Let
. Let  ,
,  . Since
. Since  ,
,  does not act trivially on the set
does not act trivially on the set  of idempotents of
of idempotents of  . By the previous reasoning, the unique non trivial action is given by
. By the previous reasoning, the unique non trivial action is given by 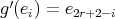 . Then
. Then  . As a consequence
. As a consequence  , that is
, that is  . Then
. Then  because
because 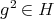 , and hence
, and hence 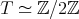 . Hence, if the group
. Hence, if the group 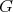 does not act trivially on the set
does not act trivially on the set  of idempotents of
of idempotents of  , in accordance with the previous analysis we have that
, in accordance with the previous analysis we have that 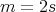 is an even number and
is an even number and 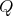 is of type
is of type 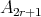 with symmetric orientation. In this case we have
with symmetric orientation. In this case we have 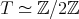 . Hence
. Hence ![∏s Λ [G] ≃ Λ [H ] * γ ℤ ∕2ℤ ≃ ( t=1 Λ) *γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a02645x.png) , see Theorem 2.2 and Theorem 2.8.
, see Theorem 2.2 and Theorem 2.8. -
Let
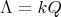 with
with 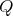 of type
of type 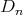 ,
, 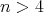 . Assume that the group
. Assume that the group 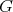 is not acting trivially on the set
is not acting trivially on the set  of idempotents of
of idempotents of 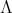 . We observe that all
. We observe that all 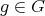 must satisfy
must satisfy 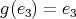 , see Proposition 2.1. If
, see Proposition 2.1. If  then
then  ,
, 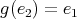 and
and  for all
for all  . This determines the orientation of the arrows, that is,
. This determines the orientation of the arrows, that is, 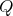 has symmetric orientation, and
has symmetric orientation, and 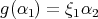 ,
, 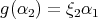 ,
,  for all
for all  , with
, with 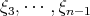
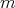 -roots of unity,
-roots of unity, 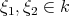 non zero. Then
non zero. Then 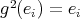 for all
for all  , that is,
, that is, 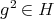 . So
. So  has even order
has even order 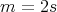 and
and 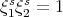 . Let
. Let 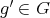 ,
, 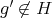 . By the previous reasoning,
. By the previous reasoning, 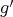 and
and 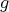 act in the unique possible non trivial way on the complete set of idempotents of
act in the unique possible non trivial way on the complete set of idempotents of  . Then
. Then  ,
, 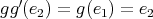 and
and 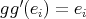 for all
for all  . Hence
. Hence 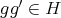 , that is
, that is 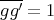 , then
, then  because
because  . Hence
. Hence  and
and  is an even number.
is an even number.It follows from the previous analysis that
 is an even number and the quiver
is an even number and the quiver  has symmetric orientation. Hence we have
has symmetric orientation. Hence we have ![Λ[G ] ≃ Λ [H ] *γ ℤ ∕2ℤ ≃ (∏s Λ) *γ ℤ ∕2ℤ t=1](/img/revistas/ruma/v50n1/1a02691x.png) .
. -
Let
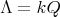 with
with 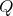 of type
of type 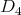 .
.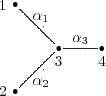
Let
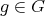 ,
, 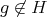 . Necessarily
. Necessarily 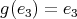 , by Proposition 2.1, and all possible cases are:
, by Proposition 2.1, and all possible cases are:-
 ,
,  ,
, 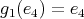 ;
; -
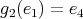 ,
, 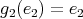 ,
,  ;
; -
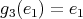 ,
, 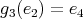 ,
, 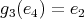 ;
; -
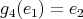 ,
, 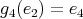 ,
, 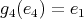 ;
; -
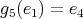 ,
, 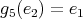 ,
,  .
.
In fact
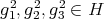 ,
, 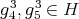 and
and 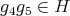 , so
, so  in
in 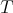 . On the other hand, since
. On the other hand, since 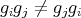 for all
for all 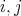 with
with 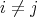 and
and 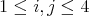 and
and  is abelian, we have that
is abelian, we have that 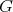 cannot contain simultaneously elements acting as
cannot contain simultaneously elements acting as 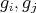 for all
for all  with
with 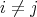 and
and 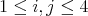 . Consequently
. Consequently  or
or 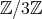 . The cases i), ii) and iii) determine the orientation of the arrows
. The cases i), ii) and iii) determine the orientation of the arrows  and
and  , that is,
, that is,  has symmetric orientation of kind (a) or (b), and the cases iv) and v) determine the orientation of all the arrows, that is,
has symmetric orientation of kind (a) or (b), and the cases iv) and v) determine the orientation of all the arrows, that is,  has symmetric orientation of kind (b).
has symmetric orientation of kind (b).In accordance with Definition 3.3 and with the previous analysis for
 of type
of type 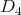 , we have that the quiver
, we have that the quiver 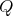 has symmetric orientation of kind (a) and
has symmetric orientation of kind (a) and 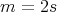 , or has symmetric orientation of kind (b) and
, or has symmetric orientation of kind (b) and  or
or 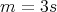 . From Theorem 2.2 and Theorem 2.8 we have that, in the first case,
. From Theorem 2.2 and Theorem 2.8 we have that, in the first case, 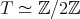 and
and ![∏ Λ [G] ≃ Λ [H ] * γ ℤ ∕2ℤ ≃ ( st=1 Λ) *γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a02742x.png) . In the second case, the order of
. In the second case, the order of  is divisible by
is divisible by  or
or 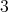 ,
,  or
or 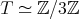 , and
, and ![∏s Λ[G ] ≃ Λ [H ] *γ ℤ ∕2ℤ ≃ ( t=1 Λ) *γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a02748x.png) or
or ![∏s Λ [G] ≃ Λ [H ] * γ ℤ ∕3ℤ ≃ ( t=1 Λ) *γ ℤ ∕3ℤ](/img/revistas/ruma/v50n1/1a02749x.png)
-
-
We need again a precise description of all the possible actions of
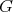 on
on  with
with 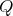 of type
of type 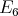 . Let
. Let 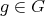 ,
, 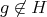 . By Proposition 2.1 ,
. By Proposition 2.1 , 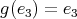 , and this implies that
, and this implies that  . On the other hand
. On the other hand  or
or  . If
. If 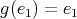 , then
, then  and
and 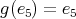 . This is a contradiction, because
. This is a contradiction, because  . Then
. Then  , and this implies that
, and this implies that 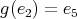 and
and  . This determines the orientation of the arrows, and we have
. This determines the orientation of the arrows, and we have 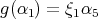 ,
, 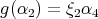 ,
,  ,
,  and
and  with
with 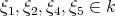 non zero and
non zero and  an
an  -root of unity. Since
-root of unity. Since 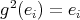 for all
for all 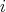 , then
, then 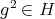 . So
. So 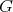 has even order
has even order 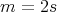 and
and 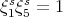 ,
, 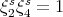 . Let
. Let 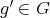 be such that
be such that  . Hence,
. Hence,  for all
for all  . Therefore
. Therefore 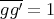 ,
,  and
and 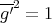 that is,
that is,  , and then
, and then  . Hence, if the group
. Hence, if the group 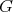 does not act trivially on the set
does not act trivially on the set  of idempotents of
of idempotents of 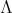 , in accordance with the previous analysis, we have that
, in accordance with the previous analysis, we have that  is an even number,
is an even number, 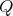 has symmetric orientation and
has symmetric orientation and  . Hence
. Hence ![∏ Λ [G] ≃ Λ [H ] * γ ℤ ∕2ℤ ≃ ( st=1 Λ) *γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a02797x.png) , see Theorem 2.2 and Theorem 2.8.
, see Theorem 2.2 and Theorem 2.8. -
If we consider the cases
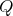 of type
of type  or
or  , the unique possible action on the set of idempotents is the trivial one. Hence
, the unique possible action on the set of idempotents is the trivial one. Hence 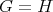 and
and 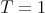 and the result follows from i).
and the result follows from i). 
Corollary 3.7. Let 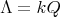 be an hereditary algebra, with
be an hereditary algebra, with  of type
of type 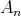 (
(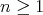 ),
), 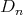 (
( ),
),  ,
,  or
or 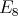 , and
, and 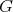 an abelian group of order
an abelian group of order  acting on
acting on  , with
, with  invertible in
invertible in  . Suppose that
. Suppose that  does not act trivially on the set
does not act trivially on the set  of idempotents of
of idempotents of 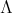 and
and 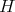 acts trivially on
acts trivially on 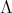 .
.
-
If
 , with
, with  of type
of type 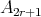 with symmetric orientation, then
with symmetric orientation, then ![∏s Λ[G ] ≃ ( t=1Λ )[ℤ∕2ℤ ]](/img/revistas/ruma/v50n1/1a02826x.png) ;
; -
If
 , with
, with 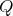 of type
of type  ,
, 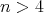 , with symmetric orientation, then
, with symmetric orientation, then ![Λ[G ] ≃ (∏s Λ )[ℤ∕2ℤ ] t=1](/img/revistas/ruma/v50n1/1a02831x.png) ;
; -
If
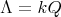 , with
, with 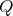 of type
of type 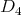 with symmetric orientation of kind (a), then
with symmetric orientation of kind (a), then ![∏s Λ [G] ≃ ( t=1Λ )[ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a02835x.png) ;
; -
If
 , with
, with 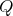 of type
of type  with symmetric orientation of kind (b), then
with symmetric orientation of kind (b), then ![Λ [G] ≃ (∏m ∕2Λ )[ℤ∕2ℤ ] t=1](/img/revistas/ruma/v50n1/1a02839x.png) or
or ![∏m ∕3 Λ [G] ≃ ( t=1 Λ)[ℤ∕3ℤ ]](/img/revistas/ruma/v50n1/1a02840x.png) .
. -
If
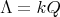 , with
, with 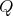 of type
of type 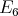 with symmetric orientation, then
with symmetric orientation, then ![Λ [G] ≃ (∏s Λ )[ℤ ∕2ℤ ] t=1](/img/revistas/ruma/v50n1/1a02844x.png) .
.
Proof. It follows from Theorem 3.6 and Corollary 2.7. 
The following Corollary follows easily from [16, (2.3), (2.4)].
Corollary 3.8. Let 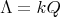 be an hereditary algebra, with
be an hereditary algebra, with 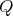 of type
of type 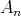 (
(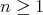 ),
),  (
( ),
),  ,
,  or
or 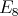 , and
, and  a cyclic group of order
a cyclic group of order 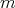 acting on
acting on 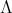 , with
, with  invertible in
invertible in 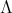 .
.
-
Let
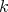 be a field such that
be a field such that  . If
. If 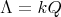 is an hereditary algebra with
is an hereditary algebra with  of type
of type 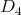 and
and 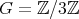 is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of 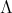 , then the skew group algebra
, then the skew group algebra ![Λ [ℤ ∕3ℤ ]](/img/revistas/ruma/v50n1/1a02868x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra  with
with  of type
of type 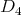 . If
. If 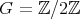 is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of  , then the skew group algebra
, then the skew group algebra ![Λ [ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a02875x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra 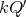 with
with  of type
of type  .
. -
Let
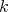 be a field such that
be a field such that 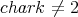 . If
. If 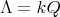 is an hereditary algebra, with
is an hereditary algebra, with 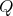 of type
of type 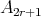 and
and 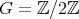 is acting non trivially on the set
is acting non trivially on the set 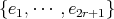 of idempotents of
of idempotents of 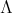 , then the skew group algebra
, then the skew group algebra ![Λ[ℤ∕2 ℤ]](/img/revistas/ruma/v50n1/1a02887x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra  with
with 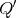 of type
of type 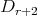 if
if  and of type
and of type  if
if 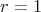 .
. -
Let
 be a field such that
be a field such that 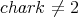 . If
. If 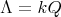 is an hereditary algebra, with
is an hereditary algebra, with 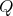 of type
of type  ,
, 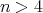 , and
, and 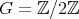 is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of  , then the skew group algebra
, then the skew group algebra ![Λ[ℤ∕2ℤ ]](/img/revistas/ruma/v50n1/1a02903x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra 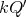 with
with 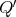 of type
of type  .
. -
Let
 be a field such that
be a field such that  . If
. If  is an hereditary algebra, with
is an hereditary algebra, with 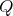 of type
of type 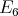 , and
, and 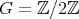 is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of  , then the skew group algebra
, then the skew group algebra ![Λ [ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a02915x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra  with
with 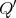 of type
of type 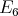 .
.
For an example of Corollary 3.8 see [16, (2.3), (2.4)].
4. ![Λ[G ]](/img/revistas/ruma/v50n1/1a02919x.png) with
with  an abelian group and
an abelian group and 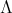 an hereditary algebra of tame representation type
an hereditary algebra of tame representation type
The aim of this section is to describe all possible actions of a finite abelian group on an hereditary algebra of tame representation type, to give a description of the skew group algebra for each action and finally to determinate their representation type.
It is well known that a connected hereditary algebra is of tame representation type if and only if the underlying graph of its quiver is one of the euclidean diagrams  (
( ),
),  (
( ),
),  ,
, 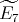 or
or  where an euclidean diagram
where an euclidean diagram 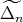 has
has  points. Then, in order to classify the tame representation type hereditary skew group algebras, it suffices to study the group actions on the euclidean quivers. It is necessary to clarify that the case
points. Then, in order to classify the tame representation type hereditary skew group algebras, it suffices to study the group actions on the euclidean quivers. It is necessary to clarify that the case  will be considered separately later on.
will be considered separately later on.

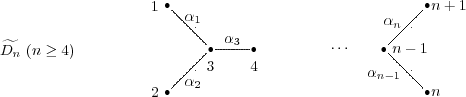
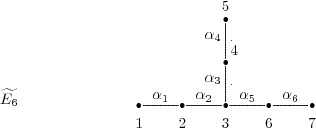
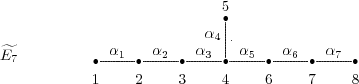

Before we present the results, we need some definitions.
Definition 4.1. We say that an quiver of type 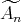 (
( ) has
) has
-
symmetric orientation if
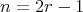 is odd and the quiver is symmetric with respect to an axis
is odd and the quiver is symmetric with respect to an axis 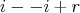 ,
, -
cyclic orientation of order
 if the full subquivers with vertices
if the full subquivers with vertices  are all equal, and
are all equal, and  is minimal with respect to this property (
is minimal with respect to this property (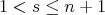 ).
).
Remark 4.2. Supose you have 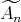 with a fixed oritentation. Choose
with a fixed oritentation. Choose  such that
such that 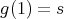 , for any action
, for any action  . This set, a non-empty set of the natural numbers, has a first element and this is the
. This set, a non-empty set of the natural numbers, has a first element and this is the  of the definition.
of the definition.
Definition 4.3. We say that an quiver of type  ,
,  , has
, has
-
symmetric orientation of kind
 if
if-
 , or
, or -
 , or
, or -
 , or
, or -
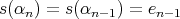 ,
,
-
-
symmetric orientation of kind
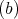 if
if  is even and the quiver is symmetric with respect to the middle point
is even and the quiver is symmetric with respect to the middle point 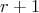 ;
;
Definition 4.4. We say that an quiver of type 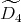 has symmetric orientation of order
has symmetric orientation of order  if the number of arrows starting at the vertex
if the number of arrows starting at the vertex  is equal to
is equal to  , for
, for 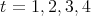 .
.
Definition 4.5. We say that an quiver of type 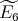 has
has
-
symmetric orientation of kind
 if
if  ,
, 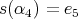 ,
,  or
or 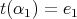 ,
, 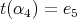
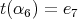 and
and 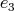 is a source or a sink;
is a source or a sink; -
symmetric orientation of kind
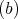 if it is not symmetric of kind (a) and it is symmetric with respect to the side
if it is not symmetric of kind (a) and it is symmetric with respect to the side 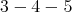 .
.
Definition 4.6. We say that an quiver of type 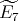 has symmetric orientation if it is symmetric with respect to the side
has symmetric orientation if it is symmetric with respect to the side 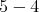 .
.
-
We say that the quiver
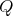 is symmetric with respect to the middle point
is symmetric with respect to the middle point 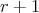 if that point is center of symmetry of the quiver
if that point is center of symmetry of the quiver  .
. -
We say that the quiver
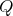 is symmetric with respect to an axis
is symmetric with respect to an axis  , if the line obtained with the points
, if the line obtained with the points 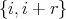 is symmetry axis of the quiver.
is symmetry axis of the quiver.
Let 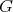 be a group and we will assume that
be a group and we will assume that 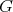 is acting trivially on
is acting trivially on 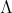 , we have
, we have ![∏m Λ[G ] = t=1 Λ](/img/revistas/ruma/v50n1/1a02987x.png) . Hence, from now on, we will assume that
. Hence, from now on, we will assume that  is acting non trivially on
is acting non trivially on 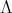 . Let
. Let 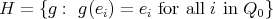 . Clearly
. Clearly  is a normal subgroup of
is a normal subgroup of  . Let
. Let 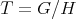 , then
, then 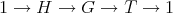 is a short exact sequence of groups.
is a short exact sequence of groups.
Theorem 4.8. Let  be a tame hereditary algebra, with
be a tame hereditary algebra, with 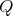 of type
of type  (
(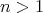 ),
),  (
(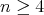 ),
),  ,
,  or
or  , and
, and 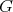 a finite abelian group of order
a finite abelian group of order  acting non trivially on
acting non trivially on 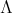 , with
, with 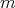 invertible in
invertible in 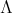 .
.
-
If
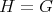 then
then ![∏ Λ [G ] = mt=1 Λ](/img/revistas/ruma/v50n1/1a021010x.png) ;
; -
If
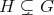 and
and 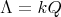 with
with 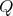 of type
of type 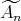 then
then-
 is symmetric not cyclic,
is symmetric not cyclic,  if it is symmetric with respect to one axis, or
if it is symmetric with respect to one axis, or 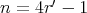 if it is symmetric with respect to a pair of perpendicular axes, the order of
if it is symmetric with respect to a pair of perpendicular axes, the order of 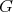 is divisible by
is divisible by  or
or 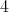 respectively, and
respectively, and ![Λ [G ] ≃ (∏m ∕2Λ ) * ℤ∕2 ℤ t=1 γ](/img/revistas/ruma/v50n1/1a021021x.png) or
or ![∏m ∕4 Λ [G ] ≃ ( t=1 Λ ) *γ (ℤ∕2ℤ × ℤ∕2 ℤ)](/img/revistas/ruma/v50n1/1a021022x.png) ;
; -
 is cyclic of order
is cyclic of order  , not symmetric,
, not symmetric, 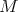 is the smallest natural number such that
is the smallest natural number such that  is divisible by
is divisible by  , the order of
, the order of  is divisible by
is divisible by  and
and ![∏m ∕M Λ [G ] ≃ ( t=1 Λ ) *γ ℤ∕M ℤ](/img/revistas/ruma/v50n1/1a021030x.png) ;
;or
-
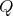 is symmetric and cyclic of order
is symmetric and cyclic of order  ,
,  , the order of
, the order of 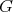 is divisible by
is divisible by  or
or 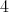 and
and ![∏m ∕2 Λ [G] ≃ ( t=1 Λ) * γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a021037x.png) or
or ![∏ Λ [G ] ≃ ( mt=∕14Λ ) *γ (ℤ∕2ℤ × ℤ∕2 ℤ)](/img/revistas/ruma/v50n1/1a021038x.png) .
.
-
-
If
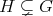 and
and 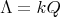 with
with  of type
of type 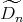 ,
, 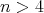 then
then-
 has symmetric orientation of kind
has symmetric orientation of kind 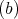 , not (a), the order of
, not (a), the order of 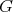 is even and
is even and ![∏ Λ[G ] ≃ ( mt=∕21 Λ) *γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a021047x.png) ,
, -
 has symmetric orientation of kind
has symmetric orientation of kind 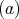 , not
, not 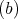 , the order of
, the order of 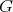 is divisible by
is divisible by  or
or  , and
, and ![∏m ∕2 Λ [G ] ≃ ( t=1 Λ ) *γ ℤ∕2 ℤ](/img/revistas/ruma/v50n1/1a021054x.png) or
or ![Λ [G ] ≃ (∏m ∕4Λ ) *γ (ℤ∕2ℤ × ℤ∕2ℤ ) t=1](/img/revistas/ruma/v50n1/1a021055x.png) ,
,or
-
 has symmetric orientation of kind
has symmetric orientation of kind 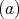 and (b), the order of
and (b), the order of 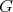 is divisible by
is divisible by  or
or 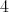 and
and ![∏ Λ [G] ≃ ( m ∕2 Λ) *γ ℤ ∕2ℤ t=1](/img/revistas/ruma/v50n1/1a021061x.png) ,
, ![∏m ∕4 Λ [G ] ≃ ( t=1 Λ ) *γ (ℤ∕2ℤ × ℤ∕2 ℤ)](/img/revistas/ruma/v50n1/1a021062x.png) or
or ![∏m ∕4 Λ [G ] ≃ ( t=1 Λ ) *γ ℤ∕4 ℤ](/img/revistas/ruma/v50n1/1a021063x.png) .
.
-
-
If
 and
and  with
with  of type
of type 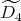 then
then-
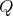 is symmetric of order
is symmetric of order 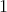 or
or  , the order of
, the order of  is divisible by
is divisible by  or
or 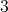 and
and ![∏m ∕2 Λ [G ] ≃ ( t=1 Λ ) *γ ℤ∕2 ℤ](/img/revistas/ruma/v50n1/1a021074x.png) or
or ![∏ Λ [G ] ≃ ( mt=∕13Λ ) *γ ℤ∕3 ℤ](/img/revistas/ruma/v50n1/1a021075x.png) ;
; -
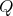 is symmetric of order
is symmetric of order  , the order of
, the order of 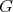 is divisible by
is divisible by  or
or  and
and ![∏m ∕2 Λ [G ] ≃ ( t=1 Λ ) *γ ℤ∕2 ℤ](/img/revistas/ruma/v50n1/1a021081x.png) or
or ![∏ Λ [G ] ≃ ( mt=∕14Λ ) *γ (ℤ∕2ℤ × ℤ∕2 ℤ)](/img/revistas/ruma/v50n1/1a021082x.png) ;
;or
-
 is symmetric of order
is symmetric of order  , the order of
, the order of  is divisible by
is divisible by  ,
, 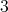 or
or  and
and ![∏m ∕2 Λ [G] ≃ ( t=1 Λ) *γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a021089x.png) ,
, ![∏ Λ [G ] ≃ ( mt=∕13Λ ) *γ ℤ∕3 ℤ](/img/revistas/ruma/v50n1/1a021090x.png) ,
, ![Λ [G ] ≃ (∏m ∕4Λ ) * (ℤ∕2ℤ × ℤ∕2 ℤ) t=1 γ](/img/revistas/ruma/v50n1/1a021091x.png) or
or ![∏m ∕4 Λ [G ] ≃ ( t=1 Λ ) *γ ℤ∕4 ℤ](/img/revistas/ruma/v50n1/1a021092x.png) ;
;
-
-
If
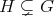 and
and 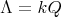 with
with  of type
of type 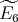 then
then-
 has symmetric orientation of kind (a), the order of
has symmetric orientation of kind (a), the order of 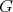 is divisible by
is divisible by  or
or 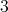 and
and ![∏m ∕2 Λ [G] ≃ ( t=1 Λ) * γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a021101x.png) or
or ![∏ Λ [G ] ≃ ( mt=∕13Λ ) *γ ℤ∕3 ℤ](/img/revistas/ruma/v50n1/1a021102x.png) ;
;or
-
 has symmetric orientation of kind (b), the order of
has symmetric orientation of kind (b), the order of  is divisible by
is divisible by  and
and ![∏ Λ[G ] ≃ ( mt=∕12Λ) *γ ℤ∕2ℤ](/img/revistas/ruma/v50n1/1a021106x.png) ;
;
-
-
If
 and
and 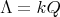 with
with 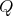 of type
of type 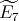 then
then  has symmetric orientation,
has symmetric orientation, 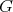 is a group of even order and
is a group of even order and ![∏m ∕2 Λ [G] ≃ ( t=1 Λ) *γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a021113x.png) ;
; -
If
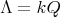 with
with 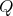 of type
of type  then
then 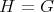 and
and ![∏ Λ [G ] = mt=1 Λ](/img/revistas/ruma/v50n1/1a021118x.png) .
.
Proof. In order to prove the theorem, we need a precise description of all the possible actions of 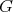 on
on 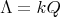 , for each type and orientation of
, for each type and orientation of  . We use Proposition 2.1 to describe all possible actions of
. We use Proposition 2.1 to describe all possible actions of 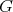 on
on  with
with 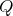 of type
of type 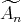 ,
, 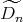 ,
, 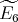 ,
, 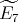 or
or 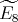 . We observe that we identify the elements of
. We observe that we identify the elements of 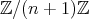 with the natural numbers
with the natural numbers 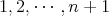 in the indexes of the idempotents
in the indexes of the idempotents 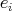 .
.
-
Theorem 2.8 cannot be applied because
 is not simply connected. Using [16, (2.3), (2.4)] for this case we have
is not simply connected. Using [16, (2.3), (2.4)] for this case we have ![∏ Λ [G] = mt=1Λ](/img/revistas/ruma/v50n1/1a021134x.png) (where
(where 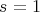 ,
,  ,
, 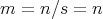 ,
,  under the conditions of [16, (2.3)]) .
under the conditions of [16, (2.3)]) . -
Let
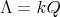 with
with  of type
of type  and let
and let 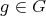 ,
,  . Assume that
. Assume that  fixes at least one point, say
fixes at least one point, say 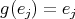 . Then
. Then 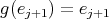 or
or 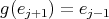 . In the first case, repeating this procedure we have that
. In the first case, repeating this procedure we have that  for all
for all 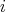 , and so
, and so 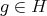 , a contradiction. In the second case, we get that
, a contradiction. In the second case, we get that 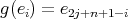 , for all
, for all 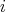 , and this determines the orientation of the arrows. If
, and this determines the orientation of the arrows. If 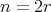 , we have
, we have  and
and 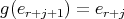 , a contradiction since there is only one arrow joining
, a contradiction since there is only one arrow joining 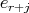 and
and 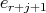 . So
. So 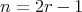 and
and 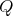 has symmetric orientation. Moreover,
has symmetric orientation. Moreover, 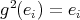 for all
for all 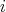 , so
, so 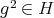 .
.Now let
 ,
, 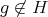 ,
,  for all
for all 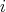 . Let
. Let 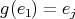 . If
. If 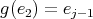 , the previous reasoning says that there must exist a middle point between
, the previous reasoning says that there must exist a middle point between  and
and  that will be fixed by
that will be fixed by 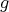 , a contradiction. So
, a contradiction. So 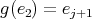 , and inductively we get that
, and inductively we get that  . This determines the orientation of the arrows, and so
. This determines the orientation of the arrows, and so 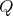 is cyclic of order
is cyclic of order  , where
, where  is the first element in the set
is the first element in the set  . Let
. Let  be such that
be such that  . Let
. Let  , with
, with  . Then
. Then 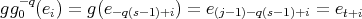 . If
. If 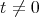 , we get a contradiction to the minimality of
, we get a contradiction to the minimality of  . So
. So 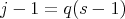 and
and 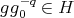 and
and 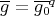 in
in 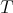 .
.We denote by

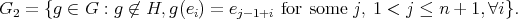
We have already proved that
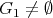 if and only if
if and only if  has symmetric orientation, and
has symmetric orientation, and 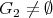 if and only if
if and only if 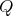 is cyclic of order
is cyclic of order  .
.Assume first that
 is cyclic of order
is cyclic of order  and is not symmetric. We have seen that
and is not symmetric. We have seen that 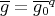 in
in  for any
for any 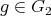 . Moreover,
. Moreover, 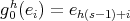 , so
, so 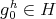 if and only if
if and only if 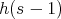 is divisible by
is divisible by  . Let
. Let 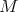 be the smallest natural number such that
be the smallest natural number such that 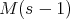 is divisible by
is divisible by  . We conclude that
. We conclude that 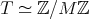 in this case.
in this case.Assume now that
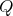 is symmetric but not cyclic, and let
is symmetric but not cyclic, and let 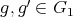 , that is,
, that is, 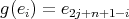 and
and 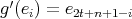 for some
for some 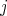 and
and  ,
, 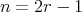 . We assume, without loss of generality, that
. We assume, without loss of generality, that 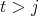 . If
. If 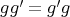 , then
, then 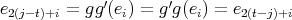 , so
, so 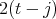 is divisible by
is divisible by  . Since
. Since  , we have that
, we have that  for
for  . If
. If 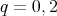 then
then  and hence
and hence 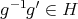 , that is,
, that is,  in
in 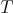 , and hence
, and hence  in this case. If
in this case. If  then
then  and
and  is symmetric with respect to the axes
is symmetric with respect to the axes 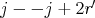 and
and  and in this case
and in this case  .
.Finally, assume that
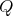 is symmetric (
is symmetric (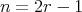 ) and cyclic of order
) and cyclic of order  , and let
, and let 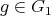 and
and  , that is,
, that is,  and
and 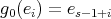 . If
. If 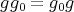 , then
, then 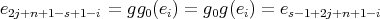 , so
, so  is divisible by
is divisible by  . Since
. Since 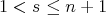 , we have that
, we have that 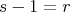 and in this case
and in this case 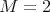 and
and 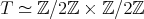 .
.Finally, from Theorem 2.2 and [16, (2.3)] we have the conclusions, that is
![Λ[G ] ≃ Λ [H ] *γ T](/img/revistas/ruma/v50n1/1a021251x.png) or
or ![∏s Λ[G ] ≃ Λ[H ] *γ T ≃ ( t=1Λ ) *γ T](/img/revistas/ruma/v50n1/1a021252x.png) .
. -
Let
 with
with 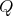 of type
of type  ,
, 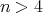 . Let
. Let  ,
, 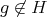 . We observe first that
. We observe first that 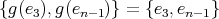 , see Proposition 2.1.
, see Proposition 2.1.Assume first that
 and
and 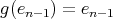 . Then
. Then  for all
for all 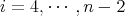 . Since
. Since  , we must have
, we must have  or
or 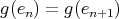 . This implies that
. This implies that 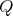 has symmetric orientation of kind
has symmetric orientation of kind 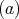 and all possible actions are given by:
and all possible actions are given by:-
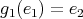 ,
, 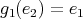 ,
, 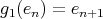 ,
, 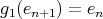 ;
; -
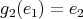 ,
, 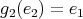 ,
, 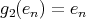 ,
,  ;
; -
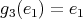 ,
, 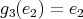 ,
, 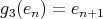 ,
, 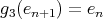 .
.
Since
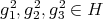 and
and  , we conclude that
, we conclude that 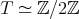 or
or  .
.Assume now that
 and
and 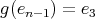 . Then, using the same argument as in the proof of Theorem 3.6 in the case of
. Then, using the same argument as in the proof of Theorem 3.6 in the case of 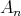 , we conclude that
, we conclude that 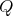 is symmetric of kind
is symmetric of kind  . If
. If 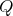 is not of kind
is not of kind 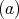 , the unique possible non trivial action on the complete set of idempotents is given by
, the unique possible non trivial action on the complete set of idempotents is given by 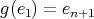 ,
, 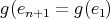 ,
, 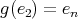 ,
,  and
and 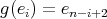 for all
for all  . In this case,
. In this case,  .
.To finish with this case, we have to assume that
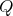 is symmetric of kind
is symmetric of kind  and
and 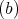 . Then all the possible non trivial actions are given by
. Then all the possible non trivial actions are given by-
 ,
,  ,
, 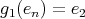 ,
, 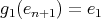 ,
, 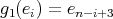 for all
for all  ;
; -
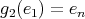 ,
, 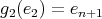 ,
, 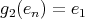 ,
,  ,
,  for all
for all 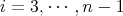 ;
; -
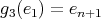 ,
, 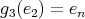 ,
, 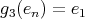 ,
, 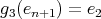 ,
,  for all
for all 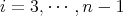 ;
; -
 ,
, 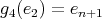 ,
, 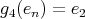 ,
,  ,
, 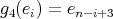 for all
for all  ;
; -
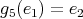 ,
,  ,
,  ,
, 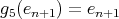 ,
, 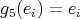 for all
for all  ;
; -
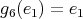 ,
,  ,
,  ,
, 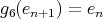 ,
, 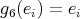 for all
for all  ;
; -
 ,
, 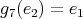 ,
, 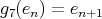 ,
,  ,
, 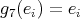 for all
for all  .
.
Now
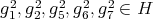 ,
, 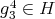 ,
,  and
and 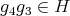 . Moreover, if
. Moreover, if  , then
, then 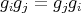 implies that
implies that 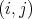 is equal to
is equal to 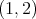 ,
,  ,
, 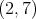 ,
,  ,
, 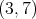 or
or  . Moreover
. Moreover  . Hence
. Hence 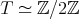 ,
, 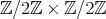 or
or  .
. -
-
Let
 with
with 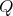 of type
of type 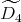 . Let
. Let 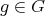 ,
, 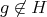 . Necessarily, by Proposition 2.1,
. Necessarily, by Proposition 2.1, 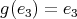 . If
. If  is symmetric of order
is symmetric of order  or
or  , the same reasoning made for
, the same reasoning made for  in the proof of Theorem 3.6 holds, and hence
in the proof of Theorem 3.6 holds, and hence  or
or 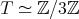 .
.If
 is symmetric of order
is symmetric of order  , assume that
, assume that 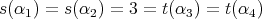 . Hence all the possible cases for
. Hence all the possible cases for 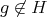 are:
are:-
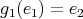 ,
, 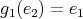 ,
, 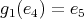 ,
, 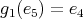 ;
; -
 ,
, 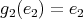 ,
, 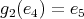 ,
, 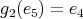 ;
; -
 ,
, 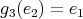 ,
,  ,
, 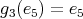 .
.
In fact
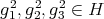 ,
,  and
and 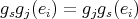 for all
for all 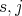 with
with 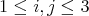 and for all
and for all  . Consequently
. Consequently 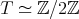 or
or 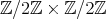 .
.If
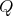 is symmetric of order
is symmetric of order 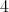 , all the possible cases for
, all the possible cases for 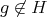 are in one to one correspondence with the non trivial permutations of
are in one to one correspondence with the non trivial permutations of 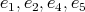 . Hence
. Hence  ,
,  ,
,  or
or 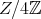 (all the possible abelian subgroups of
(all the possible abelian subgroups of  ).
). -
-
This case follows from an argument similar to what has been done in the proof of Theorem 3.6 for the case
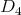 (for any
(for any 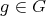 ,
, 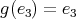 and the action of
and the action of  on
on  is uniquely determined by the action of
is uniquely determined by the action of 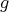 in
in  and
and  ).
). -
Let
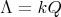 with
with  of type
of type 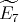 , and let
, and let 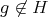 . By Proposition 2.1,
. By Proposition 2.1, 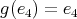 and then
and then 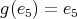 . Now
. Now 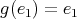 or
or  . In the first case we get that
. In the first case we get that 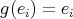 for all
for all 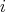 , and so
, and so  , a contradiction. Then
, a contradiction. Then  and this determines completely the orientation of the arrows, that is,
and this determines completely the orientation of the arrows, that is, 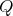 has symmetric orientation, and the action of
has symmetric orientation, and the action of 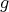 on the complete set of idempotents of
on the complete set of idempotents of  . Since
. Since 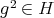 , we can deduce that
, we can deduce that 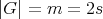 is an even number. Let
is an even number. Let 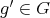 ,
,  . By the previous reasoning,
. By the previous reasoning,  and
and 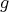 act in the unique possible way on the complete set of idempotents of
act in the unique possible way on the complete set of idempotents of 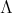 . Then
. Then 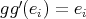 for all
for all  , hence
, hence 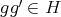 , that is,
, that is,  in
in  . So
. So 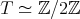 and
and ![∏ Λ [G] ≃ Λ [H ] * γ ℤ ∕2ℤ ≃ ( st=1 Λ) *γ ℤ ∕2ℤ](/img/revistas/ruma/v50n1/1a021444x.png) , see Theorem 2.2 and Theorem 2.8.
, see Theorem 2.2 and Theorem 2.8. -
If we consider the case
 of type
of type  , the unique possible action on the set of idempotents is the trivial one. Hence
, the unique possible action on the set of idempotents is the trivial one. Hence  ,
, 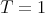 and the result follows from i).
and the result follows from i). 
Corollary 4.9. Let  be an hereditary algebra, with
be an hereditary algebra, with  of type
of type  (
(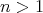 ),
), 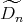 (
( ),
),  ,
, 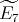 or
or 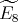 , and
, and 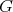 an abelian group of order
an abelian group of order 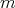 acting on
acting on  , with
, with  invertible in
invertible in  . Suppose that
. Suppose that 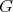 does not act trivially on the set
does not act trivially on the set  of idempotents of
of idempotents of 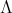 and
and 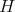 acts trivially on
acts trivially on  .
.
-
If
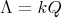 with
with 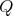 of type
of type  (
(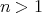 ) and
) and-
 is symmetric not cyclic,
is symmetric not cyclic, 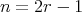 then
then ![Λ [G ] ≃ (∏m ∕2Λ )[ℤ ∕2ℤ ] t=1](/img/revistas/ruma/v50n1/1a021475x.png) or
or ![∏m ∕4 Λ [G ] ≃ ( t=1 Λ )[ℤ ∕2ℤ × ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021476x.png) ;
; -
 is cyclic of order
is cyclic of order  , not symmetric, then
, not symmetric, then ![∏ Λ [G ] ≃ ( m∕M Λ )[ℤ ∕M ℤ ] t=1](/img/revistas/ruma/v50n1/1a021479x.png) ;
;or
-
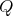 is symmetric and cyclic of order
is symmetric and cyclic of order 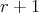 ,
,  , then
, then ![∏ Λ [G ] ≃ ( mt=∕12Λ )[ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021483x.png) or
or ![Λ [G ] ≃ (∏m ∕4Λ )[ℤ ∕2ℤ × ℤ ∕2ℤ ] t=1](/img/revistas/ruma/v50n1/1a021484x.png) .
.
-
-
If
 with
with  of type
of type 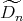 ,
, 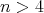 , and
, and-
 with symmetric orientation of kind
with symmetric orientation of kind  , not (a), then
, not (a), then
![Λ [G ] ≃](/img/revistas/ruma/v50n1/1a021491x.png)
![(∏m ∕2Λ )[ℤ ∕2ℤ] t=1](/img/revistas/ruma/v50n1/1a021492x.png) ,
, -
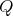 with symmetric orientation of kind
with symmetric orientation of kind 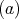 , not
, not 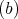 , then
, then ![∏m ∕2 Λ [G] ≃ ( t=1 Λ)[ℤ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021496x.png) or
or ![Λ [G ] ≃ (∏m ∕4Λ )[ℤ ∕2ℤ × ℤ ∕2ℤ ] t=1](/img/revistas/ruma/v50n1/1a021497x.png) ,
,or
-
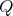 with symmetric orientation of kind
with symmetric orientation of kind  and (b) then
and (b) then
![∏ Λ [G ] ≃ ( mt=∕12Λ )[ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021500x.png) ,
, ![∏m ∕4 Λ [G ] ≃ ( t=1 Λ )[ℤ ∕2ℤ × ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021501x.png) or
or ![∏m ∕4 Λ [G ] ≃ ( t=1 Λ )[ℤ ∕4ℤ ]](/img/revistas/ruma/v50n1/1a021502x.png) .
.
-
-
If
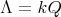 with
with  of type
of type  and
and-
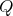 is symmetric of order
is symmetric of order 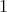 or
or  then
then ![∏m ∕2 Λ [G ] ≃ ( t=1 Λ )[ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021509x.png) or
or ![∏m ∕3 Λ [G] ≃ ( t=1 Λ)[ℤ∕3ℤ ]](/img/revistas/ruma/v50n1/1a021510x.png) ;
; -
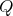 is symmetric of order
is symmetric of order  then
then ![Λ [G ] ≃ (∏m ∕2Λ )[ℤ ∕2ℤ] t=1](/img/revistas/ruma/v50n1/1a021513x.png) or
or ![∏m ∕4 Λ [G ] ≃ ( t=1 Λ )[ℤ ∕2ℤ × ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021514x.png) ;
;or
-
 is symmetric of order
is symmetric of order 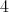 then
then ![∏m ∕2 Λ [G] ≃ ( t=1 Λ)[ℤ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021517x.png) ,
, ![∏m ∕3 Λ [G ] ≃ ( t=1 Λ )[ℤ ∕3ℤ ]](/img/revistas/ruma/v50n1/1a021518x.png) or
or ![Λ[G ] ≃ (∏m ∕4Λ )[ℤ ∕2ℤ × ℤ ∕2ℤ] t=1](/img/revistas/ruma/v50n1/1a021519x.png) ;
;
-
-
If
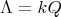 with
with 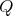 of type
of type  and
and-
 with symmetric orientation of kind (a) then
with symmetric orientation of kind (a) then ![Λ [G ] ≃ (∏m ∕2Λ )[ℤ ∕2ℤ ] t=1](/img/revistas/ruma/v50n1/1a021524x.png) or
or ![Λ [G] ≃ (∏m ∕3 Λ)[ℤ∕3ℤ ] t=1](/img/revistas/ruma/v50n1/1a021525x.png) ;
;or
-
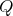 with symmetric orientation of kind (b) then
with symmetric orientation of kind (b) then ![Λ [G ] ≃ (∏m ∕2Λ )[ℤ ∕2ℤ ] t=1](/img/revistas/ruma/v50n1/1a021527x.png) ;
;
-
-
If
 with
with 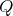 of type
of type  and
and  with symmetric orientation then
with symmetric orientation then ![∏m ∕2 Λ [G ] ≃ ( t=1 Λ )[ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021532x.png) .
.
Proof. It follows from Theorem 4.8 and Corollary 2.7. 
The following corollary follows easily from [16, (2.3), (2.4)].
Corollary 4.10. Let 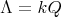 be an hereditary algebra, with
be an hereditary algebra, with  of type
of type  (
( ),
), 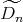 (
(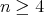 ),
),  ,
,  or
or  , and
, and 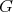 an cyclic group of order
an cyclic group of order  acting on
acting on 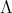 , with
, with  invertible in
invertible in 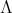 .
.
-
If
 with
with  of type
of type 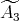 and
and 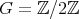 is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of 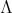 then the skew group algebra
then the skew group algebra ![Λ [ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021554x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra 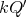 with
with  of type
of type  .
. -
If
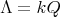 with
with 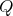 of type
of type 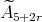 ,
, 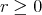 and
and 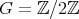 is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of 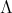 then the skew group algebra
then the skew group algebra ![Λ[ℤ ∕2ℤ]](/img/revistas/ruma/v50n1/1a021565x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra 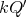 with
with 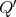 of type
of type 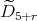 .
. -
If
 with
with 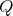 of type
of type 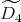 , and
, and  is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of  then the skew group algebra
then the skew group algebra ![Λ [ℤ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021575x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra  with
with 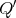 of type
of type  . If
. If  is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of  then the skew group algebra
then the skew group algebra ![Λ [ℤ∕3ℤ ]](/img/revistas/ruma/v50n1/1a021582x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra  with
with  of type
of type 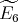 . If
. If 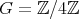 is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of 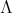 then the skew group algebra
then the skew group algebra ![Λ [ℤ ∕4ℤ ]](/img/revistas/ruma/v50n1/1a021589x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra 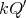 with
with 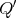 of type
of type 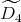 .
. -
If
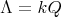 with
with 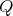 of type
of type  ,
,  and
and  is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of  and the action of
and the action of 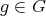 on
on  is induced by a reflection in the quiver, then the skew group algebra
is induced by a reflection in the quiver, then the skew group algebra ![Λ [ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021602x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra 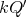 with
with  of type
of type  .
. -
If
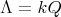 with
with  of type
of type 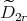 ,
, 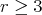 and
and 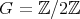 is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of 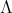 and the action of
and the action of  on
on 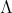 is induced by a reflection with respect the middle point
is induced by a reflection with respect the middle point  in the quiver,
in the quiver,-
if
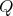 is of type
is of type  then the skew group algebra
then the skew group algebra ![Λ [ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021618x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra  with
with  of type
of type 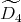 ;
; -
if
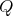 is of type
is of type 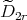 ,
,  then the skew group algebra
then the skew group algebra ![Λ [ℤ ∕2ℤ]](/img/revistas/ruma/v50n1/1a021625x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra  with
with  of type
of type 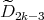 .
.
-
-
If
 with
with 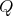 of type
of type 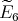 and
and  is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of  then the skew group algebra
then the skew group algebra ![Λ [ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021635x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra 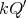 with
with 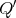 of type
of type 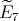 . If
. If 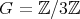 is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of 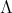 then the skew group algebra
then the skew group algebra ![Λ [ℤ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021642x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra  with
with  of type
of type 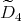 .
. -
If
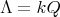 with
with 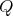 of type
of type  and
and 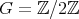 is acting non trivially on the set
is acting non trivially on the set  of idempotents of
of idempotents of 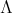 then the skew group algebra
then the skew group algebra ![Λ [ℤ ∕2ℤ ]](/img/revistas/ruma/v50n1/1a021652x.png) is Morita equivalent to an algebra
is Morita equivalent to an algebra 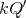 with
with  of type
of type  .
.
The case 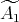 is not considered in Theorem 4.8 because the techniques we use do not hold in this case. In fact,
is not considered in Theorem 4.8 because the techniques we use do not hold in this case. In fact, 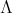 is the Kronecker algebra and Proposition 2.1 does not hold since this algebra has double arrows. Moreover, Theorem 2.8 cannot be applied because
is the Kronecker algebra and Proposition 2.1 does not hold since this algebra has double arrows. Moreover, Theorem 2.8 cannot be applied because 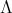 is not simply connected. We will only consider the case of a cyclic group acting on the Kronecker algebra, then it is possible to apply directly [16, (2.3)].
is not simply connected. We will only consider the case of a cyclic group acting on the Kronecker algebra, then it is possible to apply directly [16, (2.3)].
If 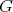 is a cyclic group acting on
is a cyclic group acting on 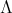 , the Kronecker algebra,
, the Kronecker algebra, 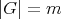 with
with  invertible in
invertible in 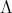 then all possible actions are given by:
then all possible actions are given by:

-
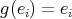 ,
, 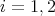 ,
, 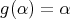 ,
,  and in this case the skew group algebra
and in this case the skew group algebra ![Λ[G ] ≃ (∏m Λ) t=1](/img/revistas/ruma/v50n1/1a021669x.png) . [16, (2.3)]
. [16, (2.3)] -
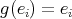 ,
, 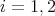 ,
, 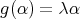 ,
, 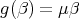 with
with  ,
, -
 ,
, 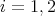 ,
, 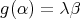 ,
,  with
with  , and in this case the skew group algebra
, and in this case the skew group algebra ![Λ[G ]](/img/revistas/ruma/v50n1/1a021687x.png) is hereditary of type
is hereditary of type 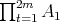 . [16, (2.3)]
. [16, (2.3)]
[1] M. Auslander, O. Goldman, The Brauer group of a commutative ring, Trans. Amer. Math. Soc. 97 (1960), 367-409. [ Links ]
[2] M. Auslander, I. Reiten and S. Smalø, Representation theory of Artin algebras, Cambridge Studies in Advanced Mathematics, vol. 36, Cambridge University Press, Cambridge, 1995. [ Links ]
[3] M. Auslander and D. Rim, Ramification index and multiplicity, Illinois J.Math. 7 (1963), 566-581. [ Links ]
[4] P. Donovan and M. Freislich, The representation theory of finite graphs and associated algebras, Carleton Lecture Notes 5, Ottawa, 1973. [ Links ]
[5] O. Funes and M.J. Redondo, Skew group algebras of simply connected algebras, Ann. Sci. Math. Québec 26 (2002), no.2, 171-180. [ Links ]
[6] P. Gabriel, Unzerlegbare Darstellungen I, Manuscripta Math. 6 (1972), 71-103. [ Links ]
[7] D. Haile, On crossed product algebras arising from weak cocycles, Journal of Algebra 74 (1982), 270-279. [ Links ]
[8] P. Hilton and U. Stammbach, A course in homological algebra, Graduate Texts in Mathematics, Vol. 4. Springer-Verlag, New York-Berlin, 1971. ix+338 pp. [ Links ]
[9] M. Lorenz and D. Passman, Two applications of Maschke's theorem, Comm. Algebra 8 (1980), 1853-1866. [ Links ]
[10] Y. Miyashita, On Galois extensions and crossed products, J. Fac. Sci. Hokkaido Univ. Ser. I 21 (1970), 97-121. [ Links ]
[11] S. Montgomery and D. Passman, Crossed products over prime rings, Israel J. Math. 31 (1978), no. 3-4, 224-256. [ Links ]
[12] L. Nazarova, Representations of quivers of infinite type, Izv. Akad. Nauk SSSR, Ser. Mat. 37 (1973) 752-791. [ Links ]
[13] D. Passman, It's essentially Maschke's theorem, Rocky Mountain J. Math. 13 (1983), 37-54. [ Links ]
[14] D. Passman, The algebraic structure of group rings, Pure and Applied Mathematics, Wiley-Interscience (John Wiley and Sons), New York-London-Sydney, 1977. xiv+720 pp. [ Links ]
[15] J.A. de la Peña, Automorfismos, álgebras torcidas y cubiertas, Ph.D. Thesis, 1983. [ Links ]
[16] I. Reiten and C. Riedtmann, Skew group algebras in the representation theory of Artin algebras, J. Algebra 92 (1985), 224-282. [ Links ]
[17] C. M. Ringel, The canonical algebras, Topics in algebra, Part 1, Banach Center Publ. 26 (Warsaw 1990), 407-432. [ Links ]
Olga Funes
Universidad Nacional de la Patagonia San Juan Bosco, Comodoro Rivadavia, Argentina.
funes@ing.unp.edu.ar
Recibido: 20 de octubre de 2006
Aceptado: 10 de marzo de 2008













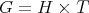 or
or 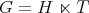 then
then ![Λ [G ] = Λ[H ][T ].](/img/revistas/ruma/v50n1/1a02360x.png)
![∏ Λ [G] ≃ Λ [H ] * γ T ≃ ( st=1 Λ) *γ T](/img/revistas/ruma/v50n1/1a021361x.png) .
.![∏ Λ [G] ≃ Λ [H ] * γ T ≃ ( st=1 Λ) *γ T](/img/revistas/ruma/v50n1/1a021407x.png) .
.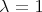 and
and 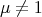 then the skew group algebra
then the skew group algebra ![Λ[G ]](/img/revistas/ruma/v50n1/1a021677x.png) is hereditary of type
is hereditary of type 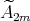 . [
. [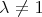 and
and 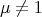 then the skew group algebra
then the skew group algebra ![∏ Λ [G ] ≃ mt=1 Λ](/img/revistas/ruma/v50n1/1a021681x.png) . [
. [
