Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932
Rev. Unión Mat. Argent. vol.50 no.1 Bahía Blanca June 2009
A Compact trace theorem for domains with external cusps
Carlos Zuppa
Abstract. This paper deals with the compact trace theorem in domains 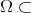
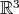 with external cusps. We show that if the power sharpness of the cusp is bellow a critical exponent, then the trace operator
with external cusps. We show that if the power sharpness of the cusp is bellow a critical exponent, then the trace operator  exists and it is compact.
exists and it is compact.
2000 Mathematics Subject Classification. 35J25,46E35
Key words and phrases. Cuspidal domains; Compact trace operator
Up to now, Lipschitz domains make up the most general class of domains where a rich function theory can be developed. However, domains with external cusps could appear at several branches of mathematics and applications. In obstacle problems, for example, the free boundary with external cusps may enter into corner points of the fixed boundary (e.g. [8]). Therefore, it is important to know what kind of results in the theory of Sobolev spaces remain valid in cuspidal domains.
Key tools in harmonic analysis and numerical application are the Rellich's theorem and the compact trace theorem. This paper deals with the compact trace theorem in domains 
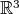 with external cusps. We show that if the power sharpness
with external cusps. We show that if the power sharpness  of the cusp is bellow a critical exponent
of the cusp is bellow a critical exponent  , then the trace operator
, then the trace operator 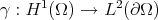 exists and it is compact. For cuspidal models in
exists and it is compact. For cuspidal models in 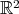 ,
,  (see [1]).
(see [1]).
Several classical results of harmonic analysis can be extended in this context, to begin with the divergence theorem, for example, or the characterization of the spaces 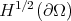 via the Steklov eigenfunction expansions [3, 4]. In several branch of harmonic analysis, the compacity of the operators
via the Steklov eigenfunction expansions [3, 4]. In several branch of harmonic analysis, the compacity of the operators  and
and  are key tools.
are key tools.
It is worth to remark here that certain classical counterexamples of analysis in cuspidal domains, like those of Friedrichs related to Korn inequality [5], have cusps of power sharpness equal to the critical exponent.
In [7] the authors characterize the traces of the Sobolev spaces  , by using some weighted norm on the boundary. In [1] a different kind of trace result was obtained by introducing a weighted Sobolev space in
, by using some weighted norm on the boundary. In [1] a different kind of trace result was obtained by introducing a weighted Sobolev space in  , such that the restriction to the boundary of functions in that space are in
, such that the restriction to the boundary of functions in that space are in 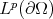 . We extended the arguments in this work to domains in
. We extended the arguments in this work to domains in 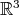 with some slight modification in the trace estimate, which is more useful in order to prove the compacity of the trace operator.
with some slight modification in the trace estimate, which is more useful in order to prove the compacity of the trace operator.
We shall consider a family of standard models or especial domains 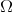 in
in  which have cusps of power sharpness
which have cusps of power sharpness  . We follow the standard notation for the Sobolev spaces
. We follow the standard notation for the Sobolev spaces 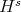 and Sobolev norms. For simplicity, we consider only the case
and Sobolev norms. For simplicity, we consider only the case 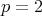 , and we do not consider other Sobolev spaces
, and we do not consider other Sobolev spaces 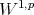 .
.
Definition 1. Let 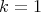 ,
,  . We shall say that
. We shall say that 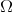 is a
is a  cusp if
cusp if
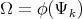 |
where the map 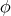 is defined by
is defined by
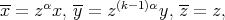 |
 |
and
 |
is a bounded connected region with Lipschitz boundary such that 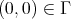 .
.
The Jacobian of the desingularizing map is 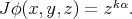
Trace theorems for domains with external cusps could be obtained in weighted Sobolev spaces [1]. For  , we define
, we define
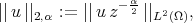 |
and we introduce the weighted Sobolev space 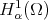 as the closure of
as the closure of 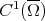 in the norm
in the norm
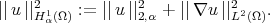 |
In what follows, we use the letter 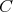 to denote a generic constant which depends only on
to denote a generic constant which depends only on  .
.
Theorem 2. Let 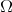 be a
be a 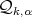 model. Then, there exists a constant
model. Then, there exists a constant  such that for any
such that for any  , the trace function
, the trace function 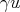 is in
is in 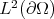 and
and
 | (1) |
The proof of this theorem will be given later in the last section. We shall first explore some consequences of this result.
Let 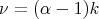 . In the next theorem we will make use of the inclusion
. In the next theorem we will make use of the inclusion
 | (2) |
which is a particular case of the results given in [2].
We can obtain the inclusion 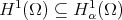 under appropriate assumptions on the values of
under appropriate assumptions on the values of  and
and 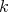 .
.
Definition 3. The 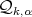 cusp
cusp 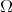 satisfies Condition A1 if
satisfies Condition A1 if
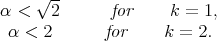 |
Theorem 4. If 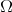 satisfies Condition A1, then
satisfies Condition A1, then 
Proof. We shall follow the arguments in [1]. By Hölder's inequality with an exponent 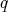 to be chosen below
to be chosen below
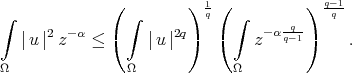 | (3) |
From (2), if  we have
we have
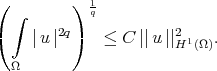 |
On the other hand, 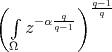 is bounded if
is bounded if  .
.
If  , we must take
, we must take  such that
such that
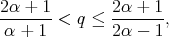 |
and this is possible only if 
For  , we have
, we have
 |
Hence,  .
.
Corollary 5. If 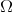 satisfies Condition A1, then the trace function
satisfies Condition A1, then the trace function  is in
is in 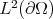 for any
for any 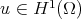 . Furthermore, the trace operator
. Furthermore, the trace operator 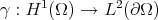 is compact.
is compact.
Proof. It only remains to show that  is compact. Then, let
is compact. Then, let  be a bounded sequence in
be a bounded sequence in  and, since we know that the inclusion
and, since we know that the inclusion 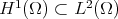 is compact [6], we can also assume that
is compact [6], we can also assume that  is a Cauchy sequence in
is a Cauchy sequence in  . We shall see now that
. We shall see now that  is a Cauchy sequence in the
is a Cauchy sequence in the  norm.
norm.
For 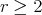 , let
, let  . By (3), we have
. By (3), we have
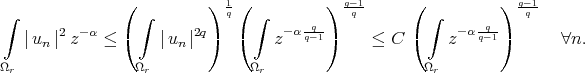 |
Since
 |
given  , we can chose
, we can chose  such that
such that
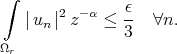 |
On the other hand,
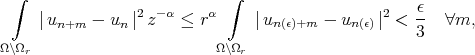 |
if 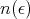 is chosen such that
is chosen such that
 |
Then,
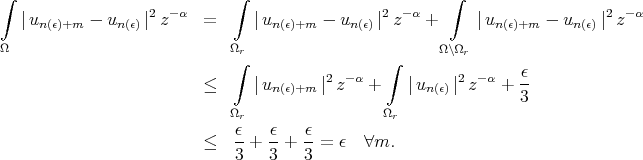
Now, the result follows easily by estimate (1).
Remark 6. In the bidimensional case, Theorem 4 for 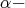 cups was obtained in [1]. The compacity of the trace operator follows by the same arguments given above. The key tool is estimate (1) in this appropriate form.
cups was obtained in [1]. The compacity of the trace operator follows by the same arguments given above. The key tool is estimate (1) in this appropriate form.
2. ALMOST LIPSCHITZ DOMAINS WITH EXTERNAL CUSPS
Let denote 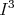 the open cube
the open cube  .
.
Definition 7. A bounded domain  satisfies Condition A2 if and only if:
satisfies Condition A2 if and only if:
(i) There exists a finite family of open subsets  of
of 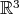 such that
such that  .
.
(ii) A Lipschitz diffeomorhism 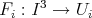
such that one of the two possibilities occurs:
(iii)  is the image of a standard cusp
is the image of a standard cusp 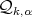 in
in 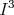 which satisfies Condition A1.
which satisfies Condition A1.
(iv) There exists a Lipschitz map 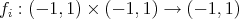 such that
such that  and
and
 |
When Condition A2 holds, there is an outward unit normal  defined at
defined at  a.e.point of
a.e.point of 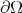 , where
, where  represents Hausdorff 2-dimensional measure and functions in
represents Hausdorff 2-dimensional measure and functions in 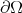 are integrated with respect to this measure . Furthermore, by a partition of unity argument we can obtain the following result.
are integrated with respect to this measure . Furthermore, by a partition of unity argument we can obtain the following result.
Theorem 8. Let  be a bounded domain which satisfies Condition A2. Then, the trace operator
be a bounded domain which satisfies Condition A2. Then, the trace operator  .
.
We proceed first with case  . Thus,
. Thus, 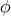 is defined by
is defined by
 |
and the Jacobian of 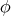 is
is  . Let
. Let 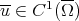 and
and 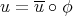 . Then,
. Then,
 |
On the other hand,
 |
and
 |
Now, let 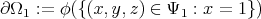 . Then,
. Then,  is parametrized by
is parametrized by
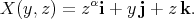 |
Thus,
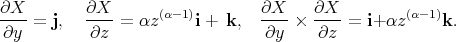 |
and it follows that
 |
Let ![ω : [- 1,1] → ℝ +](/img/revistas/ruma/v50n1/1a03132x.png) be a
be a  function such that
function such that 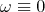 in
in ![[- 1,0]](/img/revistas/ruma/v50n1/1a03135x.png) and
and  in
in ![[0,1]](/img/revistas/ruma/v50n1/1a03137x.png) , and define
, and define 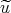 by
by 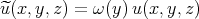 .
.
Setting
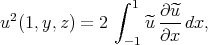 |
by Hölder's inequality we have
 |
Now, it is clear that  . On the other hand,
. On the other hand,
 |
From this, we can easily obtain that
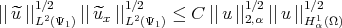 |
and the result follows. The proof for  is the same.
is the same.
Case 
We shall explain the main arguments for the curve  . It will be clear from the proof that the general case follows along the same lines via a partition of unity.
. It will be clear from the proof that the general case follows along the same lines via a partition of unity.
We consider 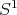 parametrized by
parametrized by 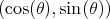 and the parametrization
and the parametrization ![X : [0,2π] × [0, 1] →](/img/revistas/ruma/v50n1/1a03150x.png)
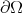 given by
given by
 |
It follows that
 |
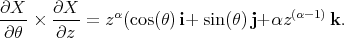 |
Thus,
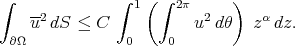 |
For 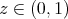 , we want now to estimate
, we want now to estimate  with the same arguments as above. We introduce polar coordinates in
with the same arguments as above. We introduce polar coordinates in  and we define
and we define
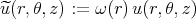 |
where ![ω ∈ C1 [0,1 ]](/img/revistas/ruma/v50n1/1a03160x.png) such that
such that  for
for  and
and  for
for  .
.
Thus,

First, we have
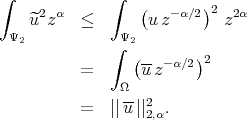
To complete the proof, we must take into account that
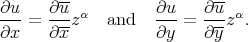 |
Then, calculating for the first derivative, we get
 |
Hence,
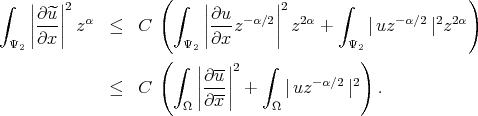
The same inequality is valid for the second derivative and we get
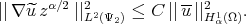 |
Considering these facts together, it is easy to see that we have concluded the proof of the theorem.
[1] G. Acosta, M. G. Armentano, R. G. Durán, and A. L. Lombardi, Finite Element Approximations in a NonLipschitz Domain. SIAM J. Numer. Anal. 45 (2007), 277-295 [ Links ]
[2] R. A. Adams, Sobolev Spaces, Academic Press, New York, 1975. [ Links ]
[3] G. Auchmuty, Steklov Eigenproblems and the Representation of Solutions of Elliptic Boundary Value Problems, Num. Functional Analysis and Optimization, 25, (2004), 321-348. [ Links ]
[4] G. Auchmuty, Spectral Characterization of the Trace Spaces 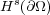 , SIAM J of Math. Anal. 38/3, (2006), 894-905. [ Links ]
, SIAM J of Math. Anal. 38/3, (2006), 894-905. [ Links ]
[5] K. O. Friedrichs, On certain inequalities and characteristic value problems for analytic functions and for functions of two variables, Trans. Amer. Math. Soc. 41, 321-364, 1937. [ Links ]
[6] V. G. Maz'ja, Sobolev Spaces, Springer Verlag, New York, 1980. [ Links ]
[7] V. G. Maz'ja, Yu. V. Netrusov and V. Poborchi, Boundary values of functions in Sobolev Spaces on certain non-lipschitzian domains, St. Petersburg Math. J. 11, 107-128, 2000. [ Links ]
[8] H. Shahgholian, When does the free boundary enter into corner points of the fixed boundary?, J. Math. Sci. 132, No. 3, 371-377, 2006. [ Links ]
Carlos Zuppa
Departamento de Matemáticas
Universidad Nacional de San Luis
Chacabuco 985, San Luis. 5700. Argentina
zuppa@unsl.edu.ar
Recibido: 13 de noviembre de 2006
Aceptado: 3 de octubre de 2008













 MODELS.
MODELS.
