Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932
Rev. Unión Mat. Argent. vol.50 no.1 Bahía Blanca jun. 2009
The subvariety of Q-Heyting algebras generated by chains
Laura A. Rueda
Abstract. The variety 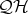 of Heyting algebras with a quantifier [14] corresponds to the algebraic study of the modal intuitionistic propositional calculus without the necessity operator. This paper is concerned with the subvariety
of Heyting algebras with a quantifier [14] corresponds to the algebraic study of the modal intuitionistic propositional calculus without the necessity operator. This paper is concerned with the subvariety  of
of 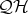 generated by chains. We prove that this subvariety is characterized within
generated by chains. We prove that this subvariety is characterized within 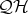 by the equations
by the equations 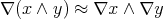 and
and 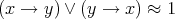 . We investigate free objects in
. We investigate free objects in 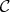 .
.
1. Introduction and Preliminaries
Distributive lattices with a quantifier were considered as algebras for the first time by Cignoli in [7] who studied them under the name of  -distributive lattices. A
-distributive lattices. A  -distributive lattice is an algebra
-distributive lattice is an algebra  of type
of type  such that
such that 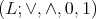 is a bounded distributive lattice and the unary operation
is a bounded distributive lattice and the unary operation 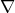 satisfies the following conditions, for any
satisfies the following conditions, for any  ,
, 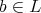 :
:  ,
, 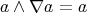 ,
, 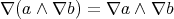 and
and 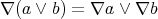 . These conditions were introduced by Halmos [9] as an algebraic counterpart of the logical notion of an existential quantifier.
. These conditions were introduced by Halmos [9] as an algebraic counterpart of the logical notion of an existential quantifier.
Various further investigations have been carried out since [7] (see R. Cignoli [8], H. Priestley [13], M. Adams and W. Dziobiak [4], M. Abad and J. P. Díaz Varela [2] and A. Petrovich [11]). As a natural generalization, the operation of quantification was considered for Heyting algebras in [3] and [15]. A Heyting algebra is an algebra 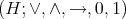 of type
of type 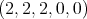 for which
for which 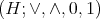 is a bounded distributive lattice and for
is a bounded distributive lattice and for  ,
,  ,
,  is the relative pseudocomplement of
is the relative pseudocomplement of  with respect to
with respect to  , i.e.,
, i.e., 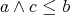 if and only if
if and only if 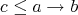 . It is known that the class of Heyting algebras forms a variety. An important subvariety of Heyting algebras is the class of linear Heyting algebras [5]. A linear Heyting algebra is a Heyting algebra that satisfies the equation
. It is known that the class of Heyting algebras forms a variety. An important subvariety of Heyting algebras is the class of linear Heyting algebras [5]. A linear Heyting algebra is a Heyting algebra that satisfies the equation 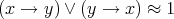 . Throughout this paper
. Throughout this paper 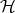 will denote the category of Heyting algebras and Heyting algebra homomorphisms and
will denote the category of Heyting algebras and Heyting algebra homomorphisms and 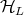 will denote the subcategory of linear Heyting algebras.
will denote the subcategory of linear Heyting algebras.
A 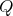 -Heyting algebra is an algebra
-Heyting algebra is an algebra  such that
such that 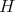 is an object of
is an object of 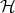 and
and  is a quantifier on
is a quantifier on 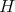 , that is,
, that is, 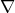 is a unary operation defined as for
is a unary operation defined as for 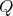 -distributive lattices. Monadic Boolean algebras are the simplest examples of
-distributive lattices. Monadic Boolean algebras are the simplest examples of 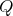 -Heyting algebras. The class of
-Heyting algebras. The class of 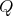 -Heyting algebras forms a variety, which we denote
-Heyting algebras forms a variety, which we denote 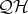 . The subvariety of
. The subvariety of 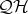 characterized within
characterized within  by the equation
by the equation  , that is, the subvariety of linear
, that is, the subvariety of linear  -Heyting algebras will be denoted by
-Heyting algebras will be denoted by 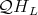 .
.  -Heyting algebras were first introduced in [14] and have been investigated in [14, 15, 3].
-Heyting algebras were first introduced in [14] and have been investigated in [14, 15, 3].
In this paper we investigate the subvariety 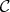 of the variety of
of the variety of 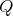 -Heyting algebras generated by chains. We characterize
-Heyting algebras generated by chains. We characterize  by identities in Section 2 and we investigate free objects in this variety in Section 3.
by identities in Section 2 and we investigate free objects in this variety in Section 3.
We will usually use the same notation for a variety and for the algebraic category associated with it. And, similarly we will use the same notation for a structure and for its universe.
Recall that Heyting algebras are algebraic models of the intuitionistic propositional logic and that the study of extensions of Intuitionistic Propositional Calculus (IPC) reduces to the study of subvarieties of the variety 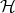 . The language of intuitionistic modal logic (MIPC) is the language of IPC enriched with two modal unary operators of necessity
. The language of intuitionistic modal logic (MIPC) is the language of IPC enriched with two modal unary operators of necessity  and of posibility
and of posibility 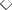 . The algebraic models of MIPC are the monadic Heyting algebras.
. The algebraic models of MIPC are the monadic Heyting algebras.
Now, in MIPC the operators  and
and  are independent from each other, that is
are independent from each other, that is  and
and 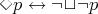 are not theorems in MIPC. Hence, the set of theorems of the propositional calculus without of the necessity operator
are not theorems in MIPC. Hence, the set of theorems of the propositional calculus without of the necessity operator  , called the
, called the  -free fragment of MIPC is different from that of MIPC. Similarly, the set of theorems of the propositional calculus without of the possibility operator
-free fragment of MIPC is different from that of MIPC. Similarly, the set of theorems of the propositional calculus without of the possibility operator 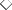 , called the
, called the 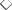 -free fragment of MIPC is different from that of MIPC.
-free fragment of MIPC is different from that of MIPC.
It turns out that the behaviour of the  -free fragment of MIPC is very much similar to that of MIPC. However, surprisingly enough, the
-free fragment of MIPC is very much similar to that of MIPC. However, surprisingly enough, the  -free fragment of MIPC behaves pretty diferent from MIPC.
-free fragment of MIPC behaves pretty diferent from MIPC.
 -Heyting algebras are the algebraic models of the
-Heyting algebras are the algebraic models of the  -free fragment of MIPC, that is,
-free fragment of MIPC, that is, 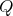 -Heyting algebras are the
-Heyting algebras are the  -free reducts of monadic Heyting algebras.
-free reducts of monadic Heyting algebras.
For a poset  and
and  , let
, let ![(Y] = {u : u ≤ v for some v ∈ Y }](/img/revistas/ruma/v50n1/1a0672x.png) and
and  . We write
. We write 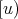 ,
, ![(u]](/img/revistas/ruma/v50n1/1a0675x.png) instead of
instead of 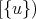 ,
, ![({u} ]](/img/revistas/ruma/v50n1/1a0677x.png) respectively. We say that
respectively. We say that  is decreasing if
is decreasing if ![Y = (Y ]](/img/revistas/ruma/v50n1/1a0679x.png) , increasing if
, increasing if  and convex if
and convex if ![Y = (Y ] ∩ [Y )](/img/revistas/ruma/v50n1/1a0681x.png) . A mapping
. A mapping  is order preserving if
is order preserving if 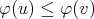 whenever
whenever 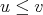 .
.
In order to describe the dual category of  we recall that a Priestley space is a triple
we recall that a Priestley space is a triple 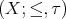 such that
such that 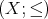 is a partially ordered set,
is a partially ordered set, 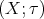 is a compact topological space, and the triple is totally order-disconnected (that is, for
is a compact topological space, and the triple is totally order-disconnected (that is, for  ,
, 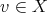 , if
, if  then there exists a clopen increasing
then there exists a clopen increasing  such that
such that  and
and  ). Priestley showed that the category of bounded distributive lattices and lattice homomorphisms is dually equivalent to the category of Priestley spaces and order preserving continuous functions (see the survey paper [12]).
). Priestley showed that the category of bounded distributive lattices and lattice homomorphisms is dually equivalent to the category of Priestley spaces and order preserving continuous functions (see the survey paper [12]).
A 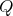 -Heyting space
-Heyting space 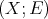 (see [7, 14, 15]) is a Priestley space
(see [7, 14, 15]) is a Priestley space 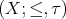 together with an equivalence relation
together with an equivalence relation  defined on
defined on 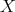 such that
such that 
![(Y ]](/img/revistas/ruma/v50n1/1a06101x.png) is clopen for every convex clopen
is clopen for every convex clopen 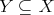 ,
, 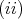
 for each
for each 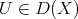 , where
, where 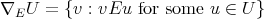 and
and 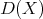 is the lattice of clopen increasing subsets of
is the lattice of clopen increasing subsets of 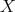 , and
, and 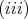 the blocks of
the blocks of 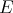 are closed in
are closed in  . For
. For  , let
, let 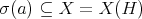 denote the clopen increasing set that represents
denote the clopen increasing set that represents  , where
, where 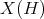 is the set of prime filters of
is the set of prime filters of  , ordered by set inclusion and with the topology having as a sub-basis the sets
, ordered by set inclusion and with the topology having as a sub-basis the sets  and
and 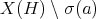 for
for 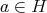 . If
. If 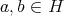 then, under the duality,
then, under the duality, 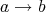 corresponds to the clopen increasing set
corresponds to the clopen increasing set ![X \ (σ (a ) \ σ(b)]](/img/revistas/ruma/v50n1/1a06122x.png) .
.
For  -Heyting spaces
-Heyting spaces 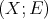 and
and  , a
, a 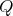 -Heyting morphism is a continuous order-preserving mapping
-Heyting morphism is a continuous order-preserving mapping 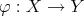 such that
such that 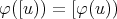 and
and 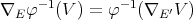 , for each
, for each  .
.
It can be proved in the usual way that the category of 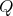 -Heyting algebras and homomorphisms is dually equivalent to the category of
-Heyting algebras and homomorphisms is dually equivalent to the category of  -Heyting spaces and
-Heyting spaces and 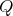 -Heyting morphisms [14, 15]. For each
-Heyting morphisms [14, 15]. For each 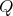 -Heyting algebra
-Heyting algebra 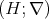 the corresponding
the corresponding  -Heyting space is
-Heyting space is  , where
, where  . Conversely, if
. Conversely, if 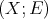 is a
is a  -Heyting space, the corresponding
-Heyting space, the corresponding  -Heyting algebra is
-Heyting algebra is  , where
, where 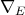 is defined as in
is defined as in  .
.
In this section we will study the subvariety 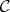 generated by chains within
generated by chains within 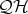 . Observe that if
. Observe that if 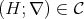 , then
, then 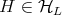 , that is,
, that is, 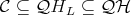 . Consequently,
. Consequently, 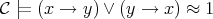 .
.
Recall that in the variety of Heyting algebras, congruences are determined by filters. Precisely, if 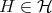 and
and  is a filter of
is a filter of  , then
, then 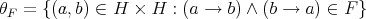 is a congruence on
is a congruence on 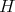 , and the correspondence
, and the correspondence 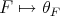 establishes an isomorphism from the lattice of filters of
establishes an isomorphism from the lattice of filters of 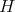 on
on  , the lattice of congruences of
, the lattice of congruences of  . If
. If 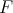 is generated by an element
is generated by an element  ,
, 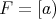 , we write
, we write 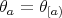 .
.
Observe that if 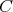 is a Heyting chain and
is a Heyting chain and 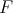 is a filter of
is a filter of 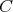 ,
,  if and only if
if and only if  or
or 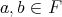 . Then,
. Then, 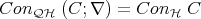 . As a consequence of this, we have that if
. As a consequence of this, we have that if 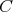 is a chain,
is a chain, 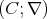 is a subdirectly irreducible algebra in
is a subdirectly irreducible algebra in 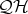 if and only if
if and only if 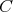 is a subdirectly irreducible algebra in
is a subdirectly irreducible algebra in  , that is,
, that is,  has a unique dual atom.
has a unique dual atom.
A quantifier  on an algebra
on an algebra  is said to be multiplicative if
is said to be multiplicative if 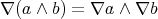 , for every
, for every 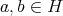 .
.
Let 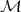 be the subvariety of
be the subvariety of 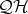 characterized by the equation
characterized by the equation  .
.
Proof Let 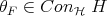 and
and 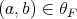 , i.e.,
, i.e., 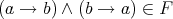 . As
. As  , then
, then 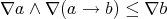 , that is,
, that is,  . So
. So 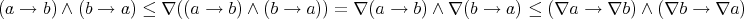 . Thus
. Thus 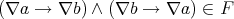 , so
, so  . Therefore,
. Therefore, 
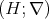 .
. 
Observe that 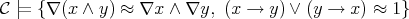 , that is,
, that is,  . Let us see that
. Let us see that  .
.
Lemma 2.2. Let 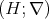 be a subdirectly irreducible algebra in
be a subdirectly irreducible algebra in  . Then
. Then 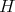 is a chain.
is a chain.
Proof Let  be a subdirectly irreducible algebra. Then
be a subdirectly irreducible algebra. Then  and hence
and hence 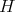 is subdirectly irreducible in
is subdirectly irreducible in 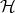 , that is,
, that is, 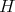 has a unique dual atom. Since for every
has a unique dual atom. Since for every 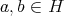 ,
, 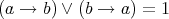 , then
, then 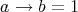 or
or 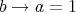 , that is,
, that is, 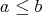 or
or 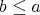 . So
. So 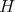 is a chain.
is a chain. 
As a consequence of this corollary we have that 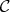 is characterized within
is characterized within 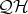 by the identities
by the identities 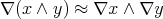 and
and 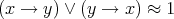 .
.
The following theorem characterizes the dual space of an algebra in 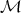 .
.
Theorem 2.4. Let 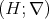 be a
be a 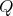 -Heyting algebra, let
-Heyting algebra, let 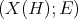 be the associated
be the associated 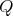 -Heyting space and
-Heyting space and 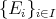 the partition of
the partition of  determined by
determined by 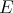 . Then,
. Then,  if and only if each
if and only if each  has exactly one maximal element.
has exactly one maximal element.
Proof Suppose that 
 and there exists
and there exists  such that
such that  has two maximal elements
has two maximal elements 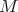 ,
, 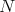 ,
, 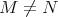 . Let
. Let  be such that
be such that 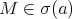 and
and  . For each
. For each 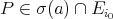 , we have that
, we have that 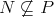 . Thus there exists
. Thus there exists  such that
such that  and
and  . Consequently
. Consequently

As 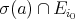 is closed, by a compacteness argument
is closed, by a compacteness argument
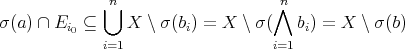
and 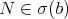 . So
. So  and
and 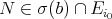 . This implies that
. This implies that 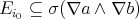 and consequently
and consequently 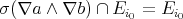 . On the other hand,
. On the other hand, 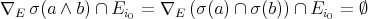 , which contradicts that
, which contradicts that 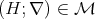 .
.
Conversely, we know that 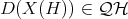 . Let us see that
. Let us see that 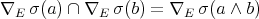 . Since
. Since  is a quantifier,
is a quantifier, 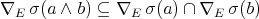 . Let us prove the other inclusion. Let
. Let us prove the other inclusion. Let 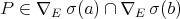 and
and  such that
such that 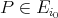 . Since
. Since 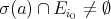 and
and 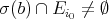 , if
, if  , then
, then 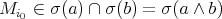 . Therefore
. Therefore  and so
and so 

Lemma 2.5. 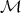 is the greatest subvariety of
is the greatest subvariety of 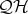 such that every filter determines a congruence.
such that every filter determines a congruence.
Proof Let  such that
such that 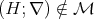 . We are going to construct a filter in
. We are going to construct a filter in  which does not determine a congruence. From
which does not determine a congruence. From  , there exist
, there exist 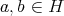 such that
such that  . Then there exists a prime ideal
. Then there exists a prime ideal 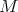 such that
such that  and
and 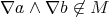 . Since
. Since  is an ideal we have that
is an ideal we have that 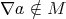 and
and 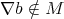 . Consider the filter
. Consider the filter 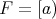 . Then
. Then  , being that
, being that 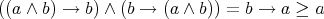 . Let us see that
. Let us see that  . Suppose on the contrary that
. Suppose on the contrary that 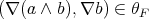 . Thus
. Thus 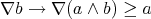 , which implies that
, which implies that  (*) since the image of
(*) since the image of 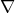 is closed under implication. On the other hand,
is closed under implication. On the other hand,  , so
, so  . Since
. Since 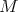 is a prime ideal and
is a prime ideal and 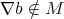 we have that
we have that  . This, together with (*), implies that
. This, together with (*), implies that  , which is a contradiction.
, which is a contradiction. 
In this section we characterize the free algebra in  with
with  generators. Following a path analogous to that of M. Abad and L. Monteiro in [1], we will provide a method to construct the order set
generators. Following a path analogous to that of M. Abad and L. Monteiro in [1], we will provide a method to construct the order set 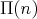 of all join-irreducible elements of the free algebra, and as a consequence, we will obtain a formula to compute
of all join-irreducible elements of the free algebra, and as a consequence, we will obtain a formula to compute 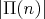 .
.
It is clear that for any subset 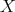 of a chain
of a chain 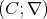 , the subalgebra of
, the subalgebra of 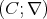 generated by
generated by 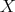 is
is 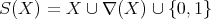 . Thus, every
. Thus, every  -generated subalgebra of a chain of
-generated subalgebra of a chain of 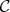 has at most
has at most  elements, that is, the class of all chains in
elements, that is, the class of all chains in  is uniformly locally finite. So
is uniformly locally finite. So 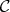 is generated by a uniformly locally finite class, and consequently,
is generated by a uniformly locally finite class, and consequently,  is a variety locally finite [6, Theorem 3.7].
is a variety locally finite [6, Theorem 3.7].
If 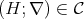 is a finite algebra, the
is a finite algebra, the 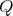 -Heyting space
-Heyting space 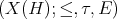 has the discrete topology and
has the discrete topology and  is anti-isomorphic to the ordered set
is anti-isomorphic to the ordered set 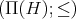 of join-irreducible elements of
of join-irreducible elements of  . In this section we will use the set
. In this section we will use the set 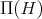 instead of
instead of  and we will consider the relation
and we will consider the relation 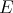 defined on
defined on  , that is we consider
, that is we consider 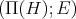 . If
. If  is the partition determined by
is the partition determined by 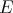 in
in 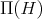 , we say that
, we say that 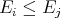 if and only if
if and only if  . This is an order relation.
. This is an order relation.
Theorem 3.1. [10] A Heyting algebra is linear if and only if the family of prime filters which contain a prime filter is a chain.
Definition 3.2. Let 
 be a finite algebra. Let
be a finite algebra. Let 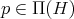 and let
and let 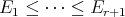 , such that
, such that ![(p] ∩ Ej ⁄= ∅](/img/revistas/ruma/v50n1/1a06337x.png) ,
,  , where
, where ![(p] = {q ∈ Π(H ) : q ≤ p}](/img/revistas/ruma/v50n1/1a06339x.png) . We say that
. We say that 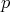 has coordinates
has coordinates  , if the chain
, if the chain ![(p]](/img/revistas/ruma/v50n1/1a06342x.png) is of length
is of length 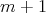 and if
and if ![mj = |(p] ∩ Ej|](/img/revistas/ruma/v50n1/1a06344x.png) ,
,  .
.
Notice that the set ![(p]](/img/revistas/ruma/v50n1/1a06346x.png) of the previous definition is considered within
of the previous definition is considered within 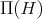 .
.
Let  be a non negative integer. Let
be a non negative integer. Let  be the chain with
be the chain with  elements. Let
elements. Let 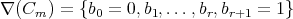 ,
, 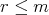 , with
, with 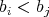 for
for 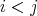 . Let
. Let ![(bi,bj]](/img/revistas/ruma/v50n1/1a06355x.png) be the interval in
be the interval in 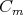 consisting of the elements
consisting of the elements 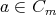 such that
such that  . We denote
. We denote 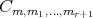 the algebra
the algebra 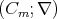 , where
, where ![mi = |(bi- 1,bi]|](/img/revistas/ruma/v50n1/1a06361x.png) ,
,  .
.
Observe that if  ,
, 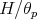 is a chain. More precisely,
is a chain. More precisely, ![(p]](/img/revistas/ruma/v50n1/1a06365x.png) is of length
is of length  if and only if
if and only if  is a chain with
is a chain with 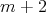 elements [1, p. 7]. If
elements [1, p. 7]. If 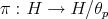 is the natural homomorphism and
is the natural homomorphism and 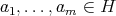 are such that
are such that  , then there exist join-irreducible elements
, then there exist join-irreducible elements  in
in  such that
such that  and
and  ,
, 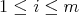 . Moreover, taking into account that
. Moreover, taking into account that 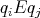 en
en 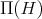 if and only if
if and only if 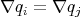 en
en  , it follows that
, it follows that  has coordinates
has coordinates  ,
, 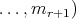 if and only if
if and only if 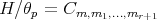 . Since
. Since 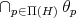 is the trivial relation, we have that
is the trivial relation, we have that 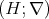 is a subdirect product of the chains
is a subdirect product of the chains  .
.
Let  be the free
be the free  -algebra with a finite set of generators of cardinal
-algebra with a finite set of generators of cardinal 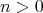 . For the sake of simplicity we will write
. For the sake of simplicity we will write 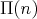 instead of
instead of  .
.
We know that every  -generated subalgebra of a chain of
-generated subalgebra of a chain of 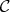 has at most
has at most  elements. Since
elements. Since  is a chain generated by at most
is a chain generated by at most 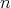 elements, we have the following
elements, we have the following
If 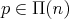 then from Lemma 3.3,
then from Lemma 3.3, 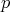 has coordinates
has coordinates  , for some
, for some 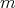 ,
,  and
and  such that
such that 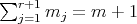 .
.
Consider the following sets:
![M1 = {bj : |(bj- 1,bj]| = 1,1 ≤ j ≤ r}](/img/revistas/ruma/v50n1/1a06407x.png)
and
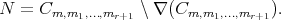
For a subset  of
of  to generate the algebra
to generate the algebra  , every non constant element must be contained in
, every non constant element must be contained in 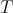 , that is,
, that is,  . Besides, every constant can be obtained from
. Besides, every constant can be obtained from  , except the constants of
, except the constants of  . So we have that
. So we have that  and consequently,
and consequently, 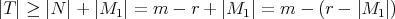 .
.
For every  ,
, 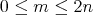 , consider the sets
, consider the sets
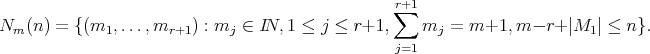
We will denote  instead of
instead of 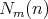 . Observe that
. Observe that 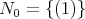 ,
, 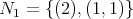 and
and 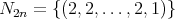 for every
for every  , that is,
, that is,  consists of one
consists of one 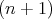 -tuple whose
-tuple whose  first coordinates are equal to 2. Moreover, if
first coordinates are equal to 2. Moreover, if 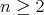 , we have that
, we have that 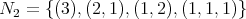 , but if
, but if  ,
,  .
.
Let 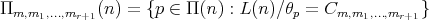 . It is clear that
. It is clear that

and that 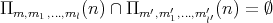 for
for 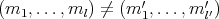 .
.
Let  be the set of all functions
be the set of all functions 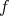 from the set
from the set 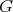 of free generators of
of free generators of 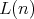 into
into 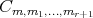 such that
such that  . Observe that every
. Observe that every  is nonempty, as
is nonempty, as  if and only if
if and only if 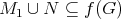 , that is
, that is  .
.
Recall that a filter  in a finite Heyting algebra is prime if and only if
in a finite Heyting algebra is prime if and only if 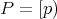 , where
, where 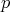 is join-irreducible element.
is join-irreducible element.
If 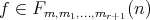 ,
,  can be extended to a unique homomorphism
can be extended to a unique homomorphism 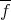 from
from  onto
onto 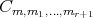 . If
. If  is the kernel of
is the kernel of 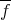 , it is well known that
, it is well known that 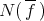 is a prime filter in
is a prime filter in  , so
, so 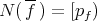 , with
, with  . Thus, for each
. Thus, for each 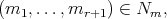
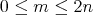 , we have a function
, we have a function
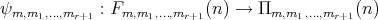
defined by 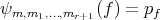 .
.
Lemma 3.4. The following holds 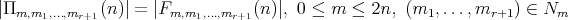 .
.
Proof Let us see that 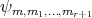 is onto. For
is onto. For 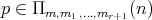 , consider
, consider 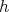 the natural homomorphism from
the natural homomorphism from 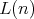 onto
onto 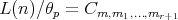 , and
, and 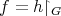 the restriction of
the restriction of 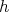 to
to 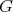 . Then
. Then  and therefore
and therefore 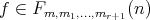 . Let
. Let 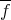 be the extension of
be the extension of 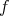 . Since
. Since  , then
, then 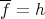 and therefore
and therefore 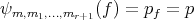 .
.
Let us prove that the function  , is one-to-one. If the functions
, is one-to-one. If the functions 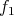 ,
, 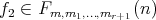 satisfy
satisfy 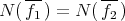 then there is an automorphism
then there is an automorphism  of
of 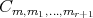 such that
such that  . But the only automorphism of
. But the only automorphism of 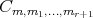 is the identity, then
is the identity, then 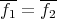 and then
and then  .
. 
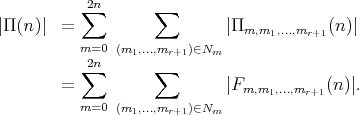
If 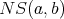 is the number of functions from a set with
is the number of functions from a set with  elements onto a set with
elements onto a set with  elements, then:
elements, then:

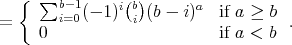
Let 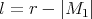 . Then, for each
. Then, for each 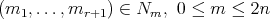 ,
,
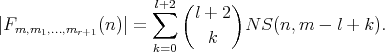
In particular, for  ,
,  and then
and then 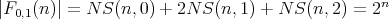 . For
. For  ,
, 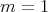 ,
,  and for
and for  ,
,  . So in both cases,
. So in both cases, 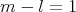 , then
, then  . And for
. And for  ,
, 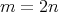 ,
,  ,
,  , then
, then 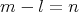 and
and 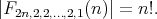
Consequently,

Consider the set
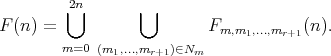
If 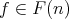 , there is a unique
, there is a unique  and a unique
and a unique 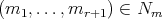 such that
such that 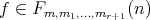 . If we put
. If we put 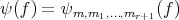 we have a one-to-one mapping from
we have a one-to-one mapping from 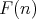 onto
onto  .
.
The following lemma is immediate (recall that ![(pf] = {q ∈ Π (n ) : q ≤ pf}](/img/revistas/ruma/v50n1/1a06527x.png) ).
).
Lemma 3.6.  has coordinates
has coordinates  if and only if
if and only if 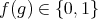 for all
for all  .
.
As a consequence, the set  has
has 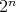 minimal elements.
minimal elements.
Lemma 3.7. For 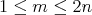 , and
, and 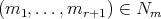 ,
, 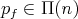 has coordinates
has coordinates  if and only if
if and only if  .
.
Proof From the proof of Lemma 3.4, 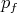 has coordinates
has coordinates  if and only if
if and only if  , and from the comment preceding that lemma, this is equivalent to
, and from the comment preceding that lemma, this is equivalent to 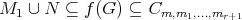 .
. 
Remark 3.8. We know that if 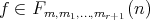 , the extension homomorphism
, the extension homomorphism 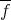 and the natural homomorphism
and the natural homomorphism  from
from 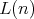 into
into 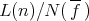 satisfy
satisfy  . Then if in
. Then if in 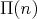 ,
, ![(pf] = {p1,...,pm, pm+1 = pf }](/img/revistas/ruma/v50n1/1a06551x.png) , we have
, we have
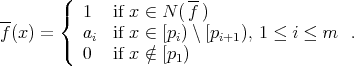
The proof of the following lemma will be omitted since it is an adaptation of that of [1, Lemma 3.13].
We say 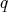 covers
covers 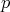 if
if  and
and 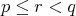 implies
implies 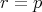 .
.
Lemma 3.9. If  ,
, 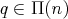 ,
,  covers
covers 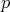 if and only if the following conditions hold:
if and only if the following conditions hold:
-
(i)
 ,
, -
(ii)
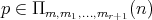 ,
, 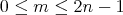 ,
, 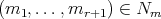 .
. -
(iii)
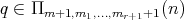 or
or 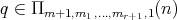 ,
, 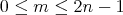 ,
, 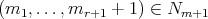 and
and  .
.
In the following theorem we denote 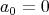 .
.
Theorem 3.10. Let 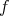 ,
, 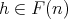 . Then
. Then 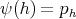 covers
covers 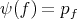 if and only if
if and only if 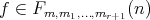 ,
, 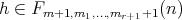 or
or  ,
,  ,
,  , and for
, and for 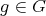 the following conditions hold:
the following conditions hold:
-
(I)
 if and only if
if and only if  ,
, 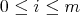 .
. -
(II)
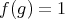 if and only if
if and only if 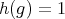 or
or 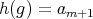 .
.
Proof Suppose that 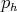 covers
covers 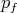 . The first part of the theorem is an immediate consequence of Lemma 3.9
. The first part of the theorem is an immediate consequence of Lemma 3.9
Since in  ,
,  , we have
, we have
 if and only if
if and only if 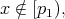
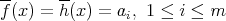 if and only if
if and only if 
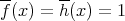 if and only if
if and only if 
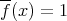 and
and  if and only if
if and only if 
In particular, we have the conditions 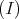 and
and 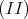 .
.
Conversely, let 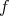 ,
,  be such that
be such that
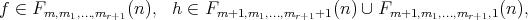
and satisfying  and
and  . Then,
. Then,
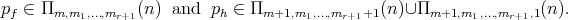
From Lemma 3.9 , we must prove that  .
.
Consider in 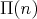
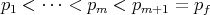
and
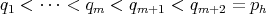
the chains ![(pf]](/img/revistas/ruma/v50n1/1a06618x.png) and
and ![(ph]](/img/revistas/ruma/v50n1/1a06619x.png) respectively and consider the following sets:
respectively and consider the following sets:
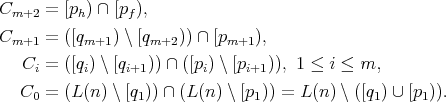
Then
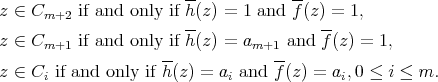
We have that 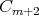 is a filter,
is a filter, 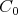 is an ideal and
is an ideal and  ,
, 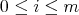 , are nonempty sets, being that
, are nonempty sets, being that  ,
,  ,
, 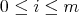 .
. 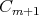 is also nonempty. Indeed, if
is also nonempty. Indeed, if 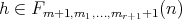 , since
, since 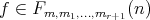 , there is
, there is 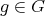 such that
such that  , then from
, then from  and
and 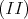 ,
,  and
and  , that is
, that is 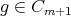 . If
. If  , there is
, there is 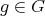 such that
such that 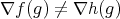 , then from
, then from 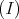 and
and  ,
, 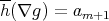 and
and 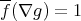 , that is
, that is 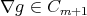 .
.
It is clear that the sets 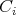 ,
,  , are pairwise disjoint. Observe that
, are pairwise disjoint. Observe that  , and so it is a filter. Using these remarks it is a routine matter to show that the set
, and so it is a filter. Using these remarks it is a routine matter to show that the set  is a subalgebra of
is a subalgebra of 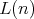 .
.
Let us see that  . If
. If  ,
,  .
.
If 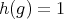 ,
, 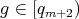 and from
and from  ,
, 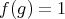 , that is,
, that is, 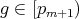 . Then
. Then 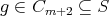 .
.
If  ,
,  and from
and from 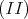 ,
, 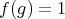 , that is
, that is 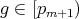 . So
. So 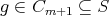 .
.
If 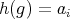 ,
, 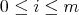 , then
, then  and from
and from 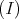 ,
, 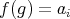 , that is,
, that is, 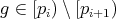 . Then
. Then 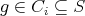 .
.
Therefore, 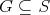 and consequently
and consequently  .
.
Then we can write,  .
.
Since 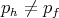 , we have
, we have 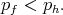

The previous theorem allows us to construct the ordered set of join-irreducible elements of the free algebra 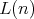 . By virtue of Lemma 3.6, there exists a one-to-one correspondence between the set of minimal elements of
. By virtue of Lemma 3.6, there exists a one-to-one correspondence between the set of minimal elements of  and the set of functions
and the set of functions  from
from  into
into 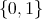 . Since
. Since ![(p ]](/img/revistas/ruma/v50n1/1a06685x.png) is a chain, for every
is a chain, for every 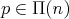 , then
, then ![(f]](/img/revistas/ruma/v50n1/1a06687x.png) is also a chain for
is also a chain for  . So, the ordered-connected components of
. So, the ordered-connected components of 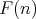 are
are  , where
, where 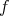 is minimal, that is, the order-connected components of
is minimal, that is, the order-connected components of  are the sets
are the sets 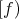 , where
, where 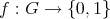 .
.
We have constructed the  -Heyting space
-Heyting space 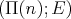 . The free algebra
. The free algebra 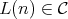 with a finite set of generators of cardinality
with a finite set of generators of cardinality 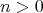 , is the algebra obtained from
, is the algebra obtained from 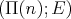 considering the decreasing subsets of
considering the decreasing subsets of  with the quantifier given by
with the quantifier given by  , for each
, for each 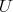 decreasing set of
decreasing set of 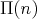 .
.
Example 3.11. In the next figure we give the free algebra  generated by an element
generated by an element 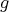 , and the ordered set
, and the ordered set 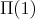 of its join-irreducible elements, with the equivalence relation which determines the quantifier.
of its join-irreducible elements, with the equivalence relation which determines the quantifier.
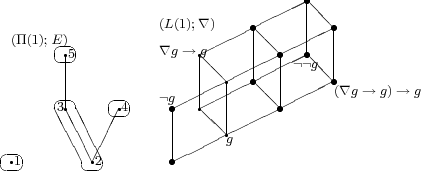
Where 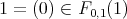 ,
, 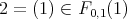 ,
, 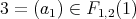 ,
,  and
and 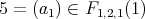 . We denote
. We denote 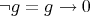 .
.
In the rest of this section we investigate the poset 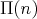 in order to obtain a recursive formula for the number of elements of
in order to obtain a recursive formula for the number of elements of  .
.
Let 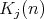 be the family of order-connected components
be the family of order-connected components  , with
, with  minimal, such that
minimal, such that  ,
,  . It is clear that
. It is clear that  , and if
, and if 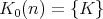 , then
, then  . In general,
. In general, 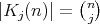 .
.
For a given  , all the order-connected components in
, all the order-connected components in  have the same number of elements. So if
have the same number of elements. So if 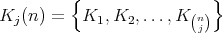 and
and  for
for 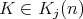 , then
, then

We are going to determine  .
.
Consider  . From Theorem 3.10, we know that
. From Theorem 3.10, we know that 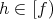 covers
covers  if and only if
if and only if 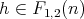 or
or 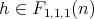 and
and
-
(I)
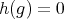 if and only if
if and only if  .
. -
(II)
 if and only if
if and only if  .
.
In particular, there are  funtions
funtions 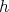 in
in 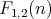 covering
covering 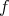 , and similarly there are
, and similarly there are  funtions
funtions  in
in 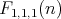 covering
covering  . So, there are
. So, there are 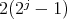 functions
functions  covering
covering 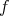 ,
, 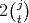 of which satisfy
of which satisfy 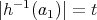 ,
, 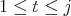 .
.
In these conditions we have the following result.
-
(1) If
 , there exists
, there exists 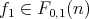 with
with  such that
such that  and
and 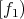 are order-isomorphic.
are order-isomorphic. -
(2) If
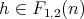 and
and 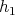 covers
covers 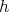 , with
, with  and
and 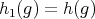 , for every
, for every  , then there exists
, then there exists  ,
, 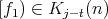 such that
such that 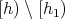 ,
,  and
and  are order-isomorphic.
are order-isomorphic.
Proof
-
(1) If
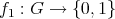 is the function defined by:
is the function defined by: 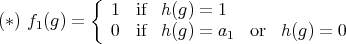 ,
,  is clearly a minimal element of
is clearly a minimal element of 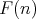 ,
,  and
and 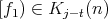 .
. Let us see that
 and
and  are order-isomorphic. Observe that if
are order-isomorphic. Observe that if 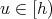 , then
, then  , where
, where 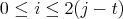 and
and 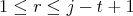 . We define
. We define  by means of
by means of  , where
, where  ,
,  .
. Clearly
 is an isomorphism.
is an isomorphism. -
(2) Observe that, if
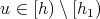 ,
, 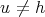 , then
, then 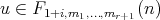 ,
, 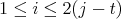 ,
,  and
and 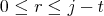 . If
. If  is the function defined by
is the function defined by  , then
, then  and
and 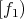 are order-isomorphic. Indeed, if we define
are order-isomorphic. Indeed, if we define  by means of
by means of 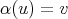 , where
, where 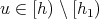 and
and  defined as in
defined as in 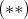 ,
,  and it can be proved that
and it can be proved that  is an isomorphism.
is an isomorphism. Finally, consider
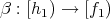 defined by
defined by 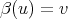 , where
, where  ,
,  ,
,  ,
, 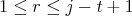 and
and 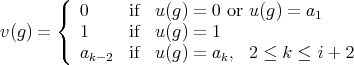 ,
, 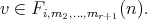
Clearly
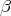 is an isomorphism.
is an isomorphism.

From the previous proposition,
![∑j [ (j ) ] N (n,j) = 3 N (n, j - t) + 1. t=1 t](/img/revistas/ruma/v50n1/1a06821x.png)
Therefore
![||n || [ ] |(⋃j) | (n ) ∑j [ (j ) ] || Ki ||= 3 N (n, j - t) + 1 , ||i=1 || j t=1 t](/img/revistas/ruma/v50n1/1a06822x.png)
and then
![[ n ( ) [ j [ ( ) ] ] ] ∑ n ∑ j |F (n)| = |Π (n)| = 1 + j 3 t N (n, j - t) + 1 . j=1 t=1](/img/revistas/ruma/v50n1/1a06823x.png)
Acknowledgment: I gratefully acknowledge helpful comments of the referees. In particular, one of them suggested the algebraic proof of Lemma 2.5.
[1] M. Abad and L. Monteiro, On free L-algebras, Notas de Lógica Matemática 35(1987), 1-20. [ Links ]
[2] M. Abad and J. P. Díaz Varela, Free Q-distributive lattices from meet semilattices, Discrete Math. 224 (2000), 1-14. [ Links ]
[3] M. Abad, J. P. Díaz Varela, L. Rueda and A. Suardíaz, Varieties of three-valued Heyting algebras with a quantifier, Studia Logica 65 (2000), 181-198. [ Links ]
[4] M. E. Adams and W. Dziobiak, Quasivarieties of distributive lattices with a quantifier, Discrete Math. 135(1994), 12-28. [ Links ]
[5] R. Balbes and Ph. Dwinger, Distributive Lattices, University of Missouri Press, Columbia, Missouri, 1974. [ Links ]
[6] G. Bezhanishvili, Locally finite varieties, Algebra Universalis 46(2001), No.4, 531-548. [ Links ]
[7] R. Cignoli, Quantifiers on distributive lattices, Discrete Math. 96(1991), 183-197. [ Links ]
[8] R. Cignoli, Free Q-distributive lattices, Studia Logica 56(1996), 23-29. [ Links ]
[9] P. R. Halmos, Algebraic Logic I. Monadic Boolean algebras, Compositio Math. 12 (1955), 217-249. [ Links ]
[10] A. Monteiro, Sur les Algèbres de Heyting Symétriques, Portugaliae Mathematica, 39 (1980), 1-237. [ Links ]
[11] A. Petrovich, Equations in the theory of Q-distributive lattices, Discrete Math. 17(1997), 211-219. [ Links ]
[12] H. A. Priestley, Ordered sets and duality for distributive lattices, Ann. Discrete Math. 23(1984), 39-60. [ Links ]
[13] H. A. Priestley, Natural dualities for varieties of distributive lattices with a quantifier, Banach Center Publications, Volume 28, Warszawa 1993, 291-310. [ Links ]
[14] L. Rueda, Algebras de Heyting lineales con un cuantificador Ph. D. Thesis, Universidad Nacional del Sur, Bahía Blanca, 2000. [ Links ]
[15] L. Rueda, Linear Heyting algebras with a quantifier, Annals of Pure and Applied Logic 108 (2001), 327-343. [ Links ]
Laura A. Rueda
Departamento de Matemática,
Universidad Nacional del Sur
Bahía Blanca, Argentina
larueda@criba.edu.ar
Recibido: 12 de noviembre de 2007
Aceptado: 2 de junio de 2009















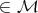 ,
, 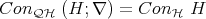 .
. 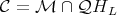 .
. 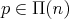 , then
, then  .
. 
