Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932
Rev. Unión Mat. Argent. vol.50 no.1 Bahía Blanca jun. 2009
Exponents of Modular Reductions of Families of Elliptic Curves
Igor E. Shparlinski
Abstract. For some natural families of elliptic curves we show that "on average" the exponent of the point group of their reductions modulo a prime 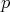 grows as
grows as 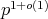 .
.
2000 Mathematics Subject Classification. 11B57, 11G07, 14H52
Key words and phrases. Elliptic curves; Group exponent; Farey fractions.
For integers  and
and  such that
such that 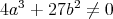 , we denote by
, we denote by  the elliptic curve defined by the affine Weierstraß equation:
the elliptic curve defined by the affine Weierstraß equation:

For a basic background on elliptic curves, we refer to [11].
For a prime 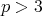 , we denote by
, we denote by 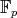 the finite field of
the finite field of 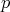 elements, which we identify with the set of integers
elements, which we identify with the set of integers  .
.
When 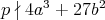 , the set
, the set 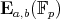 , consisting of the
, consisting of the  -rational points of
-rational points of  together with a point at infinity
together with a point at infinity 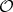 , forms an abelian group under an appropriate composition rule called addition, and the number of elements in the group
, forms an abelian group under an appropriate composition rule called addition, and the number of elements in the group  satisfies the Hasse bound:
satisfies the Hasse bound:
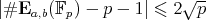 | (1) |
(see, for example, [11, Chapter V, Theorem 1.1]).
It is well-known that  is of rank at most two, that is,
is of rank at most two, that is, 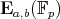 is isomorphic to
is isomorphic to
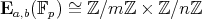 | (2) |
for unique integers  and
and 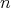 with
with 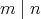 and
and 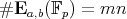 . The number
. The number  is called the exponent of
is called the exponent of 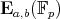 which we denote by
which we denote by 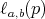 . In other words,
. In other words, 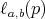 is the smallest positive
is the smallest positive 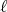 such that
such that 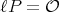 for all points
for all points 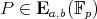 .
.
We also put 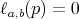 if
if 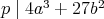 .
.
Thus we see that (1) and (2) imply the following trivial bound
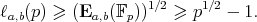 | (3) |
The exponent of elliptic curves has been studied in a number of works, see [4, 7, 8, 9, 10], with a variety of results, each of them indicating that in a "typical case" the exponent tends to be substantially larger than the bound (3) (and its analogue for curves over arbitrary finite fields) guarantees.
W. Duke [4], among other results, has proved that, assuming the Generalised Riemann Hypothesis, for every fixed integer  and
and 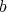 with
with 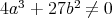 , and arbitrary small
, and arbitrary small 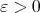 , the bound
, the bound
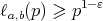 | (4) |
holds for all but 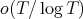 of primes
of primes 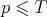 .
.
It is also shown in [10] that (4 ) holds for all but 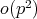 pairs
pairs 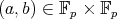 .
.
Here we use a combination of the results and ideas of [1, 10] to prove unconditionally that (4 ) is satisfied for almost all pairs 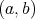 with
with  ,
,  for
for 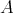 and
and 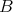 relatively small compared to
relatively small compared to  .
.
Theorem 1. For any fixed 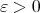 and all integers
and all integers 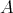 ,
, 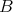 satisfying the inequalities
satisfying the inequalities
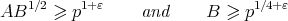
or
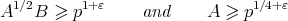
the bound

holds for all but 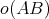 pairs
pairs  with
with 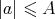 ,
, 
In particular, Theorem 1 is nontrivial if
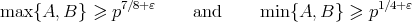
or

We also show that averaging over 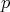 gives some additional saving.
gives some additional saving.
Theorem 2. For any fixed 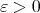 and all integers
and all integers  ,
,  and
and  satisfying the inequalities
satisfying the inequalities

the bound (4 ) holds for all but 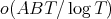 triples
triples 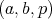 with
with 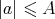 ,
,  ,
, 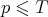 .
.
We note that the condition 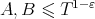 from [1], where it is used to simplify the error term, is not neccessary. One can easily extend Theorem 2 for
from [1], where it is used to simplify the error term, is not neccessary. One can easily extend Theorem 2 for 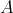 and
and 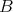 beyond this range, however since (as in [1]) small values of
beyond this range, however since (as in [1]) small values of 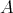 and
and  are of main interest we have not done this.
are of main interest we have not done this.
We remark that in [5] some of the results of [4] have been extended to hyperelliptic curves. It would also be interesting to obtain analogues of our result for natural families of hyperelliptic curves.
We also consider the set of Farey fractions
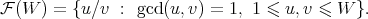
In particular
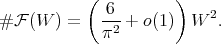
For 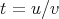 with
with 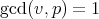 and two polynomial
and two polynomial ![A (X ),B(X ) ∈ ℤ[X ]](/img/revistas/ruma/v50n1/1a0882x.png) , the reduction
, the reduction 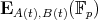 is correctly defined. Various questions concerning the behaviour of the curves
is correctly defined. Various questions concerning the behaviour of the curves 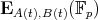 on average over
on average over 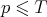 and
and  have been studied in [2]. Here we continue to study this family of curves. Certainly the most interesting case is when
have been studied in [2]. Here we continue to study this family of curves. Certainly the most interesting case is when 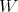 is small compared to
is small compared to 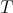 .
.
Theorem 3. Assume that the discriminant
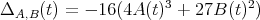
is nonzero and the 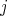 -invariant
-invariant
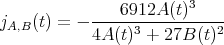
is nonconstant. Then for any fixed  and all integers
and all integers 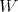 and
and 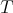 with
with
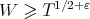
the bound
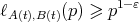
holds for all but 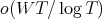 pairs
pairs 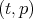 with
with  ,
, 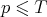 .
.
The following result follows immediately from the more precise statement of [10, Theorem 3.1].
Lemma 4. For any  , the number of triples
, the number of triples 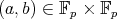 with
with
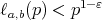
is at most 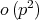 .
.
Let 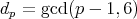 and put
and put
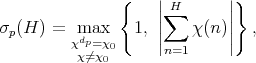
where the maximum is taken over all non-principal multiplicative characters 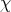 modulo
modulo 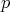 such that
such that 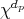 is the principal character
is the principal character  .
.
Similarly, we define 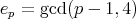 and put
and put
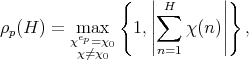
where the maximum is taken over all non-principal multiplicative characters 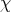 modulo
modulo 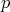 such that
such that  is the principal character
is the principal character 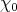 . For an arbitrary subset
. For an arbitrary subset 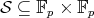 , we denote by
, we denote by 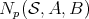 the number of pairs such that
the number of pairs such that 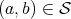 with
with 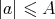 and
and 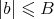 . We also denote
. We also denote

The following estimate is given in [1].
Lemma 5. For all primes  , integers
, integers 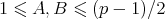 , and subsets
, and subsets 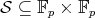 such that whenever
such that whenever 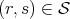 the isomorphism
the isomorphism 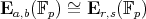 implies
implies 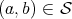 , the following bound holds:
, the following bound holds:
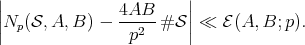
Moreover, it is shown in [1] that 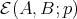 is small "on average" over
is small "on average" over 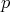 .
.
Lemma 6. The following bound holds:
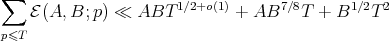
For a prime 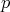 and an integer
and an integer  with
with 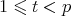 we denote by
we denote by 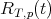 the number of fractions
the number of fractions 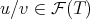 with
with 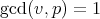 and
and  .
.
It is shown in [3] that 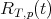 is close to its expected value
is close to its expected value 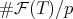 on average over
on average over  . More precisely, we have:
. More precisely, we have:
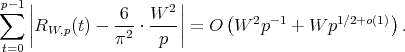
Let 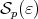 be the set of pairs
be the set of pairs 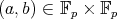 for which
for which 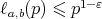 . Then it is enough to show that
. Then it is enough to show that
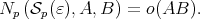
Since by Lemma 4 we have 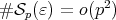 , invoking Lemma 5 we see that it is enough to check that
, invoking Lemma 5 we see that it is enough to check that 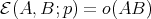 .
.
Assume that 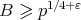 then by the Burgess bound, see [6, Theorems 12.5 and 12.6], we have
then by the Burgess bound, see [6, Theorems 12.5 and 12.6], we have 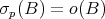 . Also, if
. Also, if 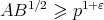 then have
then have 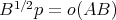 .
.
Similarly, if 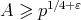 then
then  , and if
, and if  then have
then have 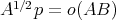 .
.
As before, let 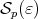 be the set of pairs
be the set of pairs  for which
for which  . Then it is enough to show that
. Then it is enough to show that
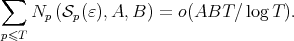 | (5) |
Let us assume that 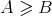 since the case
since the case  is similar.
is similar.
Using the trivial bound  for primes
for primes 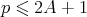 , we deduce
, we deduce
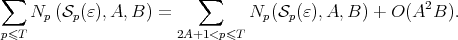 | (6) |
Noticing that for 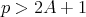 the set
the set 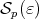 satisfies the conditions of Lemma 5 , we obtain
satisfies the conditions of Lemma 5 , we obtain
 | (7) |
By Lemma 4 we have
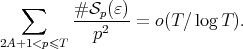 | (8) |
Substituting (7) and (8) in (6), we obtain
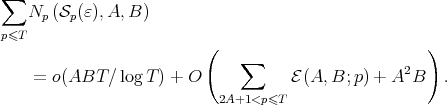 |
We now easily verify that under the conditions of the theorem, Lemma 6 implies the desired bound (5).
As before, we use 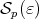 to denote the set of pairs
to denote the set of pairs 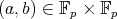 for which
for which 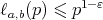 .
.
Let 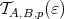 be the set of
be the set of 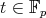 such that
such that
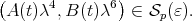
for some 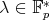 .
.
Obviously, for any 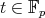 and
and 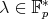 we have
we have

(since the corresponding curves are isomorphic, see [11, Section III.1]).
We also note that the system of equations

leads to the equation
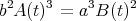
which has 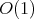 solutions (by the condition on the
solutions (by the condition on the  -invariant
-invariant 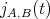 ).
).
Therefore
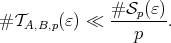
Using Lemma 7, we obtain
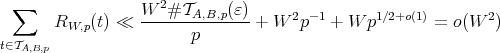
which concludes the proof.
[1] W. D. Banks and I. E. Shparlinski, 'Sato-Tate, cyclicity, and divisibility statistics on average for elliptic curves of small height', Israel J. Math., (to appear). [ Links ]
[2] A. Cojocaru and C. Hall, 'Uniform results for Serre's theorem for elliptic curves', Internat. Math. Res. Notices, 2005 (2005), 3065-3080. [ Links ]
[3] A. Cojocaru and I. E. Shparlinski, 'Distribution of Farey fractions in residue classes and Lang-Trotter conjectures on average', Proc. Amer. Math. Soc., 136 (2008), 1977-1986. [ Links ]
[4] W. Duke, 'Almost all reductions modulo p of an elliptic curve have a large exponent', Comptes Rendus Mathematique, 337 (2003), 689-692. [ Links ]
[5] K. Ford and I. E. Shparlinski, 'On finite fields with Jacobians of small exponent', Preprint, 2006 (available from http://arxiv.org/abs/math.NT/0607474). [ Links ]
[6] H. Iwaniec and E. Kowalski, On curves over finite fields with Jacobians of small exponent. Intern. J. Number Theory, 4, 2008, 819-826. [ Links ]
[7] F. Luca, J. McKee and I. E. Shparlinski, 'Small exponent point groups on elliptic curves', J. Théorie des Nombres Bordeaux, 18 (2006), 471-476. [ Links ]
[8] F. Luca and I. E. Shparlinski, 'On the exponent of the group of points on elliptic curves in extension fields', Intern. Math. Research Notices, 2005 (2005), 1391-1409. [ Links ]
[9] R. Schoof, 'The exponents of the group of points on the reduction of an elliptic curve', Arithmetic Algebraic Geometry, Progr. Math., vol. 89, Birkhäuser, Boston, MA, 1991, 325-335. [ Links ]
[10] I. E. Shparlinski, 'Orders of points on elliptic curves', Affine Algebraic Geometry, Contemp. Math., vol. 369, Amer. Math. Soc., Providence, RI, 2005, 245-252. [ Links ]
[11] J. H. Silverman, The arithmetic of elliptic curves, Springer-Verlag, Berlin, 1995. [ Links ]
Igor E. Shparlinski
Department of Computing, Macquarie University, North Ryde,
Sydney, NSW 2109, Australia
igor@ics.mq.edu.au
Recibido: 7 de octubre de 2007
Aceptado: 21 de mayo de 2008














